含裂纹纳米板振动问题的哈密顿体系方法

屈建龙, 周震寰, 徐新生

(大连理工大学 工程力学系 工业装备结构分析优化与CAE软件全国重点实验室,大连 116024)

1 引 言

随着纳米机电系统在航空航天、医学和机械电子等领域的广泛应用,对纳米结构的可靠性和安全性更加重视。纳米板作为纳米机电系统的基本构件,其出现裂纹或损伤会直接影响系统的工作状态,甚至破坏[1-3]。因此,对含裂纹或损伤纳米板动力学特性的深入研究是必要的[4]。由于尺寸效应,经典的连续介质力学理论不再适用纳米结构的相关问题[5,6]。为此,Eringen[7]提出了一种适合纳米级结构的非局部弹性理论,如纳米板的弯曲问题和振动问题等[8]。非局部弹性理论假设某点的应变状态不仅与该点的应力有关,而且与域内的应力都相关。相比于经典的连续介质力学理论,非局部弹性理论考虑了分子间的作用力对物体内某一点应变状态的影响。在纳米尺度下,分子间的范德华力是不可忽略的,因而在分析含裂纹纳米板的问题中,非局部弹性理论具有一定的优势。研究含裂纹纳米板的问题时,多采用修正的偶应力理论[9]和应变梯度理论[10],并以弹簧模型[11]拟合裂纹域内近场应力状态[12],从而建立含裂纹纳米板的控制方程。进一步得到含裂纹纳米板的固有频率和固有振型[13],结果表明,裂纹效应会导致固有频率降低。然而,这些方法仅适用于几种特殊的边界条件,因而有一定的局限性。因此,采用非局部弹性理论研究含裂纹纳米板的振动问题是一种尝试。

钟万勰院士[14]以某一空间坐标模拟虚拟的时间,并利用守恒性,开创了弹性力学问题求解新体系,从而形成一整套独特的求解系统。在该哈密顿体系下,将问题归结为辛本征值和本征解问题。由于辛本征解之间满足辛共轭正交关系,因此存在辛本征解展开定理,从而形成一种有效的方法[15-21]。本文将非局部弹性理论与哈密顿体系方法相结合,提出一种研究含裂纹纳米板振动问题的思路。

2 基本问题

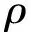
图1 含裂纹纳米板

(1-ξ22)σij=Cijklεkl

(i,j=1,2,3)

(1)

根据非局部本构关系,可以将非局部弯矩用位移表示为

(2)

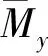
(3)

式中ξMx和ξNx为裂纹特征系数[23]。含裂纹纳米板振动的控制方程[22]为

(4)

利用关系式(2),用位移表示的控制方程(4)为

(5)

式中D1=D+ξ2N1

D2=D(1-ξMx)+ξ2N2(1+ξNx)

D12=D(2-υξMx)+ξ2N2(1+ξNx)+ξ2N1

K0=ρhω,K1=N1-ξ2K0

K2=N2(1+ξNx)-ξ2K0。

3 导入哈密顿体系

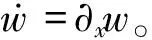
(6)

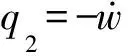
(7)

(8)

(9)

式中H为哈密顿算子矩阵

(10)

4 辛本征值和本征解

采用分离变量方法,设Ψ(x,y)=Ψμ(y)eμx,其中μ为辛本征值,Ψμ为对应的辛本征解向量。将其代入方程(9)可得

μΨμ=HΨμ

(11)

求解式(11),可得特征方程

D2λ4+(D12μ2-K2)λ2+D1μ4-K1μ2-K0=0

(12)

记方程的四个根为λ=λk(k=1,2,3,4),其中λ2=-λ1,λ4=-λ3。方程(12)同时也给出频率ω与辛本征值μ和特征根λ的关系。根据特征根,辛本征解可表示为

(13)

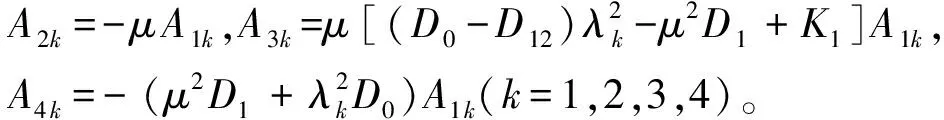
w=0,My=0

(14)

将辛本征解式(13)代入式(14),且利用非零解条件,可得

sinh(2λ1b)sinh(2λ3b)=0

(15)

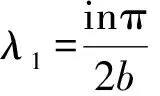
(n=1,2,…)

(16)

式中λ1和λ3的关系可由方程(12)确定。由式(15)可知,待定系数A1k(k=1,2,3,4)存在相互关系。事实上,由式(12,16)可建立频率ω与辛本征值μ的关系。

5 含裂纹纳米板的固有频率

以四边简支的纳米板为例。满足y=±b简支侧边条件的特征方程(12)可表示为

D1μ4-[D12(nπ/2b)2+K1]μ2+D2(nπ/2b)4+K2(nπ/2b)2-ρhω2=0

(n=1,2,…)

(17)

式(17)给出辛本征值与固有频率的直接关系。记满足方程(17)的四个根为±μ1和±μ2。此时辛本征解(13)可表示为

(18)

该解也称之为固有频率对应的固有振型。将解(18)代入x=±a简支条件,即w=0和Mx=0。同理存在非零解的条件为

sinh(2μ1a)sinh(2μ2a)=0

(19)

得μ1=imπ/2a或μ2=imπ/2a。对比式(17,19)的根,可得出固有频率表达式

D12(nmπ2/4ab)2+N1(mπ/2a)2+N2γ(nπ/2b)2]

(n,m=1,2,…)

(20)

式中κnm=1/[1+ξ2(mπ/2a)2+ξ2(nπ/2b)2]和γ=1+ξNx。应该指出,其他的边界条件也可得到对应的固有频率表达式。可以说,含裂纹纳米板的固有频率不仅与材料常数、非局部参数和裂纹特征有关,而且与边界条件和面内载荷有关。

6 辛本征解间的辛共轭正交关系

(21)

经过对辛本征解的辛正交归一化并重新排序,存在辛共轭正交关系,即

(22)

在以上辛本征解的讨论中,仅考虑了齐次方程和齐次边界条件问题。对于一般问题,可将非齐次边界条件转化为齐次边界条件问题,对应的方程增加一非齐次项。这样,辛本征解线性叠加解可作为齐次方程通解,即

(23)

式中Anm和Bnm(n,m=1,2,…)为待定系数。该解加上一个特解,并满足边界条件即可得到问题的解。

7 数值结果分析

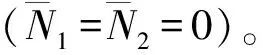
表1 含裂纹板的第一阶固有频率对比

表2 非局部参数和裂纹长度对振动基频影响

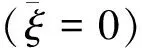
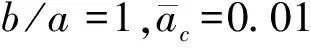
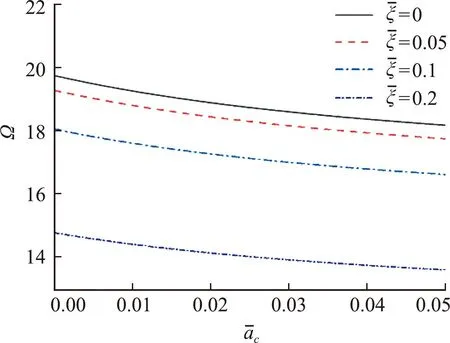
图2 裂纹长度和非局部参数对纳米板振动基频的影响

图3 非局部参数对各阶频率的影响

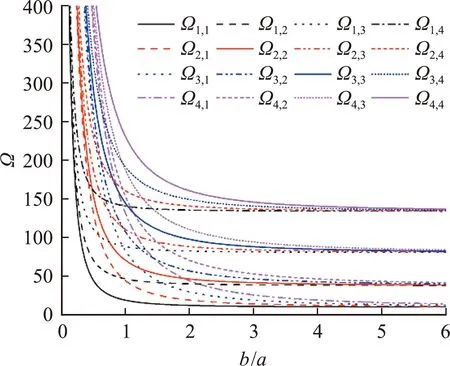
图4 纳米板长宽比对基频的影响

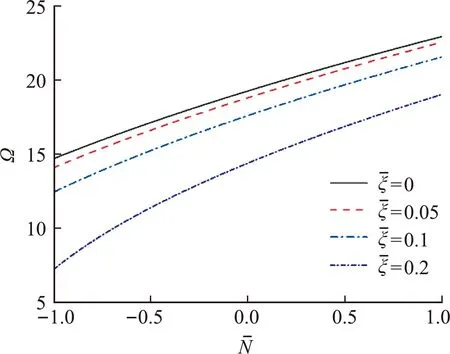
图5 面内荷载对基频的影响

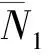
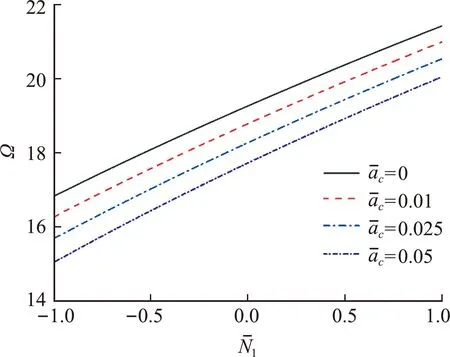
图6 x方向面内力与基频的关系

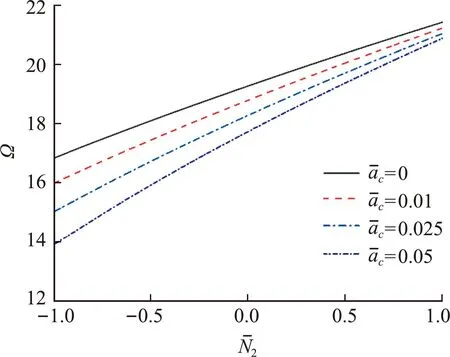
图7 y方向面内力与基频的关系

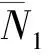
(n,m=1,2,…)

(24)

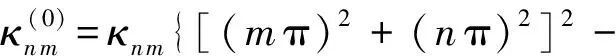
(nπ)2[ξMx(nπ)2+υξMx(mπ)2]}

8 结 论

借助于非局部弹性理论建立含裂纹纳米板振动问题的哈密顿体系可将固有频率和振型问题归结为广义辛本征值和辛本征解问题。由辛共轭正交关系,问题的解可表示为辛本征解级数的形式。结果表明,含裂纹纳米板的固有频率随着裂纹长度的增加而降低。随着非局部尺度参数增大,固有频率减小。作用在纳米板面内的拉力会使得纳米板的固有频率增加,而面内的压力则会降低纳米板的固有频率。因而,通过调整面内两个方向的拉力(压力)比例关系,可在一定范围内控制固有频率的数值。研究结果可为工程应用及相关设计提供依据。