超高速碰撞下相变效应的交错网格物质点法研究

周若璞, 曾治鑫, 张 雄

(清华大学 航天航空学院,北京 100084)

1 引 言

超高速碰撞HVI(Hyper velocity impact)是指弹体以极高的速度撞击靶体成坑或穿透的过程,其研究对于航天器空间碎片防护技术、反弹道导弹技术和核反应堆外壳安全防护设计等具有重要意义[1]。

超高速碰撞过程往往伴随着冲击波强间断、材料的极端变形和损伤破坏问题,理论分析十分困难,实验研究成本较高,周期较长,结果随机性较大,因此数值模拟是相关研究的重要手段。有限元法是目前固体力学最常用的数值分析方法。Kimsey等[2]将侵蚀算法引入EPIC有限元程序以计算超高速碰撞薄靶问题。然而,有限元法计算此类问题具有严重的网格依赖性,极易因网格畸变而产生数值困难。且侵蚀算法删除了失效单元,不能描述碎片云的产生和演化。

物质点法MPM(Material point method)是由Sulsky等[3,4]将用于流体动力学的质点网格法扩展到固体力学问题中提出的一种完全拉格朗日质点类无网格法。物质点法结合了拉格朗日方法和欧拉方法的优势,避免了网格畸变等问题,是分析超高速碰撞问题的最有效方法之一。马上等[5]基于空间碎片防护问题采用MPM研究弹丸碰撞薄板问题,并将MPM与FEM耦合应用于超高速碰撞问题。黄鹏等[6]采用并行的MPM方法模拟了铅弹超高速碰撞薄铅板问题。马上等[7]从接触算法、稳定性和计算效率等方面详细比较了MPM和SPH方法在计算超高速碰撞问题时的性能。Ren等[8]使用PAGOSA程序中的FILP和MPM功能模拟了超高音速爆炸碎片撞击壳体等问题。

物质点法采用质点积分会产生一系列数值缺陷,包括跨网格噪声、积分精度和稳定性降低等。为了消除跨网格误差,梁勇等[9]提出了交错网格物质点法SGMP(Stagger grid material point method),该方法引入了一种新颖的空间物理场重构和映射方案,实现了背景网格上的格心积分。SGMP通过交错网格实现了质点和背景网格的信息映射,提升计算精度,在模拟超高速碰撞问题中也有更好的效果。阚镭等[10]研究了SGMP在不同积分方案下的能量误差,并建立了相应的接触算法。曾治鑫等[11]采用SGMP研究金属层裂问题。阚镭等[12]基于SGMP发展了杂交交错网格物质点有限元法,研究了钢筋混凝土结构在爆炸和冲击载荷作用下的响应与破坏行为。

相较于低速或高速碰撞,超高速碰撞会产生剧烈的相变效应,在数值模拟中需要通过状态方程来描述。最初的Gruneisen状态方程[13]并不能描述材料熔融或气化的现象。Tillotson[14]提出了能够描述材料熔融和气化的Tillotson状态方程,但不能精确描述固液和液气的非均匀混合相。Ulrich等[15]将描述固液相的定标律状态方程和Young-Alder修正气体状态方程采用光滑多项式连接,建立了GRAY状态方程,其不但可以描述相态变化,还可以较好地表示固液异相间的转换。

2 交错网格物质点法

物质点法[3,4]将物质离散为一系列质点,质点携带所有物理信息,其运动就代表了物质的运动与变形。物质点法引入了背景网格计算近似函数,从而求解动量方程。物质点法的离散控制方程以弱形式动量方程为基础建立,可得到以下在背景网格上建立的离散形式运动方程

图1 物质点离散

(∀I∉Γu)

(1)

式中

(2)

为网格结点I动量的第i个分量,mp表示质点质量,np为质点总数,NIp=NI(xp)为结点I的形函数在质点p处的值,

(3)

为结点I的集中质量。

(4)

(5)

分别为结点I的内力与外力,Vp为质点p的体积,σijp为质点p的柯西应力张量,bip为质点p所受体力,h是为了将弱形式面力项的边界积分转化为体积分而引入的假象边界层厚度。

在物质点法中通常采用三线性形函数,即

(6)

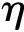
梁勇等[9,10]提出的交错网格物质点法,采用多重背景网格的方式改善了上述的跨网格误差问题。如图2所示,交错网格物质点法除了一套背景网格外,还额外引入了一套辅助网格,辅助网格的节点位于背景网格格心处,背景网格节点的物理量通过辅助网格节点的物理量映射得到,所以式(1)中各物理量的计算方式变为

(7)

式中 带下标c的即为辅助网格节点的物理量,辅助网格的物理量通过辅助网格的形函数重构质点量得到,即

(8)

图2 交错网格物质点法

在交错网格物质点法中,在背景网格求解动量方程后,并不是直接更新质点的位移、速度和应力,而是先由背景网格插值到辅助网格节点,再利用辅助网格将物理量插值到质点上,即

(9)

(10)

式中 Δεij和ΔΩij分别为应变张量增量和旋率张量增量。

交错网格物质点法的接触算法与标准物质点法类似,如果任意背景网格节点I不满足速度不可穿透接触条件即判定该节点发生接触[10],需要在背景网格节点上施加接触力使得最终的速度满足速度不可穿透条件。

3 修正金属材料模型

引入GRAY三相状态方程以描述材料的相变效应;采用Johnson-Cook强度模型描述金属本构行为,并将非线性内聚力断裂演化模型引入Johnson-Cook失效模型中,描述韧性金属材料失效后残余应力逐步归零的过程。

3.1 GRAY状态方程

GRAY状态方程[15]在固相-液相区内通过内能E判断物质相态,将相态分为固相、熔融相、液相及热液相,通过定标律状态方程得到相应的内能E和修正压力P与体积V和温度T的关系。

(1) 物质处于固相时,内能及压力计算公式为

(11)

(12)

式中E0和P0分别为冷能和冷压,R为气体热力学常数,γs(V)=γ0-ax,γe=2/3,x=1-V/V0为比体积,Ge,a和γ0为由实验测得的材料参数。

(2) 当固相物质温度升高至熔点,开始发生熔融变为熔融相,熔点Tm与体积V满足Lindemann律

(13)

仅需将固相时相应的压力修正为

[λTm+γe(T-vδT)]

(14)

式中δT为温度改变量,v为与熔化内能相关的系数,熵增ΔS=1.16R为定值,α和λ为材料参数。

(3) 物质完全熔融变为液相后,其摩尔热容CV,l随温度升高而减小

(15)

利用热力学关系,可由熵函数导出物质液相内能与压力

(16)

(17)

(4) 当液相物质的摩尔热容减小至3R/2时,其摩尔热容不再继续减小,物质进入热液区,内能与压力写为

(18)

(19)

GRAY状态方程假设物质体积V>VJ时进入气相区,采用Young-Alder修正气体状态方程描述其内能与压力

(20)

(21)

式中z=Vb/V,Vb和ay为材料参数。

在液相-气相过渡区,GRAY状态方程增加过渡相以实现Young-Alder方程与定标律方程的光滑过渡

El-g(T,V)=Eg(T,V)+FE(C1-C3T2)+(D1+D2T+D3T2)

(22)

Pl-g(T,V)=Pg(T,V)+Fp(C1+C2T+C3T2)

(23)

式中FE和Fp为过渡函数

(24)

(25)

式中zJ=Vb/VJ,θ为过渡区长度控制系数,通常取1,C1,C2,C3,D1和D2由Young-Alder方程与定标律方程光滑连接确定。

3.2 含非线性内聚力断裂的Johnson-Cook模型

3.2.1 Johnson-Cook强度模型

Johnson-Cook强度模型[16]可用于描述超高速碰撞和爆炸等涉及高温和高应变率问题下金属的力学行为,其屈服函数可表示为塑性应变、塑性应变率和温度的解耦形式,

(26)

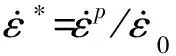
3.2.2 非线性内聚力断裂Johnson-Cook失效模型

σ=(1-Dcs)σ0

(27)

式中σ0为材料初始失效应力

(28)

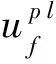
(29)

式中We为材料断裂所需的表面能。

由此可看出,非线性内聚力断裂模型通过材料韧性断裂过程中累积耗散能计算失效应力,描述金属韧性破坏演化过程。

4 超高速碰撞单层靶板数值模拟

首先分别采用MPM和SGMP并使用Gruneisen和GRAY状态方程对铝球撞击铝靶问题进行数值模拟,比较两种方法及两类状态方程计算结果,显示了SGMP方法结合GRAY状态方程在超高速碰撞问题下的计算优势。并基于此模拟了柱形弹侵彻单层钢靶问题,对碎片云进行统计分析,证明了该算法的计算准确性。

4.1 铝球撞击铝靶

球形弹丸碰撞靶板是超高速碰撞中的一类典型问题。Piekutowski等[21]进行了一系列不同冲击速度及尺寸的铝球撞击铝靶实验,并使用高速摄像机观测碎片云形貌特征,给出了碎片云特征点处的归一化速度。

选取文献[21]中试验4-1359(图3),2017-T4铝制球形弹丸直径9.55 mm,6061-T6铝制薄靶厚度0.592 mm,初始撞击速度为6.78 km/s。分别采用MPM和SGMP方法进行数值模拟,模型离散尺寸相同,均为0.1 mm。材料模型使用3.2节引入的修正Johnson-Cook模型,并分别使用Gruneisen状态方程和GRAY状态方程对比相变对结果的影响,材料参数依照文献[22,23]确定。

输出与实验图像相同物理时刻的数值模拟结果如图3所示。可以看出,由于粒子的跨网格误差,MPM计算结果碎片飞散严重,无法准确描述碎片云形貌特征。SGMP可有效消除粒子跨网格误差,碎片云形貌清晰。从图4(c,d)可以看出,使用GRAY状态方程相比于Gruneisen状态方程与实验结果更加吻合,因此在超高速碰撞下更加适用。

图3 4-1359实验图像[21]

撞击后形成的碎片云实验照片如图4所示,其前部碎片主要由靶板阻抗挤压产生,呈圆台状分布;中部碎片由压缩波破坏产生,因此碎片分布密集;尾部碎片由拉伸波破坏产生,碎片分布稀疏。与实验相比,SGMP结合GRAY状态方程可良好地模拟碎片云各部分的分布,模拟效果良好。

对冲击后靶板的速度场进行定量分析,图5定义了碎片云各特征点,点1～点4分别为碎片云轴线上各部分的交点,点5～点10分别位于碎片云径向上。数值模拟与实验所得的特征点归一化速度列入表1和表2,其中vi(i=1,2,…,10)为各特征点速度,v0为初始撞击速度。

图4 MPM和SGMP使用两种状态方程下的数值模拟结果

图5 内部碎片云形貌及特征点

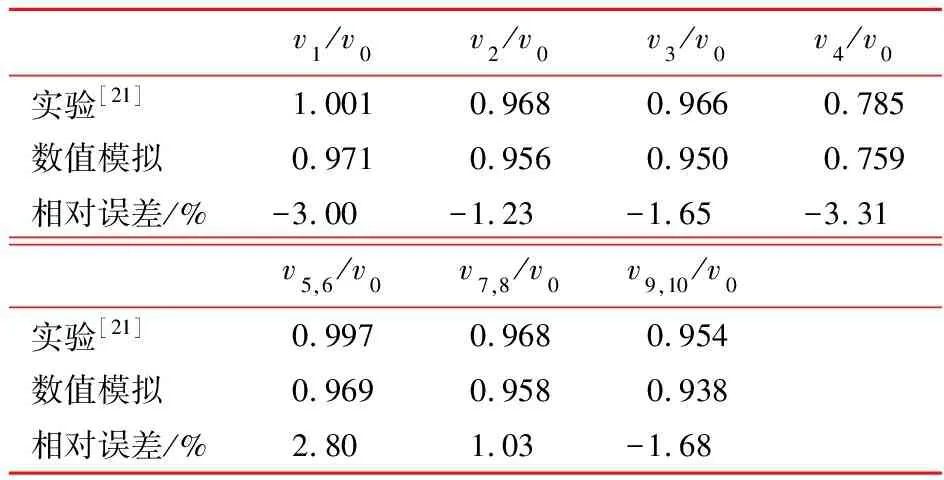
表1 弹体碎片云特征点轴向归一化速度

表2 弹体碎片云特征点径向归一化速度

由表1和表2可知,数值模拟的碎片云各特征点轴向归一化速度与实验结果相对误差均小于5%,径向速度误差稍大,这是由于碎片云径向边缘较为模糊,特征点速度无法精确捕捉,但相对误差仍在10%以内,SGMP-GRAY状态方程模拟效果良好。因此,在后续的数值模拟中,均采用SGMP方法结合GRAY状态方程进行计算。

4.2 93W柱形弹侵彻单层Q345钢靶

马坤等[24]使用二级轻气炮开展了柱形93W弹体超高速正撞击Q345薄钢板实验,并针对毁伤效应和材料相变等进行了研究。选取文献[24]中实验7,采用SGMP进行数值模拟。柱形93W弹体长10.5 mm,直径3.45 mm,Q345薄钢板厚度1.5 mm,初始撞击速度3.16 km/s,材料参数与文献[24]相同。

4.2.1 碎片云宏观形貌分析

研究发现[25],在靶板厚度小于0.72倍的弹体直径的情况下,碰撞产生的冲击波会先于弹头产生的侧向卸载波到达靶板背面,并在该自由表面反射形成较强的拉伸波,进而使靶板产生拉伸层裂破坏并形成速度较高的尖端碎片,如图6(a)所示。图6(b)表明,SGMP可有效模拟靶板层裂破坏现象,碎片云宏观形貌也与实验吻合良好。

图6 93W柱形弹侵彻单层Q345钢靶

表3给出了实验与数值模拟测得碰撞后弹体及靶板毁伤结果。其中,vp为弹体轴向残余速度,vr,max为碎片径向扩展的最大速度,ΔL为弹体残余长度,D为靶板穿孔直径。可以看出,数值模拟结果与实验结果一致性良好,误差均在10%以内。

4.2.2 碎片云统计学量分析

对数值计算结果进行碎片识别及统计分析,研究超高速碰撞单层靶板时的相变效应及碎片质量分布特性。采用Liang等[26]基于广度优先搜索算法BFC提出的粒子类碎片识别算法,得到各质量及相态的碎片质量分布情况如图7所示。可以看出,碎片质量越小,数量占比越高,质量小于25 μg的碎片占比超过99%。质量较小的碎片更容易温升而产生相变,熔融态碎片约占总数的15%,液态碎片约占比13%。

图7 碎片云质量及相态分布

n(m)∝m-β

(30)

式中β为标度指数,其对物体形状非常敏感,但与材料无关,此类现象解释为碎片分布的自组织临界特性[28,29]。碎片分布可由质量大于或等于m的碎片总数除以m来描述

(31)

图8展示了本文碎片云质量-数量指数曲线,可以看出,其满足幂律分布规律,标度指数β=0.966。这表明本文采用的数值模拟方法与碎片云统计算法计算出的碎片云满足自组织临界特性,符合超高速碰撞的碎片云分布特征。

图8 碎片云质量-数量指数曲线

5 超高速碰撞多层靶板数值模拟

采用SGMP对铝球撞击Whipple盾系统、柱形弹侵彻多层钢靶两类超高速碰撞多层靶板问题进行了数值模拟,并与实验结果进行了对比。并分析了不同层级靶板的损伤模式与破坏机理,研究相变效应对超高速碰撞毁伤的影响。

5.1 铝球碰撞Whipple盾系统

Whipple盾系统[30]是一种常用的航天器防护系统,由前防护层Front bumper和后壁Rear Wall组成,可有效保护航天器不受空间碎片冲击破坏。

文献[31]使用二级轻气炮发射铝制球形弹丸以不同速度冲击Whipple盾系统,冲击速度v分别为3.44 km/s和5.33 km/s,实验装置如图9(a)所示,本文以此建立数值模型如图9(b)所示。LY12铝制弹丸直径4 mm,前防护层与后壁材料均与弹丸相同,厚度均为3 mm,间距L=100 mm。实验中的观察窗(Witness panel)仅用于实验观测,不参与碰撞,因此在数值建模中忽略。材料参数参照文献[22]选取。

前防护层和后壁的实验及数值模拟毁伤结果分别如图10和图11所示。可以看出,前防护层受

图9 铝球碰撞Whipple盾系统

图10 前防护层毁伤结果

到剪切破坏产生规则圆形穿孔,且冲击速度越高穿孔直径越大。后壁受碎片云碰撞作用,产生大小不同的凹坑。凹坑分布总体呈现中心密集和四周分散的特点。数值模拟结果使用材料损伤量表征凹坑破坏,可以看出中心处损伤严重密集和四周逐渐轻微稀疏,结果与实验吻合。实验和数值模拟得到的前防护层穿孔直径和后壁最大损伤半径数据列入表4,两者结果吻合良好,相对误差均在10%以内。

表4 前防护层和后壁毁伤结果

文献[30]采用扫描电子显微镜SEM观测到前防护层穿孔内表面不是单纯由剪切破坏形成的光滑断口,而是存在许多熔融后凝固的粗糙组织,这说明在碰撞过程中材料产生了相变。数值模拟结果也可以观察到相同的相变效应,如图12所示。在碰撞过程中由于弹体和靶板的相互挤压与摩擦致使接触部分产生熔化,多数熔融态碎片附着在靶板断口处,在碰撞后降温凝结即形成了SEM观察到的粗糙组织。碰撞速度越高,相变效应越显著。

图12 碰撞时的相变效应

5.2 93W柱形弹侵彻多层Q345钢靶

李名锐等[32]使用二级轻气炮开展柱形93W弹体超高速正撞击多层Q345薄钢板实验,分析了不同靶板的毁伤模式。采用SGMP对文献[31]的实验2柱形弹撞击前3层靶板进行了数值模拟。柱形93W弹体长17.5 mm,直径3.45 mm,3层Q345薄钢板厚度均为1.5 mm,第2层和第3层靶板间距较第1层和第2层大,初始撞击速度2.25 km/s。

图13给出了数值模拟0 ms～0.66 ms内弹体撞击三层靶板的过程。撞击后实验及数值模拟前3层靶板正面、背面和侧面的毁伤结果分别如图14～图16所示。数值模拟的靶板破坏模式与实验结果吻合良好。第1层靶板在剪切破坏主导下形成的穿孔为规则圆形。第2层靶板在残余弹体和碎片云碰撞下以拉伸和弯曲破坏为主形成翻唇塑性变形,弹孔在残余弹体的剪切破坏下大致呈圆形,边缘由于碎片挤压破坏有不规则裂纹,弹孔附近由前端碎片撞击产生飞溅状损伤。第3层靶板同样出现翻唇变形,但由于碎片云密度的增大,其在毁伤中占主导,在中心形成不规则穿孔,弹孔附近存在孔洞和凹坑。

图13 柱形弹侵彻3层靶板数值模拟过程

图14 前3层靶板正面毁伤结果

图15 前3层靶板背面毁伤结果

图16 前3层靶板背面毁伤结果

图17为数值模拟撞击各层靶板后各相态碎片云质量占比。其中,撞击第1层靶板后仅有不到5%的碎片发生熔融或液化,相变效应不明显。撞击第2层和第3层靶板后碎片发生的相变效应类似,熔融态与液态碎片均约20%,这是由于碰撞时碎片与靶板的接触时间和切向接触力显著增大,使得大量动能转化内能,碰撞区域附近材料温升至熔点产生相变,少部分碎片由于体积膨胀气化,极少部分碎片达到热液态。

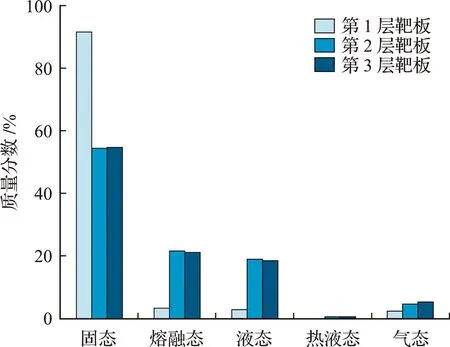
图17 撞击前3层靶板产生碎片云相态

6 结 论

将修正金属模型引入SGMP中,分别对超高速撞击单层靶板和多层靶板问题进行了数值模拟,研究超高速碰撞问题的毁伤机理和相变效应。结果表明,相比于MPM,采用SGMP方法可以有效消除跨网格误差导致的粒子飞散,从而准确描述碎片云形貌特征。使用GRAY状态方程可良好地描述材料相态转换;使用含非线性内聚力断裂的Johnson-Cook模型,可良好地描述韧性金属在高应变率下的动态响应和损伤特性。数值模拟表明,超高速碰撞多层靶板会产生明显的相变效应,靶板撞击区域附近发生大量熔化,弹体和靶板材料混合熔融物附着在弹孔断面并凝结重结晶,部分碎片云温升发生熔融相变,小部分碎片云由于体积膨胀气化。