基于粗粒化分子动力学的自由水与水化硅酸钙孔隙水冻结模拟

张 浩, 田 霞, 顾 鑫, 章 青

(河海大学 力学与材料学院,南京 211100)

1 引 言

以混凝土为代表的水泥基材料广泛应用于各种工程中。在周期性变温荷载作用下,水泥基材料孔隙内的水将发生相变,导致水泥基材料损伤开裂、力学性能劣化并影响材料的服役性能。混凝土的冻融破坏在中国北方地区非常普遍[1],严重威胁混凝土结构的安全。因此,深入开展水泥基材料的冻融破坏机制研究[2],对于提升混凝土材料的抗冻性和耐久性,保障混凝土结构的安全具有重要的现实意义[3]。

水泥水化后生成水化硅酸钙C-S-H(Calcium Silicate Hydrate)、氢氧化钙和钙矾石等产物,其中C-S-H占比60%～70%,极大地影响着水泥基材料的微观结构特征和宏观力学性能,故本文选用C-S-H表征水泥基材料的孔壁。Zhang等[4]建立了基于孔隙率变化的混凝土损伤模型,定量描述了宏观力学性能的退化规律,提出冻融循环作用下混凝土动力增长系数的经验关系。混凝土在经历冻融循环后,距离水面越近的部位孔隙率越大,其中小孔含量较少而大孔含量明显增大,即距离水面越近冻融损伤越严重[5]。水泥基材料的冻融破坏主要是其孔隙中水的冻结膨胀产生的压力所致[6],其冻融行为与受限水的相变特性直接相关,而受限水的相变特性远比自由水复杂[7,8]。Foroutan等[9]使用分子动力学方法模拟了石墨烯纳米孔隙中水的结冰过程,得到石墨烯纳米孔隙通道中水的冰点为240 K,比自由水的冰点低29 K;Jiang等[10]通过分子动力学模拟发现,6 Å纳米硅孔隙中的液态水在2.5 GPa压强和250 K温度下,自发冻结成单层冰;8 Å纳米硅孔隙中的液态水在4.0 GPa压强和300 K温度下,自发冻结成双层冰。水泥基材料的冻融破坏研究表明,水泥孔隙分布对其损伤的形成十分重要。水泥基材料孔隙水冻结时的体积膨胀是导致水泥基材料冻融破坏的重要因素,研究表明受限水相对自由水冰点更低,更加难以结冰,但目前的研究中鲜有涉及水泥基材料孔隙水的冻结模拟。本文使用分子动力学方法围绕不同孔径的C-S-H孔隙水展开研究,模拟C-S-H孔隙水的冻结过程,探究不同孔隙对水泥基材料冻融破坏的危害程度。

虽然基于全原子分子动力学方法进行微观尺度模拟精度较高,但对计算规模有较大限制,且很难模拟孔隙水的冻结过程,粗粒化分子动力学方法能够有效地提升计算效率,可望进行孔隙水的冻结模拟。Jennings[11]提出了C-S-H球形胶体颗粒模型,采用Mie势函数表示该粒子间的相互作用势,并给出了从基本结构封装形成更大尺度结构的方法。Ioannidou等[12]使用上述C-S-H球形胶体颗粒模型,计算得到了不同初始水灰比和密度下C-S-H样品的局部压力,分析了水灰比和密度对其力学性能的影响。Marrink等[13]提出脂质的粗粒化模型,其中水的粗粒化粒子是将四个水分子视为一个粗粒化水珠,即P4粒子,魏来[14]研究了该粗粒化水粒子势函数对结冰温度的影响。从目前的研究来看,国内外学者虽然分别建立了C-S-H和水的粗粒化模型,并围绕相关问题开展研究,但鲜有同时建立这两种粒子的粗粒化模型,以研究水泥基材料的冻融相关问题。

本文采用P4粒子和C-S-H胶体粒子,建立两种粒子之间的耦合势函数,采用洛伦兹-贝特洛平均法则率定势函数参数。基于上述两种粗粒化粒子,构建C-S-H孔隙及孔隙水的计算模型,模拟自由水与C-S-H孔隙水的结冰过程,研究C-S-H孔隙水的冰点与孔径关系,并探究孔隙水结冰的微观特性。

2 模型构建

水的粗粒化模型是将四个水分子合并为一个粗粒化水P4粒子,则体系的粒子数量为全原子模型的1/4。粗粒化P4粒子间的相互作用势采用LJ(Lennard-Jones)势,即

(1)

式中r为粒子间距离,ε1为P4粒子间的势阱深度,反映粒子间相互吸引作用的强弱,σ1为U1(r)=0时P4粒子间的距离。

将C-S-H粗粒化成球形胶体颗粒,粒子间采用Mie势函数[12],即

(2)

式中ε2为C-S-H胶体颗粒间的势阱深度,σ2为U2(r)=0时C-S-H胶体颗粒间的距离。

将上述两种势函数进行加权平均,得到水的粗粒化P4粒子和C-S-H的粗粒化粒子间的相互作用势函数,可表示为

Ucou(r)=λU1(r)+(1-λ)U2(r)

(3)

式中λ和1-λ分别为LJ势函数和Mie势函数的权函数,λ=1,式(3)退化为P4粒子之间的LJ势函数;λ=0,式(3)退化为C-S-H胶体颗粒之间的Mie势函数。

当λ=0.5时(后有两种粒子相互作用准确性的验证),将LJ和Mie势函数表达式代入式(3),并将粒子间的势阱深度和距离统一采用ε3和σ3表征,则有

(4)

式中ε3为P4粒子和粗粒化C-S-H粒子间的势阱深度,σ3为U3(r)=0时两种粒子间的距离。

两种粒子之间的势函数参数由洛伦兹-贝特洛法则确定,即

(5)

按上述方式形成水的粗粒化P4粒子和C-S-H的粗粒化粒子间的相互作用势函数后,便可构建C-S-H孔隙水的计算模型,离散后C-S-H孔隙通道的x-z截面如图1所示。

图1 C-S-H孔隙模型的x-z截面

3 自由水的结冰模拟

3.1 结冰判断准则

本文采用键序参数描述水的结冰程度。键序参数[15]为每个粒子键方向顺序的参数,其取值范围为0～1,0表示完全无序,1表示有序,其表达式为

(6)

(7)

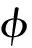
冰是由水分子有序排列形成的结晶,其有序程度高于液态水。因此,可计算粗粒化水粒子的键序参数均值,作为表征结冰的参数。

3.2 自由水冻结过程分析

首先,基于水的粗粒化粒子模型,计算粗粒化水的基本物理特性(包括密度、表面张力与扩散系数),列入表1。由表1可知,数值模拟结果与理论值吻合较好。

表1 水的物理特性

为模拟自由水结冰的演化过程并分析自由水结冰过程中的变化特征,考虑边长为10 nm的立方体模拟体系,随机生成5000个P4粒子,采用等温等压系综,温度分别设置为270 K和275 K,压强为标准大气压,为得到冻结过程中结冰演化过程细节,模拟的时间步长选为较小的1 fs,截断半径为12 Å。参考魏来[14]判断水是否结冰的方法,模拟结束后,统计等温等压系综轨迹文件的最后一帧,观察是否有晶体化现象产生,判断水分子是否冻结。以此为依据选用0.44作为临界值(未结冰的P4粒子键序参数在0.42以下,结冰后P4粒子键序参数在0.46以上):当键序参数小于0.44时,认为水处于液态;当键序参数大于0.44时,认为水开始结冰。选用键序参数作为判断结冰标准更加合理,且可以判断局部位置是否结冰。图2分别给出了270 K温度下,7.7 ns,7.8 ns,7.9 ns和8.0 ns时x-z截面的键序参数云图,为了更清楚地显示自由水结冰的演化过程,将小于0.44的键序参数均设置为0。

从图2可以看出,模拟时间小于7.7 ns时,计算区域的小部分粒子呈有序结构,大部分粒子呈无序结构;随着模拟时间的增加,具有有序结构的区域迅速扩大,且呈规则排列;当模拟时间为8 ns时,计算区域基本均呈现有序结构,表明自由水已冻结成冰。在结冰过程中,水的势能(1 Kc=4185.85 J)与流动性将发生变化,水的流动性可通过均方位移体现,图3和图4分别给出了计算得到的势能与均方位移曲线。

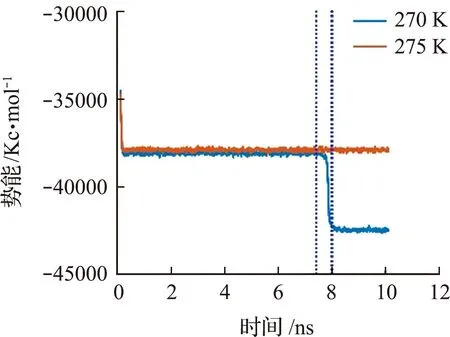
图3 不同温度下势能随时间的变化曲线

图4 不同温度下均方位移随时间的变化曲线

从图3和图4可以看出,当系统温度为275 K时,即不会发生冻结的情况下,水分子的势能基本不发生变化(弛豫过程除外),均方位移与时间呈线性关系,符合水的基本特性。当系统温度为270 K时,自由水将发生冻结,在冻结时,水分子的势能将迅速降低,冻结后水分子的势能和均方位移几乎不再发生变化,表明体系中水已经结冰,由液态变为固态,不再具有流动性。

模拟结果表明,粗粒化粒子冻结温度与理论值273.15 K比较接近。此外,计算结果呈现了水冻结时的放热过程以及从液态到固态的转变,与Matsumoto冻结模拟的现象一致[16],表明粗粒化水P4用于冻结模拟的可行性。

4 C-S-H孔隙水的结冰模拟

4.1 C-S-H与水的相互作用验证

自由水的冰点主要由水自身的性质决定(即粗粒化P4粒子势函数参数),而C-S-H孔隙水冰点受多种因素影响,除了水自身的性质外,研究表明孔隙的孔径[17]和压强影响着孔隙水的冰点[18]。本文主要采用Lammps中fix NPT命令实现控温控压,保持压强不变,研究C-S-H孔径对该体系孔隙水冰点的影响。

在建立C-S-H孔隙结构计算模型时,上下区域由随机生成的粗粒化C-S-H粒子组成,并设置粒子不发生移动,中间区域为随机生成的粗粒化水,中间区域的高表示C-S-H的孔径。设置计算体系为等温等压系综,压强为标准大气压,时间步长选用10 fs,模拟时三个方向均采用周期性边界条件,粒子间的相互作用势截断半径为12 Å。

考虑微孔半径为5 nm的C-S-H孔隙结构,孔隙水在235 K结冰时,图5和图6分别给出该温度下模拟得到的C-S-H孔隙结构x-z截面和y-z截面的粒子位置图像。

图5 235 K粒子位置图像(x-z截面)

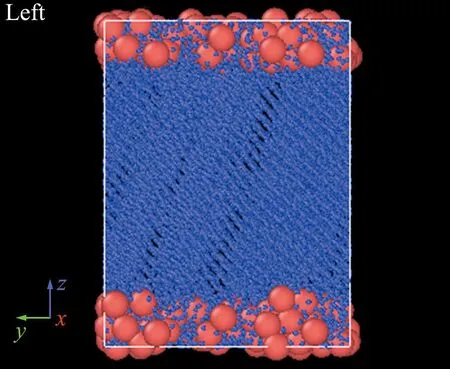
图6 235 K粒子位置图像(x-y截面)

图7给出了相应的孔隙水结冰云图。将图7与图2所示的自由水结冰云图相比,可以看出受限水的结冰特征不同于自由水。对于受限水,在靠近C-S-H孔隙壁面的蓝色区域,C-S-H吸附的水分子对应的键序参数小于0.44,呈现无序排列,未达到结冰状态;而在中间区域呈现有序排列,且键序参数大于0.44,达到结冰状态;而自由水的结冰区域覆盖了x-z截面的绝大部分区域。

图7 C-S-H孔隙x-z截面水结冰云图

本文模拟结果表明,孔隙壁上会有一层吸附水膜,在极低的温度下也不会结冰。这是因为靠近孔壁处,C-S-H与水的相互作用较大,这对水的运动有一定的束缚,从而导致C-S-H孔壁表面的水难以结冰,形成吸附水膜。C-S-H孔隙的区域2nm～12nm(红线区域内),模拟所得吸附水膜厚度约为0.5nm～0.8nm,与文献[19]描述该温度下吸附水膜厚度为0.63nm的情形相吻合。这表明该势函数可以较为准确地模拟C-S-H与水的相互作用,而C-S-H对孔隙水冰点的影响主要考虑其表面张力,因此该模型适用于C-S-H后续计算。

4.2 C-S-H孔隙水密度分布

为探究C-S-H孔隙水的密度分布特征[20],将研究对象沿x和z方向均匀离散为边长为δ的正方形,计算区域y方向长度作为高,形成有限个正四棱柱。统计每一帧正四棱柱内粗粒化水分子的个数,对时间平均,得出正四棱柱的数密度,再转换为质量密度。密度计算公式为

(8)

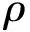
根据式(8)求出水的密度,可以得到C-S-H孔隙结构x-z截面水的密度云图,如图8所示。从图5、图6与图8可以看出,在靠近C-S-H孔隙结构的边界,受C-S-H表面张力的影响,水分子吸附在C-S-H粒子上,水分子密度较大,为1.5g/cm3～2g/cm3;在C-S-H孔隙结构的中间区域,水分子密度为1g/cm3左右,水分子呈现有序排列,已经冻结。这表明水泥基材料孔隙中,C-S-H对水的影响随着距离逐渐减小,C-S-H对孔壁表面处的水影响最大,对孔隙中间的水基本没有影响。

4.3 不同孔径中孔隙水的冰点计算

由于表面张力的作用,在水泥基材料不同孔径的孔隙中,水的结冰温度(冰点)有较大的差异。现有研究表明,孔径越小,表面张力越大,冰点越低,可表示为[17]

图8 C-S-H孔隙x-z截面水的密度云图

(9)

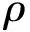
Williams[21]实验得出的-1 ℃下能结冰的最小半径为100nm左右,与上述理论值的124.4nm较为接近;谢超等[22]推导了微孔半径与冰点的关系,并参照该微孔半径与冰点关系进行了实验,该关系中-3 ℃下能结冰的最小半径为41.4nm,与理论值41.78nm较为接近。两者均与热力学理论比较吻合,而更小尺度孔径的冰点难以通过实验获得。

为研究微纳米尺度下C-S-H孔径对冰点的影响,分别设微孔半径为5nm,10nm,15nm,20nm和25nm,受限水的模型上下边界为3nm的C-S-H,中间区域生成的粗粒化水分子数量依次为8000,16000,24000,32000和40000。计算不同温度下的键序参数,列入表2。以5nm微孔半径C-S-H孔隙水为例,当温度在242K及以下时,键序参数变化不大,且有序程度较好,表明孔隙水处于结冰状态;当温度在242K以上时,键序参数迅速减小,有序程度较差,表明孔隙水处于自由状态。据此,可以认为当键序参数在1K内发生突变,则此时的温度为孔隙水的冰点。

依据键序参数的结果可得到孔径为5nm,10nm,15nm,20nm和25nm时,水的冰点依次为242K,251K,259K,262K和263K,数值模拟结果与式(9)热力学理论结果对照如图9所示。

表2 键序参数均值与温度关系

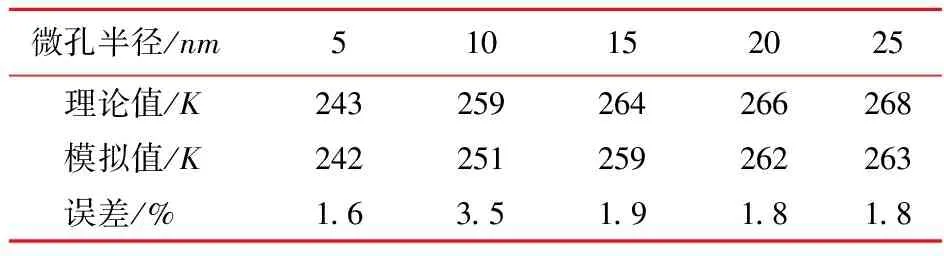
表3 误差分析

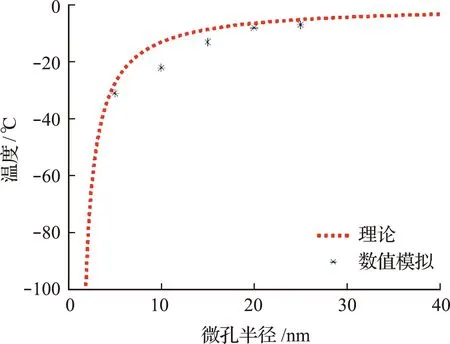
图9 微孔半径与冰点关系曲线

从图9可以看出,模拟结果与理论值吻合较好,计算得到的不同孔径的冰点略低于理论估算值,误差分别为1.6%,3.5%,1.9%,1.8%和1.8%,最大误差为3.5%。本文采用控温控压系综保持模拟系统压强不变,只考虑C-S-H孔径对受限水冰点的影响,且选用的势函数参数较为准确地表现了C-S-H与水的相互作用,故模拟结果与热力学理论值相差较小。此外,研究发现,当孔径较小时,受限水的冰点波动较大;当孔径较大时,冰点的变化缓慢。这表明水泥基材料中孔隙孔径越小,其冰点越低,结冰难度会剧烈增加。因此,水泥基材料的孔隙大小对冻融破坏的影响巨大。由模拟所得的微孔半径与冰点的关系可知,微孔半径在5nm以下的孔在-31 ℃以上不会结冰,这意味着在通常的冻融环境条件下,孔径在10nm以下的孔对水泥基材料基本没有危害;微孔半径在5nm～25nm的孔对应的孔隙水冰点在-31 ℃～-10 ℃,表明孔径在10nm～50nm范围内的孔具有一定的危害;当微孔半径在25nm以上时,孔隙水的结冰温度在-10 ℃～0 ℃,表明孔径在50nm以上的孔隙受冻融的影响较为明显,对水泥基材料的危害也较大。本文的计算结果与热力学理论相互印证,得出了实验无法测得较小孔微孔半径与冰点的关系,为进一步了解水泥基材料孔隙在冻融循环过程中的危害程度提供了基础。

5 结 论

本文选取水和C-S-H的粗粒化粒子作为基本粒子,使用两种粗粒化粒子模拟自由水与C-S-H孔隙水的结冰过程,得出以下结论。

(1)C-S-H表面张力影响着孔隙水的密度分布和冻结分布特征。由于C-S-H壁面的表面张力作用,靠近C-S-H壁面处的水吸附在C-S-H粒子上,水的密度较大,且水的运动受到一定的束缚,形成无法结冰的吸附层;而在C-S-H孔隙结构中间区域,受C-S-H表面张力影响较小,该部位孔隙水的密度与自由水基本相同。当C-S-H孔隙较小时,结冰温度非常低且吸附层占据主要区域,孔隙中水无法冻结。因此,在水泥基材料冻融破坏中,孔径小的凝胶孔难以结冰,对水泥基材料的破坏基本没有影响。

(2) 水泥基材料孔隙的孔径对孔隙水冰点有着重大的影响,进而影响内部孔隙水对水泥基材料冻融破坏的危害程度。水泥基材料孔隙的孔径越小,孔隙水的冰点越低,且结冰难度会剧烈增加;孔径在50nm以上时,C-S-H孔隙水的冰点在-10 ℃～0 ℃,孔隙水容易冻结,此类孔隙在冻融过程中危害相对较大;孔径在10nm～50nm,孔隙水的冰点在-31 ℃～-10 ℃,此孔径范围的孔隙在冻融过程中具有一定的危害性;孔径在10nm以下,孔隙水的冰点在-31 ℃以下,在冻融过程中基本不会结冰,危害很小。