融合稀疏八叉树与卷积神经网络的汽车风阻系数预测

2024-02-28张瑞昊刘学龙袁海东

计算力学学报 2024年1期

王刚, 张瑞昊,, 刘学龙, 袁海东, 韩旭*

(1.河北工业大学机械工程学院,天津 300401; 2.中汽研(天津)汽车工程研究院有限公司,天津 300300)

1 引言

风阻系数作为汽车在行驶过程中所受空气阻力大小的主要评价指标,是汽车在造型设计阶段研究的重要内容。减小风阻系数对于降低燃油消耗、延长汽车续航里程、提高车辆的行驶稳定性和安全性等具有重要意义[1]。

目前,风洞试验和计算流体力学(CFD)仿真是研究汽车风阻系数的两种主要方法。在风洞试验中,设计人员将汽车放置于由动力风扇产生的流场环境中以模拟在实际道路上的行驶工况,通过更改汽车造型以寻找最佳方案来减小空气阻力。该方法得到的风阻系数较为准确,但其准备周期长,试验成本高,且高度依赖设计人员经验。CFD仿真利用计算机求解控制流体流动的微分方程,通过改变模型的几何形状来研究汽车外造型对空气动力学性能的影响。相较于风洞试验,CFD仿真不需要大规模的试验设施,但在汽车造型设计初始阶段,外造型方案的快速迭代仍需花费大量时间进行验证。

为解决上述问题,风阻系数快速预测研究开始引起部分学者关注。目前风阻系数预测主要采用参数化方法,即通过选取对汽车风阻系数影响较大的外造型参数,利用遗传算法或响应面模型等建立造型参数与阻力系数之间的映射关系。廉玉波等[2]使用三次响应面模型对接近角、离去角和前风挡倾角等参数与风阻系数进行拟合,并采用多岛遗传算法对整车进行了多目标优化;张海林[3]使用Kriging近似模型构建了4组设计变量和阻力系数之间的快速响应关系,对某车身进行了风阻风噪协同优化;李璇等[4]将前悬距离、行李箱长度和发动机罩倾角等作为径向基神经网络模型的输入,对五种不同长细比的MIRA阶背车型进行了风阻系数预测;王正炬等[5,6]通过分析整车外流场得到对风阻影响较大的车身关键参数,利用BP神经网络实现了对车尾及整车风阻系数的快速预测。以上方法在预测模型输入参数的处理上均采用将三维复杂模型简化为低维特征的方式,但汽车外造型存在大量复杂曲面,一维或二维特征难以对其进行充分表达,使得参数化方法的预测精度普遍不高。另外,输入参数的形式也限制了预测模型的发展。

卷积神经网络最初用于二维图像处理[7,8],其模拟了动物的图像识别过程,使用图像集的像素作为输入向量。基于该原理,早期有学者将卷积神经网络拓展到三维。Wu等[9]使用3D ShapeNets对体素形式的三维形状进行分类与检索;Zhang等[10]构建了FeatureNet并应用于机械零件CAD模型的相交平面识别。基于体素化的三维卷积神经网络可以有效地提取特征,但维度的增加令其计算与存储开销呈指数级增长。针对此问题,Graham等[11]构建了关于稀疏数据存储、标记及运算的子流形稀疏网络。夏祥腾等[12]将稀疏卷积神经网络应用于点云分割,在高效计算的基础上提升了分割效果。对于高维输入数据,稀疏卷积神经网络只对输入的非零元素进行卷积操作,能显著降低计算复杂度,提高训练及推理效率。

本文融合稀疏八叉树与卷积神经网络对汽车风阻系数进行快速预测。将三维汽车模型外表面按照八叉树结构离散化,通过在离散曲面上取点采样生成结构化的平均法向量组,并将其作为整车外造型的特征。构建卷积神经网络,通过卷积和池化等操作提取模型的特征,对提取到的特征进行回归分析以预测在特定工况下汽车三维模型对应的风阻系数。相较于参数化方法,该方法能够建立整车外造型特征与风阻系数的映射关系,并且具有更高的预测精度,可以在汽车造型设计前期作为方案的减阻判断依据。

2 数据集准备

在基础车型上选取造型参数变量,通过网格变形生成不同外造型的车辆模型。对基础车型进行风阻系数仿真计算,并利用风洞试验验证仿真精度,之后对所有样本进行仿真计算得到对应风阻系数以生成本文卷积神经网络训练所用数据集。

2.1 模型构建

本文以某型号SUV为研究对象,长4.75 m,宽1.92 m,高1.62 m,按照该车型实际尺寸进行1∶1建模,在此基础上使用网格变形技术[13]对该SUV进行几何表面变形,选用变形参数如图1所示,分别为机盖前端距离地面高度H1,前保险杠下端距离地面高度H2,后备箱后沿距离地面高度H3,后备箱盖长度L1,发动机盖前缘倾角θ1,发动机盖倾角θ2,前风挡倾角θ3,后风挡倾角θ4,后备箱盖倾角θ5,前翼子板内收距离W1,后翼子板内收距离W2。为了确保生成模型的造型参数能够在设定的样本空间内均匀排列,采用均匀拉丁超立方[14,15]抽取样本点,共生成200个不同外造型的汽车几何模型。

2.2 数值仿真

在湍流的数值模拟方法中,雷诺平均法RANS相较于直接数值模拟法及大涡模拟法,能够在保证计算精度的同时减小计算开销。雷诺平均法控制方程为

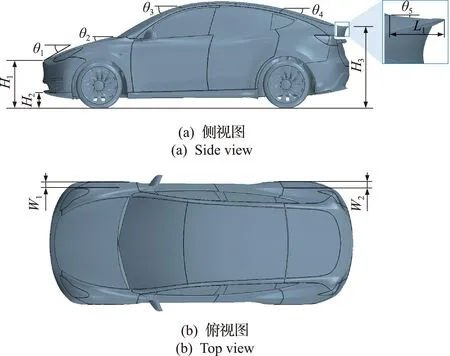
图1 外轮廓造型参数

∂ui/∂xi=0

(1)

(2)

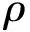
选用RANS方法中Realizablek-ε湍流模型,其湍动能k及耗散率ε可通过以下方程求解

(3)

(4)

设置计算域尺寸长60 m,宽20 m,高10 m,地面分为滑移及非滑移地面,如图2所示。选用切割体网格模型进行数值离散,为提高计算精度,在车外嵌套4层尺寸分别为16 mm,32 mm,64 mm和128 mm的加密区域,并在车体表面划分5层边界层,总厚度为8 mm,层与层之间厚度增长比为1.3,如图3所示。计算域边界条件设置列入表1,经过数值仿真计算,最终得到基础车型风阻系数Cd=0.2508。

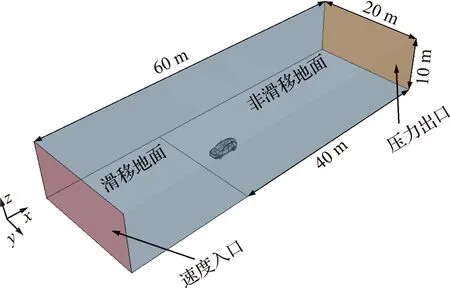
图2 计算域

图3 纵向对称面网格

表1 计算域边界条件

2.3 风洞试验与仿真验证

为验证上述计算域网格离散方式及湍流模型的计算精度,在中国汽车技术研究中心有限公司的气动-声学风洞实验室对基础车型进行了风阻系数测试,如图4所示。该风洞为3/4开放回流式风洞,最大风速为250 km/h,喷口面积为28 m2,满足本次试验的测试条件。

图4 汽车风洞试验

通过风洞试验,对仿真模型的湍流粘度、湍流强度和亚松弛因子等参数进行了标定,在车速120 km/h、格栅关闭和车轮转动的工况下,试验所得风阻系数Cd=0.2426,仿真与试验结果的相对误差为3.38%,小于5%,符合精度要求。之后将所有汽车几何模型样本依次导入计算域并生成网格,采用相同的计算域边界条件及网格加密方式,最终生成包含200个样本的数据集,每个样本包含三维汽车模型及其对应风阻系数。以上仿真计算均在中国汽车技术研究中心280核(单节点28核,10节点)服务器上进行,平均迭代时间为1.6094 s/步,最大迭代步数为3000,每个仿真的平均计算用时为4828.2 s。

3 汽车风阻系数预测模型

3.1 三维模型的八叉树表示

八叉树是一种基于递归分割的数据结构,其每个节点都有八个子节点,用于把三维空间划分成多个体素。本文提出了一种基于八叉树[16-18]结构的三维模型表示方法,如图5所示。

图5 三维模型的八叉树表示

将三维模型放置于边长为L的立方体包围盒中,该立方体为八叉树的根节点,对其进行均匀八等分,若等分之后子立方体中仍存在三维模型的几何表面,则继续对其进行分割,在每一次等分之前,遍历当前深度处三维模型占据的所有非空立方体,并将当前深度处的非空立方体在下一个深度再次等分为8个子立方体,按此递归方式操作直到达到预定深度,八叉树深度l处子立方体的边长为a=L/2l。

用一组坐标(xl,yl,zl)表示八叉树深度l处体素在其父节点中的位置,取值为0或1。定义体素在根节点中的坐标为(x,y,z),其中x=x1x2…xl,y=y1y2…yl,z=z1z2…zl。为便于管理所有体素,本文提出了一种双N型排列方式对每个深度的所有节点进行排序,体素编号及其对应坐标如图6所示。

如图7所示,使用离散曲面的平均法向量来表示三维模型,既对复杂曲面进行了简化,也能较为真实地还原模型的细节。因此,本文以规定八叉树深度内体素包含模型几何表面的平均法向量作为该体素的值,并将其按上述体素编号顺序存储在特征数组中,以此来表示三维模型的特征。

图6 八叉树节点坐标及排序

图7 三维模型的法向量表示

基于三维模型的八叉树表示方法,构建了一种卷积神经网络对三维汽车模型进行特征提取及风阻系数预测,其整体结构如图8所示,该方法只对三维形状表面占据的稀疏八分体进行卷积操作。

3.2 卷积神经网络输入形式

将在规定深度体素内模型几何表面的平均法向量组作为卷积神经网络的输入。法向量采样过程如图9所示,对于规定深度内的所有空体素,分配零向量作为输入信号;对于规定深度内的所有非空体素,在其内部的三维模型表面形状上取点采样,将所有采样点的法向量取平均值得到该体素内几何表面的平均法向量,即

(5)

图8 卷积神经网络结构

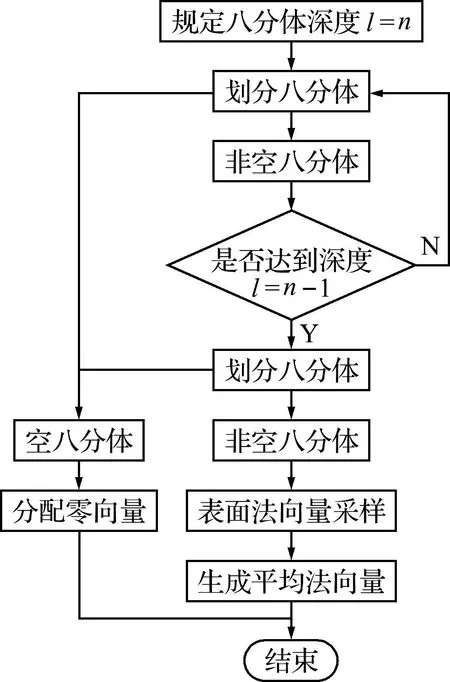
图9 体素内曲面法向量采样流程

3.3 稀疏卷积运算过程

对于规定八叉树深度内体素的卷积操作,卷积算子可以表示为

(6)

图10展示了八叉树深度l=2时输入体素的稀疏卷积运算具体过程,其中有三个节点包含非零特征值,在进行卷积运算时,卷积核只对特征值不为0的体素进行卷积操作,这样不会导致非空体素增加或减少,从而保持特征图的稀疏性。

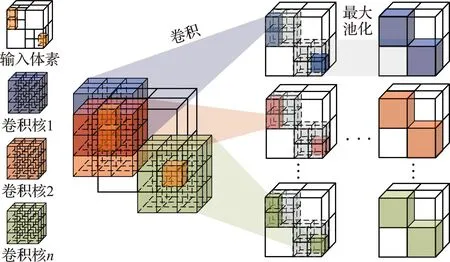
图10 八叉树结构体素的卷积和最大池化

在计算过程中,需要根据卷积核大小收集卷积核中心对应体素及其周围体素特征值,由于每个体素对应的特征值存储在数组中,若根据坐标对数组进行线性索引,随着八叉树深度的增加,计算机在执行线性索引时会产生较大的时间开销。为方便根据体素坐标快速查找其对应特征值,构建如图11所示的哈希表,规定其键为体素在根节点中坐标组合而成的数值序列K=x1y1z1x2y2z2…xnynzn,值为体素对应特征值在特征数组内的下标编号d,哈希函数可以表示为

k=|intK|,H(k)=kmodp

(7a,7b)

式中 mod为取模运算,p为小于哈希表长度m的最大素数。输入节点坐标,通过哈希表可以快速计算出特征值在数组内的下标编号,进而对特征值进行索引,以便高效地进行卷积运算。

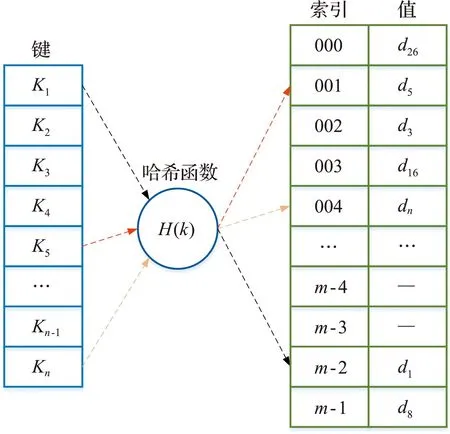
图11 哈希表

3.4 池化运算过程

池化操作是一个降采样过程,其从相应的采样窗口中提取一定的特征作为低维输出[19]。该操作可以减小特征图的空间大小,以减少网络的参数量和计算量,从而防止过拟合。如图10所示,在八叉树中应用最大池化操作可以从相同父节点的8个子节点中挑选出最大特征值并将其映射至父节点,最大池化函数可以表示为

(8)

3.5 激活函数

激活函数在深度卷积神经网络中起着至关重要的作用,其可以激活神经元的特征来解决非线性问题。目前,ReLU函数是深度卷积神经网络中最常用的激活函数,其相对于Sigmoid函数和Tanh函数能够防止梯度消失,并使网络具有较好的稀疏性。其函数曲线如图12所示。

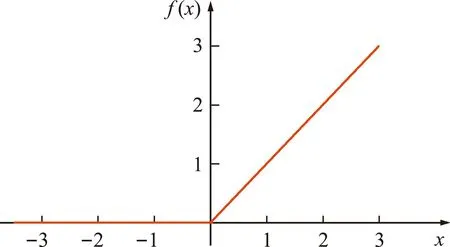
图12 ReLU激活函数曲线

本文每个卷积层之后均采用ReLU函数对网络进行非线性映射,其计算公式为

f(x)=max(0,x)

(9)

式中x为卷积之后输入激活函数的特征值。

4 仿真分析

本节构造了几种不同结构的卷积神经网络,并对构造的所有神经网络进行训练,研究了不同结构的卷积神经网络对风阻系数预测精度的影响,并与参数化预测方法进行了对比。

4.1 试验平台

神经网络训练及测试均在64位的Windows 10操作系统上进行,处理器型号为Intel(R)Core(TM)i9-11900K@3.50GHz,内存64GB,搭载Caffe深度学习框架。

4.2 模型训练

神经网络训练是一个优化过程,目的在于使损失函数最小化,使用反向传播算法训练网络的权值和偏差。采用欧几里得损失函数作为卷积神经网络的目标损失函数,即

(10)

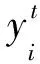
训练包括对卷积层(wc,bc)和全连接层(wf,bf)的权值及偏差的训练。将训练参数表示为W=[wc,bc,wf,bf]。为了优化训练参数,使用反向传播算法获得可训练参数的误差梯度。然后,使用随机梯度下降法SGD来更新权值和偏差,即

(11)

式中α为学习率。

采用9∶1的比例将数据集分为训练集和测试集,数据集样本数量为200,即用180个样本进行训练,20个样本用于测试模型的精度。动量为0.9,权重衰减系数为0.0005,批量大小为18,初始学习率为0.1,迭代次数为3000。对输出值进行归一化,使所有的输出值都在0～1范围内。

通过改变卷积层数与全连接层数,研究了几种卷积神经网络结构。如表2所示,将一个具有3个卷积层和2个全连接层的CNN结构作为基础模型,在基础模型中进一步添加了卷积层和全连接层,共产生6种卷积神经网络结构,之后对所有模型进行训练。训练完成后,LSCNN的收敛历史如图13所示,六种CNN结构的损失曲线在迭代2000步之后均收敛到0.01以下,展现出相同的收敛性。

表2 本文神经网络结构参数

4.3 结果分析

使用测试集中20个样本对训练好的CNN模型进行测试,将样本输入CNN模型中得到对应的风阻系数预测值。六种网络结构的预测精度如图14所示,由结构1～结构4的预测精度变化可以看出随着卷积层数量的增加,预测精度有所提高。在6个卷积层的基础上,全连接层数为2时,CNN模型预测精度最高,其风阻系数预测值与仿真值比较如图15所示。

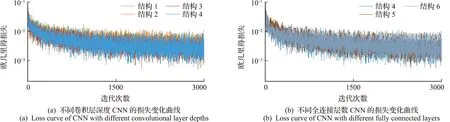
图13 欧几里得损失随迭代次数变化曲线

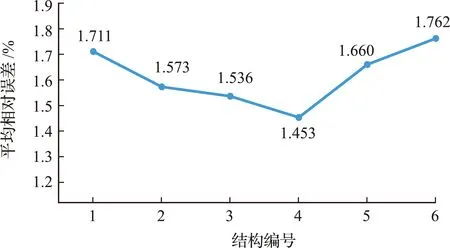
图14 不同结构的平均相对误差

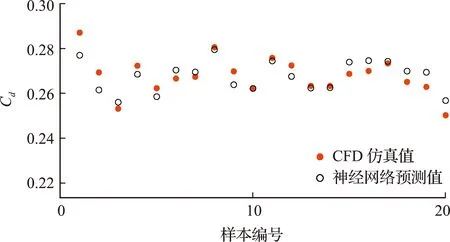
图15 结构4预测值与仿真值对比

为进一步验证本文构建的卷积神经网络模型精度,将其与径向基神经网络、Kriging代理模型和二次响应面模型等参数化预测方法进行了对比,列入表3。使用均方根误差RMSE及平均相对误差MAPE作为评价指标,其计算公式为

(12)

(13)

式中n为测试集样本个数。

参数化方法中,二次响应面模型产生的均方根误差最小,为0.00675;Kriging模型产生的平均相对误差最小,为1.918%。本文构建的六种SCNN模型预测精度均优于参数化方法,其中结构4精度最高,均方根误差及平均相对误差分别为0.00469和1.453%。相较于参数化方法,本文方法在测试集上表现出了更好的预测精度及泛化能力。