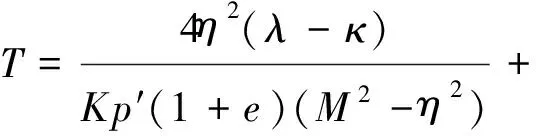弹塑性多孔介质流固耦合新理论:混合耦合理论
2024-02-28徐丽阳徐日庆陈晓辉
徐丽阳, 王 锴, 丁 智, 徐日庆, 陈晓辉
(1.浙江大学 滨海和城市岩土工程研究中心,杭州 310058;2.浙江省城市地下空间开发工程技术研究中心,杭州 310058;3.浙大城市学院 土木工程系,杭州 310015;4.浙江省城市盾构隧道安全建造与智能养护重点实验室,杭州 310015;5.北京师范大学 水科学研究院,北京 100875;6.利兹大学 土木工程系,英国利兹 LS2 9JT)
1 引 言
在全球气候变化和双碳政策的大背景下,亟需发展新能源和减碳减排技术,如开发利用地热、页岩气、天然气、水合物、核电和地质封存二氧化碳[1]。使得多孔介质中固体的变形和流体的输运问题受到越来越多研究者的广泛关注[2,3]。然而,在多孔介质中建立多场耦合模型是复杂的,面临的主要挑战是,多孔介质内部孔隙的尺度范围一般在10-9m~10-2m,而固体颗粒的尺度范围一般在宏观尺度,如黏土颗粒直径通常小于0.002 mm (2 μm),有时会小到纳米级别,具有高度的塑性和黏性。因此,多孔介质中的流固耦合现象跨越了宏观尺度到纳米尺度,即不仅要考虑宏观尺度(>10-7m)的流固耦合行为[4],如泥石流、软土的弹性变形、塑性变形和大孔隙中水的渗流;还需要考虑纳米级(10-9m~10-7m)的流固耦合作用[5],如软土微观孔隙结构的变化、吸水膨胀、毛细作用和吸附等。如果忽略这些微细观作用,对力场和流场的预测会产生较大误差,难以解释一些现象,如白垩岩遇水弱化[6](水渗透到白垩岩中时,水的渗透力可能会在颗粒之间产生冲击力,导致颗粒分离和破碎,从而降低了岩石的强度和稳定性)、北海Ekofisk油田的海底沉降[7](高孔隙率白垩的塑性变形使得Ekofisk油藏压实,造成了上覆海底的沉降)。
开展多场耦合分析有许多种思路,可归纳为力学方法和混合理论方法两类主要方法。力学方法是基于Terzaghi有效应力原理[8,9]和Biot固结理论[10]进行建模,其本质是宏观唯象关系。但对纳米级的多场耦合行为,力学方法只能基于经验和试验结果进行大量直觉性假设,因此在数学和物理上都不够严谨[11,12]。混合理论方法由Truesdell等[13,14]提出,该方法基于热力学建模,为多孔介质中的流体输运行为提供了更精确的理论方程。由于该方法假设固相和流相为独立体,需要对各相建立连续方程和动量守恒方程,并确定相界面上各相间的相互作用。然而纳米级的各相由于尺度太小,相间的作用力是很难获得的,只能依赖主观经验和特定的假设,限制了混合理论方法进一步考虑纳米尺度的作用[15]。
为了避免力学方法和混合理论方法的局限性,在多场耦合分析中实现考虑纳米尺度的作用,Chen等[16,17]提出了混合耦合理论(Mixture-Coupling Theory)。该理论源自Heidug等[18]对具有吸水膨胀效应的饱和多孔介质的研究,基于多孔介质力学和非平衡热力学,利用Helmholtz自由能和耗散熵产推导出固体变形能与耗散过程之间的关系[19]。混合耦合理论的优点是具有热力学一致性且推导方法严谨,可以建立不同尺度的平滑联系,适合于构建多尺度多场复杂耦合模型[20-23]。特别地,混合耦合理论还可以考虑大变形问题,建立弹性、塑性和固体流(泥石流)的统一理论。
然而,目前基于混合耦合理论建立的多场耦合模型,均假设固体的变形是弹性的,尚未考虑固体骨架塑性变形的影响。当固体骨架发生塑性变形时,固体颗粒会重新排列(固体颗粒的尺度范围为<0.002 m,少量在纳米尺度),储存在固体颗粒之间的自由能会变化[24,25];同时,固体颗粒重新排列,会改变流体流动的孔隙通道(10-9m~10-2m),造成孔压的变化。这些变化一方面引起宏细观的固体骨架有效应力变化和微观的孔隙结构的变化;另一方面又反过来影响微观的孔隙流体流动和压力的分布[26]。
本文首次将混合耦合理论从弹性变形假设推广到弹塑性变形,推导了饱和多孔介质的弹塑性流固耦合控制方程(即HM模型),模型实现了考虑从宏观尺度到纳米尺度的流固耦合行为,也为后续在弹塑性多孔介质中耦合更多纳米尺度的物理化学作用提供了参考。
2 平衡方程
混合耦合理论是基于非平衡热力学的方法,假设满足局域平衡条件,即饱和多孔介质整体虽然是变化的,但是局部可以近似视为平衡,并满足平衡体系中的热力学关系。在饱和多孔介质中任意选择代表单元体(REV)(图1),要求REV在宏观尺度上足够小,则其内部近似均匀;REV在微观尺度上要足够大,包含有足够多的分子,以进行统计分析。因此,饱和多孔介质系统整体的描述方程可采用局部形式的微分方程表示。假设REV具有体积V(单位:m3),由固体骨架、孔隙流体和边界S(单位:m2)组成,只允许孔隙流体的流入/流出。
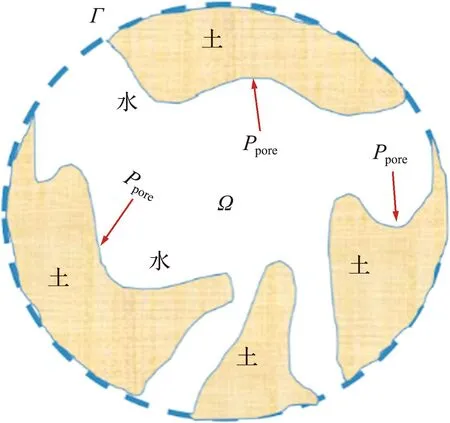
图1 代表单元体(REV)
2.1 质量平衡方程
饱和多孔介质中固相和液相的质量平衡方程可以统一表示为
(1)
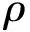
(2)
式中 ∂t为时间导数,为梯度算子。因此,由式(1)可以得到固相质量平衡方程的局部形式为
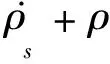
(3)
液相质量平衡方程的局部形式为
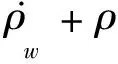
(4)
式中Iw为液体单位面积的质量通量(单位:kg/(m2·s)-1)。
(5)
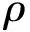
2.2 Helmholtz自由能平衡方程

2.2.1 内能平衡
饱和多孔介质的内能平衡方程为
(6)
则式(6)的局部形式为
(7)
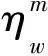
2.2.2 熵平衡
饱和多孔介质的熵平衡方程为
(8)
式中Iη为REV与周围环境交换的熵通量(单位:J/(K·m2·s)),γ为单位体积单位时间内的熵产[28](单位:J/(K·m3·s))。方程(8)的局部形式就是REV的熵密度平衡方程,
(9)
2.2.3 自由能平衡方程

(10)
3 本构关系
3.1 熵产
下一步需要确定REV的耗散过程,即确定方程(9)的γ。本文假设固体经历了不可逆的弹塑性变形,因此,REV中有两个耗散机制,即固体骨架的塑性变形,以及当流体通过多孔骨架时在固体/流体相边界产生的摩擦。其中,土壤在受力变形时,骨架颗粒重新排列产生功,一部分功是可恢复的弹性功(当土壤受的外力解除后,弹性功会完全释放),另一部分功是塑性功。假设所有的塑性功都会耗散,参考文献[29-31]的研究得到塑性变形耗散熵产的表达式
(11)

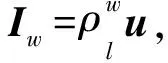
0≤Tγ2=-Iw·μw=-u·pw
(12)
因此,耗散过程的总熵产为
(13)
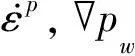
(14)
(15)
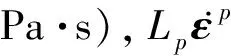
(16)
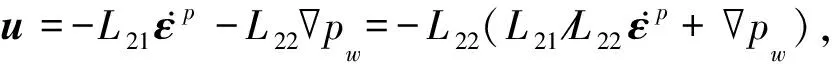
(17)
综上,得到耦合矩阵如下,
(18)
(19)
方程(19)的σd表达式与经典的耗散应力与塑性应变率的关系[31,33]一致,即较高的应变率通常会导致材料更快地发生变形,则固体颗粒更容易发生滑移,从而产生更多的耗散力;方程(19)的u表达式与经典的达西定律完全一致。以上验证了方程(14,15)的正确性。
3.2 连续介质力学方程
依据经典的连续介质力学理论,可以定义固体骨架的变形状态。一些基本的关系式为
T=JF-1σF-T,J=dV/dV0
(20)
式中F为变形梯度,X为参考组构REV所在的位置,且在t时刻的位置(当前位置)是x,E为Green应变,T为第二Piola-Kirchhoff应力(PK2),I为单位张量,J为函数的雅可比(Jacobian)矩阵,是函数输出相对于其输入的变化率,V0为参考组构REV的体积,V为当前组构REV的体积。
假设试验土样一直保持着力学平衡,因此,在不考虑外部体力的情况下,平衡方程为·σ=0。将方程(13)代入Helmholtz自由能密度平衡方程(10)得
(21)
方程(21)描述了当前组构REV的自由能平衡方程,在式(21)的两边乘以J,可推导得到参考组构的自由能平衡方程为
(22)
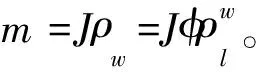
3.3 孔隙水的Helmholtz自由能
根据经典热力学可推导得到饱和多孔介质中,孔隙水的 Helmholtz自由能密度Ψpore为[15]
(23)
式中p为孔隙水压力(单位:Pa)。根据Gibbs-Duhem方程,不考虑温度变化,对方程进行时间微分,推导得
(24)
将方程(23)两边对时间求偏导,再将方程(24)代入,可得
(25)
3.4 固体骨架的Helmholtz自由能
(26)
3.5 本构方程
方程(26)采用v作为变量,但在岩土工程中,使用p作为变量比较方便,因此采用Legendre变换为

(27)
方程(27)两边对时间求偏导,再将方程(26)代入,可得方程为
(28)
W可理解为REV的总变形能,方程(28)表明,W为E,εp和p的函数。因此,T,σd和ν的表达式为
(29)
(30)
因此,应力T、耗散应力σd和孔隙体积分数v的本构方程为
(31)
(32)
(33)
式中 下标i,j,k,l=1,2,3。参数Lijkl,Sijkl,Mij,Rijkl,Bij和Q分别计算为
(34)
4 弹塑性多孔介质HM模型控制方程
方程(31~33)给出了Tij,σdij和v的一般形式耦合方程。这些方程适用于非线性、大变形和各向异性条件下的一般情况。本文主要用到Tij和v,为了简化讨论和关注土骨架塑性变形的影响,只讨论方程(31,33),并作了如下假设。

(35)
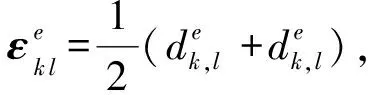
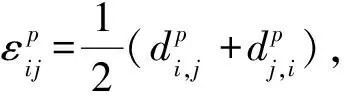
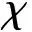
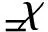
(36)
ζ=1-(K/Ks)
(37)
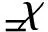
此外,Q为孔隙的压缩性能,即
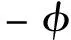
(38)
式中 当假设固体颗粒为不可压缩时(Ks=∞),Q=0。
4.1 流固耦合控制方程
4.1.1 固相的控制方程
根据上述假设,方程(31)可简化为
(39)
由于REV保持力学平衡,不考虑体力,因此应力满足平衡条件∂σij/∂x=0,推导得到固相的控制方程为
(40)
式中D为弹塑性刚度系数,由于本文研究的流固耦合行为需要考虑土骨架弹塑性变形,采用修正Cam-Clay模型描述弹塑性本构关系,因此,D可以由式(41)计算[34](详细推导过程见附录)。
(41)
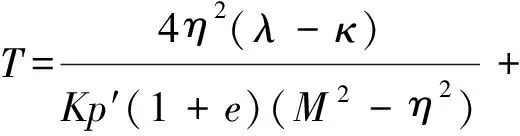
(42)
此时,力学平衡方程包含有塑性的影响和流体的影响

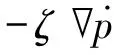
4.1.2 液相的控制方程

(43)
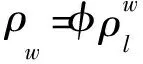
(44)
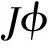
(45)
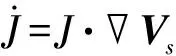
(46)
4.1.3 创新分析
本文提出的HM本构框架由方程(18,40,46)组成。这是一个统一的模型,将弹性变形、塑性变形和液体渗透都纳入了混合耦合理论框架,实现了对从宏观尺度到微观尺度的流固耦合行为的表征与分析。可以用于不同的场景实现更准确的预测,如模拟基坑降水、石油和天然气在地下储层中的流动等,特别是固体颗粒尺度大量处于纳米级的多孔介质的弹塑性流固耦合情况。此外,方程(18)精确描述了固体塑性变形对塑性耗散应力和液体输运方程的影响,方程(40,46)精确描述了固体塑性变形对力学平衡方程和流体均衡方程的影响。建立的HM模型具有准确的推导过程和多种形式的比较验证,在数学和物理上都很严谨。
本文提出的HM-塑性模型与Chen等[15]采用非平衡热力学方法提出的模型相比,力学变形方程和流体传输方程都有相似的形式,但是Chen等[15]的模型假设土体只发生弹性变形,没有考虑土的塑性变形。同时,如果不考虑塑性变形,可将方程(40,46)退化成为力学方法推导得到的经典Biot方程[10]。此外,考虑塑性变形的HM方程与文献[26,31,35]提出的方程相比,具有类似的形式。最后,本文的数值模拟部分对HM-塑性模型也进行了验证。
5 数值模拟
5.1 数值模型简介
基于Heidug等[18]设计的实验装置,建立一个长度为0.2 m、高度为0.1 m的二维轴对称模型(图2)。模型中的试样是饱和软土(0.1 m×0.2 m),用上述建立的弹塑性流固耦合模型表征,试样固定在两个坚硬且无摩擦的上下两个边界之间,因此试样只能产生水平方向(x方向)的位移。选择试样的中心点作为观测点C(图2)。基于COMSOL Multiphysics平台采用传统有限元方法计算。将弹塑性流固耦合模型的计算结果与李培超等[26]的弹塑性HM模型的计算结果进行对比分析。同时,选用剑桥模型表征软土的力学行为,模型参数列入表1。

图2 几何模型和边界条件
模型的边界和初始条件如下。
(1) 边界条件。边界A是自由的,而边界B是固定的(位移=0)。两个边界都是可透水的,可以让水在饱和软土试样中流进和流出。上下边界是不可透水的固定边界,不允许水的流动,也不能产生竖向位移。
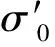
(3) 模拟的开始。在t=0时刻,自由边界A上的水压力从5 MPa突然增加到10 MPa,并且在后续的分析时间段里(即t>0)都保持这个水压力数值;固定边界B的水压力一直保持在5 MPa。

表1 考虑塑性的流固耦合模型参数
5.2 数值模拟结果
图3是观测点C的孔隙率、孔隙水压力p、有效应力和水平位移随时间的发展趋势。本文模型和李培超等[26]的模型计算结果是相似的。本文模型计算的孔隙率比文献模型的略大(图3(a)),体现了饱和软土发生塑性变形时土颗粒重排,使得孔隙结构变化。
该塑性变形会影响孔隙水压力。由于李培超等[26]的模型中,忽略重力项的水输运方程为
(47)
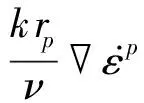
外部荷载相同的情况下,根据有效应力原理可知,孔隙水压力降低,相应的有效应力将增加。如图3(c)所示,本文模型的有效应力比文献模型略大;同时,本文模型的水平位移也比文献模型略大,如图3(d)所示。
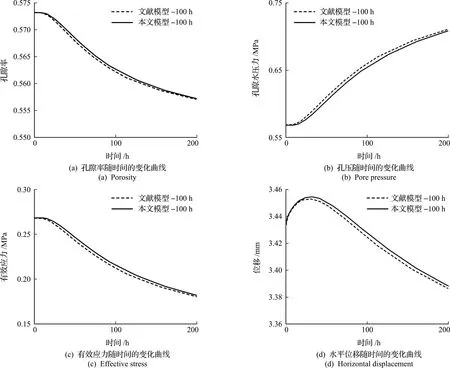
图3 观测点C的性质参数随时间的变化曲线
通过上述对比分析可知,如果忽略塑性变形的影响,对力场和流场的预测会产生较大误差。这是由于多孔介质中的流固耦合现象跨越了宏观尺度到纳米尺度,本文模型通过混合耦合理论推导得到的HM-塑性模型,可以考虑纳米尺度的流固耦合作用。
6 结 论
本文提出了一个弹塑性多孔介质流固耦合模型,在同一个理论框架内研究了弹性变形、塑性变形和液体渗流,实现了将混合耦合理论扩展到弹塑性变形范围。基于非平衡热力学的混合耦合理论,确定塑性变形时土骨架结构变化土颗粒重排产生的耗散熵,并利用Helmholtz自由能来连接宏观尺度上的力学变形和纳米尺度上的液体输运之间的相互作用,通过唯象定律进一步发展了考虑固体塑性变形的拓展达西定律。然后通过与文献中模型的比较,验证了该模型的有效性。最后,数值分析表明塑性变形对多孔介质中的流固耦合行为具有比较显著的影响。
附 录:
对于弹塑性本构模型,[Dep]的一般表达式
(A1)
按相容条件
(A2)
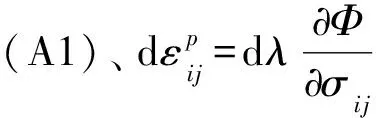
(A3)
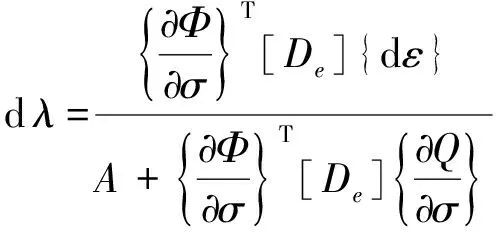
(A4)
代入式(A1),有
([De]-[Dp]){dε}=[Dep]{dε}
(A5)
式中 [Dep]=[De]-[Dp]
(A6)

(A7)
当弹塑性本构模型选用修正Cam-Clay模型时,模型中,土的状态用平均有效应力p′、偏应力q和孔隙比e共同描述。弹塑性刚度系数[Dep](即D(Dijkl))的推导过程如下。
(1) 总应变。多孔介质的总应变包括弹性应变和塑性应变两部分,即
ε=εe+εp
(A8)
式中ε为多孔介质的总应变,εe为多孔介质的弹性应变,εp为多孔介质的塑性应变。
(2) 弹性应变增量
(A9,A10)
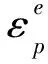
(3) 塑性应变增量
① 屈服方程
(A11)

② 流动法则。修正剑桥模型假设相关联塑性,因此,塑性势方程g和屈服方程f一样
(A12)
因此,描述塑性应变的流动法则是
(A13)

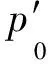
(A14,A15)
式中λ为正常固结曲线的斜率。
④ 塑性应变和应力的关系。根据上述方程,可以推导得到塑性应变和应力的关系为
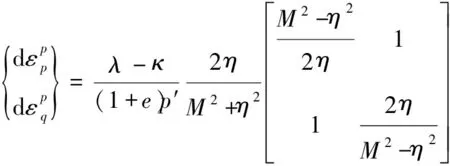
(A16)
(4) 修正的刚度D(Dijkl)。将方程(A9,A10,A16)代入方程(A8),可计算出总应变为
(A17)

(A18)