脱氧核糖核酸柔性的分子动力学模拟:Amber bsc1和bsc0力场的对比研究∗
2018-06-14熊开欣席昆鲍磊张忠良谭志杰
熊开欣 席昆 鲍磊 张忠良 谭志杰
(武汉大学物理科学与技术学院,武汉 430072)
1 引 言
脱氧核糖核酸(deoxyribonucleic acid,DNA)作为重要的遗传物质,在生命过程中扮演着核心角色.DNA的结构柔性与其生物功能的实现密切相关,DNA一般是以较为致密的折叠形态存在[1−5],如DNA在病毒中的包装、核小体的折叠和染色质的形成等[6−9].因此对DNA结构及柔性的研究对其功能的了解非常重要[10−14].现有研究表明[2,15,16],在体内或体外溶液中,DNA会发生弯曲、伸缩和扭转,其对应柔性可由弯曲持久长度lp、拉伸模量S以及扭转持久长度C等弹性参量描述[17−23].此外,人们还发现DNA的伸缩和扭转之间存在一定的耦合,DNA在低拉伸力下扭转-伸缩耦合为负,即DNA在其伸长时会旋紧[24−27].
研究生物分子柔性的实验技术包括原子力显微镜技术(AFM)[28,29]、荧光共振能量转移(FRET)[30]、小角度X射线散射实验(SAXS)[31,32]、磁镊技术(MT)和光镊技术(OT)等[3,33−39].近年来,随着计算机技术的快速发展,全原子分子动力学(all-atom molecular dynamics,MD)模拟已经成为研究生物分子结构、柔性和动力学等性质的重要手段[1,40−54].尽管实验结合弹性模型可以测量DNA的弹性性质并给出相关弹性参量,却无法给出DNA微观结构变化的信息,而MD模拟可以在原子层面对DNA等生物分子的结构、柔性和动力学进行研究.在过去的十几年中,对于核酸分子MD模拟所得到结构、弹性参量等性质能够较好地符合实验结果,并且在碱基对层面揭示了DNA结构及柔性的序列依赖性[40,55−57].在MD模拟中,精确合适的力场对模拟结果的可靠性非常关键,对于生物大分子体系,常用的模拟力场有Amber力场和Charmm力场等[52,58,59],其中Amber力场常应用于研究核酸系统.最近,针对DNA的MD模拟,Orozco等[60]在上一代Amber力场bsc0的基础上提出了新的力场bsc1,对bsc1力场的检验表明该力场得到的DNA扭转角与实验值更为接近[54].然而,到目前为止,关于新力场bsc1对DNA柔性的全面检验依然缺乏,尤其是关于DNA的宏观柔性参量及其对应的微观机理.
本文分别使用Amber bsc0和bsc1力场对DNA进行MD模拟,全面计算了在两个力场下DNA的宏观柔性,包括弯曲持久长度lp、拉伸模量S、扭转持久长度C和扭转-伸缩耦合比D等,并在碱基对层面分析了两种力场下的微观结构参量.进一步,对两种力场模拟得到的宏观弹性参量和微观结构参量与相关实验值进行全面对比,并在宏观和微观层面得到了新力场bsc1对描述DNA结构柔性不同参量的改善程度.结果表明:相比于bsc0力场,bsc1力场MD模拟所得到的宏观参量有一定改善,与相关实验更接近;在微观参量上,bsc1力场模拟得到的参量值基本上也与实验值有更好的符合.分析了bsc1力场下宏观柔性参量的改善与微观结构参量及其涨落的关系.
2 模型和方法
2.1 全原子分子动力学模拟
首先通过Amber软件自带的Nucleic Acid Builder程序包[61]产生了一根序列为5′-GCTCGACAGC TCGACGTCTA CCATGACTGA-3′的30个碱基对(30-bp)长度的DNA,此序列中间26个碱基对(26-bp)的G-C碱基配对比例约为54%,与前人模拟选取序列G-C比例相当[13,27,45].接下来,先将DNA的初始结构置于(120×120×120)Å3的立方体模拟盒子中心,并加入TIP3P水分子.由于DNA带负电荷,故加入了1 M NaCl来保证DNA分子上的负电荷被充分地屏蔽以消除静电效应对DNA柔性的影响,并添加了58个Na+作为补偿离子来中和DNA自身的负电荷[5,52,53,62−66].
利用Gromacs 4.6进行Amber bsc0和bsc1两种力场下的MD模拟[60,67,68].具体模拟过程如下:首先使用最陡下降法对系统进行约5000步的能量最小化处理;接着用热浴法将系统缓慢加热到298.15 K;然后在固定粒子数-压强-温度(NPT)系综下对整个系统利用Parrinello-Rahman压强耦合法[69,70]进行了约20 ns的预平衡模拟;最后在NPT(时间步长为2 fs,P=1 atm,T=298.15 K)系综下用蛙跳(leap-frog)算法[71]进行了600 ns的MD模拟.DNA的结构参数都是通过Curves+程序包提取得到的[72],为避免末端碱基的影响[13],在以下分析中,该DNA两端各去掉了两个碱基对,即只考虑DNA中间的26-bp片段,如图1(a)所示.本文针对DNA所要分析的相关微观结构参量如图1(b)所示.图1(c)和图1(d)展示了DNA中间26-bp片段分别在bsc0和bsc1力场下的末端距离Ree和累积扭转角度Φ随MD模拟时间的变化,可见所有轨迹在约100 ns后基本上达到了平衡,因而在以下的分析中只统计100 ns以后的模拟轨迹.
2.2 DNA的宏观柔性参量
因为在单个碱基对步(base pair step)层面上很难统计DNA的弯曲角度[13],因此可以跨越多个碱基对取一个弯曲角度θ,并得到其角度分布概率,进而通过以下公式拟合得到弯曲持久长度lp[73]:
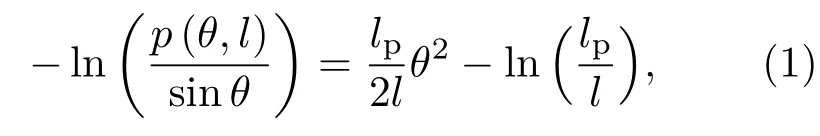
这里,θ为跨越10-bp得到的弯曲角度,因为10-bp约为DNA的一个螺旋周期;l表示10-bp的平均轮廓长度;p(θ,l)则表示θ角分布概率.
由于DNA的扭转-伸缩耦合特性,DNA的拉伸模量S和扭转持久长度C可以由下式计算[16,27,72,74]:
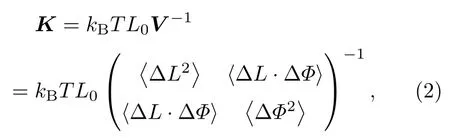
这里K代表一个弹性矩阵,其对角元K11和K22分别对应着DNA的拉伸模量S和扭转模量(扭转持久长度C=扭转模量/kBT)[27];V表示DNA中间26-bp片段的轮廓长度L和累积扭转角度Φ组成的协方差矩阵;kB为玻尔兹曼常数;T为模拟温度;L0为平均轮廓长度;∆L和∆Φ分别表示轮廓长度L和累积扭转角Φ的变化;⟨∆L2⟩和⟨∆Φ2⟩分别表示轮廓长度L和累积扭转角度Φ的方差.在实验中,通常测量∆L/∆Φ来确定扭转-伸缩耦合比D(=∆L/∆Φ),为了与实验对应,本文中也使用∆L/∆Φ来描述DNA的扭转-伸缩耦合特性[3,24,35].
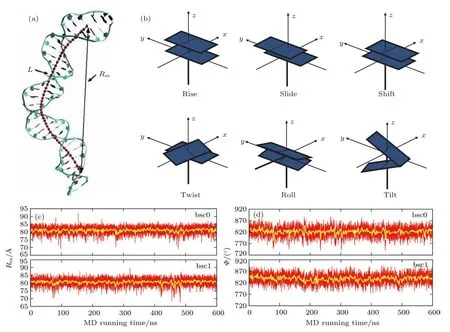
图1 (a)DNA的结构示意图,其中连着的红色小球表示该30-bp DNA中间26-bp片段的中心轴,该DNA片段轮廓长度为L,其端-端距离为Ree;(b)DNA中相邻碱基对间微观结构参量的示意图,其中包括3个平移类参量和3个旋转类参量[75];(c),(d)端-端距离Ree(c)和累积扭转角Φ(d)在Amber bsc0和bsc1力场模拟中随模拟时间的变化,其中黄色线表示每2 ns轨迹的相关参量的平均值Fig.1.(a)The diagram for the structure of the 30-bp DNA used in the work,the connected red balls represent the central axis of the central 26-bp segment of the DNA,L and Reedenote the contour length and end-to-end distance for the central 26-bp segment of the 30-bp DNA;(b)six microscopic parameters characterizing the relative orientation between two adjacent base pairs(base pair step)in the DNA,including 3 translational and 3 rotational parameters;(c),(d)the end-to-end distance Ree(c)and the cumulative H-twist Φ(d)versus MD running time(600 ns)for the central 26-bp segment of DNA from the Amber bsc0 and bsc1 force fields MD simulations,respectively,the yellow lines represent the average end-to-end distance and the cumulative H-twist Φ over every 2 ns MD simulations of the DNA.
2.3 DNA的微观结构参量
DNA双螺旋结构在碱基对层面的结构可由六个螺旋结构参数表征,其中包括三个平移参量和三个转动参量[75].如图1(b)所示,三个平移参量包括相邻碱基对堆积高度rise、相邻碱基对沿y轴滑移slide和沿x轴的滑移shift;三个转动参量包括相邻碱基对平面的夹角分别在yz平面的投影角tilt、在xz平面的投影角roll和在xy平面的投影角twist.此外,由于DNA的螺旋轴并不完全垂直于碱基对平面,考虑到碱基对平面相对DNA中心轴的倾斜角(inclination),一般将rise和twist在DNA中心轴上进行投影并标记为H-rise和H-twist,这是三个重要的碱基对螺旋轴参量[27].以上所涉及的微观结构参量的定义与1988年剑桥会议上制定的DNA结构参数公约是一致的[75].
3 结果与讨论
本文通过全原子MD模拟,利用两种力场Amber bsc1和bsc0对DNA的柔性进行对比研究.首先,研究了DNA的宏观柔性,即计算了两种力场得到的DNA宏观弹性参量,包括弯曲持久长度lp,拉伸模量S,扭转持久长度C和扭转-伸缩耦合比D,并与实验值进行了全面对比;其次考察了两种力场下DNA的微观结构,并与相关实验进行对比;最后分析了bsc1力场下宏观参量的改善与微观参量的关系.
3.1 两种力场下DNA的宏观结构柔性
由于DNA为具有螺旋结构的线性分子,描述其宏观结构需用几个方面的柔性参量:描述弯曲柔性的弯曲持久长度lp,描述伸缩柔性的拉伸模量S,描述DNA螺旋扭转柔性的扭转持久长度C和描述扭转-伸缩耦合强度的扭转-伸缩耦合比D.
3.1.1 DNA的弯曲柔性
DNA的弯曲柔性可由统计得到的弯曲角度θ分布直接反映,由于很难在单个碱基对层面描述短链DNA的弯曲,因此本文统计DNA中间26-bp片段中连续十个碱基对形成的弯曲角度θ,得到了该弯曲角度θ的分布概率p(θ).如图2(a)所示,两个力场(bsc1和bsc0)得到的角度分布概率p(θ)比较接近.基于弯曲角θ的分布概率p(θ)可通过(1)式拟合得到DNA在两种力场下的弯曲持久长度lp,如图2(b)所示.在bsc0力场下lp约为(47.9±0.1)nm,在bsc1力场下的lp约为(46.3±0.2)nm,表明bsc1和bsc0两个力场所描述的DNA的弯曲柔性很接近,并且与实验上测得的DNA持久长度约45.0—50.0 nm基本一致[1,33,36,37,76,77].
遇到错误资料很难完全避免,因此遇到资料错误时,我们应该调整好心态,把这当成是挑战自我的机会。遇到错误资料时,建议用倒推法解决,顺着执行部件的连线反向倒推,对相关线路进行逐一排查。

图2 (a)DNA中间26-bp片段弯曲角度θ的归一化分布;(b)−ln(p(θ,l)/sinθ)和弯曲角度θ的关系,可以通过(1)式对数据点拟合计算DNA片段的弯曲持久长度lpFig.2.(a)The normalized probability distribution of bending angle for the central 26-bp segment of DNA;(b)the relationship between −ln(p(θ,l)/sinθ)and bending angle θ for the central 26-bp segment of the DNA,the bending persistence length lpcan be estimated by fitting the data to Eq.(1).
3.1.2 DNA的伸缩柔性
DNA的宏观伸缩柔性可由统计得到的轮廓长度分布来描述.图3(a)给出了bsc1和bsc0两个力场下的DNA中间26-bp片段的轮廓长度概率分布,我们根据轮廓长度的概率分布计算了在bsc0和bsc1力场下DNA中间26-bp片段的平均轮廓长度分别约为83.20 Å和82.88 Å,其对应的方差分别约为1.74 Å和1.83 Å.进一步通过(2)式,计算出bsc0力场下DNA的拉伸模量S约为(1964±41)pN,而bsc1力场下的拉伸模量S约为(1860±41)pN.上述结果表明力场改进(bsc0→bsc1)降低了对DNA的拉伸模量,实验上测得的DNA拉伸模量S约为(1100—1600)pN[38,78]两种力场模拟结果与实验测量值基本一致,而bsc1力场下拉伸模量S与实验值更为接近.
3.1.3 DNA的扭转柔性
由于DNA为螺旋结构,因而其除具有线性分子的柔性(弯曲和伸缩)外,还具有扭转柔性.DNA的宏观扭转柔性可由统计得到的扭转角分布描述,图3(b)为DNA中间26-bp片段的累积扭转角Φ的概率归一化分布.由图可见DNA在bsc1力场下的扭转角整体比bsc0的稍大,这是合理的,因为bsc1力场相对bsc0力场主要的提升就是可以得到更大的与实验值更加接近的碱基对步(base pair step)扭转角[60].基于以上数据和(2)式,进而得到了bsc0力场下DNA的扭转持久长度C约为(98±2)nm,bsc1下C约为(105±2)nm,两种力场得到的C皆与实验值(100±10 nm)一致[12,35,37,79].
3.1.4 DNA的扭转-伸缩耦合
DNA伸缩和扭转之间存在耦合,实验表明DNA在伸长过程中其螺旋结构会相对旋紧,即其扭转角会增大,此效应对其生物功能有重要的作用,比如会影响DNA与蛋白质相互作用时DNA构象的调整[4,9,24,27].通过MD模拟的数据,我们统计了100 ns以后每个构象的平均H-rise(轮廓长度/碱基对步数)和H-twist(累积扭转角度/碱基对步数),它们间的耦合关系如图3(c)所示,通过拟合分别得到bsc0力场下DNA的扭转-伸缩耦合比D约为(0.62±0.02)nm/turn,bsc1力场下DNA的扭转-伸缩耦合比D约为(0.47±0.02)nm/turn.综上可见,在不同力场下,扭转-伸缩耦合比D基本一致,即DNA在拉伸下会旋紧,而新力场(bsc1)的扭转-伸缩耦合比D比bsc0力场下得到的略小,也与实验测量值(0.50±0.10)nm/turn更为接近[3,24,35].
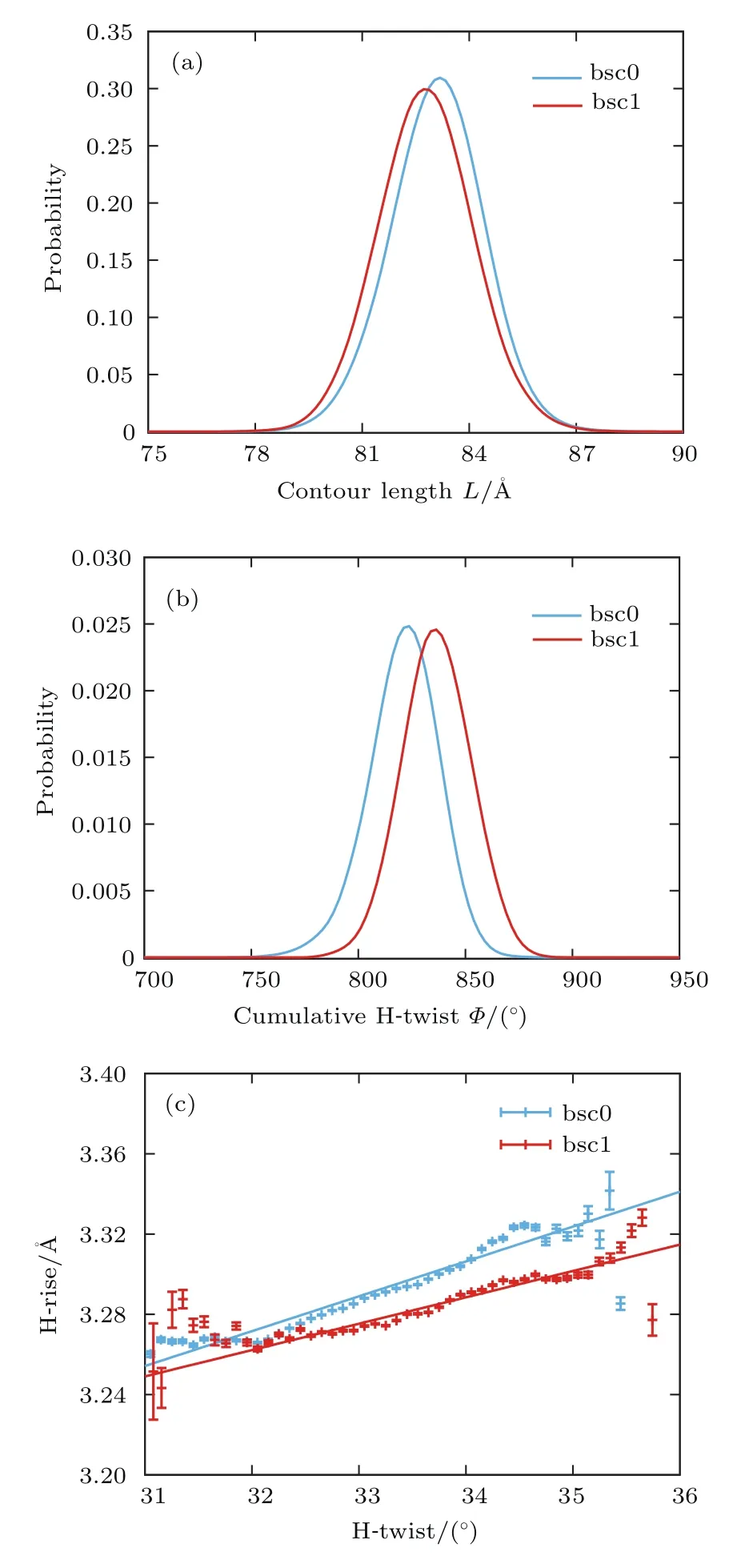
图3 (a),(b)DNA中间26-bp片段的轮廓长度L(a)和累积扭转角Φ(b)的归一化分布;(c)DNA的H-rise和H-twist的耦合关系,其中数据点是对H-twist在跨越0.1◦范围内的所有数据求平均得到,误差棒对应的是标准差Fig.3.(a),(b)The normalized probability distribution of contour length L(a)and the cumulative H-twist Φ(b)for the central 26-bp segment of DNA;(c)the coupling relationship between H-rise and H-twist of DNA;the data are obtained by averaging all the data of the H-twist within the range of 0.1◦,and the error bars correspond to the standard deviation.
3.2 两种力场下的DNA微观结构及其涨落
DNA的柔性与其微观结构及结构涨落紧密相关,我们将在碱基对层面分析bsc1和bsc0两种力场下DNA的微观结构及柔性,并与实验结构进行比较.如2.3节所述,DNA的双螺旋结构在碱基对层面可由三个平移参量(rise,slide和shift)和三个转动参量(twist,roll和tilt)表征,如图1(b)所示.此外,考虑倾斜角(inclination)、H-rise和H-twist这三个比较重要的碱基对-螺旋轴参量[27].表1列出了以上述DNA所有微观结构参数的平均值及其标准差,标准差的大小表示相关参量涨落的强弱.表1显示,两种力场下DNA的微观螺旋结构参量略有差异,相对于bsc0力场,bsc1力场下的微观结构参量更接近于实验测量值,其中bsc1力场在微观结构参量H-twist,twist和inclination上的改善较为显著,与实验值较为明显地接近,而其他微观结构参量的改善程度较为有限.我们也注意到bsc1力场下slide略微远离实验值.这里需要指出的是,虽然在不同力场下DNA微观结构参量有差异,但它们的方差的差别较小.DNA宏观柔性与微观结构参量的涨落有关,这可能是在两种力场下DNA宏观柔性参量差别不太大的原因.
如3.1节所述,尽管Amber bsc1和bsc0两种力场下DNA宏观柔性参量差别不大,但本文的计算显示,bsc1和bsc0力场下的DNA宏观柔性参量依然存在如下相对关系:弯曲持久长度lp(bsc1)6lp(bsc0)、伸缩模量S(bsc1)6S(bsc0)、扭转持久长度C(bsc1)>C(bsc0)以及扭转-伸缩耦合比D(bsc1)6D(bsc0),这里 6和 >分别意味着略小于和略大于.上述bsc1和bsc0力场下DNA宏观参量的相对关系与其微观结构参量及涨落具有相关性.首先是DNA弯曲持久长度lp(bsc1)6lp(bsc0),前人研究已显示,DNA更倾向于朝大沟弯曲,其弯曲柔性与其大沟宽度的涨落紧密相关[82,83],大沟宽度涨落越大,DNA弯曲柔性越强.本文模拟结果显示,bsc1力场下DNA的大沟宽涨落比bsc0力场下大(见表2),意味着bsc1力场下DNA有略强的弯曲柔性,即lp(bsc1)会略小.其次是拉伸模量S(bsc1)6S(bsc0),这是由于bsc1力场下DNA H-rise的涨落比bsc0力场下要略大(见表1),因而更容易实现伸缩,从而导致bsc1下DNA的拉伸模量S稍小.进而扭转持久长度C(bsc1)>C(bsc0),是由于新力场bsc1下DNA具有更大的扭转角(H-twist)和稍小的扭转角涨落(标准差),因而bsc1力场下DNA更难实现扭转并具有更大的扭转持久长度C.最后是扭转-伸缩耦合比D(bsc1)6D(bsc0),此相对关系可由Bustamante等[24]提出的简化模型理解,DNA可模型化为一体积不变,外面紧紧绕着长度为B磷酸基主链的柱体,其柱体长度为L,半径为R,磷酸基主链绕圆柱体,角度为Φ(即累积扭转角),则有B2=L2+R2Φ2.由于磷酸基主链B不可伸缩,所以扭转-伸缩耦合比D= ∆L/∆Φ=2LR2Φ/(Φ2R2−2L2). 由于bsc1力场相对bsc0得到了明显较大的Φ(或H-twist)、略小的L(或H-rise)和略小的DNA半径R(在bsc1力场下R约为9.94 Å,在bsc0力场下R约为10.02 Å),导致D(bsc1)略小.
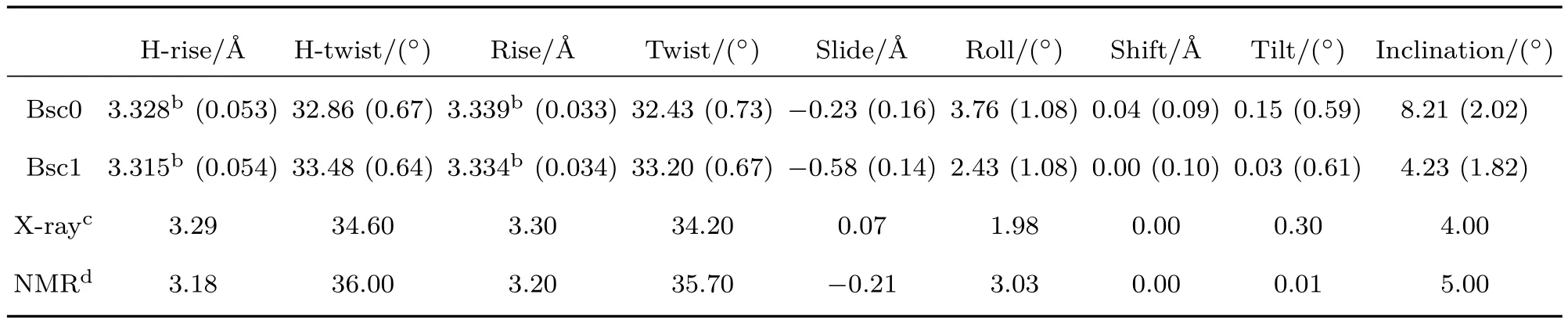
表1 MD模拟得到的DNA中间26-bp片段的平均螺旋结构参量aTable 1.Average helical structure parameters of the central 26-bp segment of DNA obtained by MD simulationsa.
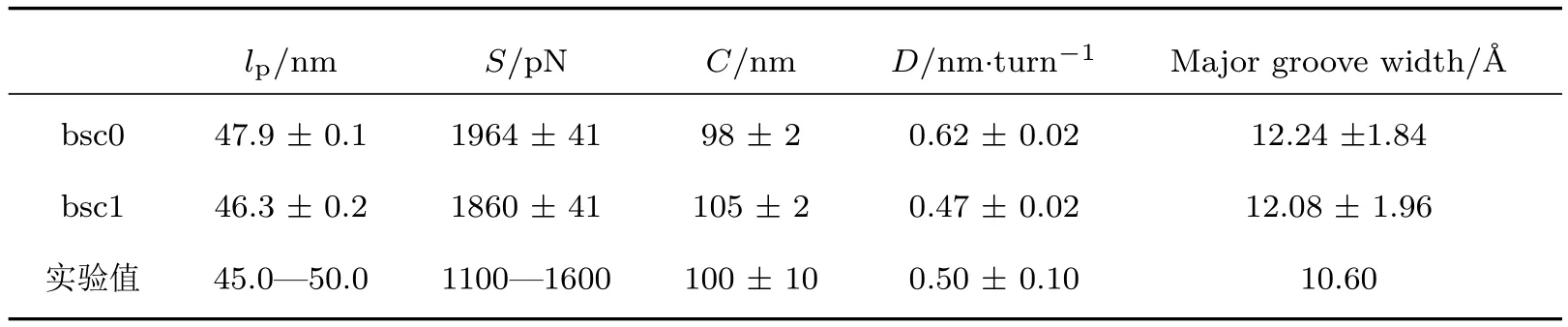
表2 DNA在Amber bsc0和bsc1两种力场下的宏观参量与实验测量值aTable 2.The macroscopic parameters of DNA under the force fields of Amber bsc0 and bsc1 and experimental valuesa.
4 结 论
本文采用Amber bsc1和bsc0两种力场对DNA进行了长时间的全原子分子动力学模拟,并从宏观和微观两个层面对DNA的结构柔性进行了深入的对比研究.本文的主要结论如下.
1)对于DNA的宏观弯曲和扭转柔性,bsc0和bsc1力场给出的弯曲持久长度lp和扭转持久长度C几乎相同,皆与实验值符合,说明这两个力场对DNA弯曲和扭转柔性的描述是比较一致和准确的;而bsc1力场下拉伸模量S和扭转-伸缩耦合比D相对于bsc0力场下的值与实验值更为接近,因而新力场bsc1对预测DNA的宏观柔性有一定的改善.
2)总体而言,bsc1力场下的DNA微观结构参量相对于bsc0力场更为接近于实验值,除了滑移(slide),其中最显著的是bsc1力场对于微观结构参量H-twist,twist和inclination有较为明显的提升.而bsc1和bsc0力场下DNA宏观柔性参量的相对关系与其微观结构参量及其涨落紧密相关.
随着单分子等实验技术的发展,DNA的柔性已经得到了较为全面的关注,但实验较难观察到DNA微观结构的变化,因而MD模拟可以作为一种有效的手段在微观层面研究DNA柔性及其微观机理,而对MD模拟而言,选择合适可靠的力场非常关键.本文针对DNA的柔性这一典型问题,利用最近新发展的Amber bsc1力场和已经广泛使用较长时间的bsc0力场进行了对比研究,发现bsc1力场下相对于bsc0力场在DNA的主要宏观柔性参量以及主要微观结构上有小幅的提升,尤其是微观结构参量如H-twist,twist和inclination有较为明显改善.本文研究将有助于人们对DNA柔性以及对新力场对描述DNA柔性改善程度的全面深入理解.
[1]Peters J P,Maher L J 2010Q.Rev.Biophys.43 23
[2]Bao L,Zhang X,Jin L,Tan Z J 2015Chin.Phys.B24 018703
[3]Lionnet T,Joubaud S,Lavery R,Bensimon D,Croquette V 2006Phys.Rev.Lett.96 178102
[4]Forth S,Sheinin M Y,Inman J,Wang M D 2013Ann.Rev.Biophys.42 583
[5]Zhang Z L,Wu Y Y,Xi K,Sang J P,Tan Z J 2017Biophys.J.113 517
[6]Richmond T J,Davey C A 2003Nature423 145
[7]Noll M 1977J.Mol.Biol.116 49
[8]Felsenfeld G,Boyes J,Chung J H,Clark D J,Studitsky V M 1996Proc.Natl.Acad.Sci.USA93 9384
[9]Li W,Wang P Y,Yan J,Li M 2012Phys.Rev.Lett.109 218102
[10]Xiao S Y,Zhu H,Wang L,Liang H J 2014Soft Matter10 1045
[11]Xiao S Y,Liang H J 2012J.Chem.Phys.136 205102
[12]Bryant Z,Stone M D,Gore J,Smith S B,Cozzarelli N R,Bustamante C 2003Nature424 338
[13]Wu Y Y,Bao L,Zhang X,Tan Z J 2015J.Chem.Phys.142 125103
[14]Wang F H,Wu Y Y,Tan Z J 2013Biopolymers99 370
[15]Kratky O,Porod G 2010Rel.Trav.Chim.Pays-Bas.68 1106
[16]Noy A,Golestanian R 2012Phys.Rev.Lett.109 228101
[17]Zhang X H,Chen H,Fu H X,Doyle P S,Yan J 2012Proc.Natl.Acad.Sci.USA109 8103
[18]Fu W B,Wang X L,Zhang X H,Ran S Y,Yan J,Li M 2006J.Am.Chem.Soc.128 15040
[19]Zhang X,Bao L,Wu Y Y,Zhu X L,Tan Z J 2017J.Chem.Phys.147 054901
[20]Travers A A 2004Phil.Trans.R.Soc.Lond.A362 1423
[21]Tan Z J,Chen S J 2008Biophys.J.94 3137
[22]Zhou H J,Zhang Y,Ouyang Z C 1998Phys.Rev.Lett.82 4560
[23]Zhou H,Zhang Y,Ouyang Z C 2000Phys.Rev.E62 1045
[24]Gore J,Bryant Z,Nöllmann M,Le M U,Cozzarelli N R,Bustamante C 2006Nature442 836
[25]Moroz J D,Nelson P C 1997Proc.Natl.Acad.Sci.USA94 14418
[26]Marko J F 1998Phys.Rev.E57 2134
[27]Bao L,Zhang X,Shi Y Z,Wu Y Y,Tan Z J 2017Biophys.J.112 1094
[28]Mazur A K,Maaloum M 2014Phys.Rev.Lett.112 068104
[29]Abels J A,Moreno-Herrero F,van der Heiden T,Dekker C,Dekker N H 2005Biophys.J.88 2737
[30]Yuan C,Chen H,Lou X W,Archer L A 2008Phys.Rev.Lett.100 018102
[31]Mathew-Fenn R S,Das R,Harbury P A B 2008Science322 446
[32]Mastroianni A J,Sivak D A,Geissler P L,Alivisatos A P 2009Biophys.J.97 1408
[33]Smith S B,Cui Y,Bustamante C 1996Science271 795
[34]Wang X L,Zhang X H,Cao M,Zheng H Z,Xiao B,Wang Y,Li M 2009J.Phys.Chem.B113 2328
[35]Lipfert J,Skinner G M,Keegstra J M,Hensgens T,Jager T,Dulin D,Kober M,Yu Z,Donkers S P,Chou F C,Das R,Dekker N H 2014Proc.Natl.Acad.Sci.USA111 15408
[36]Herrero-Galán E,Fuentes-Perez M E,Carrasco C,Valpuesta J M,Carrascosa J L,Moreno-Herrero F,Arias-Gonzalez J R 2013J.Am.Chem.Soc.135 122
[37]Lipfert J,Kerssemakers J W,Jager T,Dekker N H 2010Nat.Methods7 977
[38]Baumann C G,Smith S B,Bloomfield V A,Bustamante C 1997Proc.Natl.Acad.Sci.USA94 6185
[39]Zhang X H,Qu Y Y,Chen H,Rouzina I,Zhang S L,Doyle P S,Yan J 2014J.Am.Chem.Soc.136 16073
[40]Orozco M,Noy A,Pérez A 2008Curr.Opin.Struct.Biol.18 185
[41]Wang Y,Gong S,Wang Z,Zhang W 2016J.Chem.Phys.144 115101
[42]Qi W P,Lei X L,Fang H P 2010ChemPhysChem11 2146
[43]Qi W P,Song B,Lei X L,Wang C L,Fang H P 2011Biochemistry50 9628
[44]Yin Y D,Yang L J,Zheng G Q,Gu C,Yi C Q,He C,Gao Y Q,Zhao X S 2014Proc.Natl.Acad.Sci.USA111 8043
[45]Gu C,Zhang J,Yang Y I,Chen X,Ge H,Sun Y,Su X,Yang L,Xie S,Gao Y Q 2015J.Phys.Chem.B119 13980
[46]Lankaš F,Šponer J,Langowski J,Iii T E C 2003Biophys.J.85 2872
[47]Perez A,Lankas F,Luque F J,Orozco M 2008Nucleic Acids Res.36 2379
[48]Zuo G,Li W,Zhang J,Wang J,Wang W 2010J.Phys.Chem.B114 5835
[49]Zhang Y J,Zhang J,Wang W 2011J.Am.Chem.Soc.133 6882
[50]Bian Y,Tan C,Wang J,Sheng Y,Zhang J,Wang W 2014PLoS Comput.Biol.10 25
[51]Wang J,Zhao Y,Wang J,Xiao Y 2015Phys.Rev.E92 062705
[52]Wang J,Xiao Y 2016Phys.Rev.E94 040401
[53]Wu Y Y,Zhang Z L,Zhang J S,Zhu X L,Tan Z J 2015Nucleic Acids Res.43 6156
[54]Galindomurillo R,Robertson J,Zgarbová M,Šponer J,Otyepka M,Jurečka P,Iii T E C 2016J.Chem.Theory Comput.12 4114
[55]Cheatham T E,Young M A 2000Biopolymers56 232
[56]Fujii S,Kono H,Takenaka S,Go N,Sarai A 2007Nucleic Acids.Res.35 6063
[57]Zhang Y,Zhou H J,Ouyang Z C 2001Biophys.J.81 1133
[58]Wang J,Wolf R M,Caldwell J W,Kollman P A,Case D A 2004J.Comput.Chem.25 1157
[59]Cornell W D,Cieplak P,Bayly C I,Gould I R,Merz K M,Ferguson D M,Spellmeyer D C,Fox T,Caldwell J W,Kollman P A 2015J.Am.Chem.Soc.117 5179
[60]Ivani I,Dans P D,Noy A,Perez A,Faustino I,Hospital A,Walther J,Andrio P,Goni R,Balaceanu A,Portella G,Battistini F,Gelpi J L,Gonzalez C,Vendruscolo M,Laughton C A,Harris S A,Case D A,Orozco M 2016Nat.Methods13 55
[61]Case D A,Cheatham T E,Darden T,Gohlke H,Luo R,Merz K M,Onufriev A,Simmerling C,Wang B,Woods R J 2010J.Comput.Chem.26 1668
[62]Joung I S 2008J.Phys.Chem.B112 9020
[63]Tan Z J,Chen S J 2006Biophys.J.90 1175
[64]Tan Z J,Chen S J 2007Biophys.J.92 3615
[65]Shi Y Z,Wang F H,Wu Y Y,Tan Z J 2014J.Chem.Phys.141 2654
[66]Shi Y Z,Jin L,Wang F H,Zhu X L,Tan Z J 2015Biophys.J.109 2654
[67]Hess B,Kutzner C,van der Spoel D,Lindahl E 2008J.Chem.Theory Comput.4 435
[68]Pérez A,Marchán I,Svozil D,Sponer J,Rd C T,Laughton C A,Orozco M 2007Biophys.J.92 3817
[69]Parrinello M,Rahman A 1981J.Appl.Phys.52 7182
[70]Martonák R,Laio A,Parrinello M 2003Phys.Rev.Lett.90 075503
[71]Gunsteren W F V,Berendsen H J C 1988Mol.Simulat.1 173
[72]Lavery R,Moakher M,Maddocks J H,Petkeviciute D,Zakrzewska K 2009Nucleic Acids.Res.37 5917
[73]Mazur A K 2006Biophys.J.91 4507
[74]Faustino I,Pérez A,Orozco M 2010Biophys.J.99 1876
[75]Lavery R,Sklenar H 1989J.Biomol.Struct.Dyn.6 655
[76]Forth S,Deufel C,Sheinin M Y,Daniels B,Sethna J P,Wang M D 2008Phys.Rev.Lett.100 148301
[77]Manning G S 2006Biophys.J.91 3607
[78]Wenner J R,Williams M C,Rouzina I,Bloomfield V A 2002Biophys.J.82 3160
[79]Moroz J D,Nelson P 1997Macromolecules31 6333
[80]Drew H R,Wing R M,Takano T,Broka C,Tanaka S,Itakura K,Dickerson R E 1981Proc.Natl.Acad.Sci.USA78 2179
[81]Wu Z R,Delaglio F,Tjandra N,Zhurkin V B,Bax A 2003J.Biomol.NMR26 297
[82]Noy A,Perez A,Lankas F,Javier Luque F,Orozco M 2004J.Mol.Biol.343 627
[83]Ma N,van der Vaart A 2016J.Am.Chem.Soc.138 9951
