数值耗散对压气机流动分离涡模拟的影响研究

2024-02-27江思雅

计算力学学报 2024年1期

田铖, 江思雅,2,3, 符松*

(1.清华大学航天航空学院,北京 100084; 2.中物院高性能数值模拟软件中心,北京 100088; 3.北京应用物理与计算数学研究所,北京 100088)

1 引言

航空发动机是飞机的心脏。现代航空发动机的核心部件包括压气机、燃烧室和涡轮。其中,压气机承担增加空气压力的任务,是发动机热力循环必不可少的一部分。我国正大力发展更先进的航空发动机,这要求压气机具有更好的气动性能。为实现这一目标,必须深入理解压气机内部流动机理。然而,由于压气机部件高速旋转,而且内部空间狭小,流动实验测量受到很多限制。计算流体力学CFD(Computational Fluid Dynamics)可以复现压气机内部流动细节,是压气机流动研究的有力工具。

在压气机流动模拟中,湍流模式起关键作用。目前,工程上最常用的湍流模式是雷诺平均方法RANS(Reynolds-Averaged Navier-Stokes)。然而,压气机内部流动有强旋转特性,且包含叶尖泄漏涡和端壁分离涡等复杂涡系。对于这样复杂的流动,RANS方法在准确性方面存在缺陷。大涡模拟LES(Large Eddy Simulation)和直接数值模拟DNS(Direct Numerical Simulation)是更准确的湍流模拟方法,但计算成本很高,目前主要应用于雷诺数较低的流动。为了兼顾湍流模拟的准确度和计算效率,学者们提出了RANS/LES混合方法。

分离涡模拟DES(Detached Eddy Simulation)是一类RANS/LES混合方法,其基本思想是在附着边界层使用RANS进行模拟,而在大分离区域使用LES进行模拟。通过混合,DES既克服了RANS对大分离流动模拟不准确的缺陷,又克服了LES在附着边界层要求网格过密的缺陷。DES首先由Spalart等[1]提出,至今已有很大发展,主要改进版本包括DDES(Delayed DES)[2]和IDDES(Improved Delayed DES)[3],本文统称为DES类方法。采用DES类方法能以适中的计算成本获得较为准确的湍流流场。目前,已有很多学者将DES类方法用于压气机流动模拟,表1列出了其中一部分工作。

应用DES类方法模拟压气机流动时,需要特别关注数值耗散的影响。Marty等[5]对比了三阶和五阶重构格式的计算效果,发现高阶重构格式能显著提高小尺度相干结构的分辨率,认为这是因为高阶格式的数值耗散更低。高丽敏等[16]总结了DES类方法在叶轮机械流动中的应用,评论道:“DES类方法在叶轮机械中应用时多采用二阶或三阶精度的格式,虽然在恶劣工况下对宏观性能的预测能力提高,但仍然存在盲目性。”He等[13]在使用DES类方法模拟压气机流动时,也强调了数值耗散的影响,认为全场使用高耗散数值格式有利于RANS分支的稳定性,但会损害LES分支的湍流解析能力。因此,其推荐使用混合型格式,即在RANS分支使用高耗散的迎风格式,而在LES分支使用低耗散的中心格式。

表1 DES类方法在压气机中应用总结

然而,由表1可知,在压气机流动DES计算中,高耗散的二阶或三阶迎风格式仍非常流行,应用低耗散数值格式尚未形成共识。因此,本文认为该类计算中数值耗散的作用值得进一步研究。

2 数值方法

2.1 压气机流动求解器

本文用的流动求解程序是自主编写的UNITs,其准确性在跨声速轴流压气机[4]和离心压气机[17]中得到了良好验证。

流动求解采用有限体积法。粘性项离散采用二阶中心格式,时间推进采用双时间步隐式LU-SGS(Lower-upper Symmetric Gauss-Seidel)格式。湍流模式采用基于SSTk-ω湍流模式的IDDES方法[3]。

N-S(Navier-Stokes)方程对流项的离散格式对数值耗散影响最大。在有限体积框架下,对流项的离散过程通常分为两步,一是变量重构,二是通量演化。相应的,对流项离散格式由变量重构格式和近似Riemann求解器这两部分组成。为了对比不同数值格式的作用,本文采用了多种不同对流项离散格式,重构格式包括三阶MUSCL格式[18]、四阶MDCD格式[19]和五阶WENO格式[20];近似Riemann求解器包括标准Roe格式[21]和自适应耗散Roe格式[22]。

四阶MDCD重构和自适应耗散Roe格式组合成自适应耗散格式,与IDDES方法相配合,能够较准确模拟湍流,将在下文详细介绍。

2.2 MDCD重构格式

MDCD(Minimized Dispersion and Controllable Dissipation)是孙振生等[19]提出的先进通量重构格式。MDCD在每个方向使用六个模版点进行变量重构,但只取四阶名义精度,从而获得两个自由参量。这两个参量分别称为色散系数γdisp和耗散系数γdiss,各自独立地控制重构格式的色散和耗散特性。经过优化,MDCD格式可以得到最优色散系数,而耗散系数大小则根据算例特点进行人为调整。

为了捕捉激波,孙振生等[19]将WENO格式[20]的子模版加权思想引入MDCD格式,只是线性权用MDCD色散和耗散系数来表示。从这个角度来看,MDCD可以视为WENO线性权的优化技术。MDCD的变量重构计算式为

(1)

式中W为流动变量,下标i+1/2为网格界面指标,上标L代表界面左侧,上标(m)为第m个子模版重构结果,ωm为第m个子模版的非线性权。式(1)只给出了界面左侧变量重构的计算式,而界面右侧变量重构是完全对称的。

(2)

(3)

(4)

(5)

式中下标i-1,i和i+1等代表网格中心指标。式(1)中非线性权ωm计算为

(6)

式中Cm为线性权,ISm为光滑因子,具体表达式见文献[20]。从式(1～6),MDCD格式和WENO格式完全相同,但其中线性权Cm的取值并不相同。MDCD格式中,线性权的计算式为

(7)

(8)

(9)

(10)

如前所述,γdisp为色散系数,其最优值为0.0463783;γdiss为耗散系数,根据算例特点进行调整,本文取0.012。

2.3 自适应耗散Roe格式

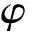
(11)

自适应耗散函数φ表达式为

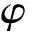
(12)

详细展开后较为复杂,包含多个开关函数,即

A=max{[(lgrid/lturb)/g0-0.5],0}

lgrid=CDESmax(Δx,Δy,Δz)

B0=2Ωmax(Ω,S)/max[(S2+Ω2)/2,10-20]

Ks=max{[(S2+Ω2)/2]1/2,0.1}

CDESε=0.61,CDESω=0.78,Cμ=0.09

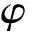
(13)

3 结果与讨论

3.1 各向同性衰减湍流

各向同性衰减湍流DIT(Decaying Isotropic Turbulence)是最简单的湍流流动之一。从系综平均观点看,该流动的平均速度处处为零,只有脉动速度非零,而且湍流统计量在空间均匀分布。湍动能k输运方程的对流项、生成项和扩散项均为零,只余下非定常项和耗散项ε,即

∂k/∂t=-ε

(14)

因此,DIT非常适合于定量测试数值耗散。本文用IDDES方法对DIT进行了模拟,并比较了不同数值格式的效果。值得注意的是,因为DIT不存在壁面,所以全计算域都激活LES分支,而RANS分支并不生效。

本文所用程序主要求解可压缩流动,故选择初始湍流马赫数为0.3的可压缩DIT作为测试算例。计算域是立方体,每条边长度均为2π,网格总数是64×64×64。所有边界都设置为周期性边界。本文计算结果与相应DNS计算结果对比。DNS工作由闫博文[25]完成。

不同数值格式预测的湍动能随时间衰减曲线如图1所示。可以看出,数值耗散从低到高的排列顺序为,(1) 四阶中心格式; (2) MDCD重构+自适应耗散Roe格式; (3) MDCD重构+标准Roe格式; (4) 五阶WENO重构+标准Roe格式; (5) 三阶MUSCL重构+标准Roe格式。定量地来看,在t=1时刻,这五种数值格式预测湍动能分别是DNS结果的89%,84%,69%,50%和32%。即使是耗散最低的中心格式,IDDES预测的湍动能衰减也快于DNS结果,这种现象产生的原因稍后将结合湍流能谱进行分析。

图1 采用不同数值格式模拟DIT,湍动能随时间的衰减曲线(横轴表示时间,用大涡翻转时间无量纲化;纵轴表示湍动能,用初始湍动能无量纲化)

针对t=1时刻的流场,用Fourier变换分析湍动能能谱,并和DNS预测的能谱作比较,结果如图2所示。图中横轴是Fourier波数,用K表示,以便与代表湍动能的k作区分。图2反映出来的数值格式耗散高低排列顺序,与图1一致。在K<5的低波数区域,各种数值格式预测的结果差别不大,而且都与DNS结果吻合较好。然而,在中高波数区域,各数值格式的耗散特性出现明显区别。三阶MUSCL+标准Roe格式的耗散最强,在K>5时其预测的能谱就远低于DNS结果。这意味着,三阶MUSCL+标准Roe格式只能捕捉大尺度相干结构,且会耗散掉绝大多数的小尺度结构。采用高阶重构后,湍流能谱预测结果得到改善,但在中高波数区域的耗散仍然过高。五阶WENO重构+标准Roe格式在K>7区域预测的能谱明显低于DNS结果,而MDCD重构+标准Roe格式在K>9区域预测的能谱明显低于DNS结果。这说明,如果只改变重构格式,而不改变近似Riemann求解器,数值耗散并不能达到LES分支要求的理想值。

分析四阶中心格式预测的湍流能谱。在K<11的区域,中心格式和DNS结果总体吻合较好,略微偏高。在1123的高波数区域,中心格式预测的能谱高于DNS结果,即能谱有翘起的趋势。这种现象称为能量累积(energy accumulation),主要由色散误差和混淆误差引起。如果把四阶中心格式直接用于压气机流动模拟,因为流场非常复杂,能谱高波数区域会出现更加严重的能量累积,引起强烈数值振荡,导致计算发散。所以,对于复杂流动,必须引入适当的数值耗散来抑制高波数区域的能量累积现象。

MDCD重构配合自适应耗散Roe格式的预测结果最好。在中低波数区域,该格式的表现和中心格式类似,基本吻合DNS结果。而且,该格式有适度数值耗散,抑制了高波数区域的能量累积现象。

图2 t=1时刻不同数值格式预测的DIT湍动能能谱

总体来说,DIT模拟结果表明,对于IDDES的LES分支,三阶MUSCL+标准Roe格式的耗散过高,只能分辨大尺度湍流结构,无法完全发挥LES对湍流的解析能力。如果仅采用高阶的重构格式,如WENO或MDCD重构,可以在一定程度上提高数值分辨率,但对中、高波数区域的能量耗散仍然过高。纯中心格式能够比较准确地预测中低波数的湍流能谱,但在最高波数区域会出现能量累积现象,这很容易引起计算发散。MDCD重构配合自适应耗散Roe格式可以抑制高波数的能量累积现象,在全波数范围内都表现出较好的性能。

3.2 跨声速离心压气机

比较两种不同数值格式在跨声速离心压气机上的IDDES计算结果。该跨声速离心压气机由清华大学设计[26],主要参数列入表2。本文模拟了离心叶轮和无叶扩压器内部流动。表2列出的70500 转/分是60%设计转速,也是本文计算采用的转速。

表2 跨声速离心压气机主要参数

本文主要讨论数值格式的影响,为提高计算效率,计算域只包括单个叶片通道及其对应的无叶扩压器,如图3所示。总网格数约340万,叶高方向使用91个网格,其中26个网格位于叶尖间隙内。绝大多数壁面上的第一层网格大小满足y+<1,而且Δx+和Δz+均小于60,这符合IDDES湍流模式的一般要求。时间步长取为转子旋转周期的1/1440,即每个叶片通过周期内包括60个物理时间步。每个物理时间步内进行20次子迭代,计算残差可降低一个数量级。非定常计算收敛的判断依据是:压气机总体性能参数,包括质量流量和静总压比,时间平均值基本不再变化。

进口边界给定总温288 K,总压101 kPa,速度取为轴向。出口边界给定均匀分布的静压,取值为145 kPa～205 kPa。不同的出口静压值对应压气机不同的工作点。环向取旋转周期性边界条件。所有固体壁面都给定绝热无滑移条件。

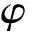
图3 跨声速离心压气机计算域和网格

作为一种RANS/LES混合方法,IDDES通过混合函数fd来控制两个分支的生效区域。采用自适应耗散格式计算时,该混合函数fd的分布如图4所示。在靠近壁面的区域,fd趋近于1,RANS分支生效;在远离壁面的主流区域,fd趋近于0,LES分支生效。可以看出,fd分布基本符合IDDES方法的设计预期。但同时,图4也显示出其模拟压气机流动的一个缺陷,即叶尖间隙区域内fd趋近于1。这说明叶尖间隙流动全部采用了RANS模式计算,这很可能会造成叶尖泄漏涡模拟不准。目前有学者[13]正尝试改进DES类方法,以解决该问题。

图4 自适应耗散格式计算时,RANS/LES混合函数fd分布

图5 数值格式的自适应耗散函数分布

CFD预测的压气机性能曲线和实验测量结果对比如图6所示,图中横轴是质量流量,纵轴是静总压比。可以看出,两种格式的模拟结果均低估了压比,而自适应耗散格式相比于三阶迎风格式,结果与实验吻合得更好。在流量0.33 kg/s附近,两种数值格式结果的差异最大,自适应耗散格式预测压比与实验结果误差为1%,三阶迎风格式与实验结果误差为7.3%;在流量0.29 kg/s附近,两种数值格式差异最小,自适应耗散格式预测压比与实验结果误差为4.6%,三阶迎风格式与实验结果误差为6.8%。在大多数工作点,自适应耗散格式预测压比与实验结果的相对误差约为4%～5%;三阶迎风格式预测的压比与实验结果的相对误差约为6%～7%。

在DIT模拟中,本文发现自适应耗散格式可以更准确地预测高波数能谱,这说明其对湍流小尺度结构的分辨率更高。在跨声速离心压气机计算中,自适应耗散格式同样在小尺度结构分辨率方面表现出了优势。图7用熵云图展示了两种数值格式预测的叶片尾迹流动,图8则用涡识别判据λ2等值面展示了叶片通道内的三维涡结构。图7和图8都反映出自适应耗散格式比三阶迎风格式捕捉了更多的小尺度相干结构。在图7中,自适应耗散格式可以捕捉到叶片尾迹的非定常脱落涡,而三阶迎风格式预测的尾迹涡几乎呈现定常状态。在图8中,自适应耗散格式可以捕捉到丰富的小尺度涡结构,而三阶迎风格式只能捕捉大尺度涡结构。