Statistical higher-order multi-scale method for nonlinear thermo-mechanical simulation of composite structures with periodically random configurations

DONG Hao, CUI Jun-zhi

(1.School of Mathematics and Statistics,Xidian University,Xi’an 710071,China;2.Academy of Mathematics and Systems Science,Chinese Academy of Sciences,Beijing 100190,China)

Abstract： Stochastic multi-scale modeling and simulation for nonlinear thermo-mechanical problems of composite structures with complicated random microstructures remains a challenging issue.In this paper,we develop a novel statistical higher-order multi-scale (SHOMS) method for nonlinear thermo-mechanical simulation of composite structures with periodically random configurations,which is designed to overcome limitations of prohibitive computation involving the macro-scale and micro-scale.By virtue of statistical multi-scale asymptotic analysis and Taylor series method,the SHOMS computational model is rigorously derived for accurately analyzing nonlinear thermo-mechanical responses of random composite structures both in the macro-scale and micro-scale.Moreover,the local error analysis of SHOMS solutions in the point-wise sense clearly illustrates the crucial indispensability of establishing the higher-order asymptotic corrected terms in SHOMS computational model for keeping the conservation of local energy and momentum.Then,the corresponding space-time multi-scale numerical algorithm with off-line and on-line stages is designed to efficiently simulate nonlinear thermo-mechanical behaviors of random composite structures.Finally,extensive numerical experiments are presented to gauge the efficiency and accuracy of the proposed SHOMS approach.

Key words： random composite structures;nonlinear thermo-mechanical simulation;SHOMS computational model;space-time multi-scale algorithm;local error analysis

1 Introduction

Random composite materials have been extensively applied in a variety of engineering sectors,such as aviation,aerospace,civil construction and smart structures,etc.By randomly distributing high-performance fibrous or particulate materials into ordinary matrix material,these synthetic composite materials exhibit high temperature resistance,high fatigue resistance and high fracture resistance,etc[1,2].Especially in aviation and aerospace industries,engineering structures often served under extreme heat environment while the thermal and mechanical properties of component materials exhibit obviously temperature-dependent feature.These complicated nonlinear behaviors and randomly geometric heterogeneities of the composite structures raise a grand challenge to effective numerical simulation[3].

To the best of our knowledge,traditional numerical methods including the finite element method(FEM)[4],boundary element method[5]and meshless method[6]have been adopted to the simulation of nonlinear thermo-mechanical problems.Moreover,Abdoun et al.[7]used homotopy and asymptotic numerical method to simulate and analyze the thermal buckling and vibration of laminated composite plates with temperature-dependent properties.Najibi et al.[8]employed higher-order graded finite element method to conduct thermal stress analysis for a hollow FGM cylinder with nonlinear temperature-dependent material properties.In Ref.[9],the state space method and transfer-matrix method are adopted to obtain the displacements and stresses for the thick beams with temperature-dependent material properties under thermo-mechanical loads.However,the direct numerical simulation for composite materials needs a tremendous amount of computational resources or even ineffective to capture their microscopic behaviors due to highly heterogeneous components.

To accomplish effective modeling and efficient simulation for inhomogeneous materials,scientists and engineers presented a variety of multi-scale methods,such as asymptotic homogenization method(AHM)[10],multi-scale finite element method (MsFEM)[11],heterogeneous multi-scale method(HMM)[12],variational multi-scale method(VMS)[13],multi-scale eigenelement method (MEM)[14],localized orthogonal decomposition method (LOD)[15]and finite volume based asymptotic homogenization theory(FVBAHT)[16],etc.However,numerical computation and theoretical analysis find that most of above-mentioned multi-scale methods are lower-order(first-order) multi-scale method in essence[17,18],which can only capture macroscopic and inadequate microscopic information of heterogeneous materials,especially for high-contrast composite materials.To improve inadequate numerical accuracy of classical lower-order multi-scale approaches,Cui and his research team systematically developed a class of higher-order (second-order) multi-scale methods,whose numerical accuracy is significantly improved for simulating authentic composite materials.Hence,these higher-order multi-scale approaches are extensively used in multi-physics coupling problem,stochastic problem,structural mechanics problem and nonlinear multi-scale problem of heterogeneous materials,etc[19-23].The reviews of above-mentioned multi-scale approaches show that these methods have a strong potential to encourage important advances in modeling and simulating a certain range of composites’ behaviors.However,they still need to be improved for random composite materials with complex non-deterministic microstructure.The uncertainties in the microstructure prominently affect the mechanical properties of the composite materials.Some stochastic multi-scale computational schemes have been established in recent years based on perturbation-based stochastic finite element method[24-26],spectral stochastic finite element method[27-30]and stochastic collocation method[31,32]for specific problems.Especially in Ref.[30],the spectral stochastic FEM is applied to analysis multiple-random field RC structures.Furthermore,combining with Monte Carlo method,the higher-order multi-scale methods proposed by Cui and his research team have been applied to simulate a wide range of physical behaviors of random composite materials[19,20,23,33,34].However,there are few works about multi-scale thermo-mechanical simulation of random composite materials with temperature-dependent properties.Hence,it is of great theoretical and engineering values to develop effective multi-scale approaches for nonlinear thermo-mechanical simulation of random composite materials.

2 Statistical higher-order multi-scale computational model

2.1 Microscopic representation of random composite

The primary challenge for solving random multi-scale problems pertains to their auxiliary cell problems defined on the entire spaceΝ(Ν=2,3).To tackle this challenge,by using “periodization” and “cutoff” techniques in previous studies[19,20,23],the unit cell problems defined on macroscopic composite structureΩare approximated by transforming them into unit cell problems on a finite domain so-called microscopic unit cellYs(s=1,2,3,…denotes the index of random samples) with spatial sizeεand infinite random sampling,see Fig.1 for a schematic explanation,which corresponds to random sampleωsobeying a given probability distribution modelP(ω) with random variableω.

In this study,the investigated composite structures are comprised of matrix and randomly distributed reinforced (or soften) particles or fibers,or porous media[35,36],as shown in Fig.2.Based on computer representation idea and its improved algorithm devised by Li et al.[37,38],we employ open-source Freefem++ software to establish the detailed computer representation algorithm for generating microscopic configurations of random composite materials as follows.

Fig.1 Composite structures with periodically random configurations

Fig.2 Random composite structures with different microscopic configurations

(S1) Regarding random particulate and fibrous materials in Fig.2,the probability distribution model is first employed to generate the random geometric parameters (x1,x2,a,b,θ1) or (x1,x2,x3,a,b,c,θ1,θ2,θ3) for 2D or 3D randomly distributed configurations.

(S2) Then,judge whether the newly generated configuration is located inside RVE and whether the newly generated configuration intersects with other previously generated configurations.We use whether the distance between the central points of the previously generated configurations and newly generated configuration is greater than the sum of the radii of both configurations as criterion.Additionally,to enhance the packing ratio of microscopic inclusions,we use the following rule as revised discriminate criterion:There exist such intersection points on previous configuration those connect the centers of previous ones with the points on the surfaces of new generated configuration.

(S3) When generating a sufficient amount of microscopic configurations,mesh generation algorithm based on Delaunay Refinement method (Freefem++ command:“buildmesh” or “tetg” for 2D or 3D geometrical configurations,respectively) is adopted to create the microscopic configurations of the investigated random composites[39].

For geometric parameters(x1,x2,a,b,θ1)in 2D case,x1andx2represent the central coordinates of the elliptical inclusion for thex-axis andy-axis.aandbdenote the lengths of the long half-axis and short half-axis of the elliptical inclusion andθ1represents the intersection angle between the long half-axis of the elliptical inclusion and thex-axis.For geometric parameters (x1,x2,x3,a,b,c,θ1,θ2,θ3) in 3D case,x1,x2andx3are the central coordinates of the ellipsoidal inclusion for thex-axis,y-axis andz-axis.a,bandcdenote the lengths of the long half-axis,middle half-axis and short half-axis of the ellipsoidal inclusion.θ1,θ2andθ3are the three Euler angles of the ellipsoidal inclusion,respectively.Moreover,by increasing the ratio of their long half-axis to short half-axis,the elliptical or ellipsoidal particles can be changed as fibrous inclusions.To sum up,the above methodologies accomplish the effective generation of finite element mesh for random composites.

2.2 Stochastic multi-scale nonlinear thermo-mechanical problems

Based on the classical thermo-mechanical model[3],the stochastic governing equations for describing the nonlinear thermo-mechanical problems of composite structures with periodically random configurations are set up,whose material parameters all possess the temperature-dependent properties.

(1)

where notationΩrepresents a bounded convex domain inΝ(Ν=2,3) with a boundary ∂ΩT∪∂Ωu∪∂Ωq∪∂Ωσ.In the micro-scale,the domainΩcan be defined by a statistical periodic layout of microscopic unit cellYscorresponding to random sampleωs.The characteristic size of microscopic cellYsis characterized by a parameterε.TheTε(x,t,ω) andε(x,Tε,ω) is the mass density;cε(x,Tε,ω) is specificthe second order thermal modulus tensor.Furthermore,we assume that all material parameters satisfy Lipschitz continuous condition with respect to temperature variableTεand are statistical periodicis the prescribed temperature on the boundaryis the prescribed heat flux normal to the boundary ∂Ωqwith the normal vectorni,andis the prescribed traction on the boundary ∂Ωσwith the normal vectoris the initial temperature;The internal heat source and body forces are represented byh(x,t) andfi(x,t),respectively.To begin with,let us sety=x/εas microscopic coordinates of statistical periodic unit cellYs=[0,1]N.With this notation,we have the chain rule for the spatial scales as follows.

(2)

which will be extensively used in the sequel.

2.3 Statistical higher-order multi-scale computational model

(3)

By aid of the above Taylor’s formula(4) and multi-index notation(5),the material parameters depending on temperatureTεthus can be expanded as follows[22]

kij(y,T0+εT1+ε2T2+O(ε3),ω)=

kij(y,T0,ω)+D(0,1,0)kij(y,T0,ω)[εT1+ε2T2+

O(ε3)]2+O([εT1+ε2T2+O(ε3)]3)=

kij(y,T0,ω)+εT1D(0,1,0)kij+

(4)

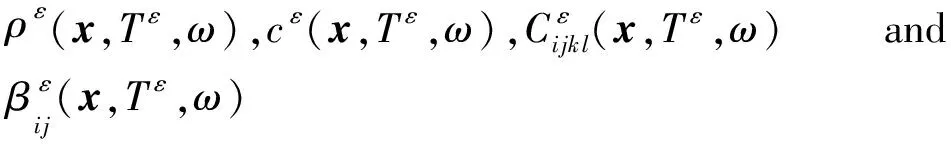
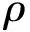
cε(x,Tε,ω)=c(0)+εc(1)+ε2c(2)+O(ε3)

(5)

By substituting equations (3)-(5) into the multi-scale coupling problem (1) and utilizing the chain rule (2),we can expand the derivatives and match terms with the same order of the small parameterε.Then,according to the similar higher-order multi-scale analysis in Ref.[22],O(ε-2)-order equations allow us to reasonably obtain the following results

(6)

And then,according to O(ε-1)-order equations,the first-order correctorsT1andui1can be individually constructed as follows

(7)

(8)

(9)

(10)

Subsequently,we perform a volume integral on both sides ofO(ε0)-order equations on microscopic unit cellYsand apply the Gauss theorem onO(ε-1)-order equations.By further applying the Kolmogorov’s strong law of large numbers,the macroscopic homogenized equations associated with multi-scale problem (1) are derived as follows

(11)

where the macroscopic homogenized material parameters in (11) are defined as follows

(12)

The effective material coefficients in (12) are evaluated using the following formulas,which correspond to microscopic unit cellYswith random sampleωs

(13)

After that,by substituting (6,7) intoO(ε0)-order equations,and then subtractingO(ε0)-order equations from (11),the concrete expressions forT2andui2can be defined as follows

(14)

(15)

(16)

(17)

(18)

(19)

(20)

(21)

(22)

(23)

(24)

Summing up,the macro-micro coupled SHOMS asymptotic solutions of the multi-scale nonlinear dynamic thermo-mechanical problem (1) are established.

2.4 Local error analysis of statistical multi-scale solutions in point-wise sense

To begin with,two kinds of the multi-scale approximate solutions of stochastic multi-scale problem (1) are defined as follows

(25)

Next,we introduce the following residual functions for thelocal numerical accuracy analysis.

(26)

(27)

(28)

Noting the residual equations (27),it can be concluded that the residual error of SLOMS solutions is of order-O (1) in the point-wise sense,primarily due to the presence of terms F0and S0i.Comparing with the residual equations (28),the residual error of SHOMS solutions is of order-O(ε) in the point-wise sense.This implies that the SHOMS solutions can satisfy the local energy conservation of thermal equation and local momentum conservation of mechanical equations of the original stochastic multi-scale equations (1) in the point-wise sense,which can still provide the required accuracy for engineering computation and accurately capture the microscopic oscillating behaviors exhibited by random composite materials.

3 Space-time multi-scale numerical algorithm

In this section,a new space-time multi-scale numerical algorithm with off-line and on-line stages is presented for the stochastic nonlinear governing equations (1) based on the FEM in spatial region and the finite difference method (FDM) in time direction.The detailed algorithm is listed as follows.

3.1 Off-line computation for microscopic cell problems

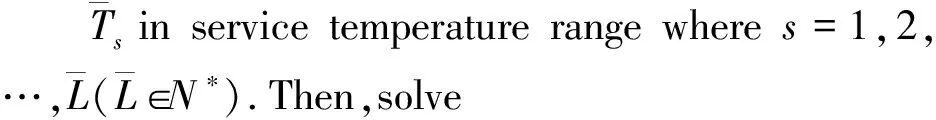
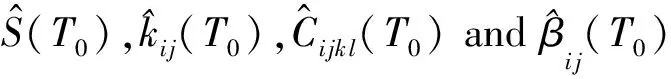
3.2 On-line computation for macroscopic homogenized problem and statistical higher-order multi-scale solutions

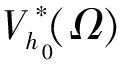
(3) It should be highlighted that,decoupled thermal equation is a nonlinear system which can not be computed directly.Herein,the direct iterative method is employed for simulating the nonlinear system.

(4) For arbitrary point (x,t)∈Ω×(0,T*),to apply the interpolation method to acquire the corresponding values of first-order auxiliary cell functions,second-order auxiliary cell functions and homogenized solutions.The spatial derivatives in formulas (7,14) are evaluated by the average technique on relative elements[40],and the temporal derivatives in formula (14) are evaluated by using the difference scheme at every time steps.Then,the temperature fieldT(2ε)(x,t,ω) and displacement fieldu(2ε)(x,t,ω) are computed.Moreover,we can further employ the higher-order interpolation method and post-processing technique in[41,42]to obtain the high-accuracy SHOMS solutions.

4 Numerical experiments

In this section,the numerical accuracy andefficiency of the proposed SHOMS method are demonstrated by several numerical examples.Since obtaining the exact solutions for the multi-scale nonlinear problem (1) is extremely difficult or even impossible,direct numerical simulation (DNS) solutions on the fine grid for the multi-scale nonlinear problem (1) are taken as the reference solutions denoted asTDNS(x,t) anduDNS(x,t).In the following numerical experiments,some error notations are introduced,Terr0,Terr1 and Terr2 represent theL2norm errors,TErr0,TErr1 and TErr2 represent theH1semi-norm errors for macroscopic homogenized solution,SLOMS solutions and SHOMS solutions of temperature field respectively;Uerr0,Uerr1 and Uerr2 represent theL2norm errors,UErr0,UErr1 and UErr2 represent theH1semi-norm errors for macroscopic homogenized solution,SLOMS solutions and SHOMS solutions of displacement field respectively.

Example 1Validation of the SHOMS me-thod for nonlinear thermo-mechanical simulation in periodic composite structure.

A 2D composite structure with periodically microscopic configurations is investigated here,whose macrostructureΩand unit cellY^sare shown in Fig.3,whereΩ=(x1,x2)=[0,1]×[0,1] cm2and periodic unit cell sizeε=1/5.This 2D composite structure is clamped on its four boundaries,and the temperature at the boundaries is kept at 373.15 K.In addition,the internal heat source and body forces are set ash=5000 J/(cm2·s) and (f1,f2)=(-2000,-2000) N/cm2.And,the material parameters of 2D composite structure are demonstrated in Table 1.

Fig.3 Illustration of investigated 2D composite structure Implementing the SHOMS method to multi-scale nonlinear coupling equations (1) in time interval t∈[0,1] s with temporal step Δt=0.002 s,we define service temperature range [273.15,873.15] K of investigated composite structure and 60 representative macroscopic parameters in temperature range.In this example,the total auxiliary cell problems need to be solved off-line 4380 times,in which the 13 first-order cell functions and 60 second-order cell functions are solved on 60 macroscopic temperature interpolation points.The information of FEM meshes is listed in Tab.2.After off-line computation for microscopic cell problems and on-line computation for macroscopic homogenized problems and higher-order multi-scale solutions,we depict the computational results in Fig.4～Fig.8.

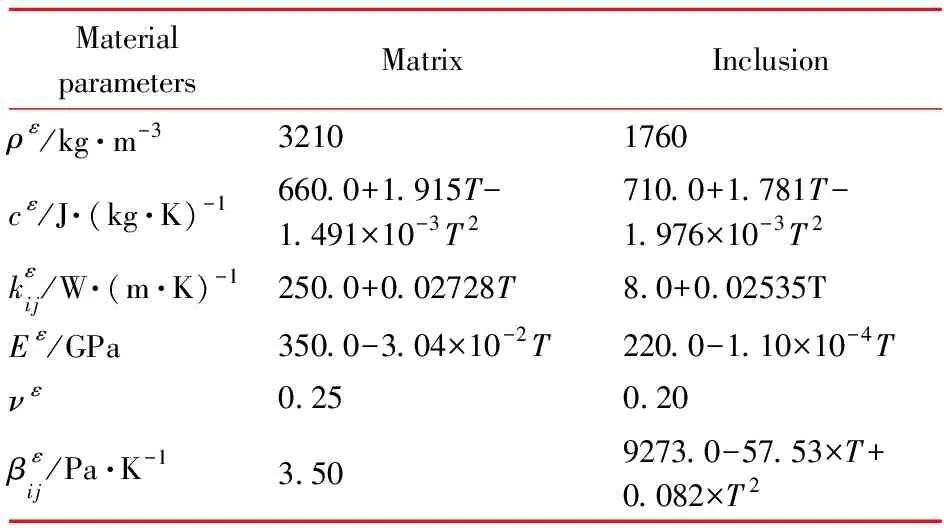
Tab.1 Material parameters of 2D composite structure

Tab.2 Summary of computational cost

Fig.4 Numerical results of temperature field at t=0.2 s

Fig.5 Numerical results of displacement field at t=0.2 s

Fig.6 Numerical results of temperature field at t=1.0 s

Fig.7 Numerical results of displacement field at t=1.0 s

Fig.8 Evolutive relative errors of temperature and displacement fields According to the computational resource cost in Tab.2,the SHOMS method can greatly economize computer memory without losing precision.Actually,both the SHOMS method and direct numerical simulation are performed on a HP desktop workstation equipped with an Intel(R) Core(TM) i7-8750H processor (2.20 GHz) and 16.0 GB of internal memory.As illustrated in Fig.4～Fig.7,we can conclude that the higher-order multi-scale solutions can accurately capture the microscopic oscillatory behaviors and preferably approximate the exact solutions of the investigated 2D composite structure compared with macroscopic homogenized solutions and lower-order multi-scale solutions,especially for temperature field.From the evolutive relative errors in Fig.8,it can clearly demonstrate that the two-stages space-time multi-scale numerical algorithm is accurate and stable in the long-time numerical simulation.Furthermore,it is worth emphasizing that the presented SHOMS approach remains effective even for a relatively small parameter ε,namely existing a great number of microscopic unit cells in inhomogeneous structures.At this time,the high-resolution DNS simulation can not guarantee the convergence for the investigated large-scale problems.This obvious advantage of the SHOMS approach is of great application values for engineering computation.

Example 2Application of the SHOMS method for equivalent material parameters computation of random composite structure.

In this example,two kinds of composite materials with matrix Ti-6Al-4V and random inclusion ZrO2,and matrix SiC and random inclusion C are investigated by the SHOMS method,as exhibited in Fig.9.The detailed material parameters for the investigated composite materials are presented in the following Tab.3 and Tab.4.

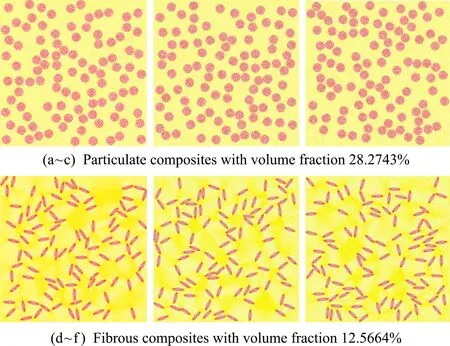
Fig.9 Several random RVEs of the composites employed for predicting equivalent material parameters

Tab.3 Material property parameters of Ti-6Al-4V/ZrO2 composite

Tab.4 Material property parameters of SiC/C composite

By using the SHOMS method,the equivalent material parameters at macro-scale are obtained by the mean value of 50 randomly microscopic samples.The corresponding results are depicted in Fig.10.According to the numerical results in Fig.10,we can conclude that the predictive values of Ti-6Al-4V/ZrO2composite and SiC/C composite fall between lower and upper bounds of Voigt-Reuss method,Hashin-Shtrikman method and also approximate the predicted values of Hobbs method.Hence,the proposed SHOMS can be employed to predict the temperature-dependent equivalent material properties of Ti-6Al-4V/ZrO2composite and SiC/C composite.

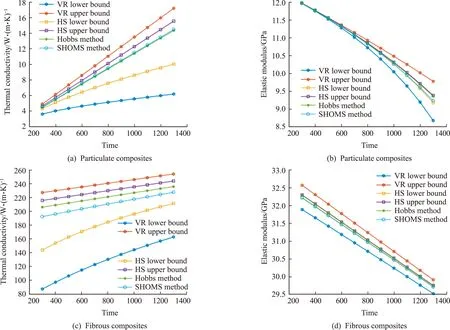
Fig.10 A comparison of the predictive results of equivalent material parameters

Example 3Application of the SHOMS method fornonlinear thermo-mechanical simulation in random composite structure.

This example mainly study the nonlinear thermo-mechanical simulation of 2D composite structure with randomly microscopic configurations,as depicted in Fig.11.In addition,the setting of initial-boundary conditions,heat source,body forces and material parameters in this example is the same as those of Example 1.

Fig.11 Illustration of investigated 2D composite structure Applying thenovel SHOMS method to multi-scale nonlinear coupling equations (1) within time interval t∈[0,1] s with temporal step Δt=0.002 s,we establish the service temperature range of the investigated composite structure as [273.15,873.15] K.In this service temperature range,we distribute 60 representative macroscopic parameters detailed information of FEM meshes is listed in Tab.5.After off-line computation for microscopic cell problems and on-line computation for macroscopic homogenized problems and higher-order multi-scale solutions,we present the computational results in Fig.12～Fig.16.

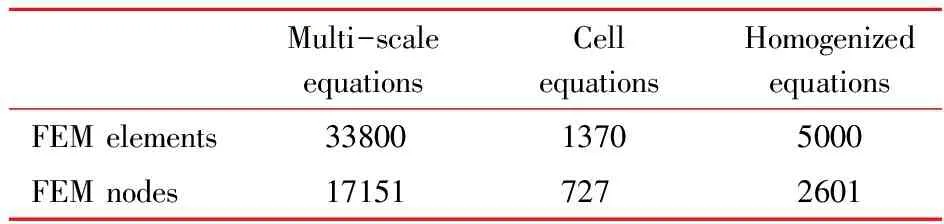
Tab.5 Summary of computational cost

Fig.12 Numerical results of temperature field at t=0.2 s

Fig.13 Numerical results of displacement field at t=0.2 s

Fig.14 Numerical results of temperature field at t=1.0 s

Fig.15 Numerical results of displacement field at t=1.0 s As indicated Tab.5,thenovel SHOMS method can significantly reduce computer memory without losing precision.Moreover,the numerical results in Fig.12～Fig.15 reveal that the higher-order multi-scale solutions can accurately capture the microscopic oscillatory behaviors and provide preferable approximations to the exact solutions compared with macroscopic homogenized solutions

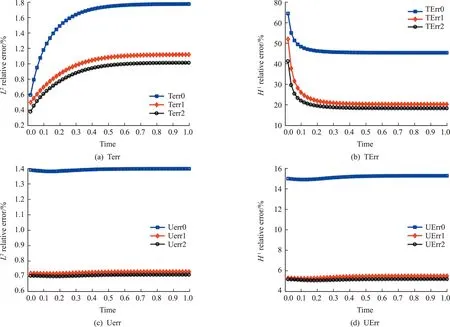
Fig.16 Evolutive relative errors of temperature and displacement fields and lower-order multi-scale solutions,especially for temperature field.The evolutive relative errors shown in Fig.16 clearly demonstrate the accuracy and stability of the two-stages space-time multi-scale numerical algorithm in the long-time numerical simulation.Furthermore,it is important to highlight that the SHOMS approach remains effective even for a relatively small parameter ε,which corresponds to a large number of microscopic unit cells in heterogeneous structures.In contrast,the high-resolution DNS simulation fails to converge for the investigated large-scale problems.This prominent computational advantage is of significant practical value of the SHOMS approach in engineering computations.

5 Conclusions and outlook

In the present work,a novel statistical higher-order multi-scale method is developed for effectively simulating nonlinear thermo-mechanical problems of composite structures with periodically random configurations and temperature-dependent properties,which serve under extreme heat environment.The main contributions of this work are threefold:First,the statistical multi-scale formulations with the higher-order correction terms are established for composite structures with periodically random configurations.Second,the local error estimations for the statistical multi-scale solutions of nonlinear thermo-mechanical systems are derived in detail.Third,a space-time numerical algorithm with off-line and on-line stages is designed to overcome the prohibitive computation of direct numerical simulation.Furthermore,numerical results demonstrate that the presented SHOMS approach can effectively simulate nonlinear thermo-mechanical coupling behaviors with less computational cost and accurately capture the microscopic oscillatory information caused by randomly heterogeneous configurations.Besides,the proposed SHOMS approach can accurately predict the equivalent material parameters of random composite structures compared with the predictive results of some theoretical models,which illustrate that high temperature field has a remarkable effect on macroscopic thermo-mechanical properties.

In the future,the SHOMS method will be extended to more complex nonlinear problems including thermal convection and radiation effects under extreme thermal environment.Additionally,machine learning approaches and parallel algorithm will be introduced in the off-line stage of SHOMS framework,in order to avoid repetitive statistical computation and improve computational efficiency.