绳驱桁架结构伸展臂的主动振动控制

蔡志勤, 曹彬彬, 彭海军,2

(1.大连理工大学 工程力学系,大连 116024;2.大连理工大学 工业装备结构分析优化与CAE软件全国重点实验室,大连 116024)

1 引 言

近年来,由于航天任务的逐渐复杂化,航天器结构逐渐向大型化和柔性化方向发展。空间可展桁架结构伸展臂具有展开刚度高和展收比高等优点[1],经常用作航天器工作平台的支撑结构。但是在空间环境中,伸展臂会受到空间温度变化和太阳光压等外界因素的影响,另外在进行位姿变化和太空作业等主动工作过程时,都很容易导致伸展臂发生振动[2],在阻尼较低的空间环境中,结构振动能量衰减速度很慢,如果不加以控制,可能会对整个系统造成不利影响。

针对伸展臂的结构振动问题,学者们提出的振动抑制方案主要分为被动控制和主动控制。被动控制主要通过提升结构自身的阻尼来加速振动衰减。Moshrefi-Torbati等[3]用遗传算法优化设计出一种具有隔振特点的伸展臂。但是遗传算法在计算最优构型过程中计算成本很高,Wei等[4]提出混合并行遗传算法,显著降低计算成本的同时进一步提高求解质量。但是被动控制无法在复杂多变的环境干扰下实现灵活的控制,而且振动抑制效率偏低。

主动控制是利用传感器得到的实时反馈信号对被控对象主动施加控制力的控制方法,可以实现高效率的、具有针对性的振动抑制。随着智能材料的不断涌出,由具有良好的形状固定和回复性能的形状记忆合金和碳纤维复合材料制作出的复合材料铰链,可以减轻展开过程中带来的振动[5]。Lan等[6]制备出环氧基形状记忆聚合物以及复合材料,并基于此制备出复合材料铰链,此铰链能在回复率接近100%的前提下有效降低结构的振动效应。压电陶瓷材料由于具有良好的承载能力也用于振动控制,可以将压电陶瓷贴片粘贴在伸展臂上充当传感器来检测结构的动态响应,也可以将压电陶瓷材料制作压电杆集成到伸展臂中充当作动器来实现主动振动控制[7-9]。目前,压电作动器广泛用于控制空间结构的振动,但其在大型结构中的放置和布线都比较复杂。

为了对上述情况进行改进,Lu等[10]通过PSO算法选择出18根伸展臂上用来减小铰链间隙的拉绳充当作动器,和压电材料充当作动器相比,这个方法不会增加结构的复杂度。但是由于充当作动器的拉绳并不是串联在一起的,所以需要在结构的18个铰链处安装用来收放拉绳的电机,这种设计会增加伸展臂的质量。而且这些拉绳均在伸展臂每一段中的连接铰和连接铰之间,这也会限制优化算法的搜索空间。

本文采用拉绳作为作动器,但并非利用的用来减小铰链间隙的张力绳。这样就解除了只能在连接铰和连接铰之间连接的限制,而且充当作动器的拉绳还可以串联在一起,进而驱动作动绳的电机在数量上可以减少的同时,也可以将电机的安装位置转移到基座上,进一步降低结构的复杂度。本文伸展臂的每一面分别有一个作动绳,通过遗传算法寻找出每一个作动绳在当前面的铰链中的最佳串联顺序。在数值仿真中,通过模型预测控制方法对伸展臂进行振动控制。

2 系统动力学模型

本文研究三棱柱式桁架结构伸展臂[11],每段由竖梁、横梁、张力绳以及驱动铰和连接铰组成,如图1所示。在大多数空间结构中,为了避免结构的低频振动,都会安装张力绳来提高结构的刚度。当这些结构发生变形时,结构中的拉绳会随着变形产生拉力。但是从图1可以看出,张力绳均是在连接铰之间,而且每段之间相互独立。如果将张力绳充当作动器,除了无法利用驱动铰外,也需要根据优化结果在连接铰安装电机,影响伸展的质量以及稳定性。

对于本文研究的伸展臂,产生极大幅度的非线性振动需要相当极端的条件,所以大部分振动仍处于线性范围内。换言之,线性振动的主动控制更具有实际意义。基于这些因素,在进行振动控制分析时,将伸展臂视为线性系统。值得注意的是,虽然可以在线弹性范围内考虑结构振动,但这种振动仍然会严重影响伸展臂的正常工作。因此,发展一种合适的振动控制方法是必要的。

图1 伸展臂

基于有限元法建立的结构动力学方程为

(1)

式中M,C和K分别为整体质量阵、阻尼阵和刚度阵。Fu为作动器的控制力,H为作动器分布矩阵,Fe为干扰外力向量。

模态分析是分析结构动力性能最成熟的线性分析技术,主要是将结构系统从物理坐标转换为模态坐标,使得方程解耦,从建立的有限元模型中可以获得结构的固有频率和模态信息。模型的前p阶模态振型和模态坐标可以表示为

x=Φq

(2)

式中Φ为前p阶振型组成的矩阵,q为对应的模态坐标,将式(2)代入式(1),并且统一左乘ΦT,则动力学方程可以写为

(3)

再将模态空间的动力学方程(3)改写为状态空间的形式为

(4)

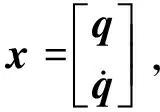
(5,6)

3 作动器位置优化及控制率设计

首先通过遗传算法计算出三根作动绳上铰链的最优串联顺序。以此为基础,再通过模型预测控制方法对三根作动绳上的拉力进行控制,抑制伸展臂的振动。

3.1 作动器位置优化

基于系统可控性的优化准则和遗传算法,对作动绳上铰链的串联顺序进行优化分析。根据文献[10,12],系统的可控性Gramian矩阵可以表示为

(7)

且满足Lyapunov方程

AWc+WcAT+BBT=0

(8)

文献[13]定义了优化准则

(9)

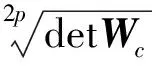
本文采用遗传算法寻找出每一个作动器串联的铰链数量以及最优串联顺序。从图2可以看出,伸展臂每一面有18个铰链,按图2所示的顺序依次对伸展臂的所有面的铰链进行编号。作动器1所连铰链的编号范围为1～18,作动器2所连铰链的编号范围为19～36,作动器3所连铰链的编号范围为37～54。定义一个向量v1×54,其中1～18元素表示作动器1的连接顺序,元素取值范围(1,18),19～36元素表示作动器2的连接顺序,元素取值范围为(19,36),37～54元素表示作动器3的连接顺序,元素取值范围为(37～54)。由于作动器无法在同一个铰链连续串联两次,所以在算法迭代过程中每次对v中连续相同的元素进行合并。

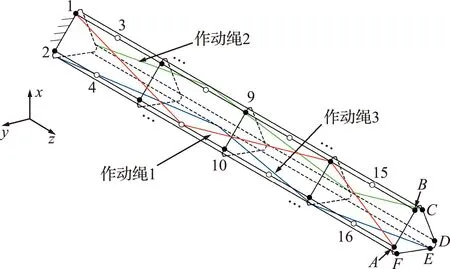
图2 作动绳上铰链串联

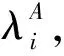
在遗传算法中考虑上述条件作为约束条件。综上所述,该优化问题的表达式为

(10)

3.2 控制率的设计

一般来说,桁架结构伸展臂,在展开过程中张力绳处于松弛状态,以确保结构的顺利展开。在展开完成后,对拉绳进行张紧,以提高结构的刚度,减少低频振动的发生。对于本文的伸展臂,结构中布置的作动绳是影响结构振动的主要因素,在控制律的设计中必须考虑拉绳的特点,即单边约束和饱和特性。综上所述,本文做出以下假设[10]。

(1) 作动绳的控制力大小范围,u∈[0,umax]。

(2) 在施加主动控制力之前,所有拉绳的张力均为零。

(3) 振动引起的变形比结构本身的尺寸小很多。

在模型预测控制器的设计过程中,通常会根据受控对象的特点建立一个模型,用于预测受控对象未来的变化趋势,并基于这个模型来制定相应的控制策略[15]。同时,模型预测控制器具备反馈校正的能力,能够确保控制器在不同工况下都能表现出良好的稳定性和鲁棒性。模型预测控制方法还能够方便地引入对控制输入的约束,以满足系统的操作限制。所以,本文主要采用模型预测控制方法调节3个作动绳的控制力。

首先,对系统状态方程(4)进行离散化,可写为

x(k+1)=As(k)x(k)+Bs(k)u(k)

y(k)=Cs(k)x(k)

(11)

式中 采样周期为ts,k为第k个采样周期,As,Bs和Cs分别为由连续状态方程转换为离散状态方程的系数矩阵。

为了求解预测控制问题,在状态空间表达式中必须计算被控变量的预测值。其可由当前状态的最佳估计值以及假设的未来输入计算。假设当前时刻为第k个采样周期,根据式(9)可以预测未来l个时间步的状态值为

(12)

式中 式(12)的项分别为

(13,14)

(15)

(16)

(17)

在满足约束条件下,模型预测控制器找到控制输入的最优序列,使得目标函数J最小化,即

(18)

式中umax为由3个作动绳拉力最大值组成的列向量,J为系统性能指标,可以表示为

(19)

式中rk为期望轨迹,在本文则为所有节点的位移,所以rk=0;Q和R为控制权矩阵。结合式(12),目标函数J可以写为

(20)

模型预测控制问题转化为最优化问题中的二次规划优化问题,利用二次规划方法求解可以得到最优解。

4 数值仿真

以一个由4个单元组成的伸展臂为例进行数值仿真。研究对象如图2所示,假设该伸展臂的左端固定,右端自由,考虑到伸展臂在工作中的负载情况,在有限元建模过程中,伸展臂右端A,B,C,D,E和F节点上分别添加质量为20kg的质量块。表1列举了该结构的几何尺寸和材料特性。采用ANSYS对结构进行建模,伸展臂中所有长梁均划分为10个空间梁单元(BEAM188),模型的前6阶模态频率列入表2。

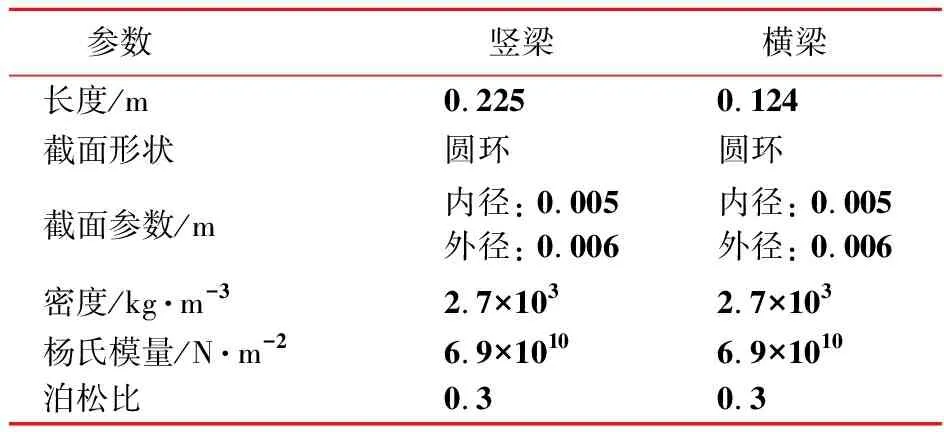
表1 结构几何尺寸及材料参数

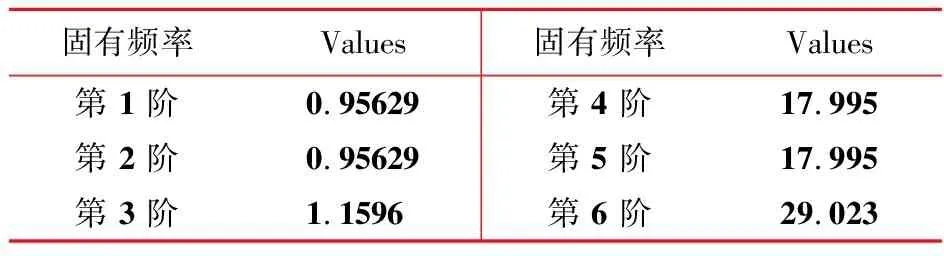
表2 伸展臂前6阶固有频率

基于上述信息,对作动绳在铰链上的串联顺序进行优化分析。遗传算法中种群染色体数为1000,交叉和变异概率分别为0.8和0.1。最大迭代次数设为1000,算法迭代到300步,最大适应度值达到稳定。最终优化结果列入表3,连接效果如图3所示。

表3 作动绳上铰链串联顺序优化结果

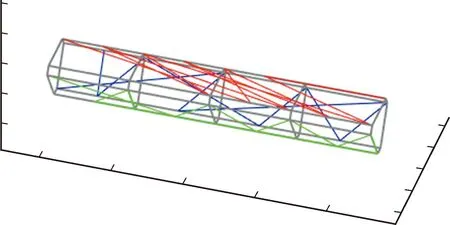
图3 作动绳上铰链的最佳串联顺序

在伸展臂右端节点A(图2)上施加100N沿y轴的力(Fy),以产生伸展臂的初始变形。t=0时,移除外力作用。模型预测控制器中采样周期为0.1 s,预测步长为100,控制步长为5,对模型的前4阶模态进行控制。

在umax=1时,进行仿真计算。图4(a)表示在伸展臂有无控制的情况下,节点A在y方向位移的对比结果。这些结果表明,在施加控制力后,由振动引起的节点A的位移在10 s内控制在1×10-3m左右。与没有主动控制的曲线相比,振动衰减时间大大缩短。在初始变形状态下,所有节点y方向位移向量的均方根为0.0134 m,在应用主动控制10 s后这些节点的均方根降低到6.4×10-4m,这个结构几乎恢复了平稳。控制力-时间曲线如图4(b)所示,清楚地表明有源电缆上的所有控制力都满足预设的0≤u≤umax范围。输出控制力可以满足单边约束和饱和约束。

为了应对不同工况,将施加在节点A上的力Fy增加到200 N。图5(a)展示了有无控制的情况下,节点A在y方向的位移对比结果。在施加控制力后,节点A的位移在10 s内降低到2.2×10-3m左右。在初始变形状态下,所有节点y方向位移的均方根为0.027 m,在应用主动控制10 s后这些节点的均方根降低到1.3×10-3m。而且作动绳的控制力仍然保持在设置的范围内(图5(b))。可以看出,提出的作动绳串联的方法可以在不同初始条件下,有效控制伸展臂的振动。

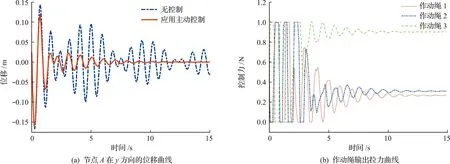
图4 Fy=100 N时的仿真结果

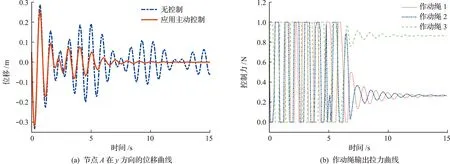
图5 Fy=200 N时的仿真结果

5 结 论

为了解决以拉绳作为作动器的伸展臂的振动控制问题,提出了拉绳串联伸展臂部分铰链的方式,将需要控制的电机从文献中的18个降低到3个,而且驱动拉绳的电机的安装位置也从铰链上移动到基座上,进一步降低伸展臂的复杂度和提高伸展臂的稳定性。在数值模拟中,首先,建立了由4个单元组成的伸展臂结构模型,然后通过遗传算法寻找出3个作动绳上铰链的最优串联顺序,结合优化结果对具有初始弯扭变形条件下的伸展臂的振动控制进行数值模拟,验证了提出的作动绳布置方式以及控制率可以有效地抑制结构的振动,同时满足控制力的单边约束和饱和约束,可以保证伸展臂迅速恢复到满足精度要求的状态,这对伸展臂的正常工作具有重要意义。