基于智能电表数据的低压配电网拓扑与线路参数联合辨识

马 尚，卫志农，黄蔓云，郑玉平，孙国强

（1.河海大学能源与电气学院，江苏省 南京市 211100；2.南瑞集团有限公司（国网电力科学研究院有限公司），江苏省 南京市 211106）

0 引言

为应对用户侧分布式电源接入所带来的不确定性［1-2］，进一步提高低压配电网的智能调度及运维管理水平，需要获取低压配电网精确的拓扑与线路参数［3-4］。然而，低压配电网中用户扩、改、接线频繁，布线隐蔽导致线路长度难以测量。此外，低压线路长时间运行后实际电阻率可能改变，使得台账上的拓扑与线路参数信息存在更新滞后、数据缺失等问题［5-6］。同时，低压配电网缺乏高级量测设备提供充足的相位及时域信息［7］，使得多数输电网及中压配电网的拓扑与线路参数辨识方法无法直接应用于低压配电网。随着高级量测体系在低压配电网中的普及，智能电能表（简称智能电表）提供了大量带有时标的用户侧电压幅值、功率等量测信息［8-9］，使得基于智能电表数据的低压配电网拓扑与线路参数辨识成为可能。

近年来，国内外在低压配电网的拓扑与线路参数辨识方面均有所研究。在拓扑辨识研究方面，文献［10］利用皮尔逊相关系数法确定低压配电网的相序和节点连接关系。文献［11］利用用户与所属变压器电压的T 形灰色关联度对拓扑图进行校核。文献［12］基于支路有功功率序列的相关性辨识分支节点的上下与并行、相序关系；文献［13］基于主成分分析法和图论进行低压配电网拓扑的构建；文献［14］基于马尔可夫随机场进行节点相关性分析获取网络拓扑。在线路参数辨识方面，文献［15］利用智能电表数据和已知拓扑推算线路功率分布，基于最小二乘法计算线路参数；文献［16］提出了基于多时间断面的同步相量测量单元（phasor measurement unit，PMU）、数据采集与监控、高级量测体系量测数据的线路参数辨识方法。上述多种辨识方法均只能实现拓扑或线路参数辨识的单一功能，不同拓扑辨识和线路参数辨识方法在数据的类型、数量和质量上的要求差别很大，难以在同一量测配置下组合进行辨识。

为此，一些学者开展了拓扑与线路参数联合辨识研究。文献［17-18］通过改进牛顿-拉夫逊法获得线路参数的精确值，但该算法仅适用于所有节点均装有智能电表的情况。而在低压配电网中，智能电表仅安装在用户节点上，中间含有大量数量未知、注入功率为零的“隐节点”［19-20］。对于含隐节点的拓扑与线路参数联合辨识问题，一些研究基于线路压降方程对支路逐条进行辨识。文献［19］基于线性压降方程从叶节点到根节点依次进行拓扑构建并计算线路参数。文献［20］建立了节点电压幅值平方形式的非线性电压降方程，通过非线性回归逐条对支路进行拓扑和线路参数辨识，但在量测误差较大的场景下无法保证辨识结果收敛于真值。另一类研究主要基于全网的“逆潮流”模型进行含隐节点的配电网拓扑与线路参数辨识。文献［21］提出了“逆潮流”的概念，利用PMU 提供的电压、电流相量，基于图论推断出含隐节点的网络节点导纳矩阵，但该方法只能应用于相角量测信息相对充足的中压配电网。文献［22］提出了可逆的线性耦合潮流模型（linear coupled power flow model，LCPF），并通过分组递归（recursive grouping，RG）算法实现含隐节点的低压配电网拓扑与线路参数的联合辨识，但所提模型在较大量测误差场景下的辨识精度有待提高。文献［23］采用电压灵敏度系数（voltage sensitivity coefficient，VSC）形式的线性逆潮流模型，通过RG算法生成一系列候选拓扑进行筛选，但筛选成功率受电压误差影响较大。文献［24］将逆潮流模型和RG 算法均改进为相量形式，模型精度更高，但不适用于无相角量测信息的低压配电网。

为了实现基于智能电表数据对含未知数量隐节点的低压配电网进行拓扑与线路参数的精确辨识，本文基于低压配电网的电气特性以及辐射状网络的结构特点，提出了一种功率-电压比形式的低压配电网逆潮流模型，并基于线性回归法求解得到阻抗距离矩阵，再通过无判定阈值形式的改进RG 算法对网络中的节点进行遍历，实现全网拓扑与线路参数的联合辨识。 通过在IEEE 欧洲低压馈线（European low-voltage test feeder，ELTF）和中国南京市某地区的实际低压配电网中进行测试分析，证明了所提辨识算法的有效性。

1 拓扑与线路参数联合辨识

1.1 拓扑与线路参数联合辨识问题描述

目前，已有研究多针对低压配电网的相序辨识、户变关系辨识。为进一步支撑智能调度与运维，需要进一步辨识低压配电网所有单元的拓扑连接关系以及各条支路的线路参数。低压配电网的拓扑与线路参数辨识主要存在以下困难：

1）智能电表往往仅安装在用户单元上，而分支单元缺乏量测装置，其数量和位置均为未知，难以获取含大量分支单元的低压配电网的完整拓扑；

2）低压配电网以智能电表量测为主，需要在无相角量测信息的前提下实现拓扑与线路参数辨识；

3）由于用户侧的分布式光伏接入，使得低压配电网中潮流反向多变，电压波动更为显著，对辨识算法的准确性产生直接影响。

1.2 拓扑与线路参数联合辨识框架

为便于分析，将配电变压器低压侧视作根节点，将辐射状低压配电网表示为树状图，如图1（a）所示。图中：蓝色表示由用户单元抽象成的负荷节点，这类节点装有智能电表，可以获取电压幅值及功率数据；白色表示由分支单元、空房抽象成的隐节点，这类节点为零注入节点且不装有任何量测装置，数量及电压数据均为未知。基于上述普遍情况进行拓扑与线路参数辨识，只考虑出度至少为3 的隐节点（至少有3 条支路与该节点相连），如节点1、3。这些节点产生了新的分支，改变了拓扑结构；而出度小于3 的零注入节点，如节点7、8，由于没有产生新的分支，不会影响拓扑与线路参数辨识结果，故将其忽略。简化图如图1（b）所示。

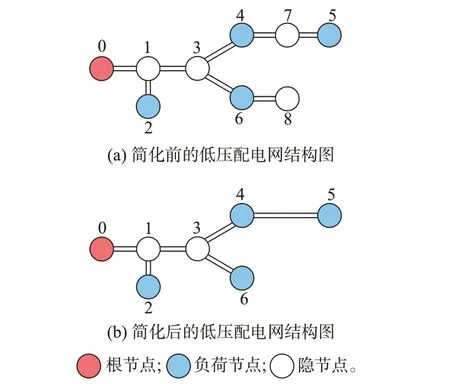
图1 拓扑简化示意图Fig.1 Schematic diagram of simplified topology

本文将基于低压配电网中智能电表提供的有功功率P、无功功率Q以及电压幅值V，辨识出低压配电网各节点间的拓扑连接关系以及各条支路的线路电阻R与电抗X，整体的辨识框架如图2 所示。

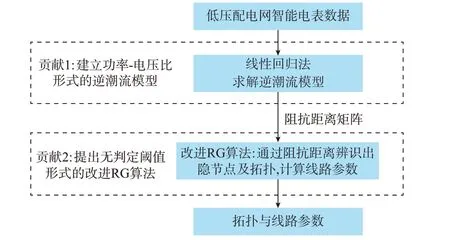
图2 联合辨识整体框架Fig.2 Overall framework of joint identification

与利用拓扑、线路参数求解节点电压的潮流模型不同，逆潮流模型将节点电压作为已知信息求解拓扑与线路参数［21］。首先，根据低压配电网中相邻节点的电压相角差较小的电气特点以及辐射状网络节点间的上下游关系，推导了功率-电压比形式的线性逆潮流模型。该模型以智能电表提供的PQV量测数据作为输入，基于线性回归法对其进行求解，获取负荷节点间的阻抗距离矩阵。进一步，基于无判定阈值形式的改进RG 算法，通过可观节点间的阻抗距离来辨识出隐节点及其拓扑连接关系并计算线路参数。需要说明的是，改进RG 算法通过遍历网络中的所有节点获得全网的拓扑与线路参数。

2 基于智能电表数据的线性逆潮流模型

本文将基于忽略相邻节点的电压相角差后所得的单支路线性压降公式，通过辐射状网络节点间的上下游关系推广至全网，得到适用于低压配电网的功率-电压比形式的线性逆潮流模型。

2.1 线性逆潮流模型的推导

在低压配电网中，两个相邻节点a、b的电压相角差接近于0［25］。在该假设条件下对支路压降方程进行近似，可以得到支路ab的功率-电压比形式的线性压降方程［26］为：

式中：va和vb分别为首端节点a和末端节点b的电压幅值；rab和xab分别为支路ab的电阻和电抗；pab和qab分别为由首端节点a流向末端节点b的支路有功和无功功率。

在该假设条件下也可以推导出支路ab与其下游支路及节点b的功率-电压比关系［26］为：

式中：E为网络中的支路集合；d为节点b的下游节点；pb和qb分别为节点b的注入有功和无功功率。例如，在图1（b）所示网络中，以支路13 为例，p13/v1可由p34/v3、p36/v3和p3/v3进行表示。

进一步，推导全网功率-电压比形式的线性逆潮流模型。在辐射状低压配电网中，由于存在明确的上下游关系，式（2）和式（3）中含支路功率的部分pbd/vb、qbd/vb可进一步向下游代换。最终，支路ab的功率-电压比可完全由支路末端节点b及其下游节点的注入功率-电压比代替，如式（4）和式（5）所示。

式中：Nb为节点b的子节点集合；vl、pl和ql分别为节点l的电压幅值、有功功率和无功功率。例如，在图1（b）所示网络中，进一步将p34/v3、p36/v3利用式（2）进行代换，得到含p45/v4的表达式，再次代换可将p13/v1完全由节点的注入功率-电压比p3/v3、p4/v4、p5/v5、p6/v6进行表示。

对于根节点与任一节点i的电压幅值差v0-vi可以表示为根节点到节点i路径上一系列相邻节点的电压幅值差的和，如式（6）所示。

式中：Ei为组成根节点到节点i的路径的所有支路集合。例如，在图1（b）所示网络中，v0-v3可以表示为组成根节点0 到节点3 路径的支路01、13 的电压差的和。

结合式（1）和式（4）—式（6），v0-vi可以用一系列的节点注入功率-电压比来表示，如式（7）所示。

为更具一般性，将式（7）进一步改写为v0-vi与除根节点外所有节点的注入功率-电压比的关系，需要将节点的范围转换为边的范围。式（7）表示对于支路ab，其对应求和的节点l的范围包括节点b及其子节点，而对于节点l来说，支路ab位于路径El上。例如，在图1（b）所示网络中，对于支路13 来说，对应的节点l的范围包括节点3、4、5、6。而对于这些节点来说，支路13 均在它们各自的路径E3、E4、E5、E6上。因此，对除根节点外的任一节点j，对应求和支路的范围应为路径Ej上的支路，即ab∈Ej。同时，支路ab∈Ei，故支路ab应处在根节点到节点i与j的共同路径上，即ab∈Ei∩Ej。据此，可将式（7）改写为：

式中：n为除了根节点外的网络节点数。例如，在图1（b）所示网络中，当i取4，j取6，p6/v6所乘的支路电阻为r01+r13，即节点4 与节点6 共同路径上支路01、13 的电阻和。

将式（8）改写为矩阵形式，表示为：

式中：v为由v1、v2、…、vn组成的列向量；v0为由n个v0组成的列向量；p为由p1、p2、…、pn组成的列向量；q为由q1、q2、…、qn组成的列向量；R、X分别为线路的电阻和电抗信息矩阵；Rij和Xij分别为矩阵R和X的元素。

式（9）为功率-电压比形式的低压配电网线性逆潮流模型。由式（10）可知，Rij与Xij分别表示根节点到节点i与节点j共同路径上的电阻与电抗和。

2.2 逆潮流模型的求解

按照隐节点及负荷节点进行划分，可以将式（9）写成分块形式为：

式中：vL、pL、qL为负荷节点的量测量列向量；vO、pO、qO为隐节点的量测量列向量；RLL和XLL分别为仅包含负荷节点的电阻和电抗信息矩阵；ROO和XOO分别为仅包含隐节点的电阻和电抗信息矩阵；RLO、ROL和XLO、XOL分别为含隐节点分量的电阻信息矩阵和电抗信息矩阵。

目前，在低压配电网中，由于仅已知负荷节点的量测量及数目，利用隐节点pO/vO=0，qO/vO=0 的特点，得到仅包含负荷节点的逆潮流模型为：

通过智能电表提供的多断面的PQV数据，利用线性回归对RLL及XLL进行求解，并进行对称化处理，表示为：

式中：PL、QL、VL分别为仅包含负荷节点的多断面有功、无功以及电压数据矩阵；V0为根节点的多断面电压数据矩阵；R'LL、X'LL分别为未对称化处理的电阻和电抗信息矩阵。

进一步，计算得到任意两负荷节点的阻抗距离，即组成两负荷节点路径所有支路的阻抗和，由此得到电阻距离矩阵dr和电抗距离矩阵dx。以节点i和j之间的电阻距离为例，表达式为：

式中：dr，ij为节点i与节点j之间的电阻距离；RLL，ii、RLL，jj、RLL，ij分别为矩阵RLL中对应位置的元素。

3 基于改进RG 算法的联合辨识模型

RG 算法利用可观节点间的可加性距离来辨识出隐节点，再更新可加性距离，以此遍历网络中的所有节点［27］。文献［22］将RG 算法引入低压配电网中，将阻抗距离矩阵dr和dx中的元素作为可加性距离，以此实现拓扑与线路参数的联合辨识。

RG 算法起始的可观节点集G即为负荷节点集L，通过引入第三方节点k判定节点i与j的连接关系。定义节点k到节点i、j的电阻距离差ϕr，ijk=dr，ik-dr，jk，k∈G{i，j}，判定节点i与j连接关系的标准如下。

1）节点i与j为父子节点

当满足式（16）时，节点i为j的子节点；当满足式（17）时，节点j为i的子节点。

式中：Ks为节点i是j的子节点的判定值；Ks'为节点j是i的子节点的判定值；τ为一较小的阈值，需根据历史经验确定。

2）节点i与j为兄弟节点

当不满足式（16）和式（17），但满足式（18）时，节点i与j拥有共同的父节点（即为兄弟节点）。

式中：Kp为节点i与j是兄弟节点的判定值。

RG 算法每次判定均针对所有节点对，不合理的τ值将会使网络中出现大量隐节点无法辨识的情况。为了消除τ的取值大小对辨识结果的影响，每次判定中仅考虑使得Kp最小的节点对(i,j)，将Ks、Ks'、Kp中的最小值所对应的连接关系作为判定结果,如式(19)所示。

当判定节点i与j为父子节点时，支路ij的电阻rij为：

当判定节点i与j为兄弟节点时，添加节点i与j共同的父节点h，支路hi的电阻rhi和支路hj的电阻rhj分别为：

更新电阻信息矩阵dr，计算节点h与其他可观节点的电阻距离，表示为：

线路电抗也依据dx中的元素进行同步计算。在初步判定节点i与j为兄弟节点后，若rhi、rhj的计算值出现小于0 的情况，则节点i与j实际应为父子节点。在判定连接关系及计算线路参数后，更新可观节点集G，即先删除子节点，若节点i与j为兄弟节点，则在可观节点集G中再加入共同的父节点h。更新完成后进行下一次迭代。改进的RG 算法一直执行至遍历可观节点集G中所有节点，由此实现全网的拓扑及线路参数的联合辨识。无判定阈值形式的改进RG 算法的流程如附录A 图A1 所示。

4 算例测试

为验证基于所提逆潮流模型的拓扑与线路参数联合辨识算法的有效性，在ELTF 中进行辨识性能测试。同时，将文献［23］提出的VSC 模型和文献［22］提出的LCPF 模型同本文所述改进RG 算法相结合组成两种联合辨识对比算法，将文献［20］提出的基于非线性压降模型的联合辨识算法作为第3 种对比算法。此外，采用中国南京市某地区16 个节点的实际低压配电网进行测试，进一步检验所提算法的实用性。

4.1 ELTF 算例介绍

ELTF 算例为额定电压416 V 的辐射状低压配电网。共有55 个负荷节点，其中，A 相21 个、B 相19 个、C 相15 个。首先，忽略出度小于3 的零注入节点，将906 个节点的网络简化到108 个节点。该算例提供了100 种采样间隔为1 min 的有功功率曲线。若每隔15 min 进行采样，每种有功功率曲线仅能提供96 个时间断面。为了获取更多的时间断面以模拟不同的负荷场景，将100 种有功功率曲线进行不同顺序的组合，生成55 个负荷的多断面有功功率数据集。无功功率数据集通过有功功率数据集和功率因数生成，其中，功率因数cosφ满足参数为（0.92，0.99）的均匀分布。电压幅值数据集通过潮流计算生成。最后，在各数据集中加入高斯噪声，分别形成P、Q、V的量测数据集。

在拓扑与线路参数辨识之前，需要对负荷节点进行相序辨识，采用文献［17］所使用的皮尔逊相关系数法，可以将所有的负荷节点分成A、B、C 三相。本文仅考虑对单相低压配电网进行拓扑与线路参数辨识。

4.2 辨识性能指标

在低压配电网的隐节点数未知的情况下，若辨识拓扑Te与真实拓扑T0的总节点数不相同，则Te与T0的各节点无法一一对应。在这种情况下，采用RF（Robinson Foulds）距离［20］、累计阻抗误差以及潮流验证误差［28］衡量所提算法的辨识性能。

1）RF 距离

RF 距离DRF(T1，T2)表示具有相同叶节点集合的两棵树之间的距离，可用于衡量具有相同负荷节点的辐射状拓扑T1与T2的距离。断开拓扑网络T中的任意一条边xy∈E(T)，得到负荷节点集的一个二分割πxy=，其中，Bxy、为断开边xy后得到的2 个负荷节点集。对于E(T)中的所有边进行切割，得到T的所有二分割集合为Π(T)={πxy：xy∈E(T)}。T1与T2的RF 距离定义为只存在于二分割集合Π(T1)或二分割集合Π(T2)中的二分割数量，表示为：

RF 距离的示例见附录B。由于本文仅针对单相网络，三相ELTF 算例的辨识拓扑Te与真实拓扑T0的RF 距离定义为A、B、C 这3 个单相网络的RF距离和，即

式中：TeA、TeB、TeC分别为A、B、C 相的辨识拓扑；T0A、T0B、T0C分别为A、B、C 相的真实拓扑。

2）累计阻抗误差

将累计阻抗误差CR和CX及对应均值CˉR和CˉX作为线路参数辨识精度的评价指标。对于网络中的任一节点i，其累计阻抗是指从根节点到该节点路径Ei上的阻抗和。累计阻抗误差及其对应均值的表达式为：

3）潮流验证误差

将数据集分成2 个部分：第1 部分加入高斯误差后形成量测数据集用于拓扑与线路参数辨识测试，第2 部分用于潮流验证。潮流验证误差为基于量测数据辨识得到的拓扑与线路参数，将用于验证的有功、无功数据经潮流计算得到的电压值与用于验证的电压数据之间的绝对误差。如节点i在断面t的潮流验证误差Fi，t为：

式中：vi，t为用于验证的数据集中节点i在断面t的电压幅值；为对应的利用辨识的拓扑及线路参数进行潮流计算得到的电压幅值。

在本文中，采用1 000 个时间断面进行拓扑即线路参数辨识测试，用100 个时间断面进行潮流验证。

4.3 ELTF 测试结果

为了测试基于所提逆潮流模型的拓扑与线路参数联合辨识算法在不同量测环境下的性能，在用于测试的数据集中添加了不同大小的高斯误差，形成了以下5 种测试场景：

场景1：P、Q的数据集中加入0.2%的误差，V的数据集中加入0.1%的误差；

场景2：P、Q的数据集中加入0.2%的误差，V的数据集中加入0.2%的误差；

场景3：P、Q的数据集中加入0.5%的误差，V的数据集中加入0.1%的误差；

场景4：P、Q的数据集中加入0.5%的误差，V的数据集中加入0.5%的误差；

场景5：P、Q的数据集中加入1%的误差，V的数据集中加入0.5%的误差。

在不同测试场景下，基于所提逆潮流模型的辨识算法和其他3 种对比算法所得拓扑与真实拓扑间的RF 距离如图3 所示。可以看出，基于所提模型的辨识算法在5 种测试场景下的RF 距离均为最小，即辨识所得拓扑和真实拓扑的差异最小，说明所提算法拓扑辨识的精确性和普适性。基于LCPF 的辨识算法RF 距离最大，即使在量测误差较小的场景中，RF 距离依然较大，即辨识所得拓扑和真实拓扑的差异较大。

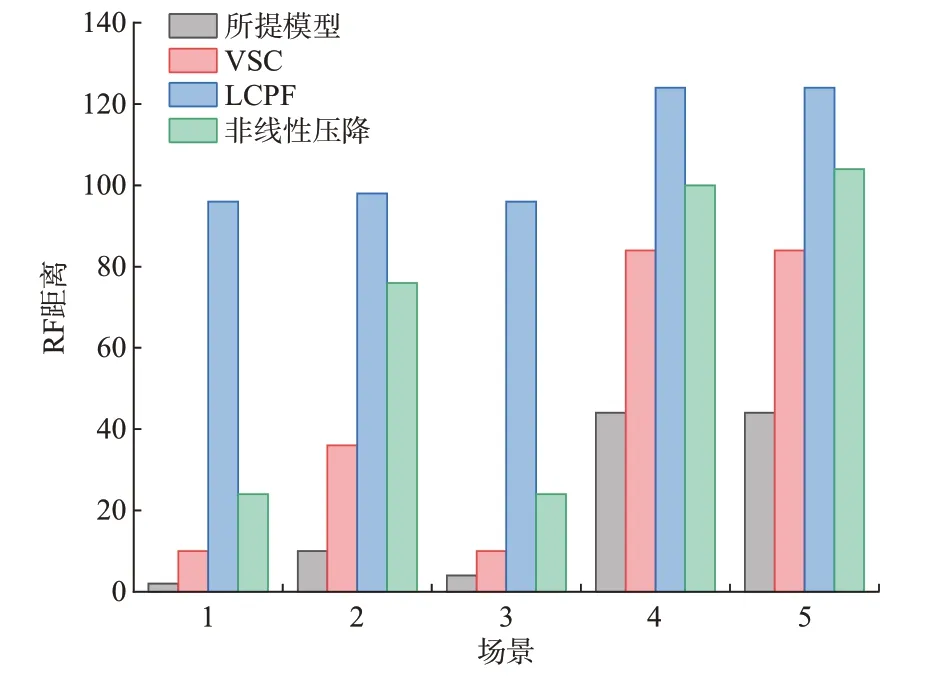
图3 不同测试场景下的RF 距离Fig.3 RF distance in different test scenarios

上述4 种辨识算法在5 种测试场景下的平均累计电阻误差CˉR和电抗误差CˉX如表1 和表2 所示。基于所提模型、VSC、非线性压降的3 种辨识算法，得到各负荷节点的累计阻抗误差分布如图4 所示。由于基于LCPF 的辨识算法误差远高于其他3 种辨识算法，在图4 中未画出。结合表1、表2 和图4 可以看出，基于所提模型的辨识算法在多场景下的辨识误差均低于其他3 种辨识算法。

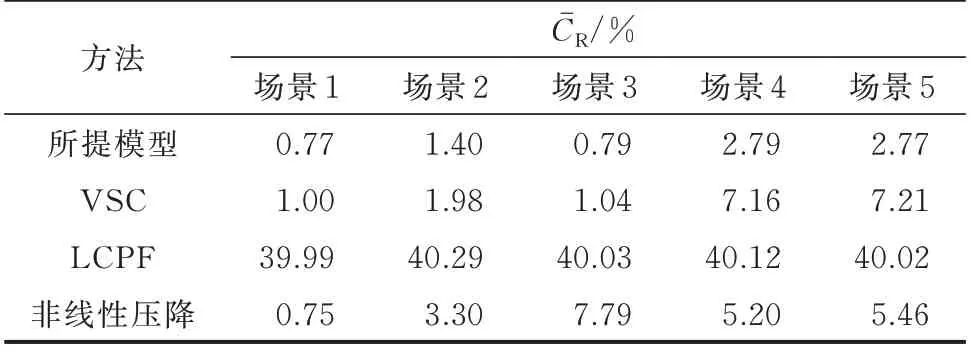
表1 不同测试场景下的平均累计电阻误差Table 1 Average cumulative resistance error in different test scenarios

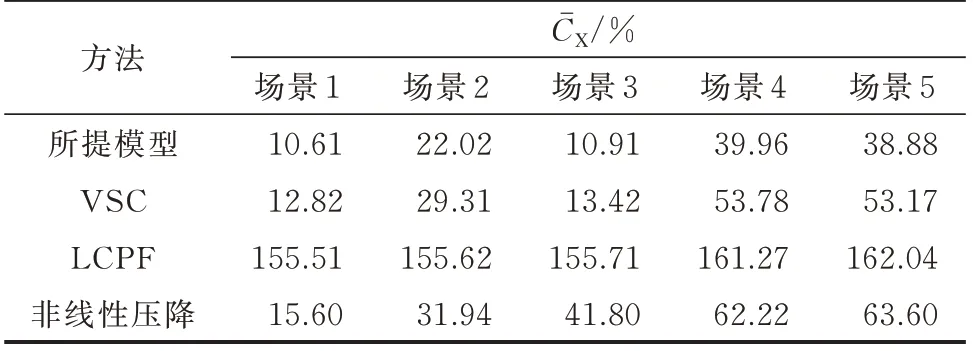
表2 不同测试场景下的平均累计电抗误差Table 2 Average cumulative reactance error in different test scenarios

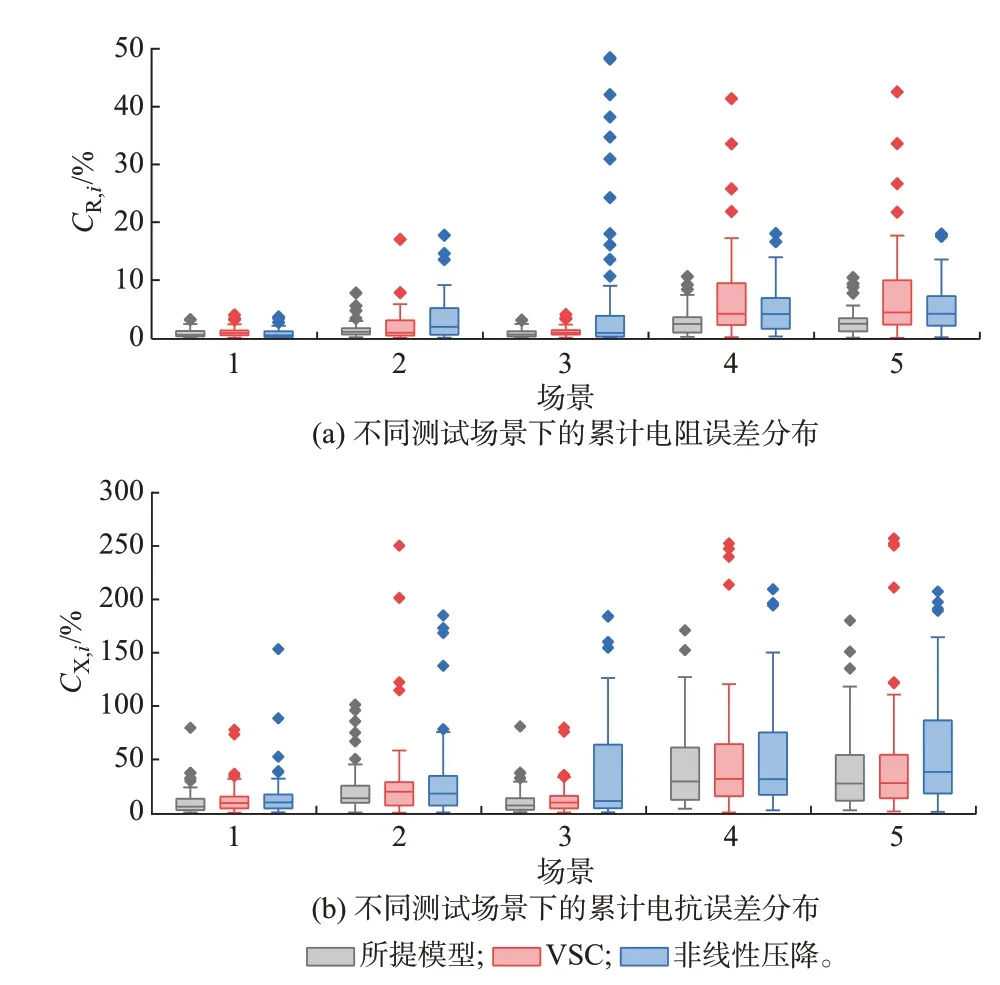
图4 不同测试场景下的累计阻抗误差分布Fig.4 Cumulative impedance error distribution in different test scenarios

考察不同类型量测误差对于拓扑与线路参数辨识的影响。结合图3 与图4 可以看出，对于单独增加电压V的量测误差（如场景1 到场景2、场景3 到场景4），基于所提模型、VSC 以及非线性压降的辨识算法拓扑与线路参数辨识误差显著增大；而单独增加注入功率P、Q的量测误差（如场景4 到场景5），上述3 种辨识算法的拓扑与线路参数辨识误差几乎不变。表明上述3 种拓扑及线路参数联合辨识算法对于电压量测误差的敏感度较注入功率量测误差的敏感度更高。

此外，结合表1、表2 和图4 可以看出，同场景下电抗的辨识误差要显著高于电阻。在ELTF 算例的系统运行参数中，数值上同一节点注入有功功率大于无功功率，同条线路电阻大于电抗。由式（1）可知，xabqab/va对于线路的压降va-vb贡献占比较小，导致线路电抗的辨识精度更低。这也是在第3 章的改进RG 算法中采用dr而不采用dx进行拓扑连接关系判定的原因。

基于所提模型、VSC 以及非线性压降辨识算法的潮流验证误差如图5 所示。由图5 可知，基于所提模型的辨识算法潮流验证误差在所有场景下略大于基于非线性压降的辨识算法。然而，通过图3 和图4可以看出，基于所提模型算法的拓扑与线路参数辨识误差均小于基于非线性压降的辨识算法。出现了辨识误差更小的算法潮流验证误差更大的现象，这一现象的原因将在4.4 节进一步分析。

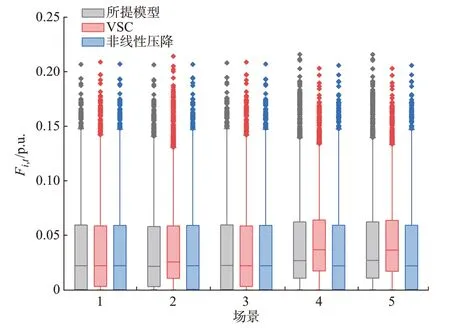
图5 不同测试场景下的潮流验证误差Fig.5 Power flow validation error in different test scenarios

4.4 ELTF 算例结果分析

为进一步分析基于所提模型的辨识算法辨识误差小的原因，考察上述4 种辨识算法的模型误差。设置场景0：在P、Q、V的数据集中均不加入误差。4 种辨识算法的拓扑与线路参数辨识指标如表3 所示。可以看出，基于非线性压降的辨识算法模型误差要远小于其他3 种方法，基于所提模型的辨识算法的模型误差略大于基于VSC 的辨识算法，而基于LCPF 的辨识算法的模型误差要远大于其他3 种算法，这是该算法在各场景下辨识误差最大的主要原因。

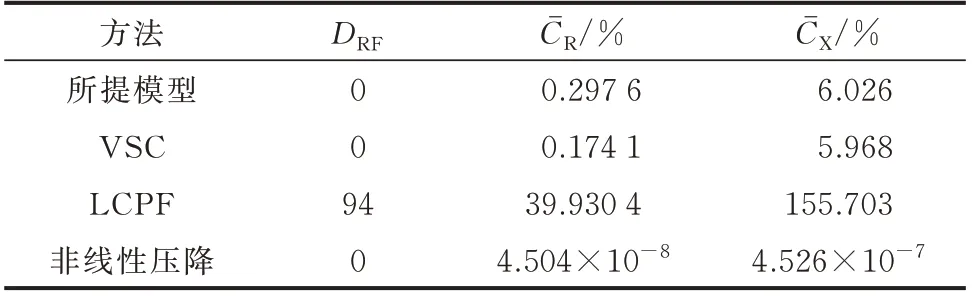
表3 场景0 下的拓扑与线路参数辨识指标Table 3 Topology and line parameter identification indexes in scenario 0

实际上，由于量测误差不会为0，基于所提模型的辨识算法在含有量测误差的情况下辨识误差小于基于VSC 的辨识算法，原因可从观测误差方面进行解释。在两种算法的模型误差相近的情况下，由于所提模型和VSC 模型数学形式上的差异，在相同测试场景下基于所提模型的辨识算法观测误差更小，辨识精度更高。具体阐述见附录C。

为了进一步分析基于所提模型的辨识算法相对于基于非线性压降的辨识方法辨识误差更小的原因，将两种辨识算法在不同测试场景下辨识的R或X小于0 的支路数展示如表4 所示。可以看出，基于非线性压降的辨识方法得到的线路参数中小于0 的支路更多，这些线路参数值与实际情况不相符。结合图5 可知，基于非线性压降的辨识算法获得了一个更为精确的整体模型，整体上的潮流验证误差更小，但部分支路的线路参数值并不收敛于真值。这是由于在量测量中加入高斯误差后，非线性压降辨识方法中的观测相量、非线性观测函数中均存在随机量测误差，使得该模型的求解无法获得线路参数的一致估计，即无法保证收敛于真值［20］。相比而言，本文所提算法基于线性回归进行求解，无需迭代，避免了收敛性的问题。

表4 不同测试场景下线路参数辨识值小于0 的数量对比Table 4 Comparison of numbers of line parameter identification values less than zero in different test scenarios

4.5 实际系统测试

采用中国南京某地区16 个节点的实际低压配电网进行测试，数据采集间隔为15 min，拓扑图如附录D 图D1 所示。利用采样得到的功率数据集进行潮流计算，得到电压数据集。在功率数据集、电压数据集中分别加入0.5%、0.2%的高斯分布的误差形成量测集。进一步探究不同断面数、不同量测误差分布以及分布式光伏接入对所提辨识算法的影响。

1）不同断面数对辨识性能的影响

在不同断面数下对拓扑与线路参数进行辨识，各指标如表5 所示。由表5 可看出，随着断面数的不断增加，拓扑和线路参数辨识的误差均不断减小。所提辨识算法的RF 距离在96 个断面时已减为0，表示已经正确辨识拓扑。当断面数量较大时，如断面数由576 增加至960 个，线路参数辨识误差已基本趋于稳定，实际应用中采用576 个断面即可。

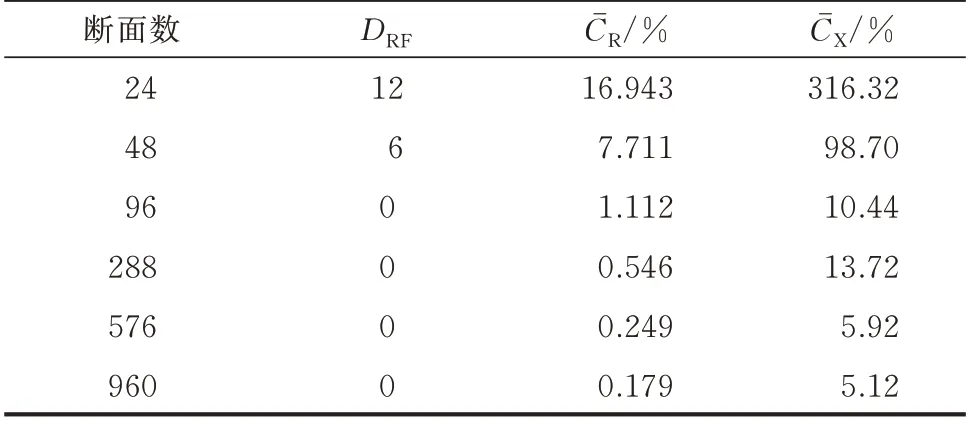
表5 不同断面数下的拓扑与线路参数辨识指标Table 5 Topology and line parameter identification indexes in different section numbers

2）不同量测误差分布对辨识性能的影响

保持功率量测误差水平0.5%、电压量测误差水平0.2%的前提下，在误差呈高斯分布、均匀分布、混合高斯分布的情形下进行拓扑与线路参数辨识。其中，高斯分布和混合高斯分布均通过参数设置使得功率量测误差在±0.5%、电压量测误差在±0.2%之间的比例大于99.7%。采用表5 所列断面数进行拓扑辨识，所提辨识算法在上述3 种不同量测误差分布情形下，RF 距离为0 所需最小断面数均为96。采用576 个断面进行线路参数辨识，不同量测误差分布对线路参数辨识的影响如表6 所示。不同分布的具体参数设置以及概率密度函数图如附录D 图D2 所示。

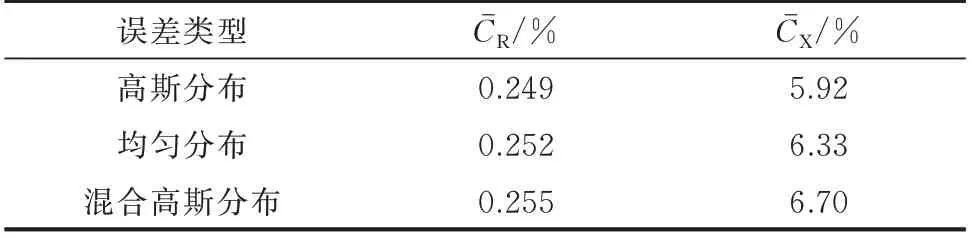
表6 不同量测误差分布下的线路参数辨识指标Table 6 Line parameter identification indexes in different measurement error distributions

由表6 可知，当量测误差服从均匀分布以及混合高斯分布时，线路参数的辨识误差相较于高斯分布略有增加，但总体辨识精度仍处于同一水平。

3）分布式光伏接入对辨识性能的影响

将多个分布式光伏接入该低压配电网，功率数据来自DKA（Desert Knowledge Australia）太阳能中心［29］。对比不接入光伏（渗透率为0%），以及先后在6、9、11 节点接入分布式光伏PV1 至PV3 的场景，对应的渗透率分别为21%、42%、63%。光伏出力曲线示意图如附录D 图D3 所示。采用表5 所列断面数进行拓扑辨识，所提辨识算法在上述4 种不同渗透率情形下，RF 距离为0 所需最小断面数均为96。采用576 个断面进行线路参数辨识，辨识结果如表7 所示。

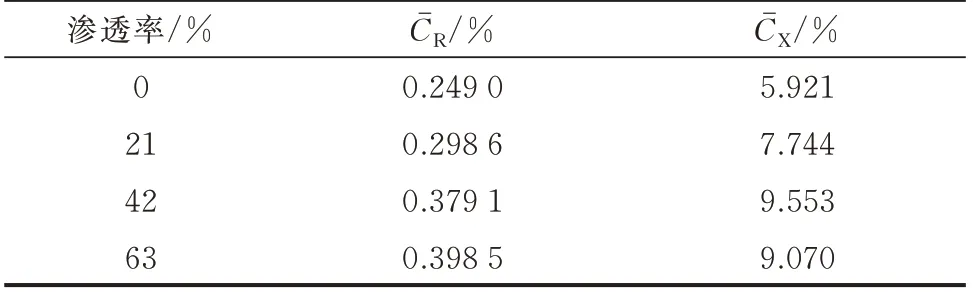
表7 不同渗透率下的线路参数辨识指标Table 7 Line parameter identification indexes with different permeabilities

由表7 可知，随着分布式光伏渗透率的增加，线路参数的辨识误差仅略有增大。分布式光伏的接入会改变功率流动方向，体现为所提逆潮流数学模型中部分节点的功率正负发生改变，并不影响模型的等式关系，即所提逆潮流模型在分布式光伏接入条件下依然成立。光伏出力使得部分线路两端节点电压差的绝对值过小，在有一定量测噪声情况下会对辨识产生干扰，但影响程度有限。

4）对智能电表非同步误差的处理

实际采样中，由于智能电表本身的时钟通常存在毫秒级到秒级的偏差，同一时刻采样得到的各电表量测值、同一电表采样得到的电压、功率值均不完全同步。这种采样的非同步性在负荷平稳的情况下引入的误差较小［15，30］，故仅考虑剔除负荷波动较大的断面。采用文献［15］的处理方法，在台区变压器出口处安装总用电量采样装置，获取每秒的全低压配电网的总用电量。根据总用电量在采样时刻附近一段时间的波动程度进行数据筛选，将总用电量波动较大的对应断面剔除，以减少负荷剧烈波动导致的智能电表非同步误差较大的情况。计及智能电表非同步性的算例测试如附录E 所示。

5 结语

针对含未知数量隐节点的低压配电网拓扑与线路参数辨识问题，本文提出了一种基于智能电表数据的低压配电网拓扑与线路参数联合辨识方法。首先，推导了适用于辐射状低压配电网的功率-电压比值形式的逆潮流模型。进而，利用智能电表数据进行线性回归求解得到阻抗距离矩阵，再通过无判定阈值形式的改进RG 算法实现拓扑及线路参数的联合辨识。最后，通过在ELTF 算例和中国南京市某地区实际低压配电网中进行测试，得出如下结论：

1）相比于其他拓扑与线路的联合辨识算法，本文所提算法在多种误差水平的场景中拓扑和线路参数辨识精度均为最高，体现了所提算法的精确性。

2）本文所提算法的辨识精度受不同量测误差分布和高渗透率分布式光伏接入的影响较小，具有较强的工程适用性。

未来将在本文的研究基础上，考虑部分量测缺失的情况，开展基于三相非线性逆潮流模型的拓扑及线路参数辨识研究，进一步提升辨识的准确性和实用性。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。