大规模海上风电场电磁暂态受控源解耦加速模型

2024-02-20许建中赵成勇

电力系统自动化 2024年2期

邹明，王焱，许建中，赵成勇

（新能源电力系统全国重点实验室（华北电力大学），北京市 102206）

0 引言

中国海上风电累计装机容量逐年提升，装机容量占比也越来越大，使得电网面临更大的稳定性风险［1］。电磁暂态（electromagnetic transient，EMT）仿真是支撑系统分析、设计、控制和运行的重要基础工具［2］。然而，大规模海上风电场（wind farm，WF）通常由上百台风电机组（wind turbine，WT）组成，每台机组都包含各种电气设备和电力电子开关器件，这极大地增加了系统节点数量，导致仿真效率极低［3］。

使用详细风电机组模型仿真虽然可以充分反映诸多动态过程，但模型太过复杂，需要耗费大量计算机资源，难以平衡仿真规模和仿真时间之间的矛盾［4］。现有文献中，为解决风电场EMT 仿真困难的方法主要有以下几类：部分机组元件简化［5-6］、聚合等值法［7-9］、戴维南/诺顿等效建模［10-11］和系统拆分解耦［12-14］。文献［5］通过忽略风电机组机侧系统（包括发电机和机侧换流器）来简化机组复杂度，然而，简化模型忽略了机-网耦合关系，会导致系统动态分析过程的误差。文献［6］构建了基于开关函数的机组换流器平均值模型，该模型虽然可以提高计算效率，但仿真精度有所降低。文献［7］提出一种风电场参数聚合单机等值方法，该方法原理简单、仿真效率高，但精度较低、应用场景较为有限，无法反映风电场内部电气特性。为了克服单机等值法的问题，文献［8］提出一种多机等值方法，相较于单机等值法仿真精度得到了提升，但随着风速、运行工况发生变化，需要实时对分群指标进行聚类，计算量大。文献［9］基于实际受扰轨迹的动态量测数据进行参数辨识聚合，这种聚合法精度较高，但存在量测较难获取、参数辨识准确度较低的问题。文献［10-11］提出一种风电场戴维南/诺顿等效模型，该方法具有极高的仿真精度且可显著缩短仿真时间，但其建模过程较为复杂，当机组拓扑发生变化时，等效电路需重新定义，灵活性不足。基于半隐式延迟解耦原理，文献［12］构建了风力发电单元的解耦模型以提高仿真速度，但该方法需要对递推格式反复迭代，且半个步长的延时带来了时序设计的问题。文献［13-14］从另一个角度利用传输线解耦分割，实现了大系统等价拆解，但在仿真步长一定的情况下，该解耦方法需要传输线长度大于一定距离，灵活性受限。文献［15-16］基于受控源的映射关系，对模块化多电平换流器（modular multilevel converter，MMC）和直流变压器（DC transformer，DCT）进行解耦，但缺乏交流端口的应用，且解耦方法的有效性分析未考虑时间延迟的问题。

上述建模方法分别从不同切入点对风电场建模和加速仿真开展了有益的研究，但仍存在建模方法复杂、无法反映风电场内部特性、灵活性不足等问题。为降低建模复杂度，在保留风电机组内部电气特性的基础上提高仿真效率，同时提高模型搭建的灵活性、可延展性及可移植性，本文提出一种大规模海上风电场电磁暂态受控源解耦加速模型（controlled source based decoupling acceleration model，CS-DAM）。所提解耦模型建模方法简单，便于修改且灵活性高，可以准确仿真风电场的启动、换流器解闭锁、次同步振荡及短路故障等工况，风电场级层面有功功率误差不超过5.86%，可实现1～2 个数量级的加速比。所提模型可与现有文献所提方法相互补充，扩展其灵活性。

1 直驱风电场系统结构和参数

永磁同步发电机（permanent magnet synchronous generator，PMSG）因其较好的低电压穿越性能、无励磁绕组、效率高、便于维护等优点，被广泛应用于国内在建海上风电场［17］。图1 给出了直驱风电场结构图。图中：uWF和iWF分别为风电场公共连接点（point of common coupling，PCC）处的交流电压和电流；uLj和iLj分别为第j条链路的端电压和输出电流，j=1，2，…，N；uk和igk分别为该链路中第k台风电机组的端电压和输出电流，k=1，2，…，n。由图1 可知，n台风电机组以链式连接方式汇集到35 kV 集电线路上构成一条链路，N条链路以并联方式连接，再通过35 kV/230 kV 联接变压器接入交流系统。场内各设备参数见附录A 表A1。

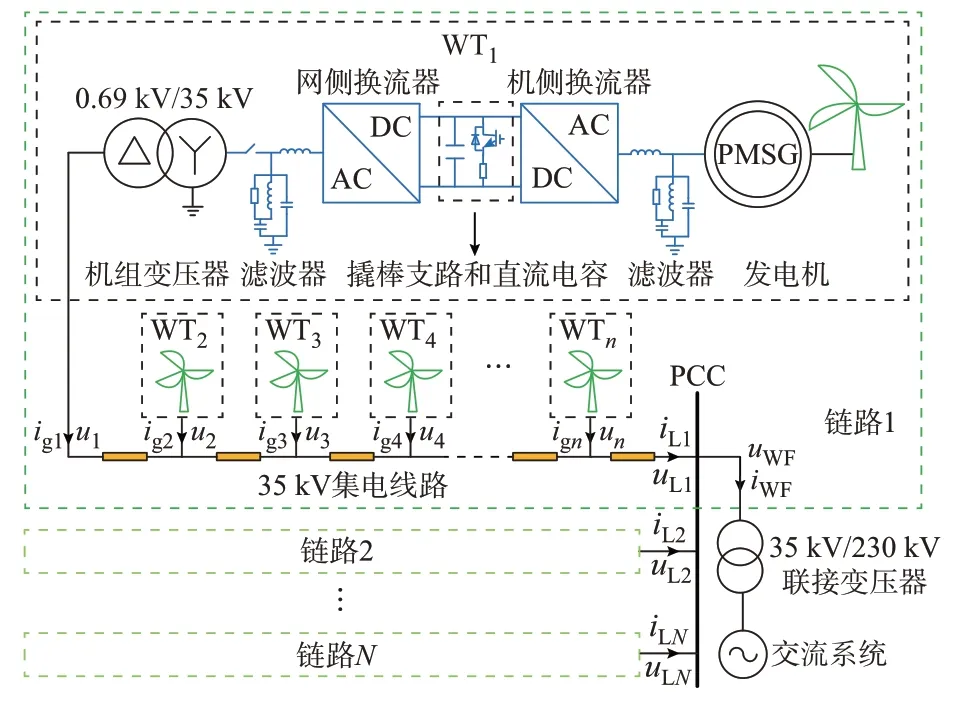
图1 直驱风电场结构图Fig.1 Structure diagram of PMSG-based wind farm

2 电磁暂态受控源解耦加速方法

2.1 解耦建模原理

利用理想变压器模型法［18］可实现风电场解耦建模，其原理如图2 所示。图中：节点l和n的等效注入电流源分别为Jl和Jn；节点间的导纳为Ylm和Ymn；im(t)和um(t)分别为t时刻节点m流过的电流和对地电压，um=um'；Δt为系统仿真步长。

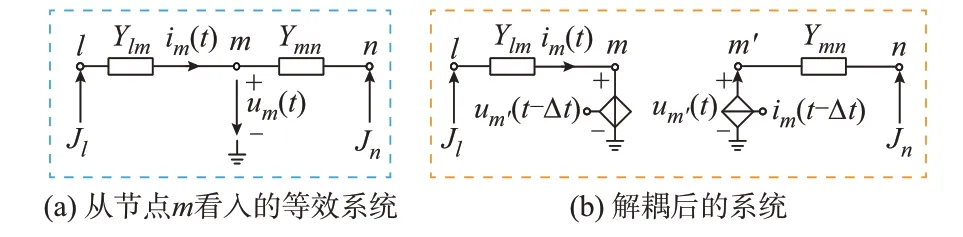
图2 解耦建模原理Fig.2 Principle of decoupling modeling

对图2（a）所示等效系统的节点m进行解耦，解耦后如图2（b）所示。拆分后解耦点一侧为受控电压源，另一侧为受控电流源。受控电流源值等于另一端受控电压源支路流过的电流，受控电压源值等于另一端受控电流源的出口电压。利用受控源解耦时，解耦点两端的信息传递延迟一个仿真步长。

2.2 风电机组外部端口解耦建模方法

风电机组外部端口包括同条链路内机组之间的链式连接以及链路出口的并联连接2 种连接方式。基于上述解耦建模原理，建立了风电机组外部端口解耦等效模型，如附录A 图A1 所示。

对于风电机组链路而言，其电网侧可等效为一个受控电压源，其电压值为PCC 处电压un+1(t-Δt)；对于电网而言，各条链路可等效为一个受控电流源，其电流值为各条链路输出电流之和iall(t-Δt)。链路内各风电机组出口与前段线路之间进行解耦，对于第k台风电机组而言，其出口侧等效为一个受控电流源，其值为其前段所有机组输出电流之和ik-1(t-Δt)；对于前段线路而言，其端口处等效为一个受控电压源uk(t-Δt)，用于传递电网侧电压值。

链路内第k台机组解耦点以及链路出口解耦点的受控电流源和电压源值如式（1）所示。

式中：fΔt[·]表示取上一个仿真步长的值。

由于受控源在传递信息时存在一个仿真步长的延时，在系统仿真步长足够小的前提下，从解耦点处向模型内部看，解耦后的模型与原始模型可认为完全等效。上述解耦方法的有效性可通过基尔霍夫定律和节点分析法证明，证明方法参考2.4 节。

2.3 风电机组内部端口解耦建模方法

由图1 可知，每台直驱风电机组中包含PMSG、滤波器、变压器、换流器等多种电气设备，其整体阶数可达25 阶。为进一步降低系统阶数，可在风电机组内部电气设备间应用前述解耦建模方法，实现各设备之间的进一步解耦，如附录A 图A2 所示，从而将大规模风电场的高阶矩阵运算分解成多个小矩阵运算同时进行。由于矩阵求逆和阶数的3 次方呈正相关，故系统分解后计算量降低，极大地提高了仿真的计算效率。由图A2 可知，该解耦建模方法不仅可应用于交流端口，也可应用于直流端口。

2.4 解耦建模方法有效性证明

通过对PMSG、滤波器、开关器件、变压器及电感、电容等元件的等效建模，单台风电机组可以表示为图3（a）所示的诺顿等效电路［11］。由于各相之间完全解耦，可构建如图3（b）所示的单相形式下风电机组链路的诺顿等效电路，对应的解耦诺顿等效电路如图3（c）所示。图中：JGA、JGB、JGC分别为风电机组三相等效电流源；YGA、YGB、YGC分别为风电机组三相等效导纳；JGk(t)为t时刻第k台风电机组注入第k个节点的诺顿等效电流源；YGk为第k台风电机组诺顿等效导纳；YLk为第k台风电机组出口线路的导纳值。其中，地节点为参考节点，单相形式仅为了推导方便，其他相同理可得，不存在三相不平衡不适用的问题。在不失通用性的前提下，假设该链路诺顿等效电路可表示风电场内任意一条链路。

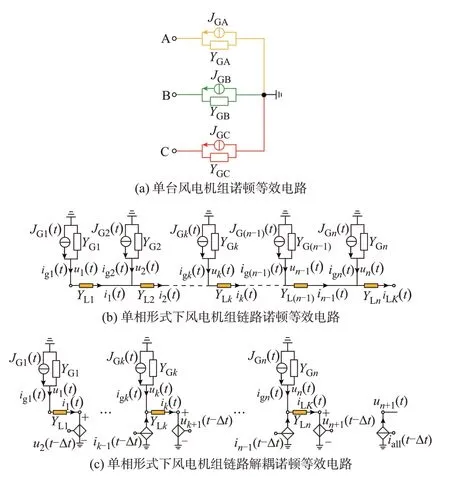
图3 风电机组及链路等效电路Fig.3 Equivalent circuit of wind turbine and link

对图3（b）所示的诺顿等效电路列写节点电压方程可得：

式中：Yk(k+1)=Y(k+1)k=-YLk，为相邻节点间的互导纳；Ykk为第k个节点的自导纳，如式（3）所示。

对图3（c）中第1、第k和第n+1 个节点应用基尔霍夫电流定律，有

为便于说明，将式（7）—式（9）中非t时刻的电压量约等为t-Δt时刻的量，结果如式（10）—式（12）所示。

将式（10）—式（12）写成矩阵形式，如式（13）所示。

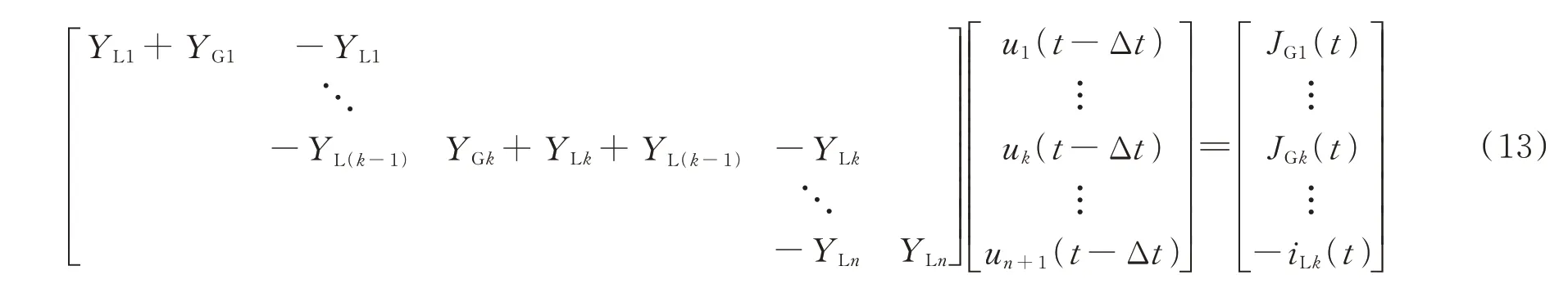
可见，解耦后等效电路的节点电压方程与原始方程的区别在于节点电压列向量存在一个仿真步长的延时。由此可知，图3（b）和（c）所示2 个诺顿等效电路在系统仿真步长较小时，可认为完全同解。由于风电场中包含了大量的电力电子器件，为准确刻画这些器件的动态特性，要求仿真步长较小。因此，所提解耦建模方法可应用于大规模风电场中。

通过一组成对的受控源，大规模风电场各子系统之间电气解耦，实现了高阶矩阵的等价降阶，提高了仿真速度。所建立的CS-DAM 不仅可以降低导纳矩阵求逆的计算量，而且可以准确仿真详细模型在启动、换流器解闭锁、次同步振荡及短路故障等工况下的所有电气特性。该建模方法原理简单、物理概念清晰、可扩展性好，可与其他建模方法实现互补。当风电场拓扑或机组结构发生变化时，采用戴维南/诺顿等效建模方法需重新建立等效电路，较为复杂。此时，可采用解耦模型搭建拓扑变化部分，其余部分则保留戴维南/诺顿模型，从而避免了再次建模，也弥补了其灵活性不足的问题。此外，所提解耦建模方法仅将系统电路部分进行解耦，而与控制方法无关。

3 仿真验证

为验证所提CS-DAM 的准确性、误差影响因素以及加速效果，在PSCAD/EMTDC 中搭建了风电场详细模型（detailed model，DM）和CS-DAM，对比其仿真精度和加速比。系统参数见附录A 表A1。

本文仿真算例中，PMSG 采用基于桨距角控制的最大功率点跟踪（maximum power point tracking，MPPT）控制，机侧换流器和网侧换流器均采用双闭环控制。其中，机侧换流器采用有功功率控制、网侧换流器采用直流电压控制。

3.1 仿真精度验证

为验证CS-DAM 的仿真精度，按照图1 所示拓扑搭建了包含20 台风电机组的风电场。其中，共包含4 条链路，每条链路由5 台风电机组经链式方式连接，用于测试不同工况下CS-DAM 的仿真精度。

3.1.1 启动阶段

工况设置：0～0.5 s，机组断路器处于断开状态，机侧和网侧换流器均闭锁，此时的风电场交流电流为0，交流电压逐渐达到额定值；0.5～0.6 s，断路器闭合，机组并入交流电网；0.6～0.7 s，网侧换流器解锁；0.7 s 后，机侧换流器解锁，机组直流电压升高导致撬棒支路动作，维持直流电压稳定，风电场交流电流逐渐增大，输出的有功功率逐渐提升至额定值、机组直流电压恢复额定值并进入稳定运行状态。

图4 给出了DM 和CS-DAM 在启动阶段风电场的输出有功功率PWF、无功功率QWF、交流电压uWF、交流电流iWF及机组直流电压UDC的波形图。图中：DM 和CS-DAM 的仿真波形基本重合，风电场有功功率、无功功率、交流电压、交流电流和机组直流电压的误差分别为：1.61%、0.570 5 Mvar、0.29%、2.10%、7.95%（其中交流量的误差基准为其额定值，下同）。由于撬棒支路触发时刻的误差，导致直流电压的误差相对较大，但实际上撬棒支路开始及结束时刻是准确的，且更关注撬棒支路能否正确动作而并不关注触发期间具体如何动作。由此可知，所提CS-DAM 在启动阶段的仿真结果具有较高的准确性。

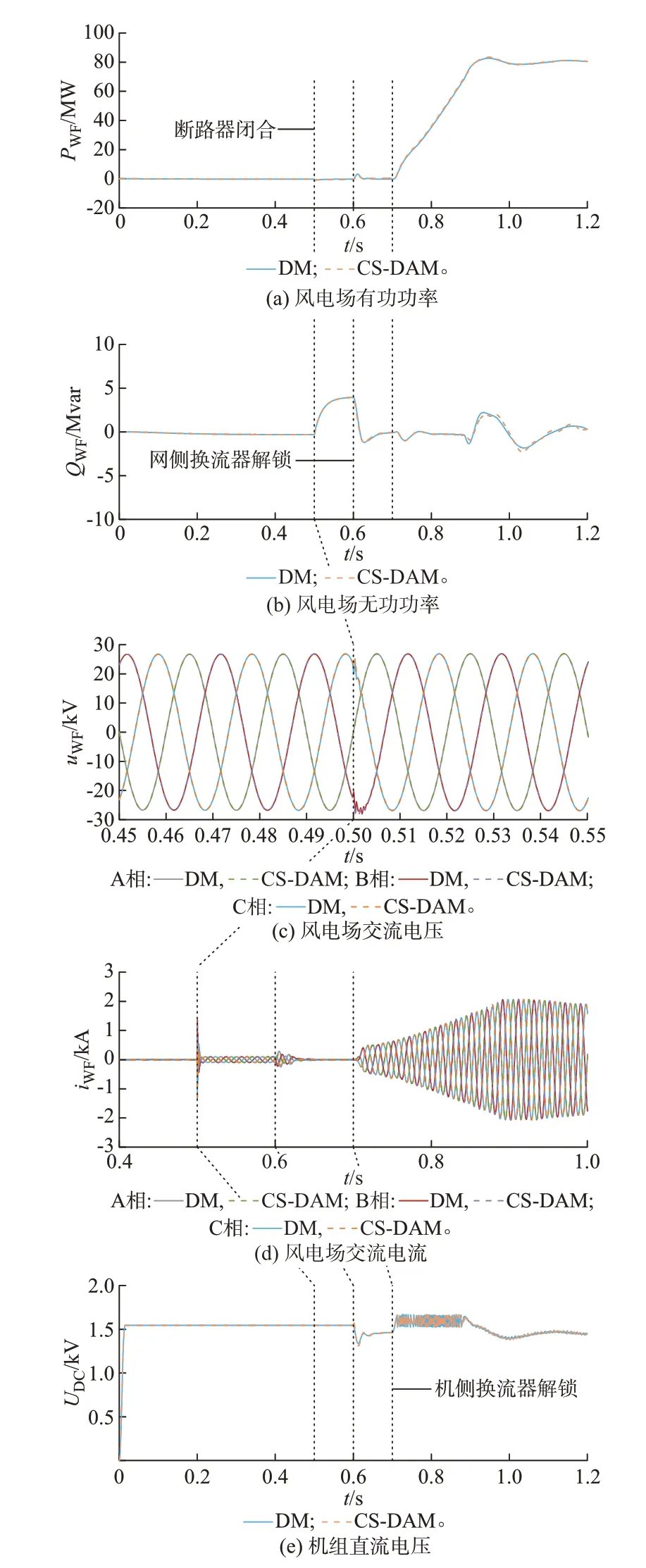
图4 启动阶段DM 和CS-DAM 的仿真波形Fig.4 Simulation waveforms of DM and CS-DAM during startup period

3.1.2 稳态阶段

1.2 s 后，系统由启动阶段进入稳态。附录A 图A3 给出了DM 和CS-DAM 在稳态阶段风电场的输出有功功率、无功功率、交流电压、交流电流及机组直流电压波形图。

稳态阶段，风电场各物理量最大相对误差为1.22%。由此可知，不论是在交流端口还是在直流端口解耦，CS-DAM 均具有较高的准确性。

3.1.3 小扰动阶段

工况设置：1.5 s 时，风电场中4 台风电机组的机侧换流器有功外环比例系数由0.25 阶跃至4，风电场输出的有功和无功功率出现振荡现象，0.5 s 后有功外环比例系数恢复至0.25，风电场振荡逐渐消失并恢复稳定运行。

附录A 图A4 给出了DM 和CS-DAM 在小扰动阶段风电场的输出有功功率、无功功率，发生小扰动机组的输出电流、有功功率和直流电压，以及未发生扰动机组的输出电流、有功功率和直流电压波形图。

风电场有功功率的最大相对误差为2.14%，相位延迟时间和振荡频率绝对误差分别为13.7 ms和0.83 Hz；风电场无功功率的最大绝对误差为1.269 8 Mvar；发生小扰动机组交流电流的相位延迟时间和振荡频率绝对误差分别为11.3 ms 和0.38 Hz；有功功率的相位延迟时间和振荡频率绝对误差分别为11.2 ms 和0.31 Hz；机组直流电压的相位延迟时间和振荡频率绝对误差分别为10.5 ms 和0.51 Hz。未发生小扰动机组的交流电流、有功功率和机组直流电压的最大相对误差分别为2.04%、0.71% 和1.87%。在小扰动过程中，虽然DM 和CS-DAM 在风电机组层面的仿真波形有一定相位的误差，但风电场级层面仍具有良好的重合度，且振荡频率误差较小，进一步验证了CS-DAM 的准确性。

3.1.4 短路故障阶段

工况设置：在2.8 s 时，风电场交流出口侧发生持续时间为625 ms、过渡电阻为50 mΩ 的三相短路故障。故障发生后，风电场出口交流电压跌落，输出有功功率受阻，出现功率倒送现象；故障清除后，系统逐渐恢复稳定运行。

附录A 图A5 给出了DM 和CS-DAM 在短路故障阶段风电场的输出有功功率、无功功率、交流电压、交流电流及机组直流电压波形图。

风电场有功功率、无功功率、交流电压、交流电流和机组直流电压的误差分别为5.86%、2.106 7 Mvar、3.32%、6.82%、9.35%。由于有功功率出现过零点，基准低导致相对误差放大。DM 和CS-DAM 在短路故障阶段的仿真波形重合度较高，在风电场级层面的最大相对误差为5.86%。

3.2 解耦建模方法误差影响因素验证

为验证受控源解耦建模方法误差的影响因素，对比了不同仿真步长下CS-DAM 各个仿真阶段的误差。附录A 图A6 给出了仿真步长分别为5 μs 和10 μs 下，各个阶段CS-DAM 的误差对比图。图A6（a）为各个阶段下CS-DAM 的相对误差，图A6（b）和（c）分别为小扰动阶段下CS-DAM 的相位延迟时间和频率绝对误差。本节工况设置与3.1 节保持一致。

由附录A 图A6 可知，启动阶段和稳态阶段的前后步长内参数变化很小。因此，仿真步长降低后，CS-DAM 的相对误差没有明显降低。系统仿真步长降低后，CS-DAM 在小扰动阶段和短路故障阶段的相对误差降低，在小扰动阶段CS-DAM 的相位延迟时间以及频率绝对误差明显降低，说明了系统仿真步长对解耦建模方法准确性的影响。

3.3 仿真加速效果验证

为验证CS-DAM 的加速效果，按照图1 所示拓扑分别搭建了包含1～30 台风电机组的风电场，用于测试不同风电机组数下，DM 和CS-DAM 的CPU仿真用时和加速比。测试所采用的计算机配置为2.10 GHz Intel Core i7-1260P，测试系统仿真步长为10 μs，仿真时间为1 s。

表1 记录了不同风电机组数下DM 和CS-DAM的CPU 仿真用时和加速比。图5 展示了两种模型的仿真用时和加速比随风电机组数变化的趋势。

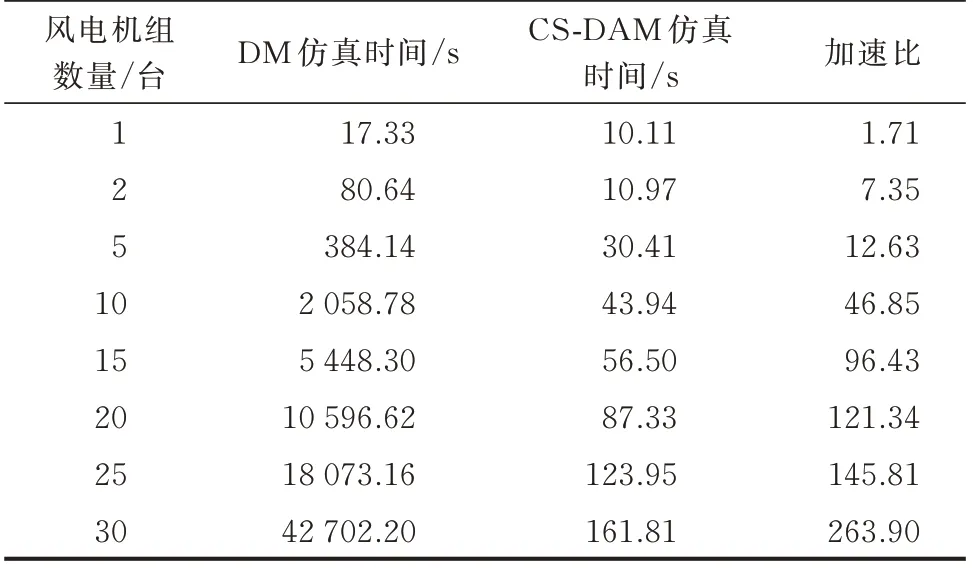
表1 DM 和CS-DAM 仿真时间和加速比对比Table 1 Comparison of simulation time and acceleration rate between DM and CS-DAM

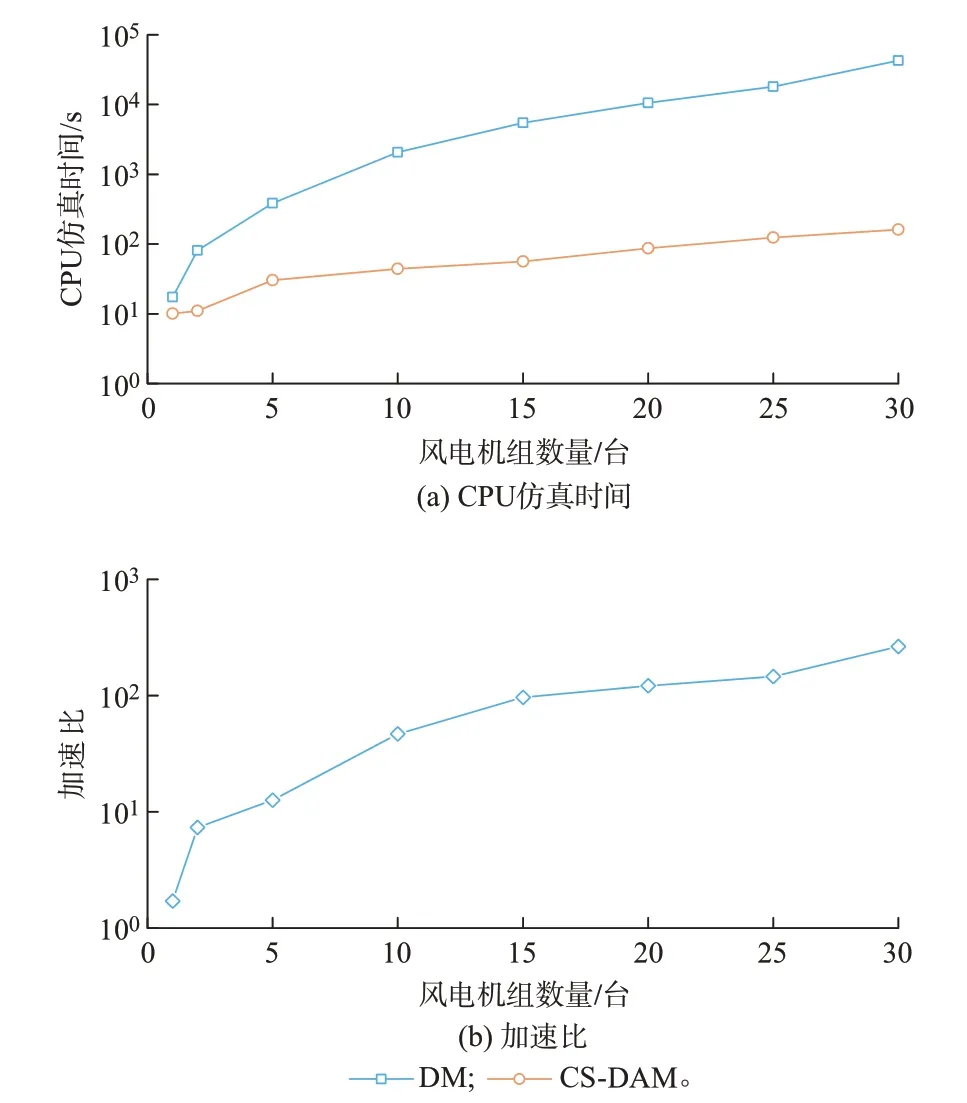
图5 不同机组数量下DM 和CS-DAM 的提速效果对比Fig.5 Comparison of acceleration effect between DM and CS-DAM under different wind turbine numbers

由图5 可知，对于单台风力发电机组，CS-DAM对于仿真速度的提升不明显。随着风电机组数的增多，CS-DAM 的CPU 仿真时间呈线性增长，加速比逐渐提高。当风电机组增加到30 台时，CS-DAM 的计算效率相较于DM 提高了2 个数量级，加速比达到了263.90 倍。

主流电力系统仿真软件电磁暂态仿真效率低的主要原因有以下2 方面：一是系统节点数；二是仿真步长。虽然CS-DAM 保留了换流器开关模型，但在仿真步长不变的前提下，影响系统计算效率的原因主要是系统节点数。因此，本文所提CS-DAM 将大系统分解为若干小系统进行求解，降低了解算过程中的矩阵阶数，实现了仿真加速。