考虑风电机组故障电压穿越特性的连锁故障关键线路辨识

徐 箭，贺中豪，廖思阳，邹曜坤，孙元章，杨 军

（武汉大学电气与自动化学院，湖北省 武汉市430072）

0 引言

随着社会用电量的爆发式增长、电网规模的持续发展以及线路复杂程度的不断提高，系统安全风险加剧。近年来，全球已发生多起大面积停电事件。研究表明，部分元件的故障可通过系统触发其他元件先后故障，从而扩大了连锁故障规模，造成连锁故障大停电的发生。

在高比例新能源并网的背景下，新能源出力的随机波动性以及电力电子设备的故障弱承载能力会导致系统安全风险加剧［1］。发生于2016 年的南澳大停电［2］、2019 年英国大停电［3］、2021 年欧洲电网解列［4］以及2021 年美国得州大停电［5］这4 起事故再次印证大规模新能源机组并网增大了电网发生停电事故的风险，其中，少数的关键元件崩溃将导致电网安全运行水平急剧下降［6］。因此，快速准确辨识含高比例可再生能源电网连锁故障的关键元件，定位导致连锁故障蔓延扩大或加剧的关键路径，对于有效实施阻断控制策略、提高电网安全稳定性具有重要意义。

目前，国内外针对连锁故障关键元件辨识的研究主要分为3 类。第1 类方法是基于系统状态分析的关键性指标，该方法利用连锁故障蔓延过程中变化的电气量构造关键性指标。例如，提出了潮流熵指标［7］、线路暂态脆弱性指标［8］、潮流转移度指标［9］和基于OPA（ORNL-PSerc-Alaska）模型［10］、隐性故障模型［11］的元件风险指标评估。此类方法可对连锁故障进行物理细节刻画，但该方法仅结合部分运行参数筛选出运行状态变化较大的元件，且连锁故障发生概率较低，计算效率与辨识准确性难以兼顾。第2 类方法是基于复杂网络理论的关键性指标，提出了平均路径长度、改进度数、改进介数等指标评估元件关键性［12-15］。此类方法具有较高的计算效率，但忽略了连锁故障传播过程的物理细节和动态特性。第3 类方法根据历史或故障仿真得到的连锁故障演化结果，对相似的故障演化规律进行分析挖掘，从而实现关键元件辨识。文献［16-17］提出了连锁故障网络图、连锁故障时空图用以分析故障传播关系，但未考虑易扩大故障传播的线路开断对连锁故障大停电的影响。文献［18-20］基于SALSA（stochastic approach for link-structure analysis）等高级算法在线路运行可靠性模型产生的故障数据基础上进行数据挖掘分析，但其算法均需大量内存空间来服务于挖掘，计算效率难以保证。

实际上，针对新型电力系统连锁故障关键元件辨识，已有学者开展了相关研究，现有研究侧重于分析新能源大规模馈入后带来的潮流不确定性。文献［21］计及新能源出力随机性，运用三点估计法并结合概率潮流定义了线路过负荷风险因子。文献［22］在不同新能源渗透率下进行蒙特卡洛故障模拟，取线路平均故障时间作为脆弱性评估指标。文献［23］提出了一种考虑出力波动性的动态辨识方法。然而，鲜有研究考虑新能源机组故障电压穿越综合控制策略对关键元件辨识的影响，其与传统控保策略在故障过程中有着动态交互作用，进而影响主网的潮流分布，而电网关键元件辨识往往需要依赖于潮流结果，使电网各元件关键性也发生了改变。

因此，为深入研究新型电力系统背景下的连锁故障关键线路辨识问题，分析线路在连锁故障发展过程中的作用及其对连锁故障大停电后果的影响，本文结合最新国标提出了同时考虑风电机组和线路运行的连锁故障仿真模型。基于状态故障网络提出关键线路的失负荷风险指标以及不均匀风险指标，基于网络结构提出关键线路的脆弱结构指标，并结合模糊熵权法提出一种同时考虑失负荷程度、失负荷不均匀性以及结构脆弱性的综合评价方法。通过对IEEE 39 节点以及IEEE 118 节点算例系统的仿真分析，验证了所提方法的有效性。

1 新型电力系统连锁故障仿真模型

尽管连锁故障的传播过程复杂、影响因素众多，其主要推动因素仍是潮流转移引起的线路相继过载开断。因此，基于稳态潮流的连锁故障仿真模型因其高计算效率和高可靠性而被广泛采用。然而，新型电力系统故障发展模式趋于复杂多变，故障造成的电压扰动以及潮流转移可能诱发新能源机组大规模脱网，采用传统连锁故障模型不能有效刻画新能源接入后对连锁故障发展过程的影响，现有连锁故障仿真模型仍待改进。

在现有连锁故障模型的基础上，本文重点关注线路过载跳闸问题和新能源机组脱网问题，基于交流潮流确定电网运行状态，结合运行可靠性理论及其评估算法建立基于运行条件的元件故障概率模型，通过所建立的新能源机组脱网模型以及线路运行可靠性模型概率选择故障元件，从而模拟连锁故障演化路径。

1.1 基于风电机组端电压运行的连锁故障模拟

目前，已有学者从数据驱动［24］或从运行可靠性角度［25］对发电机停运概率进行分析。由于大规模新能源机组连锁故障的真实数据较少，小样本数据使用复杂的数据处理方法不够可靠，文献［26］考虑风电机组故障电压穿越标准，依据风电机组并网点电压值建立了风电机组脱网概率模型。然而，该模型虽考虑到不同风机厂家的差异，却并没有与最新国标的风电机组故障电压穿越能力要求［27-28］一致。本文在此模型的基础上修正了风电机组脱网概率模型。

参考文献［26］，本文采用折线模型表示风电机组的脱网概率，该模型与现行国标一致，如附录A图A1 所示。故障电压幅值分为如下5 类：

1）并网电压大于1.3 p.u.时，允许风电机组立即脱网；

2）并网电压介于1.1～1.3 p.u.之间时，脱网概率采取线性化处理；

3）并网电压介于0.9～1.1 p.u.之间时，无论故障持续时间大小，风电机组不允许脱网；

4）并网电压介于0.2～0.9 p.u.之间时，脱网概率采取线性化处理；

5）并网电压小于0.2 p.u.时，允许风电机组立即脱网。

因此，风电机组脱网概率模型的表达式如式（1）所示，式中数值都为标幺值。

式中：poff-grid为风电机组脱网的概率；VWF为风电机组并网点电压值。

1.2 基于线路运行可靠性的连锁故障模拟

线路停运受内部、外部因素共同影响。相较于连锁故障的时间尺度，线路老化、环境等因素可等效为常数，可以主要考虑潮流变化对线路故障的影响，认为线路故障概率随潮流变化而变化［29］。本文以线路有功潮流作为线路跳闸的推动因素［30］，基于运行可靠性理论分析线路停运概率，从而进行连锁故障模拟。

停运概率与线路所载潮流关系如式（2）所示。

式中：pfl，trip为停运概率；Ffl为线路的潮流值；Ffl，c为线路fl的额定传输功率；p0为线路故障概率的历史统计平均值大小，通常取0.001［31］；Ffl，max为线路fl的功率传输最大值，考虑线路潮流过载的连锁故障模拟如附录A 图A2 所示。

1.3 同时考虑风电机组和线路运行的连锁故障模拟流程

进一步，本文提出同时考虑风电机组端电压保护和线路过负荷保护的连锁故障模型，具体流程如附录A 图A3 所示。连锁故障模型仿真步骤如下：

步骤1：输入电网运行的初始参数。

步骤2：断开初始故障线路，并将线路编号加入故障链中。

步骤3：检测系统孤岛情况，参考文献［32］对每个孤岛按照内部功率情况调整机组出力或降低负荷，直至孤岛内功率平衡，进入步骤4。

步骤4：计算系统交流潮流，若潮流不收敛则按照文献［33］方法削减负荷，同时检测是否有风电机组电压超过阈值以及是否有线路潮流超过线路容量阈值并计算系统总负荷损失。若此时故障链尚未搜索到最大深度，进入步骤5，否则进入步骤6。

步骤5：对于超过电压阈值的风电机组，基于式（1）计算风电机组的脱网概率；对于超过潮流阈值的线路，基于式（2）计算线路的停运概率。模拟风电机组脱网或线路过载断开，并统计当前累计负荷损失；当同时存在多个元件故障时，依据概率按照俄罗斯轮盘赌方式［34］随机选择一台风电机组或一条线路断开，若发生元件故障，则进入步骤3，并将故障开断的线路加入故障链中。

步骤6：单次连锁故障过程结束，统计故障链及最终系统失负荷损失。

2 基于故障数据的状态故障网络方法

为了有效进行连锁故障关键线路辨识，本文借鉴文献［35］所提出的状态故障网络方法，计算所得的相关指标能准确量化系统故障阶段、线路开断和失负荷程度的关联性，为后续计算失负荷风险指标以及不均匀风险指标提供基础。

2.1 状态故障网络的结构

连锁故障仿真模型得到了大量故障数据，本文采用系统总失负荷量作为一条故障链的停电规模度量［36-37］。根据故障数据中的故障信息，一条故障链能划分为不同的系统状态和故障阶段。随着读入故障样本的不断增加，逐渐形成了状态故障网络的结构［38］。

设有一个包含Nl条线路的系统，{f(1)，f(2)，…，f(k)，f0}为所记录的一条长度为k+1 的故障线路序列，其中，f（k）表示故障线路，下标（k）表示故障线路顺序，f0为故障链终止标识，其值设定为0。采用维度为1×Nl的0-1 向量表示当前系统运行状态，其中0表示线路正常运行，1 表示线路故障。记系统初始状态为s0，则有s0=01×Nl。因此，长度为k+1 的故障线路序列{f(1)，f(2)，…，f(k)，f0}可转化得到k+1 个系统状态{s0，s1，…，sk}，其中sk表示系统有k条线路发生故障，另外Nl-k条线路仍正常在运。

将所对应的状态与故障进行配对，得到状态故障二元组序列(s0，f(1))，(s1，f(2))，…，(sk-1，f(k))，(sk，f0)。状态故障二元组序列可在状态故障网络中定位故障线路位置，该故障链构造成状态故障网络架构的过程如图1 所示。通过大量故障数据得到的故障链共同构建了状态故障网络的结构，而状态故障网络的构造过程中存在对相同状态、相同故障的筛选、合并过程。因此，状态故障网络中的状态值S和故障值F需根据状态故障网络结构和各故障链最终负荷损失来计算。

图1 状态故障网络构造过程Fig.1 Construction process of state-failure-network

2.2 状态故障网络的状态值和故障值计算

定义状态sk(j)为第k个故障阶段的第j个状态。由于故障链具有马尔可夫性质［39］，假设状态sk(j)对应的二元组序列(sk(j)，fl)的故障值F已知，则状态sk(j)的状态值S可由式（3）计算得到：

式中：Nsk(j)为故障链数据中状态sk(j)的出现次数；F(sk(j)，fl)为线路fl作为状态sk(j)后续故障的故障值；Ssk(j)为状态sk(j)的可能故障集；N(sk(j)，fl)为线路fl作为状态sk(j)后续故障的发生次数，并且有

因此，式（3）的分数因子可视为fl在状态sk(j)发生的条件概率，即

二元组序列(sk(j)，fl)的F值分别来自本条故障链的最终负荷损失Ls以及其他故障链中存在相同后续状态sk+1(i)的S值。由于采用了系统总失负荷量作为连锁故障停电规模量度，f0记录的F值等于故障数据中所记录的最终负荷损失，即

对于其他线路实际故障，其F值等于其所指向状态的S值，即

在构造状态故障网络时，各状态的发生次数和各二元组序列的发生次数可统计得到。整个状态故障网络的S值和F值可反向沿故障阶段交替计算求得，直至初始状态s0，状态故障网络架构构建顺序和计算关系如附录B 图B1 所示。

在完成S、F值交替计算后，可得状态故障网络中各状态值及二元组序列值。终端二元组序列的F值等于该故障链所记录的最终负荷损失L，终端状态的S值等于所有为该终端状态的故障链负荷损失，而前序二元组序列的F值则表示故障发生后的系统预期负荷损失。

状态故障网络中各状态的S值可表示系统在该状态下的预期负荷损失，而二元组序列的F值大小表示当前状态下该线路故障的系统连锁故障预期负荷损失。依据事故风险理论［40］，二元组序列的F值与该状态下线路发生故障概率的乘积则可表示为该状态下线路发生故障之后的连锁故障最终风险。因此，F值可用于辨识系统中的关键线路。

3 连锁故障关键线路辨识

3.1 基于失负荷程度的失负荷风险指标和关键线路辨识

为了评估相同线路在不同状态和故障阶段下的故障风险，需要将状态故障网络中相同线路故障但位于不同状态和故障阶段的F值进行筛选并汇总。本文主要针对传播阶段故障进行预防，因此在状态故障网络识别过程中排除了初始触发故障。将故障数据中各故障链到达第k个故障阶段的次数总数记为Nk，故障数据中到达各故障阶段的次数总数之和记为N。则二元组序列发生的独立概率为：

由于二元组序列的F值衡量了线路在该状态下故障后的预期负荷损失，线路fl在任意状态下故障后的风险R(sk(j)，fl)可以表示为：

最终，可以得到线路的失负荷风险指标（security risk index，SRI）ISRI如下所示：

SRI 涵盖了所有故障链中线路的失负荷量，因此该指标与线路本身的失负荷故障风险相等。SRI越高，表明线路在系统中的失负荷风险越高，因此线路越关键。

3.2 基于泰尔熵的不均匀风险指标和关键线路辨识

泰尔熵利用信息理论中的熵概念，被广泛应用于衡量组内不均匀度和组间不均匀度对于总体不均匀度的贡献情况。传统泰尔熵评估方法［41］采用开断一条线路计及其他线路电气波动量从而实现关键线路辨识，此时泰尔熵指标仅考虑N-1 故障，不能有效反映连锁故障复杂多变工况。本文基于状态故障网络能够挖掘海量故障链的故障信息，海量故障链能反映不同故障场景下的系统运行工况。在此基础上，采用泰尔熵指标能够综合考虑N-k故障场景下的线路开断失负荷不均匀度，辨识的结果更为准确。

泰尔熵区域内一阶分解公式如下所示：

式中：Tar为a区域的属性值不均匀度指标；yas为a区域第s个量的属性值；ya为a区域属性值之和；pa为a区域属性值出现的次数。

本文基于状态故障网络结构以及S、F值，按照系统线路数量分为相应区域，分别研究相同线路在状态故障网络中故障风险分布的不均匀度，为准确定位导致系统失负荷不均匀的线路提供参考。因此，泰尔熵指标可用于分析线路失负荷的不均匀性分析。

在状态故障网络中，基于泰尔熵区域内一阶分解公式可得线路的不均匀风险指标（uneven risk index，URI）IURI如下所示：

式中：Nfl为线路fl在状态故障网络中出现的次数。

由于新型电力系统的运行随机波动性较强，在连锁故障期间电力系统潮流频繁波动，本文以线路失负荷不均匀度来衡量线路断线后功率冲击在不同运行工况下的分布规律，能够在海量故障场景中合理找出导致电力系统失负荷不均匀的关键线路，避免了低失负荷变化量但高不均衡度导致的重要度评估偏差，更能有效适应高比例可再生能源系统下的实际运行工况。

3.3 基于电气介数的脆弱结构指标和关键线路辨识

电气介数考虑了系统结构和运行状态，反映了各线路在全网潮流的贡献度及其故障对系统的影响，更符合电力系统实际运行场景。目前，已有研究提出改进电气介数指标用以进行结构脆弱性评估。基于电气介数指标的线路脆弱结构指标（vulnerable structure index，VSI）IVSI定义如下：

式中：Ifl(m，n)为在发电机-负荷节点m、n间注入单位电流源后，在线路fl上引起的电流；Wm为发电机权重，一般取发电机额定容量或正常状态下的有功功率；Wn为负荷权重，一般取正常状态下的实际或峰值负荷；G和L分别为发电机节点和负荷节点的集合。

为减少计算量，利用线性线路的可加性［42］，选取系统中某一节点为参考节点，分别在其他节点与参考节点间注入单位电流源，可得各线路上产生的电流。同时，根据式（14）可计算任意发电机-负荷节点对间注入电流源的情况。

式中：Ifl(m)、Ifl(n)分别为在发电机节点m、负荷节点n与参考节点间注入单位电流源后线路fl上产生的电流。

与集中式新能源相比，分布式新能源更侧重于满足当地负荷需求。在稳态分析中，分布式新能源一般考虑为负的负荷［43］，当系统接入分布式新能源后，在连锁故障蔓延过程中进一步影响潮流转移情况，因此会对电网脆弱结构指标产生一定影响。在此情况下脆弱结构指标VSI 的定义需做如下调整：

式中：ZDG为分布式电源节点集合。

在计算脆弱结构指标中的权值min（Wm，Wn）时，若m∈ZDG，则Wm应取为新能源分布式电源额定容量。

3.4 基于模糊熵权法的综合风险指标和关键线路辨识

基于失负荷风险指标和不均匀风险指标可以衡量线路故障对失负荷程度和失负荷不均匀性的影响，基于脆弱结构指标可以考虑集中式、分布式新能源接入后不同装机容量以及负荷水平对线路关键性的影响。为了综合考虑以上3 种影响因素，本文基于模糊熵权法［44］提出线路综合风险评价指标（comprehensive risk indicator，CRI），用于辨识新型电力系统中的薄弱环节。

分别记线路fl的失负荷风险指标SRI、不均匀风险指标URI、脆弱结构指标VSI、综合风险指标CRI为gfl，1、gfl，2、gfl，3、gfl，4，具体计算步骤如下。

1）构造维度为Nl×3 的模糊隶属度矩阵R，由式（16）计算可得其元素rfl，o：

式中：gx，o（o=1，2，3）表示线路x对应的子指标值；fl=1，2，…，Nl。

2）分别计算风险指标g1、g2、g3的熵Ho为：

3）记运行人员对严重性、不均匀性、脆弱性的风险偏好权重设定为αS、αU、αV。风险指标g1、g2、g3的模糊熵权ω1、ω2、ω3计算为：

4）计算线路fl的综合风险指标gfl，4为：

根据综合风险指标CRI，即可同时考虑严重性、不均匀性以及脆弱性对关键线路进行排序，能够更全面地辨识新型电力系统中的薄弱环节，严重性、不均匀性、脆弱性的风险偏好的权重可根据运行人员的经验判断定量化，并结合具体运行场景进行设定［45］。

随着故障链数据的读入和状态故障网络的更新，若CRI 变化趋于收敛，则可以认为此时读入的故障链数量以及生成的状态故障网络已足够可靠。本文定义状态故障网络第t次更新时CRI 的变化量如下：

4 算例分析

以IEEE 39 节点和IEEE 118 节点系统为例，利用本文方法计算的CRI 实现连锁故障关键线路辨识。设定运行人员对严重性、不均匀性、脆弱性的风险偏好权重αS、αU、αV均为1，收敛阈值ε=0.000 5。

4.1 IEEE 39 节点系统算例

4.1.1 关键线路辨识

为验证本文所提方法的正确性，基于MATLAB 对IEEE 39 节点系统进行连锁故障关键线路辨识。该系统包含10 个发电机节点和46 条线路，其中，31 和32 节点替换为等容量风电场，此时新能源渗透率约为20%，如图2 所示。系统负荷量为6 254.23 MW，Ffl，max=1.4Ffl，c，初始故障为随机N-γ故障（γ≤3）。

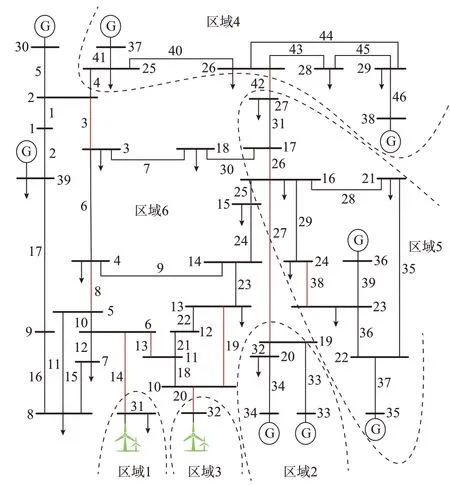
图2 IEEE 39 节点系统拓扑Fig.2 Topology of IEEE 39-bus system

下面以线路l4、l14发生断线为初始故障，举例说明故障链生成过程以及状态故障网络构建过程。初始故障发生后的连锁故障传播过程如表1 所示，故障区域如图2 所示。

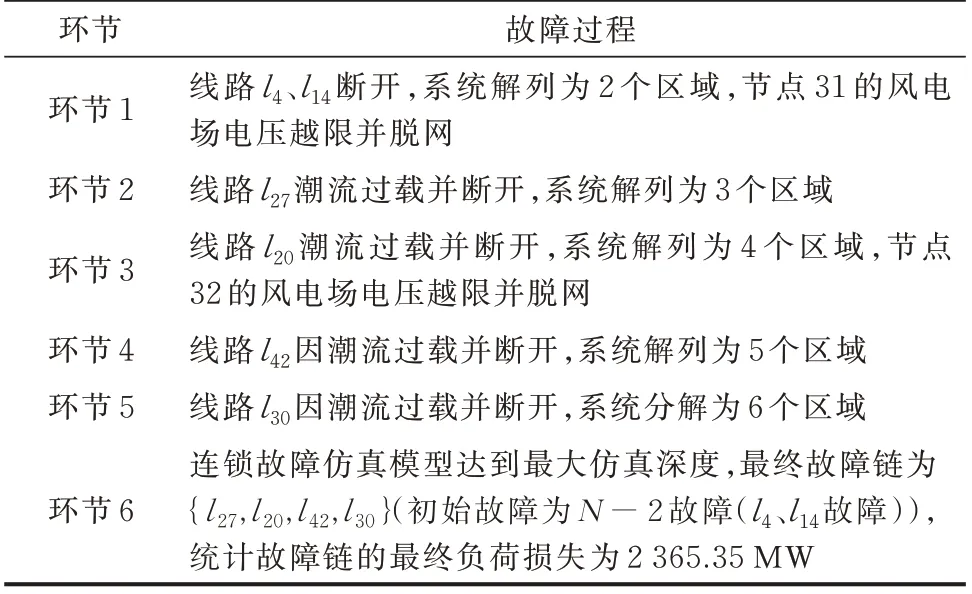
表1 初始故障发生后故障数据生成过程Table 1 Fault data generation process after initial fault occurs

本文更为关注的是在后续阶段先后故障的元件，运行人员针对传播阶段故障元件更易采取预防措施。因此，在构建状态故障网络过程中将故障链中的初始故障排除，输入状态故障网络中的该条故障链形式如下：{l27，l20，l42，l30}→2 365.35 MW。通过计算模型生成的故障数据能涵盖新能源不脱网、新能源部分脱网、新能源全部脱网等故障场景，并不断更新状态故障网络。设定每读入1 000 条故障链计算更新一次CRI，CRI 变化量指标和故障链样本的关系如附录C 图C1 所示，当更新至19 000 条故障链数据时，CRI 变化量指标低于收敛阈值。因此，本文采用19 000 条故障链来构成状态故障网络并计算CRI。 所 得 CRI 的 互 补 累 计 分 布 函 数（complementary cumulative distribution function，CCDF）如附录C 图C2 所示，在双对数坐标下，CRI分布的尾部趋于一条直线，具有幂律分布的特征。这种幂律分布表明系统中只有少数线路比其他线路更关键，连锁故障线路幂尾特性在文献［16，36］中也得到了验证。

基于本文连锁故障关键线路辨识方法，可分别计算线路的SRI、URI 和VSI，如图3 所示。可以发现，SRI、URI、VSI 在排序前10 中存在相同线路但不完全一致。这是因为SRI 所辨识的关键线路属于失负荷风险较高线路，其崩溃极易导致系统失负荷增加。URI 辨识的关键线路属于传播线路，该线路的故障极易引起系统失负荷分布不均匀，触发其他线路故障，进一步恶化故障传播。VSI 辨识的关键线路侧重于系统网络拓扑脆弱性。本文还辨别出SRI、URI、VSI 都较高的线路l3。

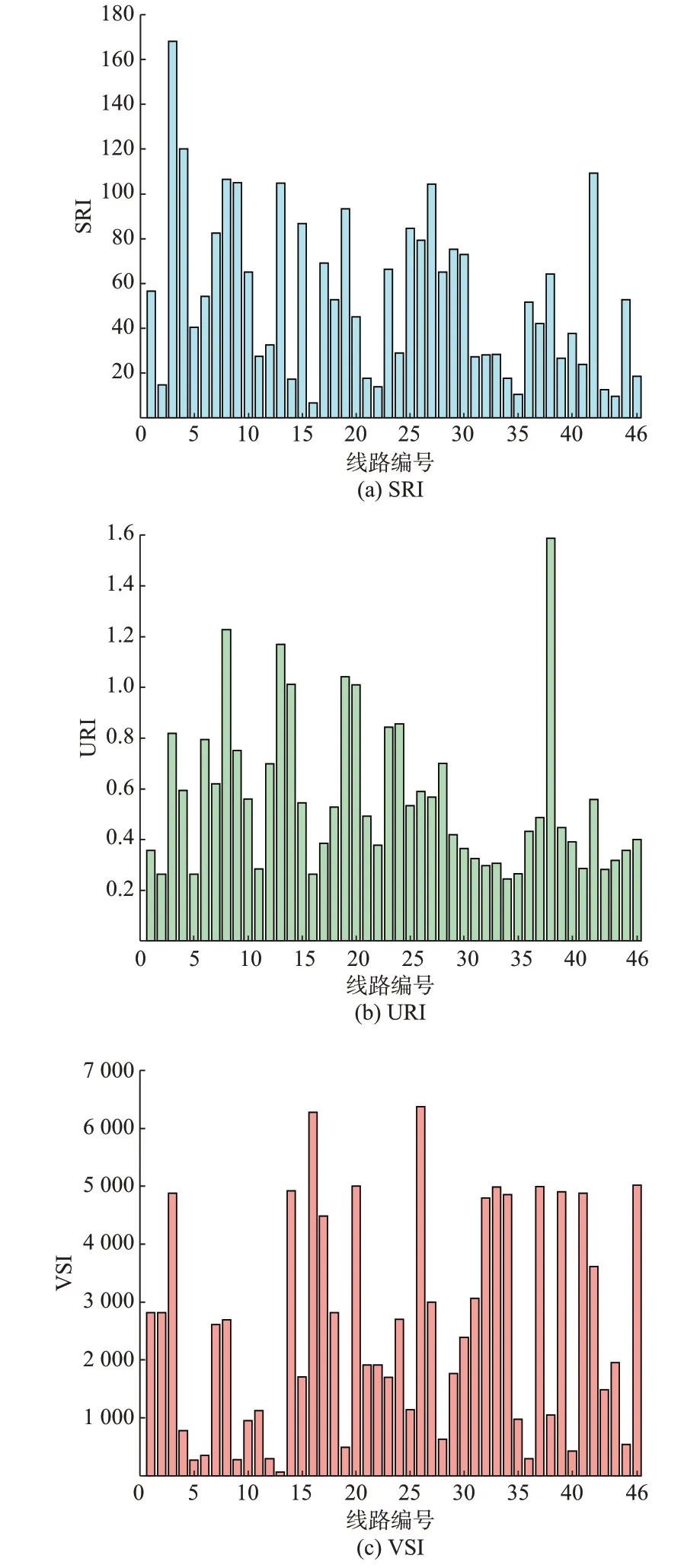
图3 IEEE 39 节点系统线路评价指标Fig.3 Evaluation indices of lines in IEEE 39-bus system

在本算例中，计算得到19 000 条故障链的时间为50 312.21 s，生成状态故障网络及计算综合风险指标的时间为2.28 s，通过本文所提方法计算的CRI指标可实现关键线路辨识。本文方法、有功潮流介数法［15］、连锁故障网络图（cascading fault graph，CFG）法［46］、频繁模式增长（FP-growth）法［18］、影响力综合指标法［47］辨识的系统关键线路如表2 所示，本文方法所辨识的系统关键线路如图2 红线所示。

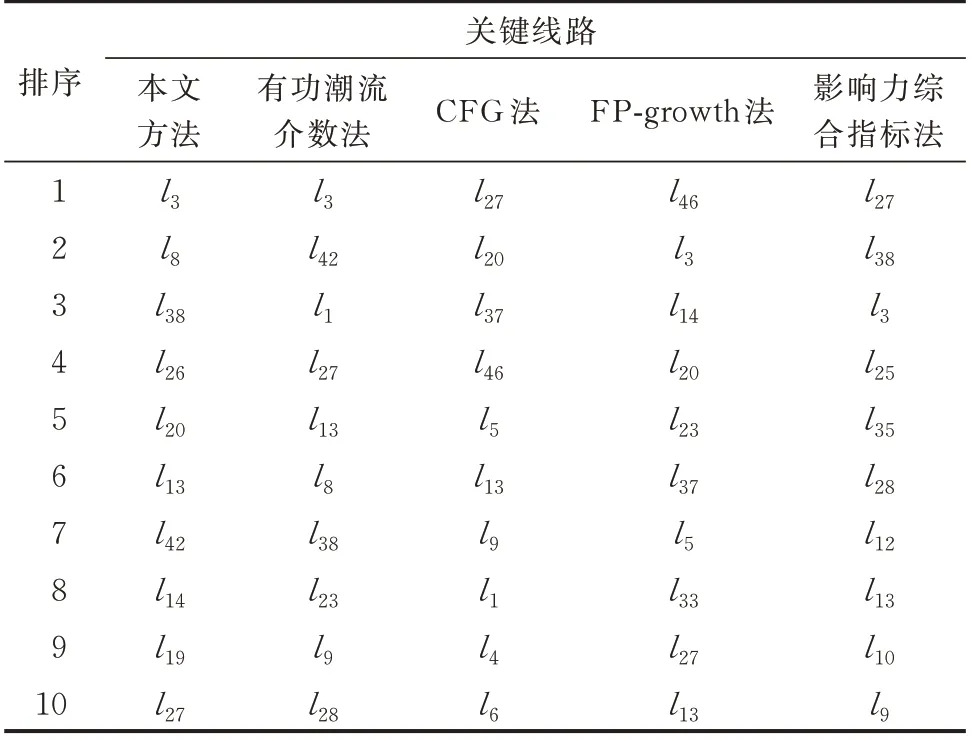
表2 5 种方法关键线路辨识结果对比Table 2 Comparison of identification results of critical lines for five methods

根据线路关键性排序结果，本文方法与有功潮流介数法、CFG 法、FP-growth 法、影响力综合指标法分别有6、3、4、5 条重合线路。4 种方法辨识的公共关键线路为l27，在图2 中位于由发电机向负荷集中区域潮流传输的重要通道。此外，发电机送出线路在本文方法中含有2 条，在CFG 法中含有3 条，在FP-growth 法中含有6 条，在有功潮流介数法和影响力综合指标法中均不含有发电机送出线路。

对于关键线路辨识结果，有功潮流介数法更关注的是电网实际潮流分布和线路输电容量的影响，其主要考虑N-1 故障情况下的潮流分布，未考虑后续连锁故障的传播过程。CFG 法虽考虑了故障的继发性传播过程，但其设置后续故障为过载最严重线路进行开断，忽略了连锁故障并发性传播的可能，不能真实反映连锁故障复杂多变的发展模式。若发电机送出线路作为故障线路，其断开极易造成潮流分布不均，发生潮流大规模转移。因此，CFG法仍包含3 条关键发电机送出线路。FP-growth 法主要考虑在故障链数据中挖掘频繁项，所辨识的关键线路为出现较为频繁的线路。因此，所辨识的关键线路含有6 条发电机送出线路。然而，该方法忽略了线路故障后产生的后果以及引起潮流分布不均的影响。影响力综合指标法综合考虑电网的拓扑结构与线路运行参数，但其并没有考虑风电机组故障电压穿越特性给关键线路辨识带来的影响。本文方法与影响力综合指标法相似，都关注系统脆弱结构和故障传播过程中的潮流分布。此外，本文方法进一步考虑了风电机组故障电压穿越特性对风电机组脱网的影响。因此，本文方法所辨识的关键线路更侧重于风电机组送出线路、传统机组送出线路以及重要潮流通道上。

由于在后续故障中存在对故障元件的概率选择开断过程，本文所提出的连锁故障仿真模型同时考虑了并发性故障和继发性故障，更能有效反映连锁故障蔓延趋势，所辨识的关键线路需要承担较大潮流转移或其位置较为关键，更容易由于潮流转移、电压越限导致系统潮流分布不均或关键元件开断，进而扩大故障传播。此外，在相同故障链数据的基础上，基于FP-growth 法的计算时间为3.87 s，大于本文方法所需的计算时间2.28 s，说明本文所提关键线路辨识方法具有较高的计算效率。

进一步考虑分布式新能源接入后对关键线路辨识结果的影响。在上述IEEE 39 节点系统中的负荷节点21、28 处分别接入额定容量为50 MW 的风电场，在本文中不考虑分布式电源的故障电压穿越特性，其余条件保持不变。同样采用本文方法，接入分布式电源和未接入分布式电源的关键线路辨识结果对比如表3 所示。

表3 接入分布式电源前后关键线路辨识结果对比Table 3 Comparison of critical line identification results with and without distributed generators

从表3 可以看出，接入分布式电源前后在前10 条关键线路中有9 条重合线路，说明了即使电网运行方式发生改变，这些线路依然承担着重要的作用。在分布式电源接入后，原先较为关键的线路l27排在了10 名以外，这是由于负荷节点21、28 接入的分布式电源等效为负的负荷，减少了系统右上方区域的负荷需求，改善了局部功率平衡，从而降低了联络线l27在系统中由发电机向负荷集中区域的传输作用。

4.1.2 结果验证

关键线路上施加的缓解措施可用以验证辨识结果的有效性。在连锁故障传播过程中，为避免潮流转移引起的保护不合理动作，本文采取将线路后备保护过载跳闸闭锁，使待闭锁线路的停运概率降低90%［48］，从而快速消除线路过载故障。将所辨识的线路按照CRI 降序排列分成3 组，分组如表4 所示。

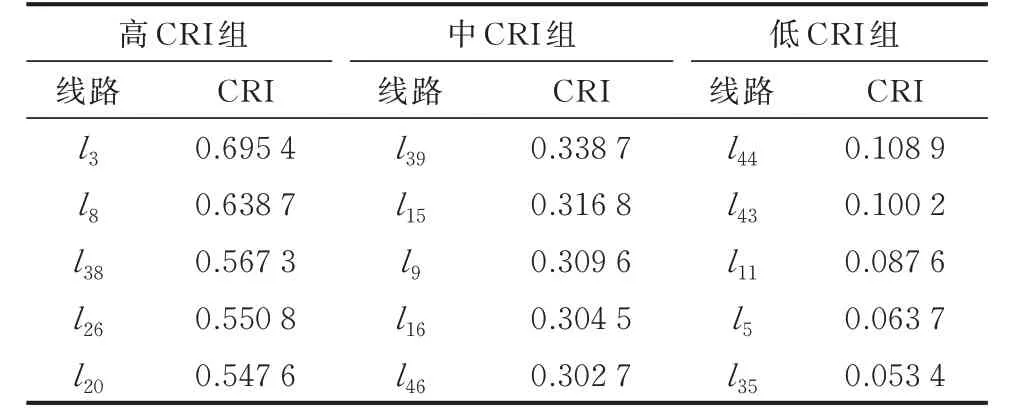
表4 IEEE 39 节点系统分组CRITable 4 Grouped CRI in IEEE 39-bus system

在表4 中，高CRI 组排序为1 至5，中CRI 组排序为18 至22，低CRI 组排序为42 至46。在系统中分别将3 组线路的停运概率降低至原概率的10%后进行连锁故障仿真，以系统失负荷量来衡量连锁故障风险大小。统计分组施加缓解措施后连锁故障风险与系统原风险的情况对比，结果如图4 所示。

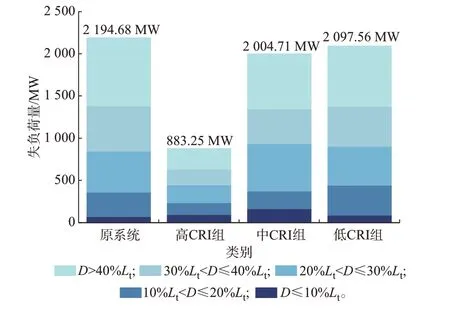
图4 IEEE 39 节点系统分组施加缓解措施风险与系统原风险对比Fig.4 Comparison between risk after applying mitigation measures in groups and original risk in IEEE 39-bus system

从图4 可以看出，对线路施加缓解措施能降低系统的连锁故障风险，3 组缓解措施分别使失负荷量从2 194.68 MW 降至883.25 MW、2 004.71 MW和2 097.56 MW。同时，3 组线路中，高CRI 组中的线路作为被识别的最关键线路，施加缓解措施后能够最大程度降低连锁故障风险。此外，高CRI 组线路施加缓解措施后，可更有效地降低高事故等级［45］（系统累积失负荷D≥30%Lt，Lt为系统总负荷）连锁故障风险，说明本文所提方法辨识的关键线路对应采取缓解措施能更有效地阻断连锁故障的蔓延发展。

为了验证本文方法的有效性，将其与CFG 法和影响力综合指标法两种方法辨识的5 条最关键线路分别施加缓解措施后进行连锁故障仿真，连锁故障风险对比结果如附录C 图C3 所示。

由附录C 图C3 可知，通过对本文方法所辨识的关键线路施加缓解措施后，失负荷量从2 194.68 MW 下降到883.25 MW，采用CFG 法下降到1 593.97 MW，采用影响力综合指标法下降到1 355.07 MW，说明本文方法仍能显著降低高事故等级的连锁故障风险。结果验证了对本文方法所辨识的关键线路施加缓解措施后，能最大程度降低连锁故障大停电风险。

分别取本文模型、基于直流潮流的稳态模型［49］的2 000 条故障链数据，得到两种模型的停电规模分布曲线，如附录C 图C4 所示。两种模型的双对数曲线呈现典型连锁故障幂律特征，且具有一致的失负荷分布，从而证明了本文模型的正确性。

为了验证本文模型的有效性，在本文模型、基于直流潮流的稳态模型以及基于稳定计算的暂态模型［43］生成的故障链数据基础上，采用本文方法辨识前5 条最关键线路结果，如表5 所示。

表5 3 种模型关键线路辨识结果对比Table 5 Comparison of critical line identification results for three models

对比表5 的辨识结果可知，本文模型与直流模型所辨识的关键线路有3 条重合线路，与暂态模型所辨识的关键线路虽在排列顺序上有差异，但关键线路全部重合。将3 种模型所辨识的5 条最关键线路分别施加缓解措施后进行连锁故障仿真，连锁故障风险对比结果如附录C 图C5 所示。通过对本文模型、暂态模型所辨识的关键线路施加缓解措施后，失负荷量从2 194.68 MW 下降到883.25 MW，采用直流模型下降到1 011.47 MW，说明对本文模型与暂态模型所辨识的关键线路施加缓解措施后，能最大程度降低连锁故障大停电风险。

4.2 IEEE 118 节点系统算例

IEEE 118 节点系统包含54 个发电机节点和186 条线路，其中，69 节点、80 节点、92 节点替换为等容量的风电场，此时新能源渗透率约为15%，系统负荷量为4 242 MW，Ffl，max=1.4Ffl，c，初始故障为随机N-γ故障(γ≤3)，生成54 000 条故障链数据时达到收敛条件。此时，系统中线路CRI 的CCDF如附录C 图C6 所示，所得线路CRI 的CCDF 在双对数坐标下同样具有幂律分布的特征。

将本文方法与CFG 法辨识的结果进行对比，两种方法关键线路辨识结果如表6 所示。通过本文辨识的关键线路排序可以看到，排序靠前的线路位于重要的潮流传输通道上和风电机组送出线路上，起到将功率输送到负荷集中区域或将功率集中转移到几条线路上，其中风电机组出线包括l106、l108、l116、l119、l127共计5 条，关键线路的先后断开将增加连锁故障大停电风险，且两种方法有4 条重合线路。CRI进一步反映了风电机组因故障电压穿越失败后引起潮流转移的特性，其辨识结果更符合含高比例新能源电力系统的运行场景。

表6 两种方法关键线路辨识结果对比Table 6 Comparison of critical line identification results for two methods

将所辨识的线路按照CRI 降序排列分成3 组，每组10 条线路，如表7 所示。同样地，分别对3 组采取缓解措施，其停电风险结果如图5 所示。

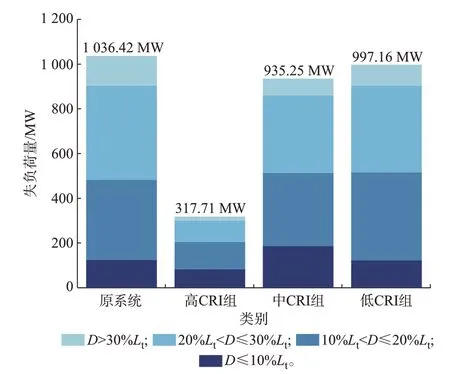
图5 IEEE 118 节点系统分组施加缓解措施后连锁故障风险对比Fig.5 Comparison of cascading failure risk in IEEE 118-bus system after applying mitigation measures in groups

由图5 可知，对线路施加缓解措施能降低系统的连锁故障风险，3 组缓解措施分别让失负荷量从1 036.42 MW 降低至317.71、935.25、997.16 MW。3 组线路中，高CRI 组中的线路作为被识别的最关键线路，施加缓解措施后能够最大程度降低连锁故障风险，且更有效地降低高事故等级（D≥30%Lt）连锁故障风险，再次验证了本文方法的有效性。

5 结语

本文结合最新国标建立了同时考虑风电机组和线路运行的连锁故障仿真模型；基于状态故障网络提出了失负荷风险指标和不均匀风险指标；基于电气介数提出了脆弱结构指标，结合模糊熵权法最终提出综合风险指标用于关键线路辨识。所述方法基于连锁故障仿真模型生成的故障数据，并通过综合考虑线路的失负荷程度、失负荷不均匀性以及结构脆弱性，能够准确辨识出造成严重大停电后果和加速连锁故障蔓延的关键线路。通过IEEE 39 节点系统和IEEE 118 节点系统的算例验证了所提方法在连锁故障传播分析和关键线路辨识的有效性。本研究为实施基于关键阻断点辨识的阻断控制策略提供了新的思路，下一步将研究连锁故障控制保护协同阻抑方法。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。