适用于直流链式储能的电池簇荷电状态自均衡控制策略

张文昕，赵志勇，于华龙，王继慷，赵志芳，韩 峰

（北京四方继保自动化股份有限公司，北京市 100085）

0 引言

随着“碳达峰·碳中和”目标的提出，直流微电网因其无须考虑无功功率、谐波电流、交直流转换损耗的优势，逐渐成为目前的研究热点［1-2］。其中，储能技术凭借其可以有效解决可再生能源发电的间歇性、波动性问题以及提高电网可再生能源消纳能力的优势，逐渐成为智能电网发展过程中的重要环节［3-4］。

电池储能系统（battery energy storage system，BESS）具有功率密度高、响应速度快、安装方便等优点［5］，近年来得到了快速发展。其中的储能变换器［6］更是储能系统中的关键组成部分。链式变换器（cascaded H-bridge converter，CHBC）将电池分散接入各级联全桥子模块的直流侧，解决了电池间的环流问题。同时，链式变换器可以省去工频变压器，直接接入中高压电网，目前已经获得了业内的广泛关注［7-8］。由于制造工艺等因素导致电池单体的容量、内阻、自放电率等内部特征存在差异［9］，电池单体通过串、并联成簇后，这种初始差异被进一步放大。电池簇差异在储能系统运行中表现出荷电状态（state of charge，SOC）不均衡。储能系统中最先达到充电上限或放电下限的电池是制约储能系统可用容量的关键因素［10-11］。

针对电池SOC 不均衡问题，以往的研究根据均衡电路的拓扑结构可以大致分为两类：能量耗散型电路和非耗散型电路［12］。能量耗散型电路中，文献［13］通过开关将电阻并联在电池单体两端构成均衡电路，以热形式消耗电压较高的电池单体的电能。该方法控制简单、易于实施，但此类拓扑结构会导致电能浪费，同时电阻发热可能会影响系统运行。

非耗散型电路中，通过转移电池能量来减小电池SOC 不均衡，一般又可大致分为电容、电感、变压器、变换器4 类均衡拓扑结构。文献［14］基于电容均衡拓扑，利用电容的储能特性，根据电池压差控制开关选通从而实现电池之间的能量流动。电容均衡拓扑易于实现、可靠性高，但更适用于对均衡精度要求不高的场合。文献［15］基于电感均衡拓扑，利用电感电流不能突变的特性，以电流的形式转移相邻电池单体的能量。由于该均衡拓扑对相邻电池单体的压差要求小，更适用于在充放电末端变化快的电池体系。文献［16］基于变压器均衡拓扑将电池组的部分能量储存在变压器绕组中，通过互感传递到另一绕组，通过选控开关使能量转移到需要均衡的电池组中。该均衡拓扑均衡速度快，但变压器绕组的存在增加了电路成本和体积。

变换器的均衡拓扑性能好、集成度高，是目前非耗散型均衡拓扑的主要发展方向之一。文献［17］基于高压直流直挂储能装置，提出一种子模块SOC 排序的改进型最近电平逼近调制策略，方法简单易于实现，但对模块数量敏感。文献［18-19］基于全桥变换器研究了线路阻抗和公共阻抗导致的SOC 不均衡，并提出均衡控制策略，减少了阻抗对电流负荷分配的影响，实现了储能单元SOC 自动均衡。文献［20-22］针对交流链式储能，提出注入零序电压或负序电压的复合SOC 均衡控制策略，通过改变相内各储能单元的调制信号来实现相间或相内SOC 均衡。但是，以往的研究仍存在以下局限性：1）固定SOC均衡参数的方法过于依赖输入参数的人为选择，不能跟随储能系统当前运行工况进行调节，应用场景有限；2）均衡策略的时间复杂度较高，需要更多的计算时间和运行内存，实时性不足。

针对以上弊端，本文以直流链式储能系统（cascaded H-bridge converter-battery energy storage system，CHBC-BESS）为研究对象，在分析链式结构拓扑的基础上，研究CHBC-BESS 的控制策略。同时，提出了一种综合考虑电池SOC 偏差、模块电容电压、直流系统电压控制裕度以及输出调制比上下限的SOC 自均衡控制策略。该策略每个控制周期进行一次SOC 均衡系数计算，能够实现控制参数实时自适应。首先，本文分析CHBC-BESS 拓扑结构；然后，研究CHBC-BESS 的整体控制系统与控制策略；接着，研究簇间电池SOC 自均衡控制策略；最后，分别在硬件在环实时仿真系统和实机装置上进行实验，验证了本文所提均衡策略的有效性。

1 基于链式结构的直流BESS

CHBC-BESS 主电路图如图1 所示。链式储能变换器由N个非隔离型DC-DC 模块串联构成，通过滤波电抗直接接入直流系统中。在该拓扑结构下，多个电池组串联形成电池簇，各簇电池在直流端无须直接连接，而是分散连接在对应功率模块的电容侧［7］。

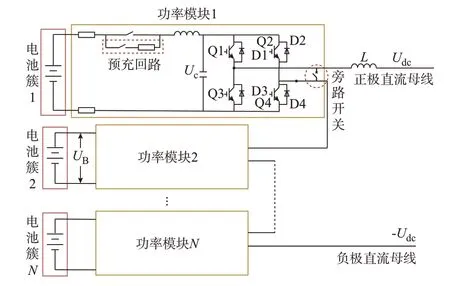
图1 CHBC-BESS 主电路拓扑Fig.1 Topology of main circuit of CHBC-BESS

功率模块由全桥变换电路及其驱动电路、母线电容、直流熔断器、旁路开关和电池侧预充电装置组成。其中的旁路开关可以隔离故障的功率模块，避免储能系统因单一模块故障导致整个系统停运，提高系统可靠性。电池预充回路能够在系统冷启动的时候降低电容充电电流，保护功率模块内的元件不会因瞬时电流而击穿损坏。该拓扑结构下，各簇电池分散在各子模块中，只须保证各模块一一对应的电池簇之间的SOC 均衡即可，无须保证整套系统的每块电池单体SOC 严格均衡，减少了需要管理的电芯数量［21］。

全桥变换电路在实际运行时分为升压模式和降压模式［6］，当功率由电池流向直流母线时，模块在降压模式下运行；当功率由直流母线流向电池时，模块在升压模式下运行。对于全桥变换电路，本文采用脉宽调制（pulse-width modulation，PWM）方式，定义调制比为调制波幅值与三角载波幅值之比。

该拓扑结构下，级联的功率模块数量N主要取决于电池簇的输出电压UB和直流系统电压Udc。当各簇电池电压之和低于直流系统电压时，直流母线会通过功率模块对电池进行不可控充电。因此，电池最小运行电压需大于直流系统电压。综合考虑直流系统电压裕度、调制比、电池最小运行电压等因素，计算链式结构中模块数量如式（1）所示。

式中：kv为直流母线电压裕度；km，max为最大调制比；UB，min为电池最低运行电压；■·■ 表示向上取整；Nrd为模块冗余数量。

2 CHBC-BESS 的整体控制

2.1 整体控制系统

CHBC-BESS 的控制系统由监控层、主控层和模块控制层构成。整体控制系统示意图如附录A图A1 所示。图中：监控层由监控系统组成，主要负责系统电气量和电池状态的数据采集以及分合闸控制；主控层由一台主控制器构成，主要负责控制算法以及下发控制命令，同时接收由电池管理系统（battery management system，BMS）采集的电池信息；模块控制层由N套模块控制器构成，每个功率模块均对应一套模块控制器，接收主控制器的控制命令并控制模块内的开关分合以及开关管的开通关断，即每簇电池对应的模块可以受控制器单独控制独立调节。模块控制器能够独立接收主控制器不同的控制命令是实现本文所提SOC 自均衡控制策略的通信基础。

2.2 整体控制策略

根据不同应用场景下的需求，CHBC-BESS 可以在功率控制模式（power control mode，PCM）和电压控制模式（voltage control mode，VCM）之间进行灵活切换［22］。在PCM 下，主控制器根据功率指令对电池簇的充放电功率进行闭环控制，通过调整各功率模块的调制波实现对各电池簇充放电功率的控制。在VCM 下，主控制器根据电压指令稳定直流链式储能的电压值，为直流母线提供电压支撑。

考虑CHBC-BESS 在各模式下的电池均衡需求，本文采取分级控制策略。第1 级控制为当前运行模式的基础控制，输出该模式下的基础调制波；第2 级控制为各模块的均衡控制，输出该模块的调制波补偿量ΔUm。两级控制的输出经叠加，即基础调制波叠加模块调制波补偿量最终得到各模块的调制波总输出。本节主要介绍第1 级基础控制，第2 级模块均衡控制中ΔUm的具体计算方法将在下一章详述。

CHBC-BESS 分级控制框图如图2 所示。

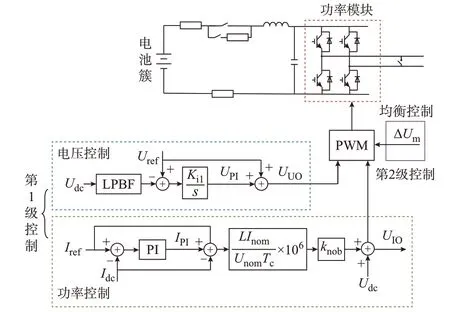
图2 CHBC-BESS 分级控制框图Fig.2 Hierarchical control block diagram of CHBC-BESS

功率控制采用无差拍控制，由电流外环比例-积分（proportional-integral，PI）控制和无差拍内环控制组成。图2 中：Uref为电压指令值；UPI为电压外环补偿输出；Ki1为电压环积分系数；UUO为电压环输出，作为电压模式下的调制波基础输出；Idc为直流系统电流采样值；Iref为直流系统电流指令值；IPI为电流外环补偿输出；1/s为积分环节；f为无差拍参数的标幺值；knob为无差拍系数；UIO为电流环输出，作为功率模式下的调制波基础输出。其中，无差拍参数的标幺值计算如式（2）所示。

式中：L为桥臂电抗值；Unom、Inom分别为直流电压、直流电流标幺化的基准值；Tc为控制周期。

电压控制采用闭环PI 控制，电压外环由电压指令前馈和电压反馈累加器组成。电压反馈可以通过快速更新数据来补偿因阻抗等原因造成的电压偏差，同时保证系统稳定性。

3 电池簇间SOC 自均衡控制

第2 级模块均衡控制的输出为各模块的调制波补偿量ΔUm。簇间SOC 自均衡的思路是通过第2级模块均衡控制实时调整各簇电池对应模块的调制波，对电池实施差异化充放电。充电时提高SOC 小的电池的充电电流，并降低SOC 大的电池充电电流；同理，放电时提高SOC 大的电池的放电电流，并降低SOC 小的电池的放电电流，从而达到各簇电池SOC 逐渐趋于一致的效果，实现电池自均衡控制。

在此基础上定义模块i的调制补偿量计算公式如式（3）所示。各模块的调制波补偿量受到该簇电池SOC 的偏移程度、系统功率方向、SOC 均衡系数共3 部分的影响，其中的SOC 均衡系数的计算是第2 级控制的核心部分。

式中：ΔUm(i)为模块i的调制波补偿量；ksoc为SOC均衡系数，为非负数；Si为第i簇电池的SOC，由BMS 提供；Save为链式结构中各簇电池SOC 的平均值；Isgn为电流方向标志位，为1 时表示放电、为-1时表示充电。

模块调制波补偿量ΔUm的计算流程描述如下：

1）判断SOC 自均衡启动条件。首先，计算簇间SOC 的最大值Smax、最小值Smin和平均值Save，将各簇电池SOC 与平均值进行比较，当任一簇电池SOC 与平均值的差值超过SOC 均衡启动阈值时，启动簇间SOC 自均衡控制。

电池簇的SOC 均值可由式（4）计算。为了衡量簇间SOC 偏移程度，定义簇间SOC 峰谷差、SOC 方差，分别由式（5）、式（6）计算。

式中：N为BESS 中电池簇数量以及功率模块数量；ΔS为SOC 峰谷差；V(S)为SOC 方差。

2）判断当前时刻电流方向。对当前直流系统电流和电流方向判断阈值进行滞环比较，得到电流方向标志位如式（7）所示。

式中：Ik1为电流方向判断阈值。

3）根据储能系统输出电压目标值和模块数量计算单模块输出电压目标值范围。

式中：Um，max、Um，min分别为输出电压目标值范围的上、下限；α1、α2分别为输出电压上限系数和输出电压下限系数，一般分别取1.1 和0.9；αUref表示储能系统需满足的输出电压可调范围，除以N表示平均到每个模块上的输出电压目标值范围。

4）综合考虑电池SOC 偏差、模块电容电压值、直流系统电压控制裕度、模块电压可调范围，实时计算均衡系数ksoc。由于SOC 不均衡，导致电池电压不均衡以及各模块电容电压不均衡，存在最大模块电容电压Uc，max、最小模块电容电压Uc，min。考虑受到最小脉宽限制的全桥变换电路调制比范围，各模块输出电压的可调范围上限为km，maxUc、下限值为km，minUc，其中，km，max、km，min分别为最大、最小输出调制比。

为了保证在输出电压目标值范围内任意电压目标值下的各模块均可控，要求各模块可调范围必须大于模块输出电压目标值范围。定义SOC 自均衡控制的可调范围，即输出电压目标值范围以外的模块电压可调范围。综合考虑均衡速度以及系统安全性，定义模块最大安全调制余量。

式中：ΔU+为正方向最大安全调制余量；ΔU-为负方向最大安全调制余量。为了较快地均衡速度、保证模块安全、防止不可控充电，要求电容电压最小的模块在最大调制比的情况下大于输出电压目标值的上限。

同理，要求电容电压最大的模块在最小调制比的情况下小于输出电压目标值的下限。定义正、负方向SOC 最大偏差为：

式中：ΔS+为正方向SOC 偏差；ΔS-为负方向SOC偏差。

在正、负方向最大安全调制余量的基础上，引入正、负方向SOC 最大偏差值计算正、负方向SOC 均衡系数。例如，模块1 电容电压最大、SOC 最大，即模块1 放电余量最大、充电余量最小；同理模块2 电容电压最小、SOC 最小，即充电余量越大、放电余量最小。在Isgn=1 的放电工况下，正方向SOC 均衡系数的计算引入模块1 的Smax定义为ΔU+/ΔS+。负方向SOC 均衡系数计算时，由于此时km，minUc，max小于输出电压目标值下限，即在负方向最大调制余量的情况下只能进行可控充电。因此，对ΔU-取反来定义放电工况下的负方向SOC 均衡系数为-ΔU-/ΔS-。同样地，在Isgn=-1 的充电工况下，负方向SOC 均衡系数定义为ΔU-/ΔS+。由于此时正方向最大安全调制余量处只能进行可控放电，对ΔU+取反来定义充电工况下的正方向SOC 均衡系数为-ΔU+/ΔS-。

在充放电工况下，取正、负方向SOC 均衡系数中较小值作为该工况下最终SOC 均衡系数，具体定义如式（14）所示。

5）如式（3）所示，根据实时计算出的SOC 均衡系数计算各个模块的调制波补偿量。

SOC 自均衡控制输出的各模块调制波补偿量，叠加上基础调制波即可得到各模块的最终输出调制波。因此，通过单独控制各模块的调制波，进而实现对电池充放电电流的分别控制，同时保证了自均衡控制前后的直流链式储能装置输出保持不变。SOC 自均衡控制计算框图如图3 所示。

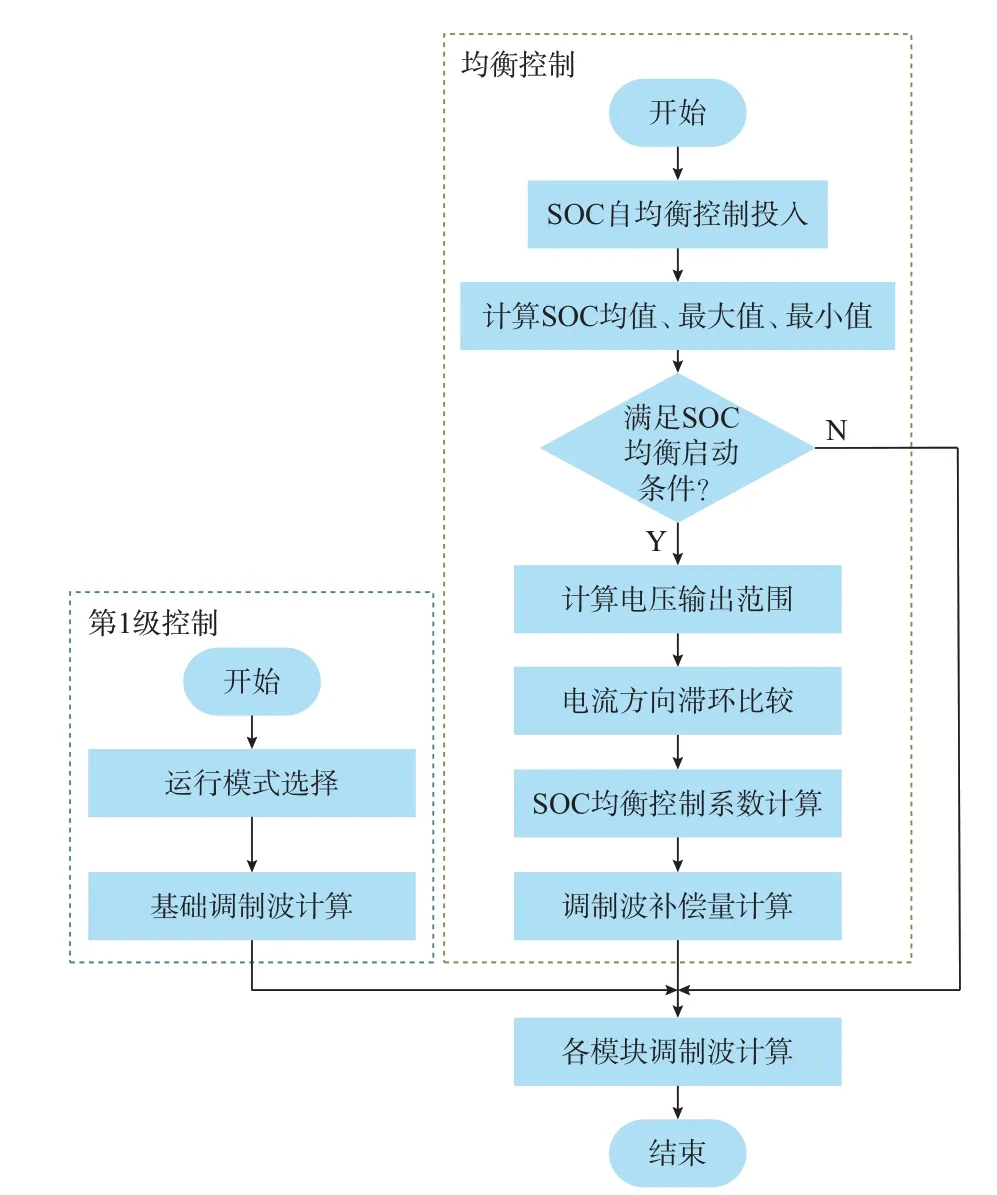
图3 SOC 自均衡控制计算框图Fig.3 Calculation block diagram of SOC self-equalizing control

本文所提算法在时间复杂度和空间复杂度上均为O（n）。随着储能系统电池数量规模增加，仍有较好的时间性能和内存空间性能。

4 实验验证

4.1 装置参数

储能系统选用磷酸铁锂电池，装置主要参数见附录A 表A1。主控制器选用Zynq 芯片，Zynq 芯片是结合ARM 处理器与现场可编程门阵列（field programmable gate array，FPGA）为一体的架构。其中，ARM 处理器主要完成以下功能：1）与上位机进行通信，接收功率指令和电压指令等；2）与BMS 进行通信，通过控制器局域网（controller area network，CAN）接收BMS 信息；3）从FPGA 读取系统采样信息，完成主要控制算法。FPGA 主要负责与单元板和模块控制器进行通信，获取模块控制器的状态和电气量采样数据，等待ARM 处理器的读取。模块控制器的主要功能是将接收到的调制波转换输出为PWM 信号，控制开关管的开通关断，进而控制电池簇的充放电电流。

4.2 实验验证

基于实时数字仿真（real-time digital simulator，RTDS）平台，搭建了硬件在环实时仿真系统来验证所提簇间SOC 自均衡控制策略的有效性。硬件在环实时仿真系统主要包含RTDS 主机、控制器及接口开发板，可实现电力电子设备快速仿真模型的短步长仿真计算，模拟控制系统的计算精度、链路延时等带来的实际影响，实现对控制算法执行效果的准确验证。

利用硬件在环实时仿真系统设计了以下实验：1）在未投入SOC 均衡控制的情况下，进行直流链式储能的充放电实验；2）在满功率放电的工况下，进行投入SOC 均衡控制前后的对比实验；3）在投入SOC 均衡控制的情况下，进行满功率的充放电切换实验；4）充电状态下的均衡效果对比实验。

值得说明的是，本文所提的SOC 自均衡控制方法在电压模式和功率模式下并不存在原理区分，该方法只区分充电和放电工况。因此，选取功率模式对充电和放电两种工况进行实验验证。

4.2.1 未投入SOC 均衡控制的充放电实验

在不投入SOC 自均衡控制的情况下，进行一次满功率的充放电切换阶跃实验。选取SOC 不一致的3 簇电池绘制满功率切换下的波形图，波形图见附录A 图A2。由图A2（a）可见，在18 s 时刻进行一次满功率的充放电切换实验。此时，功率指令由2 MW 改变为-2 MW。在Δt1=0.4 s 内正极直流电流由100 A 阶跃到-60 A，再根据设定的爬坡速率爬坡至-100 A。由图A2（b）可见，不投入SOC均衡控制的工况下，SOC 间的不一致性不会缓解，此时的SOC 峰谷差ΔS约为40%。

电池继续以2 MW 的功率进行充电，直到电池充到电压截止上限，绘制储能系统停运波形如附录A 图A3 所示。在不投入SOC 自均衡的情况下，第1簇电池即SOC 最高的电池会首先充电到电池运行电压上限，从而导致整个储能系统停运，可见SOC不均衡会严重限制储能系统容量的使用率。

4.2.2 SOC 自均衡实验

为了验证簇间SOC 自均衡控制策略的有效性，模拟SOC 不一致性，第1 簇、第2 簇、第3—34 簇电池起始时刻的SOC 分别为69%、53%、60%，在此选取电池第1—3 簇作为典型电池簇绘制波形图。储能系统运行在放电功率为2 MW 的功率模式，第16 s 时，投入SOC 自均衡控制。绘制SOC 均衡投入前后波形图见附录A 图A4。

在投入SOC 均衡的前一时刻，第1 簇、第2 簇、第3—34 簇的SOC 分别为64%、48%、56%，此时SOC 峰谷差为16，且各模块的调制波基本相同。在16 s 时刻投入SOC 均衡，实时计算出均衡系数约为0.028，此时SOC 大于均值的电池簇1 调制波增大，即放电电流增大；SOC 小于均值的电池簇2 调制波减小，即放电电流减小；约等于SOC 均值的电池簇3调制波几乎不变。该调制波的变化符合式（3）的理论。附录A 图A4（a）中，均衡投入前后直流母线电流几乎没有变化，可以说明SOC 均衡只改变电池簇间的差异化放电，并不改变母线传输功率。由图A4（b）可见，经过30 s 的持续均衡控制，在第60 s 时第1 簇，第2 簇和其余电池簇的SOC 分别为49.6%、42.4%、39.2%，均衡期间SOC 峰谷差逐渐减小到10.4%。在该工况下持续放电1 min 后的SOC 变化如图4 所示。

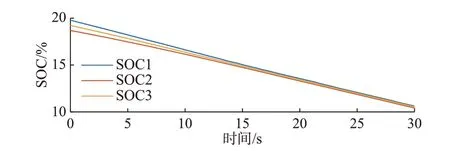
图4 放电状态下的SOC 均衡过程Fig.4 SOC equalizing process in discharging state

在SOC 均衡投入的情况下持续放电近2 min后，最终各电池簇的SOC 均为10.5%左右，达到均衡状态。

为验证本文所提策略在满功率充放电切换的极端工况下的有效性，设计实验改变功率指令由2 MW 变为-2 MW，即从2 MW 放电阶跃到2 MW充电，绘制波形图见附录A 图A5。由图A5（b）可见，峰谷差ΔS由21.7%降低为19.3%，再进一步降低至17.3%。对比图A5（b）、（c）可见，当前放电状态下，SOC1＞SOC3＞SOC2，此时模块1 的调制波最大、模块2 的调制波最小。在发生充换电状态改变时，调制波也发生改变。阶跃到充电状态下时，模块1 调制波最小而模块2 的调制波最大。可以简要总结为SOC 大的电池少充多放、SOC 小的电池多充少放。因此，认为本文所提均衡策略在充电状态、放电状态以及充放电快速转换的极端工况下均能稳定实现SOC 的自均衡控制。

可见，本文提出的簇间SOC 自均衡控制无论在充电状态还是放电状态均能达到较好的均衡效果，使簇间SOC 趋于一致，且不会改变系统总功率，仅改变功率在电池簇之间的分配。

4.2.3 均衡效果对比实验

本节对比SOC 自均衡控制、SOC 恒定均衡系数控制、基于排序算法SOC 均衡控制的均衡效果。在充电工况下，设置电池簇SOC 初始值分别为50%、52%、54%、56%、58%、60%，SOC 恒定均衡1和SOC 恒定均衡2 的系数分别取0.01、0.02，均衡过程的电池簇SOC 方差见图5。

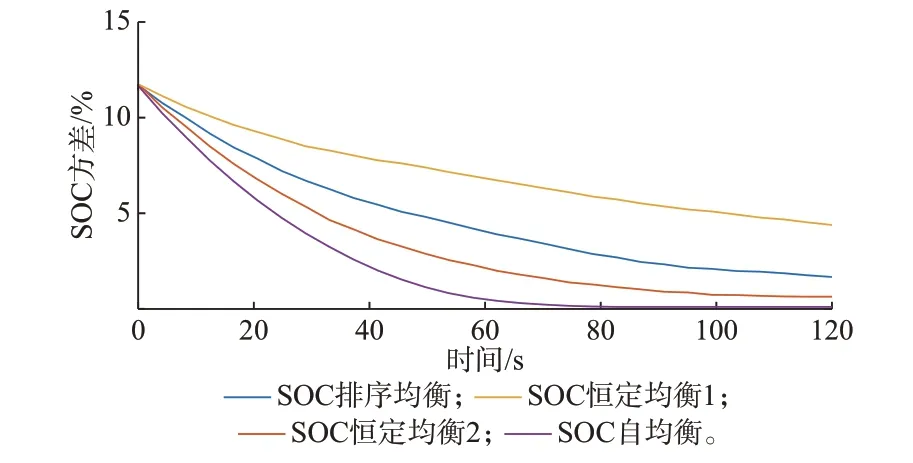
图5 充电状态下电池簇SOC 方差图Fig.5 SOC variance diagram of battery cluster in charging state

由图5 可见，3 种方法均可以降低电池簇SOC不均衡程度。基于排序的SOC 均衡控制方法均衡效率较优，但是本文设置的实验条件为6 簇电池中有1 簇可用于投切，在实际运行中考虑到成本问题很难达到如此高的可投切比例，实际均衡效果会被进一步削弱［17］。SOC 恒定均衡系数控制的均衡效果与均衡系数的选择相关，为了达到较好的均衡效果，需要预先通过仿真选择一个合理的均衡系数。而SOC 自均衡控制能够在不同的工况自适应调整均衡系数，无需额外的冗余电池成本，均衡效果较好。

4.3 实机装置

本文所提的SOC 自均衡策略已经在实际的直流链式储能装置中应用。目前，该直流链式储能装置已经应用在国家重点研发计划项目的配套工程现场。附录B 图B1、图B2 分别为直流链式储能实机装置的外观图和内部图。

在2 MW 功率放电的实际工程工况下，随机选取3 簇电池，绘制电池SOC 和电池电流变化，如附录B 图B3 所示。由图B3（a）可见，虽然实际工程中SOC 的变化缓慢，但对比图B3（a）、（b）可见，在放电状态下，SOC 最高的电池簇1 的放电电流最大，SOC 最小的电池簇3 放电电流最小。因此，本文所提方法在工程应用上通过对各模块的独立控制可以实现各簇电池的差异化充放电。

5 结语

本文对CHBC-BESS 的簇间SOC 均衡问题进行了研究，分析了CHBC-BESS 在功率模式和电压模式工况下的控制策略，在此基础上提出了一种综合考虑SOC 偏差、各模块电容电压值、直流系统电压控制裕度以及输出调制比上下限的控制参数自适应的SOC 自均衡控制策略。通过RTDS 实验得出如下结论：所提电池簇间SOC 均衡策略能够通过单独调整每个功率模块的调制波来控制各电池簇的充放电电流，通过电池簇差异化充放电实现SOC 自适应均衡控制，最终达到SOC 均衡。该策略在不改变CHBC-BESS 总功率的同时，实现了SOC 均衡参数控制自适应，根据采样结果在每个控制周期进行实时计算，均衡效率较高。

由于本文在SOC 计算时采用了相同的额定容量，当储能系统各子模块上的电池健康状态差异较大时，均衡效果将有所降低。将电池健康状态引入均衡策略将在后续工作进行研究。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。