基于时序生成对抗网络的居民用户非侵入式负荷分解

罗 平，朱振宇，樊星驰，孙博宇，张 帆，吕 强

（1.杭州电子科技大学自动化学院，浙江省 杭州市 310018；2.杭州电子科技大学圣光机联合学院，浙江省 杭州市 310018；3.杭州电子科技大学信息工程学院，浙江省 杭州市 310018）

0 引言

据统计，2022年中国居民用电量为1 336.6 TW·h，占全社会用电量的15.5%［1］。通过了解居民电器设备的能耗情况可优化能源管理，从而提高能源的利用率。同时，智能电表与通信网络和数据管理系统共同构建了足以收集海量居民用户数据的高级量测体系（advanced metering infrastructure，AMI）［2］。非侵入式负荷监测（non-intrusive load monitoring，NILM）技术通过传感用户的总能量信号来估计单个设备的运行状态和能耗［3］。但AMI 提供的居民用户数据仅为户用电信息，缺少各电器设备级负荷样本数据。此外，用户出于隐私保护，仅愿提供少量设备级负荷样本数据，这对目前以监督学习为主流的NILM 技术提出了挑战。

针对缺少电器设备级负荷样本数据的问题，现有文献的解决方法大致可分为直接法和间接法。直接法是指直接生成可用于NILM 的数据集。文献［4］使用融合了电器时序特征的隐马尔可夫模型（hidden Markov model，HMM），其电器生成数据可克服原有方法在时间特性上的不足。文献［5］提出了4 种不同的插值技术用于从低频数据集中生成高频数据。文献［6］采用了一种由基于动态时间规整的聚类算法和改进的平均序列求法组成的混合时间序列数据增强框架，用于处理负载瞬态识别中类不平衡和样本量不足的问题。随着技术的发展，生成对抗网络（generative adversarial network，GAN）在数据增强领域得到广泛应用［7］。文献［8］提出一种基于一维Wasserstein GAN 的TraceGAN 模型来合成电器功率数据，但其仅考虑了几种大功率电器，缺乏对小功率电器负荷数据生成与电器运行状态间关联性的研究。文献［9］提出了一种基于Wasserstein深度卷积GAN 的家庭总功率能耗时序生成模型，但该模型不能生成设备级负荷数据。文献［10］创建了一个数据集生成工具NILM-Synth，通过从参考负载数据库中叠加示例波形来创建适用于NILM 的数据集。

间接法主要指通过迁移学习［11］将源域学习的模型参数分享到目标域以提升模型效率。文献［12］将在ImageNet-1K 数据集上经过大量标签数据训练的ResNeXt-50 网络模型迁移到标签数据较少的目标域。文献［13］将其他楼宇的电-气负荷模型迁移到目标楼宇。迁移学习虽训练速度快，但用户习惯不同会导致电器源域和目标域的训练集并不相似，从而产生负迁移［12-13］。

现有的NILM 技术根据是否需要事件检测步骤可分为基于事件和非基于事件的方法［14］。基于事件的方法需进行事件检测才能完成负荷辨识和分解［15］。文献［16］采用滑动窗口实现对总负荷数据统计特征的跟踪。文献［17］针对阶梯状和长瞬态事件，提出改进边缘检测方法及移动平均与移动t检验相结合的两阶段事件检测方法。文献［18］给出一种具有自适应调整窗口宽度、边缘宽度和阈值的鲁棒事件检测方法，用于未知家庭及具有盲参数设置的数据集。基于事件的NILM 算法速度相对较快，但无法直接获取电器的功率序列，需借助其他优化算法进行求解。若数据集中某一电器难以检测，后续电器功率分解的精度会大大降低。

非基于事件的NILM 算法以电器状态为变量，分解得到各电器的功率序列［19］。文献［20］基于递归特征消除法选择最优特征组合并引入香农熵设置投票权重，解决了基学习器优化选择困难的问题。文献［21］提出一种根据电器功耗自动确定电器工作状态的聚类算法，利用HMM 进行负荷分解以减少对先验信息的依赖。文献［4］以深度神经网络（deep neural network，DNN）代替HMM 实现负荷分解，提升了算法的精度。文献［22］基于总负荷数据构建图信号模型，考虑负荷数据相关性求解功率损耗的约束条件以得到功率序列。但非基于事件的NILM 算法求解速度相对较慢，算法复杂度也相对较高。

时序生成对抗网络（time-series generative adversarial network，TimeGAN）既能捕捉时序序列概率分布，又能充分考虑序列间动态的时间相关性［23］，适合生成家庭用户电器的时序样本。但当输入数据维数过多时，TimeGAN 难以收敛。因此，本文将已知的少量电器设备级功率数据进行拼接，以降维网络替代TimeGAN 中原有的嵌入网络，用于生成与样本数据具有相同概率分布的生成数据。此外，采用基于电器运行状态和深度学习的NILM 方法［24］对由生成数据和原始数据组成的数据集进行处理，根据电器运行状态数量不同将电器分为状态复杂和状态简单电器。利用能深入挖掘负荷特征且能处理前后时序关联性的卷积神经网络-双向门控循环单元（convolutional neural network-bidirectional gated recurrent unit，CNN-BiGRU）对每个状态复杂电器进行负荷分解；采用DNN 对每个状态简单电器构建打分器模型，以实现负荷辨识和分解。最后，利用参考能量分解数据集（reference energy disaggregation data set，REDD）中的低频数据集和每分钟电力年鉴数据集（almanac of minutely power dataset，Ampds）对所提数据生成方法和负荷分解算法进行了验证。

1 NILM 算法流程

本文的NILM 算法流程主要分为数据生成、电器聚类、负荷特征选取和负荷分解4 个部分，具体步骤如图1 所示。

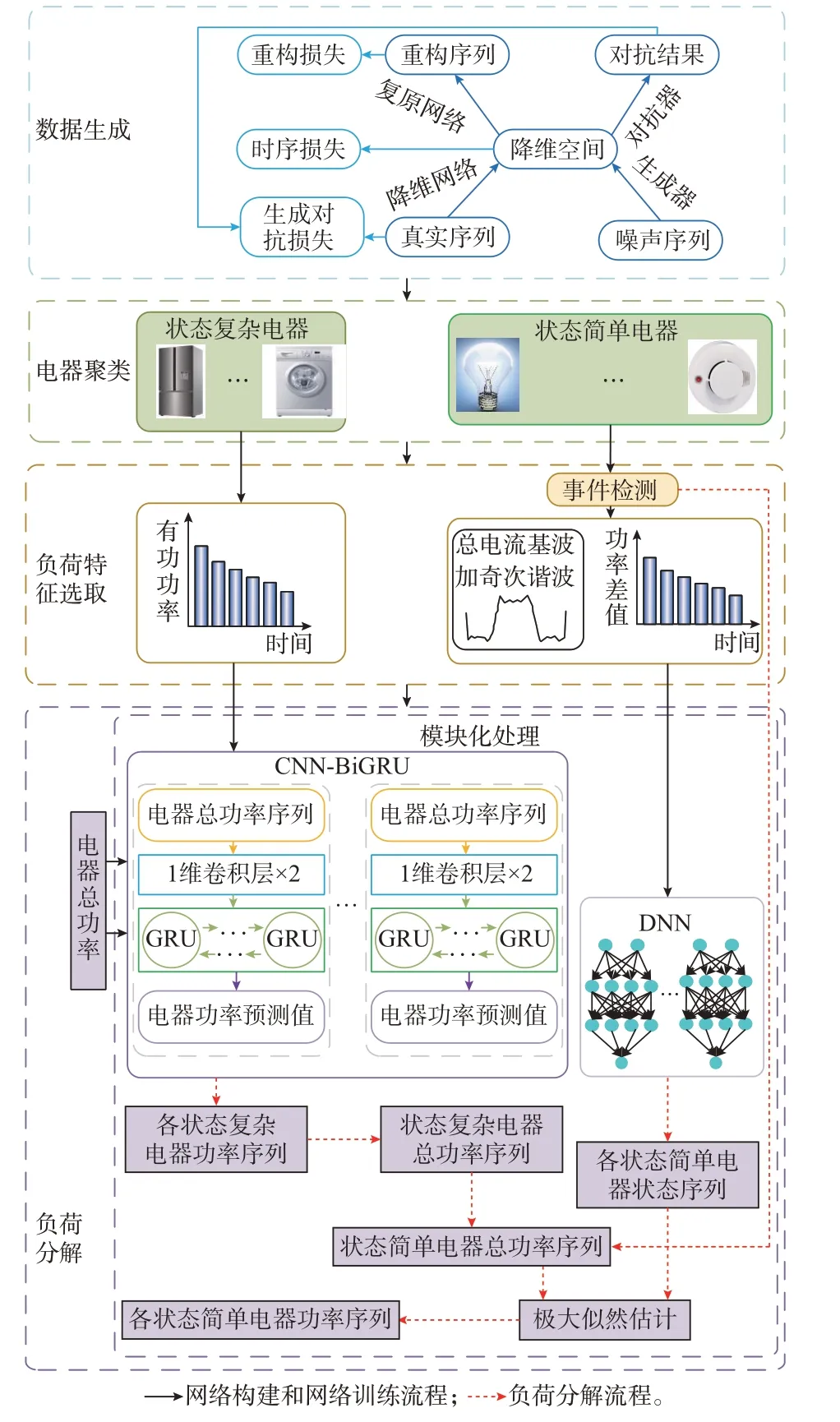
图1 NILM 算法流程Fig.1 Process of NILM algorithm

首先，在已知少量电器设备级负荷功率数据的基础上，使用TimeGAN 获取充足的负荷功率数据。然后，利用仿射传播聚类算法［25］对各电器历史有功功率序列进行聚类，通过聚类得到电器状态数将电器进行分类。状态复杂电器是指工作时会出现多个工作状态的电器，其负荷特征为电器有功功率；状态简单电器只存在关闭或开启状态，其负荷特征为切投前后总有功功率差值及总电流的基波和3、5、7 次谐波。

对每个状态复杂电器构建一个CNN-BiGRU 网络，将待分解的电器总功率序列输入训练好的网络中，得到各状态复杂电器对应的功率序列及状态简单电器的总功率序列。假设同一时刻只存在单个电器投切，对该总功率序列进行事件检测便可获得状态简单电器的切投时间。提取相应的负荷特征输入已训练好的DNN 即可输出每个状态简单电器对应的状态序列。最后，利用极大似然估计得到其功率序列。

2 基于TimeGAN 的数据生成模型

电力负荷数据由电器所处的工作状态决定，工作状态背后隐藏的是数据的时序特性。例如，电视机在深夜工作的概率远低于其他时段；洗衣机的工作状态一般分为注水、清洗和甩干。此外，各电器间的状态也隐藏着相关性：电饭煲大概率会和微波炉同时工作；洗碗机大概率会在面包机关闭后工作等。因此，研究电力负荷数据生成方法时需充分考虑数据的时序特性和电器间的相关性，从而使得生成的数据更加逼近真实数据。TimeGAN 将无监督GAN 模型与有监督自回归模型中的条件概率原理相结合［23］，能生成保留时间动态特征的序列，非常适合处理NILM 中时序数据的生成问题。

为了使得TimeGAN 能挖掘同一时刻电器间的相关性，本文将所有电器的功率序列堆叠输入TimeGAN。但输入数据维数的增加导致网络运算复杂度提升，使得TimeGAN 难以收敛的问题愈加严重。 因此，本文利用降维网络代替传统TimeGAN 中的嵌入网络，创建一个低维空间用于数据计算。计算结束后，利用复原网络将降维后的数据恢复到与样本数据相同的维度。本文所提TimeGAN 的具体结构和训练过程如图2 所示。图中：实线代表训练流程；虚线代表各组成网络参数的更新过程；θe、θr、θg和θd分别为降维网络、复原网络、生成器和对抗器中的参数；∂LR/∂θe和∂LU/∂θe分别为利用LR和LU更新降维网络参数的过程；∂LU/∂θg和∂LV/∂θg分别为利用LU和LV更新生成器参数的过程；∂LR/∂θr为利用LR更新复原网络参数的过程；∂LV/∂θd为利用LV更新对抗器参数的过程。

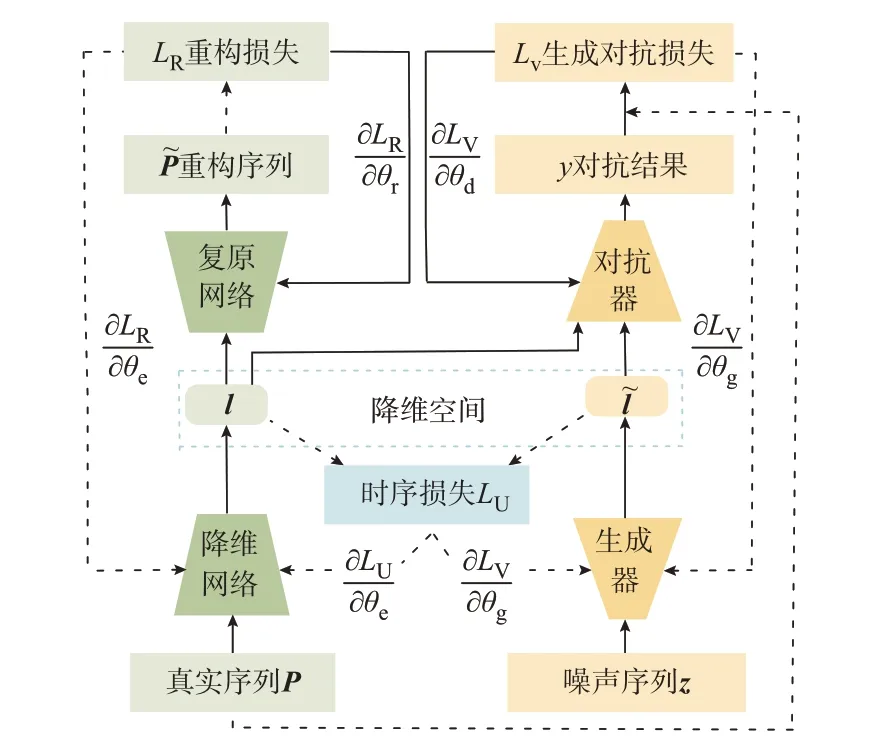
图2 优化后的TimeGAN 结构和训练过程Fig.2 Optimized structure and training process of TimeGAN

由图2 可知，TimeGAN 中包含生成器和对抗器，各组成部分都包含1 层输入层、1 层输出层和3 层隐藏层，且每层隐藏层由24 个门控循环单元（gated recurrent unit，GRU）组成。对抗器隐藏层的激活函数为sigmoid，其他部分隐藏层激活函数选择leaky-Relu。所有组成部分的优化器均选择Adam。

电器J时间长度为T的有功功率序列为P(J)=，J∈[1，m]。其中，m为家庭中电器的数量。将所有电器的P(J)拼成一个m×T的矩阵P：

TimeGAN 各组成部分的工作原理如下：

1）降维网络隐藏层中每个GRU 内神经元个数为n（n为降维后数据维度）。其输入为高维真实数据序列P，网络样本批次设置为128；输出为降维后的数据l=[l1，l2，…，lT]，其中，t时刻的输出为lt=e(lt-1，Pt)，e(·)为降维网络的映射函数，Pt为t时刻的高维真实数据序列。

2）复原网络隐藏层中每个GRU 的神经元个数为m。其输入为l，输出为，其中，=r(l)为t时刻复原网络的输出序列，r(·)为复原网络的映射函数。

构建如式（2）所示的损失函数LR来衡量降维网络和复原网络的性能：

式中：EP～pdata(P)为P的概率分布函数pdata(P)的期望。LR用于计算真实数据经过降维和复原后的损失，训练的目标是使LR接近于0。

3）生成器隐藏层中每个GRU 包含128 个神经元。其输入为随机噪声序列z，输出后的数据为͂=，其中，t时刻的输出为，g(·)为生成器的映射函数，zt为t时刻的噪声序列。为了提高生成器对时序特性的学习能力，对其单独建立一个时序损失函数LU，通过LU的数值反馈来监督生成器对数据时序特性的学习情况。LU用于计算真实低维数据lt和生成器输出的低维数据l͂t间的误差，训练目标是使LU接近于0。

4）对抗器隐藏层中每个GRU 包含128 个神经元。其输入为生成器的输出l͂（对应生成数据的概率分布信息）和降维网络的输出l（对应真实数据的概率分布信息），通过对抗器博弈后输出为y͂=d(l，l͂)，其中，d(·) 为对抗器映射函数，y͂∈(0，1)。当对抗器判定本次读取的数据为真实数据时，y͂接近于1，否则接近于0。由于输入数据的改变，此时网络的损失函数不再是衡量两个一维随机变量条件概率密度的差异，而是两个多维随机变量联合概率密度的差异。生成对抗损失函数LV为：

式中：Ez～pnoise(z)为z的概率分布函数pnoise(z)的期望。对抗损失函数需同时衡量生成器和对抗器性能，其最终的训练目标是使得两者间达到纳什均衡，即LV最终收敛于0.5。

TimeGAN 训练时，先训练降维网络和复原网络，再联合训练生成器与对抗器。训练结束后去掉降维网络和对抗器，从给定的高斯噪声分布中采样输入至生成器。生成器输出低维生成数据͂，再将输入复原网络获得生成的有功功率序列͂。

3 深度学习神经网络的选择和构建

3.1 构建CNN-BiGRU 网络

状态复杂电器包含大量的大功率电器，有功功率数据获取容易且有区分性。因此，选取有功功率作为状态复杂电器的负荷特征。

状态复杂电器的运行状态较多，利用基于事件的方法难以准确判别。因此，采用非基于事件的方法对其进行分解更为合适。双向门控循环单元（BiGRU）网络是结合前、后向GRU 网络而成的神经网络［26］，适合处理具有前后时序关联性的信息。而一维卷积神经网络（CNN）可以在有功功率特征中提取更深层的负荷特征，如电器功率水平、电器状态切换的时间点等信息，从而帮助BiGRU 网络更好地求解所构建的非线性回归问题。因此，本文选用一维CNN 和BiGRU 网络来构建状态复杂电器的模型。

CNN-BiGRU 网络结构如图3 所示，其由输入层、输出层、双层一维卷积层和正反向排列双层GRU 组成。输入层和输出层有k+1 个神经元，一维卷积层中卷积核尺寸为3×1 且步长为1，每层GRU 的数量为k+1。其中，k为输入层中输入向量的维数，各层激活函数为Relu。

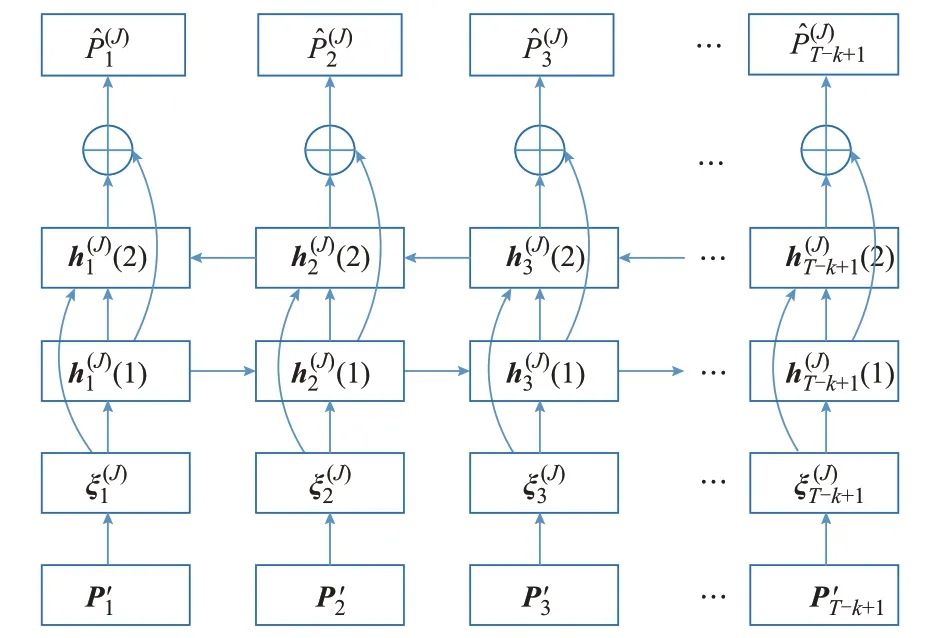
图3 CNN-BiGRU 网络结构Fig.3 Structure of CNN-BiGRU network

电器总有功功率序列P'由真实数据和生成数据构成，其时间窗从零时刻滑动，以相邻采样点的时间间隔为长度前移，最终形成T-k+1 个长度为k+1 的功率序列向量其中，为t时刻的总有功功率序列。以电器J为例，其负荷分解步骤如下：

网络训练过程利用反向传播算法进行训练，并通过优化器Adam 来修正网络中的权重参数。超参数优化采用树结构Parzen 算法［27］。

3.2 构建DNN

由于状态简单电器的状态少，总有功功率变化值的正负即可判断出其是从工作状态过渡到关闭或待机状态，反之亦然。此外，电流谐波可有效区分小功率电器，而偶次谐波分量一般较小［28］，故最终选择由切投前后总有功功率差值及总电流的基波和3、5、7 次谐波组成的复合负荷特征作为状态简单电器的负荷特征。

状态简单电器的事件类型仅有电器投切。因此，利用基于事件的方法进行求解比较方便。DNN模型是常用的分类器模型，相较于CNN，其速度更快。因此，本文利用DNN 来实现状态简单电器的负荷识别。

现有文献通常将所有电器的负荷特征利用同一个DNN 进行训练，在输出层输出一个表示负荷特征属于各电器概率的向量。当家庭中有新电器加入时，新电器的负荷特征可能会使DNN 输出向量中的元素全部接近于0.5，从而无法判别该负荷特征属于哪个电器。此时，DNN 需重新建模和训练，增加了计算的复杂度。因此，本文对每一个状态简单电器均构建一个DNN 打分器模型，将一个多分类问题转换成多个二分类问题以实现电器的模块化处理。DNN 的训练目标是当输入为相同电器的负荷特征时，网络的输出接近于1，当有新的状态简单电器加入时，其负荷特征无论输入哪个打分器，输出均接近于0。此时，只需要对新加入的电器进行特征提取，并重新搭建一个新的DNN 进行训练即可。

设a为状态简单电器负荷特征向量的维数，则DNN 输入和输出层各包含2a+1 和1 个神经元。隐藏层为5 层，每层有100 个神经元。激活函数为sigmoid，损失函数为交叉熵函数。DNN 结构如图4所示，超参数参考文献［22］进行设置，并以损失函数变化为依据进行手动调参。

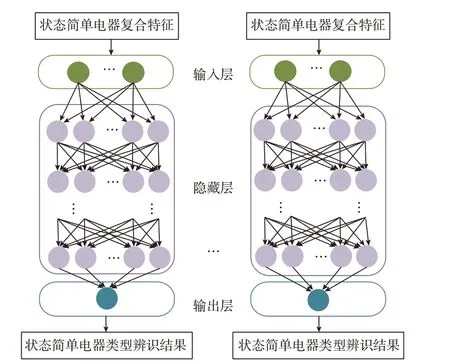
图4 DNN 结构Fig.4 Structure of DNN

在打分器将各负荷特征分类后，通过事件检测记录各状态简单电器投切的时间点，从而得到各状态简单电器的状态序列。

3.3 极大似然估计

假设状态简单电器J关闭状态不消耗功率，待机和运行状态均服从正态分布［28］，只需求解其在待机和运行状态下消耗的功率即可。利用式（5）所示的极大似然估计模型［29］对状态简单电器总功率Psim进行分解。

式中：G为状态简单电器数量；Psim，t和Psim，J，t分别为t时刻所有状态简单电器消耗的总功率和电器J的功率；fJ(Psim，J，t|sJ，t)为电器J在状态sJ，t下消耗功率为Psim，J，t的概率。

4 仿真结果及分析

选择REDD 中家庭3、5 和Ampds 中如表1 所示电器种类数据为研究对象，数据生成的基准算例选对应电器前30%的数据作为真实数据样本。表1中：REDD 和Ampds的采样间隔分别为3 s和1 min。

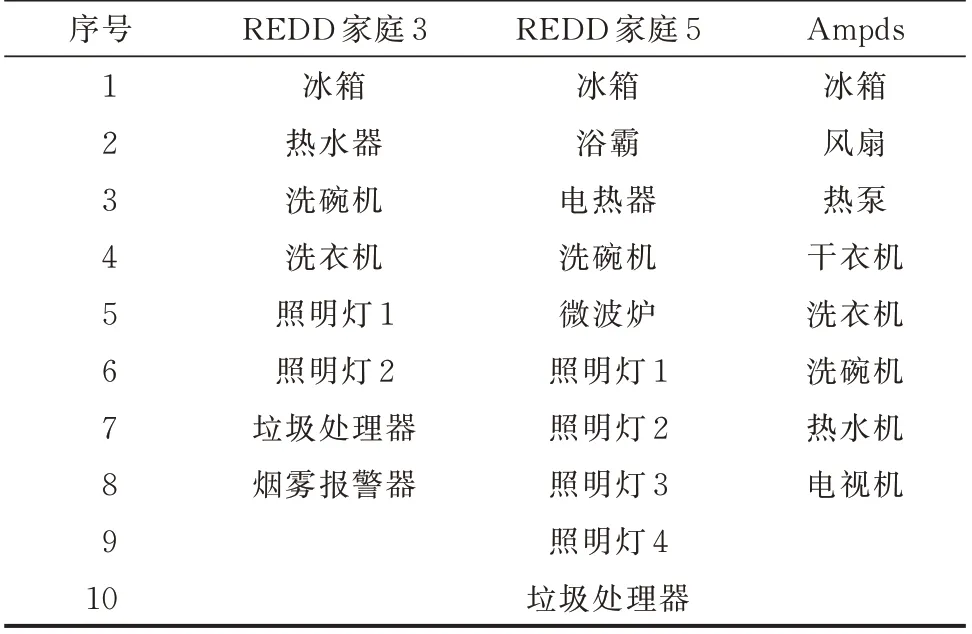
表1 电器种类Table 1 Types of electrical appliances

在负荷分解仿真分析中，将仿真家庭中真实的总电流数据，以及由不同比例生成数据和真实数据组成的功率样本作为数据集。选取数据集前80%的数据作为训练集和验证集，其中，训练集和验证集数据各占50%；选取数据集后20%的数据为测试集。 训练和测试的硬件配置为一台Nvidia RTX2080GPU 的服务器，软件平台为Pytorch。TimeGAN、CNN-BiGRU 和DNN 每个网络所需的显存为800 MB。

为了更加直观地展现本文算法，附录A 以REDD 中家庭3 为例，给出了所提算法的数据流图，包括网络训练、预测时所需各个输入/输出变量的维度、时间尺度和时间颗粒度等信息。

4.1 评价指标

利用平均绝对误差（mean absolute error，MAE）、均方根误差（root mean square error，RMSE）和 纳 什 效 率 系 数（Nash-Sutcliffe efficiency coefficient，NSE）对生成数据的精度进行评价。

MAE 指标MAE是绝对误差的平均值，可表示为：

RMSE 指标RMSE用于衡量真实值和生成值之间的离散程度：

NSE 指标NSE一般用于衡量真实值和生成值之间概率密度的接近程度，其值越接近于1 表明两者的概率密度越相似：

使用功率分解准确率cp和能量分解准确率ce作为负荷分解算法性能的评价指标：

4.2 TimeGAN 数据生成结果分析

附录B 图B1 至图B3 分别给出了REDD 中家庭3、家庭5 和Ampds 家庭中电器的生成数据和真实数据曲线。由图B1 至图B3 可知，利用TimeGAN 得到的生成数据与真实数据很接近。

利用TimeGAN 和在NILM 领域数据生成环节中应用较多的HMM［30］算法对REDD 中家庭3、5 和Ampds 家庭生成数据，对应生成数据的评价指标如表2 所示。

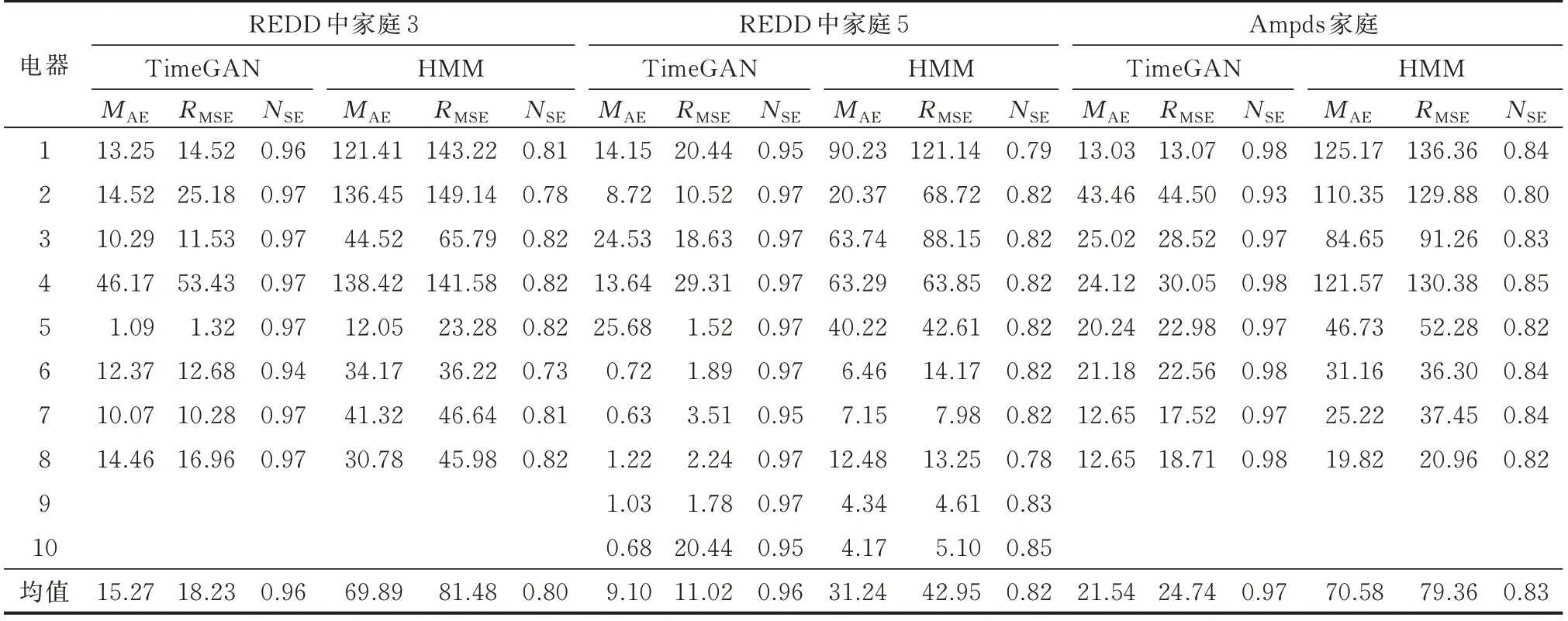
表2 REDD 中家庭3、5 和Ampds 家庭中电器基于TimeGAN 和HMM 的评价指标对比Table 2 Comparison of evaluation indices based on TimeGAN and HMM of electrical appliances in REDD families 3, 5 and Ampds family

由表2 可知：

1）3 个家庭中TimeGAN 模型的MAE和RMSE均小于HMM 模型中对应电器的MAE和RMSE，说明TimeGAN 模型的生成数据精度高于HMM 模型。3 个家庭TimeGAN 模型中大部分电器的NSE在0.97 左右，最低的是Ampds 家庭的风扇（NSE为0.93）。而HMM 大部分电器的NSE在0.82 左右，最低的为REDD 家庭3 的照明灯2（NSE为0.73）。说明TimeGAN 模型的生成数据分布更接近真实数据分布。这是由于HMM 在生成数据时假设各电器数据序列间相互独立，忽略了不同用户习惯导致的电器状态间的关联性。而TimeGAN 网络能够挖掘电器状态间的关联性，生成与真实数据在统计特性上相似的时间序列数据。

2）TimeGAN 和HMM 模型生成数据中MAE和RMSE最大的均为REDD 家庭3 中的洗衣机，原因在于洗衣机工作状态较多，使得模型难以精确捕捉每个状态间的切换。NSE较小的有REDD 家庭3 和5的照明灯2 以及Ampds 家庭的风扇，说明这3 个电器的开启或关闭与其他电器的状态切换并无太大联系。此外，风扇在使用过程中存在微风和强风之间的连续切换，使得风扇有功功率数据服从的条件概率分布不断变化，最终导致风扇的NSE值相较于其他电器略低。

3）大功率电器在工作状态下的功率波动范围较大。因此，功率较大电器的MAE和RMSE值相对较高，如REDD 家庭5 中冰箱、浴霸、电热器和洗碗机，无论是TimeGAN 模型还是HMM 模型，相较于其他电器而言，其MAE和RMSE值都比较大，但这并不代表TimeGAN 模型生成数据的精度不高，因为这些电器的NSE值均在0.95 以上，说明这些电器对应的TimeGAN 模型生成数据的概率分布接近真实数据所服从的概率分布。

4.3 真实样本数据不同比值下生成数据精度对比

以REDD 家庭3 中的电器为例，设数据生成环节中所用真实数据样本占总样本的比值为ε。表3给出了ε从10% 以步长5% 变化到40% 时，对TimeGAN 模型生成电器数据平均精度的影响。

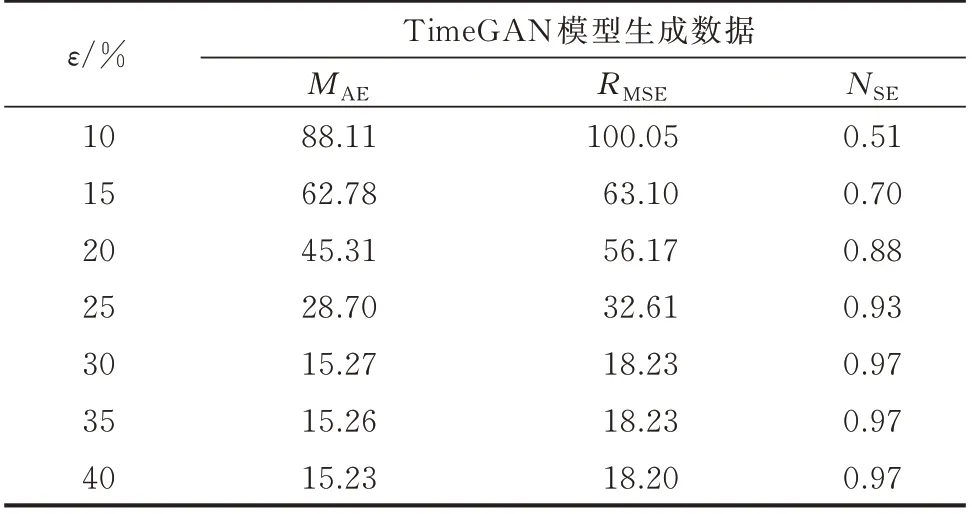
表3 ε 值对REDD 家庭3 中电器生成数据平均精度的影响Table 3 Influence of ε value on average accuracy of generated data for electrical appliances in REDD family 3

由表3 可知，当ε＞30%时，生成数据的精度更高，但随着ε的增加，对应指标的变化不明显。当ε＜30%时，生成数据的精度会逐渐下降，即NSE会大幅度下降，MAE和RMSE会大幅度提升。因此，本文数据生成算法中选用ε=30%，既满足少量数据的要求，也保证了生成数据的质量。

4.4 电器聚类结果

附录C 图C1 和图C2 分别给出了REDD 家庭3中真实数据下和ε=30%时生成数据下各电器的状态数及各状态下的功率均值μ和标准差σ。由附录B 图B1 和图B2 可知，生成数据聚类得到的状态数和真实数据聚类得到的电器状态数一致。同时，由前述定义可知，REDD 家庭3 中洗碗机、洗衣机、冰箱和热水器为状态复杂电器；烟雾报警器、照明灯1、2 以及垃圾处理器为状态简单电器。

同理可知，REDD 家庭5 中包含的状态复杂电器为洗碗机、冰箱、电热器和微波炉；状态简单电器为垃圾处理器、照明灯1、2、3、4 和浴霸。Ampds 家庭中的电器均为状态复杂电器。

4.5 负荷分解结果

为了验证数据生成算法对负荷分解结果的影响，设真实数据占训练集中所有数据样本的比值为λ，表4 给出λ=100%（即训练集中均为真实数据）时和λ=0（即训练集中负荷分解的数据均为由30%真实数据得到的生成数据）时，本文所提负荷分解算法与其他算法对REDD 家庭3、家庭5 和Ampds 家庭分解得到的结果。

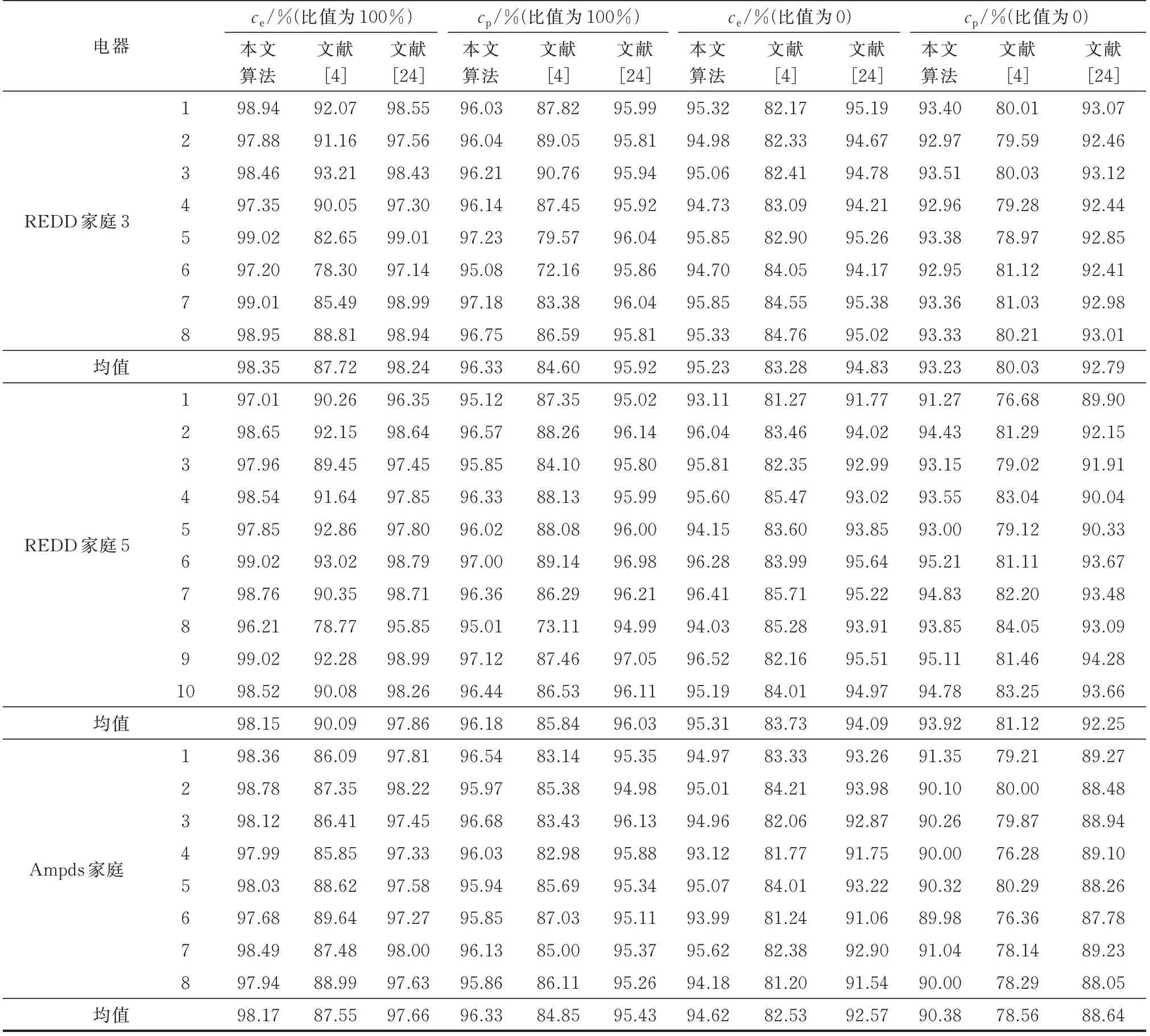
表4 λ=100%和λ=0 时不同算法所得到的不同家庭各电器的负荷分解结果Table 4 Load decomposition results of each electrical appliance in different families obtained by different algorithms when λ=100% and λ=0

由表4 可知：

1）本文算法的ce和cp均高于其他算法。其中，文献［24］和本文算法均是对电器分类后利用不同深度学习网络来实现负荷分解。因此，这两种算法的精度均高于文献［4］的算法。此外，CNN-BiGRU能够捕获序列中的长期依赖关系，处理电器时序数据时比文献［4］中DNN 的效果更好。

2）与文献［24］中采用BiLSTM 网络处理各状态复杂电器时得到的ce和cp值相比，本文采用CNN-BiGRU 网络得到的各状态复杂电器的ce和cp值均有不同程度的提升。说明CNN-BiGRU 网络对状态复杂电器的处理效果好于BiLSTM 网络。这是由于CNN 能有效提取局部特征，而BiGRU 能够捕获长距离的相关性，两者结合的表现比BiLSTM网络更好。对于状态简单电器，利用DNN 替代多层感知机，并对每个状态简单电器进行了模块化处理。因此，本文算法所得的ce和cp值比文献［24］中算法得到的ce和cp值也有所提高。

3）当λ从100%变化到0 时，对于REDD 家庭3和家庭5 而言，本文算法的ce和cp均下降3%左右。对于Ampds 家庭而言，本文算法的ce和cp分别下降4%和6%左右。原因在于生成数据和真实数据间本身存在误差，而且Ampds 家庭均为状态复杂电器，生成数据精度比状态简单电器的精度有所下降。但当λ=0 时，3 户家庭的ce和cp均值都高于90%，准确率仍处于可接受范围内，说明了本文所提数据生成算法和负荷分解算法的有效性。

当λ=0 时，3 个家庭的负荷分解结果如附录D图D1 至图D5 所示。由图可知，即使将训练集数据全部更换为由TimeGAN 生成的数据，本文负荷分解算法最终的功率分解数据，即预测值与真实值依旧相近。说明在该情况下本文算法依旧保持较高的负荷分解精度，同时也进一步说明生成的数据可以有效替代真实数据来训练深度学习网络。

当λ从100% 以20% 为步长逐渐减少至0时，3 个家庭的cp指标变化趋势如图5 所示。

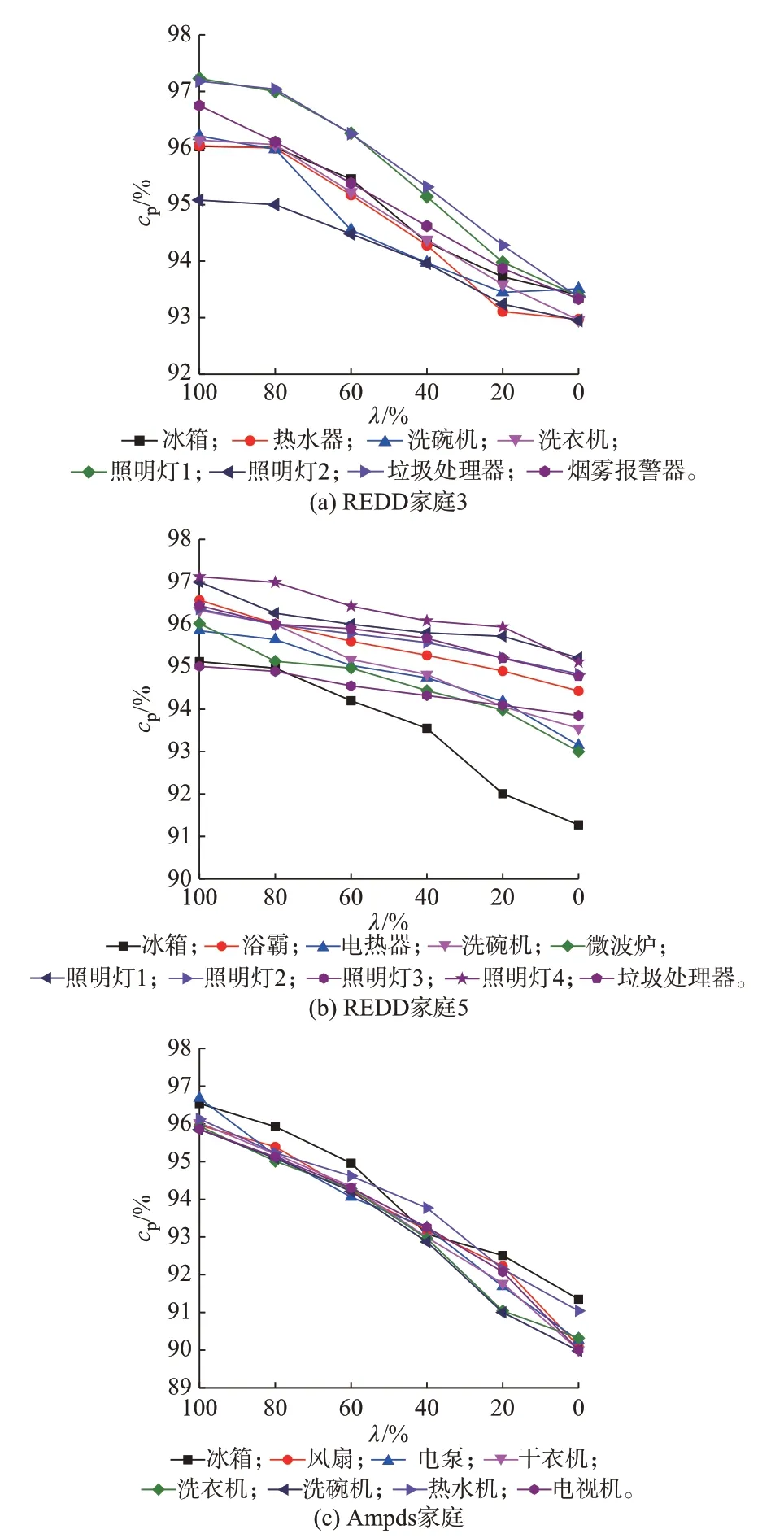
图5 λ 值对不同家庭各电器负荷分解准确率的影响Fig.5 Influence of λ value on load decomposition accuracy of each electrical appliance in different families

从图5 可知，当生成数据占比增加，即λ减小时，cp值逐渐下降，但最多下降6% 左右。说明利用TimeGAN 的数据生成方法以及基于电器运行状态和深度学习负荷分解方法，可以在少量真实电器数据场景下实现较高精度的负荷分解。

5 结语

针对现有监督学习算法难以获取大量有标签电力数据的问题，提出一种基于时序特性和电器相关性的电力数据生成方法。利用TimeGAN 网络实现横向时序特性和纵向电器相关性的学习。为了降低网络训练的复杂度，利用降维网络创建一个低维空间，进行后续网络训练过程的所有运算，最后利用复原网络将降维后的数据复原。相较于基于HMM 的数据生成模型，本文数据生成方法无须考虑电器数量的问题，适用于处理数据量较大的场景，而且生成数据更为准确。

此外，对现有基于电器运行状态和深度学习的负荷分解方法进行了改进，利用CNN-BiGRU 不仅可提取状态复杂电器有功功率特征背后隐藏的深度特征，还可以学习过去和未来状态的切换。同时，DNN 训练分类模型可以快速实现状态简单电器的负荷识别。所有电器模型都实现了模块化处理，即一个电器对应一个网络的结构。仿真结果验证了所提数据生成方法和负荷分解算法的有效性。

但本文所提的数据生成方案仍需从居民用户侧或自建平台上，获得少量电器设备级的负荷数据作为TimeGAN 的数据样本。后续可考虑通过迁移学习获得对应的数据样本，提供给TimeGAN 以实现数据生成，使得负荷数据由“少生多”到“无生多”。此外，还需考虑可能出现的状态复杂电器训练与分解时工作状态数不一致的情况，以增强算法的可迁移性。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。