基于分布式潮流控制器的海上风电系统谐波治理方法和控制策略

唐爱红，宋 幸，尚宇菲，郭国伟，余梦琪，詹细妹

（1.武汉理工大学自动化学院，湖北省 武汉市 430070；2.广东电网有限责任公司佛山供电局，广东省 佛山市 528000）

0 引言

在“双碳”目标下，中国提出构建新型电力系统，在此背景下，海上风电的开发力度将逐步加大［1］。然而，当海上风电经交流系统送出时，在长距离海缆电力传输情况下，一般在陆上风电场交流并网中并不严重的谐波谐振放大问题，在海上风电场并网中可能会变得十分严重［2-4］。

与陆上交流电网中常见的架空线路相比，交流电力电缆的正序电容是相同长度和电压等级架空线路的十几倍甚至几十倍［2］。交流电力电缆的这种效应导致了海上风电场在较低频率时就开始呈现容性，因而与表现为感性的陆上电网相作用，使得海上风电系统在低频率时就有发生谐振的可能性［2］。海上风电机组一般通过换流器进行并网，在其并网过程中将不可避免地产生电压源特性的低次谐波和高次谐波。同时，来自陆上电网的电流源特性的背景谐波也会流经海上风电系统。当这些谐波电流与谐波电压的频率在谐振频率附近时，易引发谐波放大甚至振荡的现象［5］。海上风电系统中的谐波将引起电力电子设备间的谐波振荡，导致电力电子设备或新能源发电并网不稳定甚至脱网，同时也对电力传输的电能质量造成影响［6］。因此，抑制谐波振荡是海上风电系统要解决的重要问题。

谐波治理技术分为主动谐波治理和被动谐波治理技术，主动谐波治理针对谐波源本身进行治理以降低谐波源产生的谐波，被动谐波治理通过附加滤波器来抑制谐波对电网的危害。目前，常用的谐波治理装置可以分为无源滤波器（passive power filter，PPF）和有源滤波器（active power filter，APF）［7］。PPF 是由谐波电容器和电抗器组合而成的滤波装置，通常并联在谐波源附近。这样不仅可以吸收谐波电流，还可以进行无功功率补偿，运行维护也较为简单，但是PPF 的滤波性能受系统阻抗的影响较大，在系统发生结构变化时会影响治理效果，而且与系统阻抗会发生串联或并联谐振［7］。APF 则采用了电力电子开关，实现了动态治理，能够迅速响应谐波的频率和大小的变化，同时避免了与系统阻抗产生谐振现象。并联型APF 虽然应用广泛，但其在滤波效果、滤波成本等方面仍存在问题，相比于串联型APF，在相同的负载情况下，并联型APF 所需要的容量更大，滤波效果更差，损耗更大，串联型APF 具有更广阔的发展前景［8］。

分布式潮流控制器（distributed power flow controller，DPFC）与串联型APF 同属于基于电压源换流器的调控装置，故DPFC 也可以用作滤波装置［9］。DPFC 作为一种以分布式结构为特点的柔性输电设备，可以安装在线路或者杆塔上，具有良好的经济效应。将DPFC 应用于海上风电系统中，既可以补偿谐波电压，降低海上风电系统并网点的谐波含量，发挥串联型APF 的作用，又能够进行无功补偿，发挥潮流控制器的作用。

本文从海上风电系统的谐波谐振放大问题出发，通过对海上风电系统的精细建模，分析了谐波谐振放大问题的形成机理。针对谐波谐振放大问题，采用在海上风电系统中串入DPFC 的治理方案，以降低海上风电系统并网点的谐波含量为目标，同时提出了一种DPFC 输出补偿谐波电压的控制策略。仿真结果表明，基于所提出的控制策略，在海上风电系统中串入DPFC 能够有效解决海上风电系统中的谐波谐振放大现象。

1 海上风电系统谐波问题分析

如图1 所示，海上风电场经电力海缆送出系统的一般性结构由风电机组、35 kV 集电网、场站升压变压器、220 kV 输电海缆和陆上电网组成［10］。架空线路以及电力电缆都是高度非线性的，常规的Π 形线路段元件无法反映依赖频率变化的电缆和架空线路模型。因此，为了精确地研究海上风电系统在不同频段的阻抗特性，本文基于PSCAD/EMTDC 软件的频域相关模型构建了电力电缆和架空线路，并构建了海上风电系统的其他部分［11］。相关元件的参数设置如附录A 所示。

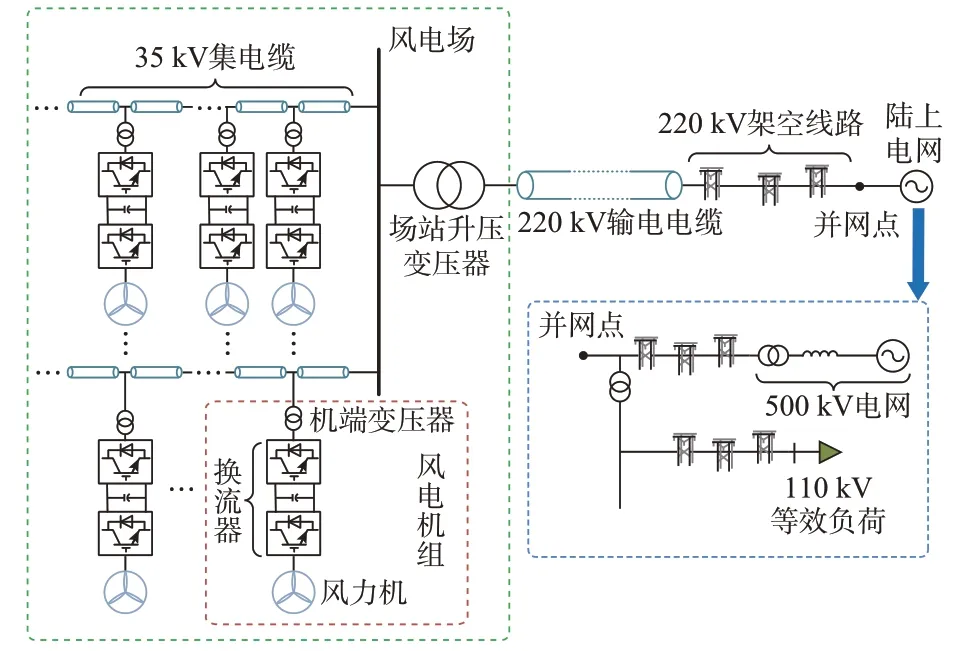
图1 海上风电场经电力海缆送出系统Fig.1 Transmission system of offshore wind farm via submarine cable

为了便于分析并网点的谐波含量，可以将从并网点看进去的风电场以及陆上电网等效为单口网络。风电机组产生的谐波主要来自电压源换流器。因此，将从并网点看进去的风电场等效为戴维南支路，开路电压与等效阻抗分别记为V̇h和Z1h，下标h表示不同的倍频。陆上电网的背景谐波主要表现为电流型谐波。因此，将从并网点看进去的陆上电网等效为诺顿支路，短路电流与等效阻抗分别记为İh和Z2h［12-13］。等效后的海上风电系统如图2 所示。

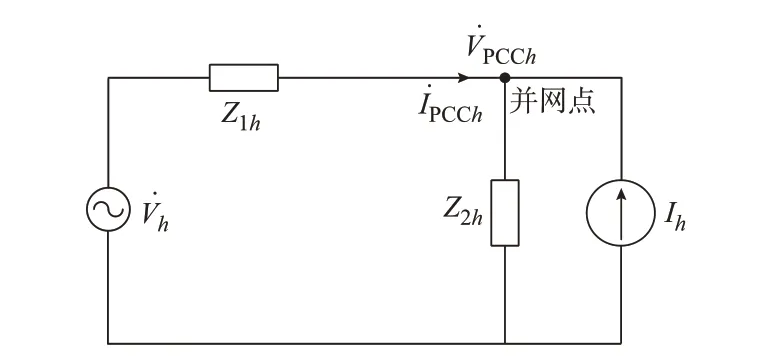
图2 海上风电系统等效模型Fig.2 Equivalent model of offshore wind power system

通过阻抗扫描，得到Z1h和Z2h在不同频率下的幅值和相角，如图3 所示。可以看出，Z1h在120 Hz时由感性进入容性，在739 Hz 时由容性变为感性，而Z2h则在1 906 Hz 时才由感性进入容性。对比Z1h和Z2h的结构可知，相比Z2h只包含架空线路，Z1h则含有一定长度的电力电缆，这导致了Z1h比Z2h在更低频率就进入了容性。因此，当海上风电系统存在低频谐波时，呈现容性的Z1h和呈现感性的Z2h就有了发生谐振的可能。

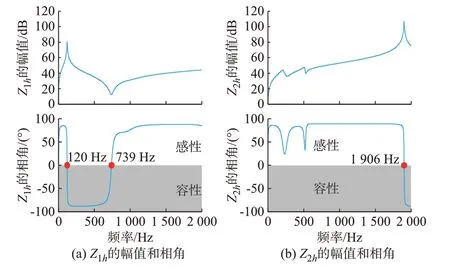
图3 海上风电系统等效阻抗随频率变化图Fig.3 Diagram of equivalent impedance of offshore wind power system varying with frequency

并网点电压谐波含量和风电场注入并网点的电流谐波含量是衡量海上风电系统电能质量的重要指标。由图2 可以得到并网点的谐波电压表达式和注入的谐波电流表达式分别为：

观察式（1）和式（2）的结构可以知道，谐波电压表达式和谐波电流表达式中含有共同的分母Z1h+Z2h。由前面的分析可知，Z1h和Z2h在低频时有发生谐振的可能性。在谐振时，Z1h+Z2h的幅值会取到较小的值，这会造成谐波电压和谐波电流取到非常大的值。为了分析不同频率下谐波电压和谐波电流的放大情况，记增益传递函数为：

增益传递函数G(ω)在不同频率下的幅值和相角如图4 所示。可以看到，G(ω)在多个频率下发生了谐振，其中，传递函数在368 Hz 附近发生了谐振并且幅值取到了最大值。因此，当海上风电系统存在该谐振频率附近的谐波时，就会在并网点上产生谐波放大和振荡现象，造成电能质量下降。

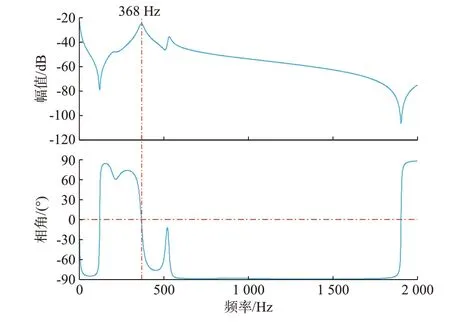
图4 不同频率下增益传递函数的幅值和相角Fig.4 Amplitude and phase angle of gain transfer function at different frequencies

2 基于DPFC 的谐波治理原理分析

DPFC 是一种由两组及以上可独立运行的单相子单元以串联的方式接入交流电网的装置，子单元的拓扑结构如图5 所示［14-15］。图中：T 表示DPFC 串联变压器；ILine为线路流入DPFC 子单元的电流；IL为流过滤波电感的电流；Vse为滤波电容的电压，同时也是DPFC 子单元的输出电压；Vr为H 桥式电压源换流器输出的调制电压；Vdc为直流电容电压；Cf为DPFC 子单元交流滤波电容；Lf为DPFC 子单元交流滤波电感；Rf为DPFC 子单元交流滤波电感的附生电阻；Cdc为DPFC 子单元直流电容。

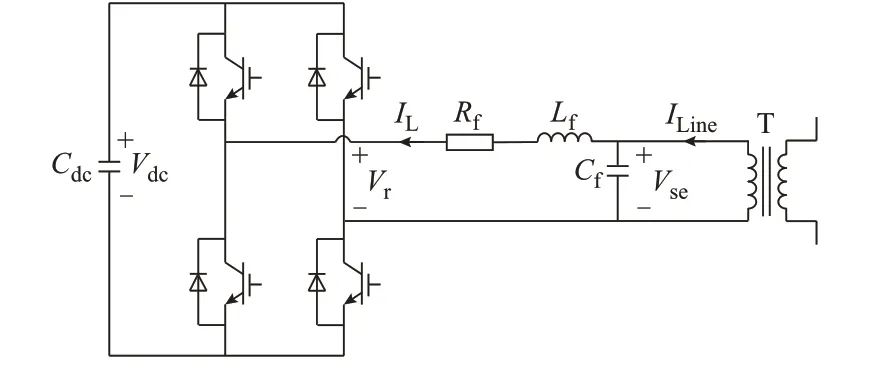
图5 DPFC 子单元拓扑结构Fig.5 Topology of DPFC sub-unit

DPFC 能够逆变出不同频率的电压，当逆变出基频电压时，可以用作潮流控制器，调节电网潮流；当逆变出倍频电压时，可以用作串联APF，进行谐波治理，可以在海上风电场按照电能质量或者潮流调控需要安装不同功能的DPFC 单元，用以满足不同的调控要求。为了降低海上风电系统并网点电压的谐波含量，本文采用了在海上风电系统中串入DPFC 的谐波治理方案，通过控制DPFC 输出对应频率的补偿电压从而对谐波进行治理。将DPFC 安装在图1 所示的海上风电系统中，在某倍频下的简化电路如图6 所示。图中：V̇DPFCh为DPFC 单元输出的补偿谐波电压。

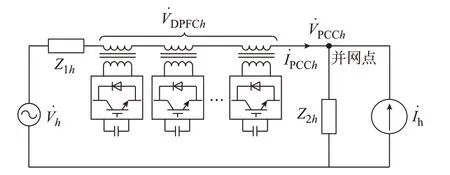
图6 海上风电系统安装DPFC 后的简化电路Fig.6 Simplified circuit of offshore wind power system after installing DPFC

由图6 可以得到安装DPFC 后并网点的谐波电压表达式为：

将式（4）中的相量写成实部和虚部形式，其中，实部下标记为d，虚部下标记为q，则有：

将式（5）代入式（4）中，可以求得并网点谐波电压的幅值VPCCh表达式为：

分析式（6）的结构可知，通过改变DPFC 输出电压的相角和幅值，可以调整并网点谐波电压的幅值。为使并网点谐波电压幅值达到最小，DPFC 输出电压要满足的方程为：

记使并网点谐波电压幅值最小时的DPFC 输出电压为(VDPFCd0，VDPFCq0)，求解式（7）可以得到：

DPFC 输出电压如式（8）所示时，并网点谐波电压幅值将变为零。式（4）—式（8）表明了安装在海上风电系统的DPFC，通过控制输出电压的幅值和相角，可以使得并网点谐波电压幅值降为零，起到治理谐波的作用。同时，在并网点谐波电压幅值降为零时，风电场注入并网点的谐波电流表达式为：

对比式（2）和式（9）的结构可以看到，式（9）的表达式中没有了分母Z1h+Z2h，此时注入并网点的谐波电流完全由陆上电网的背景谐波决定，谐波电流的幅值不再因为谐振而取到非常大的值。由此可见，DPFC 在治理并网点谐波电压的同时也能在一定程度上抑制注入并网点的谐波电流。

3 控制策略

由第2 章的分析可知，DPFC 在对谐波进行治理时，为了保持并网点谐波电压幅值为零，需要跟踪并输出式（6）所示的谐波补偿电压。因此，将DPFC的谐波治理控制策略分为两部分：1）系统级控制策略，以并网点谐波电压降到零为目标，实时跟踪使并网点谐波电压幅值为零的谐波补偿电压，并将结果作为指令值输出给DPFC 子模块；2）装置级控制策略，保持直流电容电压稳定并跟踪接收到的谐波补偿电压指令值。

3.1 系统级控制策略

在式（4）中，将并网点谐波电压幅值的平方分别对DPFC 输出电压的实部和虚部求偏导，可以得到：

将式（8）代入式（10），可以得到：

电导增量法可以实现对信号的实时跟踪［16-17］。因此，对于使并网点谐波电压幅值为零的谐波补偿电压(VDPFCd0，VDPFCq0)的实时跟踪，本文提出的方法如下。

在k+1 时刻，计算式（10）中的偏导数，可以得到：

判断式（12）中在k+1 时刻偏导数的符号，并计算出当前时刻DPFC 输出电压的指令值：

式中：上标*表示输出给DPFC 装置级控制策略的指令值；sgn［·］表示符号函数；M为每步的增量。M的选择关乎控制算法的性能，其值太小会造成追踪过程太长，其值太大则造成稳定时振荡较大。为了在跟踪过程中保证速度的同时，减小稳定时的振荡幅度，可以采用一种变增量的方法，通过预先设置阈值X1，X2，X3，…，在跟踪过程中依据并网点谐波电压幅值的变化改变M的大小，有

式（12）—式（14）即是所提出的DPFC 谐波治理控制策略的系统级控制策略部分，流程图如图7 所示。通过式（12）—式（14），可以实时地根据并网点谐波电压幅值的变化，改变输出给DPFC 装置级控制策略的指令值，实现保持并网点谐波电压幅值为零。

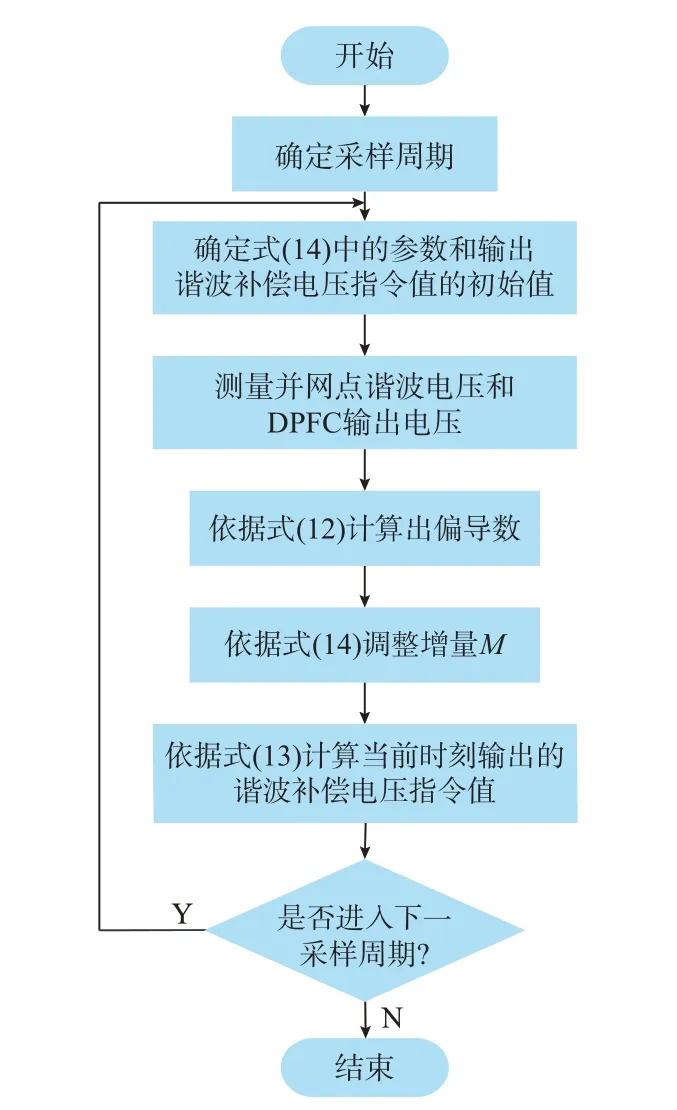
图7 系统级控制策略流程图Fig.7 Flow chart of system-level control strategy

3.2 装置级控制策略

在对某倍频的谐波进行治理时，DPFC 需要从电网吸收有功功率用以维持直流电容电压稳定，同时需要逆变出相应的倍频补偿电压用以降低并网点谐波电压含量。因此，装置级控制策略需要同时搭建基频和谐波频率两种频率的控制回路。由图5 可以得到不同倍频下DPFC 子模块在dq旋转坐标系中的数学模型为：

式中：ILdh、ILqh和ILinedh、ILineqh分别为IL和ILine的h倍频谐波分量在dq旋转坐标系下的d、q轴分量；Vrdh、Vrqh和Vsedh、Vseqh分别为Vr和Vse的h倍频谐波分量在dq旋转坐标系下的d、q轴分量；ωh为h倍频下的角频率。

在进行坐标变换时，对于基频，为了便于有功-无功解耦控制，选择参考向量为线路电流［18-19］；对于谐波频率，为了DPFC 始终输出使并网点谐波电压幅值最小的电压，选择参考向量为零向量。

《老人与海》的文体风格主要体现在简洁以及含蓄两大方面。小说中很少出现作者自己的言论或情感的流露，强调客观的描写。如圣地亚哥与大马林鱼周旋的过程中对他的手说“手啊，你觉得怎么样呢？我要替你多吃一点儿”“它上来啦，快些吧，手，请快些吧”等，在这些看似没有任何感情色彩、寥寥数语的表达中，却表达出圣地亚哥那种乐观、自信以及敢于面对现实、敢于面对困境的勇气。

DPFC 控制潮流或治理谐波的实质为控制输出电压，调节潮流和补偿谐波都可以转化为对DPFC输出电压d轴分量和q轴分量的控制。为了实现DPFC 输出电压对d轴分量指令值和q轴分量指令值的无差跟踪，本文提出不同倍频下的电压环和电流环控制如下：

式中：KP和KI分别为比例-积分（PI）控制器的比例系数和积分系数。

在确定DPFC 输出电压d轴分量指令值和q轴分量指令值的情况下，通过式（16）可以计算出内环电流的d轴和q轴分量指令值，即系统级控制策略中对应对应，继而通过式（17）计算出DPFC 换流器正弦脉宽调制（sinusoidal pulse width modulation，SPWM）的参考电压。

DPFC 需要从电网吸收基波有功功率以维持直流电容电压稳定。为了实现直流电容电压的无差控制，基频下控制回路中DPFC 的输出电压d轴分量和q轴分量的指令值［20-21］为：

谐波频率下控制回路中的DPFC 输出电压d轴分量和q轴分量的指令值则由系统级控制策略计算。

DPFC 装置级控制策略的整体框图如图8 所示。图中：FFT 表示快速傅里叶变换。

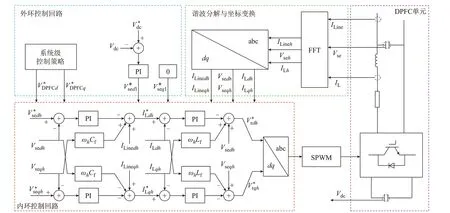
图8 DPFC 装置级控制策略框图Fig.8 Block diagram of device-level control strategy of DPFC

4 仿真验证

4.1 测试系统及参数设置

为了验证所提出的海上风电谐波治理方法和控制策略的有效性，基于图1 所示的海上风电经海缆送出系统，在PSCAD/EMTDC 搭建了仿真模型，仿真模型示意图见附录B。由于本文主要研究DPFC的谐波治理作用，故在仿真模型中，对于风电机组采用功率源等效的方法，并将风电场的谐波源以附加电压源表示，电网背景谐波放在负荷侧，以附加电流源表示。仿真模型中的谐波频率设定为5 倍频和7 倍频，在系统中串入了2 组DPFC，每组DPFC 包含6 个DPFC 子单元，第1 组DPFC 用于治理7 倍频谐波，第2 组DPFC 用于治理5 倍频谐波，仿真系统和DPFC 的主要参数如表1 所示。

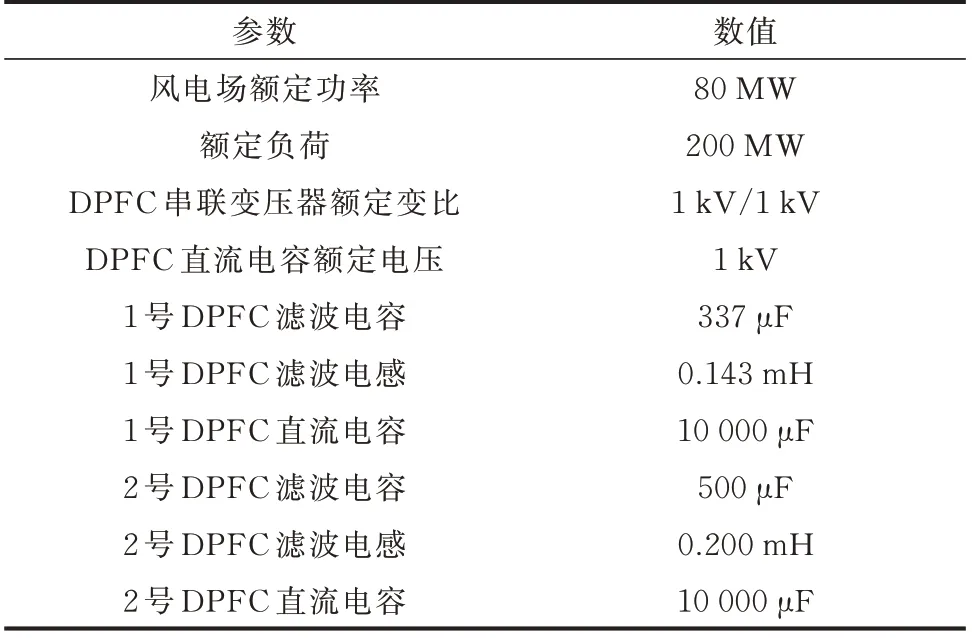
表1 仿真系统参数Table 1 Parameters of simulation system

风电场谐波源安装在风电机组机端变压器低压侧，5 倍频谐波电压源初始有效值设置为16 V、相角为0°，7 倍频谐波电压源初始有效值设置为10 V、相角为0°。陆上电网谐波源与综合负荷模型并联，5 倍频谐波电流源初始有效值设置为18 A，相角为0°，7 倍频谐波电流源初始有效值设置为15 A，相角为0°。2 组DPFC 均在0.5 s 时刻开始投入系统并对直流电容进行充电，第1 组DPFC 在1.0 s 开始输出7 倍频谐波补偿电压，第2 组DPFC 在1.5 s 开始输出5 倍频谐波补偿电压。

4.2 仿真结果及分析

4.2.1 谐波源幅值突变工况下的仿真分析

为设置谐波源幅值突变的仿真工况，风电场谐波源5 倍频谐波电压源的有效值在2.5 s 由16 V 阶跃至24 V；7 倍频谐波电压源的有效值在2.5 s 由10 V阶跃至15 V。陆上电网谐波源5 倍频谐波电流源的有效值值在3.5 s 由18 A 阶跃至25 A；7 倍频谐波电流源的有效值在3.5 s 由15 A 阶跃至20 A。

仿真结果的部分波形图如图9 所示，其余仿真波形图见附录C。由图9 可以看到，DPFC 未投入运行时，在谐波源幅值未变化时，并网点7 次谐波电压保持为5.0 kV，在2.5 s 时因风电场谐波源幅值的突变而上升为6.05 kV，在3.5 s 时则因陆上电网谐波源的突变而继续上升为7.0 kV；并网点5 次谐波电压在谐波源幅值未变化时保持为2.22 kV，在2.5 s时因风电场谐波源幅值的突变而上升为2.5 kV，在3.5 s 时则因陆上电网谐波源的突变而继续上升为3.15 kV。

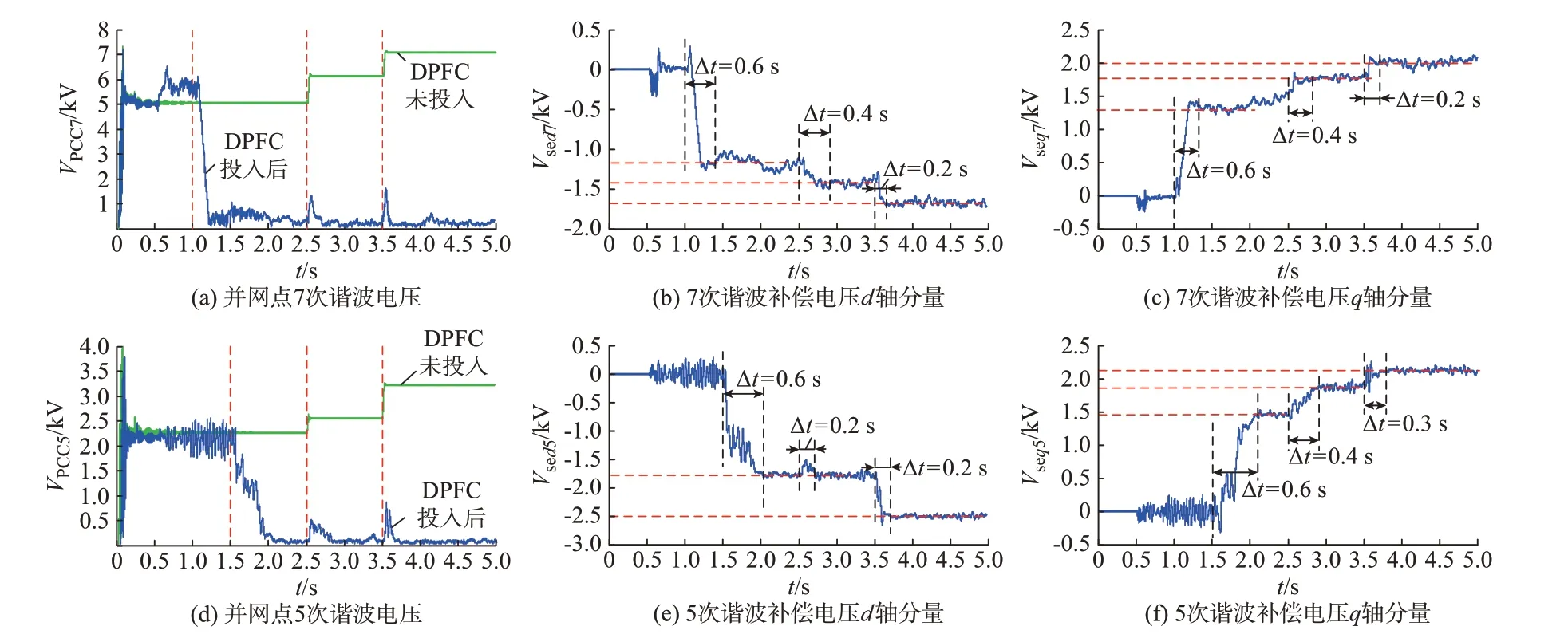
图9 谐波源幅值突变工况下的仿真波形Fig.9 Simulation waveforms under sudden change condition of harmonic source amplitude

在1.0 s 时，DPFC 开始对谐波进行治理后，DPFC 能够迅速地调整输出的7 倍频谐波电压的d轴分量和q轴分量，快速降低并网点7 倍频谐波电压的幅值，经过0.4 s 后，并网点7 倍频谐波电压的幅值降到最低点零附近。此时，DPFC 输出的7 倍频谐波电压的d轴分量稳定在-1.20 kV，q轴分量稳定在1.30 kV。在风电场谐波发生突变后，并网点谐波电压幅值会短暂上升，然后DPFC 开始改变输出的谐波补偿电压的d轴分量和q轴分量，使得并网点谐波电压幅值再次恢复到零附近，经过0.4 s 再次达到稳定状态，DPFC 输出的7 倍频谐波电压的d轴分量稳定在-1.45 kV，q轴分量稳定在1.75 kV。在陆上电网谐波突变后，并网点谐波电压幅值也会短暂上升。同时，DPFC 调整输出的谐波补偿电压的d轴分量和q轴分量，经过0.2 s 并网点谐波电压幅值稳定在零附近，DPFC 输出的7 倍频谐波电压的d轴分量稳定在-1.70 kV，q轴分量稳定在2.00 kV。

在1.5 s 时，第2 组DPFC 开始输出5 次谐波补偿电压对并网点中的5 次谐波电压进行治理，在开始对5 次谐波进行治理后，经过0.6 s 达到稳定。此时，DPFC 输出的5 倍频谐波电压的d轴分量稳定在-1.73 kV，q轴分量稳定在1.44 kV。在风电场谐波发生突变后，经过0.4 s 再次达到稳定状态，DPFC 输出的5 倍频谐波电压的d轴分量稳定在-1.73 kV，q轴分量稳定在1.83 kV。在陆上电网谐波突变后，经过0.3 s 再次稳定，DPFC 输出的5 倍频谐波电压的d轴分量稳定在-2.45 kV，q轴分量稳定在2.06 kV。

由此可见，本文所提出的倍频下的控制策略能够实时跟踪并逆变出使并网点谐波电压幅值为零的谐波补偿电压；在谐波源幅值受到扰动后，也能迅速调整输出的谐波补偿电压的d轴分量和q轴分量，将并网点谐波电压幅值恢复到零附近。

4.2.2 谐波源相角突变工况下的仿真分析

为设置谐波源相角突变的仿真工况，风电场谐波源7 倍频谐波电压源的有效值保持为10 V，相角在2.5 s 由0°阶跃至-50°。陆上电网谐波源7 倍频谐波电流源的有效值值保持为15 A，相角在3.5 s 由0°阶跃至50°。

仿真结果如图10 所示。在DPFC 未投入运行时，并网点7 次谐波电压在谐波源相角未变化时保持为5.0 kV，在2.5 s 因风电场谐波的相角突变而下降为4.56 kV，在3.5 s 则因陆上谐波电压源的相角突变而继续下降为3.31 kV。

图10 谐波源相角突变工况下的仿真波形Fig.10 Simulation waveforms under sudden change condition of harmonic source phase angel

在DPFC 开始对谐波进行治理后，DPFC 能够迅速地调整输出的7 倍频谐波电压的d轴分量和q轴分量，快速降低并网点7 倍频谐波电压的幅值。在风电场谐波源相角发生突变后，并网点谐波电压幅值会短暂上升。然后，DPFC 开始改变输出的谐波补偿电压的d轴分量和q轴分量，使得并网点谐波电压幅值再次恢复到零附近，经过0.3 s 再次达到稳定状态，DPFC 输出的7 倍频谐波电压的d轴分量稳定在-1.06 kV，q轴分量稳定在2.40 kV。在陆上电网谐波相角发生突变后，并网点谐波电压幅值也会短暂上升，同时DPFC 调整输出的谐波补偿电压的d轴分量和q轴分量，经过0.2 s 并网点谐波电压幅值稳定在零附近，DPFC 输出的7 倍频谐波电压的d轴分量稳定在-1.50 kV，q轴分量稳定在1.05 kV。

由此可见，所提出的倍频下的控制策略在谐波源相角受到扰动后，也能迅速调整输出的谐波补偿电压的d轴分量和q轴分量，将并网点谐波电压幅值恢复到零附近。

5 结语

针对海上风电系统中极易出现的谐波谐振放大现象，本文分析了海上风电系统谐波谐振放大的原因，并提出了一种基于DPFC 的海上风电系统的谐波治理方式和相应的控制策略，经过仿真验证，得出以下结论：

1）海底电缆相较于架空线路有着更大的对地电容，使得海上风电经海缆送出系统在较低频率时就呈现容性状态。此时，与呈感性的陆上电网系统相互作用，在并网点将产生谐振现象，当海上风电系统存在低频谐波时，将会产生谐波谐振放大问题；

2）所提出的控制策略能够正确地跟踪使并网点谐波电压幅值为零的谐波补偿电压，并使DPFC逆变出相应的谐波补偿电压，保持并网点对应频率的谐波电压在零附近，同时也能够抑制注入并网点的谐波电流；

3）所提出的控制策略具有一定的适应性，在谐波源幅值和相角变动时，所提出的控制策略也能迅速调整DPFC 输出的谐波补偿电压，迅速将并网点谐波电压幅值恢复到零附近。

因此，本文提出的基于DPFC 的海上风电系统谐波问题的治理方法和控制策略能够降低并网点谐波电压含量，提高海上风电系统的电能质量。

本文还存在以下不足之处需要进一步研究：1）本文未验证所提出的DPFC 治理方法及控制策略在海上风电系统不同工况下的适应性，需要进一步对DPFC 在包括电网运行方式不同及网架结构调整等多种工况下进行仿真验证；2）本文在治理海上风电系统谐波时，仅考虑了并网点电压的谐波含量，未考虑其他电能质量指标，下一步考虑对计及多电能质量指标的谐波治理目标进行优化研究。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。