基于正弦函数拟合的高动态捷联惯导姿态更新算法

路永乐，杨 杰，孙 旗，罗 毅，肖 轩，刘 宇

（重庆邮电大学 智能传感技术与微系统重庆市高校工程研究中心，重庆 400065）

捷联惯性导航系统（Strapdown Inertial Navigation System,SINS）以数学平台为导航平台，使用姿态矩阵描述数学平台相对载体坐标系的关系[1]，具有高可靠性、使用灵活的优点[2]，其核心为捷联惯导姿态更新算法[3]。然而，由于刚体有限旋转的不可交换性，姿态更新中不可避免地引入不可交换性误差[4]。高动态环境下，这种误差更加明显[5]。

1971 年Bortz[6]提出等效旋转矢量算法以补偿不可交换性误差，随后各学者基于此开展了广泛的研究。根据研究方法的不同可以分为两类[7]：一是以多项式角运动为假设前提，基于泰勒级数展开或最小二乘估计进行算法系数求取的方法：Miller[8]在纯圆锥运动条件下推导了三子样圆锥补偿算法；Savage 等[9]基于多项式角运动假设和最小二乘估计提出了显式频率整形圆锥补偿算法；王茂松等[10]同样以多项式角运动假设为基础提出了高阶等效旋转矢量姿态更新算法。二是数值迭代的方法：严恭敏等[11]基于多项式迭代提出了等效旋转矢量精确解方法；武元新[12]基于函数迭代提出了三阶旋转矢量微分方程数值解方法。

然而，利用有限次的多项式表示角运动是一种近似拟合[12]，而数值迭代类算法具有更高精度的同时意味着所需迭代时间更长[13]，同时一些传统算法推导过程中忽略了Bortz 方程三阶及以上项的影响，导致实际使用精度达不到理论效果，特别是在高动态环境下，有时高子样算法精度反而不如低子样算法[11]。本文采用第一类研究方法的思想进行误差补偿算法设计。同时，为了更好地拟合载体运动角速度，进一步提升高动态环境下姿态解算精度，本文以正弦函数代替多项式对载体运动角运动进行拟合，基于此提出了一种基于正弦函数拟合的高动态捷联惯导姿态更新算法，并在圆锥运动与大角速率转动并存的条件下，对本文算法进行仿真验证。

1 基于等效旋转矢量的姿态更新算法设计方法

等效旋转矢量算法是在高动态环境下实现高精度姿态更新的常用方法[3]，其利用姿态更新周期内的角增量构建等效旋转矢量，通过优化算法系数，实现不可交换性误差补偿。

等效旋转矢量算法对不可交换性误差进行补偿的理论基础为等效旋转矢量微分方程，即Bortz 方程[6]，工程上常用近似形式为：

其中，Φ为等效旋转矢量；ω为载体运动角速度；称为不可交换性误差。

相较于四元数姿态更新法，等效旋转矢量法进行姿态更新时需要先求取等效旋转矢量，再计算姿态变化四元数，随后才能进行四元数更新。

1.1 构建等效旋转矢量

在实际应用中，姿态更新周期常为毫秒级。以数据传输频率200 Hz 计算，四元数法姿态更新周期为5 ms，对应二子样等效旋转矢量法姿态更新周期为10 ms。由于姿态更新周期短，将等效旋转矢量用角增量代替，即：Φ≈Δθ。于是，式(1)进一步改写为：

以式(2)为理论基础，在姿态更新周期内以不同阶次的多项式对载体角速度进行拟合，得到不同的等效旋转矢量。例如，令角速度为非零常数，即零次多项式ω(t)=a(0≤t≤h)，其中a为常数向量，h=tk+1-tk表示一个姿态更新周期，tk、tk+1分别表示k、k+1时刻。此时，得到单子样算法的等效旋转矢量[8]为：

其中，Δθ表示 [tk,tk+1]内的角增量。

1.2 构造姿态变化四元数

从角位置A0到角位置A1的旋转四元数记为：

其中，Q表示旋转四元数；u表示单位向量；θ表示旋转角度。

又有四元数更新方程[8]为：

其中，Q(tk+1)、Q(tk)分别为tk+1、tk时刻导航坐标系至载体坐标系的旋转四元数；q(h)为tk至tk+1时刻的载体坐标系旋转四元数。

一个姿态更新周期内，旋转角度为旋转矢量模值Φ，因此，q(h)由旋转矢量表示为式(6)，并称为[tk,tk+1]时间段内的姿态变化四元数[7]。

2 基于正弦函数拟合的等效旋转矢量算法

逼近理论的基本问题是用一系列简单函数来逼近（拟合）一个复杂或是没有解析式的函数[14]，这些简单函数通常为一组正交基[15]。例如，Legendre 正交基：1,x,(3x2-1)/2,(5x3-3x)/2…；Chebyshev 正交基：1,cosx,cos2x,cos3x… ；Fourier 正交基 ：1,sinx,cosx,sin2x,cos2x…。正交基的特点为任意两个不同的基，其内积为 0。本文使用正交基(sinx,sin 2x,sin3x…) 对载体角速度进行拟合。

将载体运动角速度用不同频率的正弦函数之和进行拟合，具体表达式为：

其中，k1、k2…kn为系数矢量。

根据姿态更新周期内的采样点数选择合适的角速度函数。以一个姿态更新周期内进行两次采样为例，载体运动角速度表示为：

其中，a、b为系数矢量。记姿态更新周期内角增量为角速度积分：

则角速度与角增量在t=0处各阶导数分别为：

对式(2)进行毕卡迭代求解，得到Bortz 方程三阶毕卡解[16]为：

求取式(12)中等效旋转矢量各阶毕卡解在t=0处各阶导数，并将式(10)和式(11)代入得：

对Φ(h)在t=0处泰勒展开，考虑部分泰勒展开的六阶分量远大于八阶分量，且七阶分量为零，因此对等效旋转矢量进行六阶泰勒展开，并将式(13)代入，得：

为了将等效旋转矢量以角增量形式表示，求取一个姿态更新周期内两个角增量表达式。根据式(8)和式(9)所示的角速率与角增量表达式，得：

根据余弦函数的麦克劳林展开式，将式(15)中角增量之和展开为：

对比式(14)和式(16)，可得基于正弦函数拟合的二采样等效旋转矢量算法的等效旋转矢量：

其中，a、b由式(15)中角增量表达式联立求得。

同理，可得基于正弦函数拟合的三采样等效旋转矢量算法的等效旋转矢量为：

其中，d、e、f为系数矢量，表达式见式(20)。

3 圆锥运功与大角速率转动并存环境仿真分析

3.1 等效旋转矢量真实值

圆锥运动与角速率机动并存环境是指载体处于圆锥运动的同时，又有一个坐标轴处于常值角速率旋转的环境，其运动角速率ω(t)见式(21)[17]。当常值角速率转动值大于100 °/s 时，称其为圆锥运动与大角速率转动并存环境，该环境是一种典型的高动态环境[17]。

其中，α为圆锥运动半锥角；Ω 为圆锥运动角频率；ω0为常值转动角速率。

以圆锥运动与角速率机动并存环境作为仿真条件的优势在于，其等效旋转矢量的真实值是已知的。在此条件下，载体运动的真实姿态四元数Q(t)为：

因此，姿态变化四元数q(h)及其与等效旋转矢量[ΦxΦyΦz]T的对应关系表示为：

分析式(23)可知，Φx、Φy为周期项，其误差不随时间累积，对算法精度的影响可忽略不计[18]，因此，后文仅分析非周期项Φz带来的算法误差。

当式(23)中的常值转动角速率ω0较小时，可以认为q0值很小，对其中正弦函数采取一阶近似[8]，而当ω0较大时，需要对正弦函数采取二阶近似[17]，将二阶近似值代入式(23)可得：

联立式(23)和式(24)求得Φz的理论值为：

3.2 等效旋转矢量估计值

圆锥误差补偿算法子样数通常在1～4 之间[9,10]，其中单子样算法本质上为四元数算法，其对不可交换性误差补偿程度不够，而四子样算法往往复杂且效果不一定优于三子样算法[13]。因此，本文仅选择子样数为二和子样数为三的相关算法进行对比分析，各种算法的名称及缩写如表1 所示。

表1 对比分析算法名称及缩写Tab.1 Comparative analysis algorithm names and abbreviations

表1 中各算法的等效旋转矢量估计值如式(26)～式(30)所示，其中式(27)中参数a、b由式(18)求取，式(30)中参数d、e、f由式(20)求取，所有算法的角增量均由式(9)求出。

1）等效旋转矢量二子样圆锥优化算法（ERV2）

2）正弦函数拟合二子样旋转矢量算法（TRV2）

3）扩展形式频率级数三子样圆锥算法（FSR3）

4）扩展形式显示频率三子样圆锥算法（EXP3）

5）正弦函数拟合三子样旋转矢量算法（TRV3）

3.3 不同参数算法误差对比分析

由式(25)可知，等效旋转矢量算法的误差与半锥角a、角频率Ω、常值角速率ω0和姿态解算周期h均有关系，因此本文就不同参数条件下算法误差分别进行仿真对比分析。算法误差评估方法采用Musoff[19]提出的剩余误差评估方法，该值越小表明算法性能越好，其定义为进行补偿后剩余的误差，即：

1）仿真参数设置为：α=0.001 °～90°，Ω=2π rad/s，ω0=5.30 rad/s，h=0.02 s。

该环境下各算法随半锥角变化的误差仿真结果如图1 所示。从图1 可以看出：①半锥角小于1.38 °时，TRV2 与ERV2 精度相当，误差均在0.1 °/h 以内；TRV3性能较好，其中在半锥角 0.77 °时误差最小，为1.08×10-5°/h，比FSR3、EXP3 低3 个数量级。②半锥角大于1.38°时，TRV2、TRV3 表现不足；ERV2、FSR3、EXP3 三者误差在不同半锥角下各自达到最小值，如图1 局部放大图所示，EXP3 在半锥角40.07 °时误差最小，为6.89×10-7°/h；ERV2 在半锥角57.31 °时误差最小，为5.94×10-8°/h；FSR3 在半锥角57.71 °时误差最小，为7.13×10-7°/h。综上分析可知，本文所提算法在小半锥角情况下表现更好。

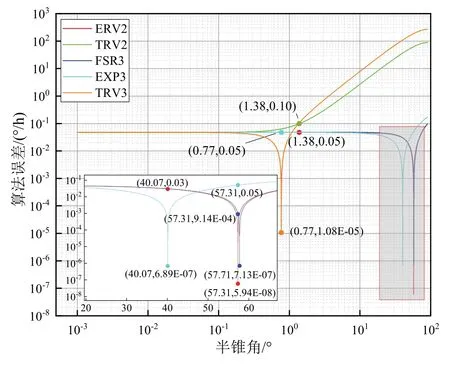
图1 各算法随半锥角变化的误差对比Fig.1 Comparison of the relative cone error of each algorithm with the half-cone angle

2 ）仿真参数设置为：α=0.5°，Ω=π rad/s～500π rad/s，ω0=5.30 rad/s，h=0.02 s。

该环境下各算法随角频率变化的误差仿真结果如图2 所示。从图2 可以看出：①角频率低于2.83π rad/s时，TRV2 与ERV2 精度相当，误差均在0.1 °/h 以内；TRV3 性能较好，其中在角频率2.26π rad/s 时误差最小，为4.36×10-4°/h，比FSR3、EXP3 低2 个数量级。②角频率高于2.83π rad/s 时，随着角频率变化，各算法分别在不同角频率条件下达到性能最佳点。例如，角频率 13.04π rad/s 时 ERV2 误差最小，为1.18×10-4°/h；角频率64.71π rad/s 时TRV2 误差最小，为3.26×10-3°/h；角频率67.88π rad/s 时FSR3 误差最小，为3.90×10-3°/h；角频率70.93π rad/s 时EXP3 误差最小，为7.44×10-3°/h。同时，可以发现，当角频率达到301.69π rad/s 左右时，所有算法的误差相同（图2 局部放大图中五角星处）。③从整体来看，所有算法的误差均随圆锥运动角频率的升高而增加，且在一定间隔后，同子样数的算法误差将变得相同，而每个间隔内各算法性能呈现交替变换的趋势。对于子样数为二的算法，该间隔为200π rad/s，对于子样数为三的算法，该间隔为300π rad/s，如图3 所示。综上分析可知，本文所提算法在低频情况下表现更好。

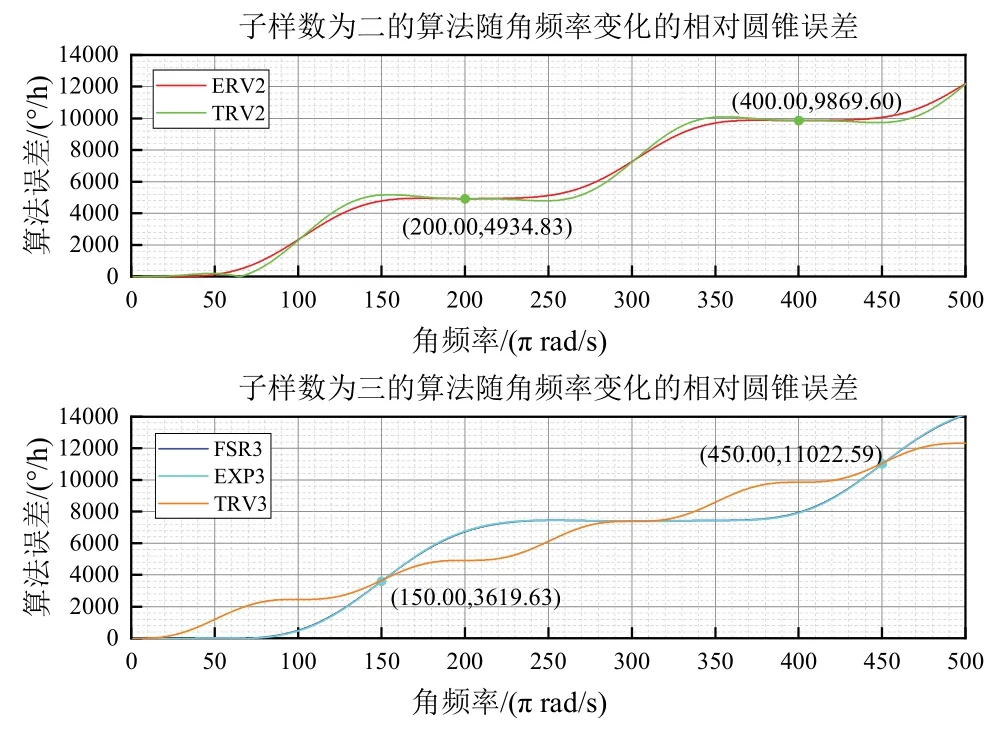
图3 不同子样数算法随角频率变化的误差对比Fig.3 Comparison of the relative cone error with the angular frequency for different subsample number algorithms

3）仿真参数设置为：α=0.5°，Ω=2π rad/s，ω0=0rad/s～ 25 rad/s，h=0.02 s。

该环境下各算法随常值角速率变化的误差仿真结果如图4 所示。从图4 可以看出：①常值角速率低于3.67 rad/s 时，ERV2、FSR3 和EXP3 的误差小于TRV2、TRV3，且 ERV2 和 EXP3 分别在常值角速率为0.81 rad/s 和 1.05 rad/s 时误差最小，分别为1.79×10-9°/h 和2.98×10-8°/h。②当常值角速率高于3.67 rad/s、低于6.28 rad/s 时，TRV3 性能较好，其中在常值角速率4.83 rad/s 时误差最小，为8.27×10-6°/h，比其余算法低 4 个数量级。③常值角速率高于6.28 rad/s 时，各算法的误差几乎相同。综上分析可知，本文所提算法在高速常值角速率转动情况下表现更好。

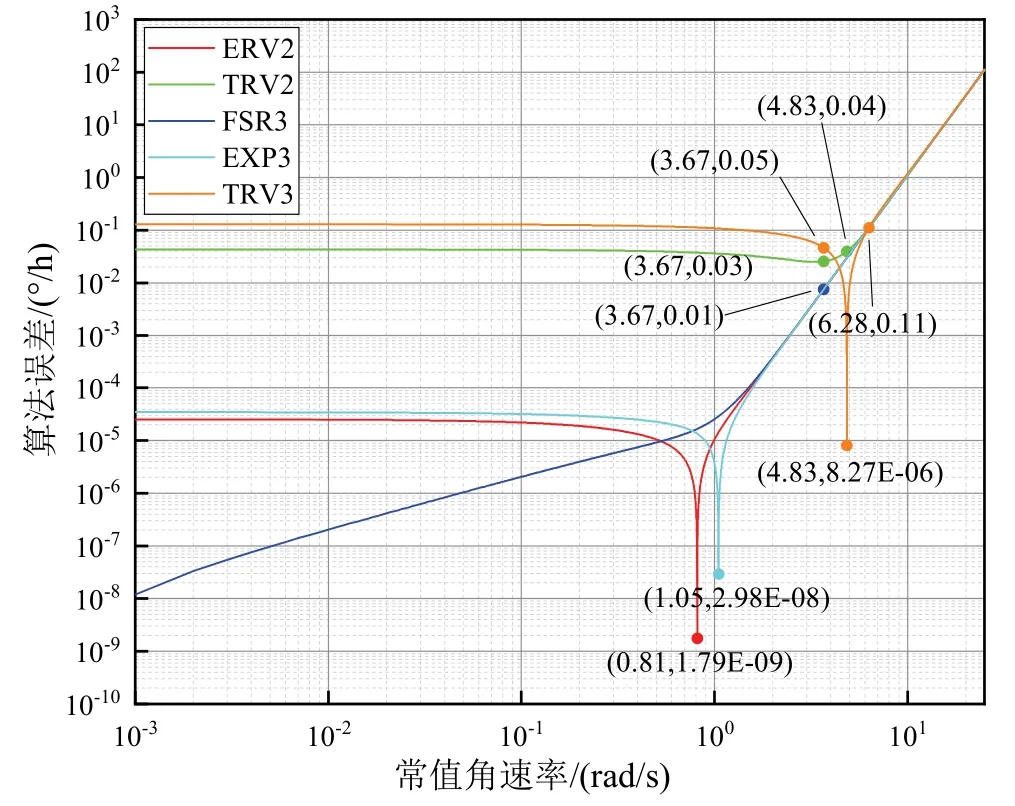
图4 各算法随常值角速率变化的误差对比Fig.4 Comparison of the relative cone error of each algorithm with the constant angular rate

4）仿真参数设置为：α=0.5°，Ω=2π rad/s，ω0=5.30 rad/s，h=0.0005s～ 0.05 s 。

该环境下各算法随姿态解算周期变化的误差仿真结果如图5 所示。

从图5 可以看出：①姿态解算周期小于0.02 s 时，各算法性能几乎相同。②姿态解算周期大于0.02 s 时，TRV3 误差略低于其余算法，在姿态解算周期为0.05 s时TRV3 误差为1.75 °/h，其余算法误差均在1.88 °/h左右。③整体而言，随着姿态解算周期增大，各算法误差均表现出增大的趋势，但TRV3 误差增速略缓于其余算法。综上分析可知，本文所提算法在姿态解算周期相同的情况下表现更好。

4 总结

降低高动态环境下姿态更新中不可交换性误差的有效手段是使用等效旋转矢量算法。本文依据等效旋转矢量算法的设计方法，通过改变算法设计的前提条件，采用正弦函数正交基对载体角速度进行拟合，提出了一种基于正弦函数拟合的高动态捷联惯导姿态更新算法。在圆锥运动与大角速率转动并存环境下进行了仿真验证，并与现有的三种典型的圆锥误差补偿算法进行了对比。仿真结果表明，在小半锥角低频圆锥运动伴随快速常值角速率转动时，本文所提方法具有一定优势，这表明该算法在大角速率转动伴随小幅圆锥运动环境下可能发挥重要的作用，为高动态环境下高精度误差补偿算法研究提供了理论参考价值。