稀土元素Lu,Sc掺杂GaN光电特性的第一性原理研究

付莎莎, 肖清泉, 姚云美, 邹梦真, 谢 泉

(贵州大学 大数据与信息工程学院 新型光电子材料与技术研究所, 贵阳550025)

1 引 言

GaN的禁带宽度为3.39 eV，作为第三代宽带隙半导体材料，它具有直接带隙、高热导率、高击穿电压、耐高温和化学稳定性好等优点[1-3]，在短波长光电器件、高温器件和高频大功率器件中具有广阔的应用前景[4].当前，越来越多的学者聚焦于GaN及其掺杂体系研究[5-9].实验方面，Dashdorj 等人[10]、Polyakov等人[11]研究了Fe掺杂GaN材料的光电性质.Khan等人[12]研究发现Cu掺杂后GaN的光催化性质有所提高；Tang等人[13]研究发现在绝缘C掺杂基片上生长的GaN薄膜具有优良的输运和光学性能；Sasaki等人[14]、Wolos等人[15]发现Mn掺杂GaN后会形成窄的自旋极化带且体系表现为强交换耦合和高居里温度铁磁性.理论研究方面，Latif等人[16]发现Au单掺杂和(C，Au)共掺杂使GaN具有磁性；Maskar等人[17]的计算结果表明Pm、Sm、Eu掺杂GaN材料在费米能级表现出100%自旋极化的半金属行为；Abdalla等人[18]研究发现Ga位掺杂Fe的GaN比在N位掺杂Fe的GaN更稳定且掺杂后材料呈现磁性半导体.

由于采用方法不同，刑海英等人[19]、饶雪等人[20]计算了本征GaN的禁带宽度，分别为1.98 eV和1.56 eV，所得计算结果较实验值3.39 eV偏小，结果均不理想；且基于以上研究发现，以稀土元素为基础的材料拥有优良的光学、电学、磁学性能以及催化性能，稀土元素掺杂有望改善GaN可见光吸收.而目前对于稀土元素Lu、Sc掺杂GaN体系相关的理论计算尚未见报道，故本文利用第一性原理，采用GGA+U(Generalized Gradient Approximation-Hubbard U)方法计算了本征GaN及稀土元素(Lu、Sc)掺杂GaN超晶胞的电子结构和光学性质，所得结果相比于其他方法更为准确；研究了掺杂对GaN电子结构和光学性质的影响，以期所得结论为后续的研究和实验提供理论依据和参考.

2 计算模型和方法

2.1 理论模型

稳定的GaN结构有两种：纤锌矿、闪锌矿[21]，而岩盐矿结构只在特定的条件下存在.本文研究的六方纤锌矿结构GaN属于P63mc空间群，其晶格常数分别为a=b=3.189 Å，c=5.185 Å，c/a=1.626[22]，α=β=90°，γ=120°.本文选取包含32个原子的2×2×2的超晶胞．掺杂时，选取Lu、Sc替代GaN中的一个Ga原子，掺杂浓度均为6.25 %，其体系的超胞模型如图1所示.

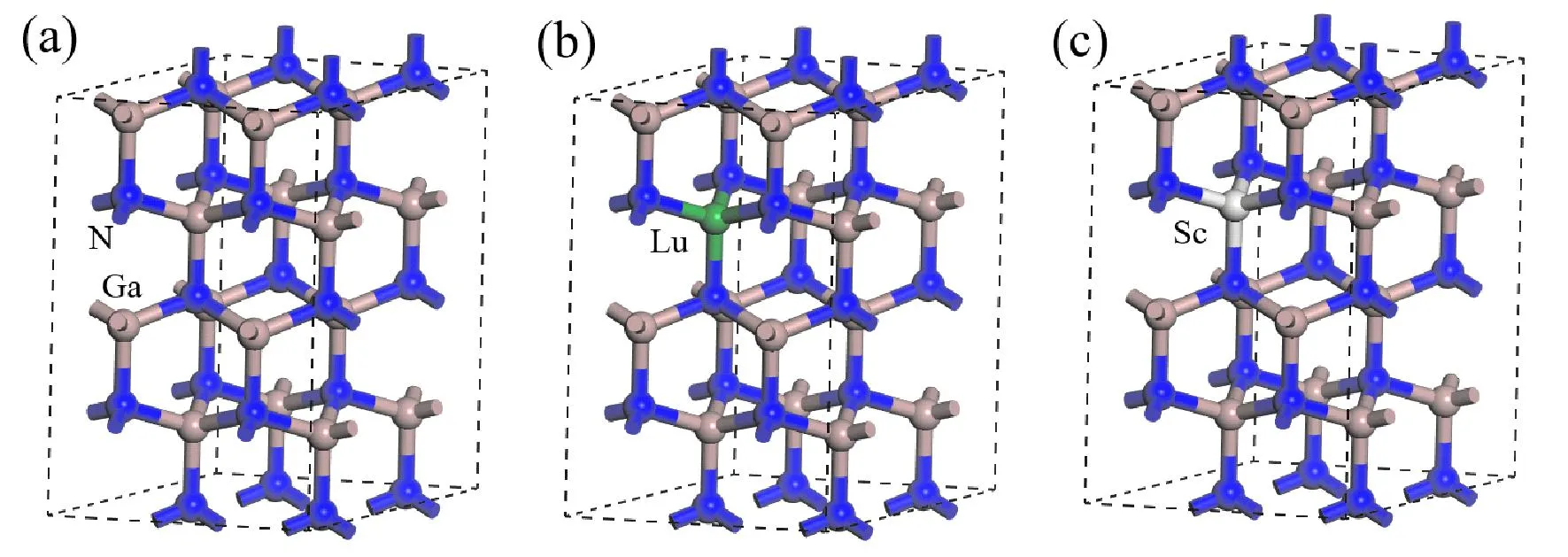
图1 稀土元素掺杂GaN体系超胞结构图 (a)GaN；(b)GaN∶Lu；(c)GaN∶ScFig. 1 Supercell structure diagrams of rare earth element doped GaN systems (a)GaN；(b)GaN∶Lu；(c)GaN∶Sc.

2.2 计算方法

基于密度泛函理论，采用Materials Studio 2019中的CSATEP[23]计算模块.在密度泛函理论(Density functional theory，DFT)下采广义梯度近似(Generalized Gradient Approximation，GGA)和交换关联函数(Perdew-Burke-Ernzerhof，PBE)[24]来处理电子间相互作用的关联能.通常情况下采用GGA方法会低估带隙宽度，为了使计算结果更准确，本文采用GGA+U平面波超赝势方法[25，26]. 参考Abdalla等人[18]和Zakrzewski等人[27]的结论，最终在N的2p态和Ga的3d态上取U值为4.90 eV和0.30 eV.考虑到由于稀土元素属于强关联体系，所以对稀土的4f轨道参考Larson等人[28]的结论，在Lu的4f态上取U值为10.95 eV；Sc的3d态上选取软件默认的2.50 eV.平面波截止能选取450 eV，参考Monkhorst方案取布里渊区k点为4×4×2，自洽收敛精度为2×10-6eV/atom，能量收敛标准为1×10-5eV/atom，内应力为0.05 GPa，原子的最大位移收敛标准设为0.001 Å.计算中，Ga、N、Lu、Sc原子的价电子分别3d104s24p1、2s22p3、4f145d16s2、3d1s2.

3 计算结果与分析

3.1 电子结构

3.1.1晶体参数

计算前先对超晶胞进行几何结构优化，所得晶胞参数见表1.

表1 优化后GaN 和 稀土掺杂GaN 体系晶胞参数值

由表1可知，优化后的c/a=1.624与实验值1.626吻合较好，误差仅为0.12%，可见本文计算方法的可靠性.稀土元素掺杂后体系的晶格参数均大于本征体系，主要是因为Lu3+离子半径(0.0861 nm)和Sc3+离子半径(0.0745 nm)大于Ga3+离子的半径(0.067 nm)，所以Lu、Sc掺杂会导致超晶胞晶格常数增大.

3.1.2能带结构

对本征GaN超胞进行结构优化后计算能带结构，所得数据见表2.由表可知，采用GGA+U方法计算所得本征GaN的禁带宽度为3.37 eV，接近实验值3.39 eV.

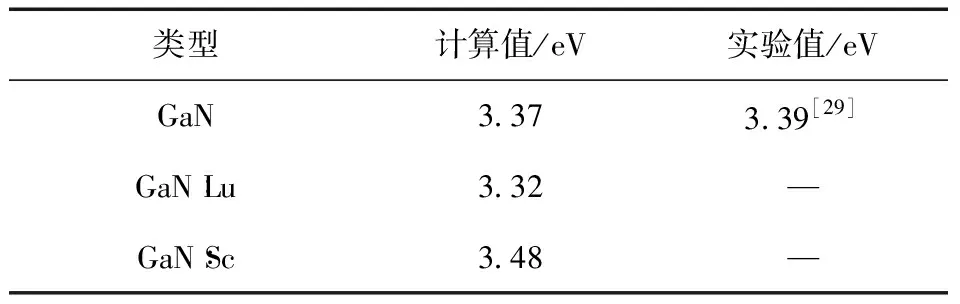
表2 GaN掺杂前后带隙.

图2为本征GaN的能带结构图，从图可以直观的看出，GaN的导带底和价带顶位于布里渊区同一点，为直接能隙半导体.计算所得的数据3.37 eV与实验值3.39 eV符合得很好，误差仅为0.59 %.

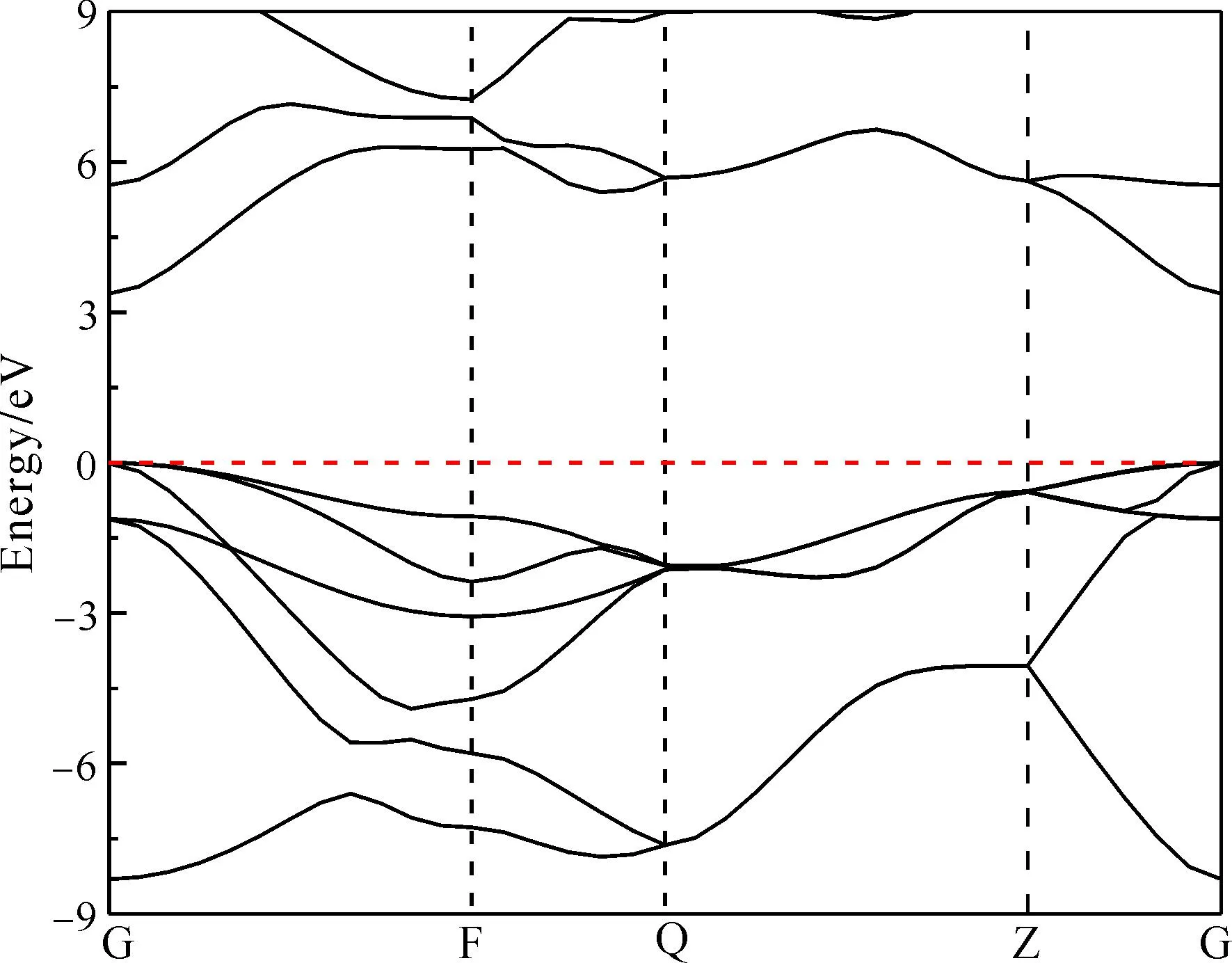
图2 本征GaN能带结构Fig. 2 Band structures of the ideal GaN.

Lu、Sc掺杂后GaN的能带结构(自旋向上和自旋向下)如图3所示.可以看出，相比于未掺杂的GaN，掺杂后系统能带结构中的价带导带数明显变多变密，在费米能级处产生了杂质能级.Lu的掺入使得导带向低能方向偏移，价带上移，从而导致带隙减小为3.32 eV，而Sc掺入后带隙变大为3.48 eV.虽然掺杂后GaN体系的电子结构发生了较大改变，但未改变体系的跃迁方式，仍为直接跃迁，满足直接带隙半导体特性. 稀土元素Lu掺杂GaN后，诱导了浅能级杂质，使得禁带宽度变窄，有利于改善 GaN 的光学性能.

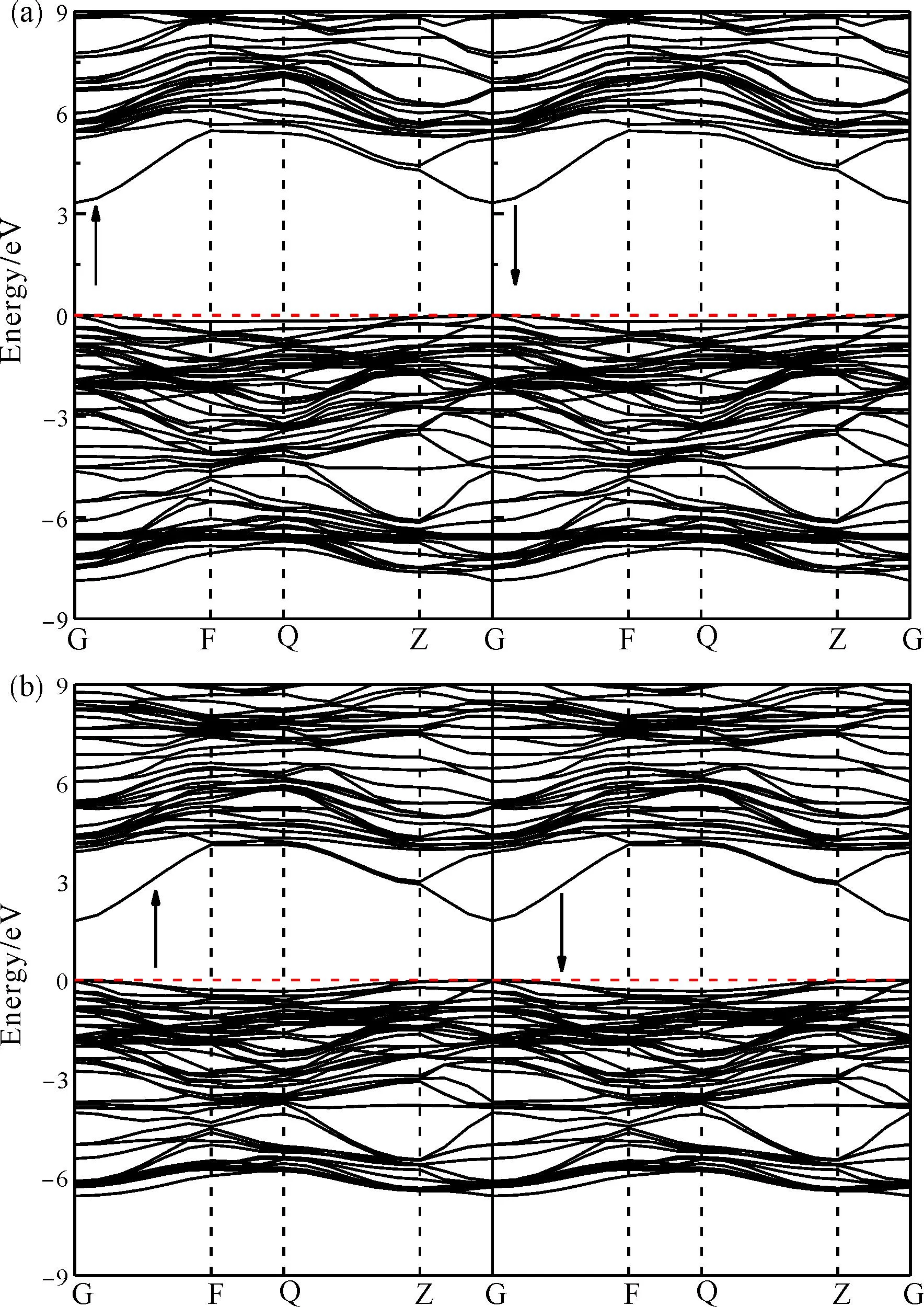
图3 稀土掺杂GaN体系能带结构：(a)GaN∶Lu；(b)GaN∶ScFig.3 Band structures of the rare-earth doped GaN systems：(a)GaN∶Lu；(b)GaN∶Sc.

3.1.3电子态密度

本征GaN和稀土掺杂GaN的总态密度(Density of States，DOS)如图4所示.从图中可以看出：-15 eV至13 eV(下价带)附近的峰主要来自N的2s态和Ga的3d态，以及少量N的2p态和Ga的4s4p态；在-13 eV至-9 eV(中价带)附近的峰主要来自Ga的3d态、N的2s和2p态以及少量Ga的4s和4p态；在-8 eV至0 eV(上价带)附近的峰主要由Ga的4s态、N的2p态以及少量Ga的4p态和N的2s态贡献.GaN的导带主要由Ga的4s和4p态、N的2s和2p态贡献.

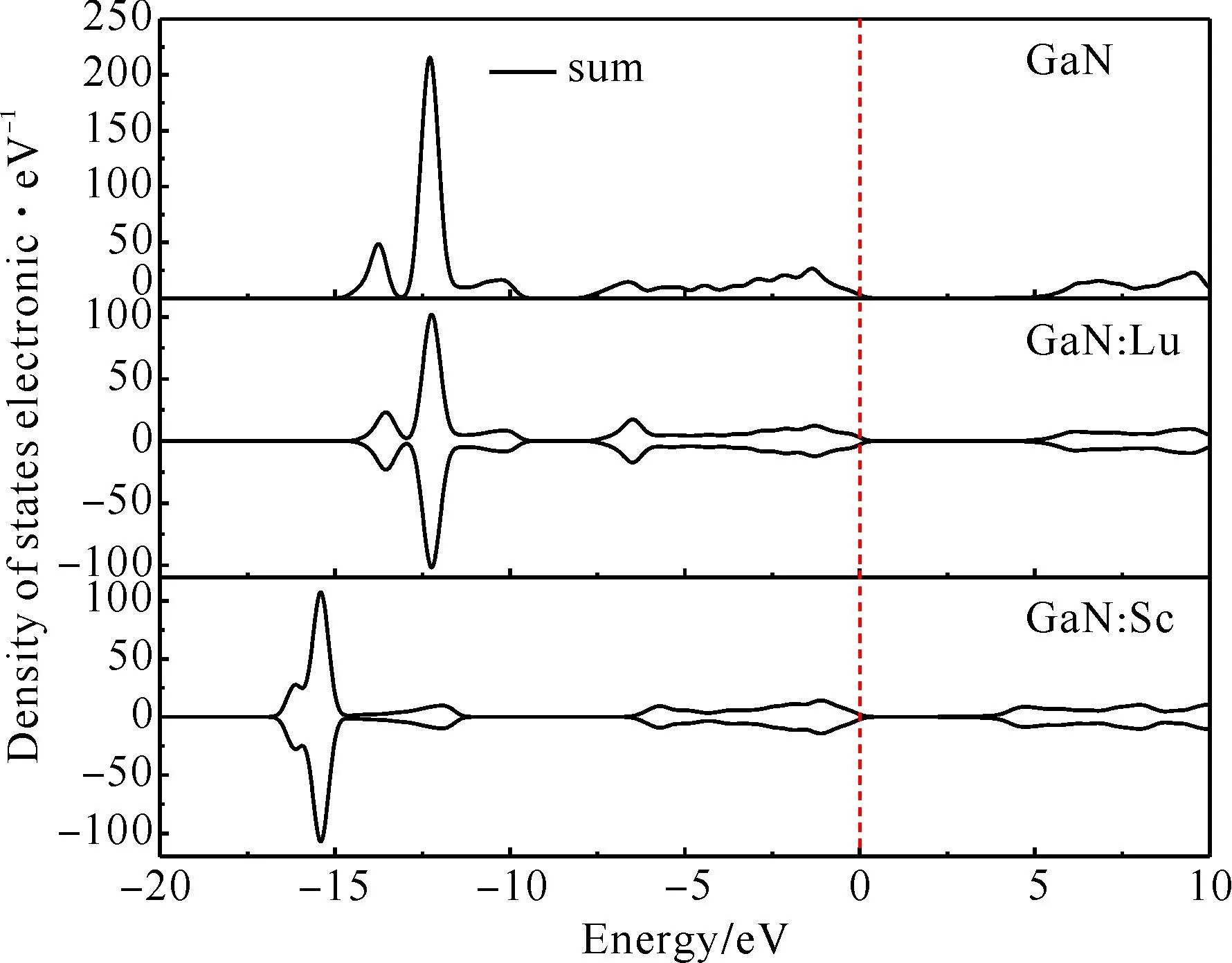
图4 GaN和稀土掺杂GaN体系总态密度图Fig. 4 Total densities-of-states for GaN and rare-earth doped GaN.

Lu掺杂GaN体系的自旋向上和自旋向下的总态密度是高度对称的.从图4结合图5-8可以看出，-15 eV--9 eV附近的峰主要来自Ga的3d态、N的2s态和Lu的4f态；在-8 eV-0 eV附近的峰主要来自N的2p态和少量Ga的4s4p态、N的2s态和Lu的5d态.

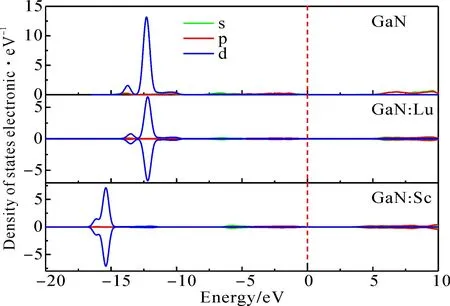
图5 GaN和稀土掺杂GaN体系Ga原子分波态密度图Fig. 5 Partial densities-of-states of Ga for GaN and rare-earth doped GaN.

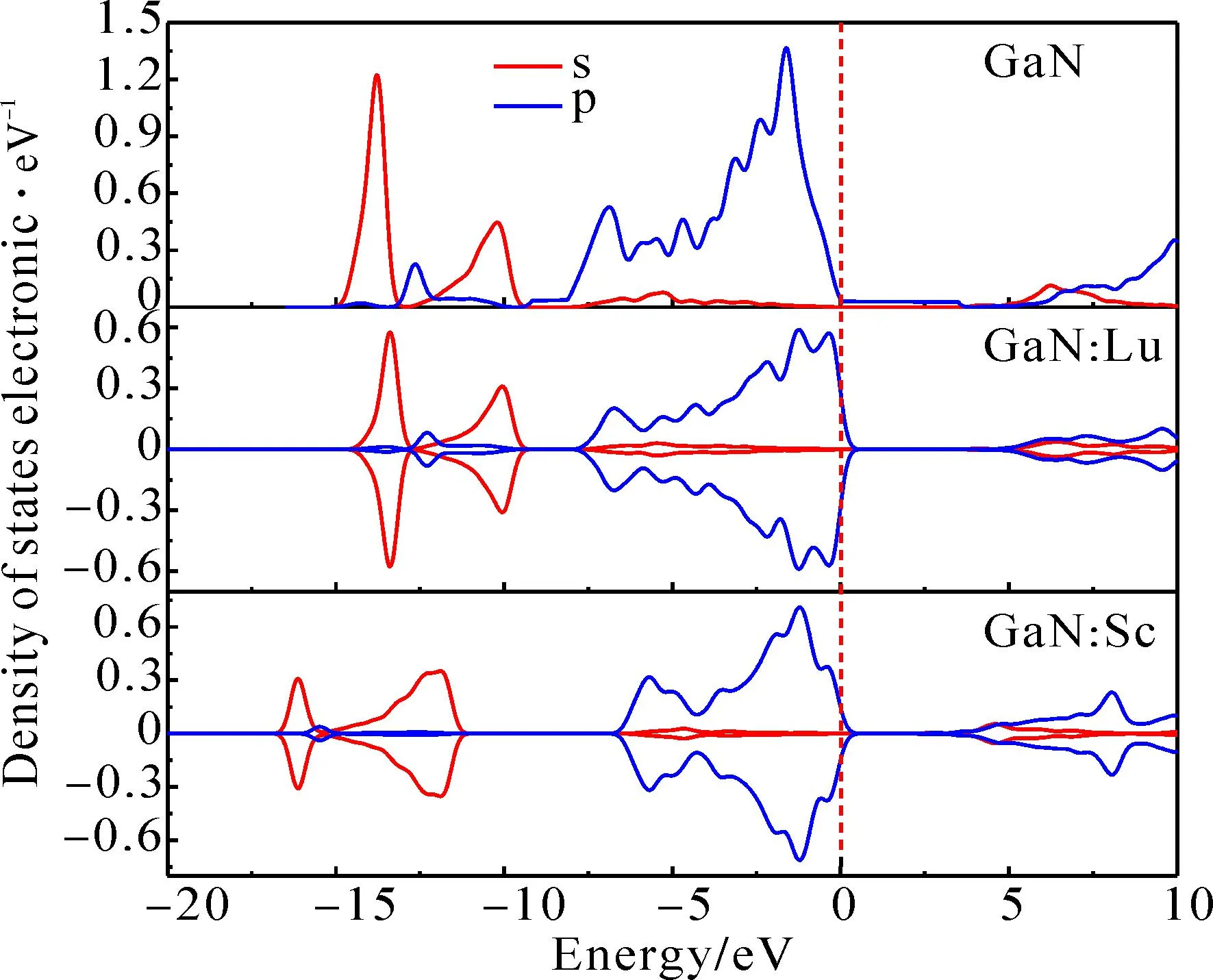
图6 GaN和稀土掺杂GaN体系N原子分波态密度图Fig. 6 Partial densities-of-states of N for GaN and rare-earth doped GaN.

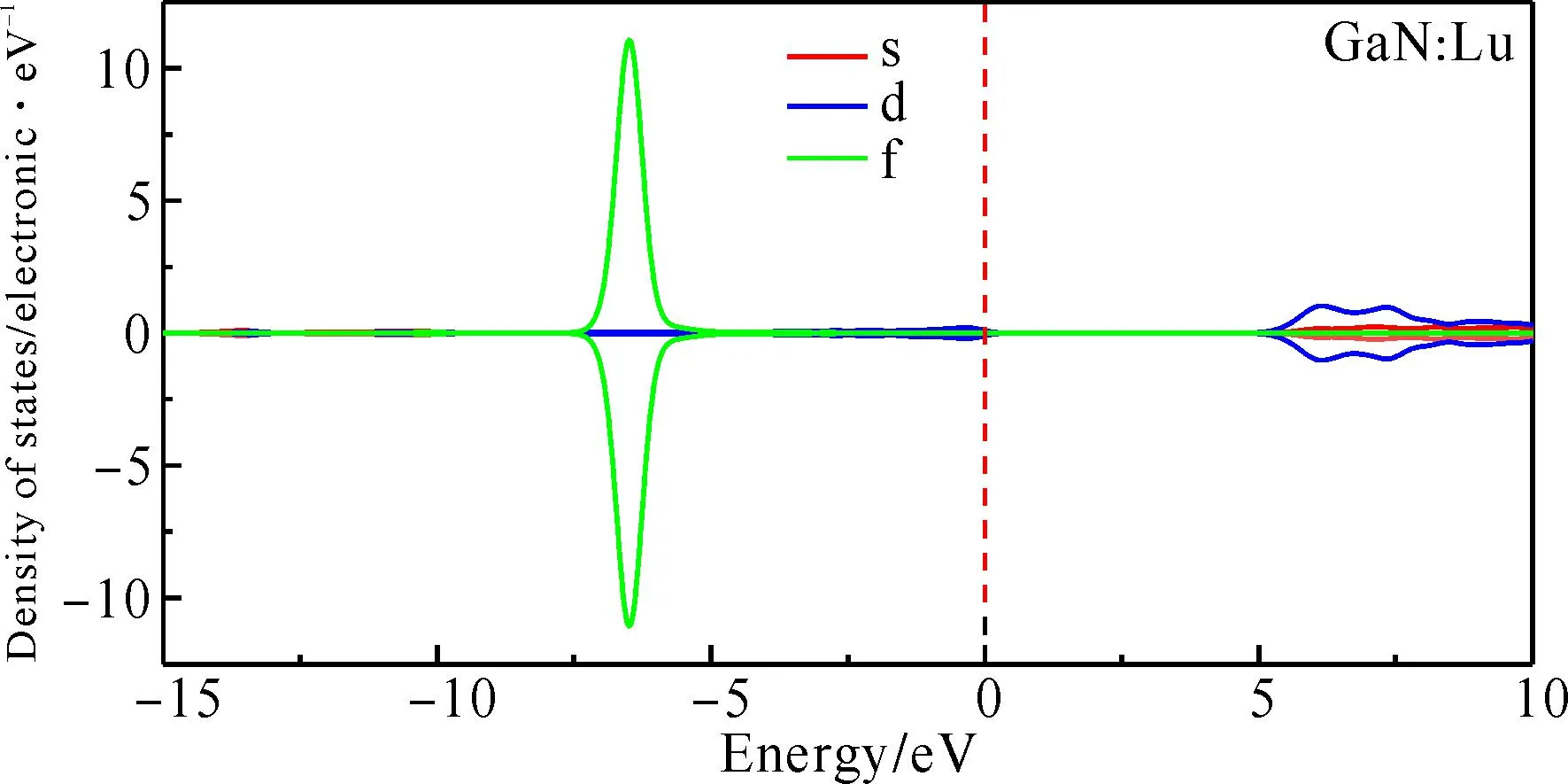
图7 GaN∶Lu体系Lu原子分波态密度图Fig. 7 Partial density-of-states of Lu for GaN∶Lu.

图8 GaN∶Sc体系Sc原子分波态密度图Fig. 8 Partial density-of-states of Sc for GaN∶Sc.

由图4可知，对于GaN∶Sc体系，其总态密度也呈现出高度的对称性.在-17 eV--11 eV附近的峰值主要来自Ga的3d态、N的2s态；处于-6 eV-0 eV附近的峰值主要由N的2p态、Sc的s态及少量Sc的3d态贡献；而导带4 eV-10 eV附近的峰值则主要来自Sc的s态和N的2p态. Lu原子的4f态和5d态以及Sc的原子3d态和s态的向上自旋部分和向下自旋部分，分别对各自掺杂体系的总态密度不同带的峰值做出了贡献.

3.2 光学性质

在一定范围内，半导体的宏观光学性质可以使用复介电函数ε(ω)=ε1(ω)+ε2(ω)和复折射率函数N(ω)=n(ω)+ik(ω)来描述.其中

ε1(ω)=n2-k2，

(1)

ε2(ω)=2nk.

(2)

式中，n为折射率，k为消光系数.

通过直接跃迁概率定义和Kramers-Kronig色散关系可以推导出半导体介电函数的实部和虚部为[30].

(3)

(4)

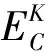
根据介电函数，半导体的其他光学常数：吸收系数α(ω)、反射率R(ω)、折射率n(ω)和能量损失函数L(ω)可以由下列公式给出[31，32].

(5)

(6)

(7)

(8)

3.2.1复介电函数

纯GaN和稀土掺杂GaN超胞的介电函数实部和虚部如图9所示.从图9(a)中可以看出，在入射光能量为零时，GaN∶Lu体系的静介电常数为4.71相比于比本征GaN的4.5有所增大. 而Sc掺杂GaN后静态介电常数也有所增大为4.62，掺杂后GaN静态介电常数均提高，说明掺杂使得体系耐高压特性有所增强.

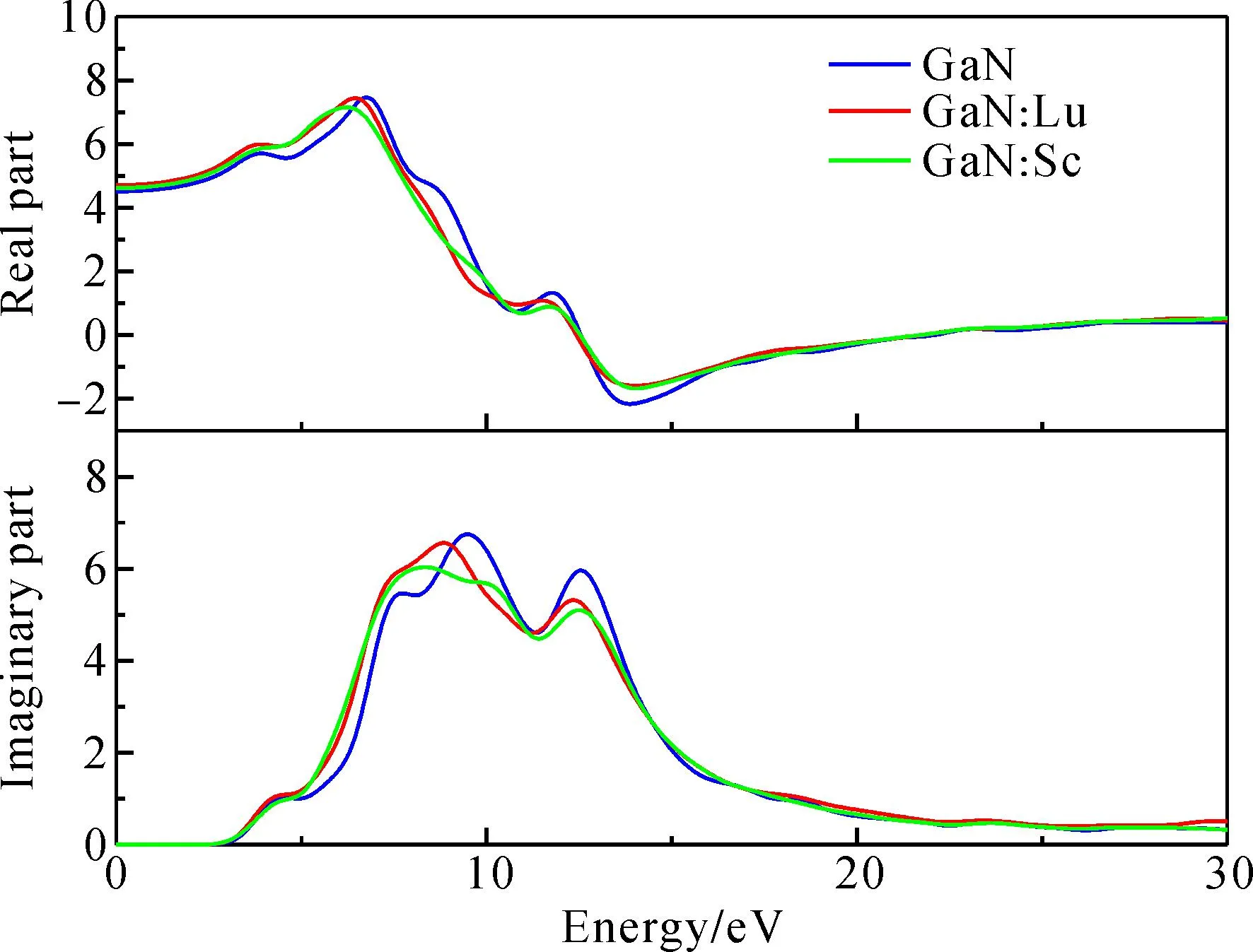
图9 GaN和稀土掺杂GaN体系的介电函数实部和虚部Fig. 9 Real and imaginary parts of dielectric function in GaN and rare-earth doped GaN systems.

介电函数虚部的峰值代表电子跃迁的数目，掺杂前后体系均为直接能隙半导体材料，其峰值可以由能带结构和电子态分布给出解释.从图9(b)可以看出，本征GaN介电函数的虚部在4.51 eV、7.57 eV、9.53 eV、12.50 eV处出现峰值，对应于价带顶到导带底的跃迁.Lu掺入后峰值数目有所减少，分别在4.55 eV、8.84 eV和12.30 eV处产生峰值.相比于本征GaN介电函数虚部曲线，GaN∶Lu体系在7.57 eV处的峰值消失，且整体发生左移，主要原因是Lu的掺入引起晶格弛豫从而导致的.由于Sc的掺杂GaN∶Sc体系介电函数的虚部发生了红移，但变化趋势与GaN∶Lu体系基本一致.

3.2.2吸收系数和折射率

图10为本征GaN和稀土掺杂 GaN结构的光吸收系数和折射率.由图10(a)可知，纯的GaN的光吸带边为3.12 eV，该能量对应价带顶到导带底的跃迁，略小于禁带隙值3.39 eV，这是因为禁带宽度还与激子能量有关. 吸收谱的变化趋势与介电函数虚部与能量的关系基本一致，在光子能量为13.30 eV时达到最大值，略高于陆稳等人[33]结果12.50 eV.Lu、Sc替位掺杂Ga后，光吸收边往低能方向移动，发生了红移现象.

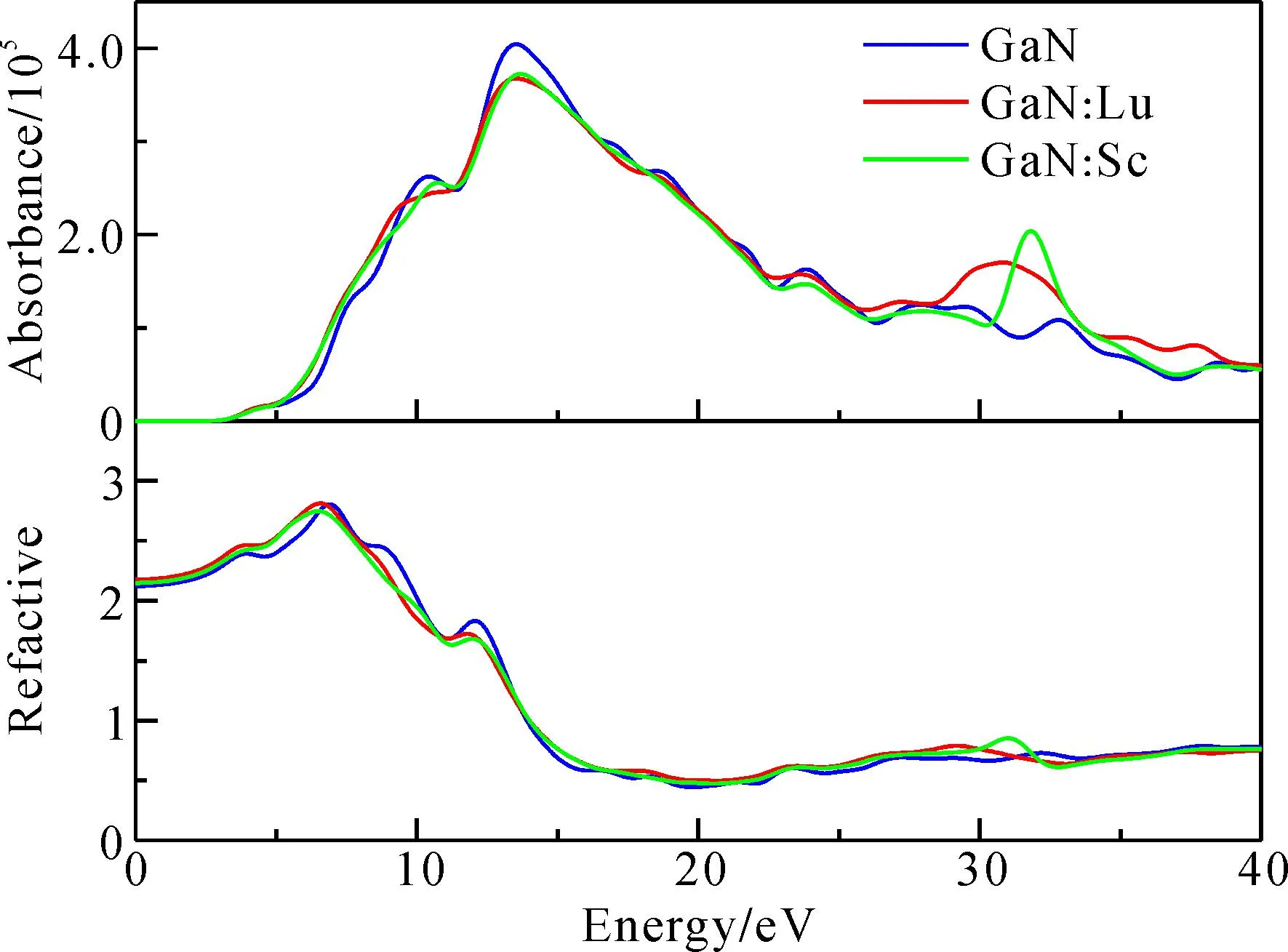
图10 GaN和稀土掺杂GaN体系的吸收系数和折射率Fig. 10 Absorbance indexs and refractive indexs of in GaN and rare-earth doped GaN systems.

从图10(b)中折射率随能量变化的关系可以看出，本征GaN在光子能量为零时的静态折射率为2.15，较理论值2.2[34]符合的很好.Lu、Sc掺杂后，静态折射率有所提高分别为2.17和2.47.能量分别为19.60 eV、20.90 eV和17.20 eV时，GaN、 GaN∶Sc、GaN∶Lu体系折射率达到最低，说明此时入射光发生折射的能力最弱.

3.2.3反射率及消光系数

GaN掺杂前后的反射率和消光系数如图11所示.从图11(a)可以看出，本征GaN的静态反射率为0.13，Lu、Sc掺杂后有所增大为0.14、0.133.当光子能量为14.90 eV时本征GaN体系的反射率达到最大.从图11(b)可以看出，本征GaN和GaN∶Lu体系都在光子能量为13.10 eV时开始减退，而GaN∶Sc体系发生了红移在11.50 eV时开始减退，且掺杂后使得体系的衰减峰值有所降低.

图11 GaN和稀土掺杂GaN体系的反射率和消光系数Fig. 11 Reflectivities and extinction coefficients of GaN and rare-earth doped GaN systems.

3.2.4能量损失谱

图12为本征GaN和Lu、Sc掺杂GaN体系的能量损失谱.由图可知，Lu、Sc掺杂后体系能量损失最大值降低，并且峰值相对左移. Sc掺杂后体系在32.60 eV附近产生新的峰值. 未掺杂GaN体系在光子能量为22.20 eV时能量损失值最大，Lu、Sc掺杂后分别左移至22.00 eV、22.10 eV.

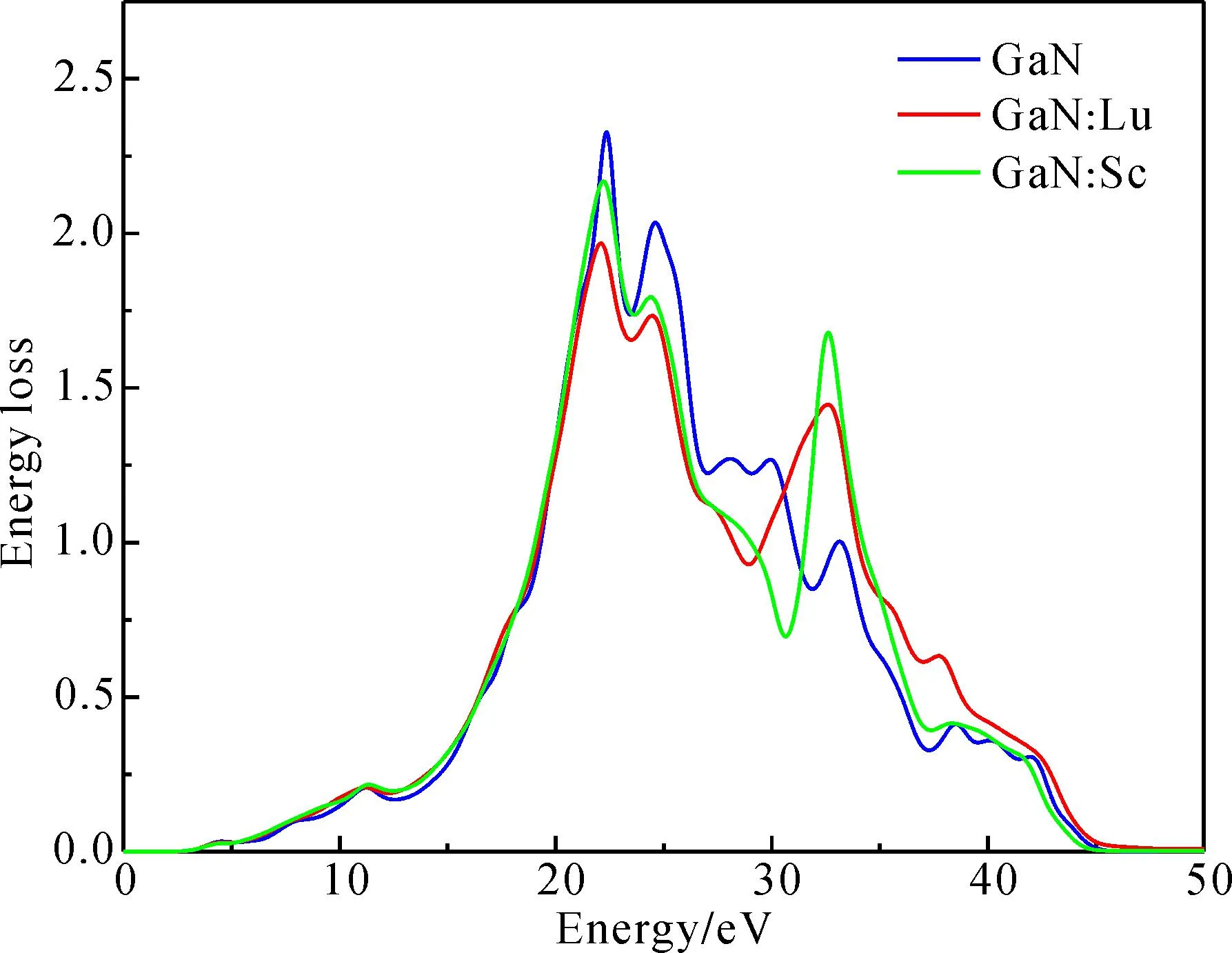
图12 GaN和稀土掺杂GaN体系的能量损失谱Fig.12 Energy loss spectra for GaN and rare-earth doped GaN systems.

4 结 论

利用第一性原理，对本征GaN和稀土元素Lu、Sc掺GaN体系的超晶胞进行优化，采用GGA+U方法对掺杂前后体系的电子结构和光学性质进行了理论计算.计算结果表明，Lu掺杂GaN后诱导了浅能级杂质带隙变小，为3.32 eV；而Sc掺杂后诱导了深能级杂质，使得带隙变宽为3.48 eV，且在靠近费米能级处引入了杂质带，该能级主要来源于Lu的4f态和5d态电子以及Sc的3d态电子. Lu、Sc的掺入，从不同程度上影响了GaN的光学性能，计算所得本征GaN光学常数与实验数据基本一致，Lu、Sc掺杂后静态介电常数较本征GaN有所增大.两种稀土元素掺杂后介电函数的虚部整体左移，峰值减小. Lu、Sc替位掺杂Ga后，光吸收边往低能方向移动，可见光区域的响应范围变宽，发生了红移现象.计算结果对稀土元素掺杂GaN红外高压光电材料的开发和研究提供了理论依据和数据支持.