双数态输入型M-Z干涉仪中量子相位的最大似然估计和贝叶斯分析

李 岩, 师昳婧, 任志红

(1．太原师范学院 物理系, 晋中030619; 2. 太原师范学院 计算物理与应用物理研究所,晋中 030619; 3. 山西师范大学 物理与信息工程学院,太原 030031)

1 引 言

基于量子力学基本原理所开展的高精度相位估计是当前国内外精密测量领域研究的重点课题[1，2]，如引力波探测[3]，重力常数测量[4]，等效性原理验证[5]等，其不仅有利于我们对自然界物理常数的准确测定，也有助于当前量子科学技术的快速发展[6]. 在物理学中，相位可以被估计，但不能被测量，就像时间一样，无法找到一个可观测物理量与其相对应，所以相位估计的原理是通过对可选择物理量的测量，结合其与相位的函数关系，获得待测相位的相关信息，如相位平均值及方差[7].

作为相位估计的理想载体，干涉仪在科学研究的发展中起到了非常重要的作用，比如早期的迈克尔逊-莫雷干涉仪，就是通过对光在不同干涉仪臂上传播的时间差所导致的相位差来探测以太是否存在[8]. 马赫-曾德尔(Mach-Zehnder，M-Z)干涉仪 是另外一种常见的光学干涉仪，广泛地应用在量子力学的基础研究中，包括量子纠缠、量子芝诺效应等[9]. 1981年，美国科学家Calton M.Caves教授指出，将M-Z干涉仪的闲置端口输入压缩真空态可以有效地提高待估参数的精度，甚至超越标准量子极限[10]. 由此揭开了以量子纠缠或量子压缩为资源的量子计量序幕[11，12]，对量子相位进行精确估计成为了精密测量研究的核心内容[13].

双数态(twin-Fock state，tFs)是Dicke态不同分类中的一种，在精密测量方面有着不错的表现[14]. 与最大纠缠态GHZ态相比，其具有较强的抗噪性，与其他类型的Dicke态(如W态)相比，其在高精度测量方面表现最优，故在实验和理论上双数态被广泛地进行研究[15-20]. 但大部分研究是从频率论角度出发，利用最大似然估计方法对其相位精度进行研究，较少采用贝叶斯分析开展研究.

本文将基于双数态输入的M-Z干涉仪，探究最大似然估计和贝叶斯分析对量子相位估计精度的影响. 通过对干涉仪输出端粒子数差和宇称测量的理论计算和数值模拟，发现采用贝叶斯分析结合粒子数差测量，可实现全相位空间的最优测量，即达到量子Fisher信息给出的测量精度极限，与此同时，采用贝叶斯分析所需的测量样本数更少. 另外，我们还对宇称测量方案进行了分析研究，通过最大似然估计方法验证了量子相位估计精度会随待估相位θ0的变化发生改变，与粒子数差测量结果对比，验证了前者的优越性.

2 模型及相关概念

2.1 M-Z干涉仪及其施温格表示

一般地，在粒子数表象中，双数态可以表示为[20]

(1)

(2)

属于Bell态中的一种，或称两比特W态. 2017年，清华大学尤力教授领导的实验小组就利用量子相变产生了近1000个原子的双数态纠缠，促进了量子计量学的发展[16].

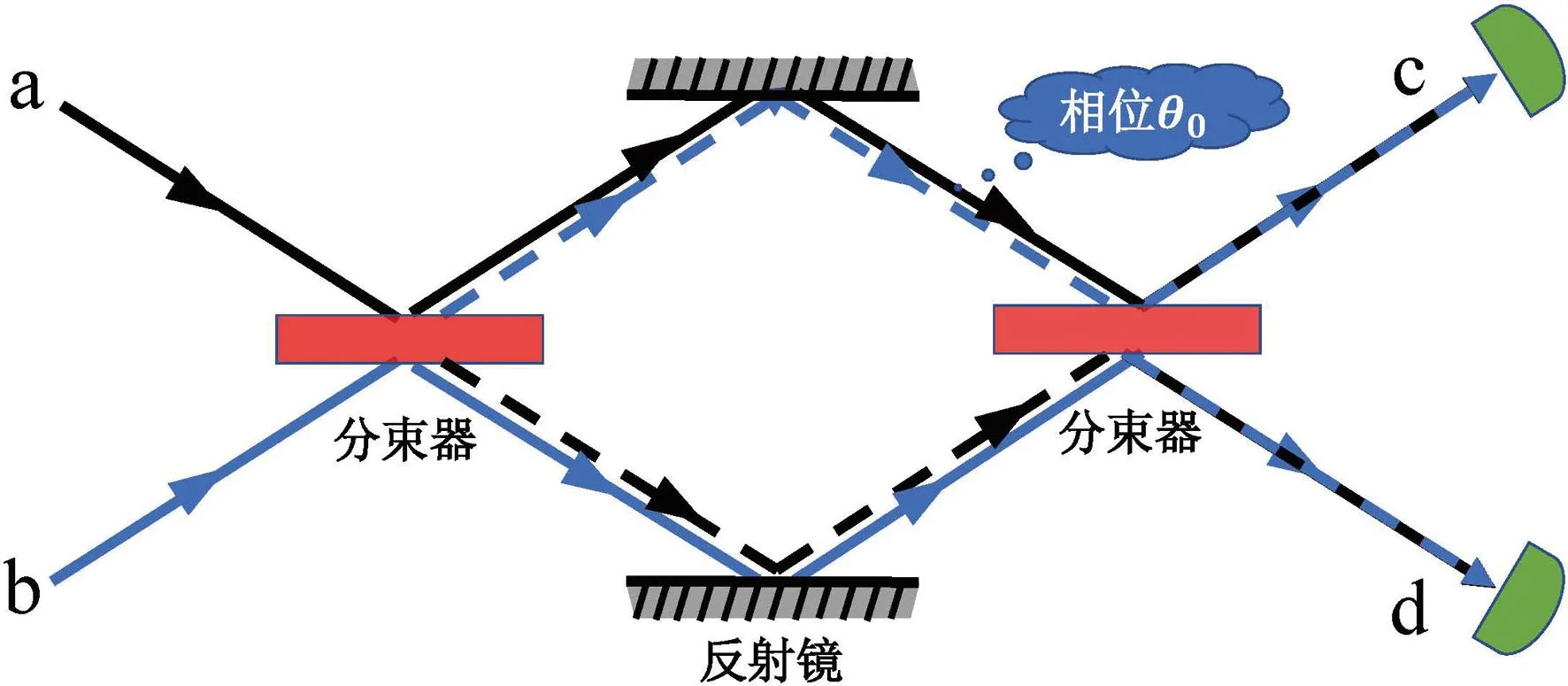
图 1 马赫曾德尔干涉仪工作示意图. Fig. 1 Schematic plot of Mach-Zehnder interferometer

双数态输入型马赫曾德干涉仪可由上图1表示，其中a，b端口进行双数态(如光子)的输入，经过分束器(红色部分)，反射镜，待测参数M以相位差θ0的形式编码到量子态上，再经分束器合并，最后在输出端c，d进行粒子数差或宇称测量，进而获取待测参数的相关信息.

依据角动量施温格表象与粒子数表象的对应关系[21]，

M-Z干涉仪三部分操作过程可以表示为

(3)

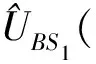
(4)

可将M-Z干涉仪输出端的双数态表示为

(5)

2.2 量子Fisher信息

在无偏差参数估计中，Fisher信息扮演着非常重要的角色，用来给定测量精度的上限. 一般地，对于试验获取的条件概率p(μ|θ)，即在给定相位θ条件下对物理量M进行测量得到的概率分布，其Fisher信息可以表示为

(6)

依据统计学中的克拉美罗下界(Cramer-Rao Lower bound)

(7)

可借助系统Fisher信息的计算，得到测量精度的理论极限.

(8)

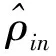
2.3 最大似然估计和贝叶斯分析

最大似然估计和贝叶斯分析是参数估计中常见的两种方法，彼此有各自的特点. 最大似然估计认为待估参数是确定的，其值可通过似然函数取极大值进行获取. 而贝叶斯分析则认为待估参数是不确定的、随机的，可通过后验概率分布来进行获取.

一般地，对于单次测量得到的条件概率p(μ|θ0)(其中θ0为待估计参数)，进行m次重复测量(作为样本)，可得似然函数，

(9)

对其求最大值，便可得到最大似然估计值，

θMLE=arg maxp(μ1，μ2，...，μm|θ0)

(10)

将m次样本测量作为整体进行重复n次，可得n个估计值，进而获取其平均值〈θest〉及标准差Δθ.

贝叶斯分析则基于贝叶斯定理，从后验概率分布的角度出发进行研究，

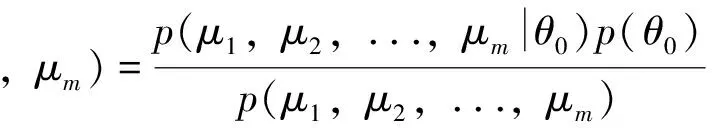
(11)

其中，p(θ0)为先验概率. 通过后验概率分布p(θ|μ1，μ2，...，μm)，可获得待估相位θ0的估计值θest及其标准差Δθest，即

(12)

(13)

与最大似然估计方法一样，重复n次，可得n个估计值及标准差，经过平均可得最后结果〈θest〉和〈Δθ〉.

3 理论分析与数值模拟

针对粒子数差和宇称测量两种方案，将首先进行进行理论计算分析；其次，通过蒙特卡洛数值模拟条件概率，获取两种测量方案所需的实验数据；最后，采用最大似然估计和贝叶斯分析方法，探究相位估计精度随实验样本数m的变化关系.

3.1 粒子数差测量

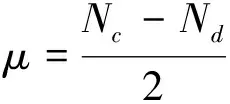
p(μ|θ)=|〈N/2，μ|e-iθJy|N/2，0〉|2

(14)

(15)

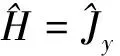
(16)

容易发现二者是一致的. 从理论上讲，这表明粒子数差测量是最优的测量方案. 那么在实际测量中，表现如何呢？通过蒙特卡洛模拟实验数据，我们分别采用最大似然估计和贝叶斯分析对其开展研究.

针对条件概率p(μ|θ)，进行数值模拟，获取粒子数差(随机变量)μ的数据，开展待估相位θ0的最大似然估计和贝叶斯分析(具体流程如2.3小节所述)，探究相位估计值θest及其精度mΔ2θ随样本数目m的变化关系. 对于双数态(1)来说，由于其条件概率分布p(μ|θ)=p(-μ|θ)具有对称性，当采用最大似然估计进行研究时，会发现无法确定真实相位θ0. 因此，在本文的研究中，我们限定了待估计θ0的变化范围，即θ0⊂[0，π/2]区间，这一点在文献[18]中也有提到.

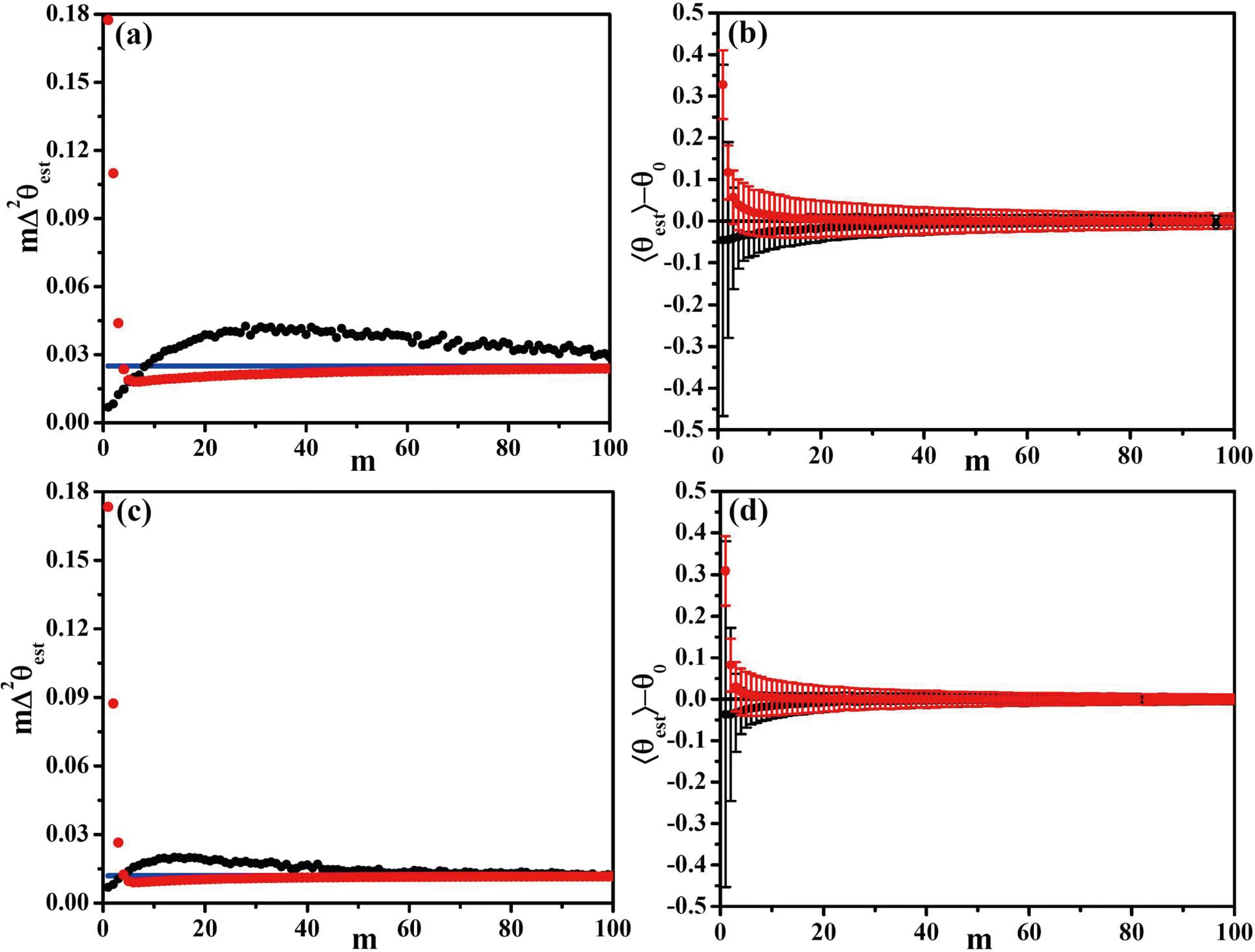
图 2 对待估相位θ0=0.02π分别采用最大似然估计(黑点)和贝叶斯推断(红点)进行分析的结果. (a)和(b)分别表示当粒子数N=8时，相位估计精度mΔ2θ和相位估计差值〈θest〉-θ0随样本数m的变化. (c)和(d)表示粒子数N=12的结果. 其中，(a)和(c)中的蓝色直线代表量子测量极限，1/FQ. Fig. 2 Maximum likelihood estimation (black point)and Bayesian inference (red dot)of the estimated phaseθ0=0.02π. (a)and (b)represent the phase estimation precision mΔ2θ and the difference value 〈θest〉-θ0 with respect to the number of sample m in N=8 tFs，respectively. (c)and (d)represent the results of N=12 tFs. The blue lines in (a)and (c)denote quantum measurement limit，1/FQ.

如图2所示，在N=8和N=12双数态输入的M-Z干涉仪中，通过粒子数差测量，对待估相位θ0=0.02π进行两种方案下的估计研究. 针对样本m=1，2，...，100，我们分别重复n=2000次试验进行研究，贝叶斯分析所采用的先验概率分布函数为0到π/2的均匀分布函数p(θ)=2/π. 研究发现，当双数态粒子数N较小时，需要更多的样本才能达到无偏差估计；当粒子数N较大时，所需的样本数m变少. 此外，采用贝叶斯分析进行相位估计，达到测量精度极限所需的需样本数m较最大似然估计更少一些. 图3是对待估相位θ0=0.01π进行了两种方法研究结果的对比，表明当待估相位值较大时，实现准确估计所需的样本数m变小，两种方法的表现近乎一致.

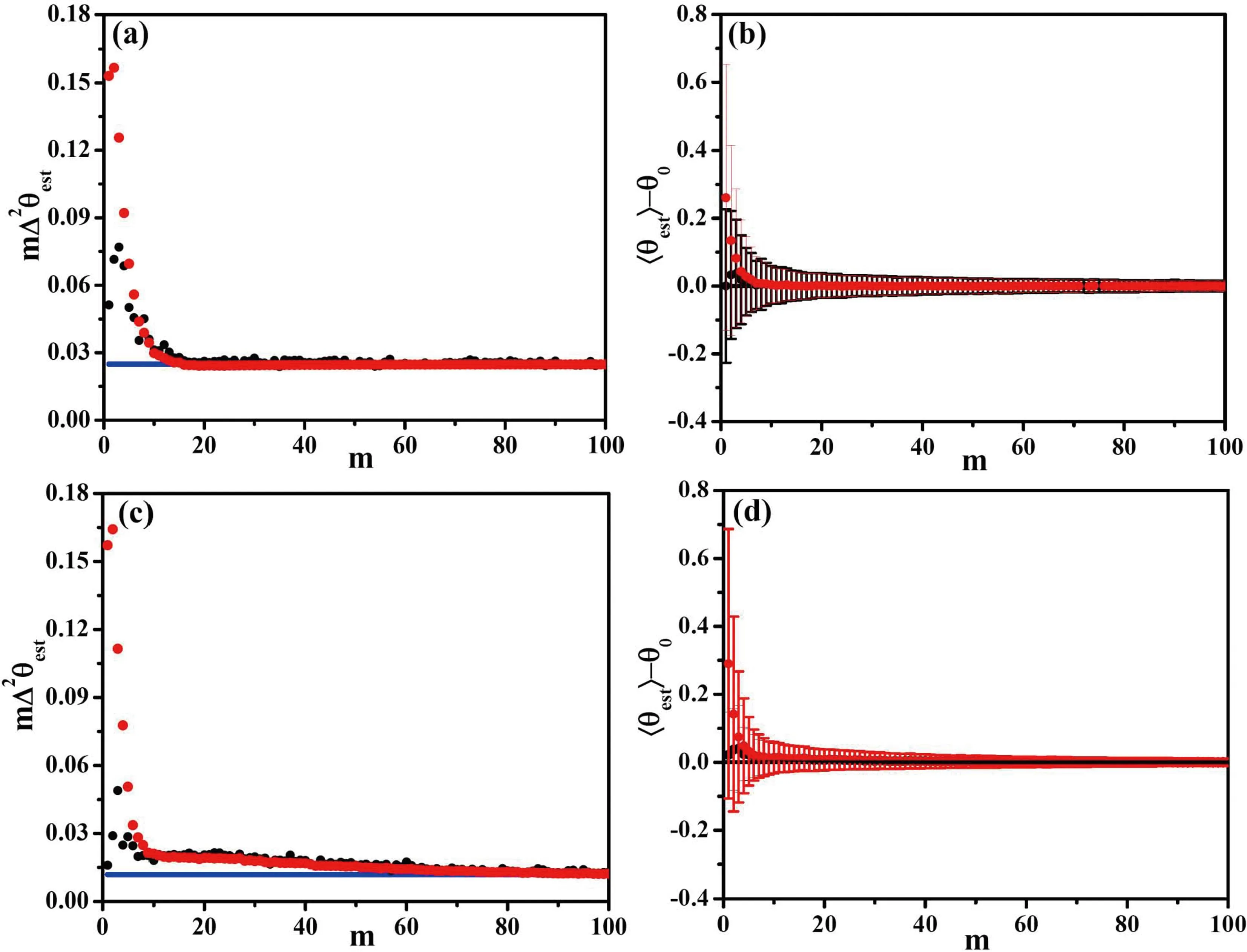
图 3 对待估相位θ0=0.01π分别采用最大似然估计(黑点)和贝叶斯推断(红点)进行分析的结果. (a)和(b)分别表示当粒子数N=8时，相位估计精度mΔ2θ和相位估计差值〈θest〉-θ0随样本数m的变化. (c)和(d)表示粒子数N=12的结果. 其中，(a)和(c)中的蓝色直线代表量子测量极限，1/FQ. Fig. 3 Maximum likelihood estimation (black point)and Bayesian inference (red dot)of the estimated phaseθ0=0.01π. (a)and (b)represent the phase estimation precision mΔ2θ and the difference value 〈θest〉-θ0 with respect to the number of sample m in N=8 tFs，respectively. (c)and (d)represent the results of N=12 tFs. The blue lines in (a)and (c)denote quantum measurement limit，1/FQ.

为了更为清晰地了解在整个相位空间[0，π/2]上的表现，我们对粒子数N=8，12，20的双数态进行了分析研究，如图4所示，这里选取样本数m=100，重复次数n=2000. 从图4(a)，图4(c)和图4(e)的对比中可以看出，当双数态所含粒子数N较小时，贝叶斯分析(红点)和最大似然估计(黑点)无法在整个相位区间实现最优估计(Δθmin)，特别是当待估相位θ0靠近中间区域时，两种方法均出现了误差. 当粒子数N较大时，贝叶斯分析在整个相位空间实现了最优相位估计，最大似然估计原则上应该也实现了最优相位估计，但由于此处样本值m较大，最大似然函数表达式复杂，导致相位估计值及其精度不准确，这也从侧面体现了贝叶斯分析的优越性.

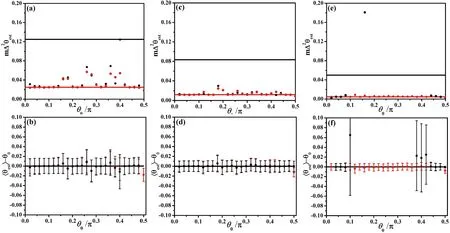
图4 对待估相位θ0⊂[0，π/2]分别采用最大似然估计(黑点)和贝叶斯估计(红点)进行分析的结果. (a)和(b)分别表示当粒子数N=8时，相位估计精度mΔ2θ和相位估计差值〈θest〉-θ0随样本数m的变化. (c)和(d)表示粒子数N=12的结果. (e)和(f)表示粒子数N=20的结果. 其中，黑色的直线代表散粒噪声极限，即1/N，红色的直线代表量子测量极限，1/FQ.Fig. 4 Maximum likelihood estimation (black point)and Bayesian inference (red dot)of the estimated phase θ0⊂[0，π/2]. (a)and (b)represent the phase estimation precision mΔ2θ and the difference value 〈θest〉-θ0 with respect to the number of sample m in N=8 tFs，respectively. (c)and (d)represent the results of N=12 tFs. (e)and (f)represent the results of N=20 tFs. The black lines in (a)，(c)，(e)denote the shot noise limit，1/N. The red lines in (a)，(c)，(e)denote quantum measurement limit，1/FQ.

需要注意的一点是，当待估相位θ0非常靠近0或π/2时，如图4(b)，图4(d)和图4(f)中π/2处所示，此时需要较大样本数m，以及较大粒子数N，才可实现最优相位估计，也可通过图2(a)和图2(c)得到验证.

3.2 粒子数差测量

3.2.1宇称测量

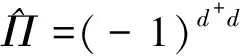
peven(+1|θ)-podd(+1|θ)=PN/2[cos(2θ)]

(17)

此处PN/2[cos(2θ)]为勒让德多项式，peven(+1|θ)(podd(+1|θ))代表d端口所测粒子数为偶数(奇数)的概率. 结合二者概率之和为1，即

peven(+1|θ)+podd(+1|θ)=1

(18)

可得端口d所测粒子数为奇数和偶数的概率分别为，

(19)

(20)

与粒子数差测量中计算Fisher信息的方法一致，将式(19)和式(20)代入Fisher信息公式(6)得，

(21)

下图5给出了在理想情况下，当粒子数N=8，12时，Fisher信息及相位精度随待估相位θ0的变化. 从图5(a)中可以看出，当待估相位取特殊相位角θ0=0，π/2时，得到Fisher信息的最大值，即量子Fisher信息(8)，表明此时为最优相位估计. 借助CRLB(式(7))可知，随着待估相位θ0的变化，其测量精度的理论极限会发生改变，如图5(b)所示.

为了验证上述理论结果，我们选取N=8和N=12的双数态对待估相位θ0=0.05π进行研究，其Fisher信息为F8(0.05π)=35.05和F12(0.05π)=58.65. 通过蒙特卡洛模拟方法获取实验数据(n=10000)，采用最大似然估计方法对其进行分析，得到结果如图6所示.

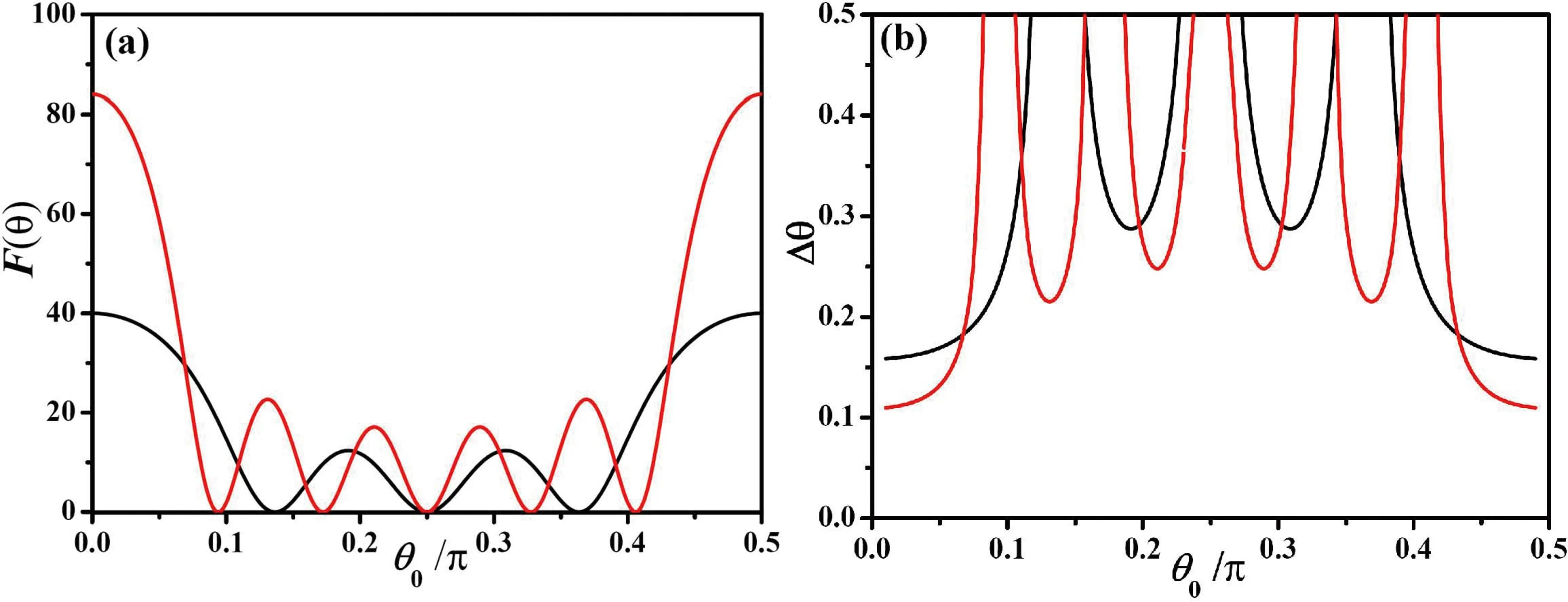
图 5 Fisher信息(21)和相位估计精度Δθ随待估相位θ0的变化. (a)红色和黑色实线分别代表粒子数N=8，12时Fisher信息随相位θ0的变化；(b)红色和黑色实线分别代表粒子数N=8，12时测量精度Δθ随相位θ0的变化. Fig.5 Fisher information (21)and theoretical precision Δθ with respect to the estimated phase θ0. (a)The solid red and black lines represent the Fisher information with respect to the phase θ0 of N=8，12 tFs；(b)The solid red and black lines represent the precision with respect to θ0 of N=8，12 tFs.

从图6(a)和图6(c)中，容易发现采用宇称测量方案和最大似然估计方法的组合，得到的相位估计精度值(蓝色点)逐渐趋近红色实线(理论测量极限)，但无法抵达黑色实线(量子Fisher信息所给定测量极限)，即1/FQ. 图6(b)和图6(d)表示估计值θest与待估相位θ0=0.05π之间的差值随样本数m的变化，可以看出，随着样本数m的增加，最大似然估计为无偏差估计. 这样，我们从数值上验证了宇称测量方案中相位估计精度随待估相位值θ0变化而改变，且仅当选取最优相位θ0=0，π/2，才能达到量子Fisher信息(8)所给出的精度. 此处，由于最大似然函数在相位区间[0，π/2]上不满足高斯分布，故经贝叶斯定理计算后所得的后验概率分布也不是高斯分布，无法实现相位估计研究.

为了更加直观地比较两种测量方案(粒子数差和宇称)对相位估计精度的影响，图7给出了在粒子数差测量方案下，双数态所含粒子数为N=8和N=12，待估相位为θ0=0.05π时，最大似然估计方法给出的结果.

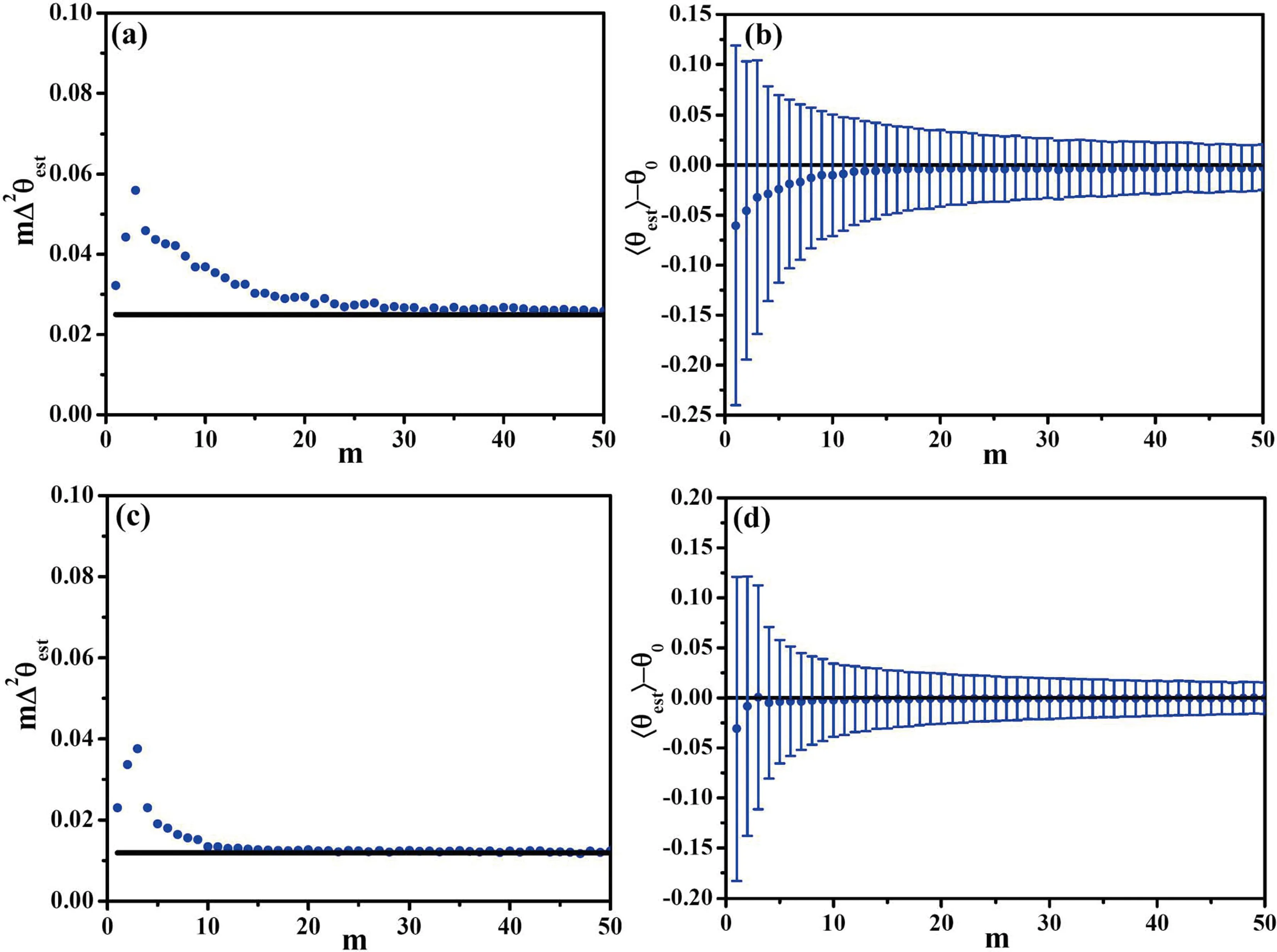
图7 针对粒子数差测量，对待估相位θ0=0.05π采用最大似然估计(蓝点)进行分析的结果. (a)和(b)分别代表粒子数N=8时，相位估计精度mΔ2θ和相位估计差值〈θest〉-θ0随样本数m的变化. (c)和(d)代表粒子数N=12的结果. 其中，黑色直线代表1/FQ. Fig.7 Maximum likelihood estimation (blue point)of the estimated phase θ0=0.05π in the scheme of particle-number difference measurement. (a)and (b)represent the phase estimation precision mΔ2θ and the difference value 〈θest〉-θ0 with respect to the number of sample m in N=8 tFs，respectively. (c)and (d)represent the results of N=12 tFs. The black lines denote 1/FQ.

将其与图6进行对比，可以看出，随着样本数m的增加，粒子数差测量方案达到了量子测量极限(黑色直线)，而宇称测量方案未达到黑色直线，再次验证了粒子数差测量方案的优越性.

4 结 论

综上所述，本文基于双数态输入的马赫曾德尔干涉仪模型，探究了在不同测量方案下，粒子数测量和宇称测量，最大似然估计和贝叶斯分析两种方法在量子相位估计方面的表现. 通过分析研究，得出贝叶斯分析结合粒子数测量是最优的相位估计方案，可在整个相位空间实现最优测量，达到量子Fisher信息所限定的量子测量极限. 同时，贝叶斯分析在相位估计中所需的样本数m较最大似然估计更少一些，节省资源. 另外，当待估相位值较小时，需要选取粒子数更多的双数态，样本数更大的测量方案，方可实现最优测量. 在宇称测量方案中，相位估计精度会随待估相位的变化而发生改变，借助蒙特卡洛数值模拟我们验证了这一点，还发现了贝叶斯分析不适合宇称测量方案下的相位估计.

通过对两种测量方案下特定相位的最大似然估计研究，再次验证了粒子数差测量是最优相位测量方案. 本文的研究结果为采用双数态进行实验上的精密测量提供了重要的理论依据.