三时间间隔圆锥补偿姿态更新算法性能分析

程思微，叶灵军，甘厚吉

CHENG Siwei,YE Lingjun,GAN Houji

海军工程大学 电子工程学院，武汉430033

College of Electronic Engineering,Naval University of Engineering,Wuhan 430033,China

1 引言

Ignagni[1]在1990 年首先提出了姿态更新算法的三时间间隔结构，并给出了一组计算公式。其基本方法是把等效旋转矢量的求解区间分为大、中、小三个时间间隔。每个大时间间隔作为一个更新周期。大时间间隔包含若干个中时间间隔，中时间间隔又包含若干个小时间间隔。在计算时，先对小时间间隔内的角速度积分，得出小时间间隔内的角增量，将这些量相加，就可以得到中时间间隔和大时间间隔的角增量；然后再利用小时间间隔内的角增量的叉乘来对中时间间隔和大时间间隔的角增量进行补偿，得到大时间间隔内的等效旋转矢量，并进行姿态更新。

以文献[1]提出的三时间间隔结构为基础，Lee[2]、Park[3]、Wu[4]等人设计了一系列相应的多子样等效旋转矢量算法。Ignagni在其总结性文献[5]中，综合了Jiang[6]和Lee[2]的部分算法，得出了三时间间隔下的另一组计算公式。

上述姿态更新方法[1-6]均采用三时间间隔结构，各有其优缺点。其中，Ignagni 和Park 等人都只计算了算法漂移，没有进行仿真验证。而Lee 和Wu 虽然进行了仿真实验，但没有涉及大时间间隔中应该包含多少个中时间间隔这一关键问题，仅仅简单地直接令大时间间隔等于中时间间隔。

为了考察三时间间隔结构在姿态更新中的作用，本文用三时间间隔结构改写了Lee 提出的四子样算法和四子样优化算法，以及Savage[7]的方法，然后对改进算法以及Ignagni、Park、Lee 等人算法分别进行了仿真，并通过与传统双速结构算法的对比分析，确定三时间间隔对姿态更新算法精度和效率的影响。

2 三时间间隔圆锥补偿算法

2.1 基本原理

姿态更新的过程实质是求解方向余弦阵、欧拉角或者姿态四元数的过程。不管采用哪种描述方法，都要先求解等效旋转矢量。等效旋转矢量的微分运动方程如下[8]：

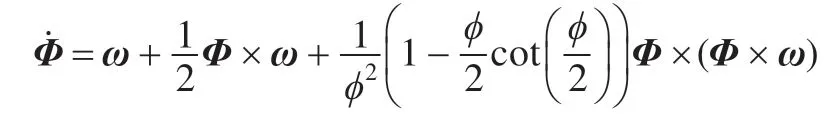
其中Φ为等效旋转矢量，表示载体tn-1到tn时刻的等效旋转，ϕ=||Φ||为旋转角度，ω为旋转角速度。由于时间间隔很短，一般情况下ϕ为小量。

旋转矢量的计算公式如下[1]：

采用三时间间隔的思想，设每个大时间间隔包含M个中时间间隔，则

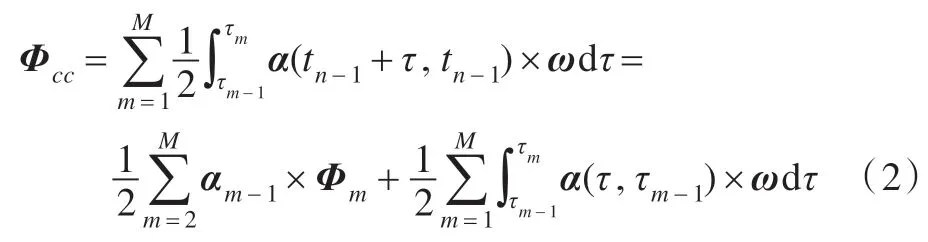
表示第m个中时间间隔内的圆锥补偿。它的计算公式和Jordan[9]、Miller[10]、Savage[7]等人提出的等效旋转矢量的计算公式类似。另外，它也是Ignagni[1，5]系列算法的不同之所在。

2.2 基于三时间间隔结构的算法改进

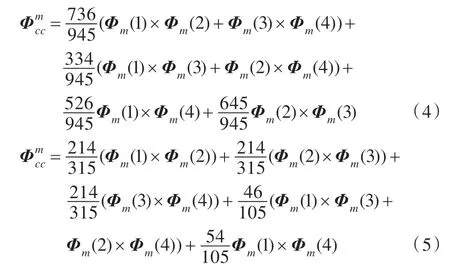
公式（4）～（6）中的任意一个，再加上式（1）～（3），就构成了一个新的三时间间隔结构的姿态更新算法。例如，先由公式（4）求解中时间间隔内的圆锥补偿，然后再根据公式（1）～（3）计算大时间间隔内的等效旋转矢量，进而对姿态进行更新，就是三时间间隔结构的四子样等效旋转矢量姿态更新算法。

3 算法分析

下面对本文将要考察的算法进行分析。

Ignagni 给出的两组算法的主要不同是中时间间隔的圆锥补偿的计算公式不同。在文献[1]中，算法A 的中时间间隔圆锥补偿，此时，中时间间隔等于小时间间隔，算法退化成两时间间隔，也就是Savage[7]所说的双速结构。算法A 的计算公式也和Savage 的类似，所不同的是，它缺少上一周期的补偿量，且补偿系数全是1/2。算法B 是Jiang[6]提出的单子样公式的三时间间隔的表示。算法C、D、E 是Jordan[9]和Miller[10]算法的三时间间隔的表示，而算法E1 和F 是从算法E 改进而来的，所不同的是，这两种算法在求解时都只需要计算一次叉乘。算法G、H 又是算法F 改进版本，它们的不同是，用到了上一个大时间间隔的角增量作为补偿量。

在文献[5]中，算法1 是Jiang[6]的二子样算法的三时间间隔表示，算法3、5、7分别是从Jordan[9]、Miller[10]、Lee[2]的算法改进得到的三子样姿态更新算法，算法9 是一种新的五子样算法。算法2、4、6、8、10 又分别是从算法1、3、5、7、9 改进而来的，它们的特点是比原方法多了一个修正量。Park[3]的算法6 是一个六子样算法。

表1 给出了文献[1-3，5]，以及本文中的算法按子样数的分类。其中，IA～IH分别表示文献[1]中的算法A～H，Lee 表示文献[2]提出的实时算法，Park6 表示文献[3]中的算法6，I1～I10 分别表示文献[5]中的算法1～10，RV43、RV4o3、S23、S33、S43 分别表示本文构造的四子样算法、优化四子样算法，以及子样数为2、3、4 的Savage方法。

为了简便起见，约定每个大时间间隔包含的中时间间隔的个数称为样本数（M值），而每个中时间间隔包含的小时间间隔的个数为子样数（N值）。如果样本数为1，则三时间间隔退化成两时间间隔，Jordan、Miller 等人提出的传统的等效旋转矢量算法就是在此基础上构造的。因为三时间间隔结构与传统的算法结构的主要差别是多了一个样本数的概念，下面主要考察样本数对算法精度和效率的影响。

表1 各算法按子样数的分类

4 实验分析

4.1 精度分析

精度分析实验分三组进行，第一组测试文献[1]中的算法，第二组测试文献[5]和文献[3]中的算法，第三组测试本文构造的算法。假设载体作典型圆锥运动，实验参数设置为：圆锥频率0.1 Hz，半锥角1°，步长0.01 s，运行时间1 h。

图1、2 给出了文献[1]中算法的欧拉角最大绝对值误差MAE随样本数的变化曲线。其中，RV3 表示三子样旋转矢量算法，样本数不变化；IA～IH 分别表示文献中的算法A～H，样本数的变化范围为[1，20]。从图1 可以看到：

（1）除了算法B、G、H 以外，其他算法的误差随样本数的变化都不明显。

（2）就算是算法B、G、H，算法误差也不会随着样本数增加而无限减小，它们存在一个极限，从图1 上看，它们的精度都不会超过RV3 的精度。

图1 文献[1]中算法误差

图2 算法A 和算法C～F 误差

（3）算法C～F 的精度与RV3 相当。

从图2 可以看到：

（1）算法B、G、H 以外的其他算法的精度随样本数的变化虽然不是很明显，但是误差随着样本数增加，还是有下降的趋势。

（2）算法C～F 按精度可以分为两部分，算法C 的精度比其他算法精度差。这是因为在算法C 中子样数为2，而其他算法子样数为3。也就是说，算法C 的中时间间隔中只包含2 个小时间间隔，所以它的精度稍微差一点。

由此可以得出以下结论：

（1）如果不用中时间间隔的补偿，那么算法精度随样本数变化不大（算法A）。

（2）如果只用单子样，那么算法精度会随样本数增大而提高，但是不会超过RV3 的精度（算法B）。

（3）如果使用二子样或者三子样，算法精度随样本数变化也不大，大致相当于RV3 的精度（算法C～F）。

（4）如果使用上一大时间间隔的补偿量，在样本数较小时会有比较大的误差，随着样本数的增加，误差会降低，但是最后的精度也不如没有使用该补偿量算法的精度（算法G、H）。因此，没有必要使用上一大时间间隔的补偿量。

图3 文献[5]和文献[3]中算法误差

图4 文献[3]中算法6 和文献[5]中算法3、7、9 误差

图3 和图4 给出了文献[5]和文献[3]中算法的误差随样本数的变化曲线。其中，RV3 表示三子样旋转矢量算法，样本数不变化。I1～I10 分别表示文献[5]中的算法1～10，Park6 表示文献[3]中的算法6，样本数的变化范围为[1，20]。从中可以得出以下结论：

（1）增加样本数，能够提高部分算法的精度（算法4、5、6、10），也会降低部分算法的精度（算法1、2、8）。

（2）样本数过大时，误差反而会更大（除算法5、6 外的所有算法，这一点在图4 中特别明显）。

（3）Ignagni 对Park 算法的改进有一些提高了精度（算法8），也有一些降低了精度（算法6、10）。

（4）Park 的算法6 随着样本数增加误差增加，但是增加的幅度不大。该算法的精度要低于三子样旋转算法，这说明过多地增加子样数，对提高算法精度并没有意义。

（5）文献[5]中所有算法随着样本数的增加，精度都趋近于三子样旋转算法精度。

在图5 中，RV3 表示三子样旋转矢量算法，它是双速结构，样本数不变化。其他算法都是三时间间隔结构，样本数的变化范围为[1，20]。其中RV43 表示四子样算法，RV4o3 表示四子样优化算法，Lee 表示文献[2]提出的实时算法，S23、S33、S43 分别表示子样数为2、3、4 的Savage算法。可以看出：

（1）所有算法的误差变化的幅度都很小，最大误差和最小误差之差在10-8量级，远小于算法误差。

（2）随着样本数的增加，所有算法的误差先降低，后增加。

（3）四子样算法的精度都差不多。

（4）在M较小时，二子样和三子样Savage 算法比四子样算法精度低，在M较大时，精度反而较高。

图5 本文构造算法的误差

4.2 效率分析

由于上述算法精度都与三子样旋转矢量算法近似，而且随样本数变化不大。出于简洁和方便的考虑，在效率分析时，只选取三子样旋转矢量算法和根据三子样旋转矢量算法改进得到的算法F 进行比较。

图6 给出了这两个算法随着样本数变化所消耗的CPU 时间的曲线。其中，RV3 表示三子样旋转矢量算法，样本数不变化。IF 表示文献[1]中的算法F，样本数的变化范围为[1，20]。可以看出：

（1）算法F 的执行效率要明显高于三子样旋转矢量算法。这是因为算法F 是三时间间隔结构，它的姿态更新周期比三子样旋转矢量算法长，因此姿态更新的次数少，计算三角函数的次数少。

（2）随着样本数增加，算法F 的耗时呈指数下降趋势。但当样本数超过8 以后，变化就十分平缓了。所以样本数也不需要取得太大。

图6 三子样旋转矢量算法和算法F 耗时

5 结论

Ignagni 的三时间间隔结构和传统的双速结构的区别在于用三时间间隔代替了两时间间隔。当样本数或子样数为1 时，三时间间隔结构就退化成双速结构。当样本数为1 时，就是熟悉的等效旋转矢量算法，当子样数为1 的时候，和Savage的方法类似。

采用三时间间隔结构以后，随着样本数的增加，不同算法的精度可能变高，也可能变低，但幅度都不大，而且最后都趋近于三子样等效旋转矢量算法的精度。尤其是从传统算法直接改进过来的算法，例如图1 中的算法C、D、E，以及图5 中的所有算法，它们的精度几乎不受样本数的影响。对传统算法进行修正后，增加样本数可能会提高精度，但主要也是抵消了修正量的影响，例如图1 中的算法G、H，图3 中的算法6、10。与双速结构类似，过分地增加样本数和子样数并不能提高精度，反而会引入计算误差。

但是，采用了三时间间隔以后，姿态更新的周期就加长了，也就是说，在固定的时间内，姿态更新的次数减少了，这就意味着它可以少计算一些三角函数。可以说，三时间间隔结构的本质是利用叉乘代替了三角函数运算。而Ignagni的那些修正算法（图1 中的算法E'、F），又减少了叉乘的计算次数。因此，如果选择合理的样本数和子样数，三时间间隔结构能够在一定程度上减少运算量。但由于样本数和子样数越多，叉乘的计算次数也会越多，算法结构也越复杂，而且在样本数和子样数比较大时，再增加样本数和子样数，效率不能有太大幅度的提高，因此它们都不宜选得太大。

综上所述，Ignagni提出的三时间间隔结构是双速结构的改进形式，继承并发展了利用角增量的叉乘作为补偿量的思想。它不能显著地提高姿态更新算法的精度，过分地增加样本数和子样数，只会增加算法的复杂度和计算误差。但它延长了姿态更新的周期，减少了三角函数运算的次数，选择合理的样本数和子样数，可以在一定程度上减少运算量。因此，在实际工程应用中，本文提出的三时间间隔结构算法能够兼顾时间和精度要求，适于求解那些对时间效率要求较高，而对精度要求不那么苛刻的问题。当姿态变化要求较大的样本数以提高计算效率而姿态变化较为平缓则样本数较小，并且根据本文实验分析，在大多数情形下取样本数不超过8 个。

[1] Ignagni M B.Optimal strapdown attitude integration algorithms[J].Journal of Guidance，1990，13（2）：363-369.

[2] Lee J G，Yoon Y J，Mark J G，et al.Extension of strapdown attitude algorithm for high-frequence base motion[J].Journal of Guidance，1990，13（4）：738-743.

[3] Park C G，Kim K J，Chung D，et al.Generalized coning compensation algorithm for strapdown system[C]//AIAA，Guidance，Navigation and Control Conference.San Diego：AIAA，1996：29-31.

[4] Wu Y X，Hu X P，Hu D W，et al.Strapdown inertial navigation system algorithms based on dual quaternion[J].IEEE Transactions on Aerospace and Electronic Systems，2005，41（1）：110-132.

[5] Ignagni M B.Efficient class of optimized coing compensation algorithm[J].Journal of Guidance，Control，and Dynamics，1996，19（2）：424-429.

[6] Jiang Y F，Lin Y P.Improved strapdown coning algorithm[J].IEEE Transactions on Aerospace and Electronic Systems，1992，28（2）：484-490.

[7] Savage P G.Strapdown inertial navigation integration algorithm design part 1：attitude algorithms[J].Journal of Guidance，Control，and Dynamics，1998，21（1）：19-28.

[8] Bortz J E.A new mathematical formulation for strapdown inertial navigation[J].IEEE Transactions on Aerospace and Electronic Systems，1971，AES-7（1）：61-66.

[9] Jordan J W.An accurate strapdown direction cosine algorithm，NASA TN-D-5384[R].1969.

[10] Miller R B.A new strapdown attitude algorithm[J].Journal of Guidance，1983，6（4）：287-291.