双钙钛矿卤化物Cs2AgFeX6(X=Cl,Br,I)电子结构和光学性质的第一性原理研究

郝久源, 张 敏, 刘 派, 李 瑞, 祖宁宁

(齐齐哈尔大学 理学院, 齐齐哈尔 161000)

1 引 言

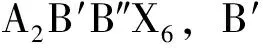
McClure等人从含有氢卤酸和次磷酸的溶液中合成了Cs2AgBiX6(X = Cl，Br)双钙钛矿，Cs2AgBiCl6和Cs2AgBiBr6带隙分别为2.62 和2.06 eV[24]. Madhvendra Nath Tripathi等人发现Cs2AgBiX6(X = Cl，Br，I)双钙钛矿，X位从Cl到I的依次取代，晶格参数增大，带隙减小，所有光谱都表现出红移的趋势[25]. 对于双钙钛矿Cs2AgCrX6(X = Cl，Br，I)，第一性原理研究发现，由于卤族元素从Cl到I的取代，带隙减小，其介电函数和损失函数光谱的阈值从高能量区向低能红外区移动[26]. 通过以上报道不难发现，X位元素的改变可以实现双钙钛矿的带隙调控，进而对其光学性质产生影响.

最近，人们在实验上成功获得了新型无铅双钙钛矿Cs2AgFeCl6晶体，为立方结构，空间群为Fm-3m(No. 225)，该材料具有稳定性好、合成低成本并且易于制造等优点，其吸收带边位于800 nm，并具有窄带隙1.55 eV[27，28]，因此该材料可以作为光伏和光催化应用的候选材料. 但据现有报道来看，Cs2AgFeCl6中Cl被Br或I取代尚未得到研究，所以本论文将采用基于密度泛函理论的第一性原理方法研究Cs2AgFeX6(X = Cl，Br，I)的电子结构和光学性质，并分析X位元素的改变对材料的晶体结构、能带结构和光吸收性质的影响.

2 计算方法

本文采用VASP软件包[29，30]对Cs2AgFeX6(X = Cl，Br，I)进行晶体结构优化. 其中电子间的交换关联能由广义梯度近似(GGA)的PBE泛函[31]处理，电子与离子间的相互作用由投影缀加平面波(PAW)[32]方法处理. 对于自洽计算，为确保计算的准确性，设置平面波截断能为500 eV，总能量收敛精度为10-5eV和相互作用力精度为10-2eV/Å. 高对称布里渊区内K点网格以Gamma点为中点，根据Monkhorst - Pack方法取样，布里渊区网格设置为5 × 5 × 5.

利用WIEN2K软件包[33，34]计算电子结构和光学性质，WIEN2K采用全势线性缀加平面波(FPLAPW)法. 电子的交换关联能也采用PBE形式的GGA处理. 在完整的布里渊区内，采用了1000个k点. 设置扩展平面截断能为7.0，自洽能量收敛小于10-5Ry/f.u..

为了准确地描述电子间的库伦关联作用，计算中采用“旋转不变”法(rotationally invariant way )进行“ + U ”计算[35]. 这里我们利用基于局域自旋密度近似加U(LSDA+U)的线性响应方法[36]计算Ag和Fe的U值，得到Ag的U值在2 ～ 3 eV之间，Fe的U值在5 ～ 6 eV之间，这一U值范围与相关研究中所使用的经验值是一致的[37 - 39]. 在计算得到的U值范围内，我们使用了多组U值对材料性质进行测试，测试结果表明，不同U值对材料的带隙大小、光谱峰值大小和峰值位置有些许影响，但对体系的物理性质所展现出的规律性是没有影响的. 因此，我们选取UAg= 2 eV，UFe= 6 eV的计算结果进行讨论.

3 结果与讨论

3.1 晶体结构

根据实验报道[27，28]，Cs2AgFeCl6晶体为立方Fm-3m(No. 225)结构，基于此，我们对Cs2AgFeX6(X = Cl，Br，I)进行了结构优化. Cs2AgFeX6的晶体结构如图1所示. 通过计算晶体不同体积下的总能(图2)，得到的结构参数如表1所示. 可以看出，X位按Cl、Br、I的顺序，相应的晶格常数和键长依次增大，这与Cl-1、Br-1、I-1的半径逐渐增大是相吻合的. 表1中还提供了以往文献中报道的关于Cs2AgFeCl6晶格常数的实验数据，通过对比可以发现，优化的Cs2AgFeCl6的晶格常数(10.441 Å)略大于立方晶格的实验数据(10.202 Å)，这是由于GGA方法本身会高估晶格常数导致.

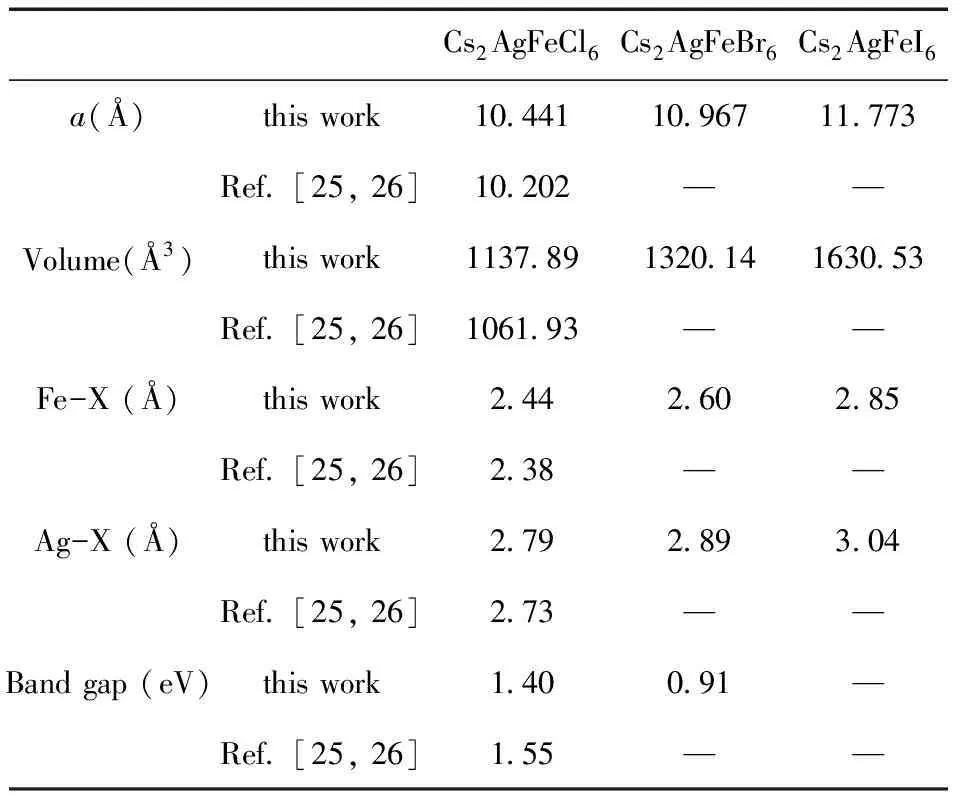
表1 Cs2AgFeX6(X = Cl，Br，I)的晶格常数、键长和带隙宽度

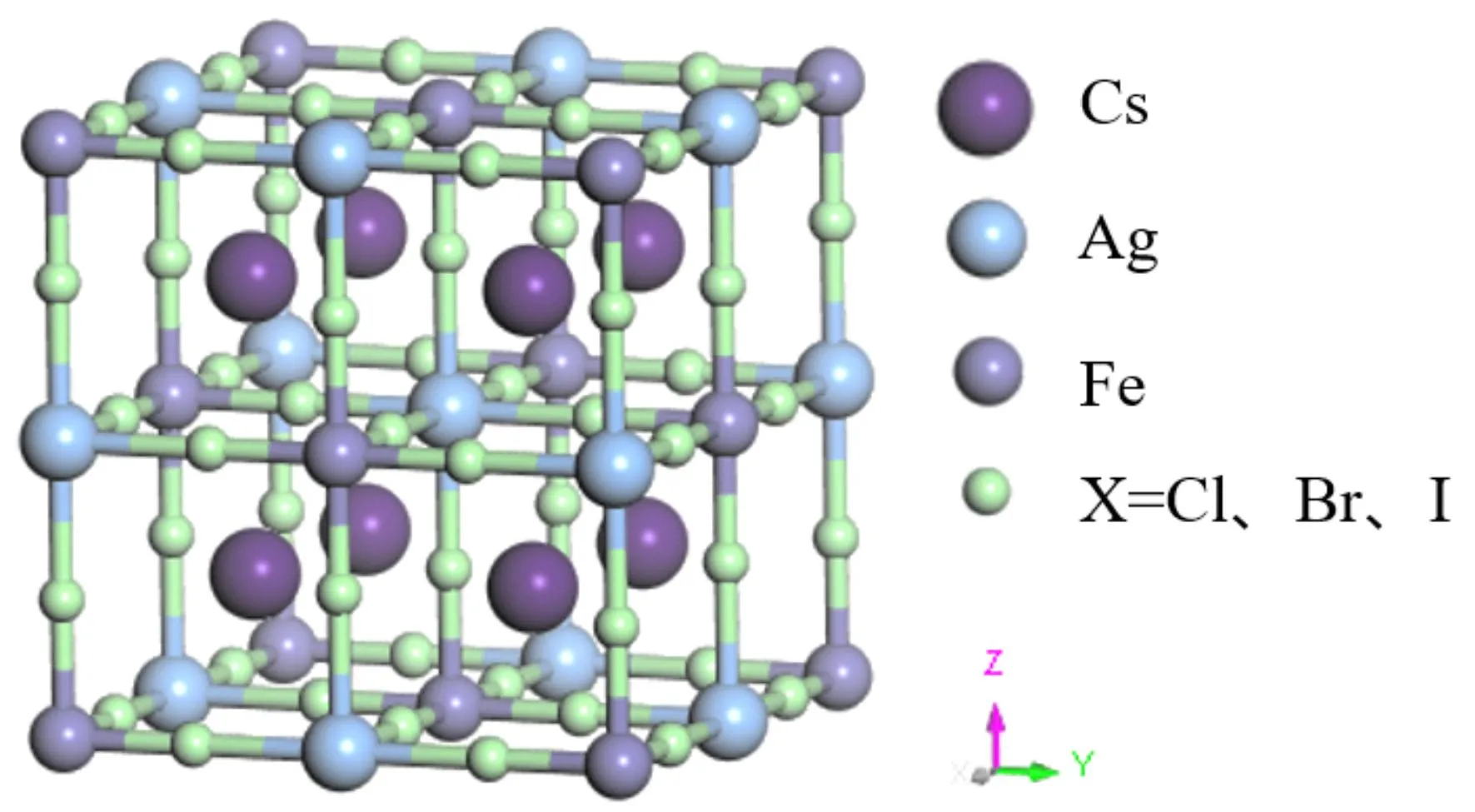
图1 Cs2AgFeX6 (X=Cl，Br，I)的立方晶体结构. 这里紫色/蓝色/灰色和绿色球代表Cs，Ag，Fe，X原子.Fig. 1 Cubic crystal structures of the Cs2AgFeX6 (X = Cl，Br，I). The purple，blue，gray and green spheres represent the Cs，Ag，Fe and X ions，respectively.

3.2 磁基态

我们设计了两种磁构型：铁磁和反铁磁，来研究Cs2AgFeX6(X = Cl，Br，I)的磁基态. 结果表明，三种材料的反铁磁态的系统能量均比铁磁态低. 因此，Cs2AgFeX6(X = Cl，Br，I)的磁基态均为反铁磁态，即Fe离子自旋反平行交错有序排列.

3.3 化学键

为了解释Cs2AgFeX6(X = Cl，Br，I)的成键特性和原子间电荷转移，我们计算了体系的电荷密度. 由于三种材料显示出的成键特性相同，所以我们以Cs2AgFeCl6为例进行讨论. 计算的Cs2AgFeX6在(100)和(110)晶面的电荷密度如图3所示[40]. 由(100)晶面的电荷密度可以看出，由于Fe和Cl、Ag和Cl之间存在杂化，即电荷共享，表明Fe - Cl键和Ag - Cl键为共价键. 同样，对于X = Br，I，Fe - X键和Ag - X键为共价键.

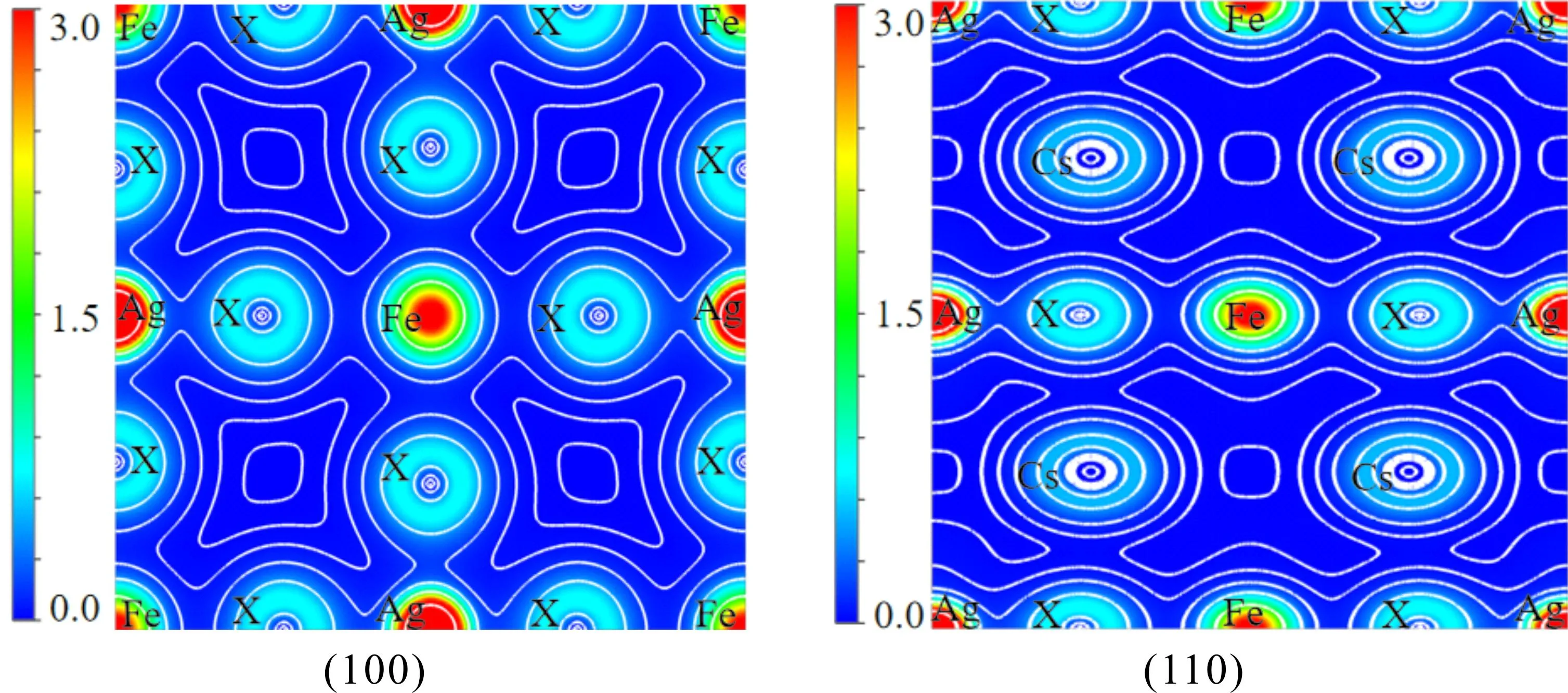
图3 Cs2AgFeX6(X=Cl，Br，I)在(100)和(110)晶面的电荷密度Fig. 3 Charge density maps of Cs2AgFeX6 (X = Cl，Br，I)in the (100)and (110)planes

图4中还绘制了Cs2AgFeCl6在(100)晶面的差分电子电荷密度. 从图中可以看出，Fe与X间的电荷密度按Cl、Br、I依次减小，这说明共价键Fe-X的强度是依次减弱的，则原子对价电子的束缚能力也是依次减弱的.

图4 Cs2AgFeX6(X = Cl，Br，I)在(100)晶面的差分电荷密度Fig. 4 Differential charge densities of Cs2AgFeX6 (X = Cl，Br，I)in the (100)plane

3.4 电子结构

图5给出了计算的Cs2AgFeX6(X = Cl，Br，I)的总态密度和分轨道态密度图. 可以看到，在费米能级附近，占据态主要包括Ag离子的4d轨道和X离子的p轨道，未占据态主要是Fe离子的3d轨道，而Cs离子的态密度在费米能级附近没有贡献，其主要分布在6 eV以下. 另外，X位元素按照Cl、Br、I的顺序，未占据的Fe的3d轨道越来越靠近费米能级，并最终穿过费米能级，使Cs2AgFeI6成为金属.

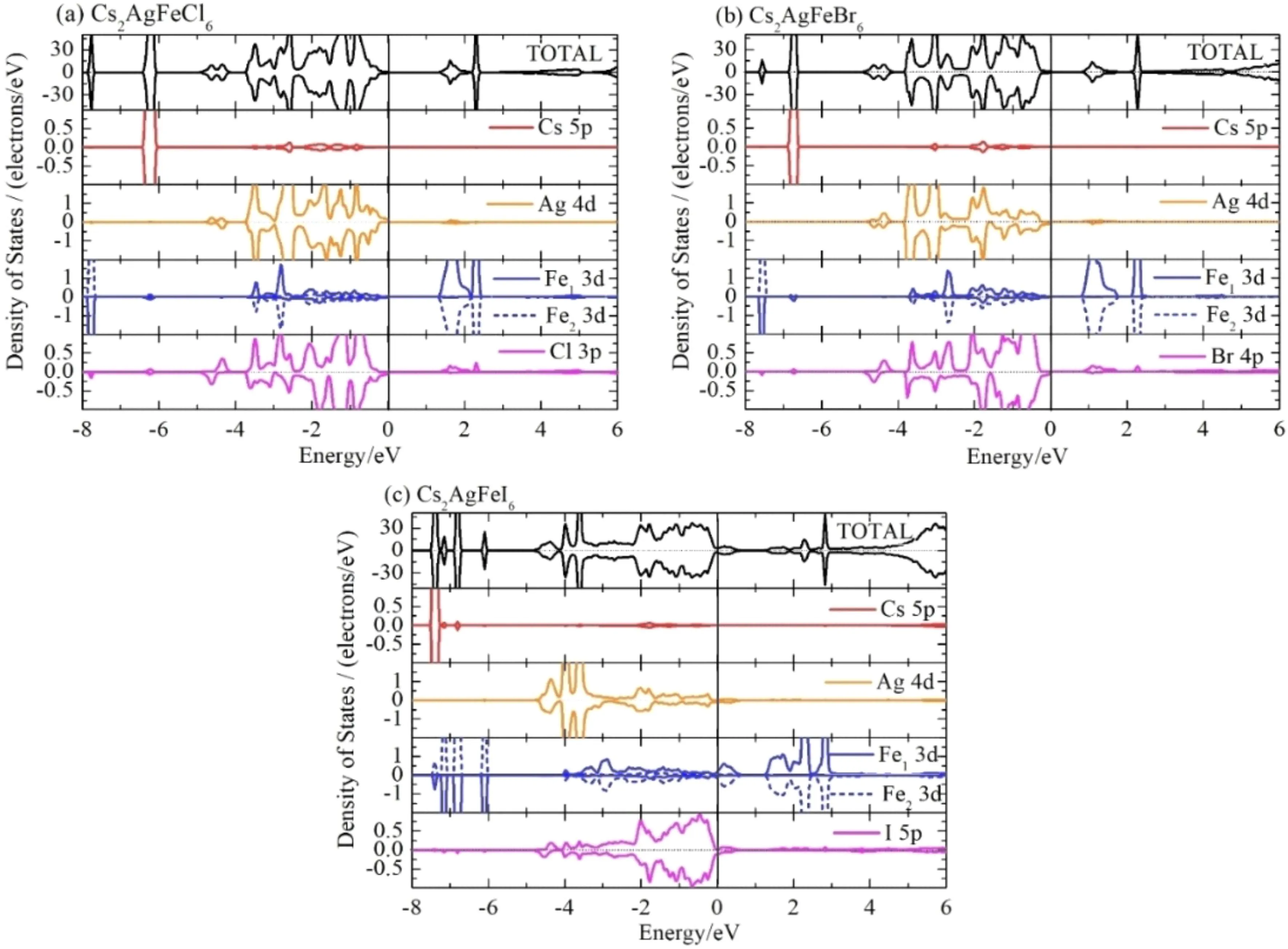
图5 Cs2AgFeX6(X = Cl，Br，I)的总态密度和分轨道态密度图. Fe1和Fe2分别代表晶胞中自旋反平行排列的两个Fe离子Fig. 5 Total and partial densities of states of Cs2AgFeX6 (X = Cl，Br，I). Here Fe1和Fe2 represent the two antiparallel - spin Fe ions in a cell，respectively

我们还计算了Cs2AgFeX6的能带结构，如图6所示. Cs2AgFeCl6带隙宽度为1.40 eV，与实验报道的1.55 eV[27，28]比较接近，Cs2AgFeBr6的带隙宽度为0.91 eV，二者的价带顶部和导带底部出现在同一个Γ高对称点上，均为直接带隙半导体. 与之相比Cs2AgFeI6在高对称点Γ处越过费米能级，呈现金属特性.

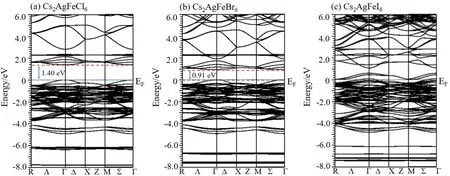
图6 Cs2AgFeX6(X = Cl，Br，I)的能带结构Fig. 6 Energy band structures of Cs2AgFeX6 (X = Cl，Br，I)

根据三种材料的电子结构，从Cs2AgFeCl6到Cs2AgFeI6，带隙逐渐减小最后变为金属，这说明电子从已占据的X离子的p轨道(上价带)到未占据的Fe离子的3d轨道(下导带)间的跃迁将会越来越容易. 另一方面，根据之前电荷密度的计算结果，共价键Fe-X的强度由Cl到I依次减弱的，这也说明了原子对价电子的束缚能力是逐渐减弱的，电子更容易发生跃迁. 因此，以上两方面的计算得到的结论是一致的.

3.5 光学性质

3.5.1复介电函数

介电函数是描述材料宏观光学性质的重要参数. 复介电函数ε(ω)由实部ε1(ω)和虚部ε2(ω)组成[41]：

ε(ω)=ε1(ω)+iε2(ω)

(1)

电子吸收光子能量进而产生带间跃迁的过程实质上是电子在电磁场的作用下从位于低能区的占据轨道跃迁到高能区的未占据轨道的过程. 介电函数虚部ε2(ω)的数值取决于电子的带间跃迁[41]：

(2)

ε1(ω)可以根据Kramer - Kronig关系由ε2(ω)得出[41]：

(3)

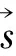
根据晶体结构对称性，由于Cs2AgFeX6(X = Cl，Br，I)属于高度对称的立方晶系，在光学性质上呈现各向同性[43，44]，主介电系数εxx(ω)=εyy(ω)=εzz(ω)，所以本文只针对材料xx方向的光学性质进行分析. 图7给出了Cs2AgFeX6(X = Cl，Br，I)沿xx方向介电函数的ε1(ω)与ε2(ω)随入射光子能量的变化关系.

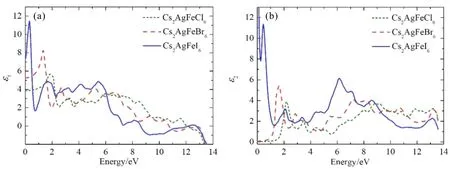
图7 Cs2AgFeX6(X = Cl，Br，I)介电函数的实部和虚部Fig. 7 The real and imaginary parts of the dielectric functions of Cs2AgFeX6 (X = Cl，Br，I )

介电函数的实部表征表示电介质在电场作用下的极化强度，即束缚电荷的能力，数值越大，束缚电荷能力越强，电荷就越不容易极化. 如图7(a)所示，Cs2AgFeX6(X = Cl，Br，I)在零频情况的值，即静态介电常数ε1(0)，分别为3.86、5.27和7.36.

由公式(2)可知，复介电函数的虚部ε2(ω)能够反映电子在能带间的跃迁过程，即能反映材料对光的吸收情况. Cs2AgFeX6(X = Cl，Br，I)的ε2(ω)光谱如图7(b)所示，整体来看，按Cl、Br、I的顺序，光谱是红移的，这与电子结构中带隙宽度的逐渐减小是相对应的. Cs2AgFeCl6的ε2(ω)的阈值能约为1.5 eV，Cs2AgFeBr6的相应阈值能约为0.8 eV，这与前面给出的二者的带隙值是相吻合的. 另外，金属Cs2AgFeI6的ε2(ω)曲线在小于1 eV的低能区具有很高的幅值，这是由于电子在能带内跃迁引起的. 每种材料的ε2(ω)曲线都可以分为两部分，低于4 eV光子能量范围内的介电特征峰主要来自于占据的Ag的4d带和X的p带到未占据的Fe 3d带之间的电子跃迁，而能量超过6 eV的介电峰则主要来源于占据的Cs的3p轨道和Fe的3d轨道到已占据的Fe 3d导带之间的电子跃迁过程.

3.5.2吸收系数

材料的吸收系数α可由以下关系来描述[45]：

(4)

式中：c为光速；n为折射率，由介电函数给出[45]：

(5)

计算得到的Cs2AgFeX6(X = Cl，Br，I)的折射率如图8所示. 可以看出，Cs2AgFeX6在零频率n(0)处的折射率随着X位从Cl到I的改变而增加.

图9中给出Cs2AgFeX6(X = Cl，Br，I)的吸收系数随光子能量的变化曲线. 由图可以看出，在0 ～ 14 eV的能量范围内，三条曲线整体呈现上升趋势. Cs2AgFeCl6和Cs2AgFeBr6的吸收阈值分别约为 1.5 eV和1.0 eV，而Cs2AgFeI6的吸收阈值接近0 eV，这与它们的介电函数虚部ε2(ω)的阈值和带隙宽度都是吻合的.

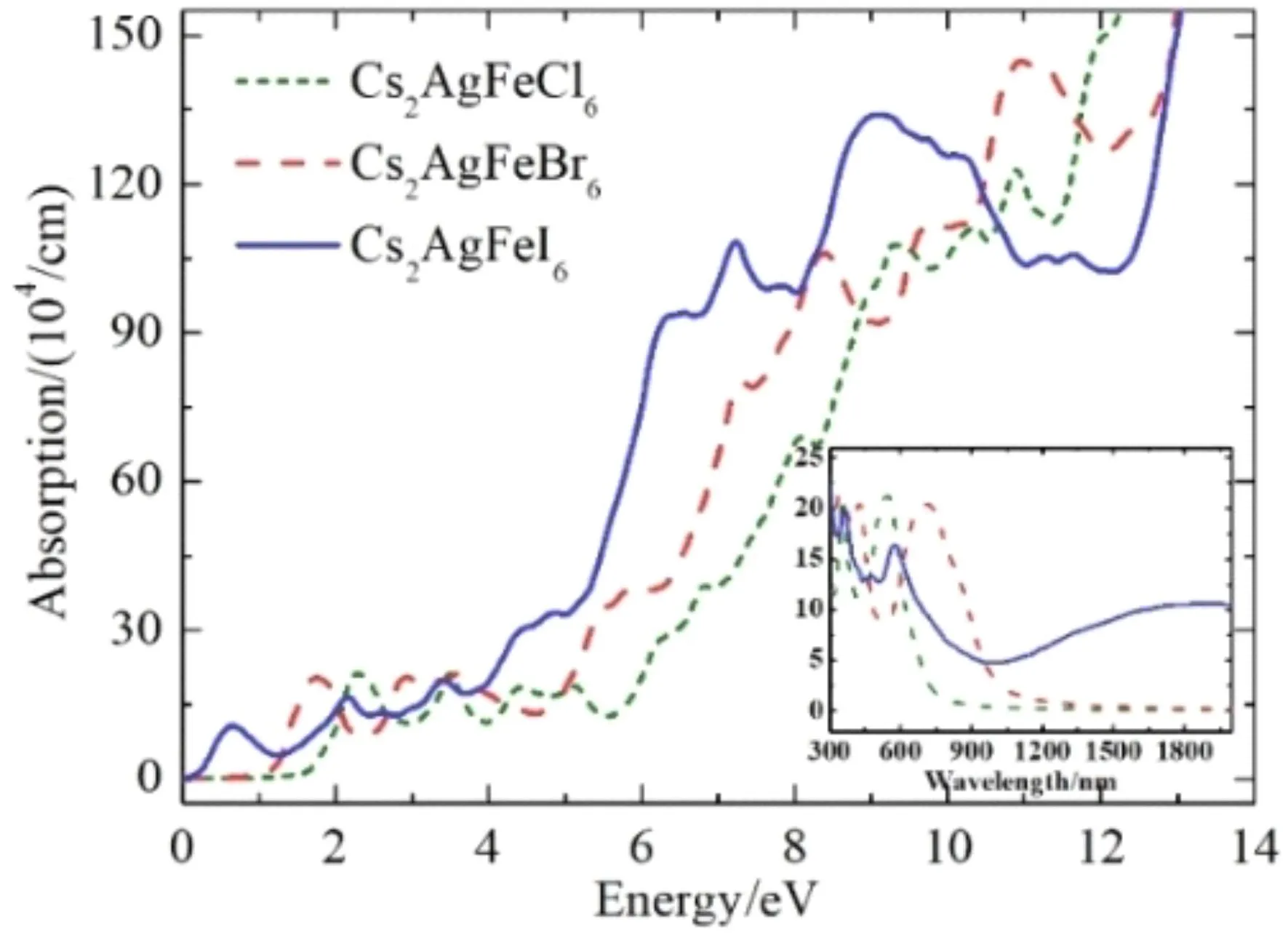
图9 Cs2AgFeX6(X = Cl，Br，I)的吸收系数Fig. 9 Absorption coefficients of Cs2AgFeX6 (X = Cl，Br，I)

为了能清楚看到Cs2AgFeX6(X = Cl，Br，I)对可见及红外波段的吸收情况，图9插图给出了吸收系数随波长的响应曲线，可以看到三种材料在可见光波段都有明显的光吸收. Cs2AgFeCl6的吸收带边在800 nm左右，这与实验报道的结果[27，28]符合得很好，吸收峰位于354 nm和534 nm处，其吸收系数的峰值分别为21.24×104cm-1和21.28×104cm-1. Cs2AgFeBr6的吸收光谱较Cs2AgFeCl6明显红移，有两个吸收峰，其一在423 nm处，峰值吸收系数为20.54×104cm-1，另一个宽吸收峰红移至712 nm，吸收系数的峰值为20.50×104cm-1. Cs2AgFeI6的吸收峰位于573 nm处，吸收系数的峰值为16.43×104cm-1，而且它在1200 nm后的红外波段仍然有一极宽的吸收峰，吸收系数可以达到10×104cm-1.

3.5.3反射率

反射率R可由如下关系得到[45]：

(6)

式中：n为折射率，由公式(5)给出；κ(ω)为消光系数[45]，即：

(7)

计算得到的Cs2AgFeX6(X = Cl，Br，I)的反射率随光子能量的变化曲线如图10所示.

图10 Cs2AgFeX6(X=Cl，Br，I)的反射率Fig. 10 Reflectivities of the Cs2AgFeX6 (X=Cl，Br，I)

由图可知，在可见光区域对应的1.6 eV ～ 3.2 eV能量范围内，Cs2AgFeCl6的反射率在8.36 % ～ 20.49 %之间；Cs2AgFeBr6的反射率在9.03 % ～ 25.09 %之间；Cs2AgFeI6的反射率在13.01 % ～ 18.20 %之间. 通常认为反射率大于25 %，材料具有金属光泽. 因此，Cs2AgFeX6(X = Cl，Br，I)无金属光泽，反射损耗较小.

4 结 论

本文采用第一性原理对双钙钛矿卤化物Cs2AgFeX6(X = Cl，Br，I)的电子结构和光学性质进行了计算. 按Cl、Br、I的顺序X位离子半径逐渐增大，导致晶体的晶格常数和键长依次增大. 根据电荷密度的计算结果，Fe - X键和Ag - X键为共价键，且由Cl到I，共价键Fe - X的强度是依次减弱的. Cs2AgFeCl6和Cs2AgFeBr6是禁带宽度分别为1.40 eV和0.91 eV的直接带隙半导体，Cs2AgFeI6为金属. 三种材料禁带宽度的大小说明电子从占据态到非占据态的跃迁需要的阈值光子能量从Cl到I逐渐减小. 通过对介电函数进行分析，可见光波段的介电特征峰主要来自于Ag、Fe间的d-d的跃迁和X、Fe间的的p - d跃迁过程. Cs2AgFeX6(X = Cl，Br，I)在可见至红外光波段均有明显的光吸收：Cs2AgFeCl6的吸收带边在800 nm左右，与文献报道的实验结果一致，在534 nm处的吸收系数达到21.28×104cm-1；Cs2AgFeBr6的吸收光谱较Cs2AgFeCl6明显红移，在712 nm处的吸收系数为20.54×104cm-1；Cs2AgFeI6在1200 nm后的红外波段有一极宽的吸收峰，吸收系数可以达到10×104cm-1. 三种材料在可见光波段的反射率小于25 %，反射损耗较小.