食品包装热成型机电动八杆开合模机构的运动及受力分析

谢志刚 陈小芹 许智扬

(1. 汕头职业技术学院,广东 汕头 515078;2. 广东依明机械科技有限公司,广东 潮州 521000)

食品包装热成型机(简称热成形机)是将塑料片材经加热、合模夹紧密封、正负压成型、冷却定型和开模取件等一系列连续动作,加工成杯、碟和盘等开口空心状制品的塑料加工机械。其制品质量和成型效率不仅与高精度模具有关,还与辅助模具成型、冷却及脱模等工序的开合模机构性能有关。开合模机构作为热成型机的核心部件,既要保持一定的锁模力,又需满足成型所需要的停歇时间,并在既定工艺时间内完成开模及合模动作[1],因而必须针对不同的制品及其生产工艺参数而定制设计,且相关杆件设计及其分析已成为业内工程技术人员普遍面临的技术难题。

陆鹏飞等[2-4]使用ADAMS软件分别对挤压成形六杆机构、执行机构末端夹爪和理盖机等进行了运动和动力分析,以期提高机构运动平稳性,从而提高加工精度。郭永增[5]提出了采用多软件协同开展电动合模机构的优化设计,涉及软件包括ADAMS、MATLAB和ANSYS等。何添成等[6-7]基于遗传算法分别进行了肘杆机构和回转复合压曲机的优化设计。王晨光等[8]对制杯机五孔斜排双曲肘合模机构进行了稳健设计研究。这些方法需要扎实的理论基础和娴熟的软件使用经验,尤其在不具备专业软件的条件下,其工程实际应用性受到一定限制。

在广东某食品包装机械厂生产实践基础上,研究拟采用解析法对塑料热成形机的八杆开合模机构进行运动和力学分析,以期缩短设计和试制周期,适应现代化生产对专机的供给需求,从而提高市场竞争力。

1 热成型机八杆开合模机构设计

热成型机的开合模机构在辅助完成合模、成型、冷却和开模等动作时,要求工作过程无冲击,开模合模迅速、成型稳定,并能够实现停留保证一定的冷却时间。目前的开合模机构多为六杆曲肘式,以液压或电机为原动件,也有设计成凸轮曲柄连杆式,凸轮虽然可以通过轮廓曲线的设计实现对工作行程、停留时间等技术要求,但由于引入高副,传力性能往往不足,并降低了设备寿命。研究在液压六杆曲肘式开模机构的基础上,将液压缸换成电动曲柄滑块,进而设计更加精准、快捷的八杆开合模机构(见图1)。

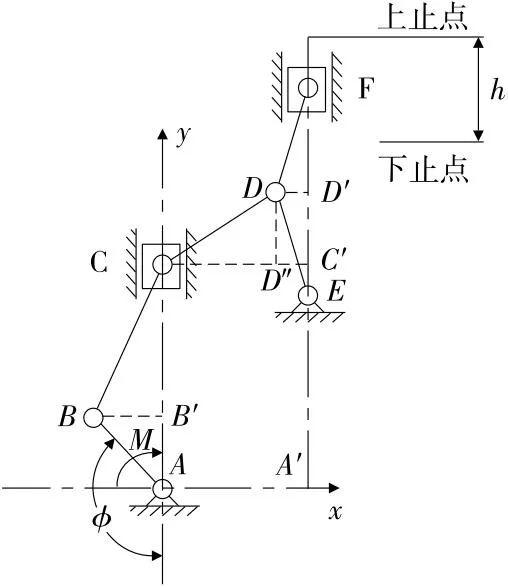
图1 开合模机构运动简图

1.1 机构运动简图

图1的开合模机构运动简图采用双滑块八杆机构,自由度为f=3n-2PL-PH=3×7-2×10-0=1,原动件为曲柄AB,以匀角速度ω转动,通过滑块C及各杆件进行运动和动力的传递,并实现机械增益,最终传递给起执行作用的滑块F,滑块F为热成型机的下模板,在连杆推动下其与上模板合模,完成制件成型动作。

1.2 运动分析

双滑块机构设计的关键条件必须满足lAA′=lCD,此条件下,滑块F位移s与7个参数相关,即

s=s(lAB,lBC,lCD,lDE,lDF,lA′E,Φ)。

(1)

绘制图1所示曲柄AB某转角时各构件位置关系,其难点在于如何确定D点:先确定C点位置,以C点为圆心,以lCD为半径画圆弧,同时,以固定铰支点E为圆心,以lDE为半径画圆弧,两个圆弧的交点即为D点。将图1中的下止点位置定义为位移0点,此时原动件曲柄AB处于竖直位置,定义其初始转角Φ为0°,经几何解析法分析及计算,得到滑块F位移与曲柄AB转角的关系,其计算过程详见表1。

为便于计算,令

(2)

其中,a=4lCD2+4W2,b=4W(lDE-W)2-8lCD2lDE,c=(lDE-W)2。

当Φ=180°时,DF杆y轴投影缩减量

(3)

当转角Φ=180°下模板行程

h=[Δ(0)+Δ′(0)]-[Δ(180)+Δ′(180)]。

(4)

当转角Φ为任意角度时,最终求得下模板距离下止点的位移

s=s(lAB,lBC,lCD,lDE,lDF,lA′E,Φ)=Δ(0)+Δ′(0)-[Δ(Φ)+Δ′(Φ)]。

(5)

1.3 算例分析

根据热成形机的规格尺寸并结合类比法确定各杆件长度:LAB=180 mm,LBC=260 mm,LCD=180 mm,LDE=180 mm,LDF=240 mm。

利用上述公式在Excel电子表格中计算曲柄AB不同的转角Φ所对应的滑块F的位移数据,计算结果与工程实际测量数据完全一致,其中Φ=180°时,最大行程为h=280 mm,整理转角Φ与位移s数据,得到如图2所示曲线。

图2 开合模机构滑块F位移与曲柄转角曲线

由图2可知,开合模机构具有“快—慢—快”的运动特征,由下止点向上止点方向的合模动作先快后慢,由上止点向下止点的开模动作先慢后快,且在上止点合模极限位置作短暂停留,减少了动模板与静模板之间的冲击,并使夹紧密封时间延长,有利于正负压的成型。该曲线近似正弦曲线,通过数据拟合得到位移s与转角Φ的关系:

(6)

式中:

s0、q、ΦC——与杆长条件相关的材料常数。

令k为整数,当kπ≤Φ≤(k+1/3)π时,s0=94.178,q=-93.987,Φc=278.049;当(k+1/3)π≤Φ≤(k+2/3)π时,s0=263.631,q=-262.565,Φc=301.059;当(k+2/3)π≤Φ≤(k+1)π时,s0=180.415,q=-101.897,Φc=251.506。

对式(6)进一步求导,得到滑块速度v、加速度a与曲柄转角Φ的关系:

(7)

(8)

2 机构力学分析

根据构件运动状态及其刚性程度,相应的动力学分析可以分为静力分析、动态静力分析、动力分析及弹性动力分析。对于运动速度较低且惯性力可忽略的机构,其驱动力和约束反力的求解通过静力分析展开;以较快均匀速度运动的重型杆件,由于惯性力太大,可进行动态静力分析(即考虑惯性力和惯性力矩的静力学分析);而采用非匀速转动原动件的机构,则需进行动力学分析;对于大柔性的弹杆件则进行弹性动力学分析[9]。研究的八杆开合模机构,在匀速转动电机的驱动下,工作速度平稳,尤其是片材挤压阶段速度较低,其惯性力可忽略,因此采用静力分析杆件在片材挤压阶段的受力并求解约束反力。

2.1 静力分析

由于不考虑惯性力的影响,假设自重和摩擦力忽略不计,并假定下模板始终处于片材挤压阶段(低速且载荷平衡状态),且原动件保持恒定输出力矩运行。各构件静力平衡的特点为:杆件BC、CD、DF和DE均为二力杠,即杆件两端所受的两个力等值、共线、方向相反;杆件AB为原动件,受到电机驱动力矩M和FBC作用,所受力矩平衡;铰接点D、滑块C和滑块F均处于三力交汇状态且平衡。因此,各构件受力情况如图3所示。

图3 机构受力分析图

(1) 分析AB杆:其受力如图3(a)所示。

由∑MA=0,得FBCLBA′-M=0,其中,LBA′=LABcosa,则

(9)

(2) 分析滑块C:其受力如图3(b)所示。

由∑Fy=0,得FBCsinβ-FCDsinγ=0,因此

(10)

(3) 分析铰接点D:其受力如图3(c)所示。

由∑Fx=0,得FCDcosγ-FDEsinθ-FDFsinφ=0;

由∑Fy=0,得FCEsinγ-FDEcosθ-FDFcosφ=0,因此

(11)

(12)

(4) 分析滑块F:设F模为理论合模力,其受力如图3(d)所示。

由∑Fy=0,得FDEcosδ-F模=0,因此

F模=FDFcosδ=FDFcosφ。

(13)

只有进入片材挤压阶段后,实际合模力才可按式(9)～式(13)的顺序计算,并同时进行其余各杆件受力分析;而空载阶段的实际合模力远小于理论合模力,主要取决于工作台和模具的重量[10-11],各杆件受力分析次序刚好相反。最终分析获得的杆件受力数据可作为杆件、销轴设计以及轴承选型的参考依据。此外,分析式(9)～ 式(13)可知,增大曲柄AB长度,各杆件受力下降,应根据开合模工艺要求及设备规格合理确定曲柄长度以获得较大机械增益。

2.2 不同行程时各杆件的受力情况

针对1.3的算例,选用厚度为0.5～3.0 mm的系列塑料片材,该类片材经热压后剩余厚度为原始厚度的60%～80%,假定电动机恒定输出力矩为M=2 362.67 N·m,此条件下计算合模挤压过程中的二力杆BC、CD、DF受力情况以及滑块F的理论合模力F模,并绘制各杆件受力随合模间隙变化的关系曲线,如图4所示。

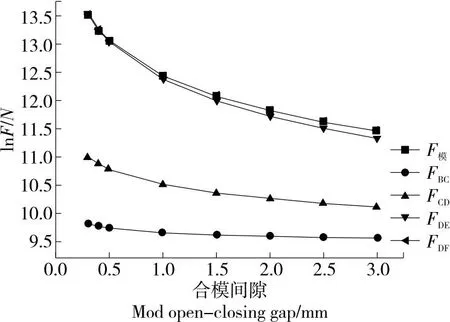
图4 开合模间隙与各杆件受力曲线

由图4可知,随着合模间隙(片材厚度)逐渐变小,开合模机构进入片材热挤压过程中,各杆件受力逐步增大,且FDF>F模>FDE>FCD>FBC,其中,FDF、F模和FDE的增大趋势较为明显,且数值也远大于FCD和FBC。当合模间隙为2 mm时,FDF=136.66 kN、F模=136.17 kN、FDE=123.75 kN、FCD= 28.66 kN、FBC=14.62 kN;当合模间隙为0.5 mm时,部分件受力出现急剧升高,此时FDF=474.49 kN、F模=474.06 kN、FDE=458.72 kN、FCD=48.59 kN,FBC=17.12 kN;当合模间隙达到0.3 mm时,相当于0.5 mm厚度的片材压缩至极限位置,此时FDE=760.94 kN、F模=760.53 kN、FDE=743.72 kN、FCD=59.99 kN、FBC=18.46 kN。

由计算结果可知,若假定上模板静止不动,开合模机构能提供足够大的理论合模力,由于裁切力根据片材实际裁切厚度和展开长度计算,并据此调整不同片材所对应的上模板位置,从而获得合理的合模力,其数值远小于理论合模力。当合模间隙趋近片材挤压厚度极限时,尤其是厚度较大的片材,此时杆DE和杆DF承受载荷较大,杆件受压后的弹性变形量将直接影响合模质量,因而在其结构设计时应给予足够的重视。

3 结束语

食品包装制品模具及其生产工艺参数的差异化,衍生出型式各异的热成形机及其开合模机构,而开合模机构的运动和受力分析又与其具体结构尺寸密切相关,相关分析给工程技术人员带来一定难度。研究解决了在不具备专业软件的条件下,运用解析法对电动八杆开合模机构进行运动和受力分析,推导出滑块位移与曲柄转角的关系,并通过实例计算数据获得拟合曲线,在给定角速度的基础上,进一步分析了获取滑块速度和加速度的变化规律。同时,基于静力学分析了合模挤压阶段理论合模力和各杆件的受力,揭示了各杆件受力变化趋势及特点,对类似新型装备的连杆机构的设计与开发具有一定的指导和借鉴意义。