空间引力波探测系统中超光滑光学元件表面散射特性分析

张耘豪，钟哲强，张 彬

四川大学电子信息学院，四川 成都 610065

1 引言

空间引力波探测通过三星之间激光传输并对其进行干涉测量来探测引力波大小，而激光传输涉及星载望远镜的发射和接收[1-3]。在此过程中，视场内杂散光主要来源于引力波探测系统中超光滑光学元件(表面粗糙度小于1 nm[4])表面的粗糙度、表面疵病、表面污染等带来的残余反射、散射和衍射，以及结构件的表面散射。杂散光在引力波探测系统内部以非正常路径传输形成光噪声[5-8]，可以通过降低反射镜粗糙度来降低表面散射率，进而减弱后向散射杂光对引力波探测性能造成影响。模拟分析表明要满足设计要求，望远镜后向散射需达到10-10以下[2]。因此，对引力波探测系统中超光滑光学元件表面散射特性进行准确、快速分析和预测，可为空间引力波探测系统杂散光分析及抑制，进而为星载望远镜的优化提供参考。

经典Rayleigh-Rice (RR)表面散射理论为超光滑光学元件的散射特性分析提供了严格的矢量模型，适用于大入射角和散射角，已广泛用于清洁、光滑和超光滑表面[9-12]。然而，该理论涉及复杂的矢量计算，不利于超光滑光学元件散射特性的准确、快速分析和预测。1963 年，Beckmann 等人发展了经典Beckmann-Kirchhoff (BK)表面标量散射理论，可避免复杂的矢量模型计算问题，但仅适用于较粗糙的光学元件，且采用了近轴或小角度近似[13]。Harvey 在BK表面标量散射理论基础上，发展并提出了Modified Beckmann-Kirchhoff (MBK)标量散射理论，但MBK理论仅适用于高斯统计分布的表面散射[14-15]。1976 年，Harvey 和Shack 提出了Harvey-Shack (HS)标量散射理论，即描述表面散射特性的线性系统公式，但同样仅对近轴或小角度近似成立[16-17]。1999 年，Krywonos和Harvey 进一步将衍射辐射描述为定向余弦空间中具有平移不变特性的基本量，进而基于非傍轴标量衍射理论的线性系统公式，发展了一套既适用于光滑表面又适用于粗糙表面的非傍轴标量散射理论[18-19]。然而，在利用该理论进行数值计算时，针对每个散射角都需要运用不同的傅里叶变换，不可避免地会花费大量的计算时间，也不利于空间引力波探测系统中超光滑光学元件散射特性的准确、快速分析。

为实现对超光滑光学元件表面散射特性的快速、准确分析与预测，本文发展了一种非傍轴标量散射模型Generalized Beckmann-Kirchhoff (GBK)。通过将MBK 模型与HS 模型进行比较，发现MBK 模型在表面光滑条件下的封闭解中隐含着表面统计参量表面功率谱密度(PSD)函数，进而从MBK 模型中提取出相应的PSD 函数，并以RR 矢量散射模型的数值计算结果为参考，通过数值拟合给出了适用于超光滑表面的GBK 非傍轴标量散射公式。在此基础上，计算分析了P 偏振光和S 偏振光入射条件下，角分辨散射(ARS)分布随入射角度、散射角度及散射方位角的变化规律，并针对常见加工工艺导致的不同表面统计分布情况，讨论了不同入射角度、散射方位角、自相关长度、斜率、截止频率和表面粗糙度等因素对ARS分布的影响。

在空间引力波探测的星载望远镜系统中，科学视场分“面内”和“面外”科学视场。“面内”是指平行于卫星组成的三角形的平面，相对于黄道平面倾斜60°；“面外”指垂直于三角形的平面。为了能够适应正常科学操作中可能遇到的角度的变化范围，引力波望远镜在科学模式下“面内”的视场角为±4.2 μrad，“面外”的视场角为±7 μrad。该视场角的大小近乎0°视场角，GBK 散射模型必然是适用的。

2 GBK 表面散射模型

Beckmann 以Helmholtz-Kirchhoff 衍射积分为基础，发展了Beckmann-Kirchhoff 标量散射理论[13]。它所含的假设有：1)表面粗糙度均方根偏差σs远小于入射光波长λ；2)表面粗糙度的斜率远小于1，自相关长度远大于入射波长。

图1 描述了Nicodemus 将BRDF 定义为被入射辐照度归一化的散射辐射时所涉及的散射几何关系[20]。假定表面S的轮廓由随机函数h(x,y)描述，其均值为0，dPi为入射光，dPs为出射光，θi为入射角，θs为散射角，φi为入射方位角，φs为散射方位角。

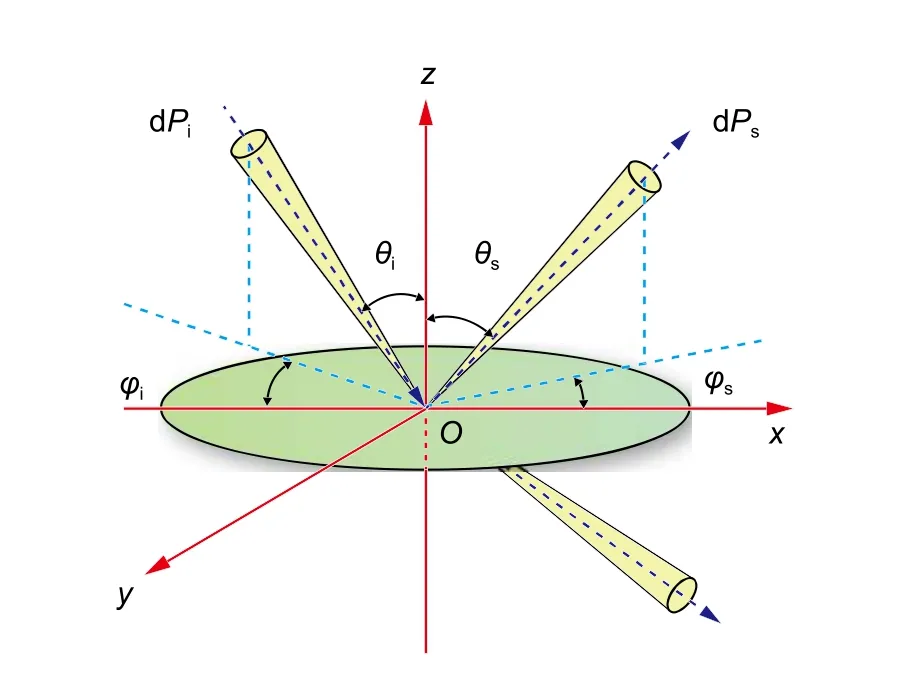
图1 随机超光滑表面散射示意图Fig.1 Scattering diagram of the random ultra-smooth surface

假设表面微观形貌统计符合高斯分布，Beckmann 给出了散射光强分布表达式[21]：

式中：lc定义为自相关函数(ACV)在1/e 高度处的半宽度，即表面自相关长度；Ai为散射表面的照射面积；F是几何因子，定义为入射角和散射角的函数[22]；ρ为贝克曼定义的一个无因次量，称之为散射系数；函数g是表面粗糙度引入的相位变化的度量，表达式如下：

若g＜＜ 1，则该表面表示为光滑表面，仅需使用式(1)中级数的第一项，若粗糙度为1 nm，波长为1064 nm，入射角和散射均为0°，则g为1.395×10-4，此条件代表超光滑表面。如果g＞＞ 1，则该表面表示为非常粗糙表面，式(1)中的级数收敛速度很慢，vxy描述粗糙表面xy平面内的位置向量。

由于BK 模型不适用于大入射角和散射角的表面散射特性分析[21]，Harvey 在BK 模型的基础上发展了MBK 标量散射模型，并提出了以下修正[22]：1)忽略几何因子F2；2)D{ρ}不再表示平均散射能量，而表示衍射辐射亮度L；3)引入归一化因子KMBK，其定义为：

式中：α=sinθscosφs，β=sinθssinφs。

经过繁杂的推导和变换运算，可得到散射面的双向反射分布函数(BRDF)[21]：

式中，λ为光波长；无量纲量Q是与偏振相关的表面反射率。

由于常规加工工艺可能存在多种不同的表面微观形貌统计分布情况，而MBK 标量散射模型仅适用于高斯统计分布，因而需进一步修正MBK 标量散射模型。通过将MBK 模型与HS 模型进行比较，我们发现MBK 模型在光滑表面条件下的封闭解中隐含着表面统计参量PSD 函数(PSD 函数是一个具有综合分析意义的概率统计函数，定义为表面轮廓函数傅里叶变换的平方)，进而从MBK 模型中提取出相应的PSD函数，并将其修正为

式中：PSDm是自相关长度为=lc/m1/2的表面相关函数的傅里叶变换，m为收敛级数，选取与粗糙度的大小有关(随粗糙度的增大，收敛级数的选取越多)。grel可以表示为

式中：n1和n2分别为入射介质和出射介质的折射率；σrel定义为对应的表面粗糙度，取表面相关部分PSD下体积的平方根即可得到其表达式 ：

式中：fc为截止频率，fx和fy分别代表x和y方向的样本空间频率，表示为

由于式(5)中的归一化因子KGBK的表达与计算较为复杂，不利于超光滑光学元件表面散射特性的快速分析，因而以RR 矢量散射模型的数值计算结果为参考(保证准确性)，通过数值拟合的方式对其进行简化(提高计算效率)。经过大量的模拟计算，我们发现在入射角度、自相关长度、表面粗糙度以及入射光波长等众多散射影响因素中，表面粗糙度和入射光波长是影响ARS 分布的主要因素。利用数值拟合方法可将归一化因子KGBK修正为拟合因子，KGBK表示为

进一步将式 (9)代入式(5)，即可得到我们提出的GBK 标量散射模型表达式：

值得指出的是，与MBK 散射模型相比，GBK 散射模型中进一步采用了表面统计参量PSD 函数，不再依赖于特定的表面统计分布函数类型。因此，可运用GBK 散射模型，对具有高斯、分形和柯西-洛伦兹统计分布函数等多种典型表面微观形貌的超光滑光学元件表面散射特性进行定量分析。

在高斯统计分布情况下，分析了GBK 散射模型和RR 散射模型的ARS 分布情况。对于具有高斯统计分布的随机超光滑表面，PSD 函数可以表示为

由式(11)可知，具有高斯分布的超光滑表面可以用表面粗糙度和自相关长度来表征。如果波长λ=1.064 μm 的光以θi的入射角从空气入射到折射率为ns=1.5 的样品表面，散射光分布主要受表面粗糙度σs、自相关长度lc和入射角θi的影响，如图2 所示。

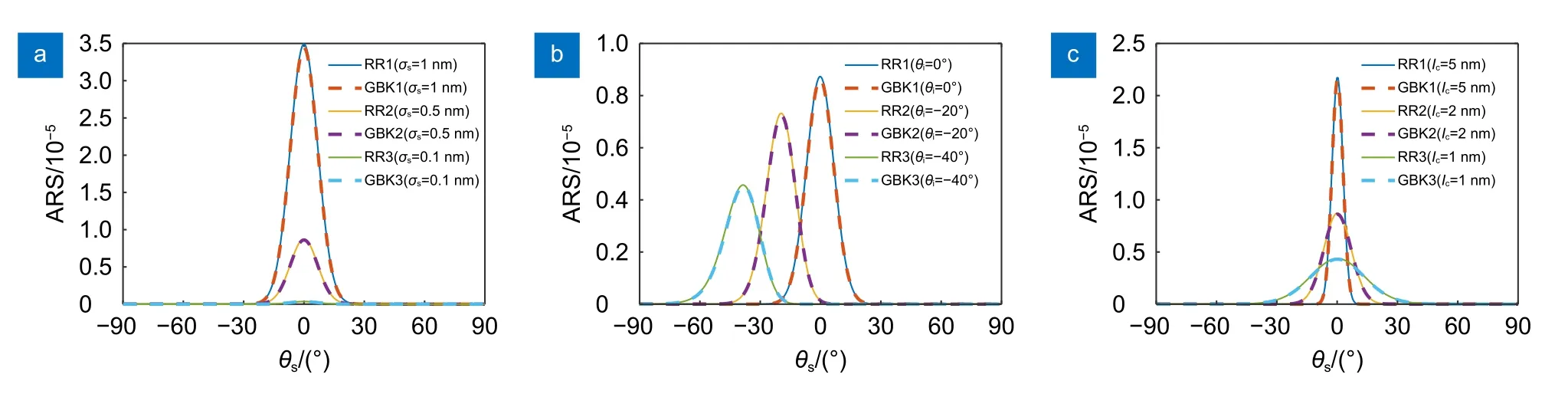
图2 不同条件下角分辨散射分布。(a)不同表面粗糙度；(b)不同入射角度；(c)不同自相关长度Fig.2 Distributions of angle resolved scattering under different conditions.(a) Different surface roughness;(b) Different incidence angles;(c) Different autocorrelation lengths

图2(a)表示不同表面粗糙度下RR 模型和GBK散射模型的ARS 分布对比；图2(b)表示不同入射角度下RR 模型和GBK 散射模型的ARS 分布对比；图2(c)表示不同自相关长度下RR 模型和GBK 散射模型的ARS 分布对比。对比分析可知，GBK 模型和RR 模型的ARS 分布情况高度一致，从而验证了GBK 模型的准确性。

此外，为进一步分析P 偏振光和S 偏振光入射条件下超光滑光学元件的表面散射特性，对于不同偏振光源和接收不同偏振光的传感器，Qss代表S 偏振光与S 偏振传感器条件下的表面反射率，Qsp代表S 偏振光与P 偏振传感器条件下的表面反射率，Qps代表P 偏振光与S 偏振传感器条件下的表面反射率，Qpp代表P 偏振光与P 偏振传感器条件下的表面反射率，分别为[23-24]：

式中，ε=n2/n1是界面的相对介电常数。

对于非偏振入射光，且传感器无偏振判别的情况，Q参数可表示为

3 超光滑光学元件散射特性分析

3.1 偏振特性分析

空间引力波探测系统中的干涉仪常采用平衡的正交四象限检测方案来检测相位信号，在发射光路中，由频率稳定激光器发出的光束通过偏振分束器分成两束，其中一束用作本地参考光束(偏振状态为S 偏振)，另一束形成出射光束(偏振状态为P 偏振)[25]。因此，有必要分析超光滑光学元件表面的偏振散射特性(包含偏振和位相变化等)。采用Stokes[26]参量-Mueller[27]矩阵可将ARS 分布函数推导变换为偏振ARS 分布函数，根据推导的偏振角分辨散射分布函数可以获取不同偏振状态下的散射特性。

3.1.1 各向同性表面偏振散射特性

对于各向同性的光学元件表面，其散射方位角为0°。因此，对于各向同性偏振反射率而言，Qsp和Qps的值为0，即散射分布中不存在交叉偏振光。若入射光为S 偏振光，散射光同样为S 偏振光；若入射光为P 偏振光，散射光同样为P 偏振光。在利用GBK 散射模型进行模拟仿真时，超光滑元件表面初始参数为：入射波长λ=1064 nm，表面统计分布服从高斯分布，折射率n=1.5，表面粗糙度σs=0.1 nm，自相关长度lc=2000 nm。图3 给出了在不同的入射角度下，各向同性超光滑光学元件表面的偏振散射特性。

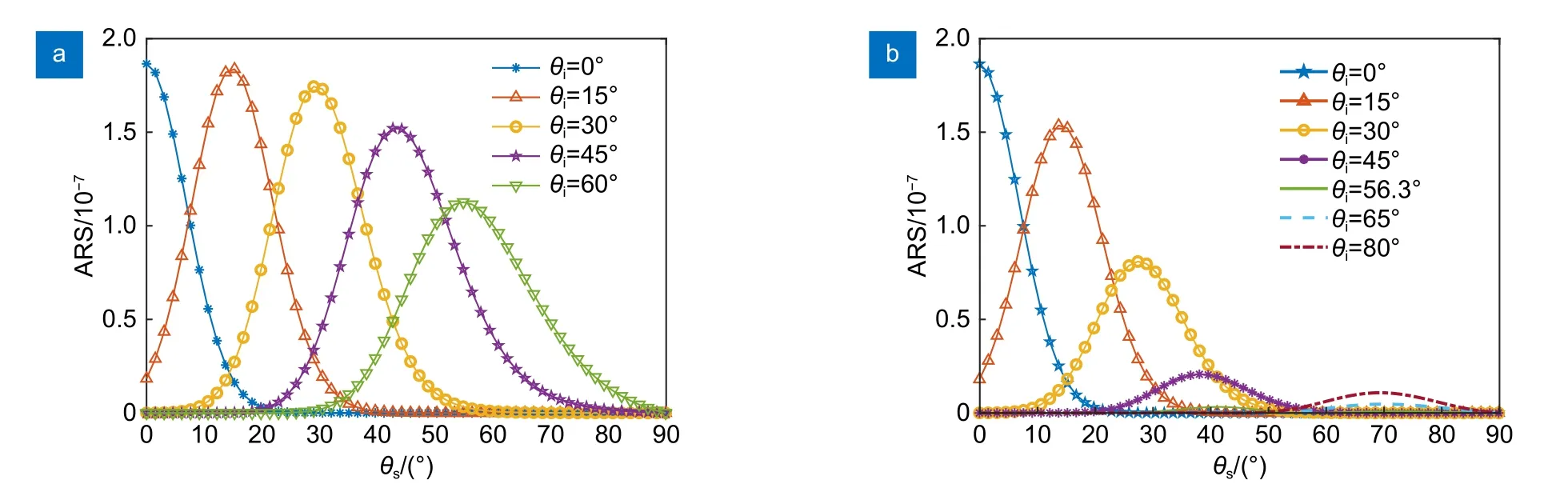
图3 各向同性光学元件偏振ARS 与散射角之间的关系。(a) S 光的偏振散射特性；(b) P 光的偏振散射特性Fig.3 Relationships between polarization ARS and scattering angles of isotropic optical elements.(a) Scattering characteristics of S-polarization light;(b) Scattering characteristics of P-polarization light

从图3(a)可以看出，随着入射角度的增大，S 偏振的ARS 峰值减少，但是散射角分布宽度变宽；其中，散射峰值(在适用范围内)是在散射角等于入射角处获得。从图3(b)可知，随着入射角度的增大，P 偏振的ARS 峰值先减小后增大，但其散射角分布宽度基本不变。特别地，当入射角度为56.3°时，ARS 值为0，这是由于布儒斯特角入射条件下P 光反射系数为0。当入射角较大时，S 光散射峰值位置并不在反射角位置处，这是由于自相关长度和波长比值大小的影响(比值越大，峰值偏离越小)。

3.1.2 散射方位角对偏振散射特性的影响

对于各向同性的光学元件表面，其交叉偏振反射率为0，散射方位角度对散射特性没有影响。然而，对于各向异性的光学元件表面而言，其散射方位角对偏振的影响特性较大。为分析在不同的散射方位角下，各向异性超光滑光学元件表面的偏振散射特性，超光滑元表面初始参数为：n=1.5，σs=0.1 nm，lc=600 nm，θi=θs=40°，散射方位角的变化范围为0°～180°，如图4 所示。

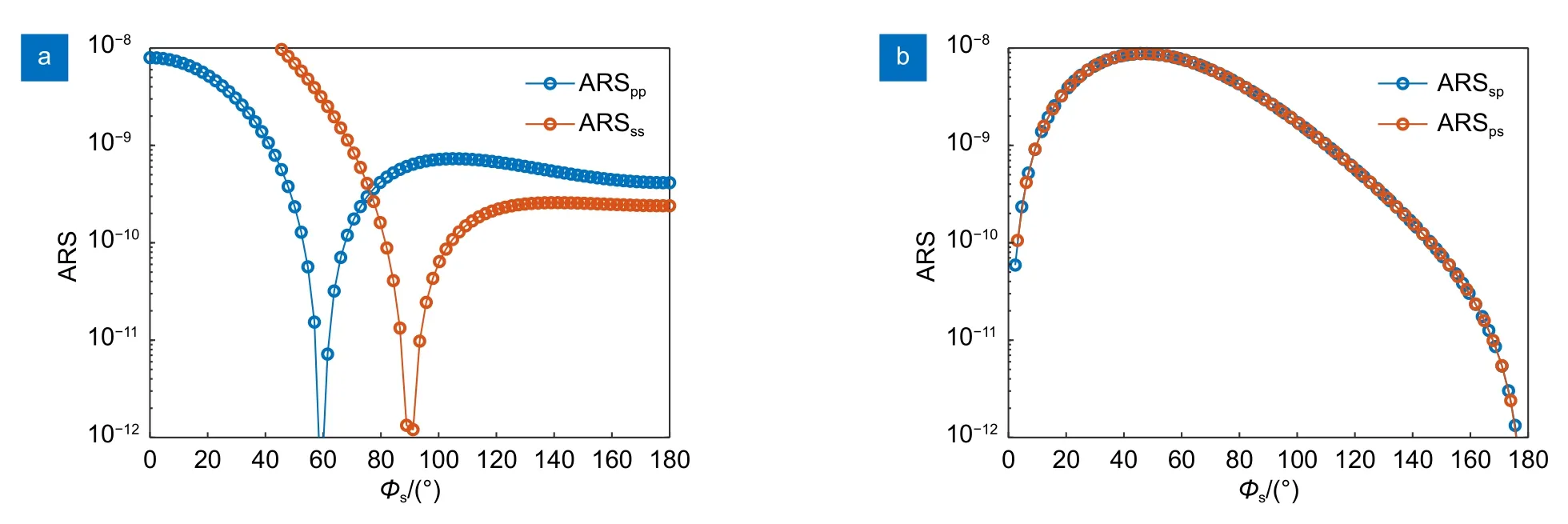
图4 四种偏振状态下，偏振ARS 与散射方位角之间的关系。(a) 平行偏振；(b) 交叉偏振Fig.4 Relationships between polarization ARS and scattering azimuth angles in four polarization states.(a) Parallel polarization;(b) Cross polarization

从图4(a)可以看出，随着散射方位角的增大，各向异性超光滑光学元件表面的ARSpp和ARSss均先减小后增大，最后趋于稳定。当散射方位角增大到与入射角相等的时候，ARSpp取得最小值；当散射方位角为90°时，ARSss取得最小值。图4(b)则表明，对于S 偏振光产生的P 偏振散射光，以及P 偏振光产生S 偏振散射光而言，ARSsp和ARSps分布几乎相同。这是由于对于同一超光滑光学元件，其表面粗糙度和自相关长度相同，致使偏振反射率Qsp、Qps也相同。随着散射方位角的增大，交叉偏振ARSsp、ARSps均先增大后减小，且当散射方位角等于入射角度时为极大值。

3.1.3 入射角度对偏振散射特性的影响

为分析在不同的入射角下，各向异性超光滑光学元件表面的偏振散射特性，超光滑元件表面初始参数为[29]：θs=45°，λ=1064 nm，n=1.5，σs=0.1 nm，lc=600 nm，如图5 所示。

图5 不同入射角度下，偏振ARS 与散射方位角的关系。(a) θi=15°；(b) θi=30°；(c) θi=45°；(d) θi=60°Fig.5 Relationships between polarization ARS and scattering azimuth angles at different incident angles.(a) θi=15°;(b) θi=30°;(c) θi=45°;(d) θi=60°

由图5(a-d)可知，在不同的入射角度下，随着散射方位角的增大，ARSsp和ARSps的变化趋势是一的。当散射方位角等于散射角时，ARSsp和ARSps都达到峰值，这是因为交叉偏振散射反射率表达式相同。然而，ARSpp和 ARSss在不同入射角下分布差异明显，存在特定的散射散方位角使得ARSpp和ARSss的值低于1×10-12。当散射方位角增大到与入射角相等的时候，ARSpp均取得最小值；而当散射方位角为90°时，ARSss均取得最小值。

总的来说，P 偏振光的偏振散射变化远大于S 偏振光的偏振散射，因而在引力波探测系统中，若采用P 偏振光，则应特别关注P 偏振光的偏振散射特性。

3.2 表面粗糙度统计特征对散射特性的影响

针对常见加工工艺导致的不同表面统计分布情况，讨论了不同入射角度、散射方位角、自相关长度、斜率、截止频率和表面粗糙度等因素对超光滑光学元件ARS 分布的影响。

3.2.1 高斯统计分布

超光滑光学元件的表面经过精细磨削、抛光、电解抛光等工艺后，其表面高度分布往往会趋于高斯统计分布，相应的PSD 函数表达式为[30]

式中：PSDGS是高斯统计分布条件下的二维表面功率谱密度函数，fx和fy表示超光滑光学元件表面的空间频率。

分析式(14)可知，影响PSDGS的主要参数有入射角度、散射方位角、自相关长度和表面粗糙度等。在利用GBK 散射模型分析高斯统计分布参数对ARS影响时，超光滑元件表面初始参数为[22-30]：n=1.5，λ=1064 nm，θi=20°，φs=0°，lc=2000 nm，σs=0.1 nm，如图6 所示。

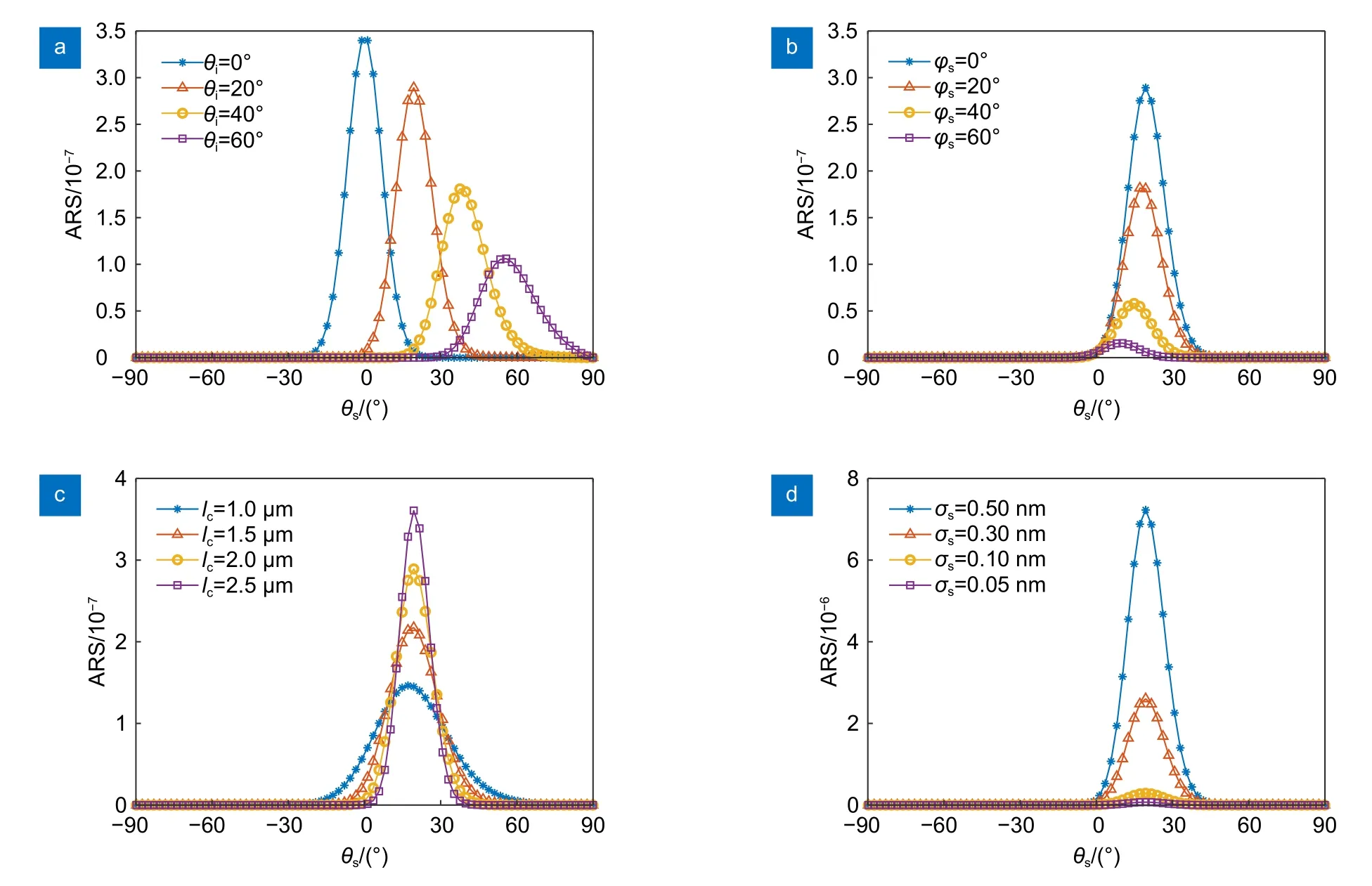
图6 在高斯统计分布下，ARS 与四种不同参数的关系。(a) 入射角度；(b) 散射方位角；(c) 自相关长度；(d) 表面粗糙度Fig.6 Relationships between ARS and four different parameters under the Gaussian statistical distribution.(a) Incidence angle;(b) Scattering azimuth angle;(c) Autocorrelation length;(d) Surface roughness

从图6(a) 可以看出，随着入射角的增大，ARS峰值减小，其分布宽度变宽；当入射角等于散射角时，ARS 取得峰值。从图6(b)可知，随着散射方位角的增大，ARS 峰值和分布宽度均减小，且其峰值向更小的散射角偏离(与ARSpp和ARSss的变化规律类似)。由图6(c)可知，随着自相关长度的增大，ARS 峰值增大，且ARS 分布宽度变窄。图6(d)表明，随着表面粗糙度的减小，ARS 的峰值快速降低，ARS 分布的宽度相应变窄。

3.2.2 分形统计分布

分形统计分布通常描述具有复杂粗糙度结构的表面，这些表面在不同尺度下均呈现出相似的形态，即局部特征与整体结构之间存在相似性。呈分形统计分布的超光滑表面可采用abc 模型描述，其二维功率谱密度函数可表示为[30]

式中：a、b和c是无量纲常数，在对数坐标系中，a为低频时光谱功率密度的大小，1/b为发生“滚降”的空间频率，它与表面形貌的表面空间波长(也称为自相关长度)成正比，c为空间频率大于1/b时光谱功率密度的斜率。具有分形统计分布表面的自相关函数表达式为：

式中：B 表示第二类修正Bessel 函数，Γ为Gamma函数。

分析式(15)可知，分形统计分布可由参量a、b和c来描述，影响PSDFD函数的主要参数包括入射角、散射方位角、斜率、表面粗糙度。在利用GBK 散射模型分析分形统计分布参数对ARS 影响时，超光滑元件表面初始参数为：n=1.5，λ=1064 nm，θi=20°，φs=0°，σs=0.1 nm，b=10，c=2.8，a参数可用b、c以及表面粗糙度来确定，如图7 所示。

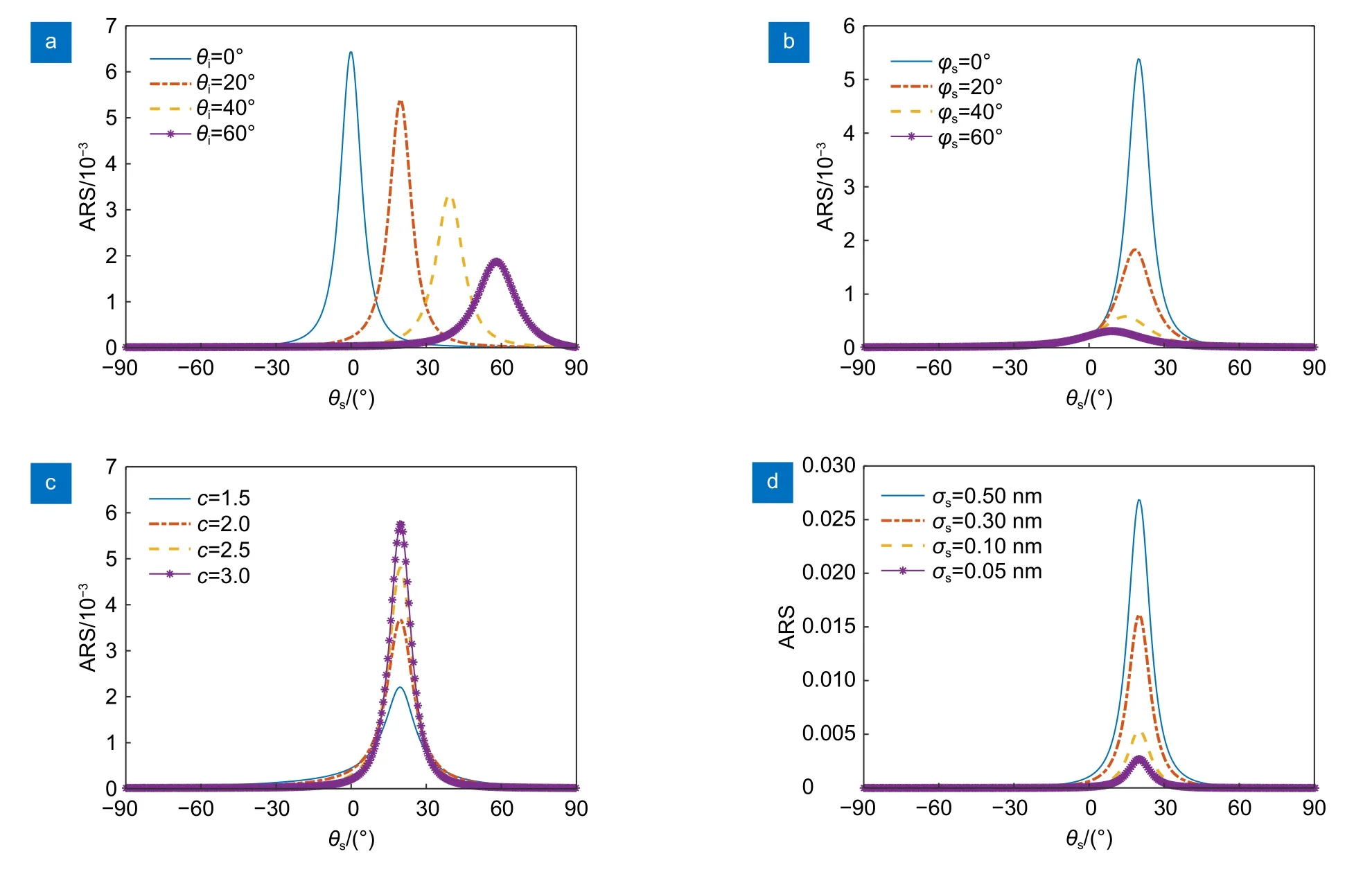
图7 在分形统计分布下ARS 与四种不同参数的关系。(a) 入射角度；(b) 散射方位角；(c) 斜率；(d) 表面粗糙度Fig.7 Relationships between ARS and four different parameters under the fractal statistical distribution.(a) Incidence angle;(b) Scattering azimuth angle;(c) Slope;(d) Surface roughness

从图7(a) 可以看出，随着入射角的增大，ARS峰值减小，ARS 分布宽度变宽；当入射角等于散射角时，ARS 取得峰值。从图7(b)可知，随着散射方位角的增大，ARS 峰值和分布宽度均减小，且其峰值向更小的散射角偏离(与ARSpp和ARSss的变化规律类似)。由图7(c)可知，随着斜率的增大，ARS 峰值增大，且ARS 分布宽度变窄。图7(d)表明，随着表面粗糙度的减小，ARS 的峰值快速降低，且ARS分布的宽度相应变窄。

3.2.3 柯西-洛伦兹统计分布

柯西-洛伦兹统计分布通常与一些特殊的加工工艺和技术相关[28]，尤其是光学薄膜制备。柯西-洛伦兹统计分布是一个重尾分布，其特点是在分布的尾部出现较慢的衰减，与高斯分布的快速衰减相比，柯西-洛伦兹统计分布的尾部扩展得更远。柯西-洛伦兹统计分布对应的二维功率谱密度表达式为

式中：a为无量纲常数，在对数坐标系中，a为低频时光谱功率密度的大小，与分形统计分布一致，参数a可采用b、c和表面粗糙度表示；fc是截止频率。

分析式(17)可知，影响PSDKX函数的参数主要有入射角、散射方位角、截止频率、表面粗糙度等。在利用GBK 散射模型分析柯西-洛伦兹统计分布参数对ARS 影响时，超光滑元件表面初始参数为：n=1.5，λ=1064 nm，θi=20°，φs=0°，fc=10-3μm-1，σs=1 nm，b=10，c=2.8，如图8 所示。

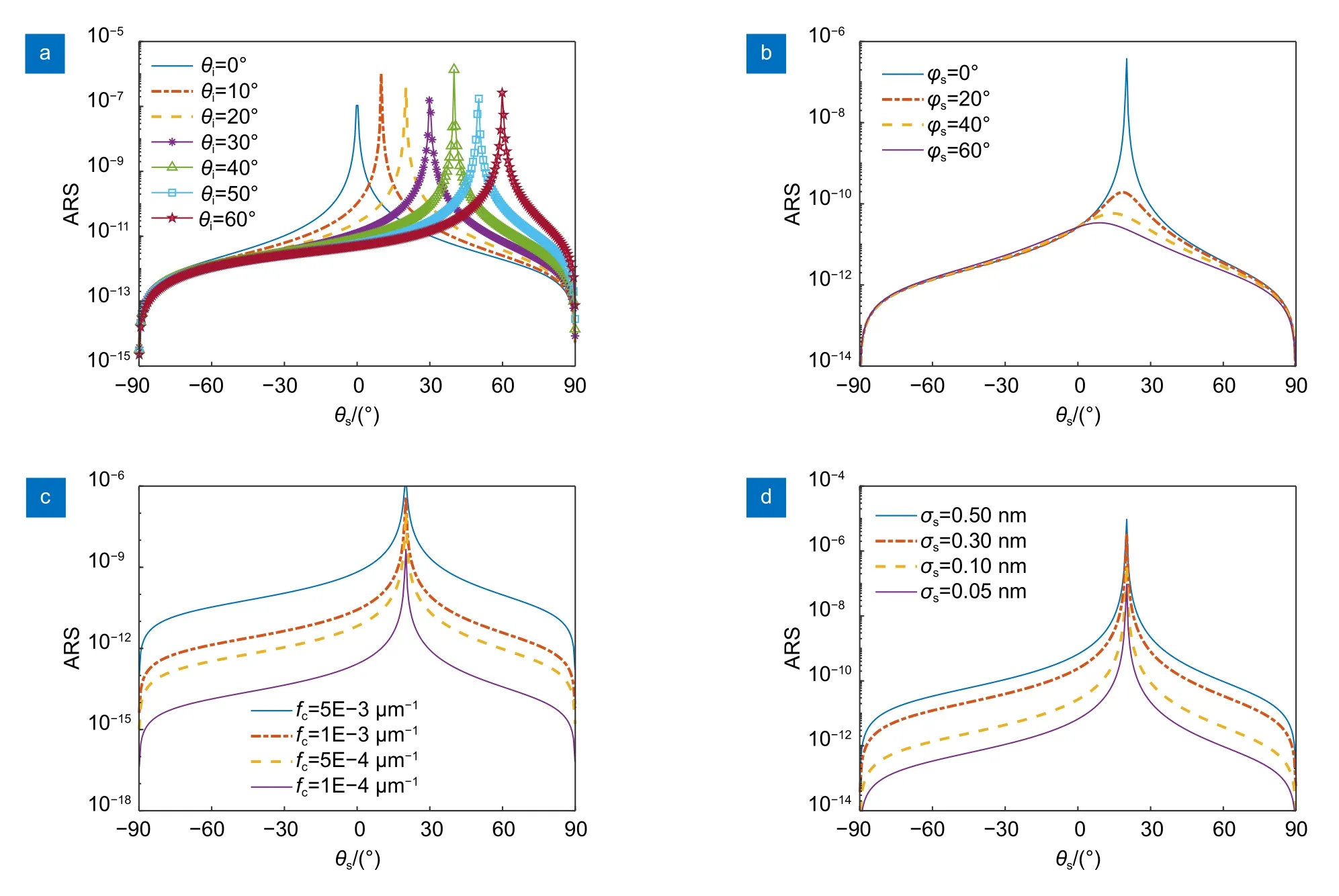
图8 在柯西-洛伦兹统计分布下，ARS 与四种不同参数的关系。(a) 入射角度；(b) 散射方位角；(c) 截止频率；(d) 表面粗糙度Fig.8 Relationships between ARS and four different parameters under the Cauchy-Lorenz statistical distribution.(a) Incidence angle;(b) Scattering azimuth angle;(c) Cut-off frequency;(d) Surface roughness

从图8(a)可以看出，随着入射角的增大，ARS峰值存在明显的涨落，ARS 分布宽度不变；当入射角等于散射角时，ARS 取得峰值。分析图8(b)可知，随着散射方位角的增大，ARS 峰值减小，但ARS 分布宽度变宽，且其峰值向更小的散射角偏离(与ARSpp和ARSss的变化规律类似)。由图8(c)可知，随着截止频率的减小，ARS 峰值减小，ARS 分布宽度变窄。图8(d)表明，随着表面粗糙度的减小，ARS的峰值减小，且ARS 分布的宽度相应变窄。

在引力波探测系统中，超光滑光学元件的表面微观形貌统计分布特性与其加工使用的高精度工具、材料选择、抛光参数的优化以及表面处理工艺等密切相关，而具有不同微观表面统计分布的超光滑光学元件，其表面散射特性规律有所不同。总体来说，随着入射角度、散射方位角和斜率的增加，ARS 峰值逐渐减小，其分布宽度变宽；随着自相关长度、截止频率和表面粗糙度的增加，ARS 峰值逐渐增大，其分布宽度变窄。

4 结论

针对空间引力波探测系统中超光滑元件表面散射特性分析，发展了一种能对超光滑光学元件表面散射特性进行快速、准确分析和预测的非傍轴标量散射模型，即GBK 模型。该模型具有偏振散射特性，且适用于超光滑光学元件表面微观形貌的不同统计分布类型。利用GBK 模型，分析了P 偏振光和S 偏振光入射条件下，角分辨散射(ARS)分布随入射角度、散射角度及散射方位角的变化规律，并针对常见加工工艺导致的不同表面统计分布情况，讨论了不同入射角度、散射方位角、自相关长度、斜率、截止频率和表面粗糙度等因素对ARS 分布的影响。结果表明，P 偏振光的偏振散射变化远大于S 偏振光的偏振散射，因而在引力波探测系统中，若采用P 偏振光，则应特别关注P 偏振光的偏振散射特性。在不同的表面微观形貌统计分布下，ARS 分布始终在镜向反射处取得峰值，并随着入射角度、散射方位角和斜率的增加，其值逐渐减小，分布宽度变宽。此外，随着自相关长度、截止频率和表面粗糙度的增加，其值逐渐增大，分布宽度变窄。在空间引力波探测系统中，应特别关注ARS 峰值大小以及分布宽度，并通过合理的设计和优化，有效抑制杂散光对引力波探测精度的影响。相关结果不仅深化了对超光滑表面散射特性的理解，还可为超光滑元件的加工提供参考。