引力波探测望远镜超低热变形桁架支撑结构设计技术

李博宏，罗 健，丘敏艳，陈文多，赵宏超

1 “天琴计划”教育部重点实验室，天琴中心 &物理与天文学院，天琴前沿科学中心，国家航天局引力波研究中心，中山大学(珠海校区)，广东 珠海 519082；

2 中山大学深圳材料学院，广东 深圳 518107；

3 中山大学深圳先进制造学院，广东 深圳 518107

1 引言

天琴计划空间引力波天文台由三颗完全相同的卫星组成，星座的任意两条臂均可构成一个迈克尔逊干涉仪，并通过星间激光干涉测量技术监控相距十几万公里的两个检验质量之间的距离变化实现对引力波的探测[1]。作为干涉测量系统的一部分，望远镜在系统中的作用主要有两个：本地激光的扩束发射和远端激光的汇聚接收[2]。

杂散光与尺寸稳定性是引力波探测望远镜设计中的两个核心问题[3-4]。受限于传统同轴望远镜中心遮拦引起的高杂散光问题，目前引力波探测望远镜方案均以离轴望远镜设计为主。但离轴望远镜结构总体稳定性较低，扰动后的任意微小变化均可引起结构变形，从而增加光程噪声。

环境温度变化是导致望远镜结构变形的主要原因。望远镜内部占据空间最大的组件为主次镜间连接结构。该结构作为提供零件支撑固定的平台，可以很大程度上反映望远镜整体的热变形行为。因此必须通过对望远镜主次镜连接结构的选材与构型优化设计，改善望远镜整体尺寸稳定性，从而降低光程噪声，提升引力波探测信噪比。

消热化设计又称无热化设计，早在上世纪50 年代就被广泛应用于光机设计之中。在早期，消热化设计主要采用一些简单的手工计算方法，估算结构的温度分布和热应力分布，以改进结构设计方案[5-6]。该方法虽然简单易行，但是准确度不高，只适用于简单的光学结构设计。经过多年的发展，当下消热化结构设计已经比较成熟。典型的消热化设计手段有：

1)低膨胀计量杆与高膨胀板的反向组合设计技术[7]；

2)利用柔性连接补偿轴向热变形技术[8-9]；

3)整机使用同种材料以消除热应力[10-11]；

4)结构消热化设计技术[12]；

5)应用超低膨胀材料以减少热变形[13-16]。

针对引力波探测望远镜而言，常规消热化手段不足以满足热变形要求，必须考虑使用更综合有效的消热化手段降低结构热变形，其中结构优化[17]和选择低热膨胀系数的材料[18]尤为重要。

本文为降低望远镜结构热变形，从CFRP (carbon fiber reinforced polymer)材料铺层优化和结构几何参数优化两个角度出发，建立了CFRP 铺层方式与热膨胀系数的数学模型，并构建了结构几何参数与间隔、偏心两自由度方向热变形之间的函数关系。同时，考虑到实际加工装调等问题，提出了三段式组装型望远镜设计方案，提高了望远镜装调的可操作性，可有效避免工艺误差带来的整机失效风险。分析结果表明，CFRP 铺层方式与热膨胀系数之间的数学模型可以准确预测材料的热膨胀系数，将其中经过设计的CFRP材料应用于桁架支撑结构设计中，在满足力学性能的前提下，可明显降低望远镜结构热变形。

2 建立结构热变形数学模型

引力波探测单链路等效位置不确定性表示为振幅谱密度，其功率谱密度是干涉测量系统(interferometric measurement system,IMS)的位移噪声和干扰减少系统(disturbance reduction system,DRS)的加速度噪声这两项的总和：

本文不涉及加速度(DRS)噪声。就干涉测量系统(IMS)而言，其位移噪声为

结构热变形与很多因素有关，如材料选择、构型设计、组件间热补偿设计等，其中材料选择非常关键，材料的热胀系数做到1 ×10-7/K是结构达标的必要条件。目前航天望远镜结构常见选材如下：

LISA 团队早在2008 年前后就选用了Zerodur 以及CFRP 两种作为望远镜主体支撑结构的选材。两种材料均可以做到材料热膨胀αCFRP＜1×10-7/K，基本满足引力波探测望远镜的选材要求。LISA 基于其中CFRP 材料制成的望远镜支架结构已经于2014 年完成实验测试。测试结果表明LISA 样机主次镜中心点相对热变形满足要求，但间隔、偏心等方向热变形不满足设计要求，仍有很大的优化空间，针对结构和材料优化需要做更深入的研究。另一方面，以Zerodur材料为基础的望远镜方案相比于CFRP 材料望远镜而言，其加工装调难度较大，实物产出较难，至今仍无整机实验。该方案对于现阶段引力波探测望远镜装调实验需求而言并不适用，因此作为备选方案研究，本文不做深入讨论。

2.1 基于铺层设计的CFRP 热物性数学模型

针对引力波探测望远镜超稳定性的需求，本文选择参数可设计的CFRP 材料作为研究对象，通过对纤维铺层角度的设计，调整CFRP 材料的热膨胀系数[19-20]，将敏感方向的热膨胀系数降低至α ＜1×10-7/K。

热膨胀系数即“单位温度变化所导致材料的应变量”：

其中：α 表示热膨胀系数，下标为热膨胀的方向，单位为 K-1；ΔT表示材料温度变化量，单位为 K ；ε0表示由温度变化引起的应变量，为变化量的绝对值与材料原长度之比，可表示为Δl/l，属无量纲物理量。

对于复合材料而言，层合板性能取决于单层板性能以及其铺层方式，根据广义胡克定律，单层板复合材料有本构关系：

其中：σ1、σ2代表面内施加的正应力，下标1 代表纤维增强方向，简称纵向；下标2 代表面内垂直纤维方向，简称横向；τ12表示面内剪切应力；Q为材料刚度矩阵，其中元素Qij为 材料在各方向的刚度系数；ε1、ε2、γ12分别为对应方向的面内纵向、横向正应变和面内剪应变。

将其纤维方向一般化，如图1 所示，得到任意角度单层板本构关系：

图1 单层CFRP 示意图。方向1 为面内纤维方向，简称纵向；方向2 与方向1 面内垂直，简称横向Fig.1 Single-layer CFRP schematic diagram.Direction 1 corresponds to the in-plane fiber direction referred to as the longitudinal direction；Direction 2 is perpendicular to direction 1 within the plane referred to as the transverse direction

其中，t为坐标系转换矩阵：

其中，m=cosθ,n=sinθ，即该式将单层板本构关系与其纤维角联系了起来。式(6)反映出复合材料单层板在任意纤维角度下的本构关系，该函数关系是层合板热膨胀系数的模型基础。将该纤维角度下的转换矩阵与单层板面内热膨胀系数关系相结合，单层板在任意角度下的热膨胀系数 α表示为

其中：α1为 单层板纵向热膨胀系数，α2为单层板纵向热膨胀系数。

单层板结构的材料参数是固定的，若想调整材料性能，需将单层板在垂直于面的z方向上层叠起来，制成层压板复合材料，如图2 所示。

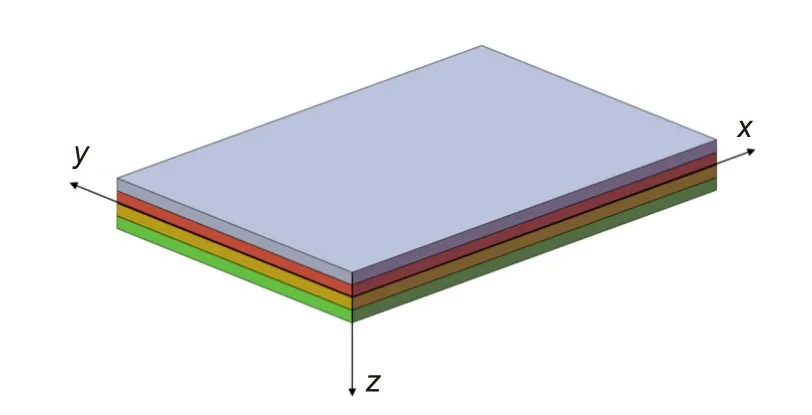
图2 层压板复合材料示意图Fig.2 Laminate composite material schematic diagram

考虑到层合板中有经典层合板理论解释层合板基础本构关系：

其中：N、M分别是层合板在面内x、y正向和剪切方向受到的单位长度上的合力与合力矩。ABD矩阵为层合板的刚度矩阵：矩阵块A为拉伸刚度矩阵，元素Aij为各方向拉伸刚度；矩阵块B为耦合刚度矩阵，元素Bij表示面内合力N和曲率K以及弯矩M和层合板中面应变 ε0之间的耦合关系；矩阵D为弯曲刚度矩阵，元素Dij为各方向弯曲刚度。ε、K为层合板中面应变和层合板弯曲曲率。

热膨胀过程不涉及弯曲应力，且铺层必须保证对称性，否则存在拉-弯耦合。因此式(9)中B矩阵为零矩阵，且不涉及D矩阵运算。可将其简化并求逆：

式中：A'带有上标，表示该元素为原ABD矩阵中拉压矩阵A的 逆矩阵的元素；NT表示层合板受到的单位宽度热应力。

若层压板共有n层，则NT与每层单层板的刚度矩阵、温度变化量 ΔT、一般坐标系下的热膨胀系数 αk及 该层厚度(zk-zk-1)之间的关系为

同时，拉伸刚度矩阵A中元素与每层单层板的刚度矩阵、温度变化量、一般坐标系下的热膨胀系数及该层厚度之间的关系为

将式(11)和(12)带入到式(10)中，得到ε；再将ε带 入式α=ε/ΔT，约去其中的温度差 ΔT，即可得到层合板热膨胀系数αl与每层单层板的性质、铺层角度和厚度的关系：

由(13)可知，单层板确定后，材料的刚度矩阵和厚度随之确定，唯一变量即单层板角度转换矩阵t，说明层合板热膨胀系数αl可通过层合板中的每层纤维铺层角度进行调节。

2.2 结构分段式设计与热变形模型

对于引力波探测望远镜而言，Zerodur 材料热膨胀系数极低，因此基于该材料的一体化设计方案更容易实现热变形稳定性的目标，但该方案生产加工难度大，装调粘接工艺要求较高。本文提出的可装配分段式结构设计相比于Zerodur 一体化的设计方案而言更加易于设计、安装和调整，且不会因局部加工误差过大导致全局失效，只需对局部组件进行重新生产加工即可，热变形稳定性的问题可以通过CFRP 材料优化、结构几何优化等方式解决。望远镜主体支撑结构分为三个部分，即主镜支撑承力板、桁架结构和副镜支撑结构，如图3。

图3 天琴望远镜三段式设计：1)主承力板；2)主支撑三杆；3)副镜支撑装调背板Fig.3 Three-stage design of the TianQin telescope:1) Main load-bearing plate;2) Three main support rods;3) Sub-mirror support adjustment backplate

各个组件之间由可更换式CFRP 连接管进行组装连接，图4 即可更换支撑管示意图。

图4 可更换式望远镜CFRP 支撑杆接头Fig.4 Replaceable telescope CFRP support tube joint

为探究结构几何参数与热变形之间的关系，可以将望远镜简化为桁架杆模型。如图5，可认为QP、MP 和OP 分别代表结构中的两侧支撑管和底部主支撑管，通过对结构参数LA、LB、LC进行优化，对副镜所在位置的P点在偏心dy和离焦dz两个方向上进行热变形分析。

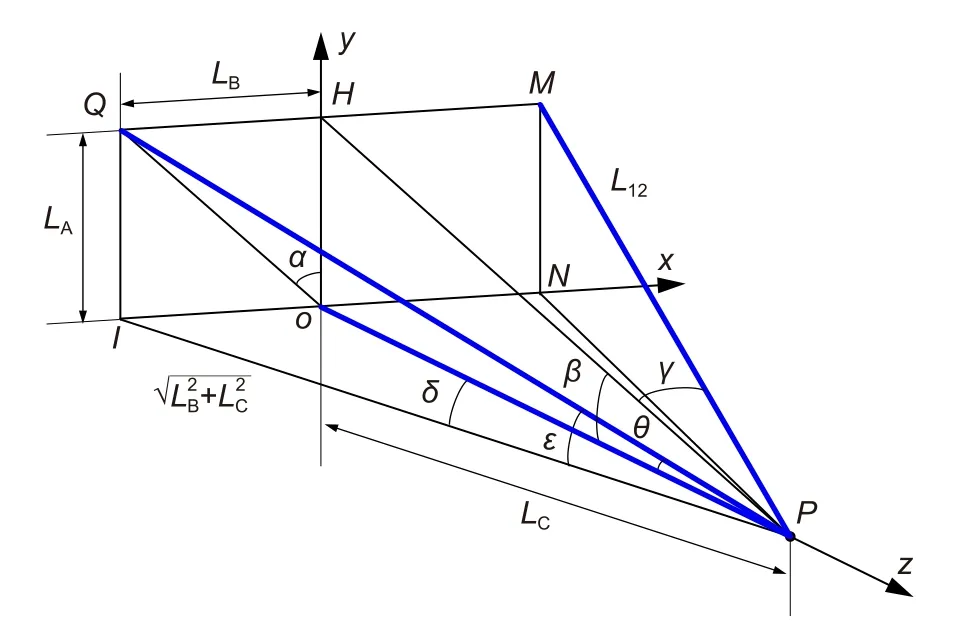
图5 桁架支撑结构的几何模型Fig.5 Geometric model of the support structure

基于结构力学理论，三杆均认为是桁架模型，仅在轴向受力，且由于三杆选用材料相同，理想状态下无内部热应力。将以上特点结合具体三杆结构的变形协调方程，得到

根据式(14)及几何关系，得到P点沿Z轴方向热变形dz：

以及P点沿Y轴方向热变形dy：

选择以结构参数LA、LB、LC为优化参数，约束条件为望远镜结构尺寸包络限制，分别为LA∈[250,275],LB∈[225,235],LC∈[825,855]。由式(15)、(16)可知，当支杆选材确定后，一定温变条件下，结构热变形只与结构的几何参数LA、LB、LC相关。

3 模型验证与参数优化

3.1 铺层-热膨胀系数的模型验证与仿真优化

本文选择M40J/wp-s3000 单层板作为基本铺层单元，每层厚度均为0.15 mm，总层数为20 层，基本性能如表1 所示。

表1 常见望远镜样机主支撑结构备选材料Table 1 Candidate materials for truss support structure of telescope prototype

考虑到优化目标函数是减少材料热变形系数αx-CFRP和 αy-CFRP，变量空间为20 层CFRP 的纤维角，因此属于多目标、多变量求最小值的问题。针对这类问题，目前较为成熟的优化算法有很多，如粒子群算法、遗传算法等。本文选用NSGA-Ⅱ，即非支配排序遗传算法。

NSGA-Ⅱ (Non-dominated sorting genetic algorithms-Ⅱ)是一种基于Pareto 最优概念的遗传算法，早在1995 年就被Srinivas 和Deb 提出，并于2000 年改良成为第二代高效成熟的优化算法，是最流行的多目标遗传算法之一，它降低了非劣排序遗传算法的复杂性，具有运行速度快，解集的收敛性好的优点，成为其他多目标优化算法性能的基准。该算法基本思路是通过寻找Pareto 前沿以及非支配优化方案来进行精英筛选，然后再将后续Pareto 前沿若干种群进行遗传算法优化，得到新的种群；保留优势种群后再重新排序迭代优化，最后收敛得到稳定的Pareto 前沿优化结果。

目前常见的CFRP 材料以各向同性铺层方式为主，但为了对比常规CFRP 铺层和特定铺层方式，这里选取6 种不同的铺层方式作为对比，其中铺层1 是准各向同性铺层方式，2～4 为常见消热化铺层设计，5～6为针对x方向热膨胀优化设计后的铺层方式。将以上CFRP 铺层参数带入到计算程序中，得到相应热膨胀系数计算结果，见表2。

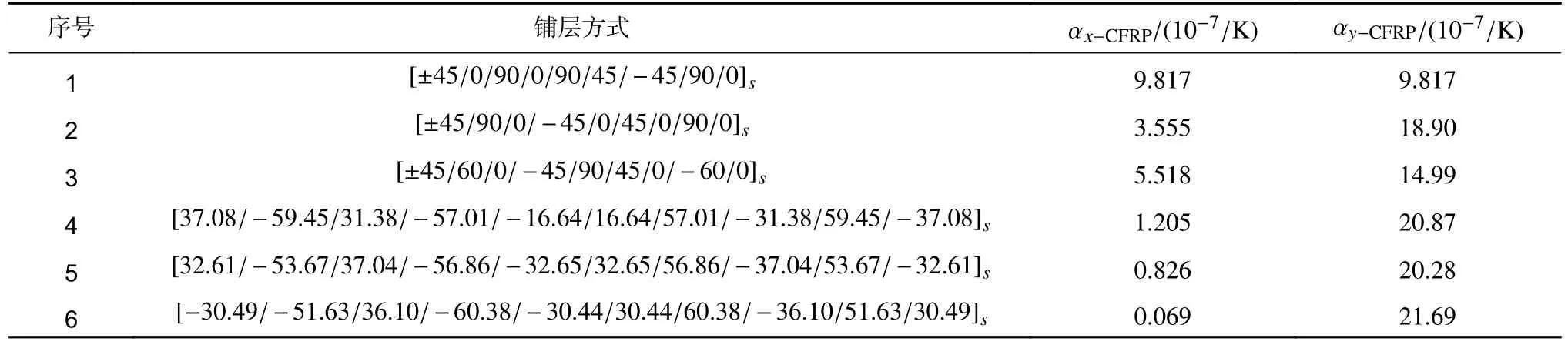
表2 备选CFRP 铺层方式Table 2 Alternative CFRP layup methods

将该结果与ABAQUS 仿真软件中的结果进行对比，这里以铺层方式6 为例，分别给出了经过设计后的CFRP 在X和Y两个方向的热膨胀系数，如图6所示。

图6 CFRP 材料热膨胀有限元仿真：以最优设计—铺层方式6 为例Fig.6 Finite element simulation of thermal expansion of CFRP material — taking laying method 6 as an example

将6 种铺层方式的有限元仿真结果与理论计算仿真结果进行对比。其中，在理论计算过程中，每层纤维角的精度不设限制，仿真中每层纤维角精度保留至小数点后两位(即仿真纤维角设置精度为0.01°)，优化对象以CFRP 中x方向热膨胀系数为主。将仿真结果与前文理论模型计算结果进行对比，以验证理论模型正确性和误差估计。对比结果见表3。

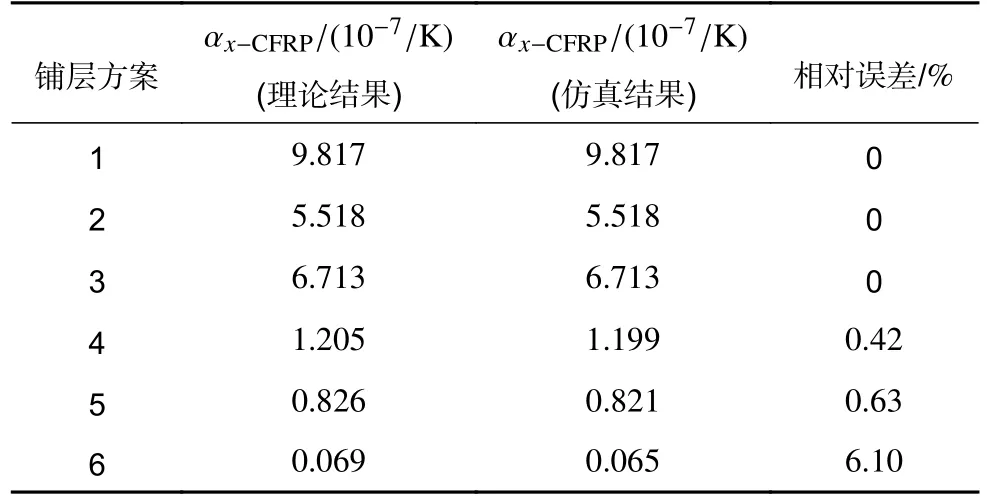
表3 理论模型计算结果与仿真结果对比Table 3 Comparison of theoretical model calculation results with simulation results

对比结果表明：

1)在一定误差范围内，式(13)对CFRP 热膨胀系数的预测值与仿真结果一致；

2)针对性铺层设计在设计方向上的热膨胀系数小于常规准各向同性铺层设计；

3)由于经过优化设计后仿真计算取小数点后两位，仿真设置精度小于理想参数设置，因此与理想结果之间有偏差。同时可经过观察发现，热胀系数设计值越低，同等精度下的偏差值越大，这也为后续CFRP 实物样件的加工提供了纤维铺层加工精度参考。

3.2 支撑结构-热变形模型验证与仿真优化

对于望远镜主支撑结构的设计必须保证：1)系统强度大，结构不受破坏；2)结构刚度大，在重力卸载后镜面之间不会产生较大的相对位置偏移而失效；3)能够抵抗一定的冲击，避免镜体位置变形过大而失效。

根据当前的调研结果给出望远镜主支撑结构的主要设计指标，见表4。

表4 望远镜样机主支撑结构设计要求Table 4 Design requirements for main support structure of telescope prototype

表中前3 项均为一般性要求，其中重力卸载需针对间隔 Δz、偏心 Δy，以及主次镜间角度变化ΔTx。重力形变主要受主副镜部分组件重量及支撑形式影响。第4 项则表示航天器在任务周期内，望远镜环境温度会产生较大温变，该情况下在间隔、偏心方向上允许热变形的最大值。第5 项表示为温控可以达到理想状态下的且IMS 噪声中除望远镜外其他噪声为0。该条件下望远镜设计要求较低，因此作为阶段性基本设计目标。同时考虑到实际情况非极限状态给出表格种第6 项，即表示环境热噪声在频段内为条件下，IMS 噪声中40%的影响由望远镜结构热变形产生。与前项相比，该条件下望远镜设计要求更高。

结构模型如图7 所示，总体结构以主镜组件固定背板底部中心为原点，以主次镜轴向方向为Z轴，以主镜背板所在面为X-Y平面。望远镜样机的主支撑结构可分为三个组成部分：1)主承力固定背板；2)主支撑方管和侧翼支撑圆管；3)副镜支撑组件。

图7 主支撑结构模型与坐标系Fig.7 Main support structure model and coordinate system

望远镜为三杆支撑结构，可以其抽象为空间桁架模型，并对该模型进行有限元仿真验证。给出理论模型计算结果、桁架单元仿真结果和实体单元仿真结果三者对比。输入条件为整体升温10 K，输出为副镜处Z、Y两自由度热变形。三杆支撑材料选择常规各向同性CFRP 铺层方式，即前文中铺层1，结构模型如图8、图9。

图8 实体单元模型(左)；桁架杆单元模型(中)；理论模型(右)Fig.8 Solid model (left);truss structure model (middle);theoretical model (right)

图9 实体仿真结果和桁架杆仿真结果—以间隔dz 方向热变形为例Fig.9 Solid simulation and truss simulation result — example of thermal deformation in the dz direction

仿真结果如表5。

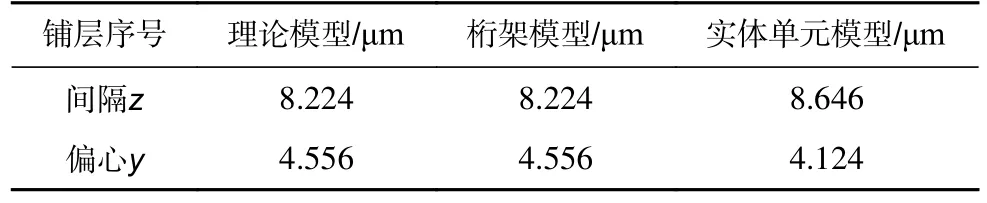
表5 三种模型之间对比验证Table 5 Comparison and verification among the three models

仿真结果表明：

1)桁架单元仿真结果与理论计算结果完全一致，即针对“结构参数-热变形”的数学模型准确，由桁架理论推导出的函数关系式(15)、式(16)有效；

2)实体单元与理论模型的相对误差在z方向是5.13%，y方向为9.68%。原因在于理论模型与桁架模型均为一维拉压杆模型，而实体模型计算过程中会引入另外两个方向的应力应变，因此计算结果一定会出现差别。但在误差允许范围内，理论模型可作为结构优化设计的重要参考。

以各向同性CFRP 铺层方式1 为三杆选材，将材料与结构几何约束带入到参数优化程序中。目标优化函数为结构在z、y两个方向的热变形dz和dy，面向LA、LB、LC三个参数做优化，属于多目标多参数优化问题，如图10 所示。

图10 对结构热变形的参数优化结果Fig.10 Optimization results for structural thermal deformations

优化采用多目标遗传算法优化手段，寻找设计Pareto 前沿。图中横纵坐标分别表示P点在优化结构LA、LB、LC参数后的热变形dy和dz。每一点均对应一种LA、LB、LC参数设计方案，不同的参数组合可以求解出不同的热变形结果，但均为相对最优解。需针对具体的加工精度、公差要求、尺寸约束等进行选择。

因此，设计方案基于其中的一种结构设计参数进行讨论，即A=260.0、B=230.3、C=837.8，桁架材料铺层为前文(表2)中铺层1，该铺层方式为准各向同性CFRP 铺层，属于非优化的常规铺层方案，可作为对照组。该设计在间隔z、偏心y和结构总体热变形方向上，结构热变形系数分别为：αz=9.817×10-7/K、αy=16.986×10-7/K、αl=10.751×10-7/K。后续以该设计作为基础设计方案，分析桁架支撑结构的机械性能，并对比常规材料、优化后铺层的热变形性能。

4 数据分析

4.1 机械性能分析

目前桁架支撑结构设计重量为6.7 kg，满足设计要求。在模态分析方面，仿真分析给出了前15 阶的模态分析结果，这里以前两阶振型为例，如图11、图12。前两阶模态的频率分别为122.61 Hz 和128.47 Hz，均满足初始设计要求。

图11 第一阶振型：沿Y 方向摆动，122.61 HzFig.11 First mode: oscillation along the Y direction,122.61 Hz

图12 第二阶振型：沿X 方向摆动，128.47 HzFig.12 Second mode: oscillation along the X direction,128.47 Hz

除模态外，对桁架支撑结构做两敏感自由度方向的重力卸载分析。整体模型基于ABAQUS 实体模型单元进行分析，三桁架杆选材为铺层方式1 的CFRP材料。以主支撑背板端面为边界条件，分三次对整体结构加载沿X、Y、Z三方向的重力载荷。最后针对主副两镜面中心点的相对位移做数据后处理，结果见表6。

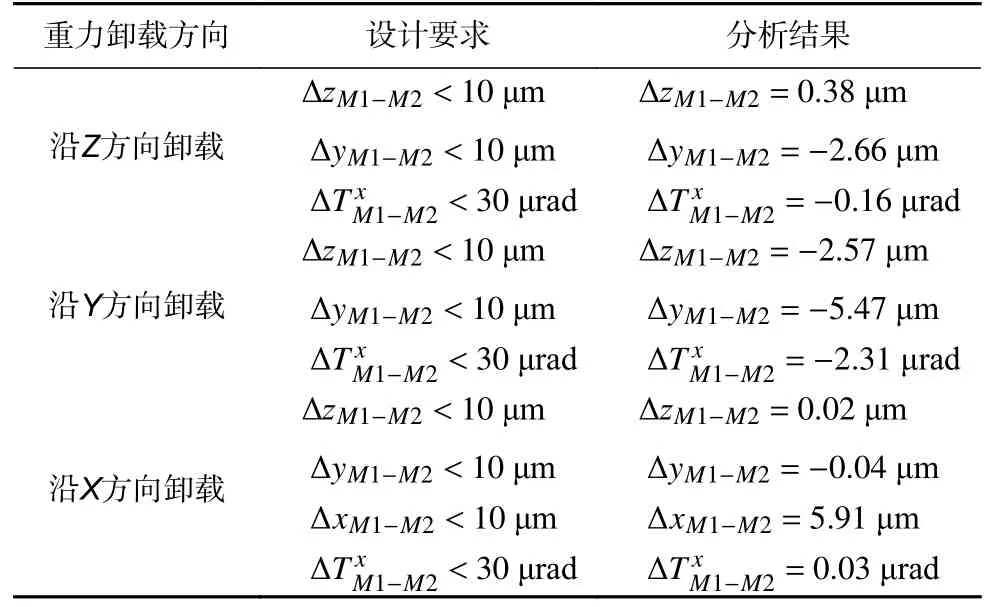
表6 重力卸载变形分析Table 6 Gravity unloading deformation analysis

要注意的是，由于整个望远镜样机的设计是相对于YOZ面对称的，即当重力卸载方向沿Y和Z时，X方向上的变形在计算过程中可以忽略不计。但如果重力卸载方向沿X方向时，就必须考虑主次镜间在X方向的相对变形。因此表格中重力沿X方向卸载时，增加一项主次镜之间在X方向的相对变形ΔxM1-M2。

根据重力卸载后的分析结果可知，由于使用CFRP 材料，整体结构较轻的同时结构刚度也很大，静力学与动力学性能均较好，满足望远镜动力学要求和在空间任意方向下重力卸载后的变形要求。

4.2 桁架支撑结构热变形稳定性分析

使用CFRP 材料的一个重要目标就是利用其可设计性降低材料热膨胀系数，达到降低结构热变形稳定性的目标。因此需要将前文中经过分析后的CFRP 应用于主支撑结构设计方案中，并分析结构热变形。以铺层方式1 为例，有限元仿真如图13。

图13 热变形有限元分析-以铺层1 为例Fig.13 Element analysis of thermal deformation of truss support structure -example with layer 1

图14 以50 μK 温度噪声为温度输入条件Fig.14 Taking 50 μK temperature noise as an example

图15 主次镜间隔相对热变形为Fig.15 The relative thermal deformation in the M1-M2 separation direction is 12

结合本文铺层设计，与其它常规望远镜材料应用于支杆作为对比，结果如表7 所示。

表7 不同选材之间结构热变形对比结果Table 7 Comparison results of structural thermal deformation between different materials

综合以上分析结果表明：

1)以CFRP 作为望远镜桁架支杆材料，相比于其他常规材料而言，可以明显降低望远镜支撑结构热变形。

2)铺层方式4 的CFRP 材料热膨胀系数为αx-CFRP=1.20×10-7/K，将其带入到实体单元结构中进行分析，发现桁架结构的热变形为αz=3.31×10-7/K。可知热变形性能还受到具体方案影响，如主镜支撑形式、连接结构设计、热补偿结构方案等。

3)同时对比不同CFRP 铺层方式，发现产生的结构热变形也有很大的差别，说明经过特定设计的CFRP 材料确实可以降低望远镜的热变形，且铺层方式对热变形影响较大，不可忽略。因此，在后续工作中既需要继续优化CFRP 铺层方式，同时也需给出多种消热化方案的综合性设计。

5 结论

本文针对引力波探测望远镜的超低热变形要求，提出了从材料和结构两方面进行优化的解决方案。材料方面，建立了CFRP 铺层方式与热膨胀系数之间的数学模型，利用有限元仿真分析验证了模型的正确性，并给出了优化纤维铺层方案。结构方面，建立了结构参数与热变形之间的数学模型，并对结构参数进行了优化，为望远镜的桁架支撑结构超低热变形设计建立了理论基础。将上述针对材料与结构的理论研究与实际结构要求相结合，提出了装配式分段设计方案，主支撑杆件、主承力板等组件均可分别更换装调，降低了望远镜的装调难度。最后结合有限元仿真，对设计结果进行机械性能、热变形性能分析，并给出了不同材料作为桁架支撑结构的热变形结果对比。综合分析结果表明：

1)通过设计CFRP 铺层方式可对材料热膨胀系数进行优化，满足材料热变形要求。

2)常规结构设计要求方面，桁架结构重量为6.7 kg，结构基频为122.61 Hz；重力卸载偏差最大值在重力沿x方向卸载时的结构变形5.91 μm；周期内环境温变为10 K 条件下，结构热变形为dz=8.224 μm、dy=4.556 μm，说明结构设计满足基本性能要求。

4)目前的结构设计相比于常规设计而言，热变形性能有明显提升，但仍未满足天琴需求。虽然目前的CFRP 铺层优化可将材料在桁架杆轴向方向保证10-7/K的热膨胀水平，但由于结构中组件间局部热应力、泊松比效应等导致结构总体热变形性能仍不能满足要求，因此后续工作应在现有工作的基础上进一步讨论结构消热化的问题，对具体的支撑组件、连接组件、消热化结构等做综合优化设计。