空间引力波望远镜内部光场计算方法研究

刘 烨，华喆怿，彭韶婧，吴 兰，刘 东，刘 崇

浙江大学 光电科学与工程学院 现代光学仪器国家重点实验室，浙江 杭州 310027

1 引言

引力波是物质与能量剧烈运动和变化所产生的一种物质波，承载了引力相互作用的基本自由度。1916 年，爱因斯坦基于广义相对论预言了引力波的存在[1]，此后一系列引力波探测与研究为揭示宇宙演化、基础物理学规律提供了新的途径。美国激光干涉引力波天文台LIGO 于2016 年首次报道探测到了双黑洞合并引力波[2]，其基于臂长数公里的迈克耳逊干涉仪，当引力波经过时探测器周围的空间发生扰动，导致空间在一个方向上拉伸而在另一个方向上压缩，两束干涉光走过的路程产生细微的差异，反映在干涉强度上，通过解调相位信息的变化进行探测。宇宙中存在大量引力波源，覆盖了10-18Hz 到104Hz 极为宽阔的频段，然而受地表震动、噪声以及干涉臂长的限制，大多数地面引力波探测项目仅能探测到10 Hz 以上频段。20 世纪 90 年代以来，空间引力波探测计划使得探测0.1 mHz～1 Hz 频段丰富的引力波源成为可能[3]。其采用外差干涉测量技术，由3 颗相同卫星组成非独立的夹角为 60°的迈克尔逊干涉仪，如图1 所示，测量间距百万公里级别的两自由悬浮测试质量间10 pm 量级的变化量[4]。国际上，欧洲空间局(ESA)的激光干涉空间天线LISA 计划已于2015 年将关键技术验证卫星LISA-Pathfinder 送上太空，展示了惊人的性能[5]；国内则有由中山大学牵头发起的“天琴计划”[6]和由中国科学院与欧洲航天局合作发起的“太极计划”[7]。

图1 空间引力波探测系统示意图[4]Fig.1 Schematic diagram of the space gravitational wave detector[4]

在空间引力波探测计划中，引力波望远镜是激光干涉测量系统的重要组成部分，起到激光信号收发与扩缩束的作用，它由多个复杂光学表面构成，不同于传统的几何成像望远镜，除了具备大倍率、高像质、杂光抑制能力强、波前误差一致性好的一系列技术要求外，其波前质量及稳定性直接影响收发信号的强度及相位分布，从而影响引力波信号的解算精度，因而有着pm 量级的光程稳定性及苛刻的杂散光要求[8]。以LISA 项目为例，其设计的望远镜系统采用离轴无焦四反系统结构，如图2 所示。其中主镜 M1 是离轴抛物面，次镜 M2 为离轴双曲面，后面的三镜M3 和四镜 M4 为平面或球面，系统在 M2 和 M3 之间设计有一次像面，在此位置设置消杂光光阑可以有效抑制杂散光[9]。

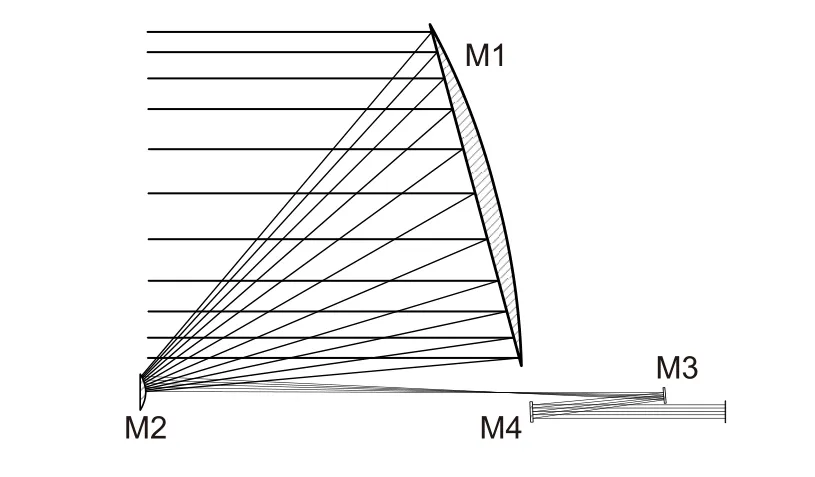
图2 引力波望远镜光学结构示意图[9]Fig.2 Schematic diagram of the optical structure of the gravitational wave telescope[9]

在激光信号发射端，望远镜系统将高斯光场进行扩束中继，出瞳处的近场复振幅光场信息作为超长空间链路的输入，若不考虑光场的矢量特性导致出瞳处相位、振幅分布计算产生误差，会对接收端远场振幅、波前与光程稳定性的仿真产生影响，降低远场波前指标评价合理性。在接收端，望远镜出瞳波前误差与抖动光程(tilt-to-length，TTL)噪声耦合，成为探测系统第二大噪声源。为控制噪声需采用复振幅计算相位信息[8]，对望远镜波前误差与光束抖动角耦合关系进行研究。若该仿真过程存在误差，会对噪声控制产生影响，劣化干涉测距解算稳定性，反过来影响系统设计指标分解有效性。

尽管基于几何光学仿真的光学设计已经可以将引力波望远镜系统的设计波前质量与全视场波前稳定性优化至低于1/30 波长RMS[9]，现阶段的光学设计并未考虑激光作为高斯光束在光学系统中的光场传输特性。从物理光学角度出发，光阑尺寸与位置、各元件结构与表面参数等都会影响光场衍射传输过程，不同性质的激光光束甚至不同参数高斯光场经过特定系统传输后的其特性也会有所不同[10]。特别地，由于偏振光场的矢量特性和离轴光学系统非近轴传播特点，望远镜出瞳处偏振光场的相位分布会呈现与几何光学的波前分布不同的特点，复振幅光场更携带了几何光学没有的信息。因此更应考虑真实边界条件对于光场作用，采用严格的矢量衍射计算，使仿真贴合物理情形。

本文论述了在空间引力波望远镜系统仿真需求中进行严格矢量衍射光场传输计算的必要性，基于矢量光线追迹衍射积分算法 (vectorial ray-based diffraction integral,VRBDI)建立了矢量光场衍射仿真计算程序，将一离轴无焦四反空间望远镜设计参数作为模型，对程序波前计算精度进行了验证，展示了光场仿真计算结果。基于该系统模型，对输入高斯光场参数、元件表面复折射率两个因素可能对输出光场矢量特性带来的影响进行了仿真讨论。

2 引力波望远镜光场衍射算法与模型

在空间超长链路激光干涉测量系统中，望远镜系统出瞳处的复振幅光场及其相位、光程稳定性密切影响着耦合进入接收端干涉系统的远场波前振幅与TTL 噪声控制水平，进而影响干涉测量的准确性和系统指标分解有效性。因而对于高斯光束在望远镜系统内部的衍射传输过程，使用高精度、全接口的算法进行精密的光场仿真分析非常必要。本章通过讨论不同衍射理论适用范围及其局限性，说明了在空间引力波望远镜系统仿真场景中基于偏振光线追迹进行严格矢量衍射光场传输计算的必要性，论述了VRBDI 算法的可行性，结合望远镜系统进行了算法具体流程的阐述。

2.1 不同衍射理论适用范围与局限性

对于像差光学系统，根据是否考虑光场矢量特性，其光场传输算法可分为标量与矢量衍射理论。对于矢量衍射理论，根据系统复杂度、元件类型、计算精度要求等可细分更多的具体算法。在一定的条件下，标量衍射理论可用于某些简单光学系统的设计和分析。然而当傍轴近似条件失效时，与近轴标量衍射理论相比，矢量衍射理论显然更为严格，它考虑了偏振与非近轴传播，是研究具有高数值孔径、离轴系统或使用特定偏振的光学系统的理论基础[11]，例如光刻系统、激光直写系统、自适应光学等领域。

矢量衍射积分计算需要被积分面(如出瞳)的边界和光场信息，对于简单的聚焦光学系统，可以基于几何参数近似计算边界场参数，例如基于Debye 近似的Richards-Wolf 矢量衍射理论[12]等。然而对于光束传播过程中会经过离轴、偏振化表面的系统，其具体光场的边界信息需要通过光线追迹得到。Foreman 等采用3×3 琼斯矩阵三维偏振光线追迹[13]的方法进行矢量衍射计算，对于一些简单的光学系统，例如平面镜、棱镜式折反系统等[14]，它能够不进行完善的光线追迹从而简单地实现对瞳孔处的光场有效计算[15]。然而对于复杂光学系统，这种方法缺少对于每个特定光束在具体边界处的角度、符号等信息，会导致计算不准确。Denis 等在Richards-Wolf 积分形式上进行了扩展，研究了任意形状旋转对称曲面的非近轴聚焦精确矢量模型[16]。但其建立在光瞳坐标系下，对于光场与元件形状参数非旋转对称的离轴系统，该方法不能准确表征每个矢量光场分量在特定表面上的作用情况。表1 总结了不同衍射理论适用范围与各自局限性。

表1 不同衍射理论适用范围与局限性Table 1 Application scope and limitations of different diffraction theories

作为对于光瞳处矢量光场分布有高精度解算需求的空间望远镜系统，其并非经典聚焦成像系统，且元件具多种面型，没有统一的衍射计算解析表达式。其次作为非旋转对称的离轴系统，处理过程中不能使用旋转对称系统常用的柱坐标系，对于不同空间位置光场或元件需要基于直角坐标系进行处理。因而，将严格的三维直角坐标系下偏振矩阵光学与高精度矢量衍射积分计算结合，进行系统内部矢量光场传输的精确计算十分必要。

2.2 望远镜系统模型算法流程

综合上节分析，基于矢量光线追迹的衍射积分(VRBDI)算法[17-19]是一种适用于空间引力波望远镜系统内部矢量光场衍射传输计算的方法。VRBDI 考虑了系统各元件的精确几何形状、边界参数以及输入矢量电磁场等多参量接口，能够模拟复杂光学系统内部矢量偏振光场非傍轴传播过程。该算法以偏振矩阵光学和矢量射线追迹为基础，将输入平面上的单色连续波电磁场进行平面波分解，用一个同时包含几何特性与偏振特性的三维偏振射线矩阵表征一个矢量平面波分量，进而对光线与场分量通过整个光学系统进行序列的跟踪计算，最后在设置的输出平面上进行分量复振幅场的合成，从而实现光学系统内部矢量光场衍射传播的仿真分析。

将VRBDI 算法应用于空间引力波望远镜中，仿真矢量光场经过整个光学系统衍射传输过程，最终得到输出探测面上的矢量光场分布，如图3 所示。

图3 引力波望远镜系统模型算法流程示意图Fig.3 Schematic diagram of the algorithm flow of the gravitational wave telescope system model

首先在输入面上对于输入矢量光场进行傅里叶变换，得到各角谱平面波分量，对于各个分量在输入面上进行采样，得到具有几何光线信息和光场复振幅信息的微分光矢量矩阵。在经过了坐标变换的各局部坐标系下建立对应元件与探测面，根据序列光线追迹原理，对每个光矢量分量进行从输入面到M1 反射面的几何追迹，在M1 反射面边界上进行光矢量计算，得到与边界作用后的光矢量分量。依据系统M1、M2、M3、M4 元件次序，在各个界面间进行光线追迹和光矢量迭代计算，最终在输出探测面上进行各角谱分量的衍射积分合成，得到输出面上矢量光场分布。

3 望远镜系统模型光场仿真

基于VRDBI 算法编写了仿真程序，建立了光学系统内部严格矢量光场衍射传输计算模型。该模型输入量有输入面和探测面全局坐标、输入矢量光场、系统参数、各元件参数等，输出量为探测面矢量光场复振幅。本章将空间引力波望远镜系统设计参数输入仿真模型，进行了理想设计波前的计算验证与光场仿真计算。

3.1 空间望远镜光学设计结构

结合空间引力波望远镜的设计要求，在商用光学设计仿真软件ZEMAX 中设计并优化了缩束比1：100，入瞳直径300 mm 的四镜离轴无焦系统，如图4 所示。考虑到空间望远镜光机结构与杂散光抑制等要求，口径300 mm 的光阑设置于主镜M1 前100 mm 处。获取各系统参数与元件参数输入仿真程序，将其作为波前与衍射光场仿真模型，主要参数如表2所示。

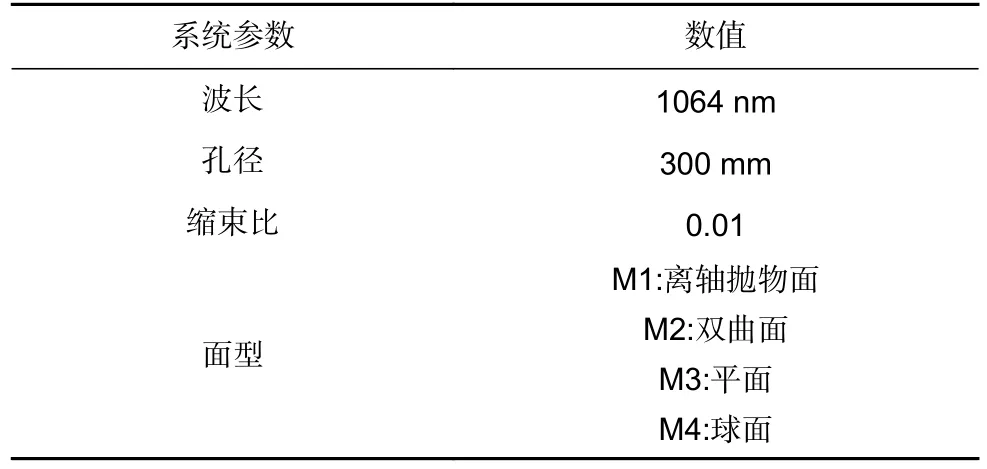
表2 望远镜系统主要参数Table 2 Main parameters of the telescope system

图4 望远镜系统结构示意图Fig.4 Schematic diagram of the telescope system structure

由于空间望远镜光学系统设计与优化传统逻辑为主镜开始至次镜再到M3、M4，设计得到的为接收望远镜端光学结构，第二节涉及的仿真内容主要为针对发射望远镜进行光场仿真与计算，因此在程序中首先进行系统倒置处理，得到发射望远镜系统结构，再进行后续的仿真计算。

3.2 波前与光场仿真计算

在0 度视场下对于倒置望远镜系统进行光程数据的计算，得到光程数据可作为系统波前的参考。在商用光学设计软件ZEMAX 中通过接口批量调用操作数，以获取内置程序计算得到的光线数据，将其作为光程计算数据的参考，对光场计算程序的波前计算精度进行验证。图5(a-c)分别为全局坐标出瞳位置下光程仿真程序计算、ZEMAX 光程计算结果、两者作差的xy二维伪彩图，其中图5(a)、5(b)共用颜色坐标。

图5 零视场下发射望远镜在出瞳光程数据。(a)光场仿真程序计算结果；(b)仿真软件ZEMAX 光程计算结果；(c)两者作差Fig.5 Optical path data at the exit pupil of the transmitting telescope at the 0 degree field angle.(a) Calculation results of the optical field simulation model;(b) Calculation results of the simulation software ZEMAX;(c) The difference between (a) and (b)

比较两个光程数据分布图，其分布一致，作为波前分布计算PV 值为0.0214λ，RMS 值为0.00496λ。从作差图看，两者差值在10-6pm 量级，验证了光场仿真模型程序的光程计算精度。

将高斯光束光场作为输入经过望远镜系统得到光场输出，展示仿真程序计算有效性。设置束腰半径1 mm，束腰位置处于输入面上的X线偏高斯光场，在设计出瞳位置即输出面进行400 mm×400 mm 尺寸的光场探测。图6 为输入面高斯光场强度分布，图7为仿真计算得到经过发射望远镜系统的输出面矢量光场分布结果。

图7 仿真计算输出面矢量光场分布。(a)光强分布图；(b) X 偏振分量振幅分布图；(c) X 偏振分量相位分布图Fig.7 Vectorial optical field distributions on the output surface of simulation calculation.(a) Intensity distribution map;(b) X polarization component amplitude distribution map;(c) X polarization component phase distribution map

在图7(c) 中，X偏振分量相位分布图区别于波前，单位采用弧度(rad)，进行比较可以发现X偏振分量相位分布与出瞳光程数据计算的波前分布趋势大致相同，振幅基本符合经过系统截断后高斯光场的振幅分布形式。计算相位分布图PV 值与RMS 值分别为0.1320 rad 和0.0302 rad，对应到波长值为0.0210λ和0.0048λ，相比使用几何光线追迹得到的波前分布结果略微降低。从光场分解角度看，几何光线追迹等效于单个理想平面波，而高斯光场在入射面上将分解为发散的多个平面波组合，该光学系统设计并非理想无光焦度，实际上存在微小的正光焦度。对于高斯光场情况，其发散降低了系统对光束的会聚作用，使其相位分布相比理想几何光线追迹产生变化。

4 光场矢量特性仿真影响

上一章基于空间引力波望远镜，进行了特定参数、理想X线偏高斯光场输入下输出复振幅光场的仿真。但在实际工程环境中，激光器性能、前置系统稳定性、环境动态变化等因素都会导致输入光场具体分布发生变化，进而影响输出光场复振幅。对矢量光场进行完善仿真需考虑各偏振光场分量，当光场与系统作用的边界条件发生变化时，特别的，不同元件材料对应表面复折射率有所区别，出射光场的矢量特性也将产生相应变化。本章基于系统仿真模型对于以上两方面进行了讨论，仿真了高斯光场参数变化对发射望远镜出射光场振幅和相位分布影响，并以表面材料金属铝为例比较了其与理想反射情况下出射光场XY偏振相位分布的变化。

4.1 输入高斯光场参数对发射望远镜出射光场影响

在实际工程中，激光高斯光束作为发射望远镜的入射光场，其参数可能存在不确定性，随环境温度等也可能发生动态变化，出射光场也会因此产生一定变化。利用仿真系统模型，改变输入二维高斯光场的参数，仿真该情形下出射光场变化及其规律。在定义输入二维高斯光场时，两个重要的参数为高斯束腰半径ω0和 束腰距离zω，束腰半径定义了光束的光斑尺寸大小，束腰距离为束腰位置到输入面的距离，zω=0时代表束腰恰好处于输入面上，正值代表在输入面上是发散光束，负值则代表聚焦。

在输入面上设置X线偏、峰值振幅归一化高斯光场，对于3 mm 输入口径的发射望远镜系统，分别进行两组情况仿真。设置束腰半径为1 mm 不变时，对束腰距离从-80 mm 至200 mm 进行8 组等间距采样，仿真得到输出光场振幅和相位分布随束腰距离变化，如图8、图9 所示。设置束腰距离为200 mm 不变时，对束腰半径从0.8 mm 到2.2 mm 进行8 组等间距采样，仿真得到输出光场振幅和相位分布随束腰距离变化，如图10、图11 所示。

图8 输出光场振幅分布随束腰距离变化(单位：V/m)Fig.8 The amplitude distributions of the output field change with the waist distance (unit: V/m)

图9 输出光场相位分布随束腰距离变化(单位：rad)Fig.9 The phase distributions of the output field change with the waist distance (unit: rad)

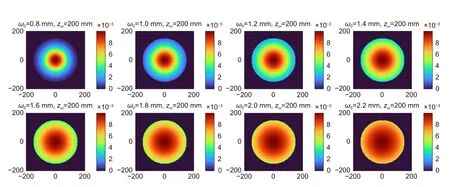
图10 输出光场振幅分布随束腰半径变化(单位：V/m)Fig.10 The amplitude distributions of the output field change with the waist radius (unit: V/m)

图11 输出光场相位分布随束腰半径变化(单位：rad)Fig.11 The phase distributions of the output field change with the waist radius (unit: rad)

比较束腰半径为1 mm 不变时输出光场随束腰距离变化，其振幅分布符合高斯光束被光阑截断后分布规律且变化较小，相位分布发生较明显变化。从数值统计上看，相位分布PV 值和RMS 值随束腰距离数值增大而增大，对应到波长值，束腰距离zω=-80 mm时PV 为0.0157λ、RMS 为0.0041λ，束腰距离zω=200 mm时 PV 为 0.0416λ、RMS 为0.0100λ。将其作为波前分布考虑变化规律，可以使用低阶Zernike 多项式进行拟合，发现其明显变化项为Z5(离焦)项系数。做出其曲线变化图如图12(a) 所示，Z5 项系数绝对值随束腰距离数值等间距增大而增大，且在仿真范围内近乎呈线性，其中Z5 项分布形式如图12(c)所示。

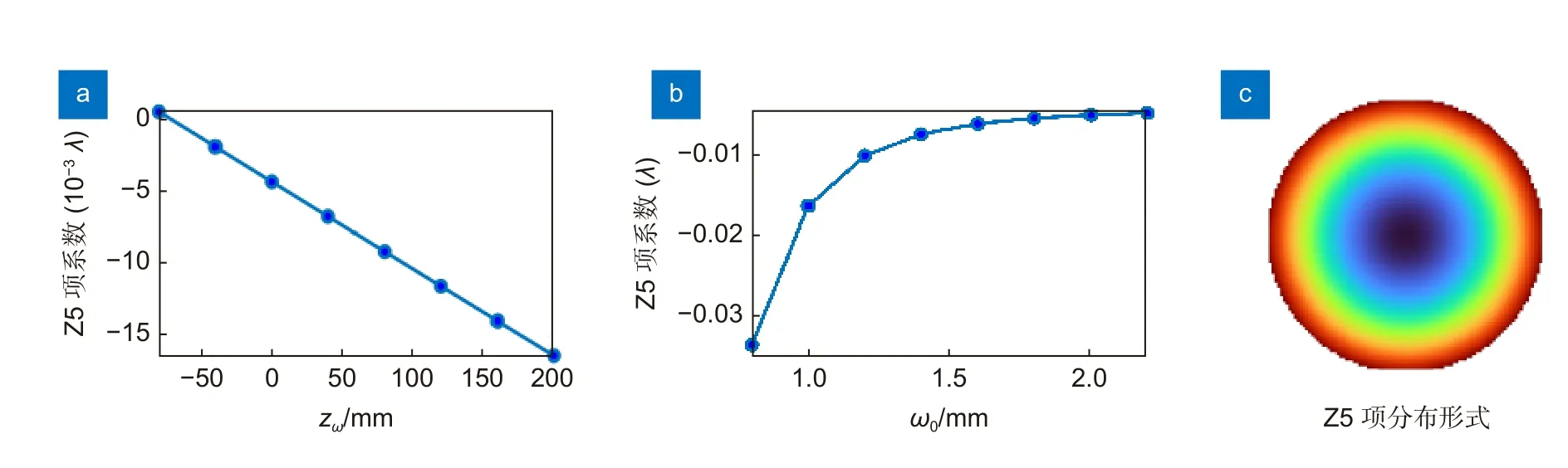
图12 Z5 项系数变化。(a)相位分布中Z5 项系数随束腰距离变化；(b)相位分布中Z5 项系数随束腰半径变化；(c) Z5(离焦)项分布形式Fig.12 The changes of Z5 coefficient.(a) Z5 coefficient in the phase distribution changes with the waist distance;(b) Z5 coefficient in the phase distribution changes with the waist radius.(c) Z5 (defocus) term distribution form

比较束腰距离为200 mm 不变时输出光场随束腰半径变化，其振幅分布符合高斯光束被光阑截断后分布，且随着束腰半径增大，经过系统传输后保留的能量比值逐渐降低。从数值统计上看，相位分布PV 值和RMS 值随束腰半径值增大而减小，对应到波长值，束腰半径 ω0=0.8 mm 时PV 为0.0750λ、RMS 为0.0198λ，束腰半径 ω0=2.2 mm时PV 为0.0218λ、RMS 为0.0050λ。将其作为波前分布考虑变化规律，进行低阶Zernike 多项式拟合，发现其在Z5 项系数上也有明显变化。做出其曲线变化图如图12(b) 所示，Z5 项系数绝对值随束腰半径等间距增大而减小，在仿真范围内变化梯度逐渐降低。

4.2 表面复折射率对出射光场相位分布影响

在本节前对于望远镜系统的仿真将四镜元件均视为理想反射镜，将光场在其界面上的作用视为理想反射。然而在实际工程中，为提高大型空间望远镜系统性能，反射镜元件表面往往需进行镀膜处理。相比于介质膜，金属膜能有效提升元件在特定波段反射率，但其会对光场偏振特性产生一定影响，即相比于理想反射情况的输出复振幅光场会产生变化。

为使仿真贴合实际情况，特别是在偏振矢量光场情况下计算发射望远镜出瞳光场精确偏振相位分布，在仿真模型中设置表面复折射率接口，对相应复折射系数与光场界面作用公式进行修正。介质的折射率一般是一个正实部，而金属的折射率是复数，由负实部和比较大虚部组成。以金属铝为例，该材料在望远镜系统工作波长1064 nm 下复折射率nAL=1.373-7.618 i。设置发射望远镜的入射高斯光场束腰半径为1 mm，束腰距离为0 mm，考虑X、Y偏振分量振幅比值为1 :1 的情况，仿真理想反射与铝镜两种情况下出射光场X、Y偏振分量的相位分布情况，得到X偏振相位分布如图13 所示，Y偏振相位分布如图14 所示。其中(a)为理想反射情况下两偏振分量相位分布，(b)为铝镜反射情况下两偏振分量相位分布，(c)为铝镜反射与理想反射情况下相位分布之差。

图13 出射X 偏振光场相位分布。(a)理想反射情况下X 偏振相位分布；(b)铝镜反射情况下X 偏振相位分布；(c) X 偏振分量铝镜与理想反射下相位分布之差Fig.13 Phase distributions of the output X polarization field.(a) X polarization phase distribution under the ideal reflection;(b) X polarization phase distribution under the aluminum mirror reflection.(c) The difference in X polarization phase distribution between the aluminum mirror reflection case and the ideal reflection case

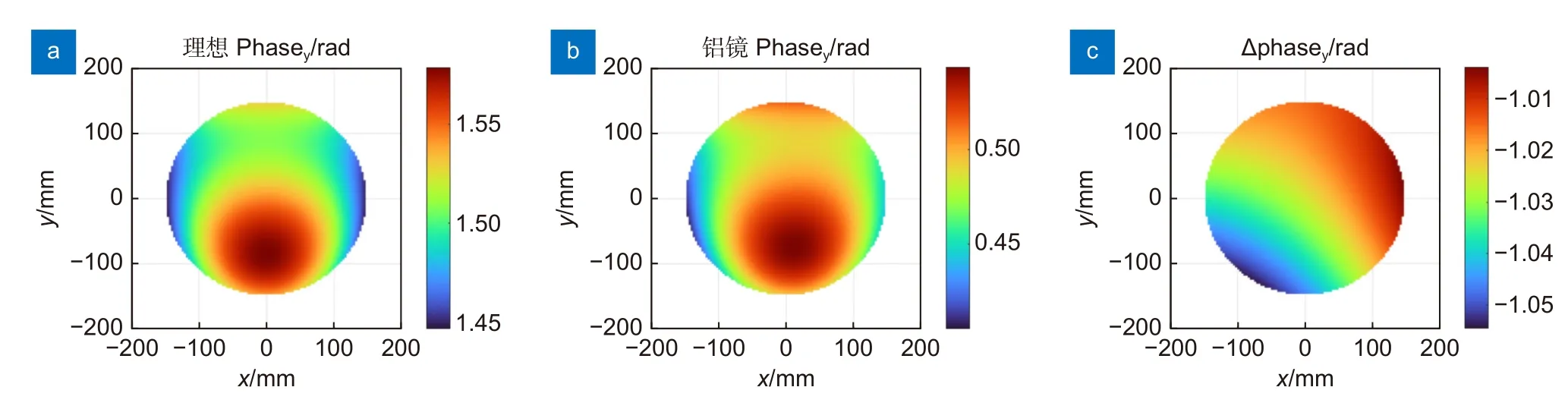
图14 出射Y 偏振光场相位分布。(a)理想反射情况下Y 偏振相位分布；(b)铝镜反射情况下Y 偏振相位分布；(c) Y 偏振分量铝镜与理想反射下相位分布之差Fig.14 Phase distributions of the output Y polarization field.(a) Y polarization phase distribution under the ideal reflection;(b) Y polarization phase distribution under the aluminum mirror reflection;(c) The difference in Y polarization phase distribution between the aluminum mirror reflection case and the ideal reflection case

可以发现理想反射情况下X、Y偏振分量的输出相位分布趋势与第三章中仅仿真X偏振分量时输出相位分布保持一致。比较理想情况与铝镜反射情况下两偏振分量相位分布趋势，均发生了明显变化。从数值统计上看，X偏振分量相位分布PV 值由理想情况下0.0210λ上升到0.0260λ，RMS 值 由0.0048λ上升到0.0059λ；Y偏振分量相位分布PV 值由理想情况下0.0210λ上升到0.0221λ，RMS 值 由0.0048λ下降到0.0043λ。图13(c)、图14(c)分别展示了X、Y偏振分量在铝镜与理想反射下输出相位差值分布趋势，对其进行低阶Zernike 多项式(Z1-Z15)拟合得到图15，条形图蓝色和红色代表X和Y偏振。两偏振分量相位差值分布Zernike 项主要集中在Z2(x倾斜)、Z3(y倾斜)、Z4(0 度像散)、Z6(45 度像散)，其中两分量相位差值Z2、Z3 系数绝对值大小相近，Z2 项均为正值，Z3项正负相反，Z4、Z6 系数绝对值大小相近，Z4 项正负相反，Z6 项均为负值。

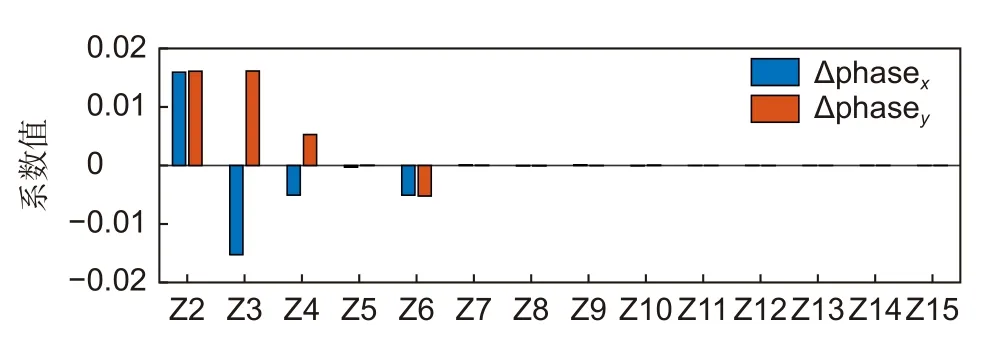
图15 X、Y 偏振相位差值分布Z2-Z15 项系数比较图Fig.15 Comparison of Z2-Z15 coefficients of the X and Y polarizations phase difference distribution

5 结论

在空间引力波激光干涉测量系统中，发射望远镜系统出瞳处的复振幅光场与光程稳定性密切影响着耦合进入接收端干涉系统的远场波前与振幅，进而影响干涉测量的准确性；同时在接收端，望远镜系统出瞳相位分布与TTL 噪声控制水平密切相关，忽略光场矢量特性导致的相位仿真误差将降低噪声控制指标分解的可信性。对于望远镜系统内部的矢量光场衍射传输高精度仿真需求，本文基于矢量光线追迹衍射积分算法编写了程序，将一空间引力波望远镜初始设计作为系统模型参数输入，对出瞳波前进行了仿真，与商用光学仿真软件ZEMAX 结果进行比较，验证了仿真程序10-6pm 量级的光线追迹计算精度，设置了特定参数输入高斯光场，进行了光场仿真计算结果的展示。对于可能导致输出矢量光场仿真偏差的两个因素，输入高斯光场参数与元件表面复折射率，进行了一系列仿真讨论，展示了输出光场矢量特性随高斯光束束腰半径、束腰距离两参数的变化规律，比较了元件表面为金属铝材料时输出X、Y偏振分量相对理想反射时的矢量特性变化。