基于夏克-哈特曼传感器的星载望远镜波前测量技术研究

位希雅，宋奇林，杨金生，张兰强，李 杨，黄林海，顾乃庭，饶长辉*

1中国科学院自适应光学重点实验室，四川 成都 610209；

2中国科学院光电技术研究所，四川 成都 610209；

3中国科学院大学，北京 100049；

4中国科学院大学电子电气与通信工程学院，北京 100049

1 引言

从1915 年爱因斯坦提出广义相对论并预测引力波的存在[1]，到2015 年LIGO 实验团队实现引力波的首次直接探测[2]，标志着引力学领域经历了一场前所未有的革命。作为一种由物质和能量剧烈运动和变化产生的物质波，引力波不仅能够揭示以往无法探测的宇宙事件，还为研究黑洞、中子星等天文难题提供了崭新的手段，并推动了力学、物理学等多个领域的突破与发展[3-5]。激光干涉仪因其高灵敏度和宽频响应等特点，在引力波多种探测方法中脱颖而出，成为主导技术[6-7]。由于地面探测受地表振动等多种限制因素的影响，探测频段非常有限，使得空间引力波探测尤为重要。到目前为止，只有LIGO[8]和VIRGO[9]这两大引力波探测器成功捕获到引力波，但多国已经开始筹划建设新的地基和空间引力波探测器[10-12]，如中国的天琴计划已明确提出在2035 年发射引力波天文台的目标。星载望远镜是其核心组件，需要具备强大的干涉测量、激光发射、接收以及高精度跟踪能力，以保证对引力波事件的准确测量和探测[13]。

引力波引发的光程变化极为微妙，导致引力波探测要求具有pm 甚至fm 量级以下的灵敏度。探测过程中，机械应力或振动以及温度变化等因素导致的波前像差成为一大挑战。波前像差直接干扰了经过数十万公里传输后的远场光斑的能量分布和空间位置，制约了干涉质量，进一步影响引力波探测的性能。因此，需要将波前像差对引力波探测精度的影响降至最低。天琴计划计划采用偏轴望远镜设计，在通光口径为220 mm，波长为1064 nm 的情况下，能够达到满足λ/300 的波前像差测量精度[14]。LISA 计划使用多块相同镜片，通过精确的对准技术，确保星载望远镜达到满足任务要求的光学波前误差标准[15]。目前地面上的波前像差测量手段有剪切干涉仪[16]、哈特曼传感器[17]、曲率传感器[18]和棱锥传感器[19]等，其中哈特曼传感器原理简单，技术成熟，且易实现，在多个领域得到了广泛应用[20-21]。

本文使用夏克-哈特曼波前传感器进行星载望远镜的波前像差测量，探测精确度的关键因素在于质心位置的确定。传统的质心算法常被用于定位光斑的质心位置，但光斑的非均匀强度分布、变化以及多种噪声等因素都可能严重影响其测量精确度[22]。为应对这些问题，研究者引入了多种优化算法，如去阈值质心算法(thresholding centroid algorithm,TCoG)、加权质心算法(weighted centroid algorithm,WCoG)和四分之一像元算法(quarter cell,QC)[23-24]等。2009 年，马晓燠等人[25]深入探讨了去阈值质心算法的阈值，成功为质心算法推导出最佳阈值。

相比于质心算法，相关算法在抑制噪声上更为出色，并具有良好的图像适应性。常见的相关算法有互相关算法(cross-correlation function,CCF)，绝对差分算法(absolute difference function,ADF)及频域上的互相关算法(cross-correlation function in frequency domain,CFF)等[26-30]，每种相关算法都代表不同的图像匹配相似度。2003 年，Poyneer[31]提出将频域上的互相关算法用于夏克-哈特曼波前传感器波前探测，并证明了其对噪声的高鲁棒性以及受光斑尺寸影响小的优势。Li 等人[32]的研究显示，在常见的相关算法中，频域上的互相关算法在波前测量精度上表现最佳，且具备出色的运算速度。

基于以上背景，本文提出一种基于夏克-哈特曼波前传感器原理的波前像差的高精度测量方法。该方法采用了频域上的互相关算法，并对其进行频域阈值去噪。与传统的质心算法相比，该算法的测量精度更高，为空间引力波星载望远镜地面波前像差的高精度测试提供了重要参考。本文第二节详细介绍了星载望远镜波前像差的测量原理。第三节利用实际的点源图像生成了已知RMS 离焦值后，结合频域上的互相关算法和去阈值质心算法进行了偏移量测量及波前复原。通过计算复原后的离焦值以及生成波面和残余波面的均方根值(RMS)，验证了频域上的互相关算法的测量精度。第四节对全文进行了总结与讨论。

2 星载望远镜波前像差测量原理

以天琴计划的星载望远镜为例，其光学布局设计如图1 所示，由一个大的抛物面主镜和三个非球面次镜组成[33]。天琴计划设计三颗卫星组成的等边三角形阵列，每个卫星之间的距离约为17 万公里，它们之间相互发射和接收激光。当引力波经过这三个卫星的区域时，会引起卫星之间距离的微妙变化。然而，望远镜在太空中会受到各种外界因素的影响。温度的变化、太空操作以及长时间运行后的机械老化和热效应，如热膨胀等，都可能导致机械应力、震动或微小的结构变化。这些因素都可能引起波前像差，对引力波的探测造成直接的影响[34-35]。

使用夏克-哈特曼波前传感器，能够实现对波前像差的精准测量和复原[36]，其工作原理如图2 所示。微透镜阵列将入射光波分解为多个子光波，在阵列透镜的作用下对波前进行分割采样。在子孔径分割过程中，子孔径内的光波波前被等效为带有倾斜平面的波前。根据每个子孔径中光线达到探测器的位置与理想位置之间的差异，可以计算出每个子孔径处的具体偏移量。每个子孔径都由多个像素组成，通过子孔径的复用，结合多个子孔径的偏移量信息推导在光波传播中的相位畸变信息。进一步生成相位补偿，并校正光学系统中的相位畸变，从而显著提升成像质量和系统的整体性能[37]。

图2 夏克-哈特曼波前传感器的原理Fig.2 The principle of the Shack-Hartmann wavefront sensor

微透镜阵列的巧妙设计确保每个子孔径能够捕获到目标不同位置的波前畸变。通过多个子孔径的测量，进一步提高波前像差的测量精度，显著提升夏克-哈特曼波前传感器子孔径光斑位置探测的信噪比及灵敏度，有效增强了整个系统的测量准确度和精度。

质心算法[38]为点源位置的估计提供了一种快速、有效的方法。在太空引力波探测中，由于望远镜接收到的信号为光斑图像，质心算法可以被用以实现波前像差的测量。以x方向为例，该算法的数学表达式为

式中：xc为x方向的质心位置，xij为像素位置，Nij表示子孔径内坐标(i，j)处的像素点接收到的光子总数，U,M则为子孔径窗口的大小。

在星载望远镜的工作过程中，光斑图像会受到如信号光子噪声、背景光子噪声、CCD 读出噪声以及离散采样误差等多种因素的影响[22]，这些干扰的存在会极大程度影响质心算法的测量精度。作为一种改进的质心算法，去阈值质心算法(以下简称为“质心算法”)旨在增强噪声和其他干扰因素下质心的测量精确度。该算法的核心思想是为光斑图像设定一个阈值，将图像中低于该阈值的强度部分视为噪声或背景，并在后续质心运算中将其排除，从而提高质心运算的精确度和鲁棒性。阈值的最佳选择为其中NB为 噪声的均值，σB为噪声的标准差。

和质心算法相比，相关算法具有更强的噪声抑制性，同时可以自适应地调节窗口尺寸，具有更出色的图像适应性。在夏克-哈特曼波前传感器中，相关算法常用于扩展目标的图像匹配。如图3所示，设实际图像为L，参考图像为R (由图中黄色框线标识的区域)。选定参考图像R 后，模版在实际图像中逐像素滑动。在每一个位置都会计算出模版和参考图像之间的相似度，通过找出和参考图像最高匹配相似度的位置，从而确定实际图像上的匹配位置。

图3 图像匹配原理图Fig.3 Image matching principle of correlation algorithm

本研究采用的频域上的互相关算法(以下简称为“互相关算法”)如式(2)所示：

式中：P(u,v) 表示位置(u,v)处的互相关函数值，F()代表傅里叶变换，F-1()代表傅里叶逆变换，L 代表实际图像，R 代表参考图像，*代表复共轭运算。为了减小噪声对相关算法计算精度的影响，对互相关算法进行了频域阈值去噪，阈值为信号均值加三倍的标准差。在获得匹配矩阵P后，由于图像像素的坐标以整数值表示，然而最佳匹配位置通常位于像素之间。因此，对算法进行亚像素插值运算，以确保对质心位置进行更精细的估计，进而获得更精准的匹配结果。亚像素插值的基本思想是对局部像素值进行插值处理，实现亚像素级别的位置估计。

Löfdahl 等人[39]采用仿真米粒图像进行实验，针对各种插值算法的计算精度进行了比较。研究结果表明，二维插值方法在精度上高于一维插值方法。本文使用二维抛物线插值方法来获取亚像素精度，通过构建如式(3)所示的二维抛物线模型，以匹配矩阵G的峰值点附近的数值为依据，将数据点代入该模型中，计算得到系数a1～a6，进而求解得到最小点坐标(xmin,ymin)，得到亚像素值，从而确保了更高精度的图像匹配。

波前复原使用Zernike 模式波前复原算法，对于哈特曼波前传感器，子孔径内的斜率数据G与Zernike多项式系数的关系为

其中：ak为第k项的Zernike 多项式系数，Zk为第k项Zernike 多项式，ϵx和 ϵy分别为波前相位在x和y方向的测量误差，m为子孔径数，n为模式阶数，Si为子孔径归一化面积。因此，2m个子孔径斜率，n项Zernike 系数的关系用矩阵可以表示为

要计算出波前相位，则要求解A，即Zernike 系数ak。对于任意的2m和n，上述方程的最小二乘解可用广义逆D+表示：

其中，Y为任意矢量。当Y=0 时，方程在最小二乘和最小范数意义下的解为

3 实验结果

为了准确评估互相关算法在点源图像上的计算精度，在实验室平台上搭建了夏克-哈特曼波前传感器的实验装置。实验光路图如图5 所示，激光器发出的点源信标直接进入波前传感相机，通过移动光源或相机的位置产生离焦像差。使用的微透镜的尺寸为0.279 mm×0.279 mm，其焦距为34 mm。实验中，我们选用了C8484-16C 型号的相机，该相机的位深为12 位，像素尺寸为 8.3µm×8.3µm。使用光源波长为532 nm，子孔径的数目为 20×16，其中，有效子孔径的分布如图6 所示，有效子孔径数为140 个，详细参数如表1 所示。

表1 微透镜阵列及相机参数Table 1 Microlens array and camera parameters

图5 实验平台光路图Fig.5 The optical path diagram of the experimental platform

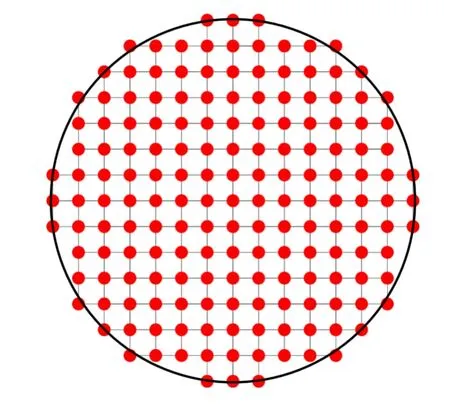
图6 点源图像的有效子孔径分布Fig.6 Effective sub-aperture distribution of the point source image

如图7 所展示的单个子孔径的点源图像中，CCD 光信号的分布范围约为 64 pixel×64 pixel，实际光信号分布约为3 0 pixel×30 pixel。选取如图7 中红色方框所示的3 2 pixel×32 pixel的区域进行质心偏移量运算。使用黄色框线所示的四个角区域来计算随机噪声大小，每个角区域的像素数为1 0 pixel×10 pixel，用b表示。

图7 单个子孔径图像及噪声计算区域(黄色框线内)和匹配区域(红色框线内)Fig.7 Individual sub-aperture image and noise calculation region(within the yellow box) and matching region (within the red box)

首先，使用标准平行光束照射夏克-哈特曼波前传感器微透镜阵列。此时，聚焦光斑展现出基本均匀的分布特点。记录图像并分别使用质心算法和互相关算法计算每一个聚焦光斑的中心坐标，这些中心坐标为各相应子孔径的参考基准零点位置。我们采集了100 帧图像，其中第w帧图像的信号强度用Ga(w)表示，这里a 代表角区域，表示第w帧图像的信号均值 。根据式(8)、式(9)分别计算每帧图像的噪声均值和 方差[40]。通过对这100 帧图像进行累加处理，求其均值，我们得到了零噪声图像，作为光斑质心偏移量测量的参考图像。

移动光源，根据光源移动距离，将其带入式(10)：

其中：f是焦距，D为子孔径尺寸，d是移动的距离，Δ为引入的离焦值[41]。移动的距离使用测微仪进行测量，其精度为0.01 mm。分别引入0.22 nm，0.44 nm和0.66 nm 的RMS 离焦值，并和原始未经离焦处理的图像，共组成四组数据，每组均包含100 个图像。这些离焦值会导致入射的光线产生相位差，从而在CCD 上生成具有偏移量的点源图像，产生波前像差。尽管这种方法无法真实模拟星载望远镜在太空中受到扰动引起的波前像差，但是通过生成离焦值引起波前像差，我们可以有效比较和筛选质心提取算法，评定其测量精度，并为空间引力波星载望远镜地面波前像差的高精度测试提供了坚实基础。

使用质心算法和互相关算法测定每组图像的光斑中心在x和y方向上的偏移量，进而计算得出整体偏移量。随后，对每帧图像分析其所有有效子孔径的平均偏移，并将各个离焦值下的平均偏移量绘制成如图8 所示。从图中可以看出，由于夏克-哈特曼波前传感器的子孔径复用和测量精度的差异，互相关算法和质心算法在每帧图像上的平均斜率存在差别，但总体上，变化趋势相近。值得注意的是，随着离焦值的增加，平均斜率依然保持着相对稳定性。

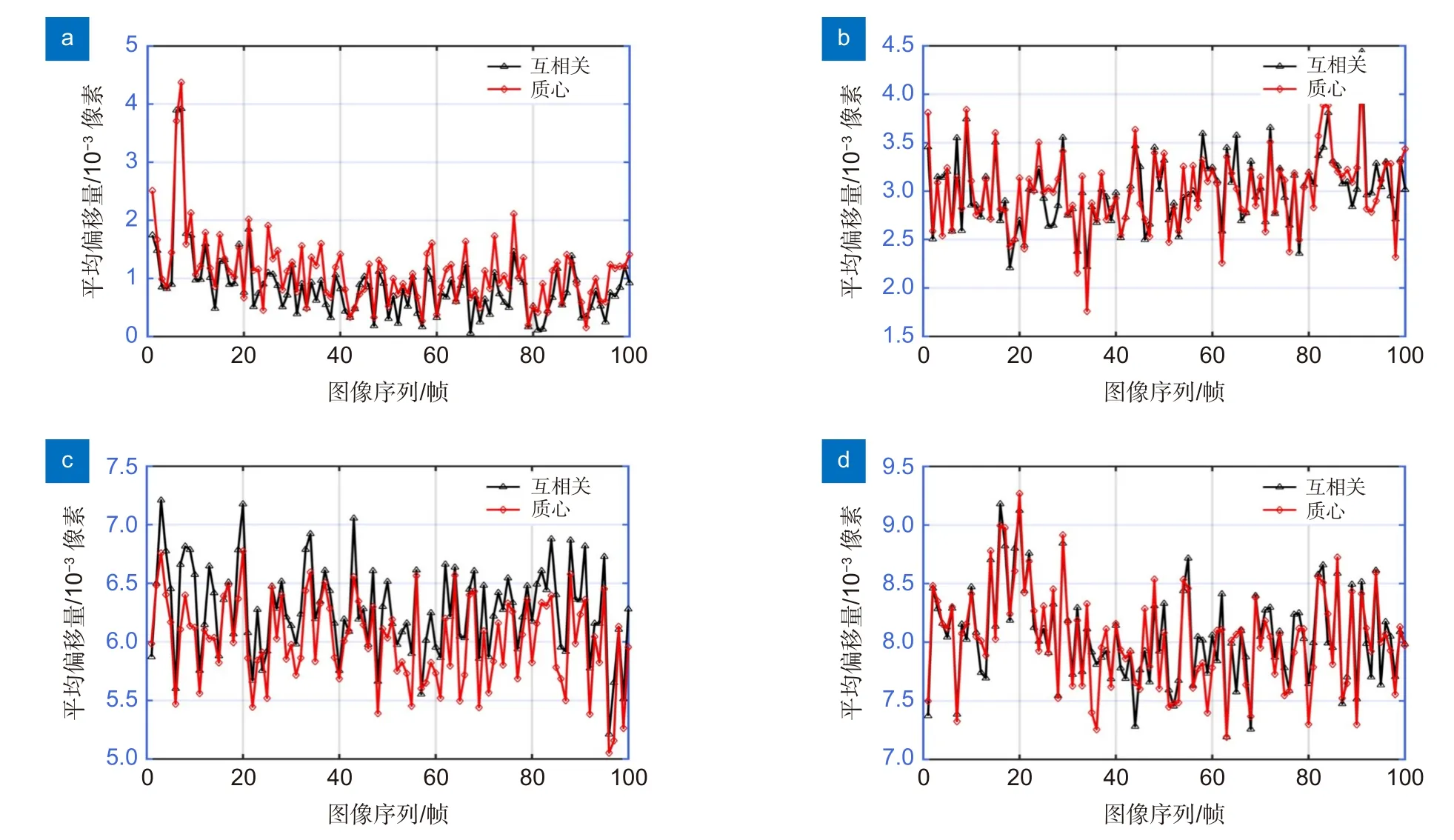
图8 互相关算法和质心算法在每帧图像上计算的平均斜率值。实际离焦值分别为(a) 0 nm，(b) 0.22 nm，(c) 0.44 nm，(d) 0.66 nmFig.8 The average shift measured on each frame image by employing the CFF and the TCoG algorithm.Defocus values are (a) 0 nm,(b) 0.22 nm,(c) 0.44 nm and (d) 0.66 nm

通过模式法复原波前像差，得到了Zernike 系数中的离焦值。在各种实际离焦值下，比较了两种算法在每帧图像上得到的离焦值及其平均值，结果如图9所示。橘色和绿色的虚线分别代表质心算法和互相关算法的复原离焦均值。从图中可明显地看出，无论在哪种离焦值下，互相关算法的复原离焦值都更接近实际值，其计算精确度显著优于质心算法。

图9 互相关算法和质心算法波在每帧图像上生成的Zernike 离焦值及平均值。实际离焦值分别为(a) 0 nm，(b) 0.22 nm，(c) 0.44 nm，(d) 0.66 nmFig.9 Zernike defocus values,and their average calculated on each frame image by employing the CFF and the TCoG algorithm.Defocus values are (a) 0 nm,(b) 0.22 nm,(c) 0.44 nm and (d) 0.66 nm

在使用模式法对波面进行复原后，对每组图像的每帧复原波面进行了平均，得到了平均复原波面。互相关算法和质心算法在不同离焦值下的平均复原波面如图10 所示。其中，图10(a-d)分别展示了质心算法和互相关算法在离焦值为0、0.22、0.44 和0.66 nm下的复原波面。我们也计算了复原波面的RMS，并在图中进行了标注。从复原的结果来看，随着离焦值的增大，两种算法均能够复原出离焦波面，但互相关算法的复原精度明显优于质心算法。

图10 互相关算法和质心算法通过复原后得到的平均复原波面。实际离焦值分别为(a) 0 nm，(b) 0.22 nm，(c) 0.44 nm，(d) 0.66 nmFig.10 The average reconstructed wavefront using the CFF and the TCoG algorithm.Defocus values are(a) 0 nm,(b) 0.22 nm,(c) 0.44 nm and (d) 0.66 nm

分别生成离焦值为0、0.22、0.44 和0.66 nm 的理想离焦值波面。通过将生成的复原波面与相应的理想离焦波面相减，生成了如图11 所示的残余波面。进一步计算了残余波面的RMS 值。结果显示，随着实际离焦值的增加，质心算法的测量误差呈现上升趋势，分别为0.0966、0.1378、0.1284 和0.1463 nm。频域上的互相关算法可以分别增加13%、7%、18%和14%的测量精度。因此，和质心算法相比，互相关算法具有更高的测量精度，这和我们在图10 中得到的结论一致。

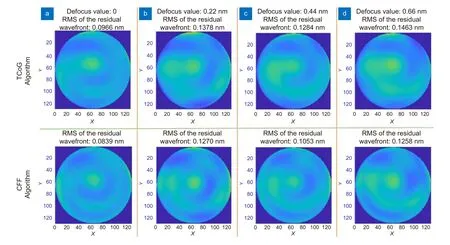
图11 互相关算法和质心算法通过复原后得到的残余波面。实际离焦值分别为(a) 0 nm，(b) 0.22 nm，(c) 0.44 nm，(d) 0 .66 nmFig.11 The residual wavefront generated using the CFF and the TCoG algorithm.Defocus values are(a) 0 nm,(b) 0.22 nm,(c) 0.44 nm and (d) 0.66 nm

由图4 可以得到，复原误差由波前空间采样误差、质心测量误差以及传感器的模式波前复原误差[42]。当光斑高斯宽度 σA大于0.5p(p为像素尺寸)时，质心探测误差均方根值小于0.02 σA，因此可以忽略离散采样误差[43]。由于我们使用的复原阶数为37 阶，子孔径数量高，模式波前复原误差约占波前总方差的不超过10%[44]。因此，复原误差主要由质心测量误差影响。

4 总结与讨论

本文深入探讨了在引力波探测中，精确测量星载望远镜波前像差的关键性。为了有效降低波前像差，提高星载望远镜的测量性能，进而提高引力波探测精度，本文提出使用夏克-哈特曼波前传感器进行波前像差的测量，使用频域上的互相关算法进行频域阈值去噪处理后，代替传统质心算法进行偏移量位置估计。通过对带有实际离焦值后的实际点源图像，使用频域上的互相关算法和去阈值质心算法进行斜率测量和波前复原后，得出了频域上的互相关算法的测量精度明显高于去阈值质心算法的结论，为空间引力波星载望远镜地面波前像差的高精度测试提供了重要参考。

本研究不仅深化了我们对波前像差在引力波探测中的理解，还探索了提升引力波探测的精度和准确性的新方法。通过采用基于夏克-哈特曼波前传感器原理的频域上的互相关算法，可以显著优化星载望远镜波前像差的测量精度，推动引力波的科学研究。然而，我们必须认识到，太空中星载望远镜所处环境的复杂性无法仅仅通过引入离焦值这类低阶像差来完全模拟，实际系统的像质更为复杂，未来应继续深入探索。