一种变转速电机转子-轴承系统故障智能诊断方法

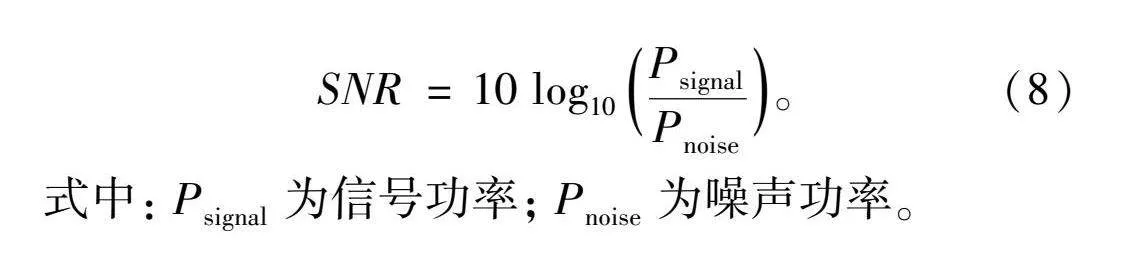
摘 要：针对变转速工况下电机转子-轴承系统的故障数据复杂和特征较难提取，提出一种角域重采样联合小波包去噪的时变信号处理方法和一种改进卷积神经网络。首先，利用角域重采样将时变信号变换为角域信号，再使用小波包软阈值法对信号进行去噪，去噪后信号作为深度学习模型输入；同时提出一种改进的第一层宽卷积核深度卷积神经网络，从卷积层、dropout和AdaBN等方面对故障诊断模型进行优化。基于自建实验平台开展正常、轴承故障、转子不平衡和转子弯曲4种状态下电机从0至1 800 r/min加速工况的模型训练，准确率均达到99%以上。在模型测试中，采用高斯白噪声、色噪声和随机均匀分布噪声并以单一和混合方式添加至测试集中，对7种加噪数据进行模型评估。结果表明，在噪声强度大于信号强度情况下，7种噪声的准确率均在76%以上；在噪声强度等于信号强度情况下，准确率均在84%以上；在噪声强度小于信号强度的情况下，准确率均在88%以上，证明所提方法具有强的抗噪性和鲁棒性。

关键词：电机；转子-轴承；变转速；故障诊断；角域重采样；小波包去噪；卷积神经网络

DOI：10.15938/j.emc.2024.11.018

中图分类号：TH113.1；TH17

文献标志码：A

文章编号：1007-449X（2024）11-0195-16

Intelligent fault diagnosis method of motor rotor-bearing system under variable speed conditions

FAN Hongwei^1，2， MENG Jin¹， REN Zhongfu¹， CAO Xiangang^1，2， ZHANG Xuhui^1，2

（1.School of Mechanical Engineering， Xi’an University of Science and Technology， Xi’an 710054， China; 2.Shaanxi Key Laboratory of Mine Electromechanical Equipment Intelligent Detection and Control， Xi’an University of Science and Technology， Xi’an 710054， China）

Abstract：Aiming at the complex fault data and difficult feature extraction of motor rotor-bearing system under variable speed conditions， a time-varying signal processing method based on angle domain resampling combined with wavelet packet denoising and an improved convolutional neural network were proposed. Firstly， the time-varying signal was transformed into angular domain signal by angular domain resampling， and then the signal was denoised by wavelet packet soft threshold method. The denoised signal was used as the input of deep learning model. At the same time， an improved first-layer wide convolution kernel deep convolution neural network was proposed to optimize the fault diagnosis model from the aspects of convolution layer， dropout and AdaBN. Based on the self-built experimental platform， the model training of the motor from 0 to 1 800 r/min acceleration conditions under four states of normal， bearing fault， rotor unbalance and rotor bending was carried out， and the accuracy rate is more than 99%. In the model test， Gaussian white noise， color noise and random uniform distribution noise were added to the test set in a single and mixed manner， and the model evaluation was performed on 7 kinds of noisy data.The results show that the accuracy of the seven kinds of noise is above 76% when the noise intensity is greater than the signal intensity. When the noise intensity is equal to the signal strength， the accuracy is above 84%. When the noise intensity is less than the signal strength， the accuracy is above 88%， which proves that the proposed method has strong anti-noise and robustness.

Keywords：motor; rotor-bearing; variable speeds; fault diagnosis; angular resampling; wavelet packet denoising; convolution neural network

0 引 言

转子-轴承系统是电机的关键部件之一，承载其连续高速运转，为机电设备提供所需运动和动力^[1]。在长期的变速、变载、温升、摩擦等作用下^[2]，电机转子-轴承系统极易发生机械故障，如轴承裂纹、转子弯曲等。如对电机的机械故障不进行及时准确的诊断，势必造成其机械结构上的不可逆损坏和服役性能的快速恶化，最终引发整台设备的计划外停机和重大经济损失。因此，对电机的转子-轴承系统进行故障诊断具有重要意义^[]。

目前，机械故障诊断广泛采用振动信号，信号分析包括时域分析、频域分析和时频分析。其中，时域分析简单，用于初步判断设备是否有故障发生，常采用均方根值、平均值、峭度、波形系数等作为评判指标^[4]。频域分析是将时域信号变换为频谱图像进一步观测信号的频率构成，常用方法是傅里叶变换。时频分析用于研究信号频谱随时间变化规律，常用的分析方法有小波变换^[5]、稀疏分解^[6]和经验模态分解^[7]。上述方法在处理变转速信号时效果欠佳。目前，针对变转速信号的处理方法分为两大类：一是采用角域重采样将时域信号转变为角域信号进行分析^[8]，LU等^[9]使用角域重采样对电机故障特征进行提取并完成诊断；二是采用时频分析将一维信号转变为二维图像进行分析^[10]，从而完成变转速故障诊断，李东东等^[11]使用Fast Kurtogram时频变换将振动信号转换为图像完成故障诊断。

在信号分析的基础上，机器学习较早开始用于数据驱动的故障诊断，如ABBASION S等^[12]利用小波分析对电机振动信号进行降噪处理，再用支持向量机对故障进行诊断；ZHOU等^[1]提出了一种单类支持向量机对电机进行故障诊断；LIU等^[14]提出了改进的BP神经网络对发动机进行故障诊断。上述研究所采用的机器学习因算法结构简单、主要适用于恒定转速工况，对变转速等复杂工况效果欠佳^[15]。

由神经网络算法演化而来的深度学习具有更强的数据特征提取能力，能够实现更复杂工况下的故障诊断^[16]。目前，主流深度学习方法有自编码器^[17]、深度信念网络^[18]、卷积神经网络（convolutional neural network， CNN）^[19]和循环神经网络^[20]]等，其中机械故障诊断多采用CNN。初期，CNN用于图像识别；后来，一维卷积神经网络（1DCNN）被用于故障诊断。与2DCNN相比，1DCNN具有直接使用原始数据、计算效率高和结构简单等优势。EREN等^[21]提出了一种改进的自适应1DCNN，将特征提取与模式识别相结合用于增强特征提取能力，但未用于变转速工况。SUN等^[22]提出了一种1DCNN与LSTM联合方法，用于提高故障诊断性能，但算法叠加使模型臃肿。LIU等^[2]提出了一种多尺度核残差CNN，增强模型的视野范围和特征提取能力，但存在算法堆叠问题，增加运行成本。LU等^[24]提出了一种可解释轻量化1DCNN，用于变转速工况，该方法采用包络分析和快速傅里叶变换对变转速工况进行分析，能够提取大部分特征信息，但会丢失部分瞬时特征。JI等^[25]基于顺序跟踪算法和1DCNN对不同转速进行重采样，能够提取大部分特征信息，实现了变工况轴承故障诊断，但顺序跟踪算法高度依赖已知结果，在未知复杂工况下具有不稳定性，而等角度重采样可以解决这个问题。ZHANG等^[26]提出一种基于角度重采样的自适应模态分解在旋转非平稳信号分析中的增强方法，该方法在提取非平稳信号的时变特征具有有较大优势。ZHANG等^[27]提出了一种第一层宽卷积核深度卷积神经网络（WDCNN），性能显著提高，但未在变转速工况下应用。

工程实际中，噪声无处不在，学者们针对噪声展开研究。ZHAO等^[28]在高斯白噪声下利用注意力机制进行了转子故障诊断。ZHANG等^[29]利用有界噪声在低速下对轴承信号进行了特征提取。SHI等^[30]研究了乘性白噪声和加性色噪声在复杂系统中的影响规律。上述学者仅针对单一噪声进行研究，实际工作环境中噪声往往不止一种，有时多种噪声同时出现，需要研究不同噪声对故障诊断结果的影响，因此将采用高斯白噪声、色噪声和随机均匀分布噪声混合情况用于模拟实际工程环境。针对实际信号被噪声污染问题，WANG等^[31]引入自适应批量归一化即AdaBN算法改善了胶囊网络在噪声环境下的适用性，改善了模型的抗噪。

综上所述，针对电机转子-轴承系统在特征提取上存在部分特征丢失与算法不稳定性问题，在模型诊断上存在模型臃肿、适用性较窄问题，本文提出一种变转速下基于角域重采样和小波包去噪的1DCNN故障诊断方法。其中，采用角域重采样联合小波包去噪将时域非平稳信号变换为角域信号并完成信号去噪，有效避免特征丢失与算法不稳定性问题，将去噪后信号输入改进的1DCNN模型，改进模型增强了视野范围，避免模型臃肿问题，最后在不同类型的噪声下对该模型进行实验验证和评价。

1 总体研究方案

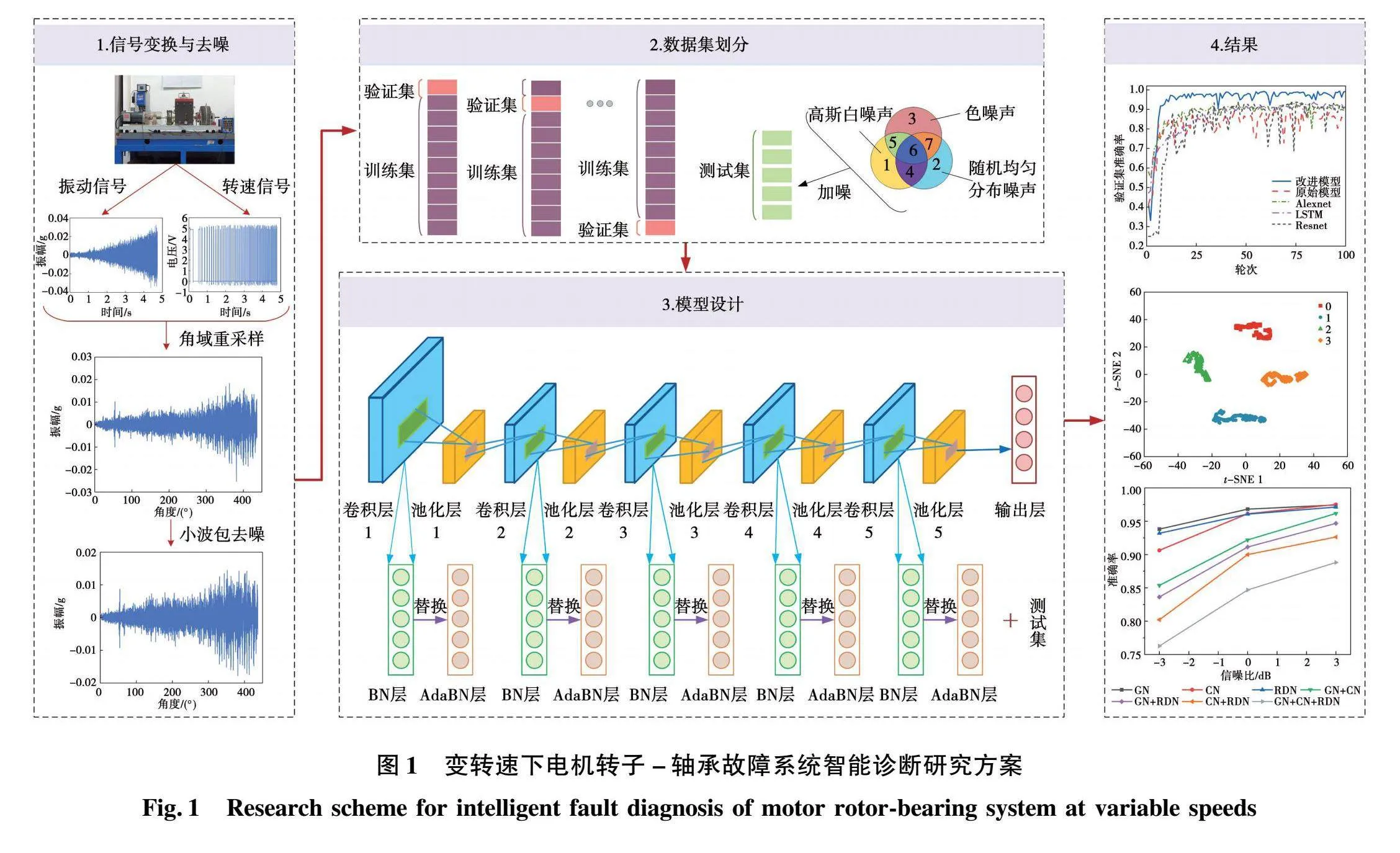
变转速下电机转子-轴承系统故障智能诊断的研究方案如图1所示，包括信号的域变换与去噪处理、深度学习模型设计和模型抗噪性验证。在信号的域变换与去噪处理中，首先对变转速下时域振动信号和转速信号采用角域重采样转换为角域信号，然后利用小波包软阈值法对变换后的信号去除噪声，使复杂时域非平稳信号变换为低噪声角域信号；其次，以上述信号为基础制备故障诊断的数据集，使用K折交叉验证进行切片划分，得到训练集、验证集和测试集，输入1DCNN中进行训练和验证；最后，使用训练集上所得最佳模型，联合AdaBN算法，对测试集上加噪数据进行模型抗噪性验证，考虑高斯白噪声、色噪声和随机均匀分布噪声及其混合出现的情况，完成对电机转子-轴承系统故障诊断方法的评价。

2 时变信号的域变换与去噪

2.1 基于角域重采样的时变信号的域变换

角域重采样的原理是利用转速信号对原始振动信号进行等角度重采样，使时变信号转变成角域信号。首先同步采集振动信号和转速信号，接着用转速脉冲拟合转角和时间函数关系，计算时间对应的角度，然后用插值法计算角度对应的信号幅值，得到等角度信号，最后用傅里叶变换得到阶次谱。对信号进行等角度重采样时，需根据电机转速及脉冲到来的时刻确定参考轴和时间关系。假设参考轴角加速度恒定，关系式为

θ（t）=a1+a2t+a3t2。（1）

式中：a1、a2、a3为系数；t为时间。

系数a1、a2和a3由三个连续上升的脉冲时间t1、t2和t3及其对应的转角增量0、Δθ和2Δθ计算。设电机转速为参考轴，电机每旋转一周产生一个脉冲即Δθ=2π。代入式（1）得

0Δθ2Δθ=1t1t211t2t221t3t23a1a2a3。（2）

根据式（2）确定任意角度对应的时间ti^[30]为

ti=12a3［a22+4a3（θ－a1）－a2］。（3）

三次样条插值具有高精度和良好平滑性，因此采用三次样条插值法利用式（3）计算角度对应的振幅，进而构造一个光滑的曲线。为避免重采样存在的重叠问题，转角增量θ^[32]需满足

θ=kΔθ。（4）

式中：Δθ角度间隔；k为插值系数。

2.2 基于小波包分解与重构的信号去噪

小波包阈值去噪包括信号分解和信号重构两个步骤，小波包分解可以同时对低频和高频部分进行分解。在分解结果中有效信号的小波包系数大，而噪声的小波包系数小，通过选择适当的阈值，对大于阈值的小波包系数认为是有效信号并保留，对小于阈值的小波包系数认为是噪声，将其置零，从而实现去噪。

小波包分解算法是由{d^j+1，nl}求{d^j，2nl}与{d^j，2n+1l}，即

d^j，2nl=∑kak－2ld^j+1，nk;

d^j，2n+1l=∑kbk－2ld^j+1，nk。（5）

式中：d^j，2nl为第n层分解的低频系数；d^j，2n+1l为第n层分解的高频系数。

小波包重构算法是由{d^j，2nl}与{d^j，2n+1l}求{d^j+1，nl}，即

d^j+1，nl=∑k（hl－2kd^j，2nk+gl－2kd^j，2n+1k）。（6）

式中：hl－2k为小波包重构的低频系数；gl－2k为小波包重构的高频系数。

2.2.1 小波包基函数和分解层数确定

信号去噪效果的好坏与小波包基函数相关。正交性好的基函数，能保留信号更多有效信息；正则性好的基函数，有利于重构光滑的曲线；对称性好的基函数，使重构曲线平稳；紧支性好的基函数，具有强的抗噪性；普遍性好的基函数，更适合于复杂信号。消失矩阵阶数越大，光滑性越好、局部化能力越强，但计算量越大、实时性越差。因此，综合考虑最终选择db3-db6和sym3-sym6基函数进行对比研究^[3]。

此外，分解层数不仅影响特征提取，还决定特征向量维度。分解层数过少，各段不能完全分解，无法获取完整特征；分解层数过多，信号分解精细，但分解后信号数量增多，特征向量维度变大，影响诊断效率。因此，综合考虑最终选择分解层数为3至7进行对比研究^[34]。

2.2.2 小波包去噪的阈值函数确定

小波包阈值去噪的关键在于选取合适的去噪阈值，常采用软阈值法^[35]。软阈值法可抑制较多噪声、保留信号特征尖峰点，去噪后信号完整且连续。

采用的软阈值法为

d-j，k=dj，k－λ，|dj，k|≥λ；

0，|dj，k|lt;λ。（7）

式中：d-j，k为去噪后小波包系数；dj，k为小波包系数；λ为阈值；j为分解层数；k=1为低频系数，k=2为高频系数。

2.2.3 小波包去噪效果的评价

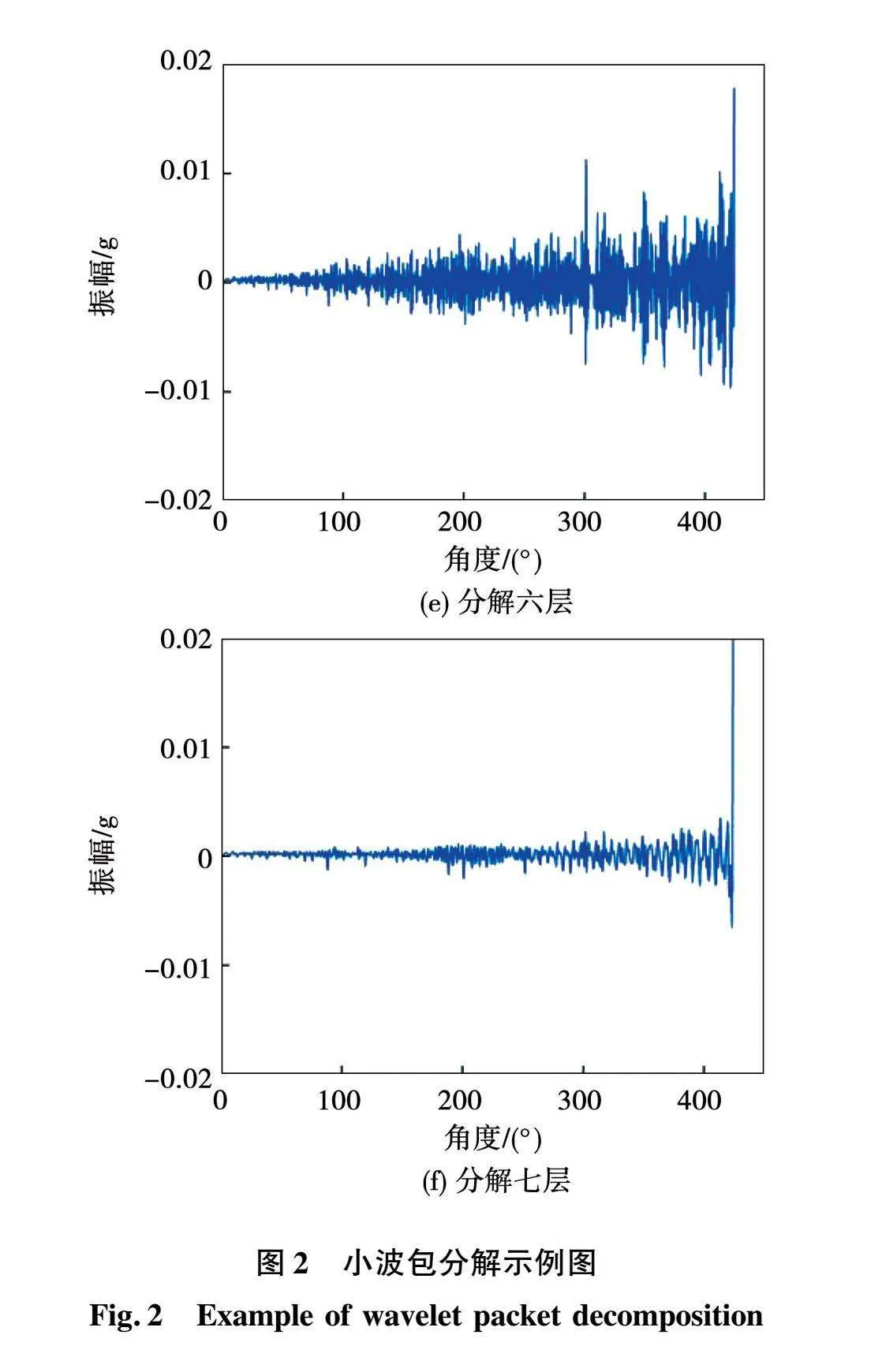
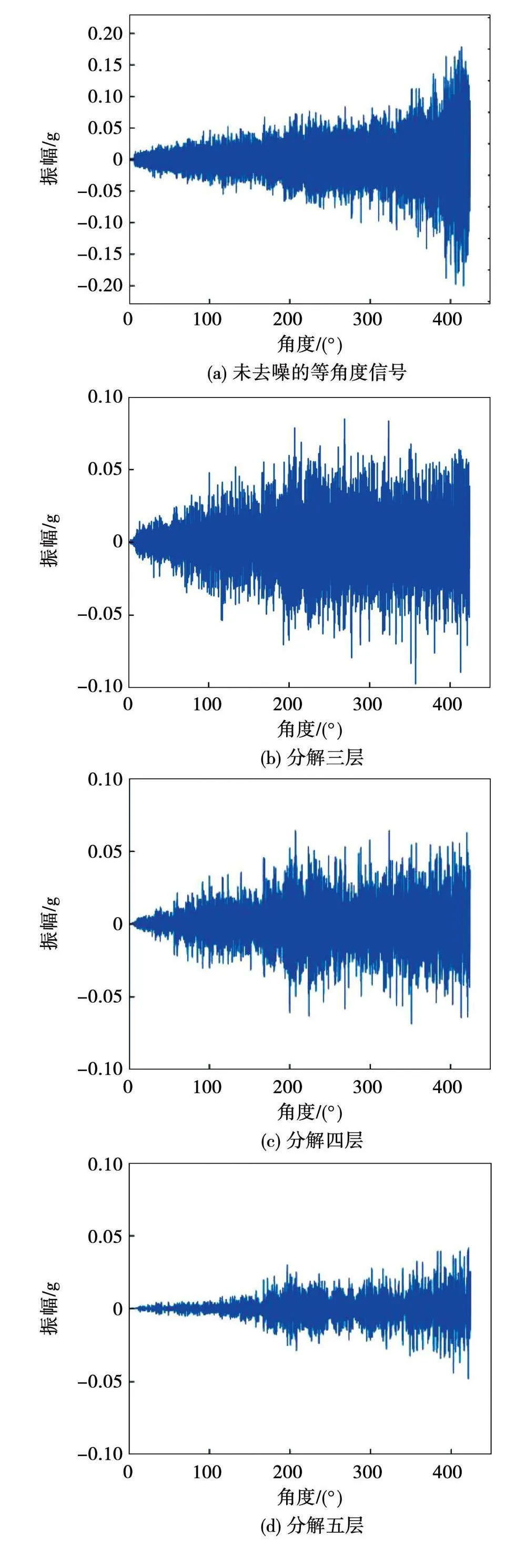
以电机轴承故障的小波包信号分解为例，如图2所示，可知3层分解与4层分解效果相差不大，5至7层分解效果较差，无法选出最佳分解层数。故需借助其他指标对分解层数与基函数进行终选。

额外采用的评价指标主要有信噪比、均方误差和畸变度。

信噪比（SNR）用于描述信号与噪声的比例，信噪比越大，去噪效果越好，表达式为

SNR=10log10PsignalPnoise。（8）

式中：Psignal为信号功率；Pnoise为噪声功率。

均方误差（MSE）用于描述去噪信号与真实信号间差异，均方误差越小，去噪效果越好，表达式为

MSE=1n∑Nn=1（Xi－Yi）2。（9）

式中：Xi为真实信号；Yi为去噪信号。

畸变度（D）用于描述去噪信号与真实信号接近程度，取值范围为0～1，畸变度越小，去噪效果越好，表达式为

D=∑Nn=1（Xi－Yi）2∑Nn=1X2i。（10）

式中：Xi为真实信号；Yi为去噪信号。

3 改进的一维卷积神经网络模型

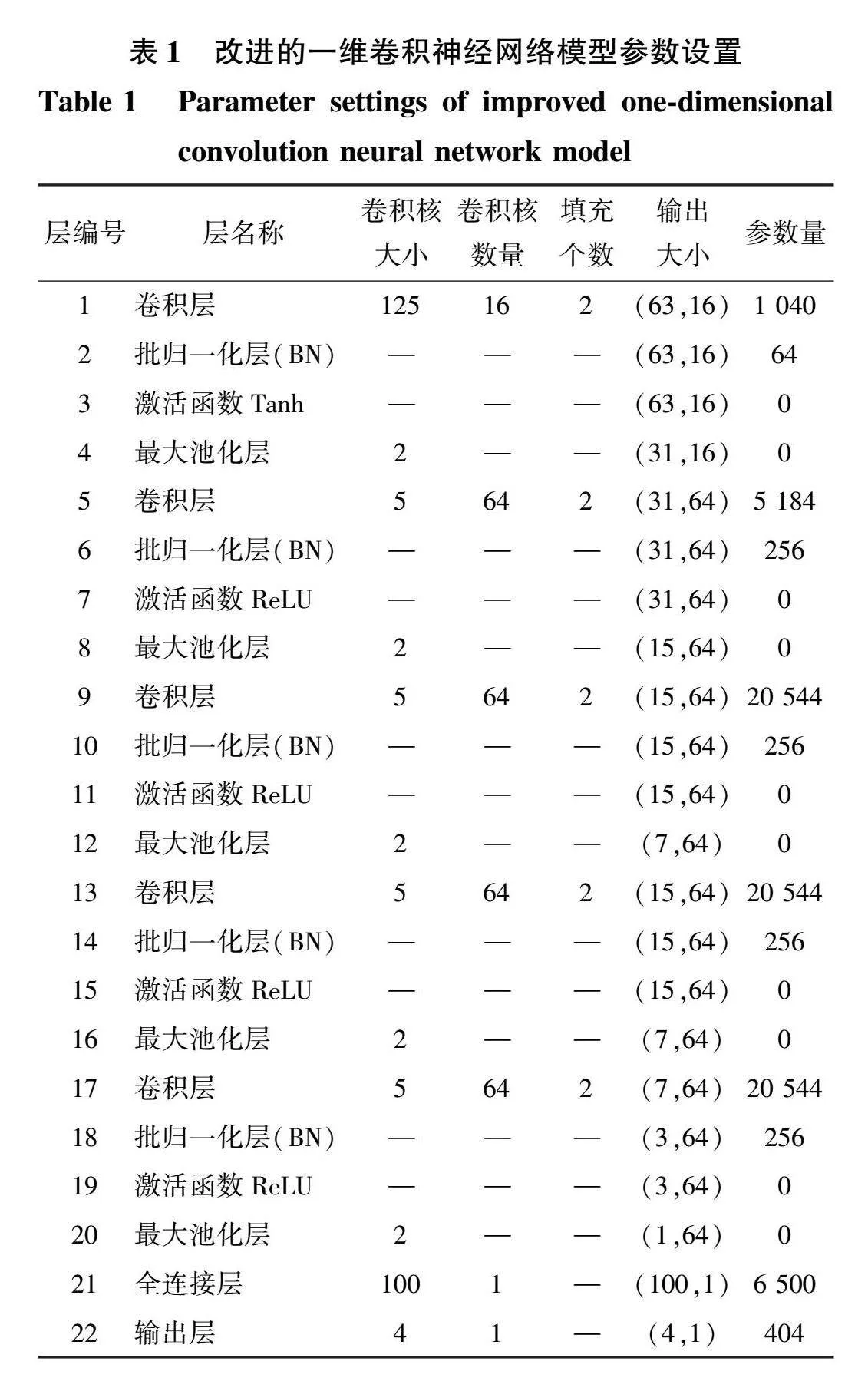
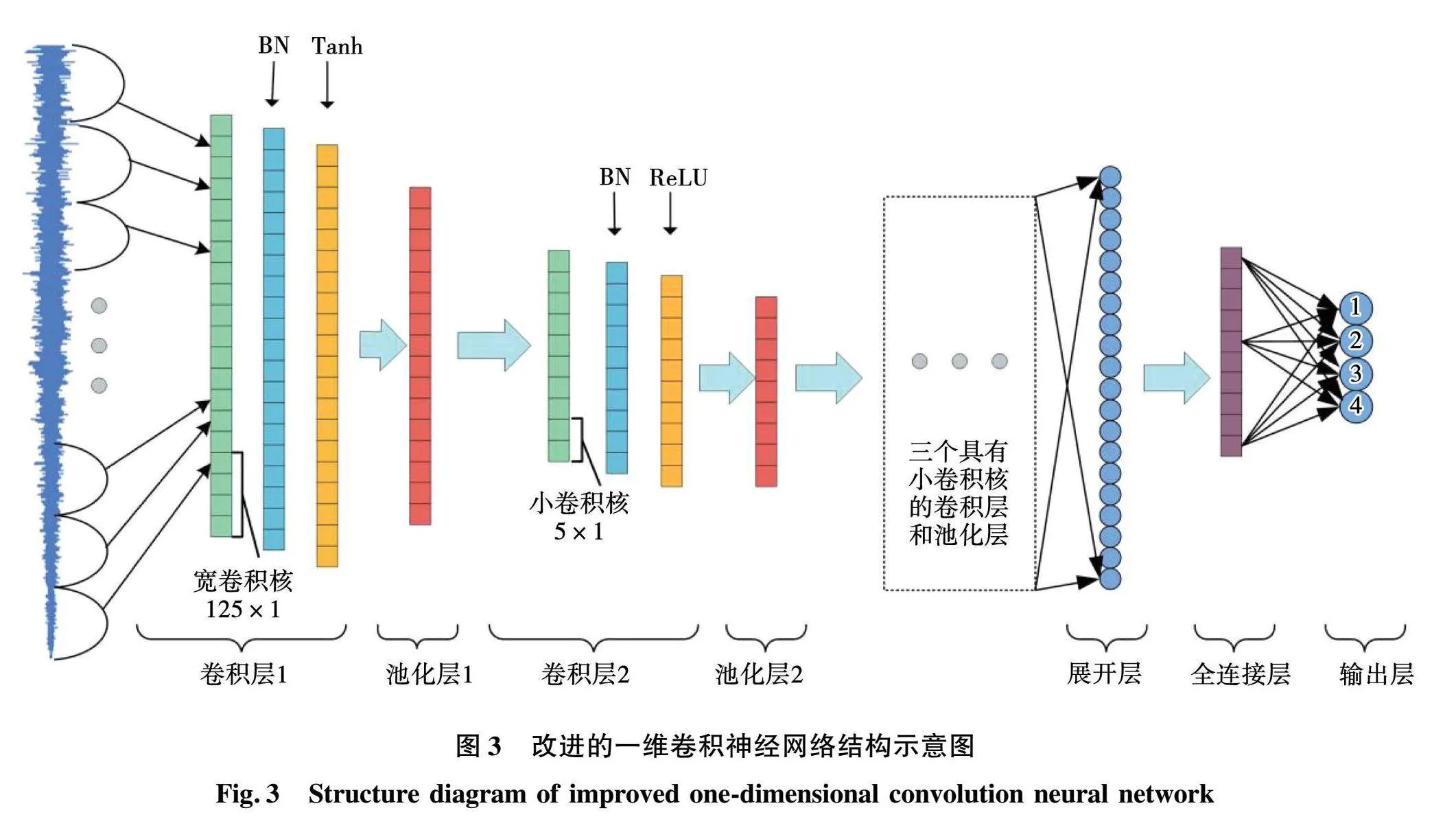
CNN模型包含卷积、池化和全连接层，卷积用于提取数据特征，池化将特征向量进行降维，全连接层完成数据分类。第一层宽卷积核深度卷积神经网络（WDCNN）^[27]是一种机械故障诊断的改良CNN模型，其特点是第一层为64×1大尺度卷积核，剩余4层均为3×1小尺度卷积核。第一层卷积具有较大视野，有利于提取短时特征和自动筛除无效特征。剩余卷积层有小卷积核，有助于加深网络深度、抑制过拟合。基于WDCNN进行改进，使其适用于变转速故障诊断，改进后的WDCNN如图3所示。

结合图3，对WDCNN的主要改进如下：

1）将第一层卷积核由64×1增大至125×1。通过增加卷积核数量，扩大第一层卷积层的感受野，更快速完整地提取短时特征，去除更多无效特征。

2）将剩余4层卷积层由3×1增大至5×1。使每个输出神经元更广泛地接收输入数据信息，捕捉更大范围的局部特征。

3）将卷积核深度由32增大至64，加深卷积核深度，增强网络表征能力，使模型具有更好的抑制过拟合能力。

4）设置dropout为0.5，dropout模块使一部分神经元停止工作，有效抑制过拟合、增加模型泛化能力，提高新样本预测准确性。

5）采用K折交叉验证，将数据集分成K个相等子集。每次训练中，随机选择K-1折用于模型训练，剩下一折用于模型验证，最大程度利用数据，避免数据只用一次，亦可抑制过拟合。

6）将BN层替换为AdaBN，以提升模型在测试集上的表现，对模型进行抗噪性改善。

综上所述，本文所设计的改进WDCNN模型的主要参数如表1所示。

4 故障诊断实验方案与方法验证

4.1 实验平台

电机故障诊断实验台如图4（a）所示，由感应电机、行星齿轮箱、平行轴齿轮箱、磁粉制动器、振动采集仪、变频器、振动传感器和光电式转速传感器等组成。其中，感应电机可进行人工更换，包括正常电机、轴承故障电机、转子不平衡故障电机和转子弯曲故障电机，如图4（b）所示。

4.2 实验参数

实验将负载设置为0 N·m，主要研究变速工况，设置升速时间为6 s，转速从0连续加速至1 800 r/min，采集电机加速过程中4.8 s的振动信号，转速及负载变化规律如图5所示。实验中选用四部具有相同结构但不同状态的三相感应电机，其状态分别为正常、轴承故障、转子不平衡和转子弯曲。电机振动信号采用压电式加速度传感器进行实时采集，其灵敏度为0.103 V/g（g代表重力加速度），安装在电机输出端的顶部，测量电机在竖直方向的振动。

4.3 实验数据

在时变转速和不同电机状态下，各种情况均采集50组原始振动信号，每组信号包含98 304个数据点。先使用角域重采样将原始振动信号转换为角域信号，再利用小波包软阈值法去除背景噪声，再将每个样本切分长度设为1 000个数据点。对每种情况，共切割2 000个样本。将这些样本按照训练集∶测试集=8∶2进行数据集划分，再使用K=10的交叉验证法，从训练集中划分出验证集，最终使训练集∶测试集∶验证集=7.2∶2∶0.8。

4.4 方法验证

4.4.1 信号角域重采样验证

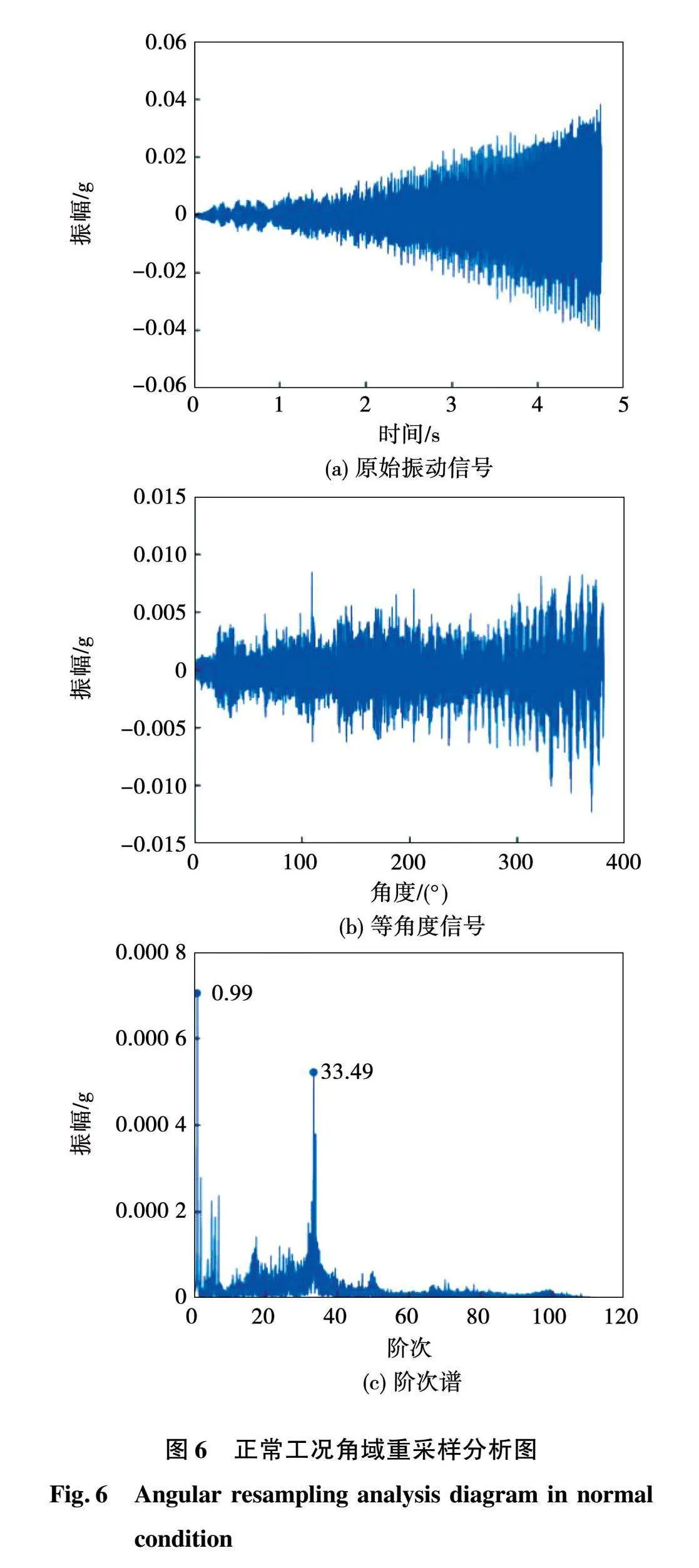
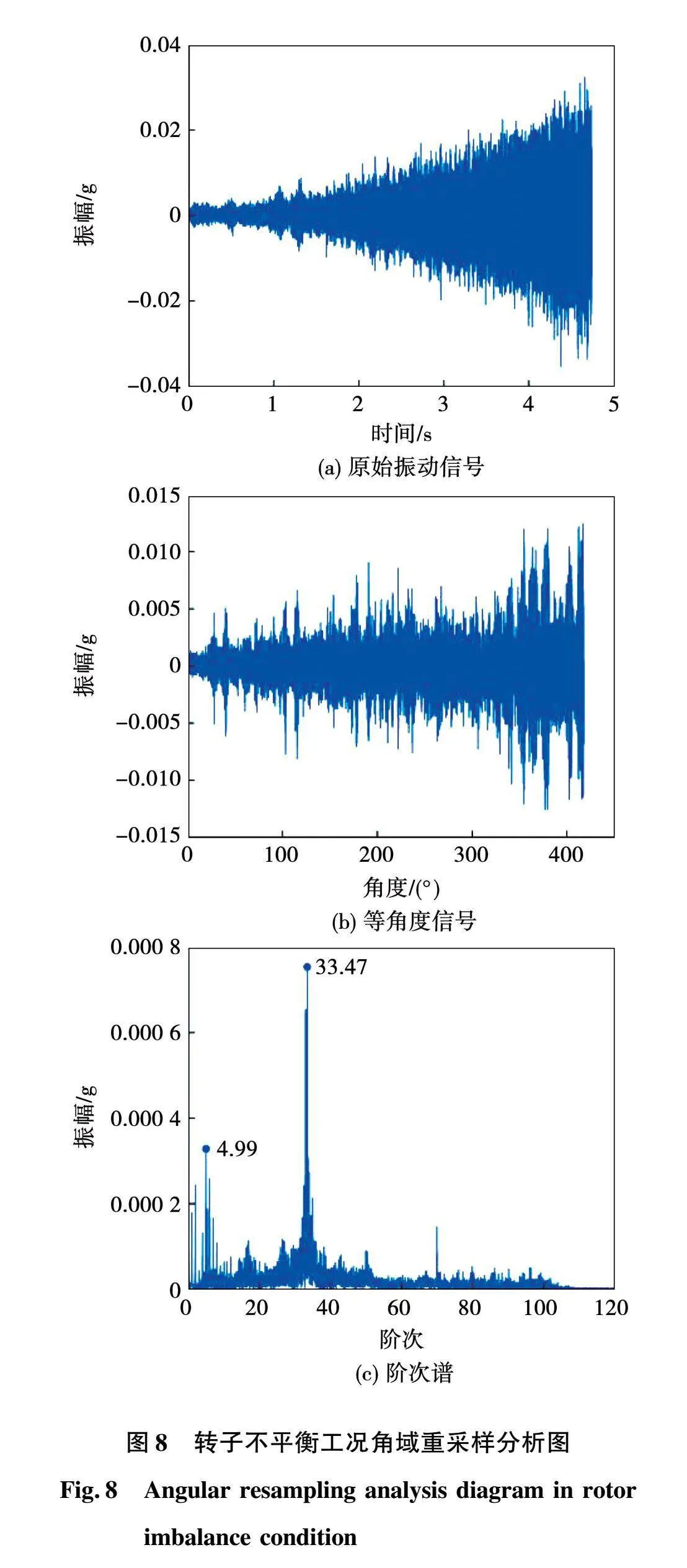
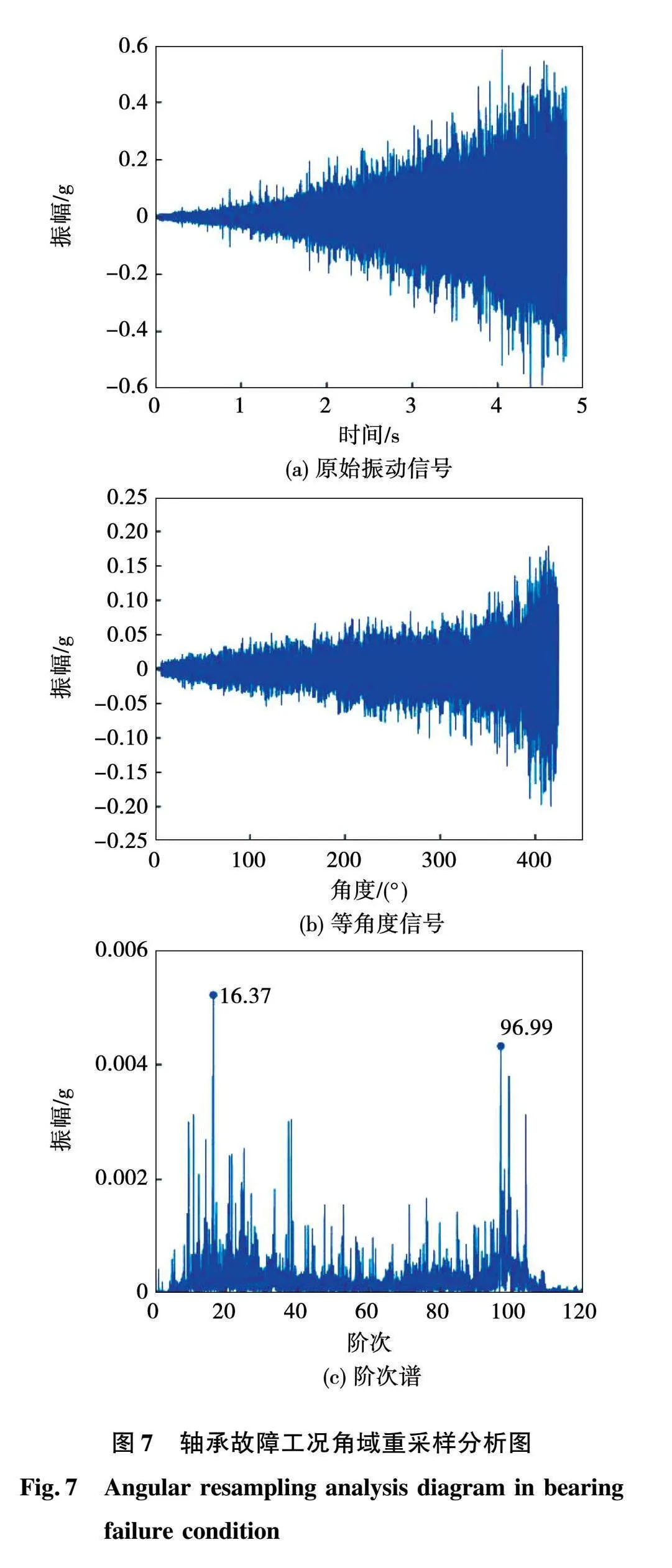
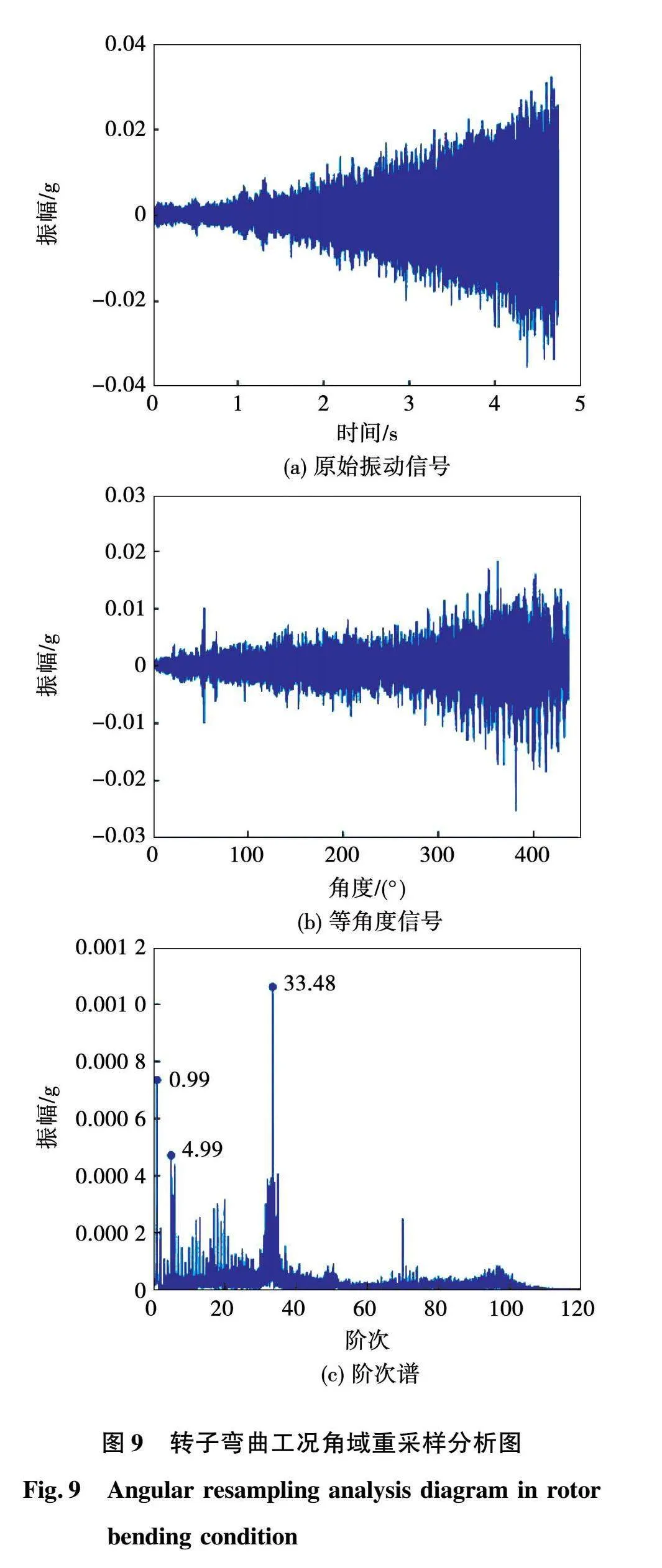
电机在正常、轴承故障、转子不平衡和转子弯曲状态运行时，其振动信号、等角度信号和阶次谱依次如图6～图9所示。可知，振动信号呈现向右开口喇叭状，振动幅值增大，为明显的时域非平稳信号，经过角域重采样后转变为角域信号。正常状态的阶次谱中突出阶次为0.99和33.49，轴承故障状态的阶次谱中突出阶次为16.37和96.99，转子不平衡状态的阶次谱中突出阶次为4.99和33.47，转子弯曲状态的阶次谱中突出阶次为0.99、4.99和33.48。综上分析，角域重采样可将时域非平稳信号转变为角域信号，并且能够很好地提取信号的特征信息。

4.4.2 信号去噪验证

信号的小波包去噪结果如表2所示，具体分析如下。

1）在相同小波包基函数下，随着分解层数逐渐增加，信噪比逐渐减小，均方误差逐渐增大，畸变度逐渐增大。从表中可以看出，3层分解时，去噪效果最理想；4至6层分解时，去噪效果相较3层分解大幅下降，去噪效果较差；7层分解时，去噪信号已发生畸变。

2）在相同分解层数下，dbN与symN系列小波包基函数随着消失矩阵阶数N增大，信噪比逐渐增大，均方误差逐渐减小，畸变度逐渐减小。从表中可以看出，在正常、轴承故障和转子不平衡状态下sym6去噪效果最理想；但在转子弯曲状态下db6去噪效果最佳。

3）在3层分解时，对比sym6与db6在转子弯曲下的评价指标。db6的信噪比sym6高0.073 7，db6的均方误差比sym6低0.026 3×10^-6，db6的畸变度比sym6低0.001 5。综合三项指标数值，发现相差较小，因此为了便于统一去噪，最终选取sym6与3层分解进行小波包去噪。

4.4.3 基于改进WDCNN的故障诊断验证

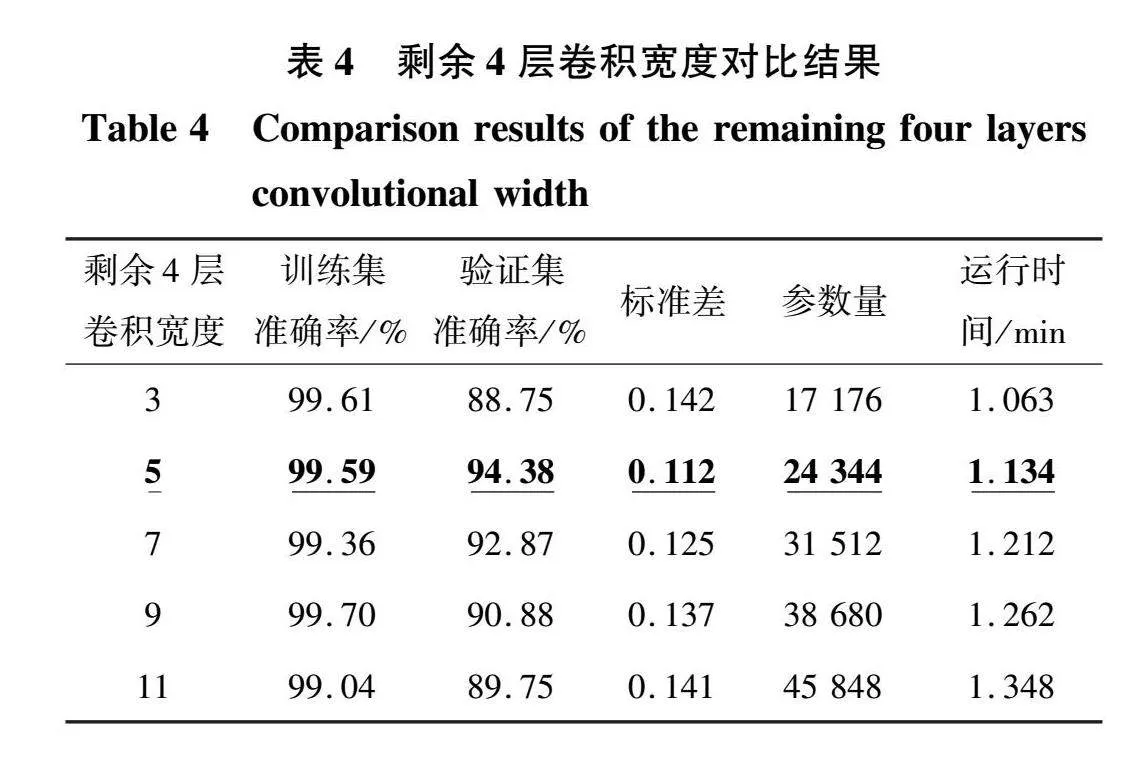
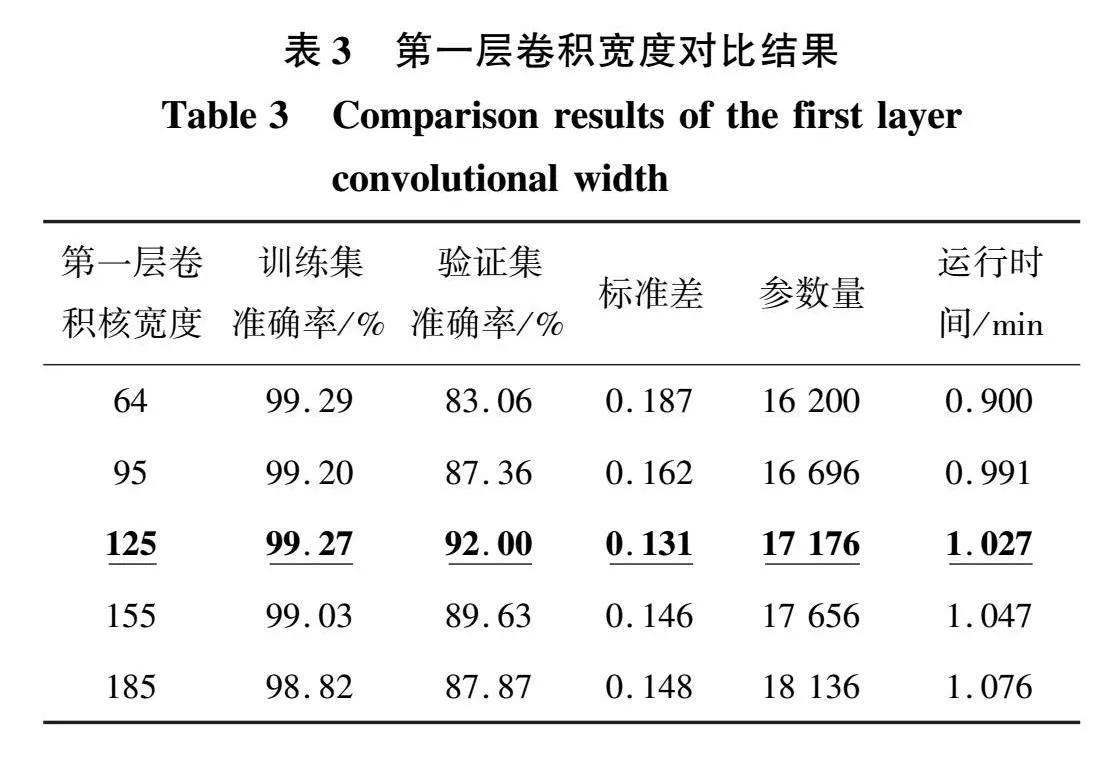
为了验证所改变的卷积层宽度和深度是最优结果，分别进行第一层卷积核宽度、剩余四层卷积核宽度以及剩余四层卷积核深度的对比实验。通过设置第一层卷积核宽度为95、125、155和185与原始模型卷积核宽度64进行对比。从图10和表3可知，当卷积核宽度为125时，训练集和验证集的准确率差距最小，均达到92%以上，标准差为0.131，模型稳定性最高，其运行时间为1.047 min，运行速度较快。随着宽度增加，验证集准确率下降，均不足90%，标准差增大，参数量增加，模型稳定性变差，运行时间也随之变长。综上所述，当卷积核宽度为125时，模型各项指标为最优结果。

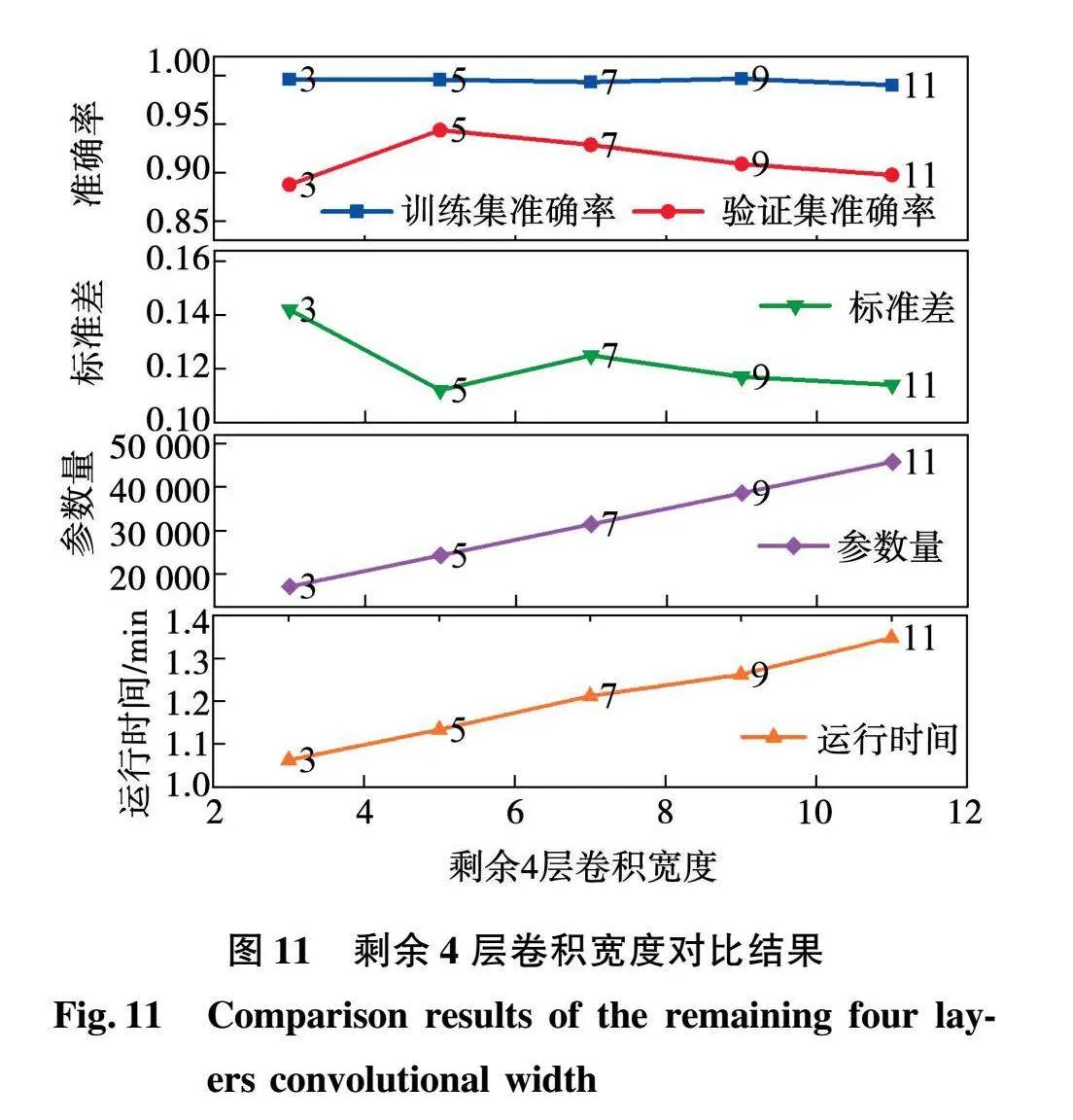
后4层卷积核普遍设置为个位数，其目的是减少参数量和资源消耗，在第一层卷积核宽度确定为125情况下，设置剩余4层卷积核宽度为3、5、7、9和11进行对比实验。结果如图11和表4所示，当卷积核宽度为5时，训练集和验证集的准确率相差最小，均在94%以上，模型拟合程度最佳，标准差为0.112，模型稳定性表现最好，其运行时间为1.134 min，运行速度较快。随着宽度增大，验证集准确率下降至89.75%，标准差增大，参数量增加，运行时间也随之增加，模型拟合效果变差，稳定性降低。综上所述，当剩余4层卷积宽度为5时，模型各项评价指标表现最佳。

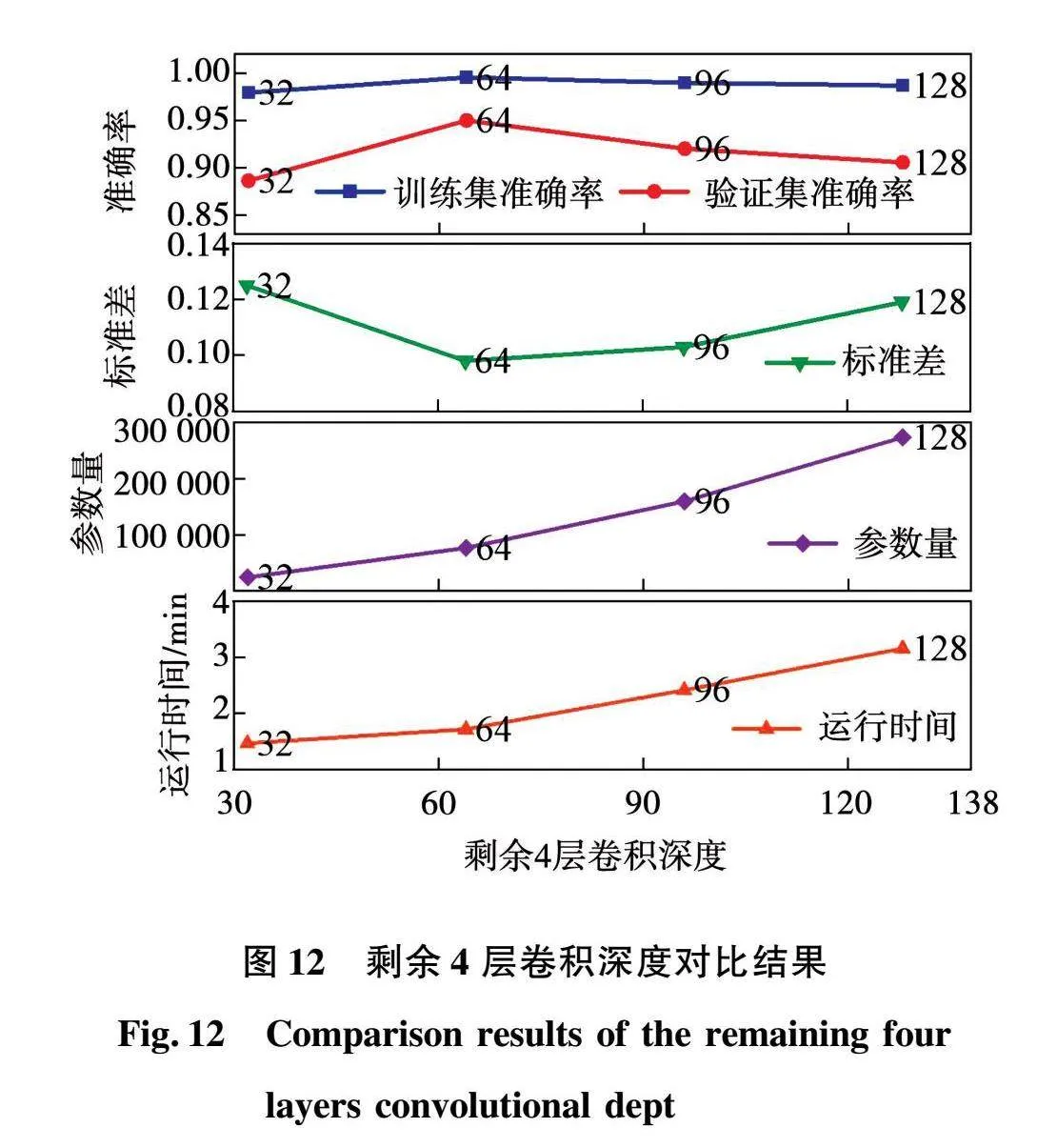
加深卷积层深度可以捕捉更高层次特征，减轻过拟合问题，提高模型的非线性能力。在上述确定第一层卷积核宽度为125，剩余4层卷积核宽度为5的情况下，设置剩余4层卷积核深度为32、64、96和128进行对比实验。结果如图12和表5所示，当卷积核深度为64时，训练集和验证集准确率均在95%以上，相差最小，标准差为0.098，模型拟合效果最佳，且具有较高的稳定性，运行时间为1.717 min，运行速度较快。随着深度的增加，验证集准确率下降至90.56%，标准差增大，参数量增加，运行时间增加至3.159 min，模型拟合效果变差，稳定性降低。综上所述，剩余4层卷积核深度为64时，模型各项评价指标最好，具有较高的准确率和稳定性。

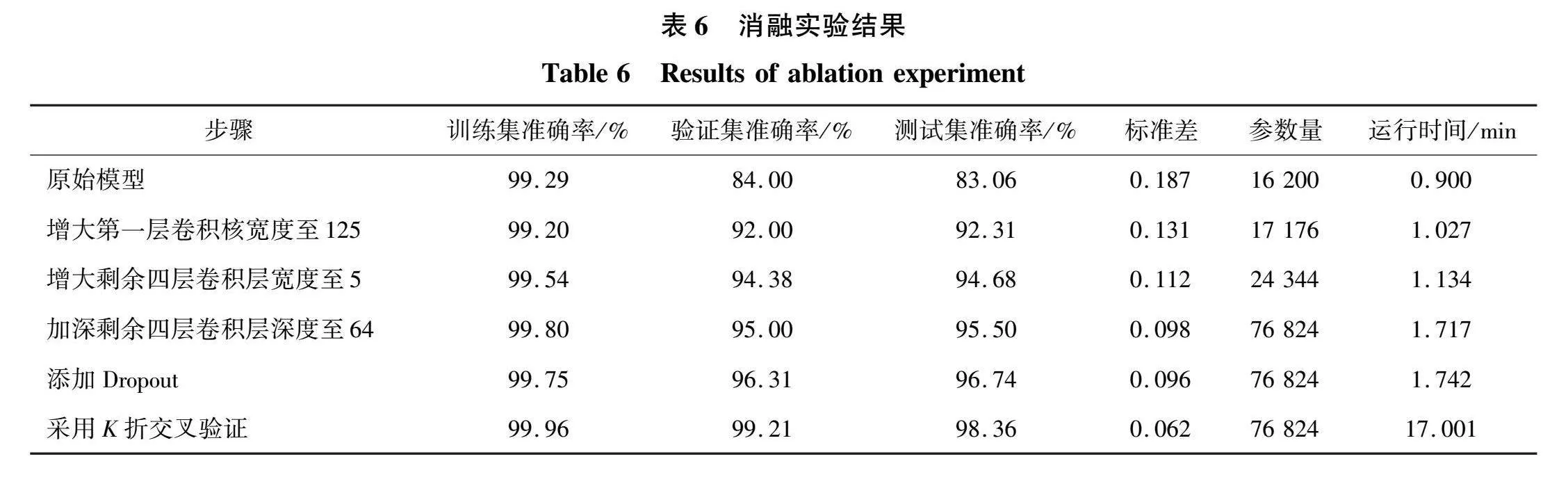
采用消融实验对改进模型的优势进行验证，结果如表6所示。在验证集和测试集上，增加第一层卷积宽度至125，准确率达到92%以上，至少提高8%，标准差为0.131，参数量增大，运行时间为1.027 min；增加剩余4层卷积宽度为5和深度为64时，准确率达到95%以上，标准差下降为0.098，模型具有较高的稳定性，运行时间为1.717 min，运行速度较快。在此基础上使用Dropout模块和K折交叉验证的训练策略，虽然运行时间达到了17 min，但最终模型准确率均在98%以上，标准差最小为0.062。综上所述，改进之处使模型具有较大优势，最终使模型具有较高的准确率和稳定性。

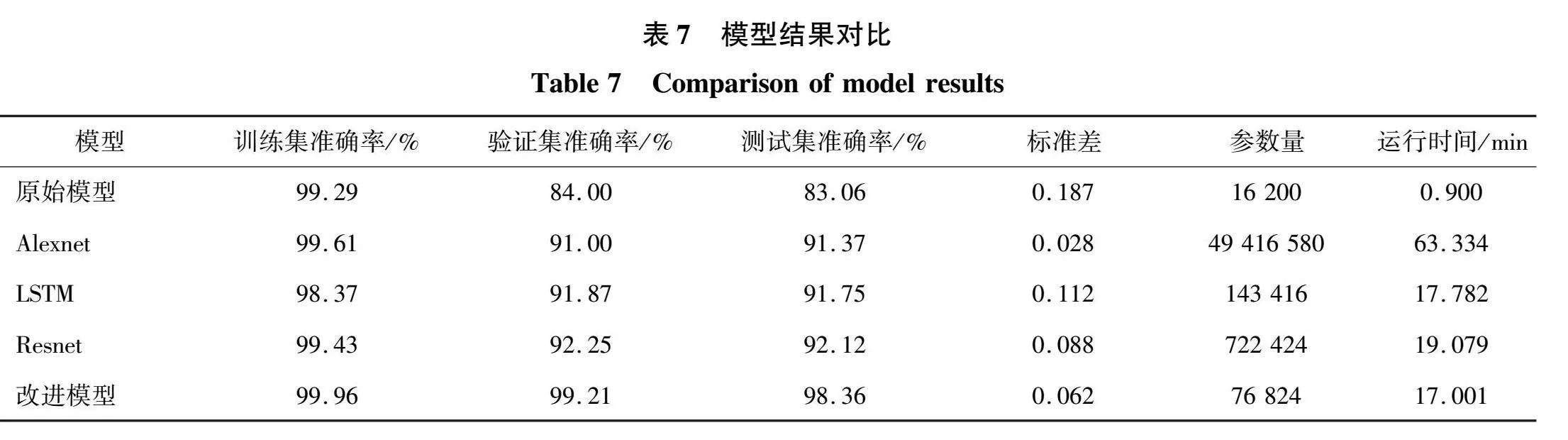
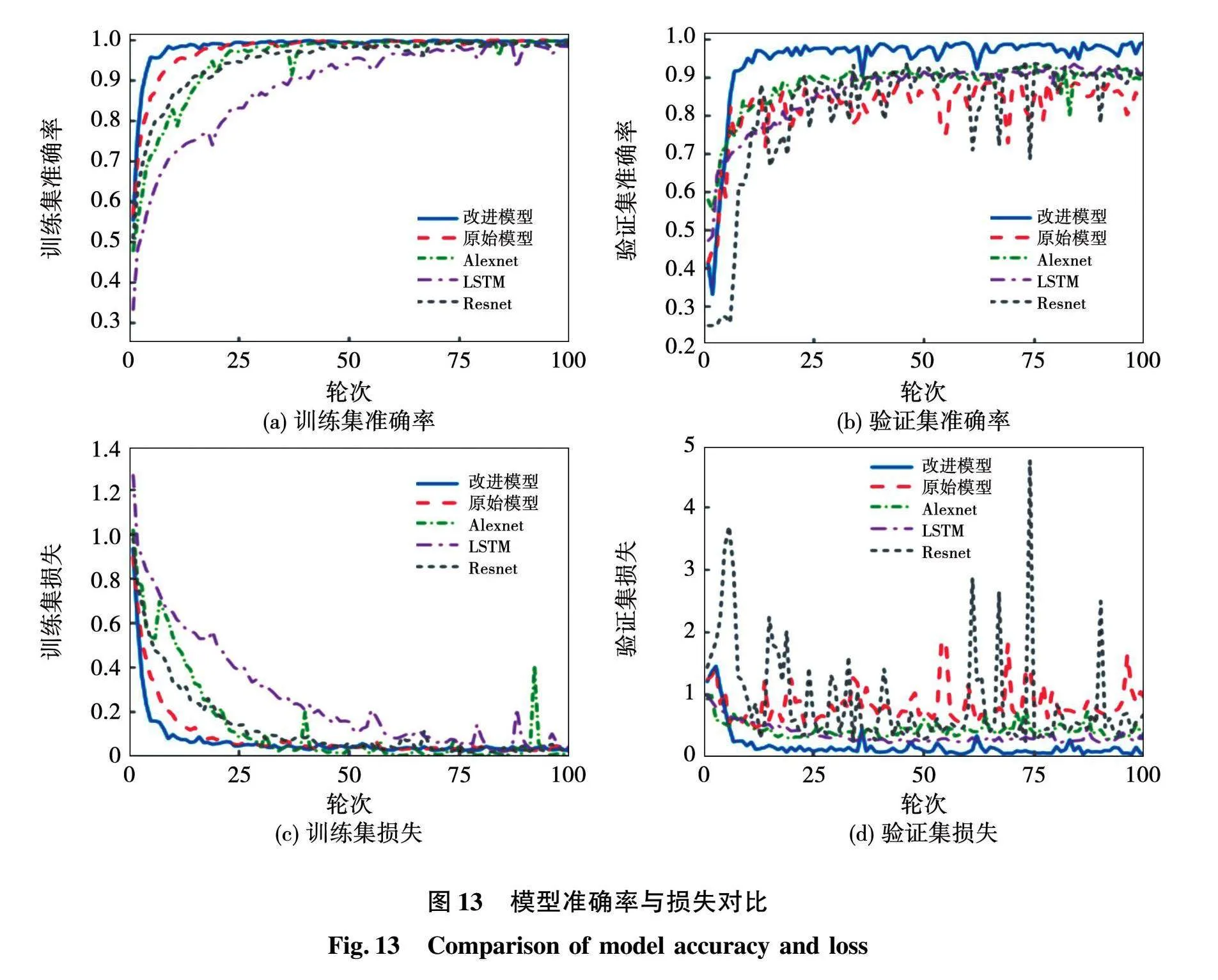
为进一步评价模型的动态学习过程，对比改进模型、原始模型、一维Alexnet网络、一维LSTM网络和一维Resnet网络的准确率与损失，如表7和图13所示。从表中可知，在验证集和测试集上，原始模型准确率最低，仅为84%左右，标准差最大为0.187，参数量为16 200，运行时间为0.9 min，运行速度最快；Alexnet网络、LSTM网络和Resnet网络准确率均在91%波动，标准差在0.1波动，其中Alexnet的标准差最低为0.028，参数量最大为49 416 580，运行时间最长为63.334 min，LSTM和Resnet网络的参数量分别为143 416和722 424，运行时间分别为17.782 min和19.079 min，运行速度较快；改进模型的准确率均在98%以上，表现最佳，标准差为0.062，参数量为76 824，运行时间为17.001 min，运行速度较快。

由图13（a）可知，5种模型在训练集上的准确率均较高、波动小且收敛，5种模型均能很好拟合训练数据；从图13（b）可知，只有改进模型的验证集准确率较高、波动小且平稳收敛，其余4种模型在验证集上准确率不足95%，波动较大，模型泛化能力较弱；从图13（c）可知，5种模型在训练集上的损失均较低、波动小且平稳收敛，模型具有较好的学习能力；由13（d）可知，在验证集上，改进模型的损失最低、波动最小且平稳收敛，其余4种模型的损失均较高，只有Alexnet网络和LSTM网络波动较小、最终平稳收敛，原始模型和Resnet网络波动明显且最终未收敛。

综上所述，改进模型在准确率和损失的对比中表现出色，模型具有较高的准确率、稳定性和泛化能力。

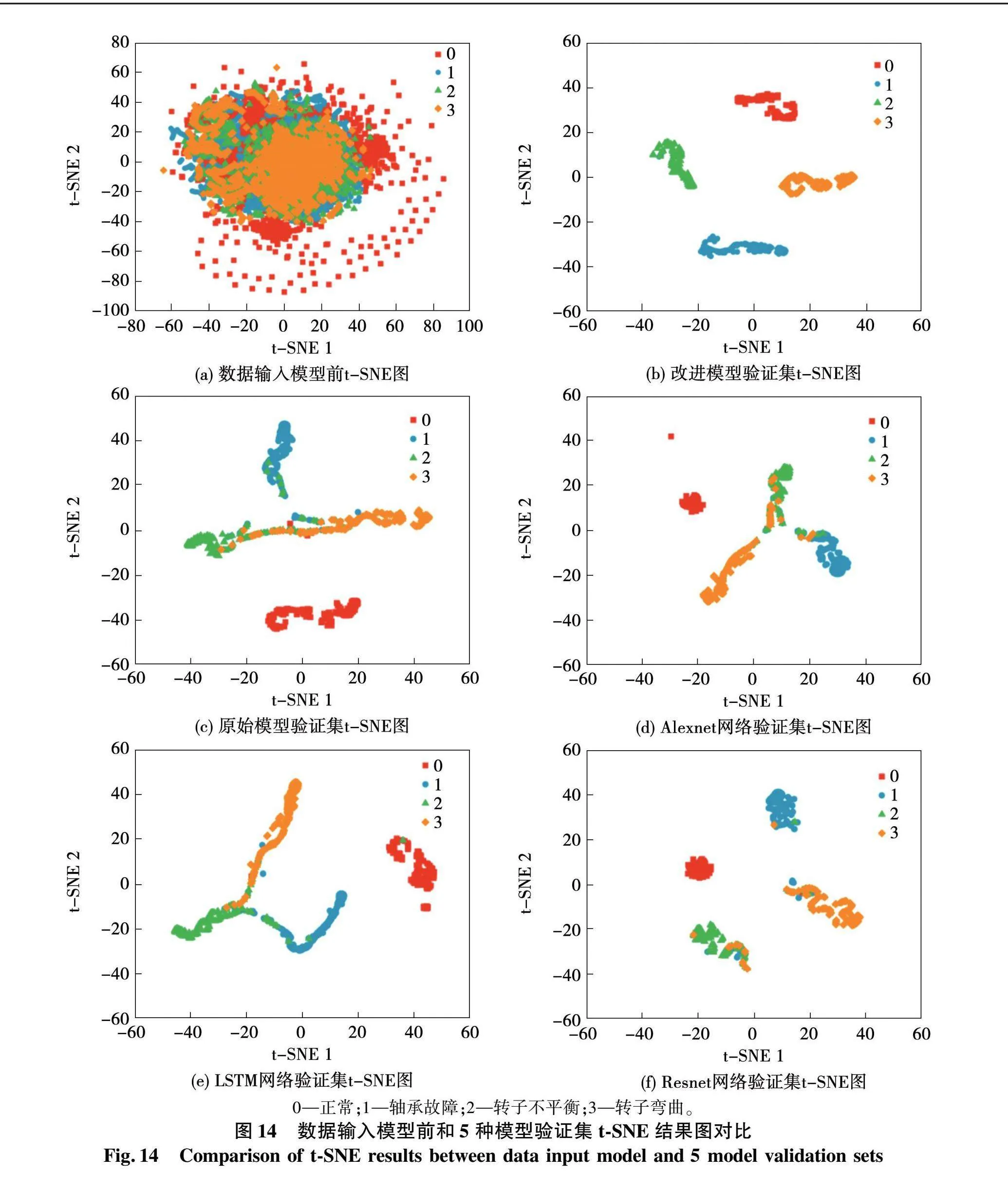
采用t-SNE（T-distribution stochastic neighbour embedding，t-SNE）非线性降维算法对数据进行可视化，将高维数据映射到二维空间，结果可从图14直观展示。为了进一步对比各模型的分类结果，利用数据输入模型前的状态作为对照组，如图14（a）所示，由图可知，数据输入模型前错综复杂且各种状态数据无法分离。从图14（b）可知，经过改进模型之后，四类不同状态的电机数据已完全分离，即故障类别被完全识别出来，未发生明显的误分和漏分情况。由图14（c）-图14（f）可知，原始模型、Alexnet网络、LSTM网络以及Resnet网络并不能将故障数据完全分离，存在误分和交错分布情况，即故障类别不能完整分离。综上所述，通过t-SNE可视化对比，改进模型具有较强的泛化能力和高稳定性。

5 抗噪性验证

5.1 所加噪声

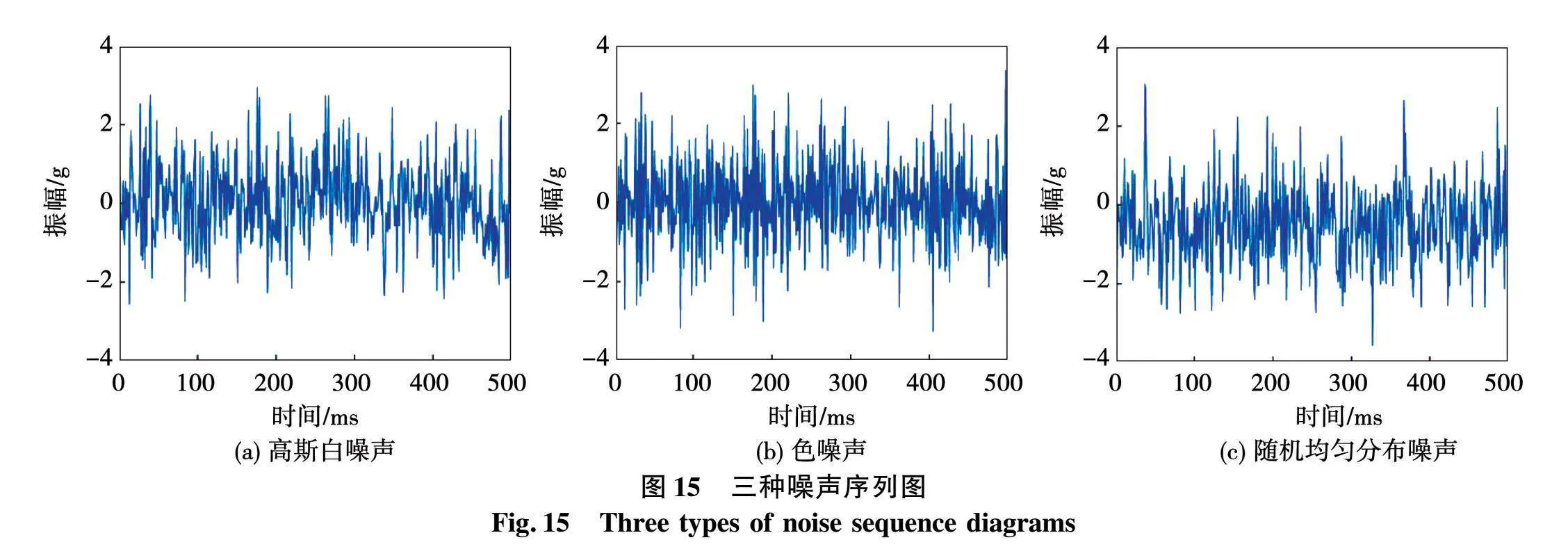
为了验证模型的抗噪性，采用高斯白噪声、色噪声和随机均匀分布噪声进行验证，三种噪声序列如图15所示。高斯白噪声具有高斯分布特征，是常见噪声；色噪声具有特定能量分布，较高斯白噪声复杂且贴近实际噪声；随机均匀分布噪声具有平均分布特点，可模拟离散、无特定规律的噪声。

5.2 抗噪实验

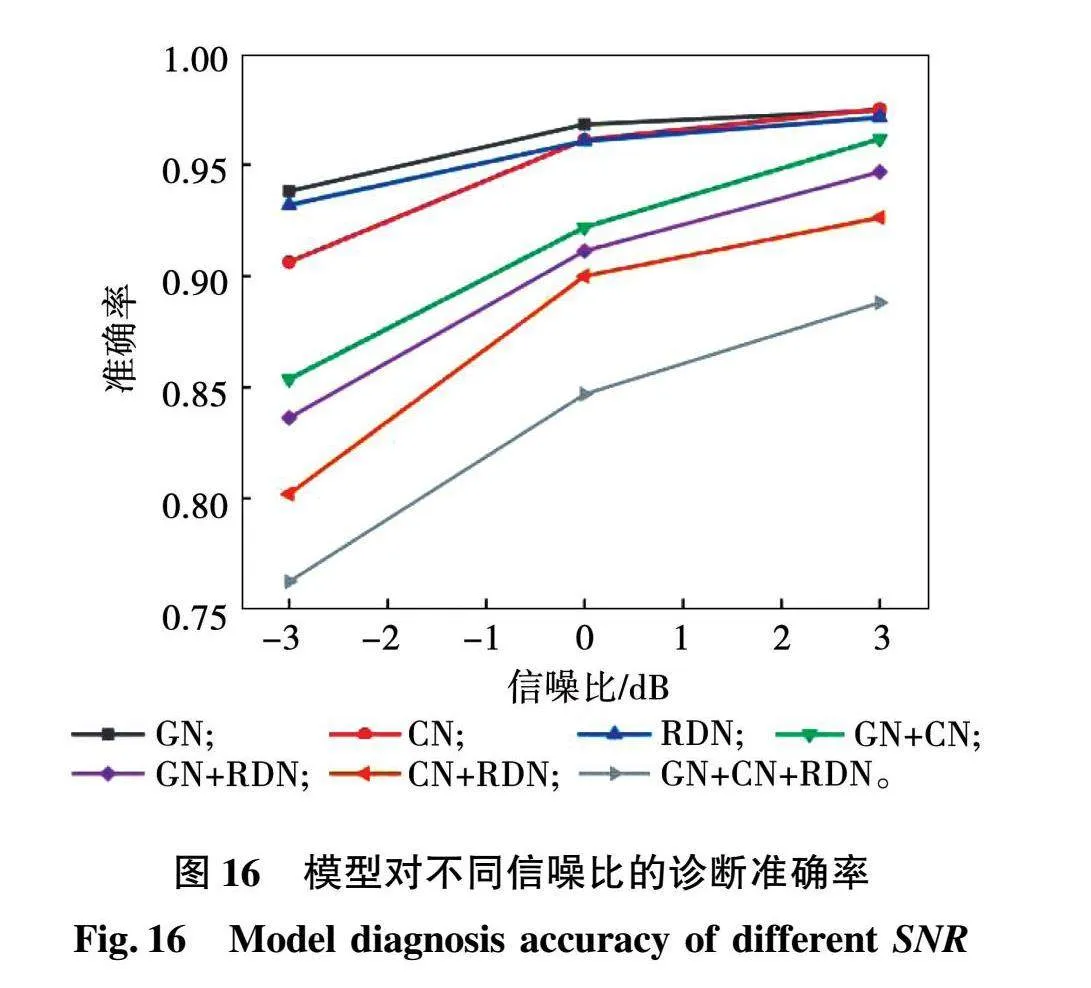
设置信噪比SNR=-3、0、3，将高斯白噪声（GN）、色噪声（CN）和随机均匀分布噪声（RDN）以单一和混合方式分别添加到原始信号中。为了评估模型对加噪数据的性能，以准确率为指标，在测试集加噪数据上使用AdaBN和训练所得最佳模型进行验证，结果如图16和表8所示。

当SNR=-3即噪声强度大于信号强度时，三种单一噪声的准确率均较高，但混合噪声的准确率相对较低，尤其三种噪声混合的准确率最低；当SNR=0即噪声强度等于信号强度时，除了三种混合噪声的准确率不足90%外，剩余六种噪声的准确率均在90%以上；当SNR=3即噪声强度小于信号强度时，除了三种混合噪声的准确率不足90%外，剩余六种噪声的准确率均在90%以上。上述结果表明在不同信噪比下所提出的方法表现良好，电机故障诊断准确率高，具有良好抗噪性和鲁棒性。

6 结 论

1）提出了一种角域重采样联合小波包去噪的变转速信号处理方法。将时变信号变换为角域信号，有效提取信号故障特征；同时，有效筛选出最佳小波包基函数，对信号进行了合理去噪处理。

2）提出了一种从卷积层、dropout、AdaBN等方面改进的WDCNN模型，结果表明在变转速四种不同电机状态下该模型具有高的准确率和稳定性，能够对电机转子-轴承系统故障类别进行有效识别。

3）验证了不同噪声对所提改进模型的影响，探讨了高斯白噪声、色噪声和随机均匀分布噪声单一和混合的情况，结果表明在三种信噪比和七种噪声类型下所提方法具有良好抗噪性和鲁棒性。

参 考 文 献：

［1］ MARTIN-DIAZ I， MORINIGO-SOTELO D， DUQUE-PEREZ O， et al. An experimental comparative evaluation of machine learning techniques for motor fault diagnosis under various operating conditions[J]. IEEE Transactions on Industry Applications， 2018， 54（3）： 2215.

［2］ 张鹏， 束小曼， 厉雪衣， 等. 基于LSTM的交流电机系统故障诊断方法研究[J]. 电机与控制学报， 2022， 26（3）： 109.

ZHANG Peng， SHU Xiaoman， LI Xueyi， et al. LSTM-based fault diagnosis of AC electric machine system[J]. Electric Machines and Control， 2022， 26（3）： 109.

［3］ HU T， TANG T， CHEN M. Data simulation by resampling—a practical data augmentation algorithm for periodical signal analysis-based fault diagnosis[J]. IEEE Access， 2019， 7： 125133.

［4］ SREEJITH B， VERMA A K， SRIVIDYA A. Fault diagnosis of rolling element bearing using time-domain features and neural networks[C]//2008 IEEE Region 10 and the Third International Conference on Industrial and Information Systems， December 15-17， 2008， Kandy， Sri Lanka. 2008：1-6.

［5］ YAN R， GAO R X， CHEN X. Wavelets for fault diagnosis of rotary machines： A review with applications[J]. Signal processing， 2014， 96： 1.

［6］ ZHENG K， BAI Y， XIONG J， et al. Simultaneously low rank and group sparse decomposition for rolling bearing fault diagnosis[J]. Sensors， 2020， 20（19）： 5541.

［7］ ZHANG X， LIU Z， MIAO Q， et al. An optimized time varying filtering based empirical mode decomposition method with grey wolf optimizer for machinery fault diagnosis[J]. Journal of Sound and Vibration， 2018， 418： 55.

［8］ CHEN X， SHU G， ZHANG K， et al. A fault characteristics extraction method for rolling bearing withvariable rotational speed using adaptive time-varying comb filtering and order tracking[J].Journal of Mechanical Science and Technology， 2022， 36（3）：1171.

［9］ LU S， GUO J， HE Q， et. A novel contactless angular resampling method for motor bearing fault diagnosis under variable speed[J]. IEEE Transactions on Instrumentation and Measurement. 2016， 65（11）： 2538.

［10］ CAO X， XU X， DUAN Y， et al. Health status recognition of rotating machinery based on deep residual shrinkage network under time-varying conditions[J]. IEEE Sensors Journal， 2022， 22（19）： 18332.

［11］ 李东东， 赵阳， 赵耀. 一种变工况下风电机组行星齿轮箱的故障诊断方法[J]. 电机与控制学报， 2023， 27（1）： 33.

LI Dongdong， ZHAO Yang， ZHAO Yao. Fault diagnosis method for wind turbine planetary gearbox under variable working conditions[J]. Electric Machines and Control， 2023， 27（1）： 33.

［12］ ABBASION S， RAFSANJANI A， FARSHIDIANFAR A， et al. Rolling element bearings multi-fault classification based on the wavelet denoising and support vector machine[J]. Mechanical Systems and Signal Processing， 2007， 21（7）： 2933.

［13］ ZHOU Z， ZHAO J， CAO F. A novel approach for fault diagnosis of induction motor with invariant character vectors[J]. Information Sciences， 2014， 281： 496.

［14］ LIU P， ZHANG W. A fault diagnosis intelligent algorithm based on improved BP neural network[J]. International Journal of Pattern Recognition and Artificial Intelligence， 2019， 33（9）： 1959028.

［15］ SUN Wenjun， ZHAO Rui， YAN Ruqiang. Convolutional discriminative feature learning for induction motor fault diagnosis[J]. IEEE Transactions on Industrial Informatics， 2017， 3（13）： 1350.

［16］ 樊红卫， 张旭辉， 曹现刚， 等. 智慧矿山背景下我国煤矿机械故障诊断研究现状与展望[J]. 振动与冲击， 2020， 39（24）： 194.

FAN Hongwei， ZHANG Xuhui， CAO Xiangang， et al. Current status and prospects of research on fault diagnosis of coal mining machinery in China under the background of smart mining[J]. Journal of Vibration and Shock， 2020，39 （24）： 194.

［17］ 李兵， 梁舒奇， 单万宁， 等. 基于改进正余弦算法优化堆叠降噪自动编码器的电机轴承故障诊断[J]. 电工技术学报， 2022， 37（16）： 4084.

LI Bing， LIANG Shuqi， SHAN Wanning， et al. Motor bearing fault diagnosis based on improved sine and cosine algorithm for stacked denoising autoencoders[J].Transactions of China Electrotechnical Society， 2022，37（16）：4084.

［18］ HINTON G E， OSINDERO S， TEH Y W. A fast learning algorithm for deep belief nets[J]. Neural Computation， 2006，18（7）： 1527.

［19］ 丁伟，宋俊材，陆思良，等.基于多通道信号二维递归融合和ECA-ConvNeXt的永磁同步电机高阻接触故障诊断[J].电工技术学报，2024，39（20）：6397.

DING Wei， SONG Juncai， LU Siliang. High-resistance connection fault diagnosis of permanent magnet synchronous motor based on two-dimensional recursive fusion of multi-channel signals and ECA-ConvNeXt[J]. Transactions of China Electrotechnical Society， 2024， 39（20）： 6397.

［20］ CHINEA A. Understanding the principles of recursive neural networks： a generative approach to tackle model complexity[C]//International Conference on Artificial Neural Networks. Springer Berlin Heidelberg， September 14-17， 2009， Rome， Italy. 2009： 952-963.

［21］ EREN L， INCE T， KIRANYAZ S. A generic intelligent bearing fault diagnosis system using compact adaptive 1DCNN classifier[J]. Journal of Signal Processing Systems， 2019， 91： 179.

［22］ SUN H， ZHAO S. Fault diagnosis for bearing based on 1DCNN and LSTM[J]. Shock and Vibration， 2021： 1-17.

［23］ LIU R， WANG F， YANG B， et al. Multiscale kernel based residual convolutional neural network for motor fault diagnosis under nonstationary conditions[J]. IEEE Transactions on Industrial Informatics， 2019， 16（6）： 3797.

［24］ LU F， TONG Q， FENG Z， et al. Explainable 1DCNN with demodulated frequency features method for fault diagnosis of rolling bearing under time-varying speed conditions[J]. Measurement Science and Technology， 2022， 33（9）：095022.

［25］ JI M， PENG G， HE J， et al. A two-stage， intelligent bearing-fault-diagnosis method using order-tracking and a one-dimensional convolutional neural network with variable speeds[J]. Sensors， 2021， 21（3）： 675.

［26］ ZHANG D， FENG Z. Enhancement of adaptive mode decomposition via angular resampling for nonstationary signal analysis of rotating machinery： principle and applications[J]. Mechanical Systems and Signal Processing， 2021， 160： 107909.

［27］ ZHANG W， PENG G， LI C， et al. A new deep learning model for fault diagnosis with good anti-noise and domain adaptation ability on raw vibration signals[J]. Sensors， 2017， 17（2）： 425.

［28］ ZHAOO Z， JIAO Y， ZHANG X. A fault diagnosis method of rotor system based on parallel convolutional neural network architecture with attention mechanism[J]. Journal of Signal Processing Systems， 2023： 1.

［29］ ZHANG J， YANG J， LITAKI G， et al. Feature extraction under bounded noise background and its application in low speed bearing fault diagnosis[J]. Journal of Mechanical Science and Technology， 2019， 33： 3193.

［30］ SHI P， XIA H， HAN D， et al. Stochastic resonance in a time polo-delayed asymmetry bistable system driven by multiplicative white noise and additive color noise[J]. Chaos， Solitons amp; Fractals， 2018， 108： 8.

［31］ WANG Y， NING D， FENG S. A novel capsule network based on wide convolution and multi-scale convolution for fault diagnosis[J]. Applied Sciences， 2020， 10： 3659.

［32］ 赵德尊.变转速下滚动轴承时变非平稳故障特征提取方法研究[D].北京：北京交通大学，2018.

［33］ 胡明宇，王先培，肖伟， 等. 基于UHF的局部放电信号小波包去噪与模式识别研究[J].仪表技术与传感器， 2016（7）： 93.

HU Mingyu， WANG Xianpei， XIAO Wei， et al. Research on wavelet packet denoising and pattern recognition of partial discharge signals based on UHF [J]. Instrument Technology and Sensors， 2016（7）： 93.

［34］ FAN H， YAN Y， ZHANG X， et al. Composite fault diagnosis of rolling bearing based on optimized wavelet packet AR spectrum energy entropy combined with adaptive no velocity term PSO-SOM-BPNN[J]. Journal of Sensors， 2021： 1-15.

［35］ DONOHO D L. De-noising by soft-thresholding[J]. IEEE Transactions on Information Theory， 1995， 41（3）： 613.

（编辑：刘素菊）