IPT系统多目标参数优化与切换控制策略研究

摘 要：针对AGV动态无线电能传输系统充电过程中负载和互感会发生波动，进而导致系统输出功率和传输效率降低的问题，提出一种基于多目标蛇算法（MOSO）的LCC-S型补偿拓扑参数优化方法以及一种基于有源阻抗匹配网络的最大功率和最大效率切换控制策略。首先，分析LCC-S型IPT系统的补偿拓扑参数对输出功率和传输效率的影响，构建多目标优化模型，利用多目标蛇算法对补偿拓扑参数进行优化设计实现传输性能最大化；其次，在副边采用基于CCM模式Buck-boost的阻抗匹配技术以实现最大功率和最大效率的切换控制。所提控制策略能适应互感和负载波动情况，保证系统在满足额定功率输出的前提下还能保持较高的传输效率。最后，搭建动态无线电能传输系统实验平台对理论分析进行验证，实验结果验证了所提优化方法和控制策略的可行性和有效性。

关键词：无线电能传输；多目标参数优化；切换控制策略；LCC-S型；最大功率；最大效率

DOI：10.15938/j.emc.2024.11.017

中图分类号：TM724

文献标志码：A

文章编号：1007-449X（2024）11-0184-11

Research on multi-objective parameter optimization and switchingcontrol strategy of IPT system

HUANG Wencong， HU Ying， HUANG Jinying， ZHANG Xiaoke， CHANG Yufang

（Hubei Collaborative Innovation Center for High-efficiency Utilization of Solar Energy， Hubei University of Technology，Wuhan 430068， China）

Abstract：Aiming at the problem that the load and mutual inductance will fluctuate during the charging process of AGV dynamic wireless power transfer system， which will lead to the reduction of system output power and transfer efficiency， an LCC-S compensation topology parameter optimization method based on multi-objective snake optimization and a control strategy based on active impedance matching network for maximum power and maximum efficiency switching were proposed. Firstly， the influence of compensation topology parameters of LCC-S IPT system on output power and transmission efficiency was analyzed， and a multi-objective optimization model was constructed. The multi-objective snake optimization was used to optimize the compensation topology parameters to maximize transmission performance. Secondly， the impedance matching technology based on CCM mode Buck-boost was adopted on the secondary side to realize the switching control of maximum power and maximum efficiency. The proposed control strategy can adapt to mutual inductance and load fluctuation， and ensure that the system can maintain high transfer efficiency under the premise of satisfying the rated power output. Finally， the experimental platform of dynamic wireless power transfer system was built to verify the theoretical analysis. The experimental results verify feasibility and effectiveness of the proposed optimization method and control strategy.

Keywords：wireless power transfer; multi-objective snake optimization; switching control strategy; LCC-S topology; maximum power; maximum efficiency

0 引 言

感应式磁耦合无线电能传输技术（inductive power transfer，IPT）基于电磁感应原理，无需导线连接即可实现从供电端到负载端的电能传输^[1-7]。相较于传统的有线充电方式，IPT技术因其具有安全、灵活、可靠等优点，被广泛应用在便携电子、轨道交通、植入医疗等诸多领域^[8-10]。

IPT技术的主要功能是实现能量传输^[11]，应当首要关注其传输特性。系统在实际运行过程中，由于收发线圈偏移引起互感变化以及负载波动都会导致其传输特性下降。通常采取添加补偿拓扑^[12]或施加控制策略^[13-14]的方式来提升系统的能量传输能力。

IPT系统补偿拓扑的选择与参数设计均会影响到系统的工作特性。文献[15]分析了不同补偿拓扑在不同负载和传输距离下的传输特性，但并未对补偿拓扑的参数设计进行研究。文献[16]将萤火虫算法应用到双边LCC补偿拓扑的参数设计中，实现线圈在非同轴放置时的效率优化。但仅仅考虑提高传输效率，并未考虑到多个目标的补偿拓扑参数设计。文献[17]对补偿拓扑的结构参数进行了优化，但并未对耦合系数进行辨识，无法适应互感变化情况。

系统运行过程中常用的提升传输性能的方式是增加有源阻抗匹配网络，通过调整DC-DC变换器的占空比来控制最大功率或最大效率输出^[18]。文献[19]针对接收端负载变化引起系统传输效率降低的问题，提出在接收侧串入Buck-boost电路并且调节占空比来实现系统的最大功率传输，但并未考虑到耦合系数变化对系统的影响以及传输效率下降问题。文献[20]提出了一种断续电流模式下的有源阻抗匹配网络最大效率跟踪方法，但并没有兼顾到输出功率。目前已有的研究较多集中在最大功率跟踪或最大效率跟踪某一方面，并未涉及到两者的切换问题。

基于以上文献研究的不足之处，本文提出一种基于多目标蛇算法（multi-objective snake optimizer，MOSO）的LCC-S型拓扑网络参数设计方法以及一种基于最大功率和最大效率切换的控制策略。在系统设计阶段，采用MOSO算法对高阶补偿拓扑进行参数寻优，提高系统输出功率和传输效率，为系统稳定且高效的运行提供了坚实的基础。在系统运行阶段，考虑耦合系数和负载变化，从控制策略层面来提升IPT系统对耦合系数的自适应性。通过最大功率和最大效率动态切换方式，提升系统的传输性能，从而满足负载的功率需求。

1 IPT系统数学模型

1.1 LCC-S拓扑电路分析

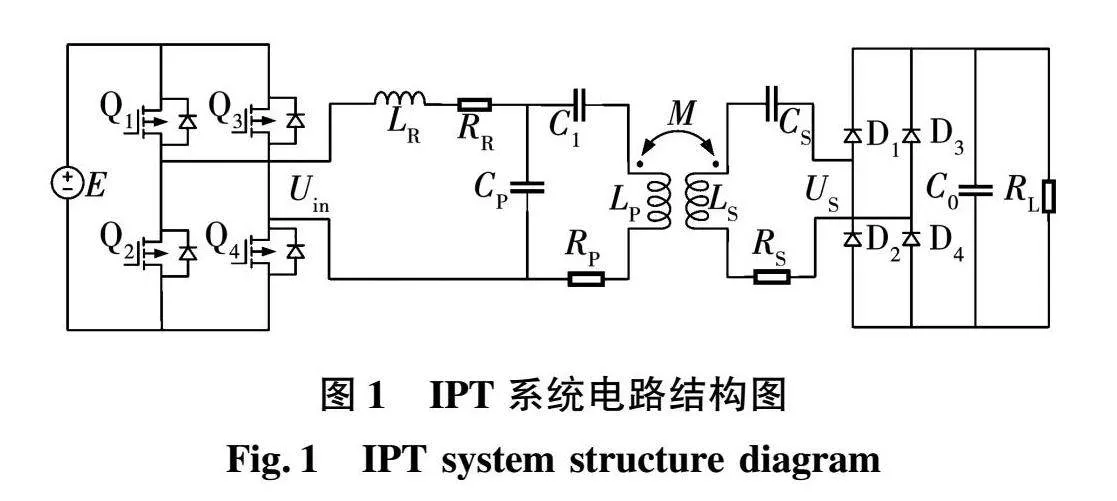
无线电能传输系统中，原、副边可通过加入谐振补偿拓扑电路来实现阻抗匹配。拓扑电路不仅能够提高系统的功率因数，还能实现恒压/恒流输出。LCC-S型拓扑结构具有发射线圈恒流，副边输出恒压的优势。此外，发射线圈恒流的特性可在耦合系数或负载变化情况下保证系统的安全稳定性。具有LCC-S型补偿拓扑的IPT系统的电路整体结构如图1所示。

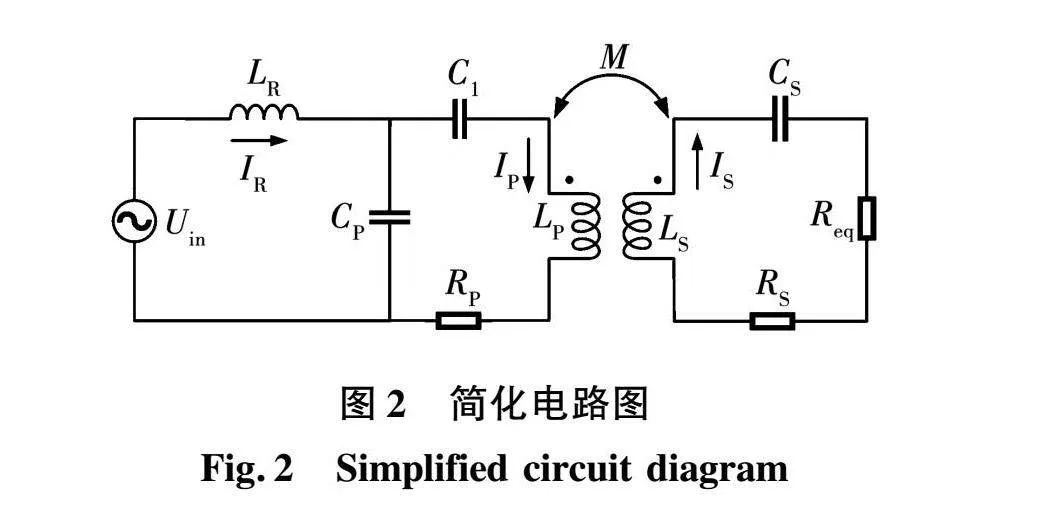
图1中，E为直流输入电压，Q1～Q4四个开关管构成全桥逆变电路将直流电压E变换为高频交流电压Uin；补偿电感LR，并联补偿电容CP和串联补偿电容C1构成原边LCC补偿拓扑，RR为补偿电感LR的内阻；CS为副边补偿电容，LP和LS分别为发射和接收线圈的自感，RS和RP分别为收发线圈的内阻；M为线圈之间的互感，D1～D4四个二极管构成整流电路，U·S为整流前的交流电压，C0为滤波电容，RL为负载电阻。采用基波等效法简化电路，简化后的等效电路如图2所示。

其中，IR、IP、IS是等效电路各回路网格电流的实际值。

依据基尔霍夫电压定律（KVL）进行推导，可得互感模型电路表达式：

（jωLR+RR）I·R+1jωCP（I·R－I·P）=U·in；

（jωLP+1jωC1+RP）I·P+1jωCP（I·P－I·R）=jωMI·S；

（jωLS+1jωCS+RS+Req）I·S=jωMI·P。（1）

式中：U·in、I·R、I·P、I·S分别为Uin、IR、IP、IS的相量；Req=8π2RL；M=kLpLS；k为两线圈的耦合系数0lt;klt;1。

当系统处于谐振状态时，存在以下关系式：

ω=1LRCP=1LSCS=1（LP－LR）C1。（2）

式中：ω为系统谐振角频率，满足ω=2πf，f是系统的谐振工作频率。

由此可得LCC-S型IPT系统的输出功率Pout和传输效率η分别为：

Pout=U·2inM2ReqL2R（Req+RS）2；（3）

η=ω2M2Req（Req+RS）2（ω2M2Req+RS+RP）。（4）

1.2 LCC-S型IPT系统传输特性分析

由式（3）和式（4）可知，系统的输出功率及传输效率与补偿拓扑参数LP、LS和LR有关。根据谐振条件，一旦补偿电感的值确定，补偿电容的值也被确定。

将接收线圈自感LS与发射线圈自感LP之间的比值定义为α，原边补偿电感LR与发射线圈自感LP之间的比值定义为β。即：

α=LSLP；β=LRLP。（5）

式中：α、β分别为LS和LP、LR和LP之间取值的差距。一般取0lt;αlt;2，0lt;βlt;1。由式（3）、式（4）可知，当交流源电压Uin、系统谐振角频率ω固定时，LP、LS、LR的值由α、β值决定。采用MATLAB分析收发线圈在不同α、β取值时对系统传输性能的影响。

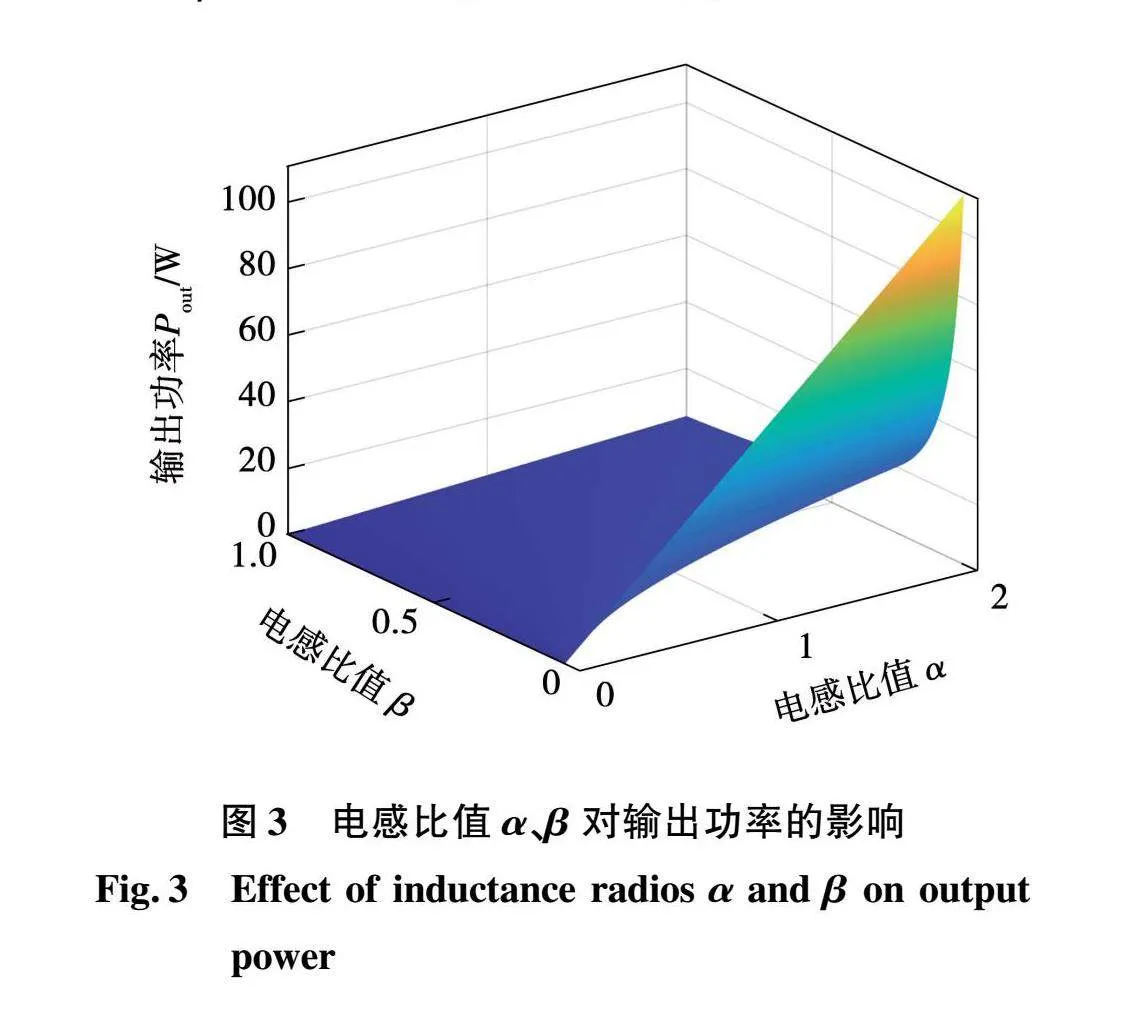
由式（3）可知，输出功率表达式与电感比值α、β均相关。当α、β在合理范围内变化时，输出功率关于α和β的三维图像如图3所示。

由图3可知，当α值一定时，β值越小，输出功率越大。当β值一定时，α值越大，输出功率越大。电感比值α、β的相对大小决定着系统的输出功率。

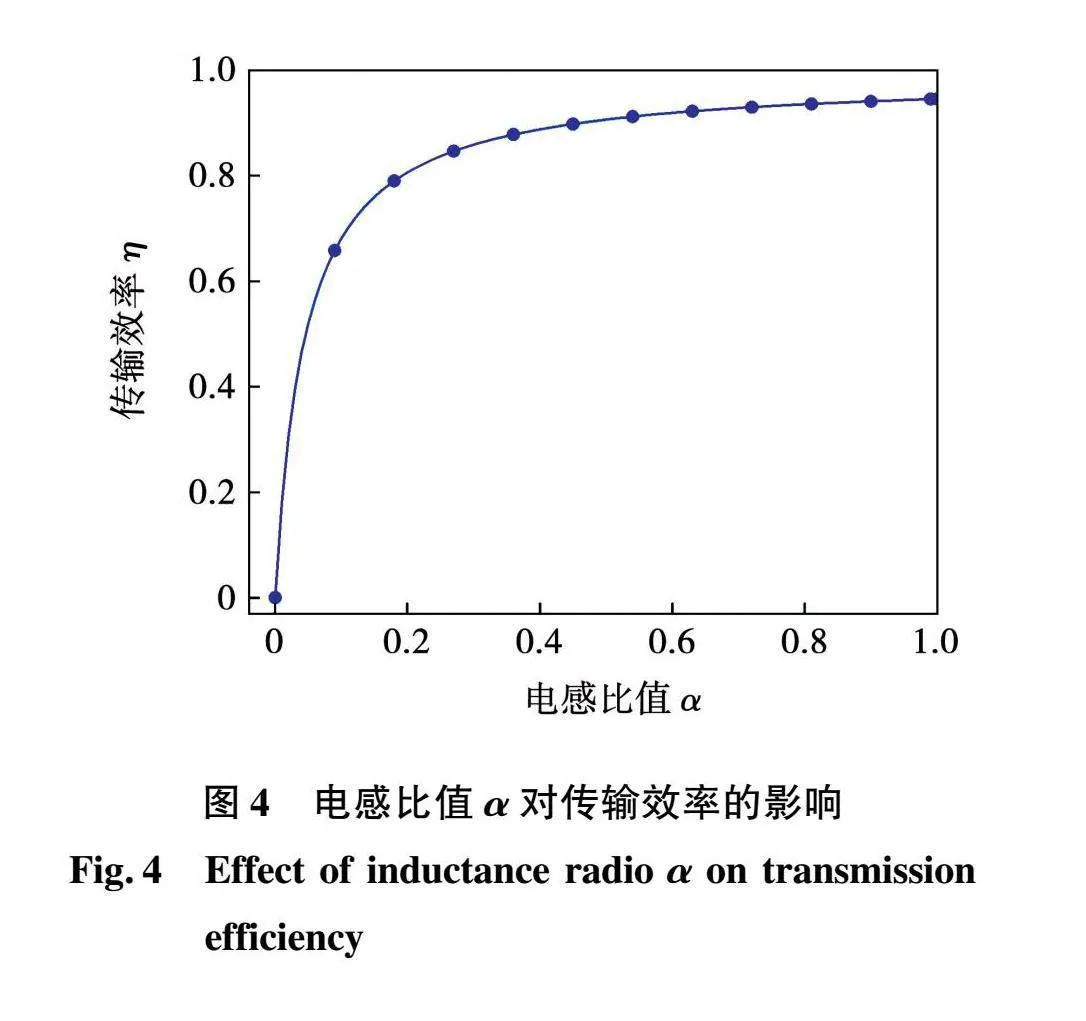
由式（4）可知，传输效率表达式仅和电感比值α相关，当α值在合理范围内变化时，传输效率关于α值的二维图像如图4所示。

如图4所示，随着α值增大，传输效率呈上升趋势。当αgt;0.2时，随着α值继续增大，传输效率变化不大。当发射线圈与接收线圈自感取值适中时，系统能够在较高的传输效率下运行。

通过上述分析发现具有LCC-S型补偿拓扑的系统，输出功率和传输效率主要受收发线圈自感以及原边补偿电感的影响，选择合适的补偿拓扑参数能够有效提高系统的传输特性。

1.3 多目标优化数学模型

1.3.1 优化目标与决策变量

由于LCC-S型高阶补偿拓扑参数之间具有非线性、强耦合等特点，在进行参数设计时不易计算，且无法同时兼顾输出功率和传输效率。通常补偿电容的取值可以根据谐振公式确定，但是对于自感以及补偿电感参数只能根据经验确定。因此对高阶补偿拓扑参数进行多目标优化是非常必要的。为了实现动态无线电能传输的输出功率和传输效率同步优化，多目标函数定义如下：

f（x）=min［1η，1Pout］。（6）

将直接影响系统传输性能的补偿拓扑参数作为优化变量，包括：发射与接收线圈自感LP、LS，原边补偿参数LR、CP、C1，副边补偿参数CS，也即：

x=［LP，LS，LR，CP，C1，CS］T。（7）

其中：LP、LS、LR为独立变量，其他非独立变量CP、C1、CS可由与独立变量间的关系求解。

1.3.2 约束条件

根据系统谐振条件和负载功率需求确定多目标优化的约束条件为：

s.t.G1=Pout－Pset≥0；

G2=ωLR－1ωCP=0；

G3=ωLP－1ωC1－1ωCP=0；

G4=ωLS－1ωCS=0；

G5=LP－LRgt;0。（8）

2 基于多目标蛇算法（MOSO）的补偿参数优化方法

为保证系统在满足功率需求的前提下提高传输效率，需要对补偿拓扑参数进行优化处理。由于补偿拓扑参数较多、公式繁琐，且在进行参数设计时需要考虑到多个约束条件。传统的参数设计方法难以同时兼顾输出功率和传输效率，因此考虑采用群智能优化算法对补偿拓扑参数进行优化。

本文采用多目标蛇算法（MOSO），旨在优化LCC-S型补偿拓扑参数，从而提升系统的输出功率及传输效率。

蛇算法（snake optimizer，SO）^[21]是HASHIM F A和HUSSIEN A G两位教授在2022年共同提出的一种元启发式智能优化算法。其设计灵感巧妙融合了自然界中蛇的觅食策略和繁殖行为。与其他算法相比，蛇算法计算参数较少，且优化效果较好，可应用在复杂非线性优化问题的求解中。对蛇算法进行改进，得到多目标蛇算法（MOSO）。

设定MOSO算法中的种群规模为100，最大迭代次数为200，外部存档大小为100。初始化IPT系统参数为Uin=300 V，Req=20 Ω，k=0.2，RP=RS=0.1 Ω。

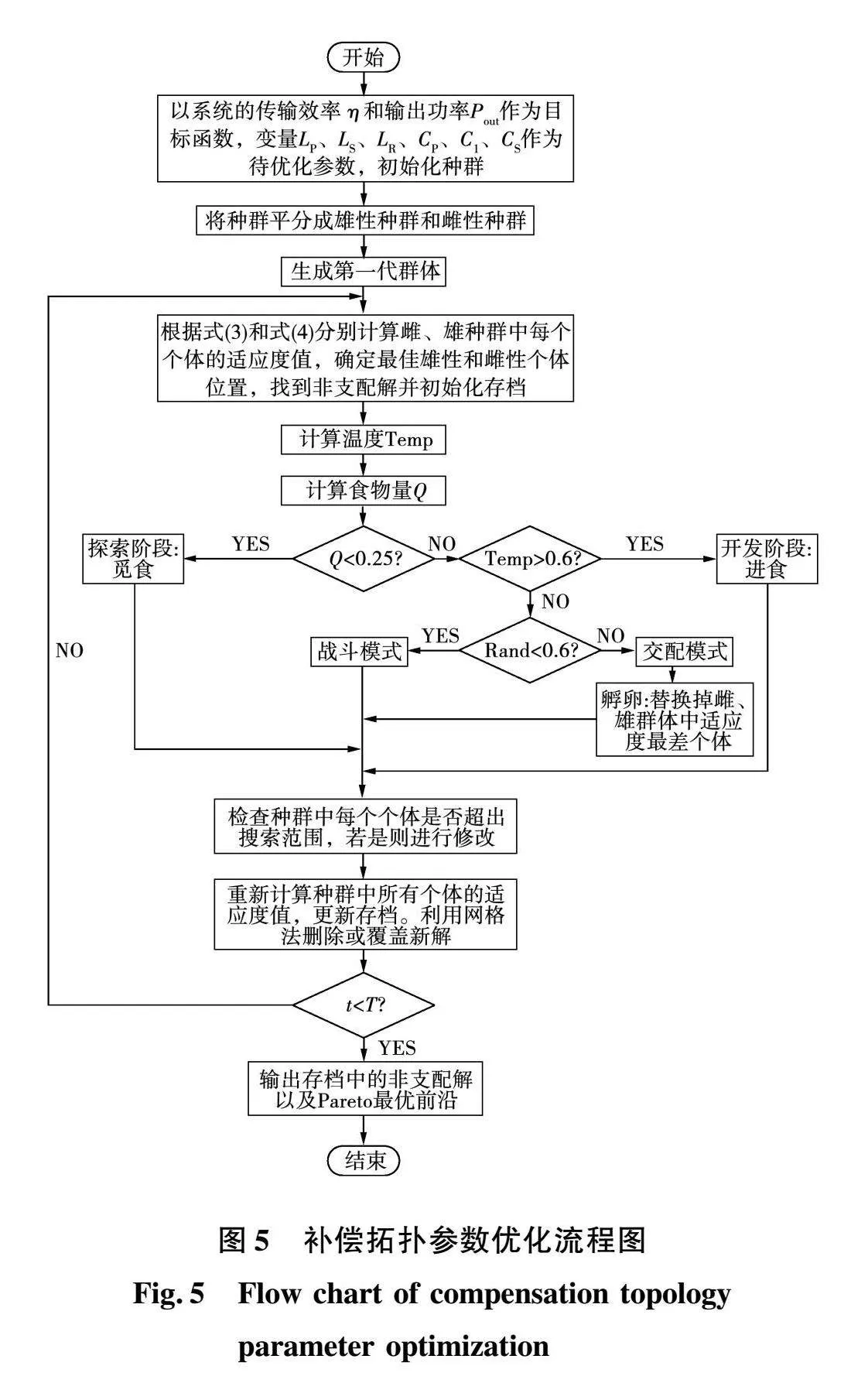
采用MOSO算法对IPT系统补偿拓扑参数进行优化设计的流程如图5所示。

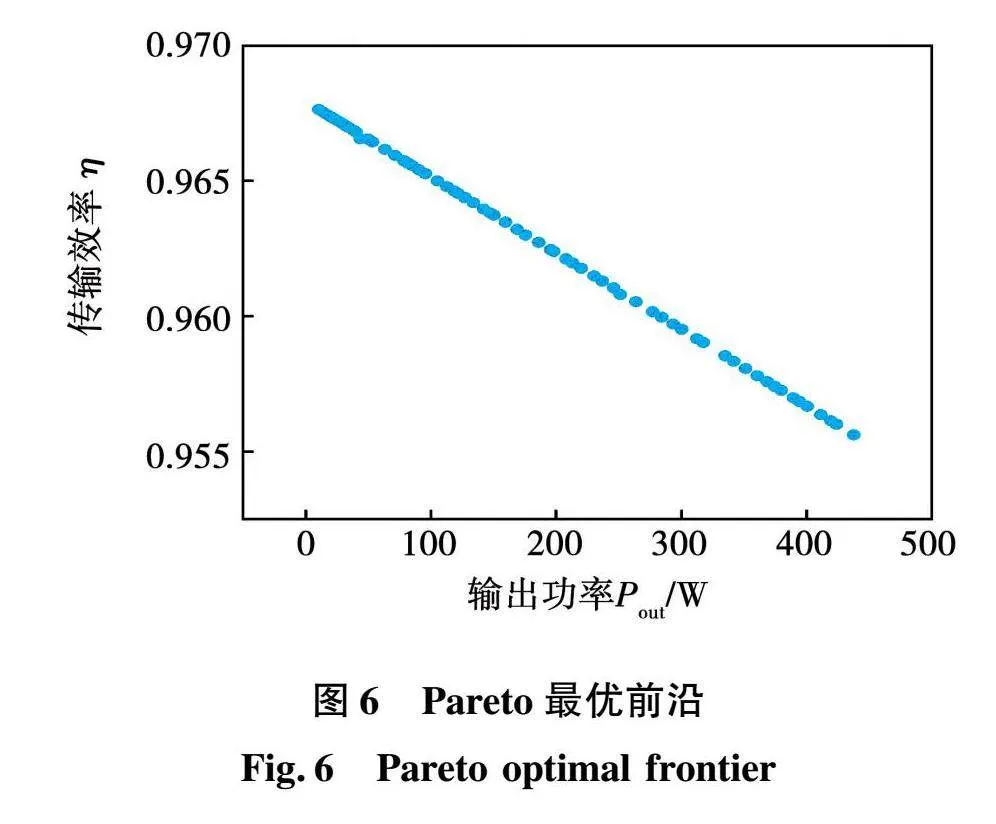
MOSO算法对LCC-S型IPT系统补偿拓扑进行多目标多约束优化得到的Pareto最优前沿如图6所示。

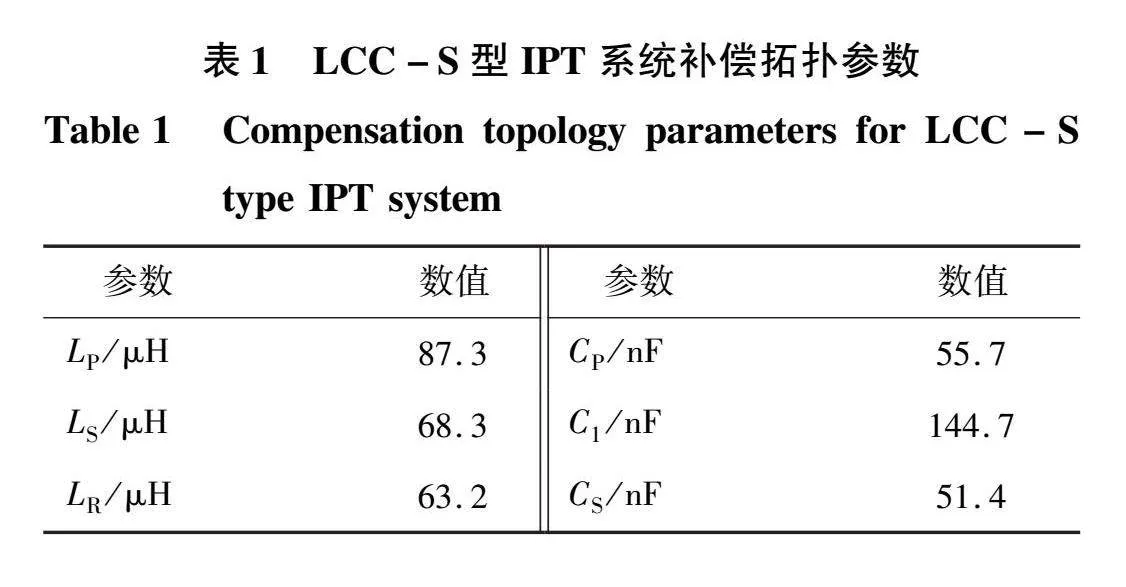
由图6可知，输出功率和传输效率无法同时达到最优，两者之间呈现负相关关系。随着输出功率的增加，传输效率反而减少。依据Pareto解的分布情况分析：各个解之间的平均距离保持适中，种群多样性表现良好。Pareto前沿呈均匀分布的特点，为决策者提供了多样化的选择空间。选定Pout=267.45 W，η=96.7%作为Pareto最优解，其对应的补偿拓扑参数如表1所示。

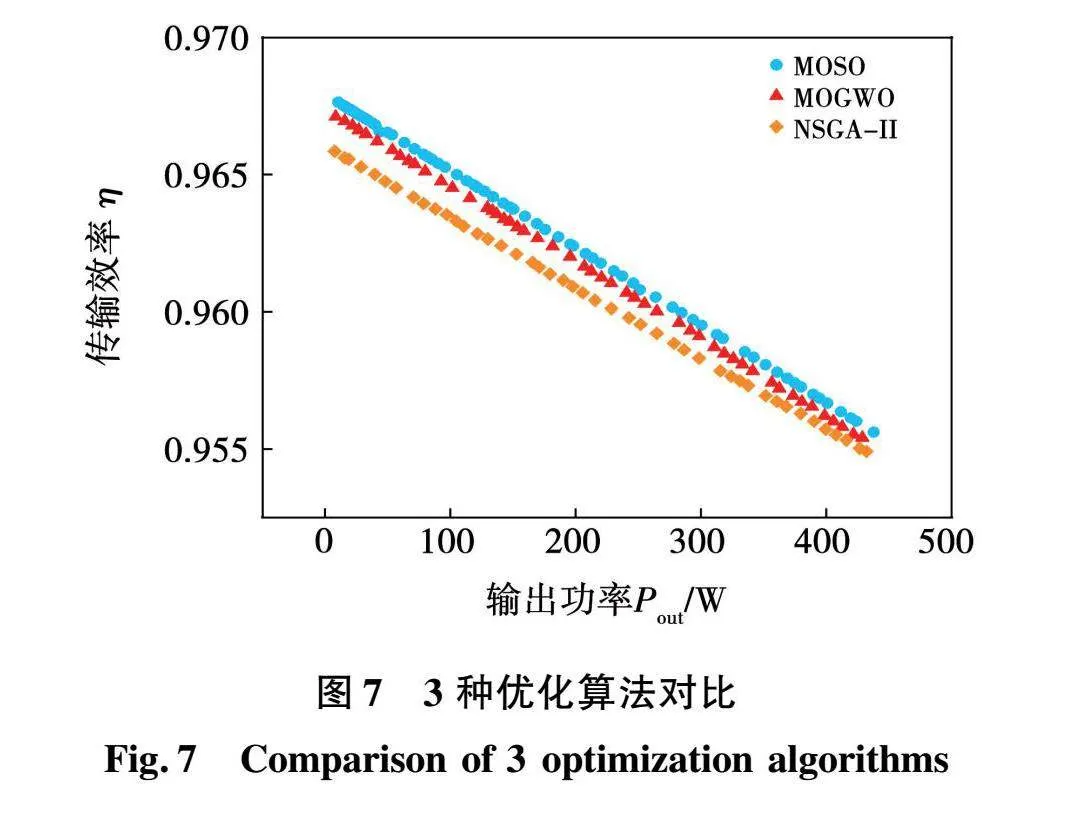
为了验证算法的有效性，本文选择基于多目标蛇算法、多目标灰狼算法（multi-objective grey wolf optimizer，MOGWO）、二代非支配排序遗传算法（non-dominated sorting genetic algorithm-II，NSGA-II）3种优化算法进行参数寻优对比，优化结果如图7所示。

从解的质量来看，本文选用的MOSO算法优化的2个目标函数均高于其他两种算法，也即MOSO算法的Pareto解全部支配了另外两种算法的解。从解的分布来看，MOSO算法求得的解在解空间上分布均匀，解的多样性较好。由此可以看出本文所提算法在解决补偿拓扑参数优化问题方面具有优越性。

3 基于最大功率和最大效率切换控制策略

针对LCC-S型IPT系统在耦合系数变化和负载波动情况下导致系统传输性能下降的问题，本文通过在副边添加有源阻抗匹配网络的方式来实现最大功率和最大效率的切换控制，从而提高系统的传输能效。

3.1 CCM模式有源阻抗匹配网络

3.1.1 两种模式的最佳负载

为获得最大输出功率或最大传输效率，首要任务是确定两种不同工作状态下各自对应的最佳等效负载值。

通过式（3）对Req求导，可得基于最大输出功率的最佳等效负载值为

Rp-max=RS。（9）

由式（9）可知，LCC-S型IPT系统在最大输出功率下的最佳负载为接收线圈内阻RS，与系统的耦合系数和工作角频率均无关。当系统的耦合情况变化时，只需保持最佳等效负载值为RS，即可实现对系统的最大功率跟踪控制。

同理，式（4）对Req求导可得基于最大传输效率的最佳等效负载值为

Rη-max=R2S+ω2k2LPLSRSRP。（10）

由式（10）可知，LCC-S型IPT系统在最大传输效率下的最佳负载随耦合系数动态变化。在耦合系数变化情况下，需要实时调整最佳负载值使得系统工作在最大传输效率状态下。

3.1.2 Buck-boost阻抗匹配网络

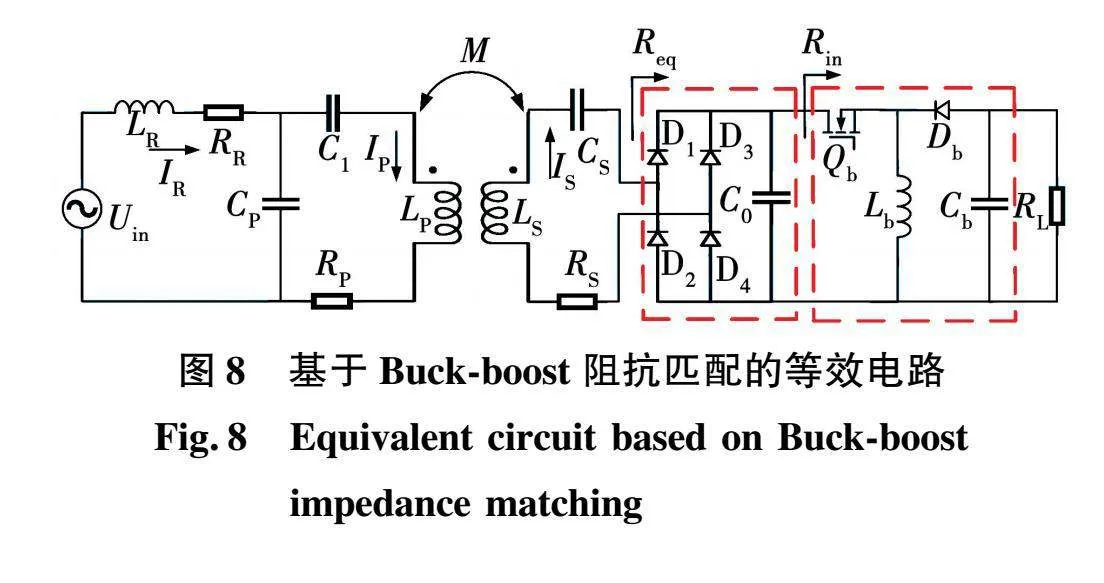
为确保系统在耦合系数及负载条件发生变化时，依然能够实现最大功率或最大效率输出，必须满足实际等效负载与最佳等效负载相匹配。本文采用在整流电路和负载电阻之间加入CCM模式Buck-boost阻抗匹配网络的方式，实现最大功率或最大效率输出。与其他阻抗匹配网络相比，Buck-boost更具优势^[20]。电路结构如图8所示。

系统接收侧的等效阻抗Req与负载电阻RL的关系式为

Req=8π2（1－DD）2RL。（11）

由式（11）可知，通过调节Buck-boost阻抗匹配网络的占空比D，能够改变等效负载Req，当Req=Rp-max或Req=Rη-max，系统可运行在最大功率或最大效率传输状态。

3.2 耦合系数辨识方法

为实现最大功率跟踪或最大效率跟踪的目标，首先要对系统耦合系数进行实时辨识。在系统谐振工作状态下，等效负载电压Ueq表达式为

Ueq=UinMReqLP（Req+RS）=22（1－D）ULπD。（12）

式中：负载两端的输出电压记作UL，求解可得耦合系数k表达式为

k=22LP（Req+RS）（1－D）ULπUinReqLPLSD。（13）

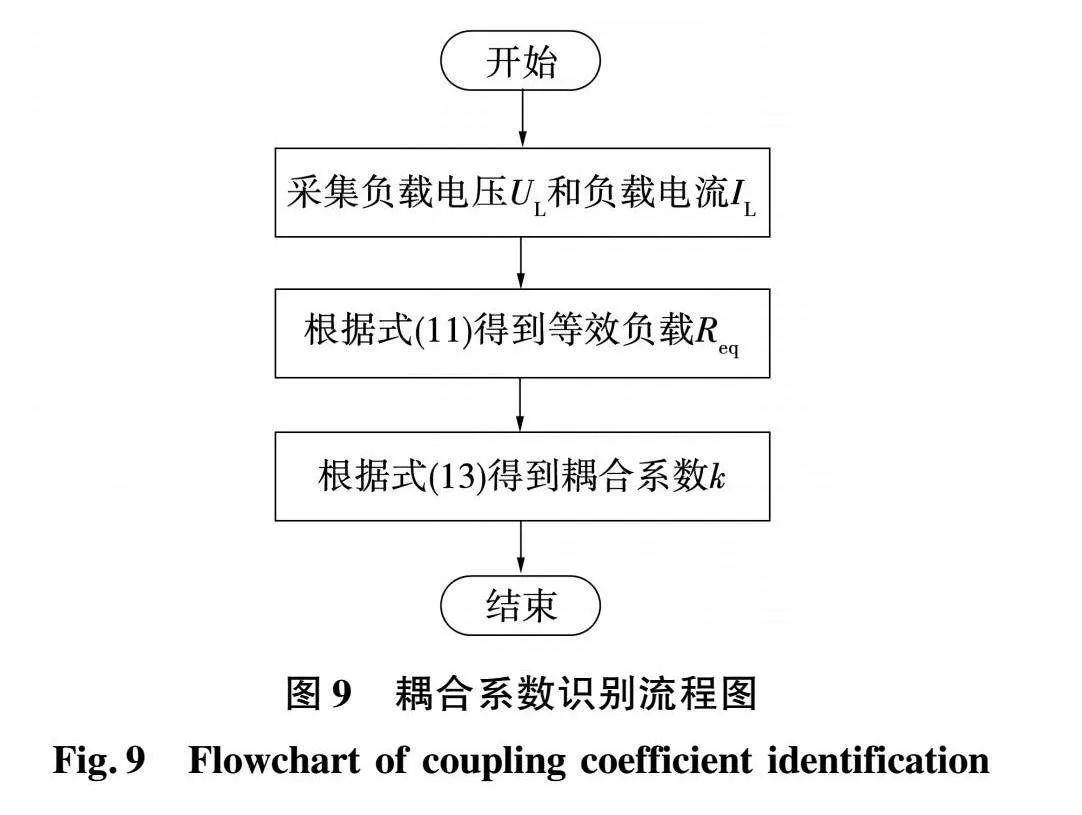
耦合系数动态辨识流程如图9所示。

由图9可知，通过检测接收侧负载的电压和电流UL、IL，即可实现对系统耦合系数k的动态辨识。

3.3 最大功率和最大效率切换控制过程

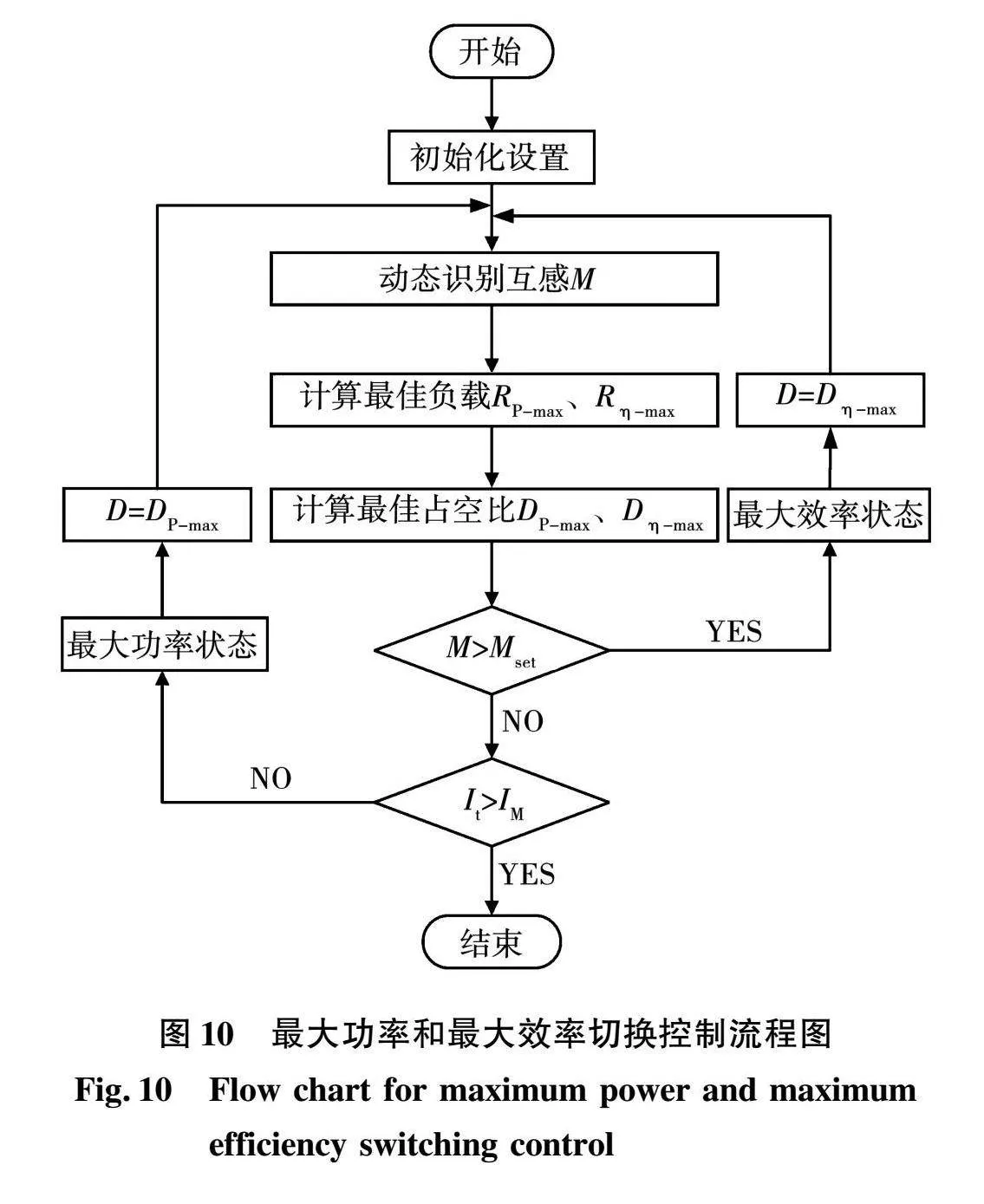
由于负载波动和耦合系数变化，IPT系统在实际工作中，无法同时兼顾输出功率和传输效率。一般在满足负载功率需求的基础上，应尽最大限度提高传输效率。因此，本文提出基于LCC-S型IPT系统的最大功率和最大效率切换控制策略，切换控制流程如图10所示。

当系统耦合系数或负载变化时，采集接收侧负载电压UL和电流IL，结合式（13）对耦合系数k进行动态辨识。根据式（9）和式（10）分别确定最佳负载RP-max、Rη-max值，结合式（11）确定最佳负载分别对应的Buck-boost电路占空比DP-max、Dη-max。将满足负载需求的功率所对应的互感值Mset作为切换点，比较系统实际互感M和Mset的大小。当系统的互感M≤Mset时，调节Buck-boost电路输出占空比DP-max，使得系统工作在最大功率状态；当Mgt;Mset时，调节Buck-boost电路输出占空比Dη-max，使得系统工作在最大效率状态。

本文所提切换控制策略根据系统当前实际耦合情况以及负载条件，动态切换工作模式，以适应不同工况。该控制策略能够有效提升LCC-S型IPT系统对耦合系数的适应性，在耦合较弱的情况下提升系统传输性能使其满足负载功率需求。

4 仿真与实验

4.1 仿真分析

4.1.1 补偿参数优化仿真验证

为验证前文所提补偿参数优化方法的有效性，本研究采用MATLAB和COMSOL软件进行了联合仿真。仿真系统设置如下：输入电压为300 V，谐振频率选定为85 kHz，负载电阻为20 Ω。

利用COMSOL软件建立了耦合机构仿真模型，具体如图11所示。

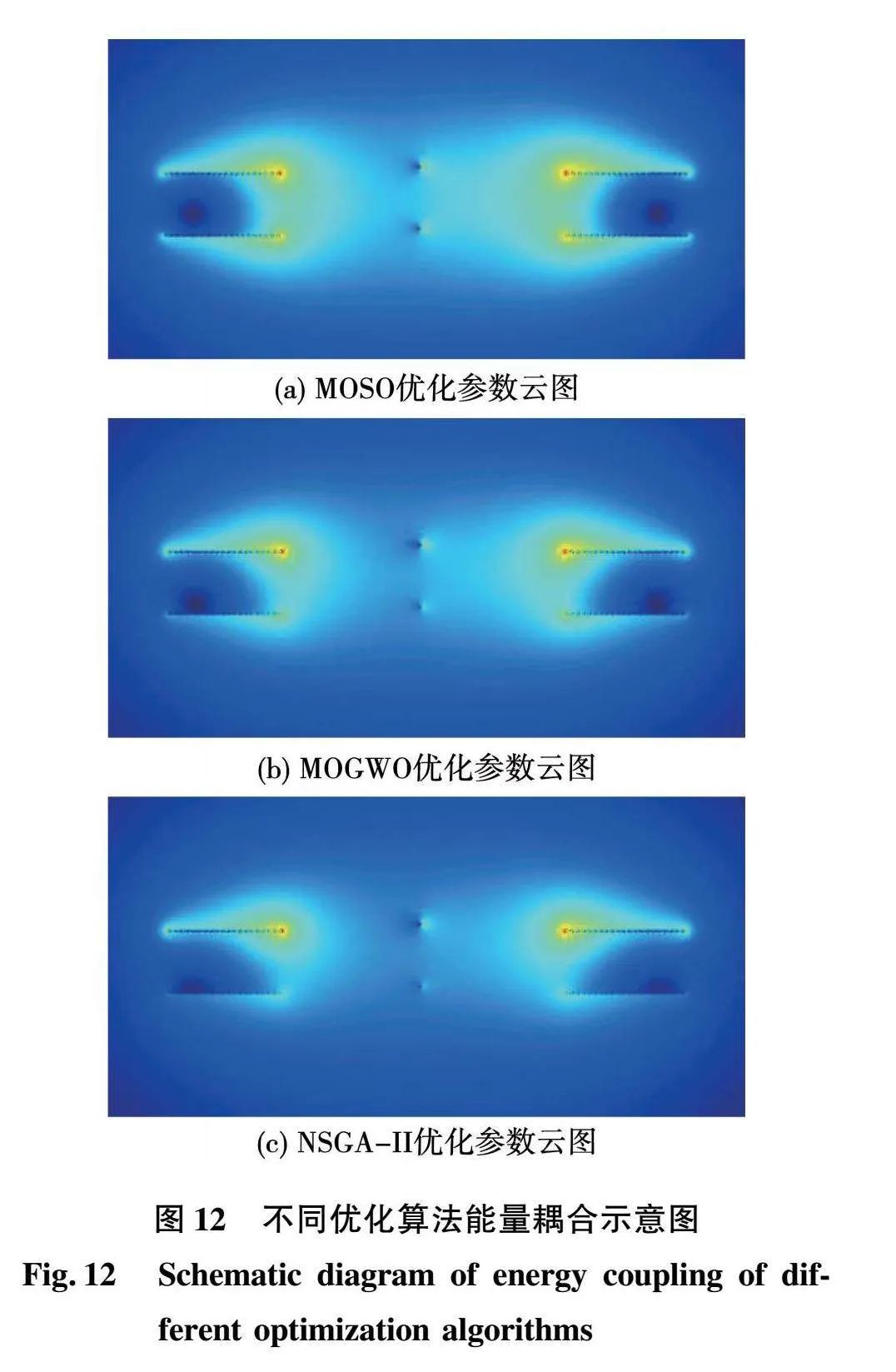
依据3种算法优化得到的LCC-S型补偿参数进行有限元仿真，线圈间能量耦合情况如图12所示。由图12可知，相较于另外2种算法，基于MOSO算法所获得的补偿参数在能量耦合程度上表现出显著优势。

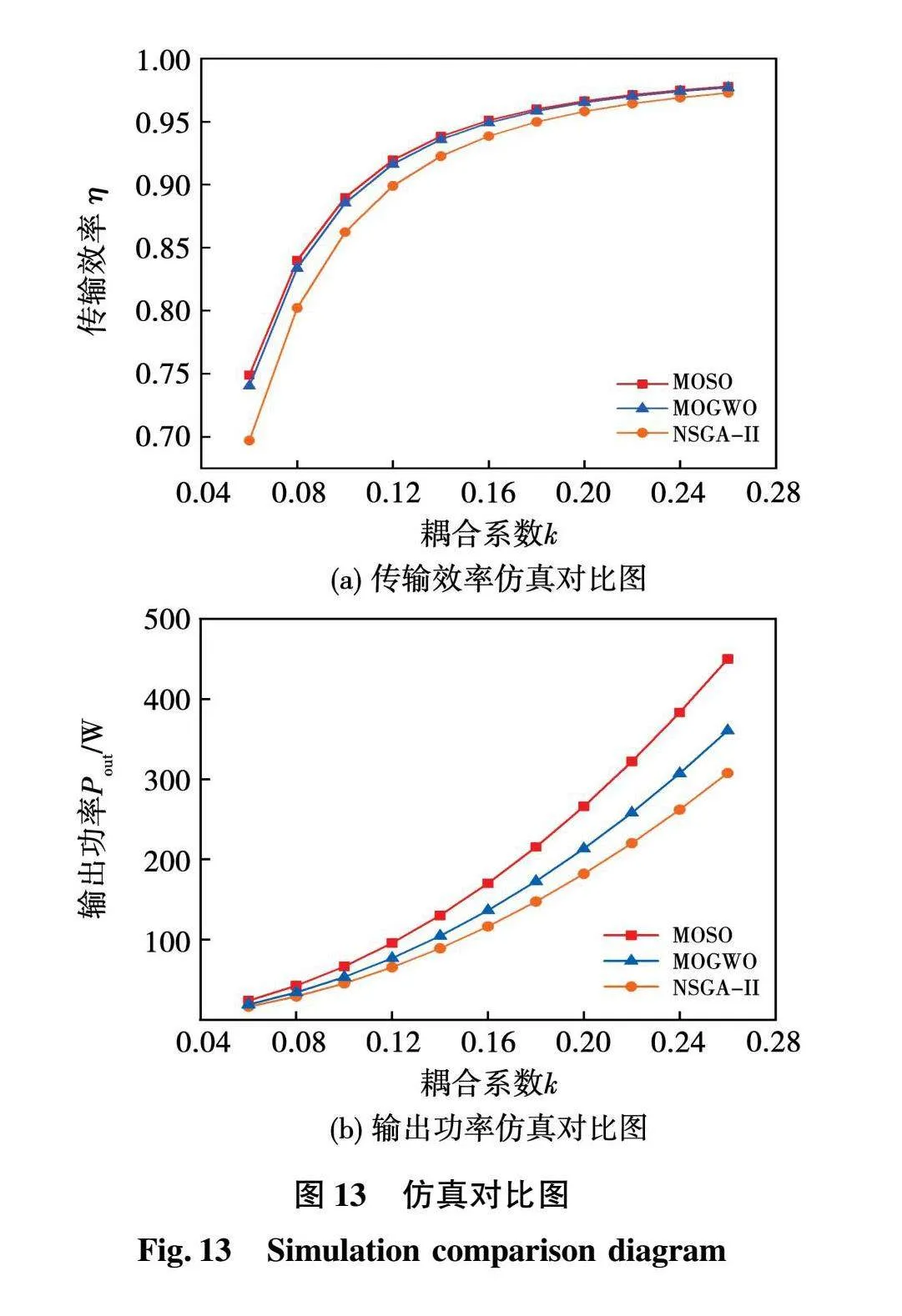
在MATLAB/Simulink软件中搭建如图1所示的电路模型，运用本文所提方法和另外2种算法优化得到的参数值作为补偿拓扑仿真参数。设定耦合系数的变化范围是[0.06，0.26]，分别记录在宽耦合系数范围下3种方法对应的传输效率及输出功率，绘制相应的拟合曲线如图13所示。

由图13可知，本文所提方法相较于另外两种算法，能够在较宽的耦合系数变化范围内获得更高的输出功率和传输效率。特别地，当偏移范围较小时，传输效率提升较为明显；当偏移范围较大时，输出功率提升较为明显。具体地，当耦合系数为0.06时，MOSO算法的传输效率比MOGWO算法提升0.85%，比NSGA-II算法提升5.18%；MOSO算法的输出功率比MOGWO算法提高4.74 W，比NSGA-II算法提高7.56 W。当耦合系数为0.26时，MOSO算法的传输效率比MOGWO算法提升0.09%，比NSGA-II算法提高0.51%；MOSO算法的输出功率比MOGWO算法提高89.08 W，比NSGA-II算法提高141.99 W。

4.1.2 最大功率和最大效率切换控制仿真验证

为了验证本文所提最大功率和最大效率切换控制策略的可行性，基于MATLAB/Simulink建立如图8所示的仿真模型。

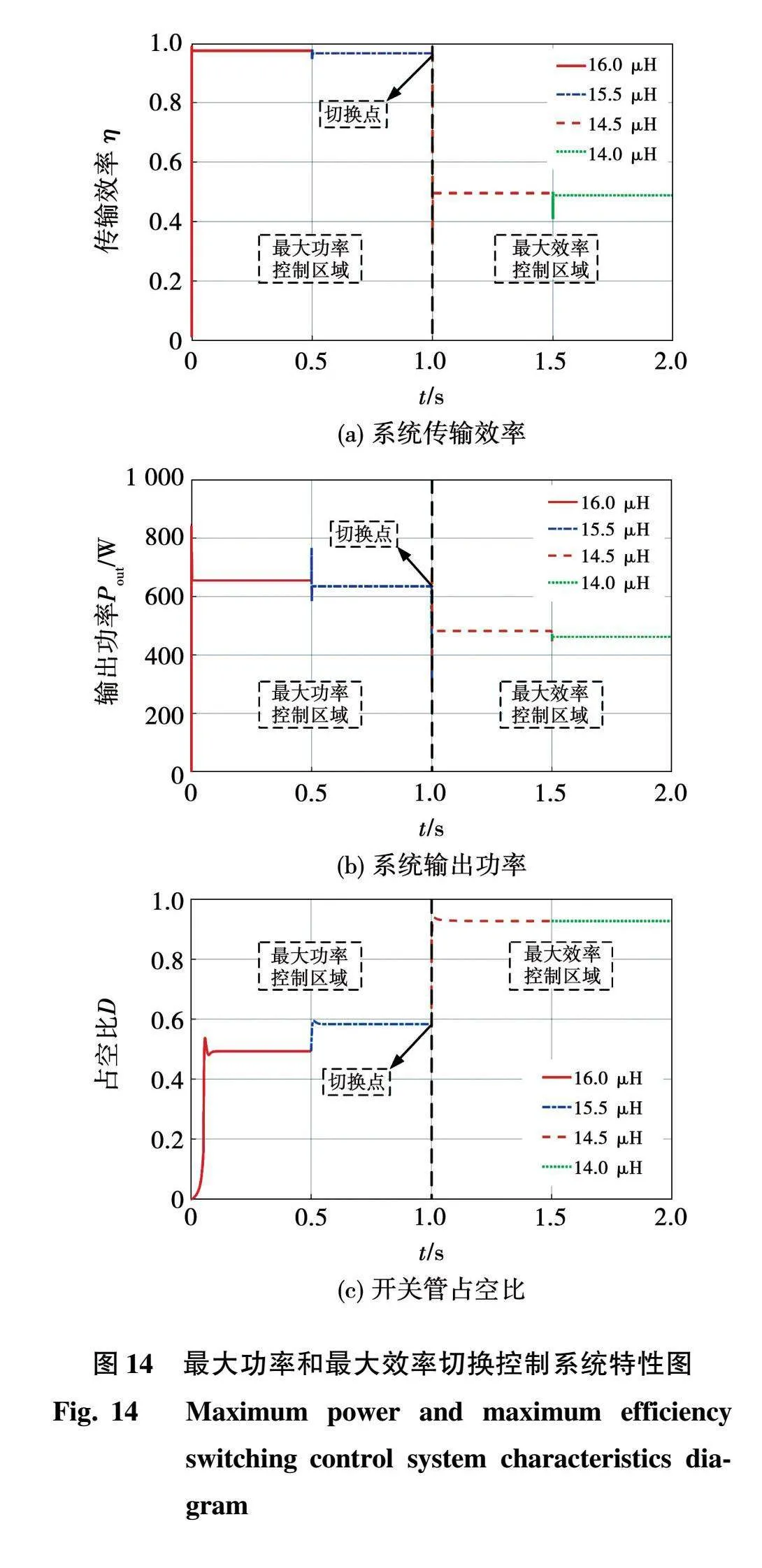
仿真模型中，主电路选用电压型全桥逆变拓扑，系统的补偿拓扑采用LCC-S型，根据MOSO算法优化得到补偿拓扑参数。系统控制器不断检测UL、IL，结合式（13）计算当前耦合系数k，从而得到实时互感值M，再结合式（11）计算Buck-boost电路占空比。根据负载的功率需求，计算可得两种模式的切换点为Mset=15 μH，设定负载阻值为20 Ω，令互感值以0.5 μH的步长从16 μH减小至14 μH。仿真结果如图14所示。

由图14可知，当互感值大于切换点Mset时，系统工作在最大效率状态。此时系统传输效率大于90%，输出功率远高于负载功率需求。在该状态下，随着互感的略微减小，输出功率和传输效率变化不大，占空比从58%减小至49%。当互感值减小至切换点Mset以下，系统切换至最大功率状态。此时系统传输效率下降至50%，系统传输性能虽然大幅下降，但输出功率依然能够满足负载需求。在该状态下，随着互感的略微下跌，输出功率和传输效率变化甚微，占空比维持在92%保持不变，此时系统的最佳负载值不会随着互感波动而发生变化。

4.2 实验验证

为了进一步验证本文所提方法的有效性和正确性，依据表1及4.1节中的仿真参数设定，建立了如图15所示的LCC-S型IPT系统实验平台。

系统选用TMS320F28335型DSP数字信号处理器作为控制器，负责信号的采集任务、控制算法的实现以及PWM波的生成工作。耦合机构是由16匝利兹线绕制的圆形螺旋线圈，线圈之间的互感使用Chroma 11050-5M高频LCR测试仪进行测量，采用Tektronix MSO 2024B示波器测量负载两端电压，结合RP1001C电流探头测量负载电流。

4.2.1 补偿参数优化实验

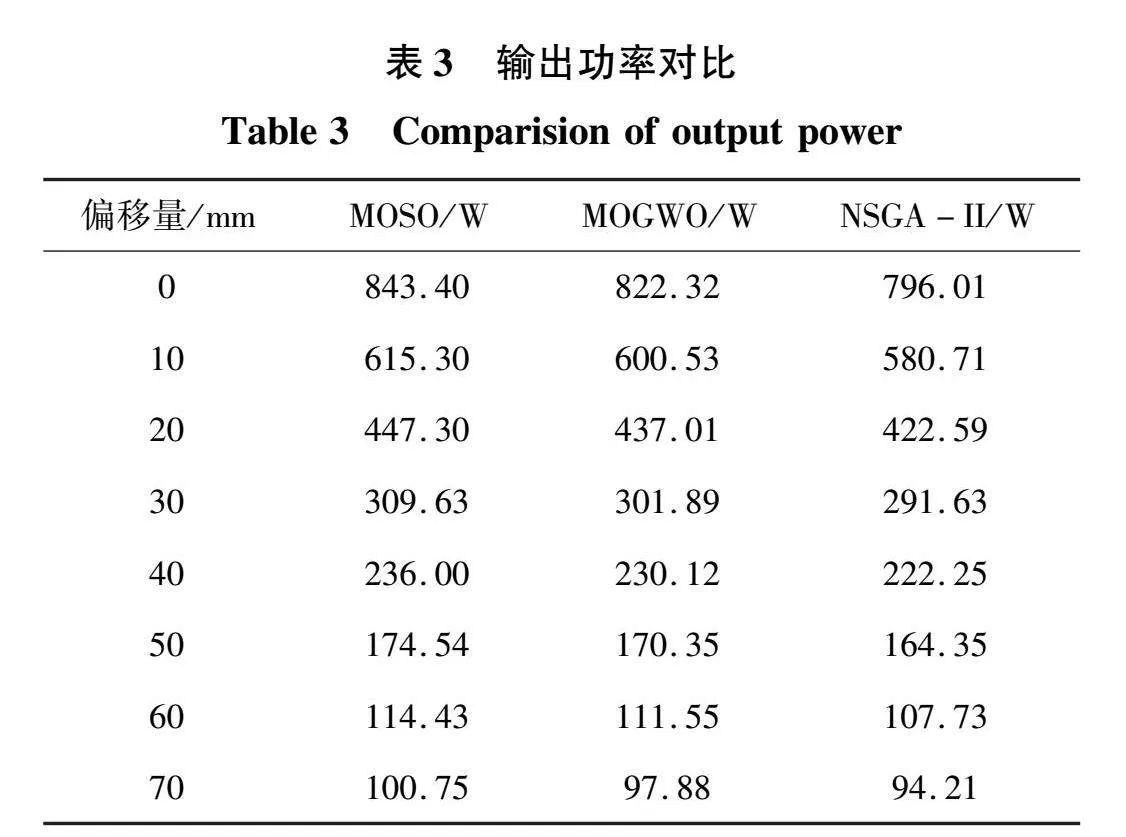
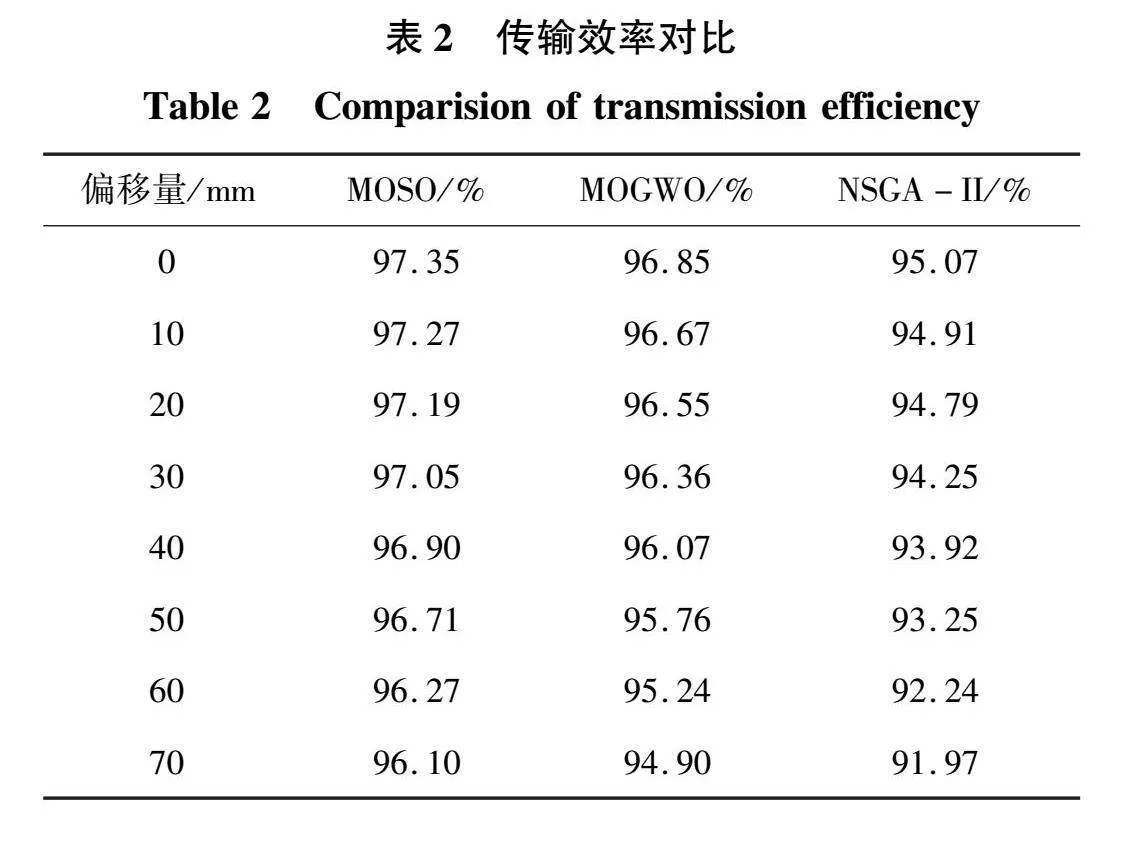
基于上述实验平台，在收发线圈间距d=[0，70]mm范围内每间隔10 mm对本文提出的方法与另外2种方法开展对比实验，得到8组系统传输效率和输出功率的比较结果分别如表2、表3所示。

由表2可知，在相同的运行条件下，与MOGWO和NSGA-II算法相比，基于MOSO算法设计的LCC-S补偿拓扑参数，在不同偏移情况下均能提高系统传输效率。当偏移量为0 mm时，MOSO算法的传输效率为97.35%，比MOGWO算法高0.5%，比NSGA-II算法高2.28%。随着偏移量的增大，MOSO算法的优势越明显。当偏移量为70 mm时，MOSO算法的传输效率为96.10%，比MOGWO算法高1.2%，比NSGA-II算法高4.13%。此外，基于MOSO算法设计的系统随着偏移量的增大，系统传输效率波动最小，约为1.25%。

由表3可知，本文所提方法在[0，70]mm横向偏移范围内均能实现更高的功率输出。当偏移量为0 mm时，MOSO算法的输出功率为843.40 W，较MOGWO算法高21.08 W，较NSGA-II算法高47.39 W。当偏移量为70 mm时，MOSO算法的输出功率为100.75 W，较MOGWO算法高2.87 W，较NSGA-II算法高6.54 W。且当横向偏移量达到70 mm时，基于MOSO算法设计的系统，依然能够满足负载功率需求。

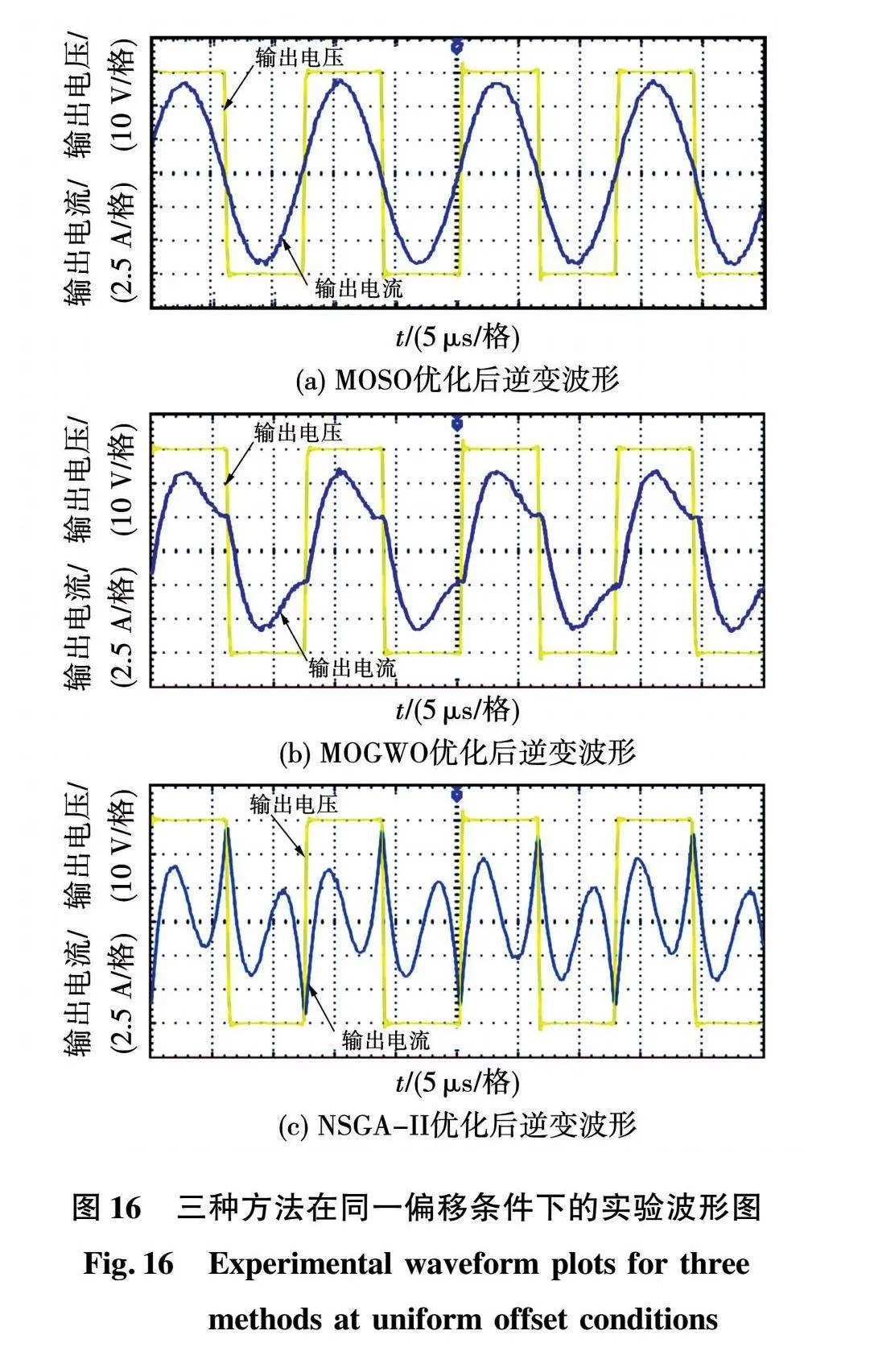
根据MOSO算法、MOGWO算法、NSGA-II算法三种方法获得的补偿拓扑参数搭建的系统在偏移距离d=60 mm（k≈0.22）时分别进行实验，系统逆变输出的电压及电流波形如图16所示。

由图16可知，在同一偏移距离下，对比三种方法优化所得的补偿拓扑参数对系统传输性能的影响，可见采用本文所提方法获得的补偿拓扑参数搭建的系统处于完全谐振状态，逆变电压和电流几乎不存在相位差，且相较于另外两种情况，逆变电流的波形近似正弦波，畸变程度明显更低，减小了谐波损耗，有利于系统高效率运行。

4.2.2 最大功率和最大效率切换控制实验

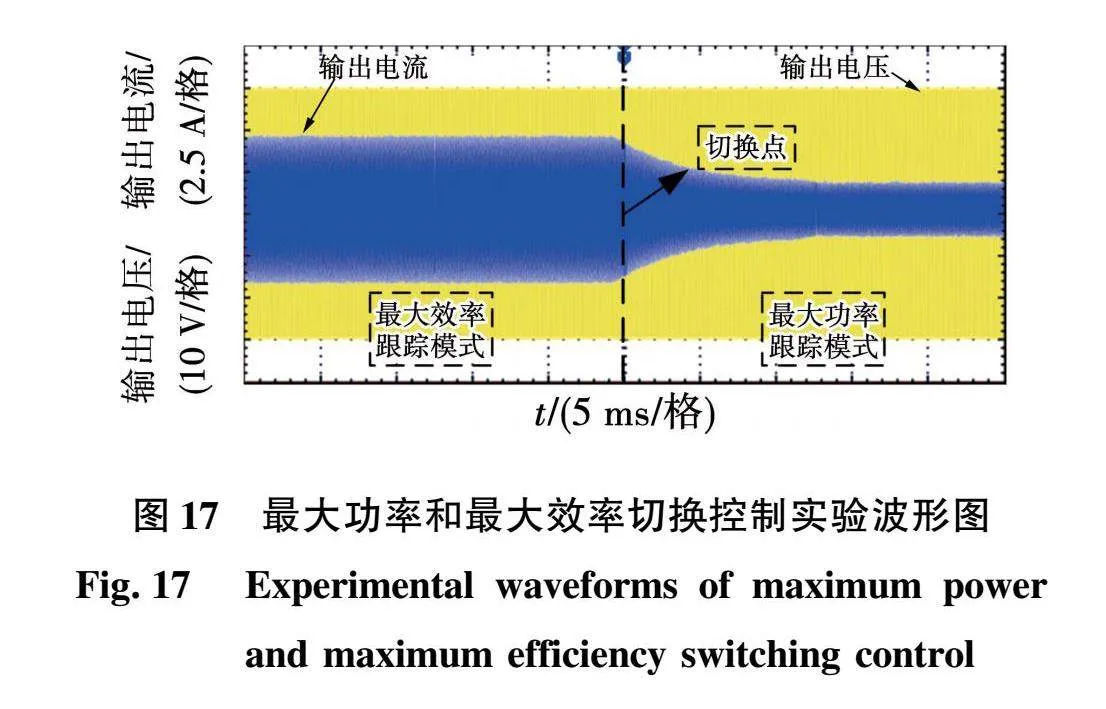
基于IPT系统实验平台，开展最大功率和最大效率切换控制实验。在保证输入电压恒定的情况下，验证当系统互感变化时，所提最大功率和最大效率切换控制策略的有效性。系统逆变输出的电压和电流波形如图17所示。

图17中，黄色为逆变输出电压，蓝色为逆变输出电流。当收发线圈的耦合状态较好，也即当前互感大于切换点时，系统处于最大效率跟踪模式。当收发线圈相对位置变化使得系统的互感跌落至切换点以下，系统切换至最大功率跟踪模式。从最大效率跟踪模式转换至最大功率跟踪模式，因系统的最佳负载值由Rη-max降低至RP-max=RS，逆变器的电流也会随之迅速减小。实验与仿真效果保持一致，所提控制策略能依据系统当前实际耦合情况，实现在最大效率和最大功率两种工作模式之间的动态切换，以此提升系统的传输能效，满足负载功率需求。

4.3 与现有技术对比

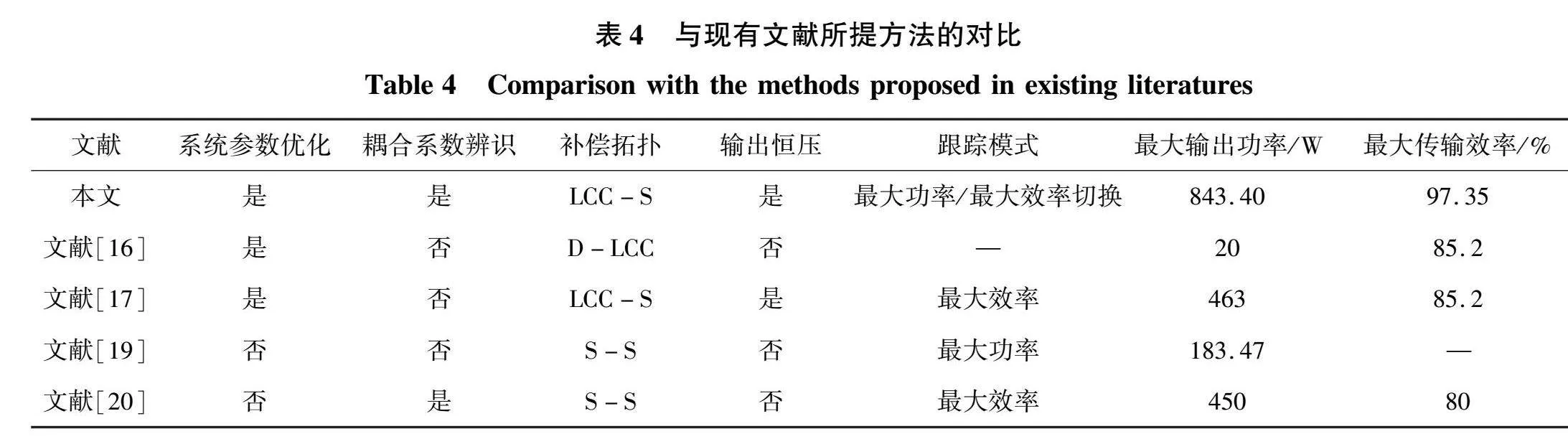
本文所提方法与现有文献介绍的其他方法对比结果如表4所示。IPT系统的传输性能与补偿拓扑参数紧密相关，文献[19-20]无法实现恒压输出，同时也没有对系统参数进行优化设计。文献[16]尽管从补偿拓扑参数优化层面提升了系统的传输效率，但并未引入控制策略实现实时最大效率追踪。为了保证系统在收发线圈发生偏移情况下仍能保持较优的传输性能，首先要对系统实际互感进行准确估算。文献[17]仅实现了系统参数优化，未对耦合系数进行实时辨识，无法应对动态无线电能传输情况。当系统耦合系数变化或负载发生波动时，需要结合控制策略提升系统的传输能效。文献[19]虽然采用最大功率跟踪方法来提升系统的输出功率，但并未考虑到系统的传输效率。与文献[20]相比，最大功率和最大效率切换控制策略相比较单一的最大功率追踪或最大效率追踪方法，在满足负载功率需求的同时，能够有效提升系统的传输效率，更具实际应用价值。综上，本文所提方法贡献在于从补偿拓扑和控制策略两个层面来提升系统的传输性能，不仅能够实现静态无线充电，同时也能适应动态充电情况，使得IPT系统在线圈相对位置变化或负载发生波动时，仍能保持高效稳定运行。

5 结 论

本文提出了IPT系统多目标参数优化与控制策略研究方法。首先，基于互感理论建立LCC-S型IPT系统数学模型，考虑谐振条件和负载需求约束建立了多目标优化模型。采用多目标蛇算法对LCC-S型高阶补偿拓扑进行多目标参数优化，使得输出功率和传输效率达到最优；在此基础上，引入最大功率和最大效率切换控制策略。即通过在整流器和负载之间添加Buck-boost变换器的方式来实现最大功率跟踪或最大效率跟踪。根据互感大小的不同，控制CCM模式变换器占空比匹配不同的最佳等效负载，实现两种模式之间的切换。该方法有效解决了因耦合系数变化及负载波动所引起的系统传输性能下降问题，在系统耦合情况较差的情形下仍然能够保证负载功率满足需求。

仿真和实验结果表明，本文所提方法在参数设计上相比其他方法具有一定优越性，在控制策略上相比单一工作模式，两种模式动态切换更能满足实际应用需求，为IPT系统在补偿拓扑与控制策略的设计上提供了参考依据。

参 考 文 献：

［1］ LI S， WANG L， GUO Y，et al. Flexible energy-transfer control of dynamic wireless power transfer system based on estimation of load and mutual inductance[J]. IEEE Transactions on Industry Applications， 2022， 58（1）： 1157.

［2］ 黄文聪， 饶天彪， 蒋煊焱， 等. 无线电能传输系统最大效率追踪及恒压输出复合控制方法[J]. 电工技术学报， 2024， 39（12）： 3589.

HUANG Wencong， RAO Tianbiao， JIANG Xuanyan， et al.Maximum efficiency tracking and constant voltage output compound control method for wireless power transfer system[J]. Transactions of China Electrotechnical Society， 2024， 39（12）： 3589.

［3］ 李争， 唐明磊， 解波， 等. 无线电能传输零电压开关角跟踪和动态电容补偿矩阵复合控制策略[J]. 电工技术学报， 2024， 39（12）： 3602.

LI Zheng， TANG Minglei， XIE Bo， et al.Composite control strategy of zero voltage switch angle tracking and dynamic capacitance compensation matrix for wireless power transfer[J]. Transactions of China Electrotechnical Society， 2024， 39（12）： 3602.

［4］ WEI G， FENG J， ZHANG J，et al. An efficient power and data synchronous transfer method for wireless power transfer system using double-D coupling coil[J]. IEEE Transactions on Industrial Electronics， 2021， 68（11）： 10643.

［5］ 姚友素， 曾明， 李刚， 等. 无线电能传输系统恒流/恒压输出切换方法[J]. 电机与控制学报， 2023， 27（6）： 8.

YAO Yousu， ZENG Ming， LI Gang， et al.Switching method from constant current mode to constant voltage mode for wireless power transfer system[J]. Electric Machines and Control， 2023， 27（6）： 8.

［6］ 靖永志， 冯伟， 谯柯，等. 基于S/LCC补偿的无线能量与信号反向同步传输系统[J]. 电机与控制学报， 2022， 26（7）： 37.

JIN Yongzhi， FENG Wei，QIAO Ke， et al. Wireless power and date reverse synchronous transmission system based on S/LCC compensation[J]. Electric Machines and Control， 2022， 26（7）： 37.

［7］ 吴凡. 具有耦合系数自适应性的最大效率与最大功率切换策略研究及实现[D]. 重庆：重庆大学， 2019.

［8］ ROY S， AZAD A N M W， BAIDYA S， et al. Powering solutions for biomedical sensors and implants inside the human body： a comprehensive review on energy harvesting units， energy storage， and wireless power transfer techniques[J]. IEEE Transactions on Power Electronics， 2022， 37（10）： 12237.

［9］ 靖永志， 谯柯， 付康， 等. 基于部分能量耦合线圈的无线能量与信号同步传输方法研究[J]. 电机与控制学报， 2024， 28（7）： 43.

JIN Yongzhi， QIAO Ke， FU Kang， et al.Research on simultaneous wireless power and data transfer method based on partial power coupling coil[J].Electric Machines and Control，2024，28（7）：43.

［10］ CAMPI T， CRUCIANI S， MARADEI F， et al. Centralized high power supply system for implanted medical devices using wireless power transfer technology[J]. IEEE Transactions on Medical Robotics and Bionics， 2021， 3（4）： 992.

［11］ 谢诗云， 杨奕， 李恋， 等. 基于双极性耦合磁场调控的高抗偏移偏转无线电能传输系统[J]. 电工技术学报， 2023， 38（18）： 4838.

XIE Shiyun， YANG Yi， LI Lian， et al.Wireless power transfer system with high misalignment tolerance based on bipolar coupling magnetic-field control[J]. Transactions of China Electrotechnical Society， 2023， 38（18）： 4838.

［12］ LIU Z， WANG L， GUO Y， et al. Primary-side linear control for constant current/voltage charging of the wireless power transfer system based on the LCC-N compensation topology[J]. IEEE Transactions on Industrial Electronics， 2022， 69（9）： 8895.

［13］ WU M， YANG X， CHEN W，et al. A dual-sided control strategy based on mode switching for efficiency optimization in wireless power transfer system[J]. IEEE Transactions on Power Electronics， 2021， 36（8）： 8835.

［14］ LI H， XU J， GAO F， et al.Duty cycle control strategy for dual-side LCC resonant converter in wireless power transfer systems[J]. IEEE Transactions on Transportation Electrification， 2022， 8（2）： 1944.

［15］ 吝伶艳， 方成刚， 宋建成， 等. 磁谐振无线输电系统不同补偿方式的传输特性[J].电机与控制学报，2019，23（12）：59.

LIN Lingyan， FANG Chenggang， SONG Jiancheng， et al. Transmission characteristics of different compensation methods in wireless power transfer system based on magnetic coupling resonance[J]. Electric Machines and Control， 2019， 23（12）： 59.

［16］ 陈晓娟， 贾敏， 李明晨. 基于线圈偏移的无线电能传输系统参数优化方法[J]. 中国电力， 2021， 54（7）： 125.

CHEN Xiaojuan， JIA Min， LI Mingchen. Coil offset based wireless power transfer system parameter optimization[J]. Electric Power， 2021， 54（7）： 125.

［17］ 田勇， 朱泽， 田劲东， 等. 基于LCC-S补偿的电动汽车动态无线充电系统拓扑参数优化[J]. 机械工程学报， 2021， 57（14）： 150.

TIAN Yong， ZHU Ze，TIAN Jindong， et al. Parameters optimization of electric vehicles dynamic wireless power transfer system based on LCC-S compensation topology[J]. Journal of Mechanical Engineering， 2021， 57（14）： 150.

［18］ 黄文聪， 胡滢， 黄津莹， 等. WPT系统的最大功率与最大效率切换控制策略[J]. 广西电力， 2022， 45（3）： 23.

HUANG Wencong， HU Ying， HUANG Jinying， et al. A maximum power and maximum efficiency switching control strategy of WPT system[J]. Guangxi Electric Power， 2022， 45（3）： 23.

［19］ 王喜升， 侯钰慧， 郭波超， 等. 无线电能传输系统基于Buck-Boost拓扑的最大功率传输研究[J]. 电子技术应用， 2022， 48（10）： 129.

WANG Xisheng， HOU Yuhui， GUO Bochao， et al. Research on maximum power transfer of wireless power transfer system based on Buck-boost topology[J]. Circuits and Systems， 2022， 48（10）： 129.

［20］ 赵进国， 赵晋斌， 张俊伟， 等. 无线电能传输系统中有源阻抗匹配网络断续电流模式最大效率跟踪研究[J]. 电工技术学报， 2022， 37（1）： 24.

ZHAO Jinguo， ZHAO Jinbin， ZHANG Junwei， et al. Maximum efficiency tracking study of active impedance matching network discontinous current mode in wireless power transfer system[J]. Transactions of China Electrotechnical Society，2022，37（1）： 24.

［21］ HASHIM F A， HUSSIEN A G. Snake optimizer： a novel meta-heuristic optimization algorithm[J]. Knowledge-Based Systems， 2022， 242： 108320.

（编辑：刘素菊）