一类线性微分方程解的增长性及Borel方向

魏文龙，杨琰琰，黄志刚

（苏州科技大学 数理学院，江苏 苏州 215009）

1 主要结果

文中将考虑二阶线性微分方程

其中A和B都是整函数。文中使用Nevanlinna值分布及角域上值分布的标准记号[1-2]，用T（r，f）表示亚纯函数f的特征函数，用σ（f），μ（f）分别表示整函数在全平面上的增长级和下级。

定义1[3-4]设0≤α＜β＜2π，复平面上的角域定义为

若f是整函数，记

f在角域上、径向上的增长级分别定义为

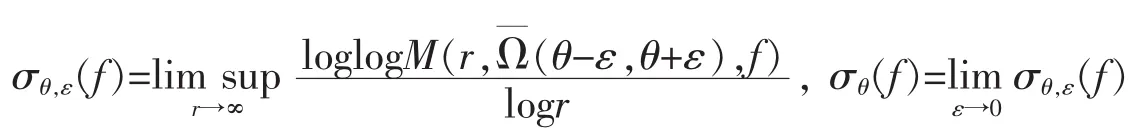
定义2[5]设f（z）在开平面|z|＜∞上的一个σ（σ≥0）级亚纯函数，如果对任意小的ε＞0和任意复数a，都有，至多除去两个值a例外，则称从原点出发的射线argz=θ是整函数f（z）的 1 条 σ（σ≥0）级 Borel方向。

定义 3[6-7]设 f（z）是角域 Ω（α，β）上的亚纯函数，0＜β＜α≤2π，k=π/（β-α），定义

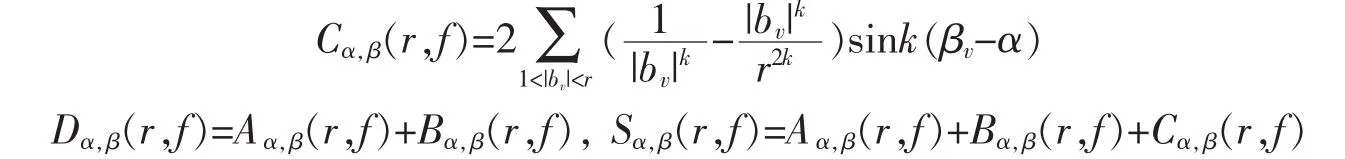
亚纯函数 f（z）在角域 Ω（α，β）上的级定义为

目前，有学者研究了二阶线性微分方程（1），考虑方程非零解的增长级为无穷的情形。由于方程中系数函数A（z）和B（z）对方程解起到决定性作用，因此，学者致力于研究当方程系数满足什么情形时，可以得到方程的任一非零解都是无穷级。 得到结论：若 A（z）和 B（z）都是整函数且 σ（A）＜σ（B）；或者 A（z）是多项式，B（z）是超越整函数；或者 σ（B）＜σ（A）＜1/2，则方程（1）的所有非零解都是无穷级。 文献[8]考虑了当 P（z）是 n次多项式，A（z）是方程 f″+P（z）f=0 的非零解，B（z）是超越整函数且 σ（B）＜1/2，同样得出方程（1）的每一个非零解都是无穷级。在此基础之上文献[9]将结论推广到了高阶方程中，使得高阶方程的任一非零解也是无穷级。之后，有学者开始研究方程解在角域内的增长性，文献[3]得出方程解在角域内增长级为无穷的充要条件。于是对于方程解在角域内的研究也逐渐展开，文献[10]研究了二阶线性微分方程的解在角域内的增长级和Borel方向的关系，并给出了如下结论。

定理 A[10]设 A（z）和 B（z）为有限级整函数，Ω（α，β）（0＜β-α≤2π）为某一角域；若 A（z）和 B（z）在Ω（α，β）内满足条件：∃θ∈（α，β），使得 argz＝θ为 B 的 1 条 λ（0＜λ≤σ（B））级 Borel方向，且 σα，β（Α）＜λ，则对方程 f″+Af′+Bf=0 的任一非平凡解 f，有 σα，β（f）＝∞，且 argz＝θ为 f的 1 条 ∞ 级 Borel方向。

随后，文献[11]考虑了高阶方程 f（n）+An-1f（n-1）+…+A0f=0 非零解在角域内的增长性和 Borel方向之间的关系，得到了下面的结论。

定理 B[11]设 A0，A1，…，An-1为有限级整函数，Ω（α，β）（0＜β-α≤2π）为某一角域，若 A0，A1，…，An-1在Ω（α，β）内满足条件：∃θ∈（α，β），使得 argz＝θ为 A0的 1 条 λ（0＜λ≤σ（A0）级 Borel方向，且 σα，β（Αj）＜λ（j＝1，2，…，n-1），则方程 f（n）+An-1f（n-1）+…+A0f=0 的任一非平凡解 f，有 σα，β（f）＝∞ 且 argz＝θ为 f的 1 条 ∞ 级Borel方向。

上述定理证明了微分方程在系数满足一定条件下，方程非平凡解在角域内的增长级是无穷，且系数和解具有相同的Borel方向，但只证明了公共Borel方向的存在性。那么如果继续考虑方程解和系数在角域内的公共Borel方向，是否能得到更多的公共Borel方向呢？

定理 1二阶线性微分方程 f″+Af′+Bf=0，设 A（z），B（z）为有限级整函数，如果 σ（B）＞1/2 和 B 有一个亏值，则存在一个夹角大于 π/σ（B）的角域 Ω（α，β），使得 f至少有两条 Borel方向。

2 相关引理

引理1[2]设f（z）为开平面亚纯的有穷正级函数且具有一个亏值。若级λ＞1/2，则其Borel方向至少有两条，且在这些方向中存在两条，夹角不超过π/λ。

引理2[12]设 f（z）为角域 Ω（α，β）（0＜β-α≤2π）上的非常数亚纯函数，则∀aj∈C∞，j＝1，2，…，q，有

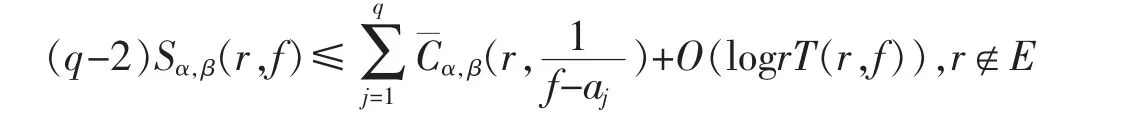
其中E是一个线性测度有限的集合。

引理 3[13]设 f（z）是一个角域内具有有限级 σ 的亚纯函数，Γ={（n1，m1），（n2，m2），…，（nj，mj）}表示满足 nj＞mj≥0（i＝1，2，…，j）的不同整数对的有限集。 设 ε＞0 和 δ＞0 为给定的正常数，则存在只与 f，ε 和 δ

有关的常数K＞0，使得

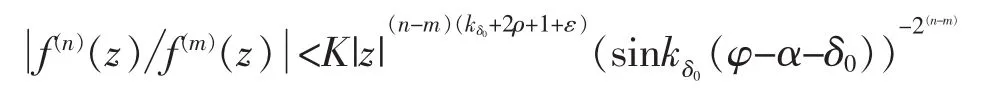
成立，其中（n，m）∈Γ，z＝reiφ∈Ω（α+δ，β-δ），z∉D，D 为由可数个半径之和为有限的圆盘并构成的一个 R-值集，kδ=π/（β-α-2δ）。

引理 4[5]设 f（z）是级 0＜σ≤∞ 的亚纯函数，假定 B：argz＝θ0（0≤θ0≤2π）为 f（z）的 1 条 σ 级 Borel方向，则在以原点为顶点，以 argz＝θ0为角平分线的任意小角域 Ω（θ0-ε，θ0+ε）内，存在 1 列 σ 级充满圆，使得在每个 Γm内，f（z）可取任意复数至少 nm次，至多可能除去一些复数含于球面半径为的 2 个圆内，其中

3 定理1的证明

对于方程

通过变形得到

于是两边同时取模并运用三角不等式有

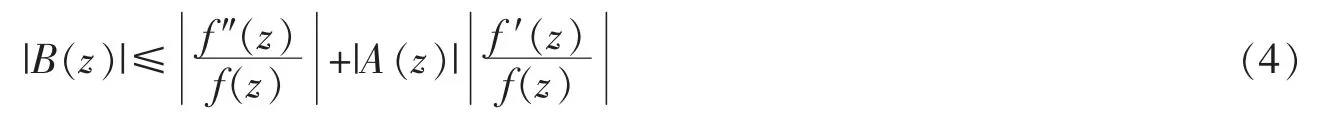
根据引理 1，因为 1/2＜σ（B）＜∞，且 B（z）有一个亏值，则 B（z）的 Borel方向至少有两条，且这些方向中存在两条，夹角不超过 π/σ（B），且令 σ（B）＝σ1。 所以存在一个夹角超过 π/σ1的角域记为 Ω（α，β），在角域Ω（α，β）内至少存在 B（z）的两条 Borel方向。

假设 σα，β（f）＝ρ＜∞，argz＝θ0（θ0∈（α，β））为 B（z）的一条 σ（B）（＜∞）级 Borel方向。

根据引理 3，取 δ0＞0，使得 θ0∈（α+δ0，β-δ0）。 对于 z＝reiφ∈Ω（α+δ0，β-δ0）且 z＝reiφ∉D，有

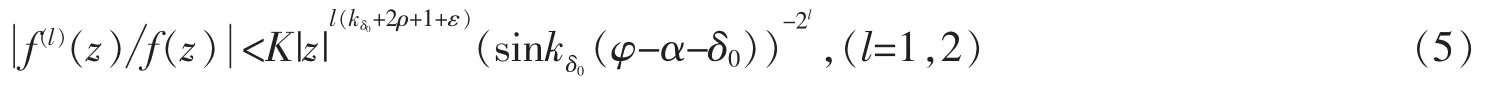
其中D是引理3中给出的例外集。

因为 argz＝θ0为 B（z）的一条 σ（B）级 Borel方向，选取适当的 η，使得 Ω（θ0－η，θ0+η）⊂Ω（α+δ0，β-δ0）。由引理 4 可得，存在一组 Borel充满圆 Γm：|z-zm|＜εm|zm|，其中

因为∞是整函数B（z）的Picard例外值，根据充满圆的性质，在充满圆定义中的两个除外球面小圆中必有一个包含∞。定义|z1，z2|为z1，z2的球面距离，当m充分大的时候，存在复数am∈Γm，于是有

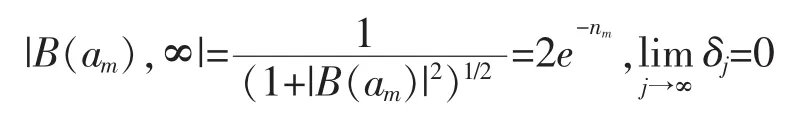
这样就可以找到与 m 无关的正常数 C，使得对充分大的 m，有因为|am|=（1+o（1））|zm|，于是有

由 Phragmen-Lindelof定理，容易知道存在区间[θ1，θ2]⊂（θ0-η，θ0+η），使∀θ∈[θ1，θ2]，有

因为D是由半径之和为有限的可数个圆盘并构成的一个R-值集，所有满足条件：射线argz＝θ与D中无穷个圆盘相交的 θ的测度为 0。 故由（5）式，可取 θ*∈[θ1，θ2]，使得∃R0＞0，当 r＞R0时，有

成立，其中

由（6）式，取 0＜ε*＜（σ1－σ0）/2，其中 σ0＝σα，β（A）＜σ1。

当n充分大时，有

成立。

又因为 σα，β（A）＜σ0，由整函数在角域内的增长级的定义，有

下证B（z）的Borel方向就是f的 Borel方向。

假设∃θ1∈（α，β），argz＝θ1为 B（z）的一条 Borel方向，则 argz＝θ1为 f的一条 Borel方向。若不然，则必然有3个例外值点，设为 a1，a2，a3，于是根据 Borel例外值定义有

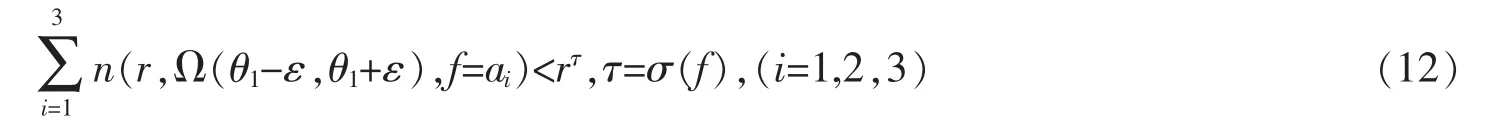
根据角域第二基本定理，即引理2可知

注意到

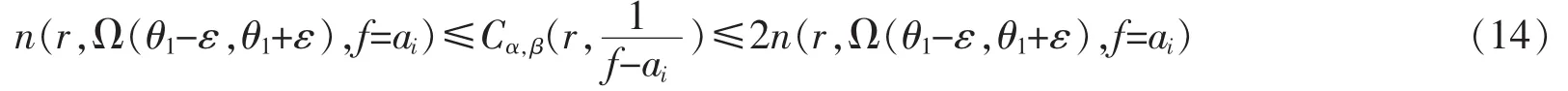
结合（12）－（14）式。 根据角域中级的定义，于是有 σθ1－ε，θ1+ε（f）＜τ，这与条件矛盾。

于是 argz＝θ1为 f的一条 Borel方向。 由于 θ1的任意性，可得出 B（z）在角域 Ω（α，β）内所有的 Borel方向都是f的Borel方向。

故f在角域Ω（α，β）至少有两条Borel方向，定理得证。