机载巡航导弹外形隐身改进的电磁散射影响

2019-12-31刘战合田秋丽王菁王晓璐石金祥

航空工程进展 2019年6期

刘战合，田秋丽，王菁，王晓璐，石金祥

(1.郑州航空工业管理学院航空工程学院，郑州 450046) (2.郑州航空工业管理学院经济学院，郑州 450046)

0 引言

随着现代战争的持续深入，巡航导弹已经成为不可或缺的战术、战略攻击性武器，其可由海、陆、空等作战平台发射[1-3]，具有作战性能优秀、航程远、攻击精度高等优势。随着探测技术尤其是雷达探测技术的发展[4-5]，对巡航导弹的生存力和突防能力提出了更高要求，隐身技术成为实现巡航导弹高突防能力的重要技术手段[6-7]。

北约和美军相继开发出了多款可挂载于B-52、B-1B、B-2、F-35、F-15等轰炸机、战斗机平台的隐身型巡航导弹，例如AGM-129、AGM-158A/B/C等，具有优秀的作战能力。与战斗机、轰炸机相比，巡航导弹为一次性使用武器系统，鉴于其作战特性不同，其隐身性能需求也有一定区别，更强调头向角域隐身性能，由于巡航导弹飞行的机动性，也可兼顾其他角域[8-10]。

针对机载导弹，国内外学者已开展了诸多研究，S.V.Babu等[11]研究了机载导弹发射过程的气动弹性问题；岳奎志等[1]、刘战合等[2]分析了挂载导弹的战斗机的电磁散射特性；刘莉等[3]以BGM-109为研究对象建立了战术导弹的气动隐身优化方法；何十全等[6]、师颖等[7]分别研究了导弹的散射特性提取方法和等离子体涂覆方案。但对机载巡航导弹本身的隐身性能影响及研究方法，研究较少。

为了研究隐身巡航导弹的电磁散射特性，本文以AGM-158C为基础，建立隐身巡航导弹电磁模型，基于物理光学法(Physical Optics，简称PO)[8]，数值计算不同状态(入射频率、俯仰角)下的RCS(radar cross section)散射曲线；以对应常规非隐身巡航导弹电磁模型为比较对象，基于RCS减缩值，详细研究并分析巡航导弹外形隐身措施对电磁散射特性的影响，以期为巡航导弹隐身设计提供技术参考。

1 巡航导弹电磁模型

以美军亚声速空射隐身反舰导弹AGM-158C为基础，建立电磁分析模型，定义为模型A，如图1(a)所示，弹身长4.959 m，弹翼展3.389 m，后掠角33.054°；模型B为常规弹身形式(旋成体)的非隐身电磁模型，如图1(b)所示，为了尽量保证与模型A的协调一致，弹翼后掠角等与模型A接近，弹身长4.756 m，弹翼展2.8 m，后掠角34.235°。

对比两种模型，结合二者RCS曲线及不同角域均值差异，研究外形隐身措施对电磁散射特性的影响规律。

(a) 隐身巡航导弹电磁模型(模型A)

(b) 常规巡航导弹模型(模型B)图1 巡航导弹电磁计算模型Fig.1 Electromagnetic computation models of cruise missile

实际执行作战任务中，巡航导弹会受到来自海、陆、空甚至是天基平台的全方位探测器的探测、识别、跟踪，给巡航导弹造成较大威胁；同时，飞行过程中，巡航导弹根据实际情况会有一定的机动动作，因此，研究时重点考虑前向角域隐身性能，同时兼顾其他角域隐身性能[1,2,8]。本文以巡航导弹电磁模型前向(即弹头方向)30°(H-30)、后向(弹尾方向)30°(T-30)角域散射特性为主要研究内容，兼顾侧向60°(S-60)、周向360°(W-360)角域。考虑到不同探测器电磁波频率的多样性，将入射电磁波频率设定为1、3、6、10、15、18 GHz；电磁波入射方位角为0°～360°，俯仰角设定为-10°、-5°、0°、5°、10°。

2 电磁散射特性分析方法

2.1 电磁散射计算方法

一般的，飞行器目标可视为金属目标，该类目标电磁散射计算方法可分为低频和高频算法。低频算法具有较高的精确度，大多为数值算法，例如矩量法(Method of Moments，简称MOM)及基于矩量法的多层快速多极子算法(Multilevel Fast Multipole Algorithm，简称MLFMA)[10,12-14]、时域有限差分法(Finite Difference Time Domain，简称FDTD)[15]、有限元法(Finite Element Method，简称FEM)。为了提高计算精度，此类算法在计算速度、内存占用上有所牺牲，分析电大尺寸复杂目标有较大难度。高频算法从物理本质上来看，是对低频精确算法的近似，例如物理光学法、等效电流方法、物理绕射理论等[16]，尽管在计算精度上有一定损失，但其高效的计算速度可满足电大尺寸目标的散射特性分析。

高频算法中的物理光学法是飞行器目标电磁散射常用求解方法之一，与低频精确矩量法基本原理一致，均为电磁场积分方程。为了提高电磁散射计算效率，物理光学法仅保留矩量法的面元自身耦合作用，而忽略不同面元间的相互弱耦合作用(例如目标局部结构之间的散射影响)，这一近似处理尤其适合处理表面光滑目标的散射计算，同时，具有一定的矩量法高精度特点。对于前述巡航导弹电磁模型A、B，可视为光滑目标，适合采用物理光学法进行分析计算。

基于切平面近似，物理光学法得到面元上的RCS平方根表示为

(1)

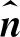
公式(1)在平面面元上展开即可计算该面元电磁散射。在对目标进行网格划分的基础上，对所有网格面元求和，按相位叠加得到总RCS：

(2)

MLFMA是矩量法的快速改进算法，同样基于严格定义下的积分方程，充分考虑了自耦合、互耦合作用，在低频算法中具有优秀的计算精度，其计算结果可用来验证本文物理光学法的计算精度。以直角边长1 m、金属柱高1 m的直角等腰三角形金属柱为对象，计算状态为：入射电磁波波长为0.1 m、俯仰角为0°、方位角0～180°(即计算等腰直角三角形高线对称的一侧角域范围)。采用物理光学法(PO)、MLFMA的RCS计算曲线对比如图2所示，其中MLFMA计算结果为水平极化情况。

图2 金属柱RCS两种计算方法对比Fig.2 Comparison of two RCS calculation methods for metal column

从图2可以看出：两种方法RCS计算曲线趋势吻合很好，在0～180°角域上，物理光学法和高精度MLFMA的算术均值误差仅为0.863 5 dB，同时，在90°～180°角域上，RCS计算曲线与平板散射效果接近，证明本文物理光学法具有较高的计算精度，可用于巡航导弹类的光滑目标电磁散射特性计算分析。

对计算目标A、B，由于二者模型建立时尽量保持典型几何尺寸接近，入射电磁波频率1、3、6、10、15、18 GHz分别对应电尺寸约为17、50、100、165、248、298，为电大尺寸，尤其是大于3 GHz情况。因此，电磁模型A、B在频率大于3 GHz时的RCS计算均适用于物理光学法计算范围，鉴于电尺寸17的1 GHz散射情况采用物理光学法精度稍差，研究RCS分布特性时采用3 GHz及以上频率，同时为了提高RCS均值和减缩值变化特性研究的完备性，也参考了1 GHz计算结果。

2.2 RCS均值

一般的，电磁散射特性与电磁波入射角、频率、目标结构特性密切相关，尤其是入射角影响较为敏感，实际分析中多采用RCS曲线分布的方法来分析散射特性，该类方法对频率、俯仰角、结构等信息涉及较少。为了有效分析导弹外形隐身技术的电磁散射特性影响，本文在曲线分布分析方法的基础上，结合重点角域RCS均值，及两种电磁模型RCS相对变化规律来综合研究外形隐身影响。

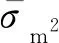
(3)

式中：σm2,i为第i个入射角上的RCS，单位为m2。

一般RCS计算或测试结果单位为dBsm，记第i个入射角的RCS为σdBsm,i，其算术均值可表示为

(4)

对巡航导弹而言，影响其生存能力最重要的角域为前向角域，若评价其隐身性能，全向即周向角域也是重要的影响因素。鉴于巡航导弹工作特点，以侧向角域和尾向角域为补充进行研究。

基于以上因素，对于巡航导弹的外形隐身电磁散射特性影响，首先对两种电磁模型的RCS散射曲线的分布特点进行对比研究，结合RCS散射曲线波峰、波谷变化特点，例如宽度、位置、幅值等，分析散射曲线与巡航导弹外形设计的影响关系；其次，采用不同角域RCS均值，研究外形隐身对不同角域内电磁散射幅值的影响关系，并分析RCS均值频率特性、俯仰角特性。

2.3 RCS减缩值

在电磁散射特性分析过程中，仅依靠RCS均值幅值大小来分析目标的散射特性有一定缺陷，尤其是在分析外形隐身、材料隐身等技术的实际效果时，不能量化分析其影响关系、频率响应、姿态角响应等特点。

区别于单独分析隐身飞行器本身的电磁散射特性的方法，本文针对两种典型几何尺寸大小基本接近的巡航导弹电磁模型，以非隐身电磁模型为基础，以不同角域的RCS减缩值来研究巡航导弹外形隐身技术的电磁散射特性影响。

在同一关注角域内，以非隐身电磁模型B为基准模型，定义隐身电磁模型A的RCS减缩值为

(5)

3 外形隐身的RCS曲线分布影响

为了分析外形隐身对RCS曲线分布的影响，采用物理光学法计算频率1～18 GHz、俯仰角-10°～10°的电磁散射特性，从频率和俯仰角变化两方面进行分析，鉴于各频率、俯仰角下的散射曲线的相似性，为了研究方便，分别取A、B模型俯仰角0°时，3、10 GHz散射曲线对比如图3所示；10 GHz时，0、10°散射曲线对比如图4所示。

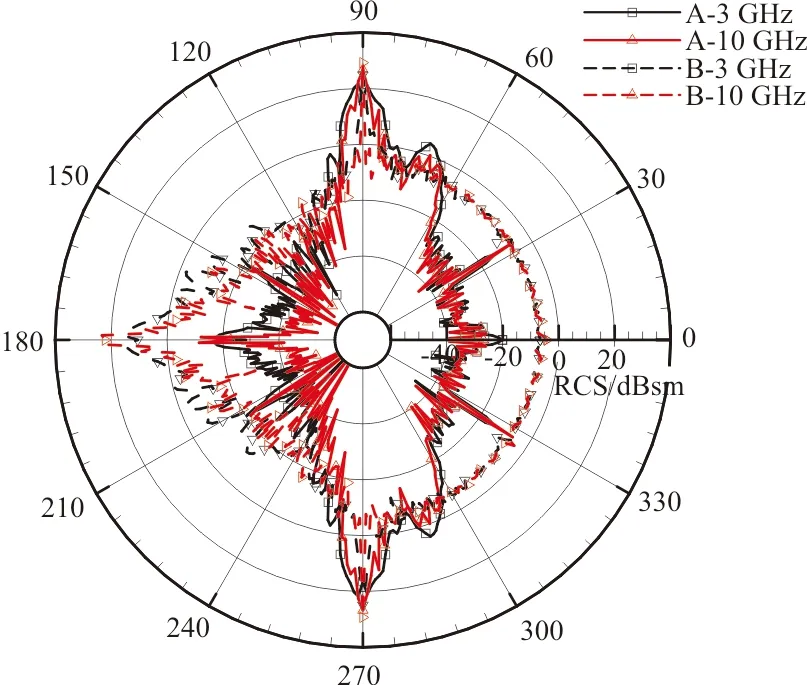
图3 不同两种模型RCS曲线(迎角0°)Fig.3 RCS curves of two models (at the pitch angle of 0°)

电磁模型A、B二者基本布局接近，模型A通过对弹身、弹头、弹尾三部分的外形改进，以提高其隐身性能。

从图3可以看出：外形隐身改进的模型A与常规非隐身模型B的RCS曲线有较大区别。

从分布上看，模型A曲线沿周向依次在33°、90°、144°、180°存在关于机身轴线对称分布的7个强度不同的散射波峰。其中33°波峰表现为机翼前缘镜面散射，且波峰较窄；侧向90°较宽波峰为弹身侧棱、弹翼和弹身二面角、垂尾及弹翼侧面等结构的综合贡献，其影响角域较大；144°附近波峰是弹翼后缘镜面散射及弹尾弧面散射耦合所致，但其影响角域较小，波峰较窄；尾向180°角域波峰为弹身尾部弧面电磁散射效果，尽管有一定峰值，但从曲线来看，波峰幅值较低，尤其是高频时波峰变窄，利于隐身性能提高。尽管布局形式基本接近，常规非隐身模型B散射曲线沿周向主要存在三个波峰，分别位于侧向90°、尾向180°、侧向270°。与模型A相似，侧向90°、270°为弹身侧棱、弹翼与弹身之间二面角的散射综合贡献，而尾向180°主要为单位平面的镜面散射作用。

从散射曲线幅值来看，尽管具有隐身性能的巡航导弹模型A的周向散射波峰较多，但从曲线来看，除侧向90°和270°角域外，其余较宽的角域上的RCS均获得了极大降低，散射曲线大幅向内收敛，尤其表现在前向角域和后向角域。在前向较大角域内(尤其是60°角域)，模型B由于弹头的圆形或近似圆形设计，会在前向表现出较高幅值的接近圆弧形分布的RCS曲线，而模型A在隐身化后，前向角域无散射波峰，且幅值有30 dB以上差异，对于模型B，33°位置波峰已经淹没在弹头形状的散射波中。在侧向，隐身模型B的侧棱设计为平面，引起该角域内电磁散射强于模型A，一般的，该角域内隐身性能对生存力提升影响较弱，因而设计时不予重点考虑。如需提高该角域隐身性能，可在保证前向、后向外形设计的前提下将侧棱斜置一定角度。对后向角域，模型A同样进行了隐身化曲面改进，大幅降低了其散射幅值，获得比常规模型B隐身性能优秀的外形设计。

同时，其他计算频率下的RCS曲线规律一致，图3仅显示了3、10 GHz曲线，可以看出：频率增加时，模型A散射曲线有内陷趋势，振荡更为明显，波峰变窄，尤其是后向和33°附近波峰，说明高频时隐身性能提高；而模型B前向角域内受频率影响较小，其后向角域曲线影响较为明显，也表现波峰降低，曲线振荡加剧的特点。对比二者发现，外形隐身对频率影响较为显著，频率提高时，外形隐身技术表现更为强烈。

图4 不同迎角下两种模型RCS曲线(10 GHz)Fig.4 RCS curves of two models at different pitch angles(10 GHz)

从图4可以看出：相对于图3的频率变化特性，俯仰角变化时，RCS曲线具有一定相似性，且变化较小。对隐身模型A，俯仰角由0°变为10°时，两条曲线基本吻合，但在入射角110°、250°附近出现两散射波峰，为弹尾弧面的近镜面散射效果，但该部位位于接近侧向位置，实际执行任务过程中对隐身性能影响不大。对模型B，俯仰角变化时，前向弧形设计基本不影响RCS曲线分布，侧向散射机理未发生改变，因此，侧向基本重合；而后向由于采用平面方式，其形成的镜面散射在俯仰角由0变为10°时，其镜面散射效果降低，故后向角域波峰宽度和幅值均有所降低。

综上，经过对弹头、弹尾及其他部位的外形隐身改进，较大地改变了RCS散射曲线分布特点，实现了控制电磁散射方向和能量的目的，提高了隐身性能。在频率和俯仰角变化时，曲线表现出一定的相似性。

4 外形隐身的电磁散射特性影响

为进一步研究导弹外形隐身的电磁散射特性影响，计算两种模型不同角域内的RCS均值、隐身模型A的减缩值等，并分析其频率响应特性和俯仰角响应特性。

4.1 频率响应特性

不同入射频率时，隐身模型A的各角域(H-30、T-30、S-60、W-360)的RCS均值、减缩值变化曲线如图5～图6所示。

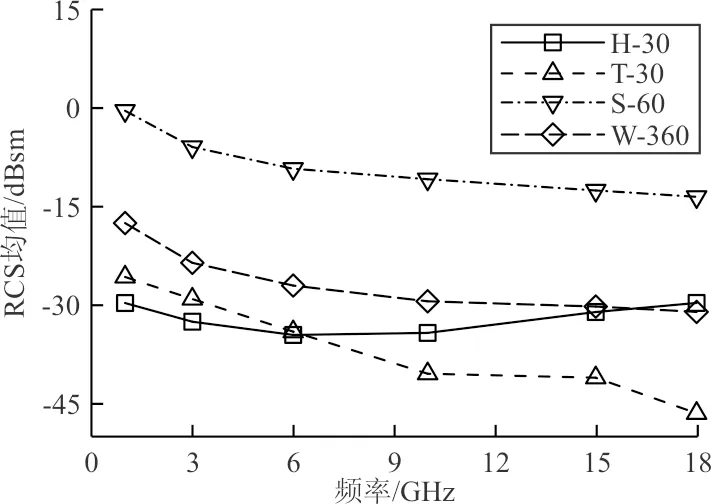
图5 不同角域RCS均值频率响应曲线Fig.5 RCS mean value-frequency response curves in different angular domains

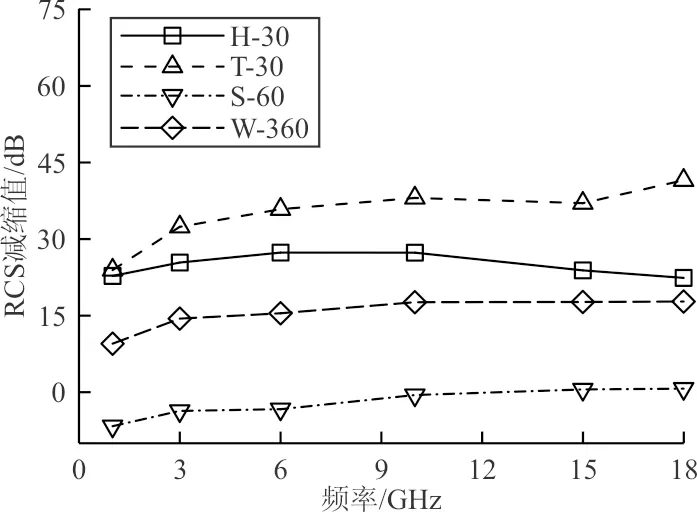
图6 不同角域RCS减缩值频率响应曲线Fig.6 RCS reduction value-frequency response curves in different angular domains

从图5可以看出：前向H-30角域内的RCS均值在-34.486 1～-29.604 1 dBsm之间(-32 dBsm左右)，随着频率的增加，先减小后增加，但均处于较低的水平，即小于-30 dBsm的振荡趋势，具有较好的隐身性能，结合RCS散射曲线，在头向无较明显较强的波峰，此为弹头隐身外形改进后的散射效果。对于后向T-30角域、侧向S-60、周向W-360角域，频率由1增加至18 GHz时，各向角域的RCS均值均有所降低，且对隐身性能影响重要的后向T-30角域，其RCS均值降速最快，由-25.642 1快速降低至-46.439 3 dBsm，隐身性能提高较快，尽管后向T-30角域上有一散射波峰，但随着频率的增加，散射波峰变窄、变弱，尤其在10、15、18 GHz频率上，在四个角域内的对应RCS均值最小，也说明弧面外形弹尾隐身处理利于降低散射。而对侧向S-60、W-360角域，频率的增加引起RCS均值的逐渐降低，且降低速度逐渐减小，但由于侧向波峰较大且较宽，侧向角域RCS均值明显强于周向角域，周向较低是由于各个角域电磁散射性能的综合效果，也是隐身改进的整体表现。

从图6可以看出：RCS减缩值从大到小依次为后向T-30、前向H-30、周向W-360、侧向S-60角域，即外形隐身改进影响效果，尽管后向T-30角域影响最强，但由于基准导弹模型B弹尾部位镜面散射，结合散射曲线，隐身改进效果强弱依次为前向H-30、后向T-30、侧向S-60、周向W-360角域。对前向H-30角域，频率增加时，减缩值表现为先增加后减小的振荡趋势，振荡幅值较小，在22.405 1～27.876 7 dB之间，说明前向角域的弹头外形隐身改进效果稳定，频率的改变不会引起散射机理的改变，保持较高的隐身性能。对后向T-30(减缩值23.934 7～41.526 8 dB)、周向W-360(减缩值9.520 1～17.771 0 dB)角域，频率增加时，减缩值逐渐增加，频率较低时，增速较快，说明外形隐身也在后向和周向表现较为明显，后向是镜面散射变为曲面散射，周向是各向散射的综合结果。侧向减缩值在-6.647 1～0.710 2 dB之间，电磁散射影响并不大，这是由于弹头和弹尾的外形隐身改进主要表现在前向和后向，如散射曲线所示，模型A为侧棱镜面散射贡献，而模型B为接近圆柱散射表现，但二者几何尺寸接近，对侧向散射影响不太明显。

综上，不同的频率下，外形改进均有较为明显的隐身效果。从RCS均值来看，前向H-30角域电磁散射信号较弱，且无明显散射波峰，隐身性能较好，受频率影响较小；后向T-30、周向W-360、侧向S-60角域电磁散射随频率增加而降低，利于实现隐身性，而后向角域存在散射波峰，降低了隐身性能。从减缩值来看，前向H-30角域上，RCS减缩值保持在25 dB左右振荡，而其余角域随频率增加而增加，隐身效果改善，但侧向S-60角域在0 dB左右，变化不大。

4.2 俯仰角响应特性

与频率响应特性的分析方法相似，入射频率10 GHz时，隐身模型A不同俯仰角的各角域(H-30、T-30、S-60、W-360)的RCS均值、减缩值变化曲线如图7～图8所示。

图7 不同角域RCS均值俯仰角响应曲线Fig.7 RCS mean value-pitch angle response curves in different angular domains

图8 不同角域RCS减缩值俯仰角响应曲线Fig.8 RCS reduction value-pitch angle response curves in different angular domains

从图7可以看出：对隐身模型A，前向H-30和后向T-30角域RCS均值在-34.034 1～-40.404 2 dBsm之间，俯仰角10°时H-30角域较低，其他俯仰角情况下，H-30角域RCS均值较高，结合图4，前向H-30无明显散射波峰，而后向T-30有一散射波峰，但该波峰较窄且波峰附近RCS较低，结合散射波峰分布情况，前向H-30角域隐身性能较好。如前所述，周向W-360角域受前向、后向角域影响，RCS均值较低，说明周向隐身性能较好，俯仰角变化时，周向W-360角域均值振荡变化且幅值较小，基本维持在-25.712 3～29.361 1 dBsm。对侧向S-60角域，由于俯仰角的变化不会引起侧向平面电磁散射机理的改变，该角域均值变化较小，在较小范围振荡。

飞行器隐身效果不仅对频率响应有影响，也对俯仰角响应有影响。从图8可以看出：在入射频率10 GHz下，俯仰角变化时，前向H-30、后向T-30角域RCS减缩值较大，其次是周向W-360角域，最小为侧向S-60角域。对前向H-30角域，由于较小的俯仰角变化不会引起弹头位置隐身外形散射机理的变化，因此，前向H-30角域减缩值对俯仰角变化并不敏感，即隐身性能基本不变，减缩值变化范围为34.001 2～36.153 7 dB。而在后向T-30角域，由于相对基准模型B的弹尾设计为较为简单的平面，其散射机理为镜面散射，俯仰角变化时，其散射有较大降低，而对应的隐身模型A弹尾的RCS均值随俯仰角变化并不剧烈，从而引起后向T-30角域减缩值在俯仰角0°最大，达41.526 3 dB，两侧逐次降低。对周向W-360角域，如前所述，为各角域综合效果，而侧向S-60角域，RCS减缩值在0 dB左右，与W-360角域均呈较小的振荡趋势。

与频率效应不同的是，在前向H-30、侧向S-60、W-360角域，较小的俯仰角变化不会改变散射机理及散射特性，即RCS均值和对应减缩值的变化区间较小，前向H-30角域的减缩值为35 dB左右；对后向T-30角域，由于尾部散射机理的不同，散射效果及RCS均值和减缩值变化随俯仰角变化较大，但外形隐身仍具有较优秀的减缩效果。