一种九电平整流器的分数阶滑模控制

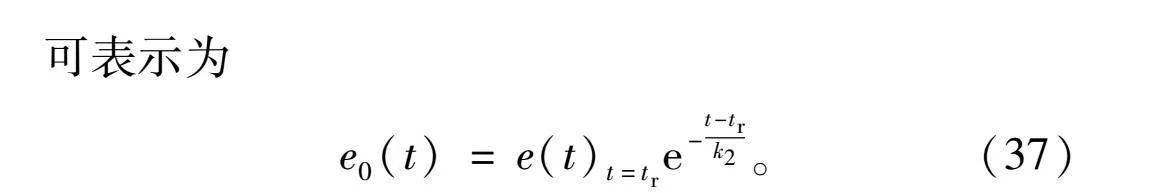
摘 要：以含耦合电感的单相九电平整流器为研究对象，首先，在分析整流器九电平产生机理及其电容电压自均衡原理的基础上建立其数学模型。其次，针对传统整数阶滑模控制（IOSMC）存在的响应速度慢、启动超调大等问题，提出一种可实现快速收敛的分数阶滑模控制（FOSMC）策略，在滑模控制中引入分数阶微积分，通过分数阶微积分算子增加的自由度改善控制系统的动态性能和收敛过程。最后，采用Lyapunov理论证明分数阶滑模控制系统的稳定性和收敛性，并就整数阶滑模和分数阶滑模的系统收敛速度的差异性进行理论分析。仿真和实验结果表明所提分数阶滑模控制与传统整数阶滑模控制相比，具有系统收敛速度快、控制时间短、鲁棒性强的优点。

关键词：九电平整流器；电容电压自均衡；分数阶微积分；分数阶滑模控制；参数整定；收敛速度

DOI：10.15938/j.emc.2024.11.015

中图分类号：TM461

文献标志码：A

文章编号：1007-449X（2024）11-0160-12

Fractional order sliding mode control of one kind of nine level rectifier

ZHU Yifeng^1，2， JIA Xiaolei^1，2， ZHOU Feishan^1，2， ZHANG Ziyang^1，2， LI Yan^1，2

（1.School of Electrical Engineering and Automation， Henan Polytechnic University， Jiaozuo 454003， China;

2.Henan Key Laboratory of Intelligent Detection and Control of Coal Mine Equipment， Jiaozuo 454003， China）

Abstract：Taking the single-phase nine-level rectifier with coupling inductor as the research object， firstly， the mathematical model was established on the basis of analyzing the nine-level generation mechanism of the rectifier and its capacitor voltage self-equalization principle. Secondly， aiming at the problems of slow response speed and startup overshoot of traditional integer-order sliding mode control （IOSMC）， a fractional-order sliding mode control （FOSMC） strategy that can achieve fast convergence was proposed， and fractional-order calculus was introduced into sliding mode control. The increased degrees of freedom of fractional calculus operators improve the dynamic performance and convergence process of the control system. Finally， Lyapunov theory was used to prove the stability and convergence of the fractional sliding mode control system， and the difference between the convergence speed of integer-order sliding mode and fractional-order sliding mode system was theoretically analyzed. Simulation and experimental results show that compared with the traditional integer-order sliding mode control， the proposed fractional sliding mode control has the advantages of fast system convergence speed， short control time and strong robustness.

Keywords：nine-level rectifier; capacitor voltage self-equalization; fractional calculus; fractional sliding mode control; parameter tuning; convergence speed

0 引 言

多电平整流器相较于传统两电平整流器有诸多优点，如降低开关器件上的电压应力，降低网侧谐波含量，降低开关频率，并且能够以更小的体积获得更高的电压输出^[1-2]。所以，近年来多电平整流器被越来越多的学者关注，并应用于中高压场合改善电能质量。

现今成熟的多电平整流器拓扑主要有飞跨电容、级联H桥和二极管箝位3种类型^[3-5]。还有不少多电平整流器拓扑是在这3种拓扑的基础上进行的改进，然而由于拓扑结构固有的特性，使得其电平数增加时存在若干问题^[6-8]。其中，电容电压平衡控制是很多多电平拓扑需要解决的一个关键问题^[9-10]。这是由于多电平拓扑具有较多的分压电容，通常需要额外的电容电压平衡电路，一般方法是在调制算法中加入复杂的控制策略。文献[11]设计了改进型同相层叠载波调制方法实现电容电压的自均衡。文献[12]提出一种基于子模块投入优先级的均压策略。但是复杂的调制策略给多电平整流器的控制带来很大的挑战。

传统整数阶滑模控制（integer-order sliding mode control，IOSMC）是一种算法简单、易于实现、响应速度快的非线性控制策略，同时滑模控制对干扰和未建模动态具有鲁棒性，因此被广泛应用于非线性控制系统^[13-14]。文献[15]针对网侧换流器提出了一种反馈线性滑模控制策略，但是实现困难，且存在超调。文献[16]提出一种快速终端滑模算法，但是控制精度差，稳态误差并未消除。文献[17]针对buck变换器电压环设计了离散积分滑模算法，虽然实现了高精度控制，但是动态性能有待进一步提升。

随着对分数阶微积分算子逼近方法的研究，近年来分数阶滑模控制（fractional-order sliding mode control，FOSMC）算法被广泛关注。分数阶滑模主要是通过在整数阶滑模控制中引入分数阶微积分，使整数阶滑模控制增加一个额外的可调参数，从而使传统整数阶滑模控制性能得到改善。文献[18]针对并网逆变器设计了模糊分数阶滑模算法，具有抗扰能力强和恢复时间短的特点。文献[19]针对风电系统设计了一种可快速收敛的分数阶滑模控制策略，使其在多种工况下的振荡得到快速抑制，实现了快速收敛的目的。文献[20]针对同步电机设计了电流环的离散型分数阶滑模控制策略，在减小抖振的同时又增加了控制精度和动态性能。可以预见的是，分数阶滑模控制在整流器上具有很好的应用前景。

针对以上问题，本文以一种含耦合电感的单相九电平整流器为研究对象，以加快系统的收敛速度，提高系统的响应能力为目标，提出一种分数阶滑模控制策略。首先，分析整流器的工作状态及电压自均衡原理，并建立dq坐标系下的数学模型；然后，针对整流器的电压环设计分数阶滑模控制策略，并对此控制策略下的系统稳定性和收敛速度进行分析；最后，将本文所提FOSMC算法与IOSMC算法和PI算法进行仿真和实验对比。

1 主电路拓扑及数学建模

1.1 单相九电平整流器电路拓扑

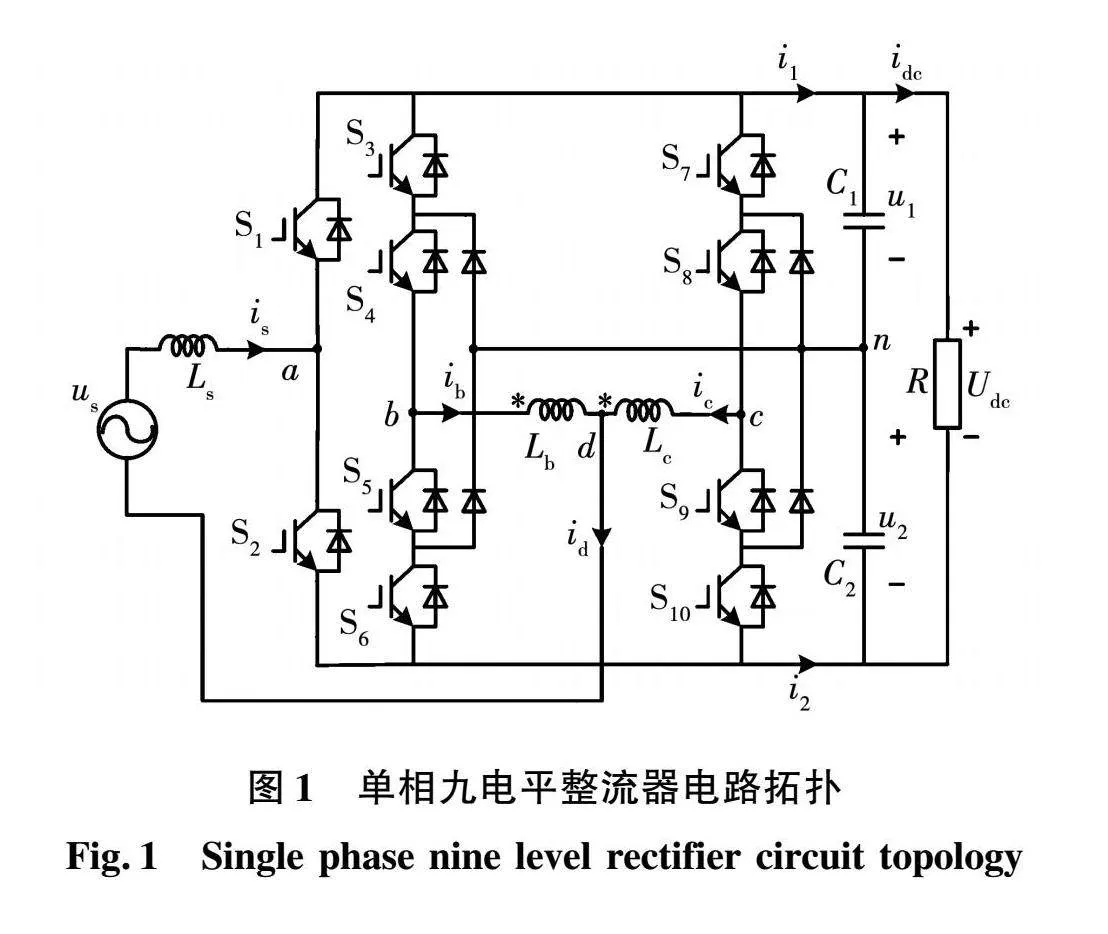
图1是含耦合电感的单相九电平整流器的电路原理图，其在二极管箝位三电平整流器的基础上添加一个耦合电感及2个功率开关管组成。

其中：us为电网电压；is为网侧输入电流；Ls为网侧电感；ib、ic为流过耦合电感上的电流；Lb、Lc为2个顺接的耦合电感；C1、C2为直流侧的2个电容；u1、u2分别为直流侧两支撑电容C1、C2上的电压；i1、i2是直流母线上正向和负向电流；R为纯电阻负载；Udc为直流母线电压；S1～S10为10个功率开关管。将第一桥臂中a点与两耦合电感公共端点d点连接，耦合电感Lb左端点b点和耦合电感Lc的右端点c点分别与第二、三桥臂相连接，则a点与d点之间的电压即为单相九电平整流器拓扑输入端电压uad。

1.2 单相九电平整流器工作原理

根据图1中电压和电流的关系，可以得到两耦合电感上面的电压：

（M+Lσ）dibdt－Mdicdt=ubn－udn；

（M+Lσ）dicdt－Mdibdt=ucn－udn。（1）

式中：Lσ为耦合电感的漏感；M为耦合电感互感；ubn、udn、ucn分别为b点、d点和c点与参考点n之间的电压。

由基尔霍夫电流定律有

ib+ic=is。（2）

将式（1）代入式（2），可得

udn=12（ubn+ucn+Lσdisdt）。（3）

忽略漏感，根据式（3）可得输入电压uad为

uad=uan－udn=uan－ubn+ucn2。（4）

该整流器拓扑有3个桥臂，左起第1个桥臂的2个开关管为互补导通工作，只有2种开关状态。第二、三桥臂上下4个开关管中的第1个开关管与第3个开关管、第2个开关管与第4个开关管为互补导通的工作方式，有3种开关状态。令T1、T2、T3分别表示第一、二、三桥臂的开关状态，则逻辑开关函数可表示为：

T1=1，S1导通，S2断开；－1，S2导通，S1断开。（5）

T2=1，S3、S4导通，S5、S6断开；0，S4、S5导通，S3、S6断开；

－1，S5、S6导通，S3、S4断开。（6）

T3=1，S7、S8导通，S9、S10断开；

0，S8、S9导通，S7、S10断开；

－1，S9、S10导通，S7、S8断开。（7）

将式（5）～式（7）代入式（4）可得：

S=T1－（T2+T3）/2；

uad=SUdc/2。（8）

式中S表示开关函数。

若整流器器件处于理想状态，忽略整流器损耗，根据功率守恒可得：

uadis=u1i1－u2i2；

u1=u2=Udc/2。（9）

将式（8）代入式（9）中，可得

i1－i2=Sis。（10）

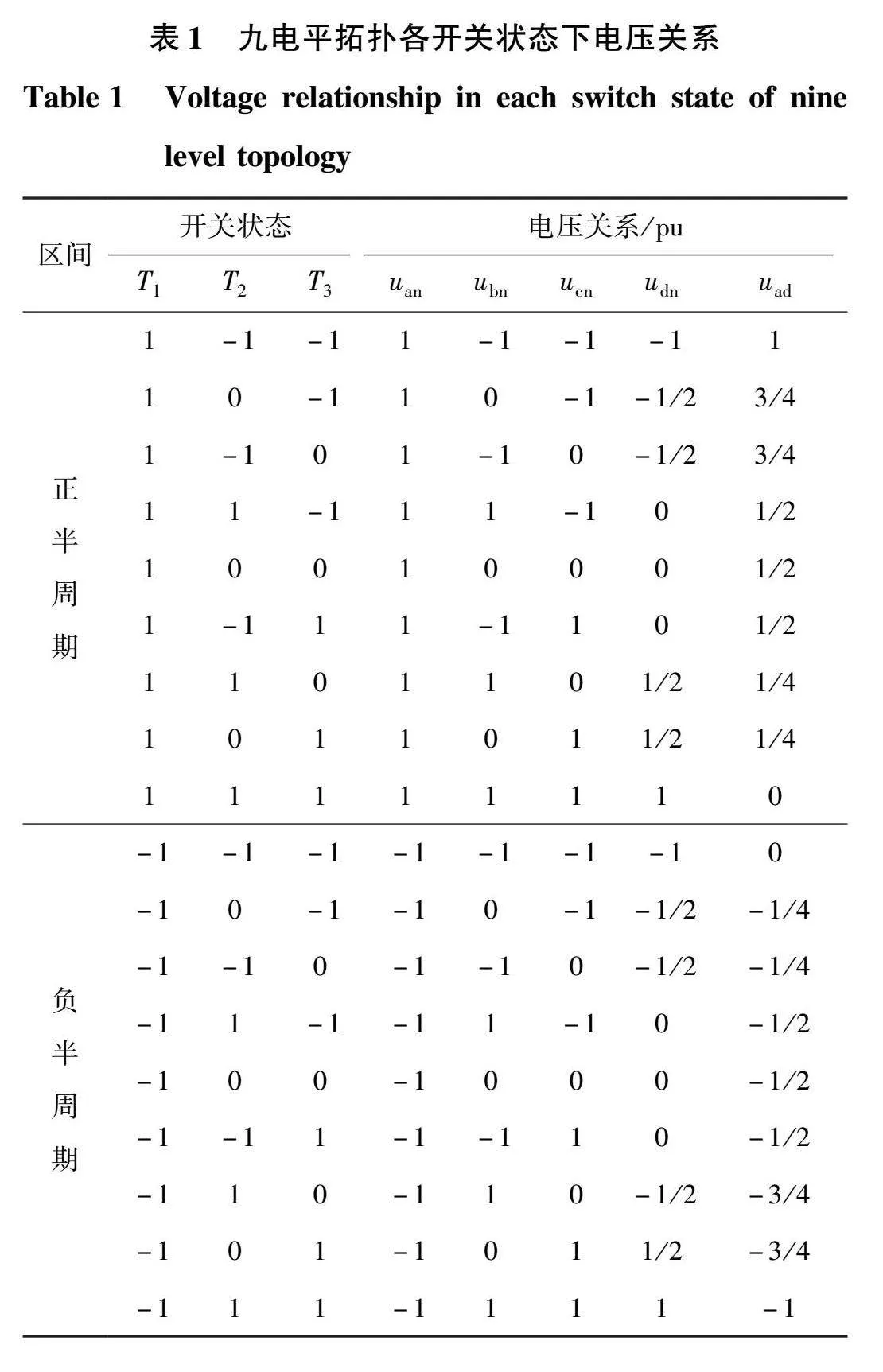
由上述分析可得出整流器正负半周期内开关状态与各电压之间的关系，如表1所示。

表1中，由于整流器在（1 1 -1）、（1 -1 1）、（0 1 -1）、（1 -1 1）这4种开关状态工作时，耦合电感上电压最大，导致基波含量最大。在满足整流器输入端电压uad九电平的前提下，耦合电感上的电流越小越好，所以这几种开关状态一般在调制中不做选择。

1.3 电容电压自均衡分析

由于正半周期和负半周期的对称关系，直流侧电容C1两端的电压u1在网侧输入电流正半周期内递增，在网侧输入电流负半周期内递减；电容C2两端的电压u2在网侧输入电流正半周期内递减，在网侧输入电流负半周期内递增，且增减的速率保持一致，即电容C1和电容C2充电和放电的速率一致。一个基波周期内，电容C1和电容C2在正半周期和负半周期交替进行充放电并且给负载供能。若两电容充放电时长一样，那么两电容电荷变化量也一致。所以电容C1和电容C2两端的的电压在1个周期内能够达到平衡。图1所示的单相九电平整流器中直流母线两支撑电容C1、C2上的电压u1、u2有自均衡的效果，不需要额外的中点电压平衡控制。

1.4 数学建模

忽略内阻，取C1=C2=C，由图1电路根据电路定理可得：

Lsdisdt=us－uad；

Cd（u1+u2）dt=i1－i2－2UdcR。（11）

由于单相系统无法进行坐标变换，需要构造虚拟正交信号，利用构造的正交虚拟电压、电流信号分别与实际的电压、电流值叠加之后即是交流侧电压、电流矢量us和is。本文选用原理简单且动态性能好的二阶广义积分（second-order generalized integral，SOGI）算法^[21]来构造虚拟正交电压、电流信号。

经过αβ/dq坐标变换，得到网侧电压us和网侧电流is以及输入端电压uad在dq坐标系下的表达式为：

us=usdcos（ωt）－usqsin（ωt）；

is=idcos（ωt）－iqsin（ωt）；

uad=udcos（ωt）－uqsin（ωt）。（12）

结合式（10）～式（12），可以得到整流器在dq坐标系下的动态方程为：

Lsdiddt=usd－ud+ωLiq；

Lsdiqdt=usq－uq+ωLid；

Cd（u1+u2）dt=（Sdid+Sqiq）－2UdcR。（13）

式中：usd、usq分别为网侧电压在dq坐标系下的分量；ud、uq、id、iq分别为整流器输入端电压、输入端电流在dq坐标系下的变量。

2 控制系统设计

2.1 整数阶滑模设计

传统整数阶滑模控制策略的核心思想是通过调节控制律使系统状态迅速收束到所设定的滑模面，并沿滑模面按照预定运动轨迹做滑动模态运动从而实现系统误差在有限时间内的最小化。在本文中，为改善直流侧输出电压的动态性能，将滑模控制算法应用于电压环的控制当中。

令e（t）表示参考电压与实际电压的误差项，其表达式为

e（t）=U*dc－Udc。（14）

为减小系统抖振，可设计整数阶滑模面为

s1=e（t）+k1e·（t）。（15）

对式（15）求导，并将Udc=u1+u2代入式（13）可得

s·1（t）=－dUdcdt+k1e··（t）=2UdcCR－Sdid+SqiqC+k1e··（t）。（16）

为了使整流器直流侧电压状态变量能够平滑的进入滑动模态，本文选用幂次趋近律进行设计。即

s·1（t）=－k|s1（t）|αsgns1（t）。（17）

式中：sgn（x）=－1，xlt;00，x=01，xgt;0；k、α为趋近律的系数，k gt;0，0lt;αlt;1。

结合式（16）、式（17）可得

－k|s1（t）|αsgns1（t）=2UdcCR－Sdid+SqiqC+k1e··（t）。（18）

当系统达到稳态时有did/dt=diq/dt=0，iq=0，usq=0，同时ud=SdUdc/2，uq=SqUdc/2，代入式（13）中可得：

Sd=2usdUdc；

Sq=2ωLidUdc。（19）

将式（19）代入式（18）中，可以得到内环电流的参考值为

i*d=U2dcRusd+kCUdc2usd|s1（t）|αsgns1（t）+k1CUdc2usde··（t）。（20）

2.2 分数阶滑模设计

2.2.1 分数阶微积分

分数阶微积分即是将经典微积分理论拓展到整数阶以外的阶次，所以相较于整数阶微积分具有更加普遍的意义。而今的控制系统领域中应用最广泛的3种分数阶微积分定义为Riemann-Liouville（RL）型、Grunwald-Letnikov（GL）型、Caputo型。本文引入RL型分数阶微积分设计FOSMC算法，其积分和微分的表达式为：

aD^－λtf（t）=1Γ（λ）∫ta（t－τ）^λ－1f（τ）dτ;（21）

aDλtf（t）=Dn［aD^－σtf（t）］=

1Γ（σ）dndtn［∫ta（t－τ）^σ－1f（τ）dτ］。（22）

式中：aD^-λt表示分数阶微积分算子，λ是分数阶次且λgt;0，a、t是算子最大、最小值；σ= n-λ，n是比λ大的最小整数；Γ（λ）是伽玛函数，其定义式为

Γ（λ）=∫∞0e^－tτ^λ－1dτ。（23）

定理1：设n为自然数m-1lt;μlt;m，且μ≠ngt;0，f（t）存在r（r=max{m，n}）阶导数，则有

Dn［aDμtf（t）］=aD^n+μtf（t）。（24）

定理2：RL型分数阶微积分的Laplace变换为：

L［0Dλtf（t）］=sλF（s）－∑n－1j=0［0D^λ－j－1tf（t）］t=0sj;

L［0D^－λtf（t）］=s^－λF（s）。（25）

式中n-1lt;λ≤n。

定理3：设α、βgt;0，Mittag-Leffler函数Eα，β（x）=∑∞k=0［xk/Γ（αk+β）］的Laplace变换为

∫∞0e^－stt^αk+β－1E^（k）α，β（±atα）dt=k！s^α－β（sαa）^k+1。（26）

2.2.2 分数阶滑模控制策略实现

针对整数阶滑模控制中收敛速度慢以及存在超调现象的问题，考虑在传统滑模控制算法中引入分数阶微积分。通过分数阶微积分算子增加的自由度改善系统的动态响应能力，同时实现系统的高精度控制。可重新设计分数阶滑模面s2为

s2（t）=e（t）+k2aDλte（t）。（27）

对式（27）求导得到

s·2（t）=e·（t）+k2D1［aDλte（t）］。（28）

根据RL型微积分定理1可得

s·2（t）=e·（t）+k2aD^λ+1te（t）。（29）

选用幂次趋近律并结合式（13）、式（29）可得

－k|s2（t）|αsgns2（t）=2UdcCR－Sdid+SqiqC+k2aD^λ+1te（t）。（30）

将式（19）代入式（30）中，可以得到内环电流的参考值为

i*d=U2dcRusd+kCUdc2usd|s2（t）|αsgns2（t）+k2CUdc2usdaD^λ+1te（t）。（31）

3 稳定性和系统收敛速度分析

3.1 稳定性分析

为分析所提FOSMC策略的稳定性和收敛性，构造正定Lyapunov函数如下：

V=12STS。（32）

对其求时间的导数为

V·=dVdt=s2（t）s·2（t）=

s2（t）［e·（t）+k10D^λ+1te（t）］=s2（t）［－k10D^λ+1te（t）－k|s2（t）|αsgns2（t）+k10D^λ+1te（t）］=

s2（t）［－k|s2（t）|αsgns2（t）］=

－k|s2|^α+1lt;0。（33）

根据式（33）可以看出，V·lt;0，即V·是负定的。由Lyapunov稳定性判据可知，受控系统是稳定且收敛的，系统状态变量能够收敛至分数阶滑模面上。

3.2 系统收敛速度分析

若系统的误差项到达滑模面所需的时间为tr，则s（tr）=0，由定理2对其进行Laplace变换，可得

E（s）+k2sλE（s）－k2e（t）t=tr=0。（34）

式中：E（s）为误差项e（t）在复频域的表达式；e（t）t=tr代表系统到达滑模面的起始误差。由式（34）可得E（s）的表达式为

E（s）=e（t）t=trsλ+1k2。（35）

由定理3可知，在分数阶滑模控制下，系统误差在时域内可表示为

e（t）=e（t）t=trEλ，λ［－（t－tr）λk2］。（36）

当λ=1时（整数阶滑模），系统误差在时域内可表示为

e0（t）=e（t）t=tre^－t－trk2。（37）

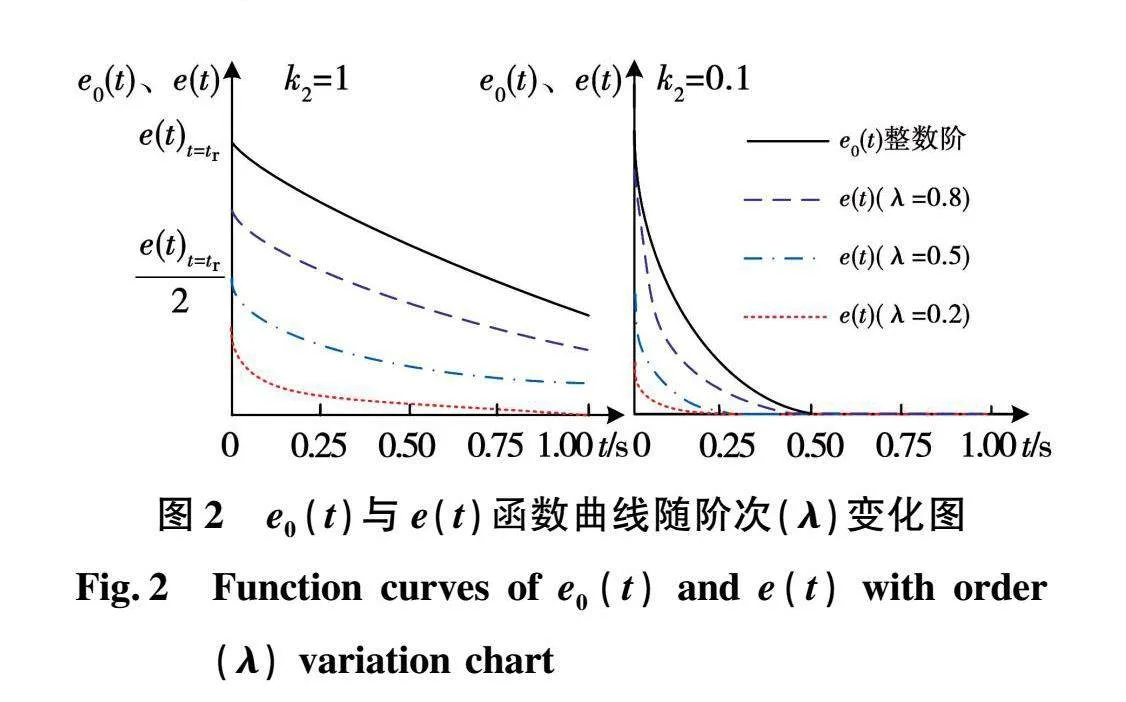
根据式（37）可以看出，当采用整数阶滑模控制时，若滑模面的参数一旦被确定后，则整个系统的收敛速度也是确定唯一的，已不可调整。而当采用分数阶滑模控制时，由式（36）可知，滑模面的参数被确定之后，仍可通过调节分数阶微积分算子λ调节系统的动态性能。所以，分数阶滑模控制通过引入分数阶微积分算子增加了控制系统的自由度，使传统整数阶滑模具备了更加灵活的调节性能，为提高系统的收敛速度创造了条件。为了更加清晰地比较整数阶和分数阶滑模控制下系统状态的收敛速度，图2展示了时域误差e0（t）与e（t）取不同阶次时的函数曲线。根据图2可以看出，相同条件下，分数阶滑模收敛速度明显快于整数阶滑模，动态响应能力更加优异，且其收敛速度随阶次（λ）减小而加快。

3.3 分数阶次（λ）的整定

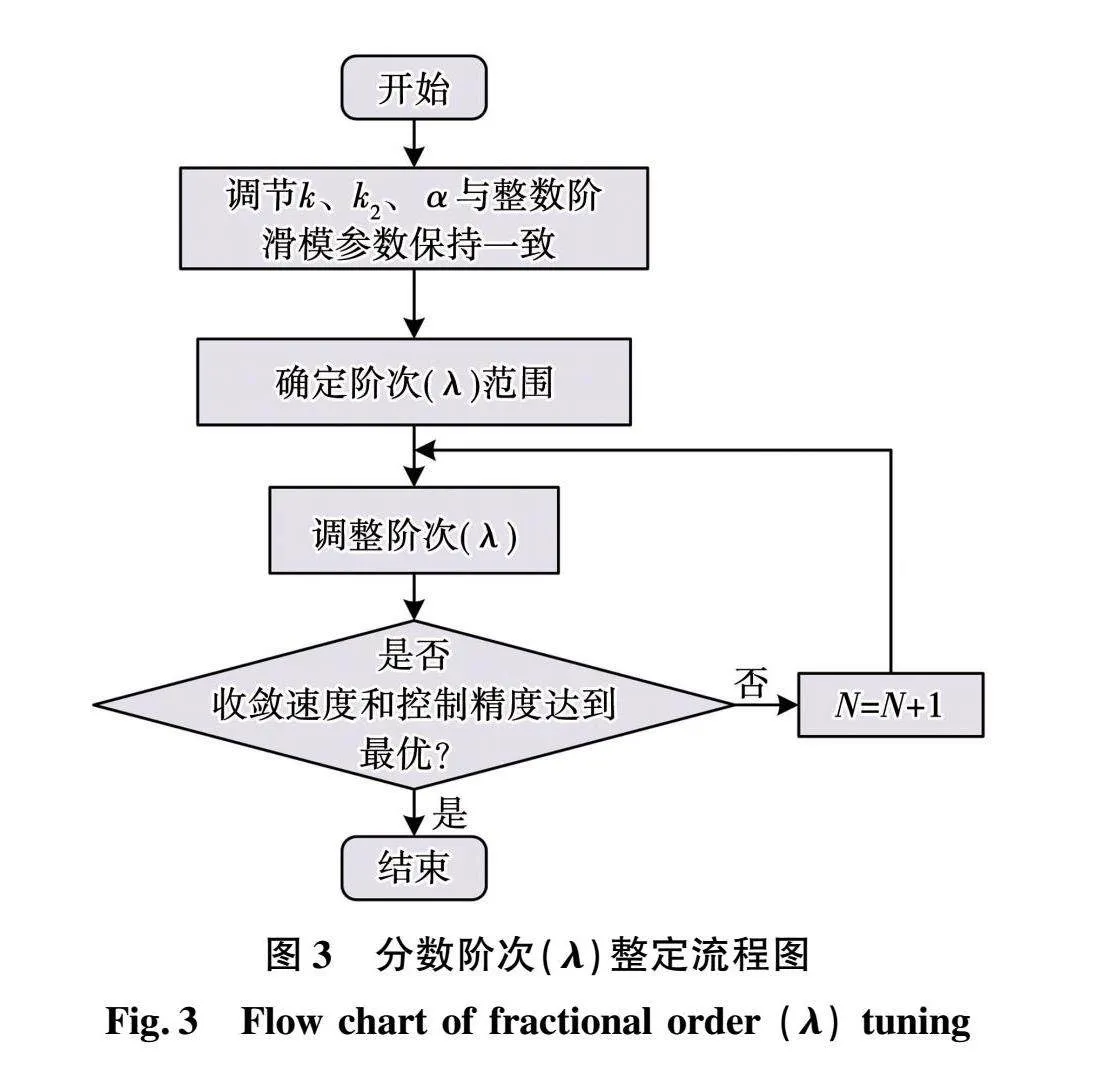
根据式（31）可知，分数阶滑模控制器参数有k、k2、α、λ，相比整数阶滑模控制器多了1个可调参数λ。其中k是滑模面切换增益，若取值太大会加剧抖振，太小会影响控制器精度。k2、α影响系统进入滑模面的速度。图3给出了控制器参数λ的整定流程图，首先调节k、k2、α三个参数与整数阶滑模控制器参数保持一致，在此基础上进而调整阶次λ直至整流器系统收敛速度和控制精度达到最优，以此来弥补整数阶滑模运用到九电平拓扑存在的缺陷。本文中分数阶微积分算子的计算采取Oustaloup滤波器拟合方法实现，该方法通过配置整数阶传递函数的零极点从而实现对分数阶微积分算子的全局逼近，实现简单且逼近精度高。

为了方便配置整数阶传递函数的零极点，分数阶传递函数的阶次一般选取为0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9，所以只需采用Oustaloup滤波器拟合方法近似九组分数阶传递函数，选出使系统控制性能达到最优的阶次即可，即本文分数阶次整定工作最多重复9次。最终的控制器参数为：k=30、k2=8、α=1、λ=0.3。

3.4 九电平整流器分数阶滑模控制算法的实现

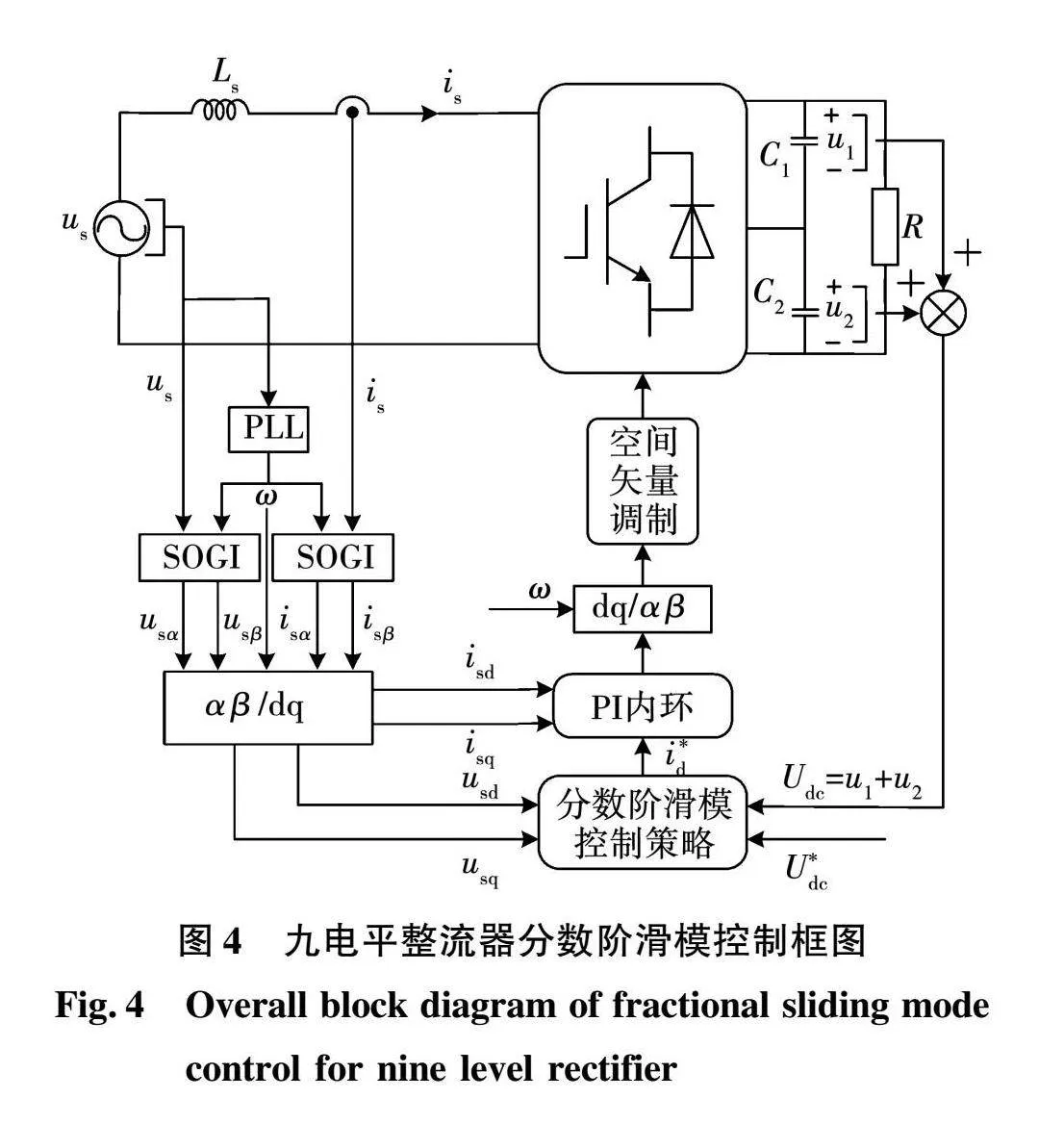
图4是九电平整流器采用分数阶滑模控制的实现框图。首先，根据直流侧电压参考值与实际值的误差形成输入分数阶滑模控制的状态变量，计算出滑模面s2，然后根据式（31）计算得到dq坐标轴下内环电流的参考值i*d，并结合内环控制输出控制信号，最后将控制信号反变换后送到空间矢量调制模块，经调制后的触发信号送至各开关管实现对整流器的控制。

4 仿真与实验结果分析

4.1 仿真分析

为验证所提FOSMC策略的正确性及其控制性能，在仿真软件上搭建了基于单相九电平整流器的PI算法、IOSMC算法以及FOSMC算法。针对3种控制策略下的整流器的稳态和动态性能进行对比研究。其中各模块的仿真参数如表2所示。

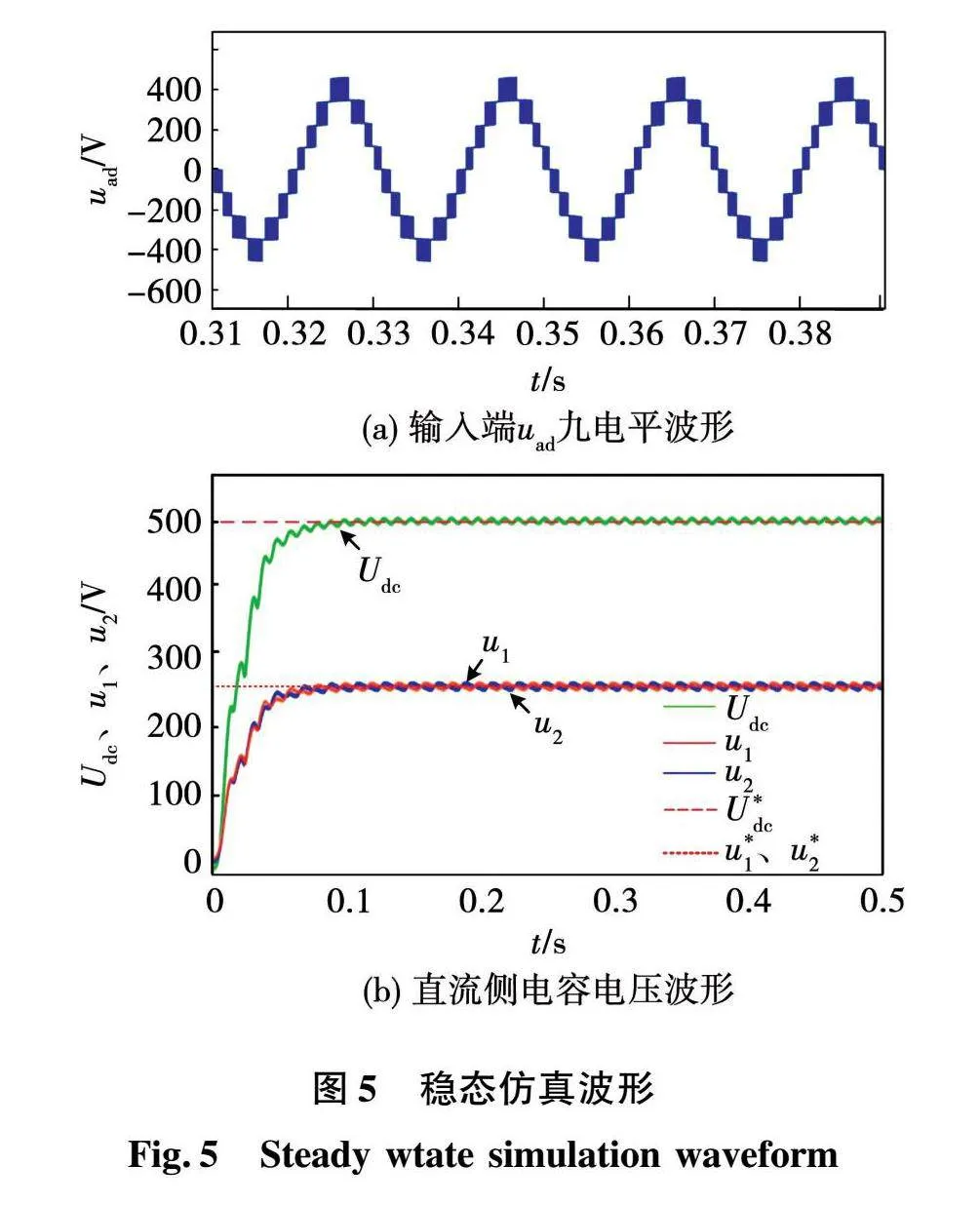
图5为施加FOSMC算法下的九电平整流器的稳态仿真波形。图5（a）为输入端电压uad的仿真波形，可以看出为九电平，且与上文所分析产生九电平的原理相对应。图5（b）是FOSMC算法控制下直流侧电压Udc和上下电容电压u1、u2的仿真波形，可以看出，直流侧电容C1两端电压u1在网侧输入电流正半周期内递增，在负半周期内递减；电容C2两端电压u2在网侧输入电流正半周期内递减，在负半周期内递增，且两电容电压u1、u2有效值均为直流侧电压Udc的一半，单相九电平整流器能够实现电容电压自均衡。

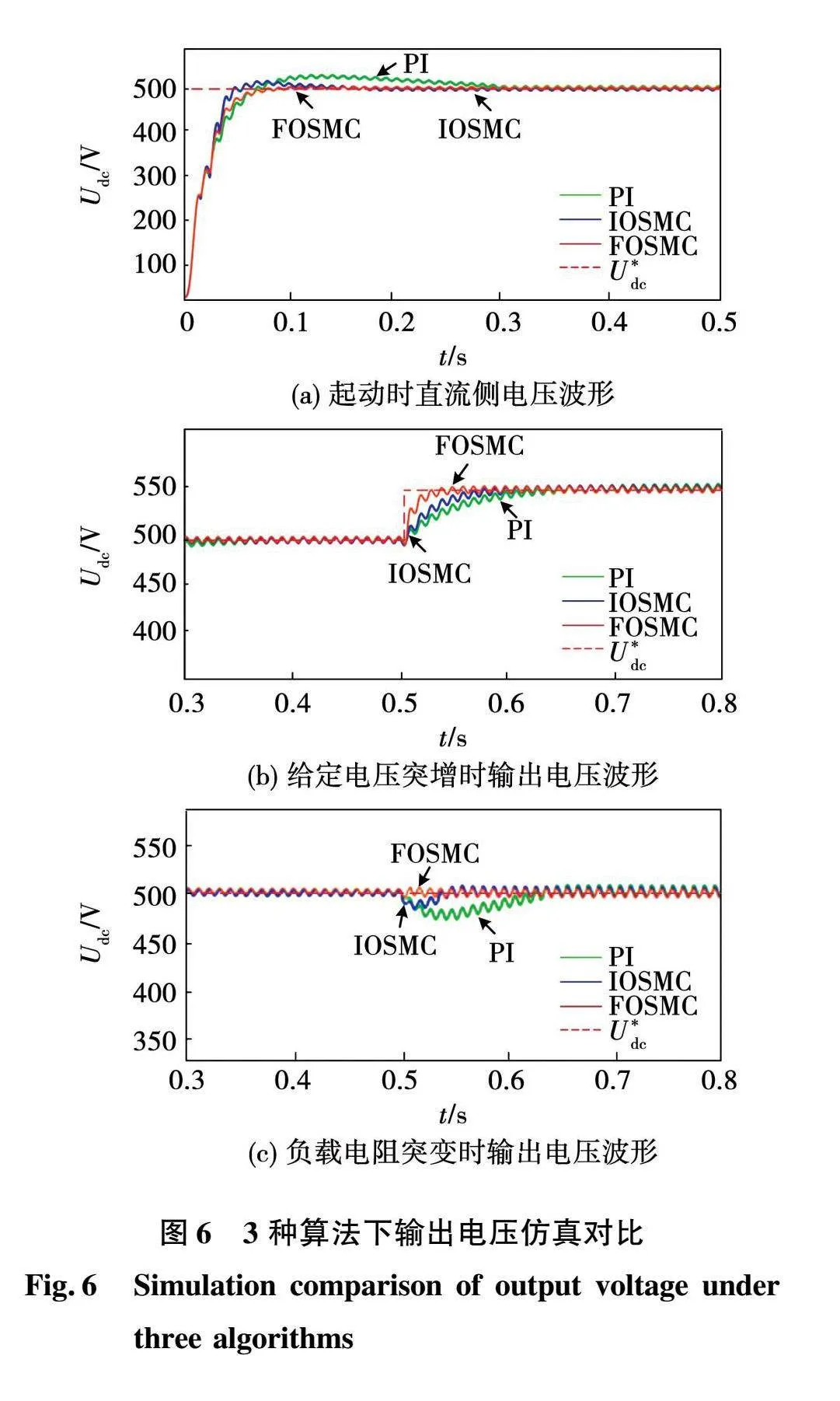
图6是分别采用PI、IOSMC以及FOSMC 3种不同控制算法下的输出电压仿真波形。图6（a）为3种控制算法的直流侧启动时电压对比波形，可以看出，3种控制策略下，直流侧电压最终都稳定在给定值，但是分数阶滑模控制算法相比于其他2种算法，收敛至稳态所需时间最短，没有起动超调，既保证了系统的快速起动，又能够实现对系统的高精度跟踪。图6（b）是给定电压突增时的输出电压波形，可以看出，给定值突变后，PI和IOSMC算法都要经过较长时间重新跟踪上给定值，而FOSMC算法很快就能够跟踪上给定值，使系统重新恢复稳定。图6（c）是直流侧负载突变时的输出电压波形，可以看出，相比于PI算法和IOSMC算法，FOSMC算法下直流侧电压波动最小，对外部干扰不敏感，鲁棒性最强。

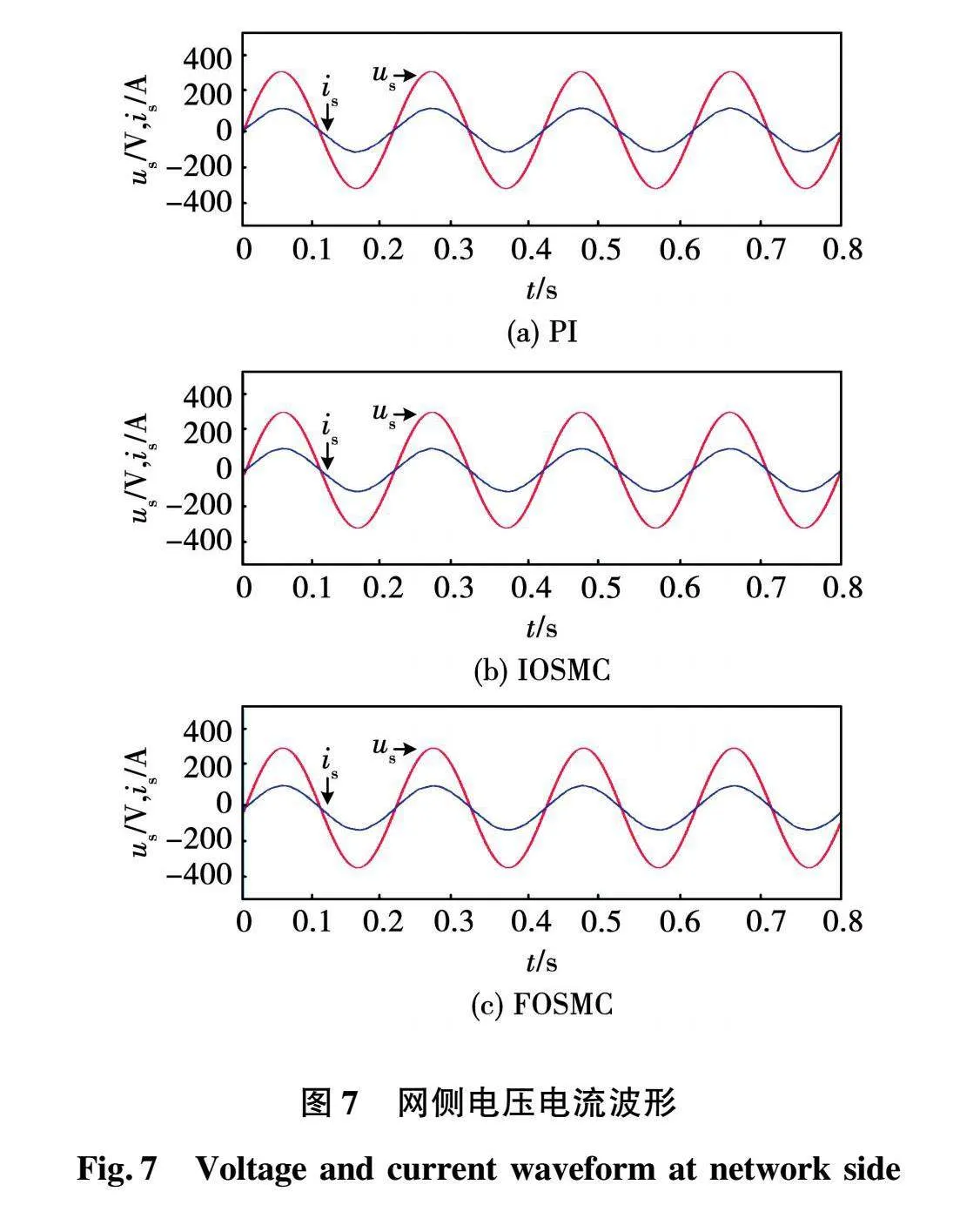
图7是3种控制算法下网侧电压和网侧电流波形，可以看出，PI、IOSMC、FOSMC 3种算法下整流器网侧和网侧电流相位差均为0，即整流器都能够实现单位功率因数运行。

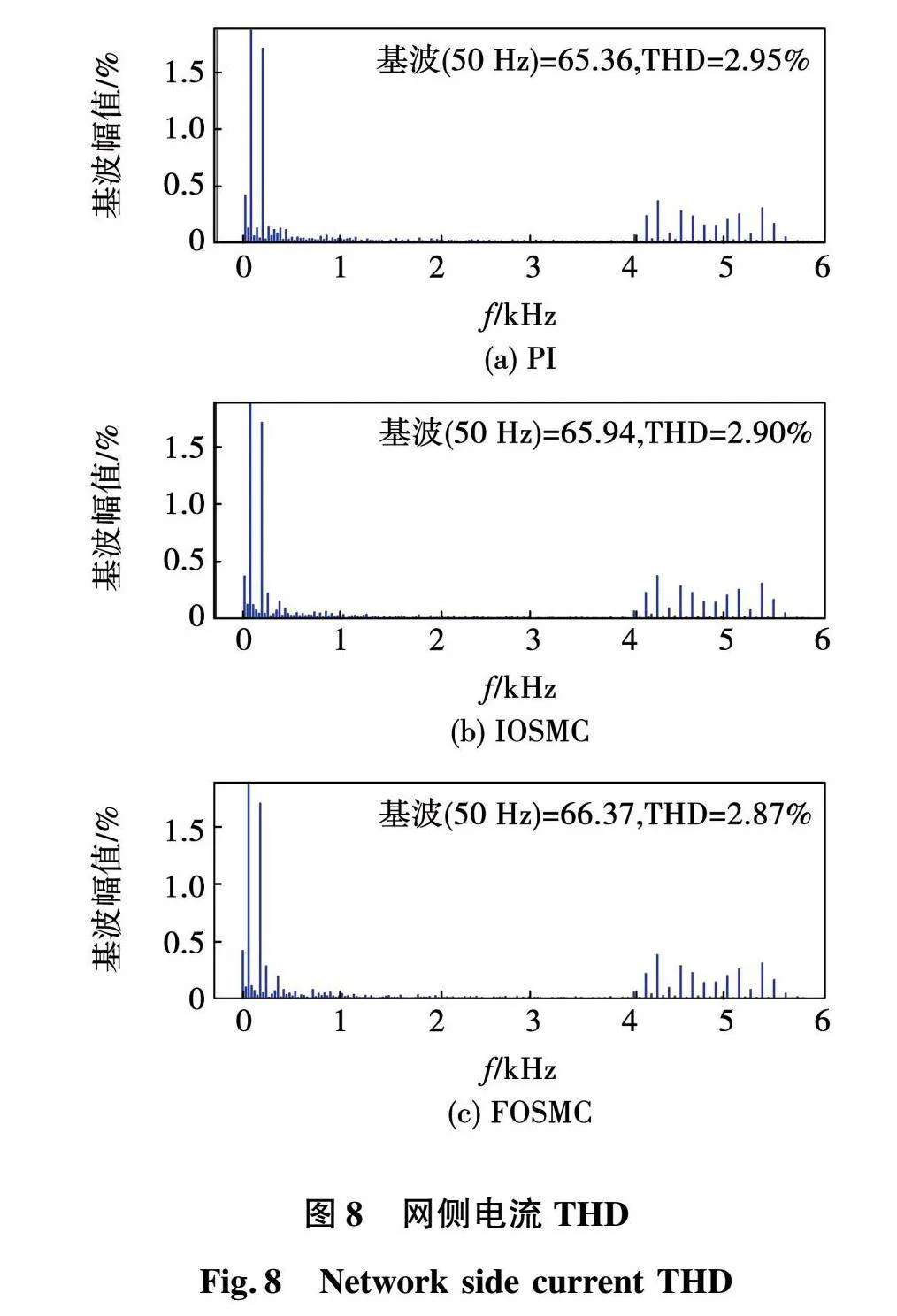
图8是3种控制算法下网侧输入电流的快速傅里叶分析（FFT）结果图，可以看出，PI控制下整流器输入端电流的总谐波畸变率（total harmonic distortion，THD）为2.95%，IOSMC的THD为2.90%，FOSMC的THD为2.87%。相比于其他2种算法，FOSMC算法下整流器的网侧电流总谐波畸变率最小。

4.2 实验验证

为了更加深入验证所提算法的有效性和可行性，搭建了DSP+RT-LAB的半实物平台，对PI算法、传统整数阶滑模算法和本文所提分数阶滑模算法这3种控制算法的稳态和动态性能进行实验对比。其中，DSP采用TI公司的TMS320F28335，RT-LAB由上位机、运算单元、模拟板和数字模块组成，如图9所示。实验中主电路各模块参数选择与仿真一致，详见表2。

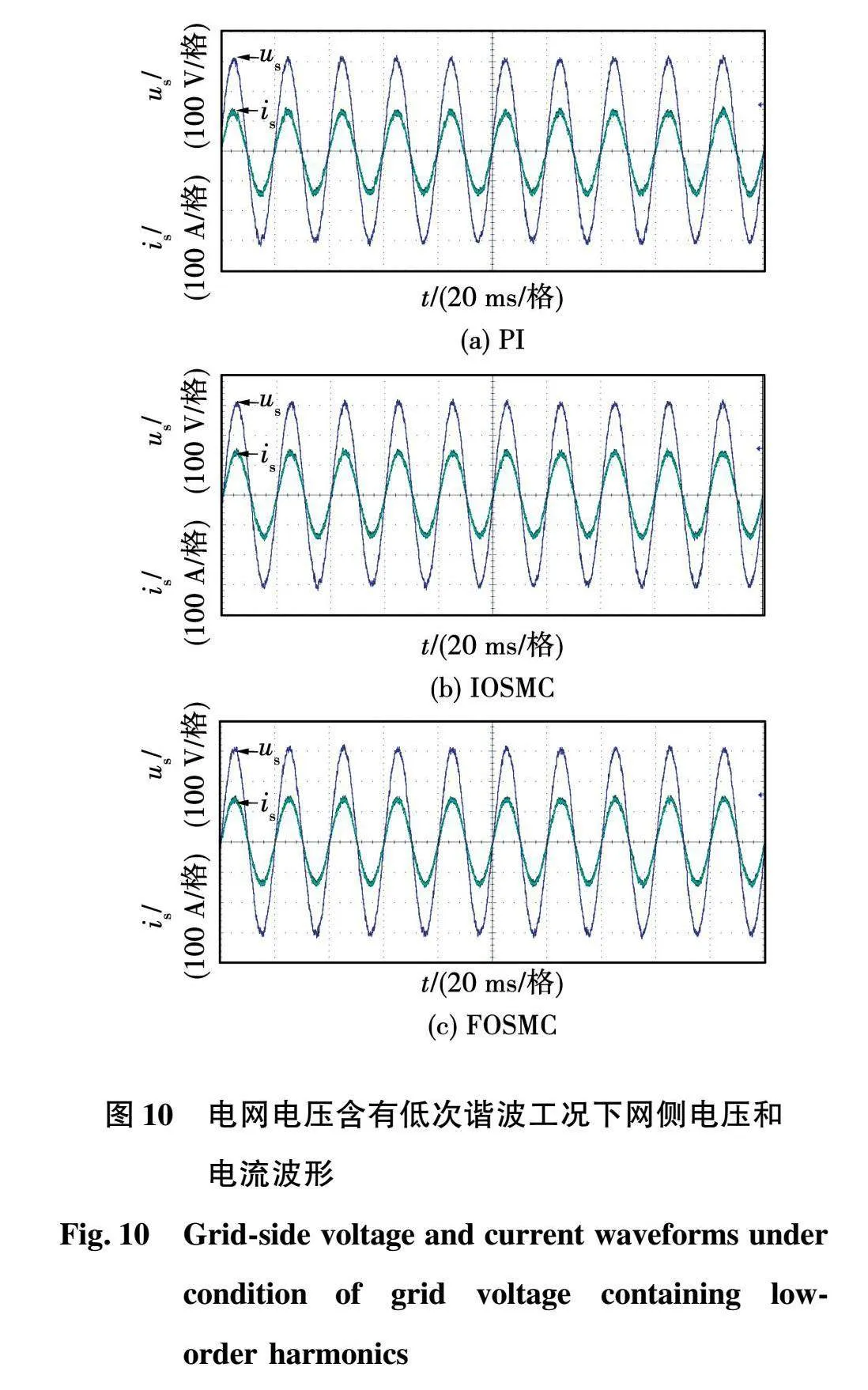
图10给出了在电网电压存在5%的3次谐波和5%的5次谐波工况下3种控制算法的实验波形。可以看出，3种控制算法在电网电压含有低次谐波工况下都能够实现单位功率因数运行，但FOSMC算法相较于PI算法和IOSMC算法网侧电流畸变程度更小，且正弦度最高，稳态性能更加优秀。

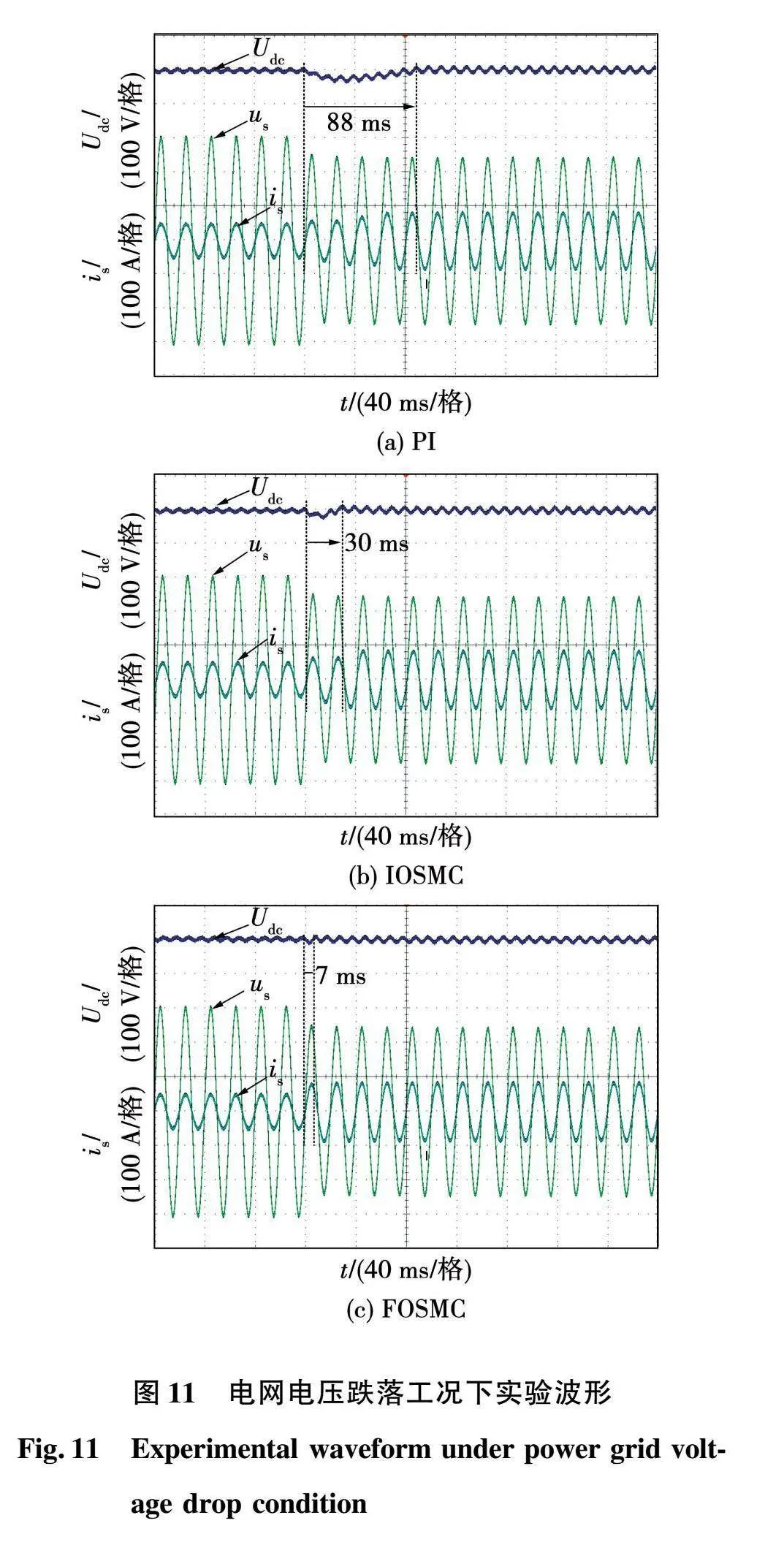
图11给出了在电网电压跌落工况下的实验波形，电压源幅值由311 V突降为255 V。由图可知，3种控制算法在电网电压跌落后直流侧电压Udc都会产生一定的电压波动，网侧电流is需要逐渐增大以补偿电网电压突降对直流侧功率产生的影响。但是图11（a）中PI算法下在电网电压跌落后需要经过88 ms才能够重新稳定，网侧电流也需要同样时间过渡到稳态，用时较长且直流侧电压具有较大的波动。图11（b）中IOSMC算法下在电网电压跌落后直流侧电压和网侧电流都需要30 ms重新恢复到稳定状态，相比PI算法控制时间有所改善，但是仍然存在较大电压波动。图11（c）中当采用FOSMC算法时，电网电压跌落后直流侧电压仅需要7 ms就能够重新稳定下来，同时网侧电流几乎不需要过渡过程就稳定下来，且直流侧电压无明显波动。综上所述，分数阶滑模控制算法在非理想工况下相比于其他2种算法具有更加优越的控制性能。

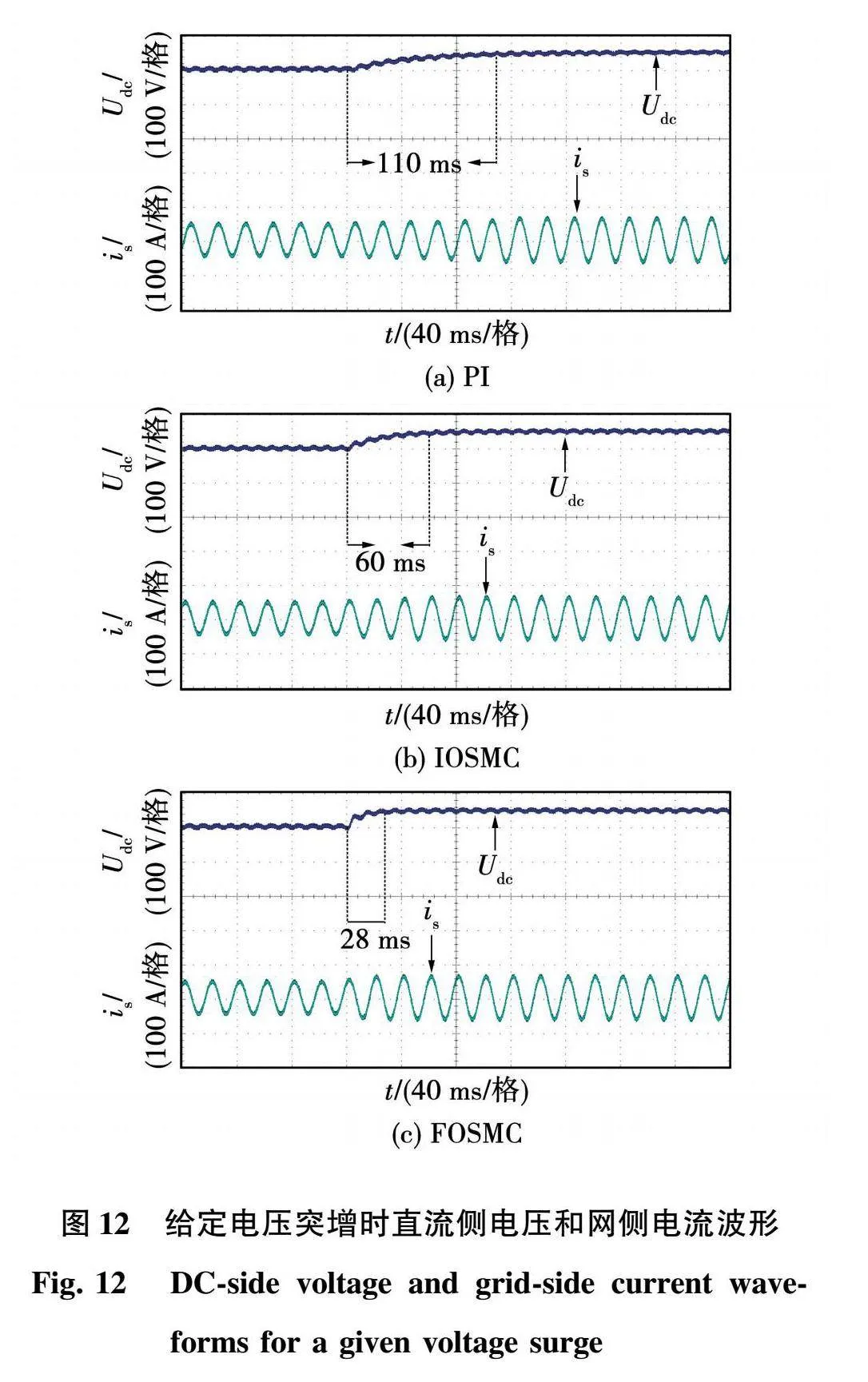
图12给出了给定电压由500 V突增到550 V时的3种控制算法下的直流侧电压Udc和网侧电流is变化情况。可以看出3种控制策略都能够使直流侧电压重新跟踪上给定值，网侧电流也重新恢复稳定。但是由图12（a）可以看出，PI控制时直流侧电压和网侧电流大约需要110 ms才能够重新达到给定值，相较于另外2种算法，用时最长。由图12（b）可以看出，施加IOSMC算法时直流侧约需60 ms重新达到给定值，网侧电流约55 ms稳定下来，恢复时间较长。而图12（c）中，当采用FOSMC算法时，仅需约28 ms直流侧电压就能够重新达到给定值，网侧电流也能够重新恢复稳定，所需时间最短。所以相较于其他2种算法，分数阶滑模控制算法具有更加优越的动态性能。

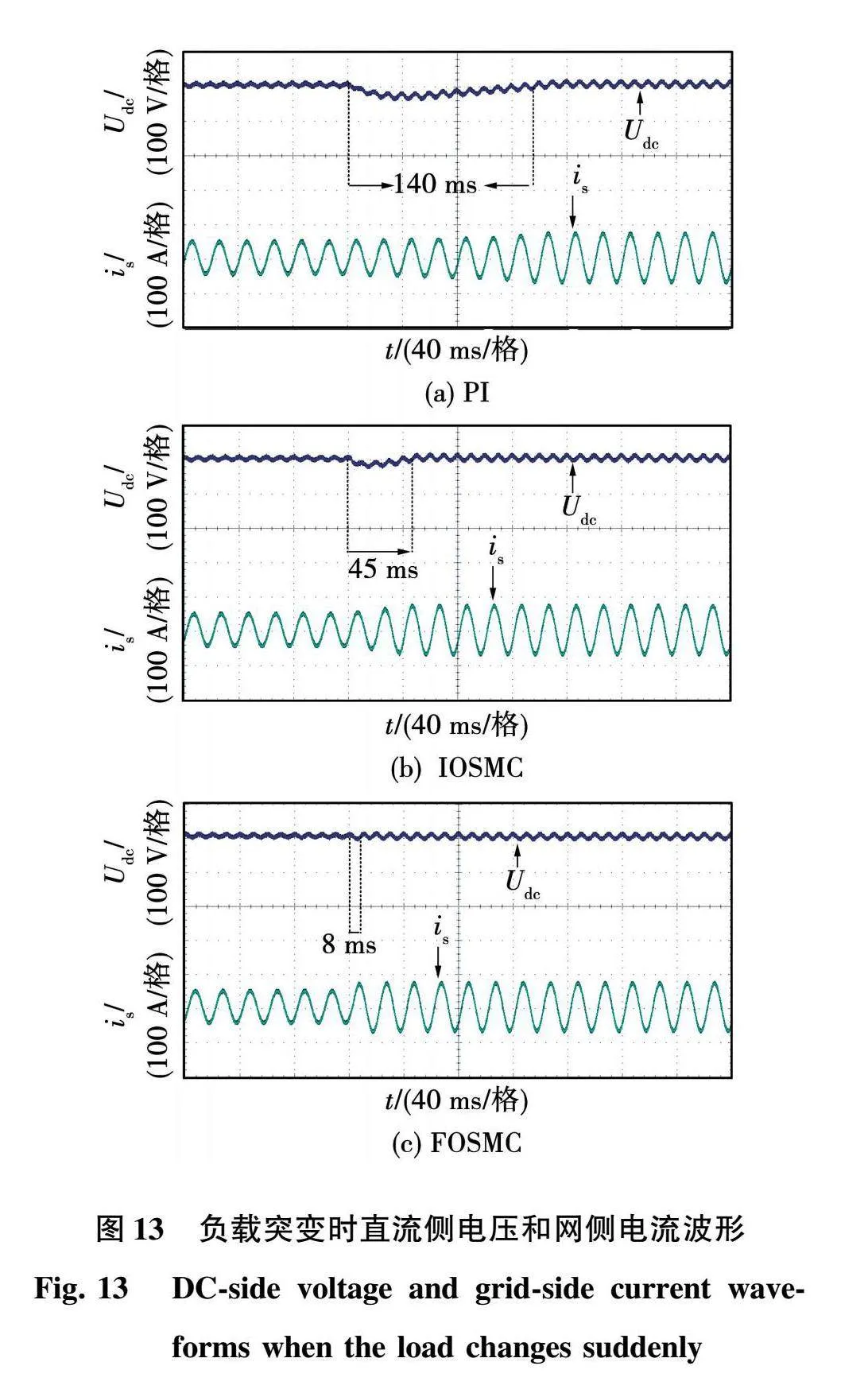
图13给出了直流侧负载突变时3种控制算法下的直流侧电压Udc和网侧电流is变化曲线图，负载由40 Ω突变为20 Ω。可以看出，图13（a）中PI控制时直流侧电压需要约140 ms才能重新跟踪给定电压，且存在很大的电压波动，电流也需要相同的时间过渡到稳态；由图13（b）可以看出IOSMC控制时直流侧电压重新达到给定值约需45 ms，电压波动有所减小，电流过渡到稳态的时间也相应减少，但仍不理想；从图13（c）中可以看出当采用FOSMC算法时，直流侧电压重新回到给定值仅需约8 ms，基本没有电压波动，网侧电流几乎无需过渡时间就能够重新稳定。所以，相较于其他2种算法，分数阶滑模算法拥有更快的收敛速度，且抗干扰能力更强。

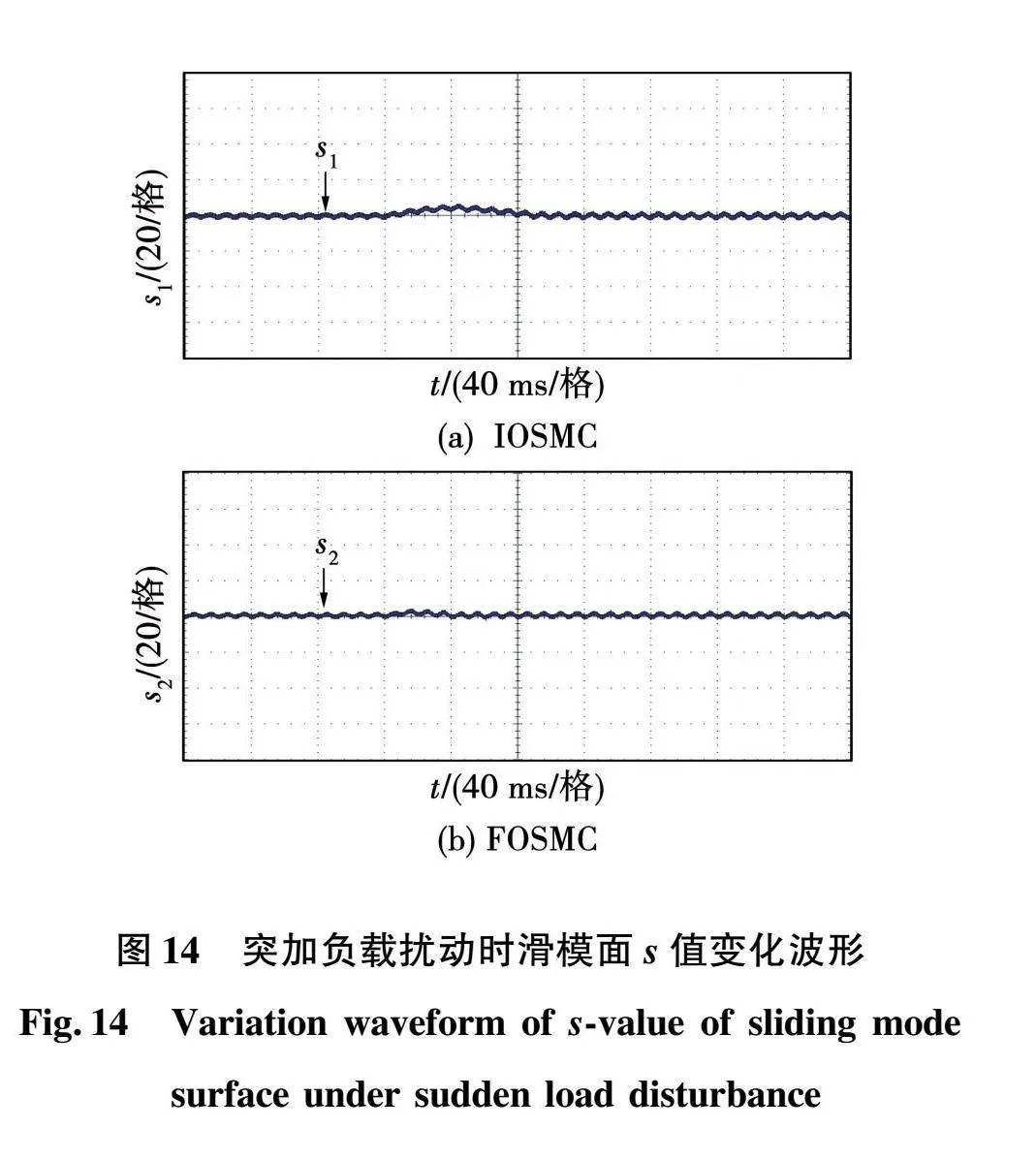
图14给出了突加负载扰动时整数阶滑模面和分数阶滑模面s值的变化曲线。通过对比可知，图14（a）中采用IOSMC算法时，在受到扰动时系统状态远离滑模面的程度更大，且重新收束到滑模面需要更长的时间。而图14（b）中采用FOSMC算法时，系统状态几乎一直沿着滑模面运动，对参数摄动性更小，收敛速度更快，鲁棒性更强。

5 结 论

本文以一种含耦合电感的单相九电平整流器为研究对象，针对传统整数阶滑模控制应用于此拓扑存在的问题，详细研究了一种分数阶滑模控制策略，并应用到整流器的控制系统中，得到如下结论：

1）通过引入分数阶微积分算子可以增加整流器控制系统的自由度，使滑模控制具备更加灵活的调节性能，为提高整流器系统的控制性能创造条件。

2）分数阶滑模控制策略相比于整数阶滑模控制和比例积分控制，响应时间更短，系统收敛速度更快。同时解决了整数阶滑模在整流器控制中存在的超调过大问题，实现了高精度控制。此外，分数阶滑模控制策略在多种工况下都能够快速跟踪给定值使系统恢复稳态，抗干扰能力强，有力地增强了系统对参数摄动的鲁棒性。

参 考 文 献：

［1］ 张云雷，王群京，胡存刚. 一种新型混合式七电平逆变器[J]. 电机与控制学报， 2020， 24（10）： 48.

ZHANG Yunlei， WANG Qunjing， HU Cungang. Hybrid seven-level inverter and control strategy[J]. Electric Machines and Control， 2020， 24（10）： 48.

［2］ KARWATZKI D， MERTENS A. Generalized control approach for a class of modular multilevel converter topologies[J]. IEEE Transactions on Power Electronics， 2018， 33（4）： 2888.

［3］ FANG J， BLAABJERG F， LIU S， et al. A review of multilevel monverters with parallel connectivity[J]. IEEE Transactions on Power Electronics， 2021， 36（11）： 12468.

［4］ 杨达亮，张轩，陈爽，等. 电网电压畸变下的单相级联H桥变流器无锁相环控制[J]. 电网技术， 2021， 45（2）： 751.

YANG Daliang， ZHANG Xuan， CHEN Shuang， et al.Single-phase cascaded H-bridge converter control without phase-locked loop under distorted grid voltage conditions [J]. Power System Technology， 2021， 45（2）： 751.

［5］ FANG J， LI Z， M-GOETZ S. Multilevel converters with symmetrical half-bridge submodules and sensorless soltage balance[J]. IEEE Transactions on Power Electronics， 2021， 36（1）： 447.

［6］ 熊成林，刁飞，吴瑕杰，等. 单相变换器简化多电平SVPWM算法[J]. 电机与控制学报， 2019， 23（4）： 56.

XIONG Chenglin， DIAO Fei， WU Xiajie， et al. A simplified multilevel space vector pulse-width modulation algorithm for single-phase converter[J]. Electric Machines and Control， 2019， 23（4）： 56.

［7］ 陈思哲， 徐梦然， 范元亮， 等. 一种基于开关电容的九电平逆变器[J]. 电工技术学报， 2022， 37（4）： 931.

CHEN Sizhe， XU Mengran， FAN Yuanliang， et al. A nine-level inverter based on switched-capacitor[J]. Transactions of China Electrotechnical Society， 2022， 37（4）： 931.

［8］ 曹宇， 李睿， 蔡旭，等. 一种交错并联型九电平光伏逆变器[J].中国电机工程学报，2020，40（11）：3602.

CAO Yu， LI Rui， CAI Xu， et al. An interleaved nine-level photovoltaic inverter[J]. Proceedings of the CSEE， 2020，40（11）：3602.

［9］ 叶满园，肖云煌，康翔，等. 混合H桥级联多电平逆变器功率均衡控制方法[J]. 电机与控制学报， 2018， 22（12）： 54.

YE Manyuan， XIAO Yunhuang， KANG Xiang， et al. Power balance control scheme of cascaded multilevel inverters with hybrid H-bridge units [J]. Electric Machines and Control， 2018， 22（12）： 54.

［10］ YE M，KANG L， XIAO Y， et al. Modified hybrid modulation strategy with power balance control for H-bridge hybrid cascaded seven-level inverter[J]. IET Power Electronics， 2018， 11（6）： 1046.

［11］ 李宋， 苗志林， 叶满园， 等. 七电平逆变器电容电压自均衡控制策略研究[J].高电压技术， 2022， 48（7）：2785.

LI Song， MIAO Zhilin， YE Manyuan， et al. Research on the control strategy of capacitor voltage self-balance for seven-level inverter[J]. High Voltage Technology， 2022， 48（7）：2785.

［12］ 苟鑫， 卢继平， 刘加林， 等. 一种基于子模块投入优先级的模块化多电平换流器电容电压均衡控制策略[J].中国电机工程学报， 2019， 39（24）： 7299.

GOU Xin， LU Jiping， LIU Jialin， et al. A capacitor voltage balancing control method for modular multilevel converter based on insertion priority of the sub-modules [J]. Proceedings of the CSEE， 2019， 39（24）： 7299.

［13］ K-JUNEJO A， XU W， MU C， et al. Adaptive speed control of PMSM drive system based a new sliding-mode reaching law[J]. IEEE Transactions on Power Electronics， 2020， 35（11）： 12110.

［14］ SHI S， GU J， XU S， et al. Globally fixed-time high-order sliding mode control for new sliding mode systems subject to mismatched terms and its application[J]. IEEE Transactions on Industrial Electronics， 2020， 67（12）： 10776.

［15］ 邵冰冰， 赵书强， 高本锋， 等. 基于反馈线性化滑模控制的直驱风电场经柔直并网系统次同步振荡抑制策略[J].中国电机工程学报， 2021， 41（9）：3090.

SHAO Bingbing， ZHAO Shuqiang， GAO Benfeng， et al. Sub-synchronous oscillation mitigation strategy of direct-drive wind farms via VSC-HVDC system based on feedback linearization sliding mode control[J]. Proceedings of the CSEE， 2021， 41（9）：3090.

［16］ SUN G， MA Z， YU J. Discrete-time fractional order terminal sliding mode tracking control for linear motor[J]. IEEE Transactions on Industrial Electronics， 2018， 65（4）： 3386.

［17］ 郑长明，张加胜，许睿，等. Buck变换器的鲁棒离散积分滑模控制[J]. 电工技术学报， 2019， 34（20）： 4306.

ZHENG Changming， ZHANG Jiasheng， XU Rui， et al. Robust discrete integral sliding mode control for buck converters [J]. Transactions of China Electrotechnical Society， 2019， 34（20）： 4306.

［18］ LONG B， J-LU P， T-CHONG K， et al. Robust fuzzy-fractional-order nonsingular terminal sliding-mode control of LCL-type grid-connected converters[J]. IEEE Transactions on Industrial Electronics， 2022， 69（6）： 5854.

［19］ 李鹏瀚，王子强，王杰. 双馈风电场次同步控制相互作用的分数阶滑模抑制策略[J]. 中国电机工程学报， 2020， 40（3）： 897.

LI Penghan， WANG Ziqiang， WANG Jie. Sub-synchronous control interaction mitigation strategy based on fractional-order sliding mode control for DFIG-based wind farm [J]. Proceedings of the CSEE， 2020， 40（3）： 897.

［20］ YIN Chun， CHEN Yangquan， ZHONG Shouming. Fractional-order sliding mode based extremum seeking control of a class of nonlinear systems[J]. Automatica， 2014， 50（12）： 3173．

［21］ MOHAMADIAN S， PAIRO H， GHASEMIAN A. A straightforward quadrature signal generator for single-phase SOGI-PLL with low susceptibility to grid harmonics[J]. IEEE Transactions on Industrial Electronics， 2022， 69（7）： 6997.

（编辑：刘琳琳）