Vienna整流器低开关频率双矢量模型预测控制策略研究

摘 要：为了解决Vienna整流器传统有限集模型预测控制计算量大、控制精度依赖于采样频率的问题，同时降低Vienna整流器的开关频率，提出一种应用于Vienna整流器的低开关频率双矢量有限集模型预测控制策略。首先，建立基于电压预测的代价函数，并在进行预测计算之前确定参考电压矢量所在的扇区以减少参与预测计算的矢量个数。其次，在控制周期中引入第二矢量与最优矢量共同作用，以提高控制系统的跟踪精度，减小传统有限集模型预测控制对采样频率的依赖。再者，为了减小系统的开关损耗，对输出的双矢量组合进行限定并对矢量的作用顺序进行调整。此外，利用冗余矢量对中点电压的相反影响解决直流侧中点电压的波动问题。最后，通过仿真和实验证明所提控制策略的有效性和可行性。

关键词：Vienna整流器；双矢量有限集模型预测控制；开关频率；低计算量；中点电压平衡；代价函数

DOI：10.15938/j.emc.2024.11.016

中图分类号：TM46

文献标志码：A

文章编号：1007-449X（2024）11-0172-12

Predictive control strategy of low switching frequency double-vector model for Vienna rectifier

FENG Xingtian， DAI Zhanjiang， SONG Xu

（College of New Energy， China University of Petroleum （East China）， Qingdao 266580， China）

Abstract：In order to solve the problem that the traditional finite set model predictive control of Vienna rectifier is computationally intensive and the control accuracy depends on the sampling frequency， and to reduce the switching frequency of Vienna rectifiers， a double-vector finite-set model predictive control strategy with low switching frequency applied to Vienna rectifiers was proposed. Firstly， a cost function based on voltage prediction was established， and the sector where the reference voltage vector is located was determined before the prediction calculation to reduce the number of vectors involved in the prediction calculation. Secondly， the second vector was introduced into the control cycle to work with the optimal vector to improve the tracking accuracy of the control system and reduce the dependence of traditional finite set model predictive control on sampling frequency. Furthermore， in order to reduce the switching loss of the system， the combination of the output double vectors was limited and the action order of the vectors was adjusted. In addition， the fluctuation problem of the neutral point voltage on the DC side was solved by using the opposite effect of the redundant vector on the neutral point voltage. Finally， effectiveness and feasibility of the proposed control strategy were proved by simulation and experiment.

Keywords：Vienna rectifier; double vector finite control set model predictive control; switching frequency; low computational load; neutral point voltage balance; cost function

0 引 言

三相三线制Vienna整流器因其低输入电流谐波畸变率、高功率密度和高效率等优点备受研究人员的关注，被广泛应用在航空电源、风力发电、电动汽车充电系统等领域^[1-4]。然而，由于拓扑结构的限制，当Vienna整流器输入电流和电压的极性不同时，输入电流会产生过零畸变。此外，Vienna整流器也存在三电平变换器固有的中点电压平衡问题，并且由于Vienna整流器多用在中、大功率场合，所以其开关损耗问题也应该被考虑。

为了解决上述问题相关学者做了大量的研究。文献[5]提出一种零序分量注入的调制方法，通过在电流畸变区间内添加补偿分量，在直流侧电压平衡和不平衡情况下都能够抑制输入电流的谐波畸变。文献[6]提出在电流过零点处设置可变钳位区域的调制方法，从原理上抑制了输入电流的过零畸变。文献[7]提出一种双层脉宽调制策略，通过调整矢量的开关顺序、开关状态和作用时间，实现抑制输入电流失真的目标。为了平衡中点电压，文献[8]在空间矢量脉宽调制环节中引入中点电压差，根据中点电压差值动态分配冗余小矢量的作用时间以平衡中点电压，文献[9]在基于载波的脉宽调制策略下设计一种平衡Vienna整流器中点电压的通用框架，在框架的基础上选择不同的零序电压就能够实现中点电压平衡。为了提高Vienna整流器在实际应用场合中的效率，文献[10-11]提出非连续脉宽调制策略，通过在开关周期中钳位某一相的桥臂电压，有效地减小功率器件的开关频率和开关损耗。

近年来，随着微处理器和数字信号处理器的快速发展，有限集模型预测控制（finite control set model predictive control，FCS-MPC）因其具有多目标约束、无需调制环节、反应速度快等优点在电力电子领域中得到了广泛的应用^[12-1]。文献[14-15]提出混合式的FCS-MPC，建立包含电流误差和中点电压误差的混合代价函数，在跟踪参考电流的同时抑制了中点电压波动。为了提高系统的效率，文献[16]在代价函数中引入开关次数的评估函数，在保证控制系统跟踪精度的前提下减小了功率器件的开关次数。文献[17]提出一种动态事件触发的模型预测控制策略，只有当系统状态满足一定的事件触发条件时才更新采样数据，在保证控制系统性能的前提下减小了控制器的计算量和系统的开关损耗。为了提高控制策略的实际应用能力，文献[18]提出一种快速矢量选择的简化FCS-MPC，在降低控制策略复杂度的同时提高了控制系统的动态响应能力。

然而上述的FCS-MPC在控制周期内都只能输出一个作用矢量，控制系统的精度严重依赖于采样频率。为了解决这一问题，文献[19-20]提出在候选矢量集中引入虚拟矢量的方法以减小预测控制的跟踪误差。虚拟矢量由相邻的实矢量组合而成，这种方法虽然能够提高系统的跟踪精度但增加了控制器的计算负担。文献[21]提出基于最优占空比的模型预测控制策略，在控制周期中输出有源电压矢量和零电压矢量，与传统FCS-MPC相比控制精度更高。文献[22]提出一种应用于Vienna整流器的有限集模型预测虚拟磁链控制，推导出一种计算作用矢量占空比的纯代数方法，在电网不平衡的情况下具有很强的鲁棒性。文献[2]提出一种Vienna整流器的定频双矢量模型预测控制，通过求导计算出控制周期内最优电压矢量和零电压矢量的占空比并经过调制环节输出开关信号，在提高控制系统跟踪精度的同时，固定了Vienna整流器的开关频率。文献[24]提出一种Vienna整流器的三层双矢量FCS-MPC，能够有效解决Vienna整流器输入电流过零畸变和中点电位平衡问题，且具有较高的电流跟踪精度。

为了解决传统FCS-MPC计算量大、控制精度受限于采样频率的问题，降低Vienna整流器的开关频率，本文提出一种应用于Vienna整流器的低开关频率双矢量有限集模型预测控制策略（low frequency double vector finite control set model predictive control，LD-MPC）。通过在控制周期中输出2个作用矢量共同跟踪参考电压矢量，以减小控制系统的跟踪误差；通过判断参考电压矢量所在的扇区，以减少参与在线寻优的矢量个数，减轻控制器的计算负担；通过明确控制周期内和相邻控制周期2个作用矢量之间的开关关系，降低功率器件的开关频率，减小系统的开关损耗；通过仿真与实验分析验证所提策略的有效性。

1 Vienna整流器模型预测控制原理

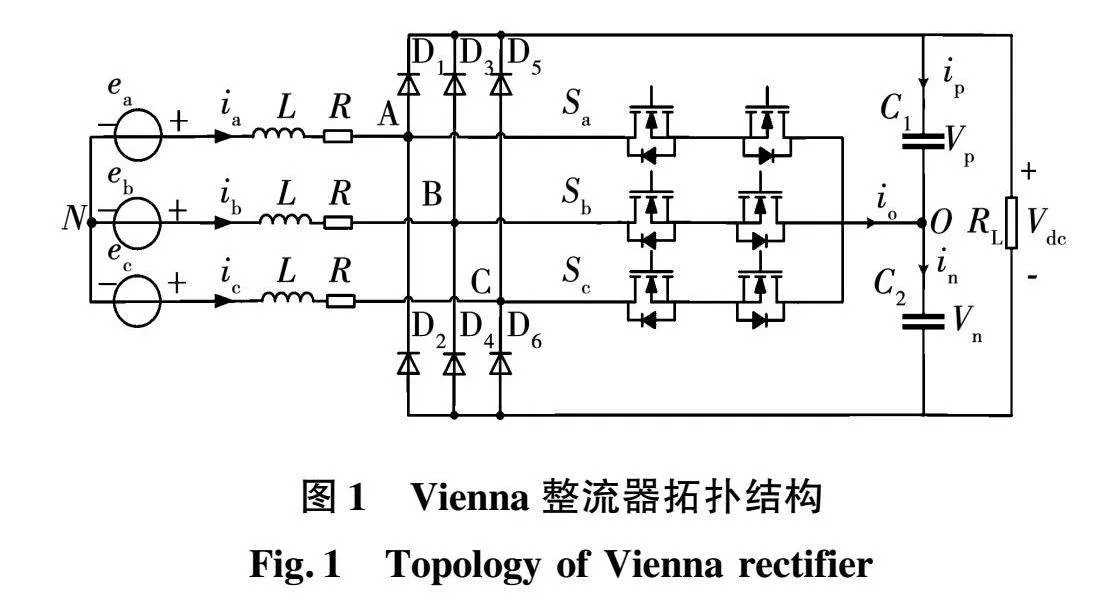
三相三线制Vienna整流器的拓扑结构如图1所示，由6个整流二极管（D1～D6）和3个连接直流侧电容中点的双向桥臂（Sa，Sb，Sc）组成，双向桥臂由2个反向串联的MOSFET构成。Vienna整流器的交流侧连接三相电网，L为交流侧滤波电感，R为交流侧输入电阻，直流侧连接负载RL，C1和C2为直流侧电容，其电容值均为C，Vp和Vn分别表示C1和C2的端电压，Vdc为直流侧的输出电压。

结合图1所示的拓扑结构和基尔霍夫电压定律，Vienna整流器在三相静止坐标系下的数学模型可以表示为：

ea=Ldiadt+Ria+uao+uon；

eb=Ldibdt+Rib+ubo+uon；

ec=Ldicdt+Ric+uco+uon。（1）

式中：ix（x=a， b， c）为三相输入电流；uon为整流器直流侧电容中点O到电网中性点N的电压；uxo（x=a，b，c）为整流桥的三相输入电压，与输入电流的极性和桥臂的开关状态有关，假设直流侧中点电压平衡，整流桥输入电压uxo可以表示为：

uxo=Vdc/2，Sx=0，ixgt;0；

0，Sx=1；

－Vdc/2，Sx=0，ixlt;0。（2）

式中Sx（x=a，b，c）为各相桥臂的开关状态，Sx=1表示桥臂导通，Sx=0表示桥臂关断。

当三相电网平衡时，由式（1）可得uon为

uon=－uao+ubo+uco3。（3）

在图1所示的拓扑结构中直流侧上下电容具有相同的参数，直流侧上下电容电流ip、in和流入电容中点的电流io可以表示为：

ip=CdVpdt；

in=CdVndt；

io=in－ip。（4）

式中流入电容中点的电流io与三相桥臂的开关状态和各相电流的方向有关，根据基尔霍夫电流定律io可以进一步表示为

io=iaSa+ibSb+icSc=∑x=a，b，cSxix。（5）

将式（4）进行离散化并结合式（5），推导出k+1时刻直流侧的中点电压为

uo（k+1）=io（k）CTs+uo（k）=

∑x=a，b，cSxixCTs+uo（k）。（6）

式中：io（k）为k时刻流入电容中点的电流；uo（k）为k时刻直流侧的中点电压；uo（k+1）为k+1时刻直流侧中点电压的预测值；Ts为采样周期。

为了进一步研究Vienna整流器的控制策略，对式（1）进行Clarke变换推导出Vienna整流器在αβ坐标系下的数学模型为：

eα=Ldiαdt+Riα+uα；

eβ=Ldiβdt+Riβ+uβ。（7）

利用前向欧拉法，式（7）可以离散化为：

Liα（k+1）－iα（k）Ts=eα（k）－Riα（k）－uα（k）；

Liβ（k+1）－iβ（k）Ts=eβ（k）－Riβ（k）－uβ（k）。（8）

式中：iα（k）、iβ（k）和eα（k）、eβ（k）分别为k时刻的输入电流和电网电压；iα（k+1）、iβ（k+1）为k+1时刻输入电流的预测值。

根据式（8），k+1时刻的电流预测值可以进一步表示为：

iα（k+1）=TsL［eα（k）－uα（k）］+（1－TsRL）iα（k）；

iβ（k+1）=TsL［eβ（k）－uβ（k）］+（1－TsRL）iβ（k）。（9）

Vienna整流器传统FCS-MPC包含两个控制目标，即跟踪参考电流和控制直流侧中点电压平衡，所以其代价函数为

F1（k）=|i*α（k+1）－iα（k+1）|+|i*β（k+1）－iβ（k+1）|+λ1uo（k+1）。（10）

式中λ1为中点电压的平衡因子。

k+1时刻的电流参考值通过拉格朗日外推法获得：

i*α（k+1）=3i*α（k）－3i*α（k－1）+i*α（k－2）；

i*β（k+1）=3i*β（k）－3i*β（k－1）+i*β（k－2）。（11）

k时刻的参考电流值通过电压外环计算得到：

i*α（k）=23［e2α（k）+e2β（k）］（eαPref+eβQref）；

i*β（k）=23［e2α（k）+e2β（k）］（eβPref－eαQref）。（12）

式中Pref和Qref分别为参考有功功率和参考无功功率，Pref通过功率外环计算得到，Qref设置为0。

从式（6）、式（9）～式（11）可知，Vienna整流器传统FCS-MPC策略是一种包含电流误差和中点电压误差的混合预测控制，在控制过程中需要计算25次中点电压预测值，25次输入电流预测值和25个代价函数值，还要在求得的25个代价函数值中找到最小值及其对应的基本电压矢量，这会给控制器带来较大的运算负担。

为了减少控制器的计算量，本文建立基于电压预测的控制模型为：

u*α（k+1）=eα－LTsi*α（k+1）+L－RTsTsiα（k）；

u*β（k+1）=eβ－LTsi*β（k+1）+L－RTsTsiβ（k）。（13）

基于式（13），Vienna整流器的代价函数被重新定义为

F2（k）=|u*α（k+1）－uα（k+1）|+|u*β（k+1）－uβ（k+1）|+λ2uo（k+1）。（14）

式中：u*α（k+1）和u*β（k+1）为k+1时刻的参考电压；uα（k+1）和uβ（k+1）为候选基本电压矢量在αβ坐标系下的投影；λ2为中点电压的平衡因子。与传统FCS-MPC相比，基于电压预测的FCS-MPC可以根据参考电压矢量所在扇区减少参与预测寻优的矢量个数。

2 双矢量低开关频率控制策略

2.1 候选电压矢量的确定

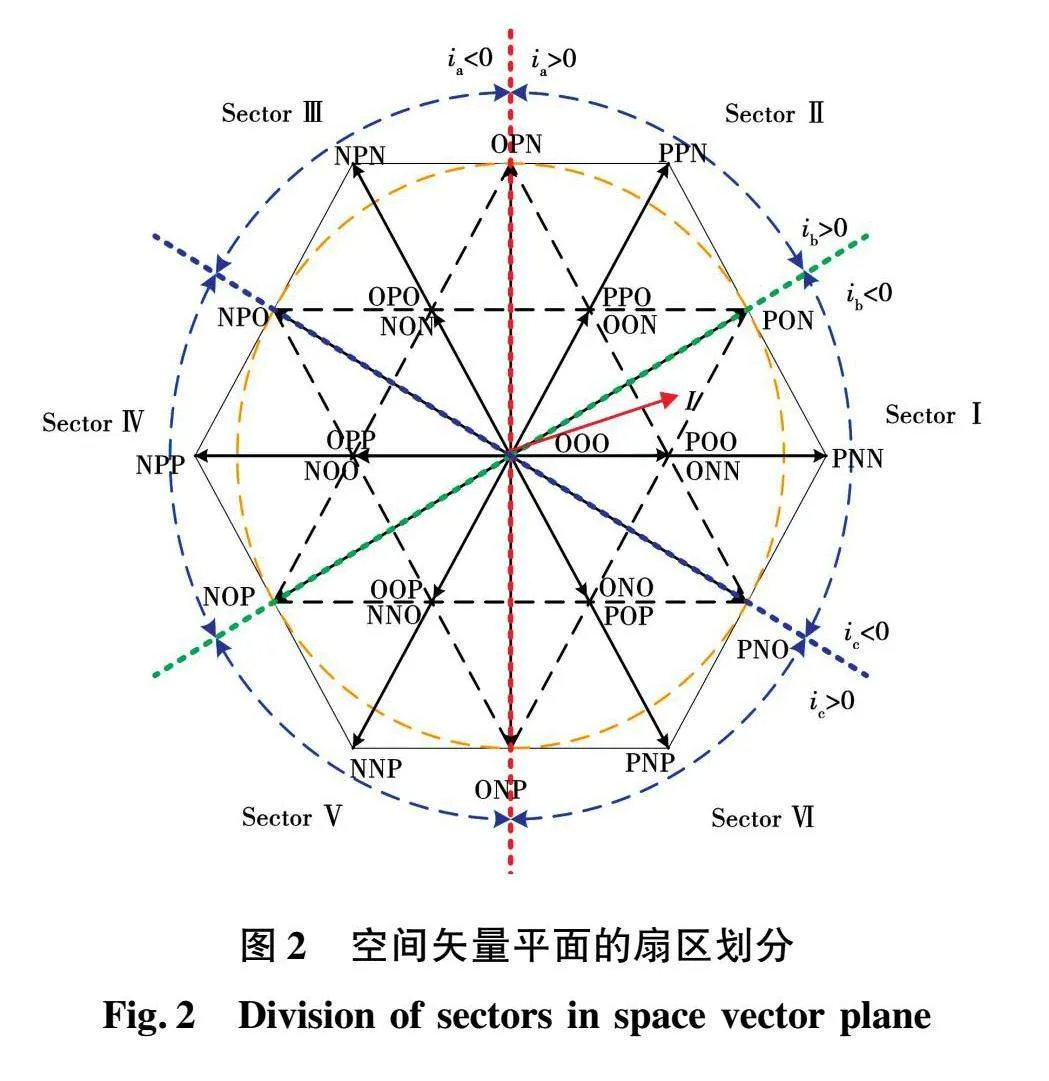
Vienna整流器由于其拓扑结构的限制，当输入电流和电压的极性不同时输入电流会出现过零畸变。为了减轻输入电流的过零畸变，本文根据输入电流的极性将空间矢量平面划分为6个大扇区（Sector I～Sector VI），如图2所示。当iagt;0、iblt;0、iclt;0时，电流矢量位于Sector I扇区，此时为了抑制输入电流过零畸变，A相允许输出的电平为P和O，B相和C相允许输出的电平为O和N。

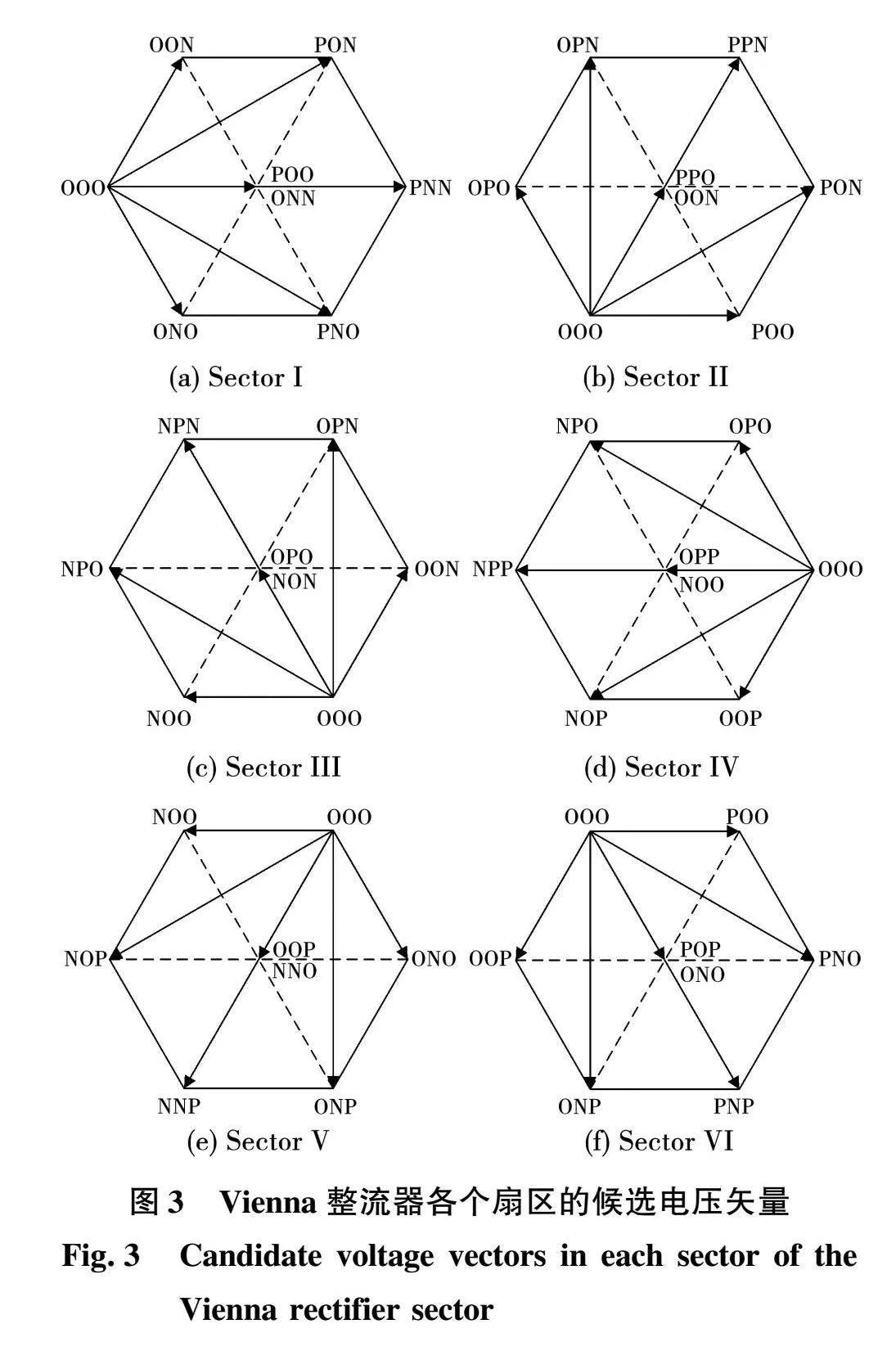
即当电流矢量位于Sector I扇区时，允许输出的基本电压矢量为[OOO]、[OON]、[PON]、[PNN]、[PNO]、[ONO]、[POO]、[ONN]，这些基本电压矢量形成一个如图3（a）所示的小六边形，类似的推导可以得到Sector II～Sector VI扇区的候选电压矢量，如图3（b）～图3（f）所示。

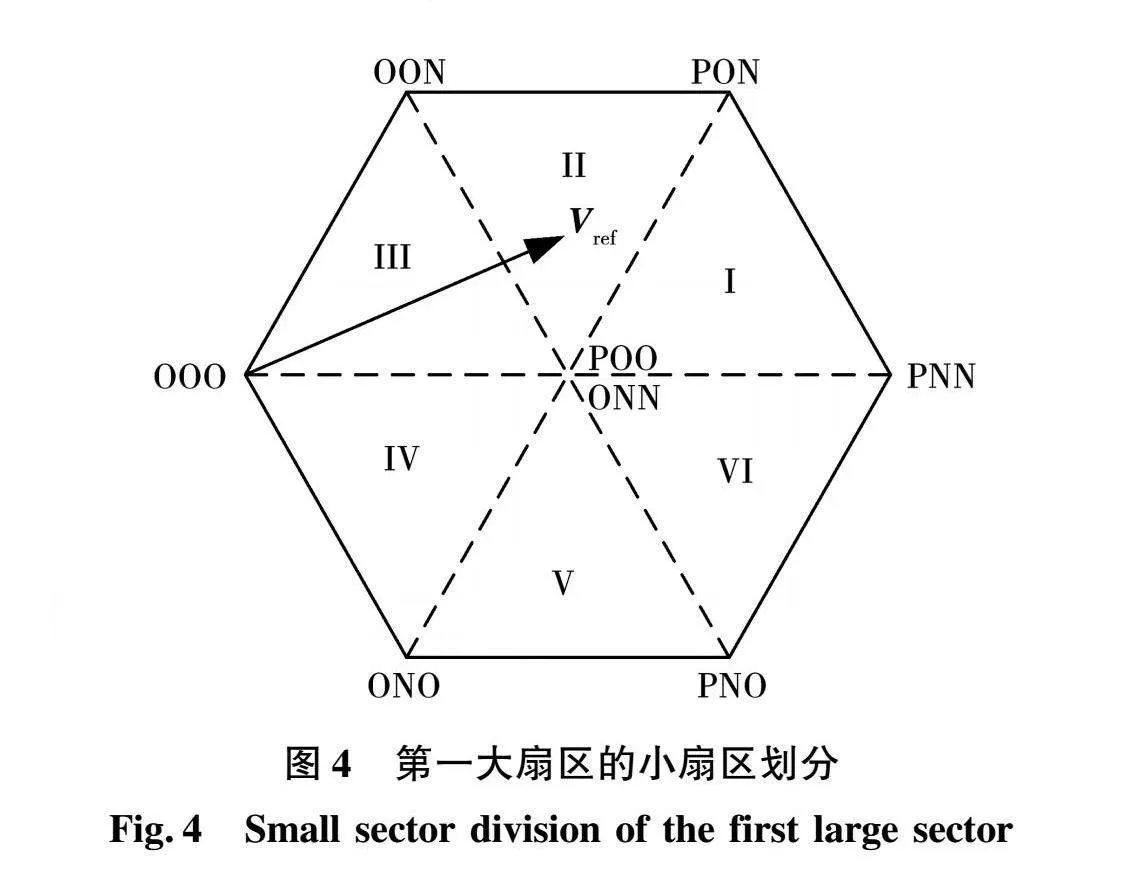
为了深入分析矢量的作用效果，本文在图3的基础上，根据相邻基本电压矢量所能够组成的小三角形，进一步将大扇区划分为6个小扇区。图4为第一大扇区的小扇区划分。当参考电压矢量位于如图4所示的第一大扇区的第二小扇区时，参与预测计算的候选电压矢量分别为[PON]、[OON]、[POO]和[ONN]。此时以式（14）为代价函数的预测模型在控制周期内需要计算4次中点电压预测值和4次代价函数值。

2.2 无平衡因子代价函数的建立

根据式（4）～式（6）可知，Vienna整流器直流侧的中点电压与作用矢量的开关状态和输入电流的极性相关。第一大扇区部分电压矢量对中点电压的影响如图5所示。在图5（a）中当大矢量[PNN]作用时，没有桥臂与直流侧中点O相连，所以大矢量[PNN]对中点电压没有影响；图5（b）中当中矢量[PON]作用时，B相电流从直流侧中点O流出，中点电压降低；图5（c）中P型小矢量[POO]作用时，B相电流流出直流侧中点O，中点电压降低；图5（d）中N型小矢量[OON]作用时，A相电流流入中点O，中点电压升高。

为了平衡直流侧的中点电压，传统FCS-MPC通常在代价函数中建立一项关于中点电压的误差函数，这不仅会增加预测控制的计算量，而且需要耗费大量的时间对平衡因子进行调整。为了省去代价函数中的中点电压误差项，本文在进行预测控制之前根据中点电压的状态判断执行不同的算法，利用冗余小矢量对中点电压的相反影响平衡中点电压。基于电压预测的代价函数式（14）可以优化为

F3（k）=|u*α（k+1）－uα（k+1）|+|u*β（k+1）－uβ（k+1）|。（15）

以式（15）为代价函数的预测模型在控制周期内无需计算中点电压的预测值，与以式（10）为代价函数的传统FCS-MPC相比计算量大大减小。

2.3 双矢量组合选择

传统FCS-MPC在控制周期中只输出一个作用矢量跟踪参考矢量，控制精度严重依赖于采样频率，本文为了提高传统FCS-MPC的跟踪精度，在控制周期内输出两个作用矢量共同跟踪参考电压矢量。

根据图4，当参考电压矢量位于第一大扇区的第二小扇区时，输出的2个作用矢量共有5种矢量组合，有2对组合（[PON]和[ONN]，[OON]和[POO]）开关动作2次，有3对组合（[PON]和[POO]，[OON]和[ONN]，[PON]和[OON]）开关动作1次。为了降低控制系统的开关频率，本文将双矢量组合限定在开关只动作1次的矢量组合中。此时第一大扇区的候选矢量组合（V1，V2）如表1所示。

根据伏秒平衡原理，控制周期内输出的矢量组合按照下式跟踪参考电压矢量，即

V1t1+V2t2=Vref。（16）

式中：V1、V2分别为最优矢量和次优矢量；t1、t2分别为最优矢量和次优矢量对应的作用时间；Vref为参考电压矢量。根据式（16）和图4可知，所提出的候选矢量组合能够跟踪第一大扇区内的任意电压矢量。

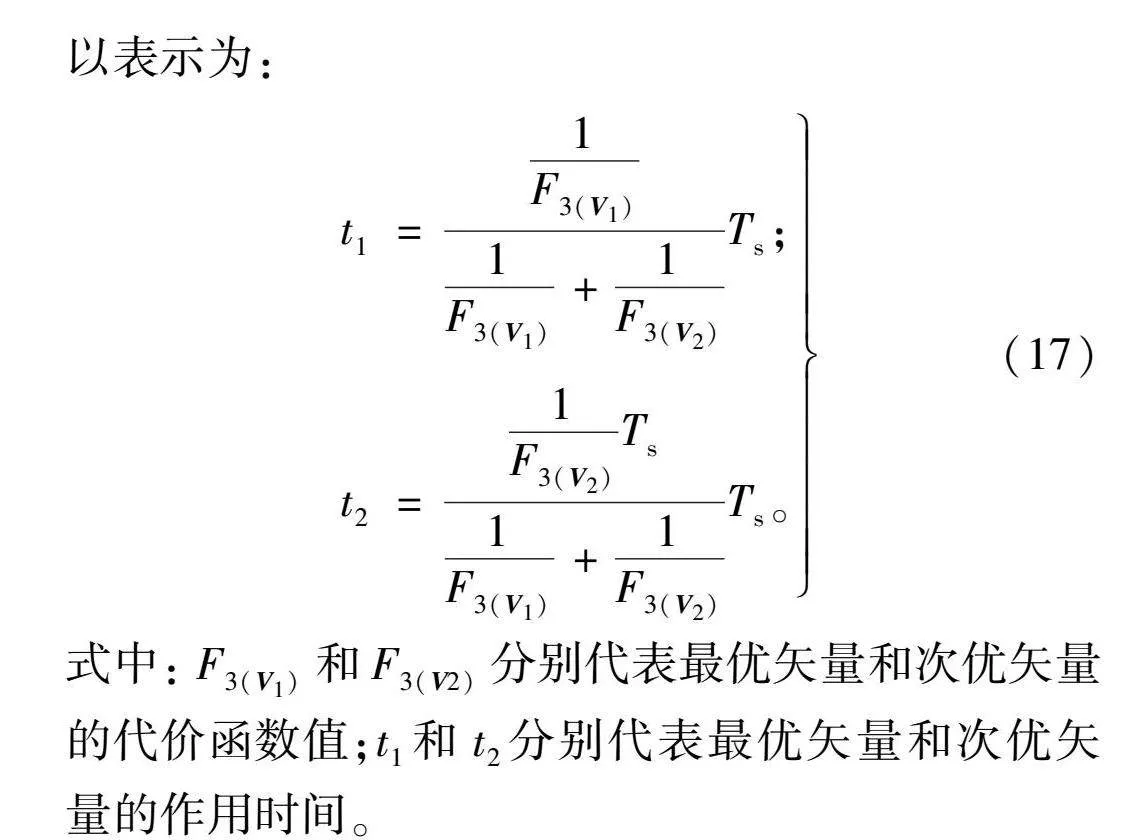
双矢量组合确定之后，矢量的作用时间根据与之对应的代价函数计算得到，矢量对应的代价函数值越小，在控制周期内的作用时间越长，反之作用时间越短。最优矢量V1和次优矢量V2的作用时间可以表示为：

t1=1F3（V1）1F3（V1）+1F3（V2）Ts；

t2=1F3（V2）Ts1F3（V1）+1F3（V2）Ts。（17）

式中：F3（V1）和F3（V2）分别代表最优矢量和次优矢量的代价函数值；t1和t2分别代表最优矢量和次优矢量的作用时间。

2.4 双矢量组合后的中点电压平衡

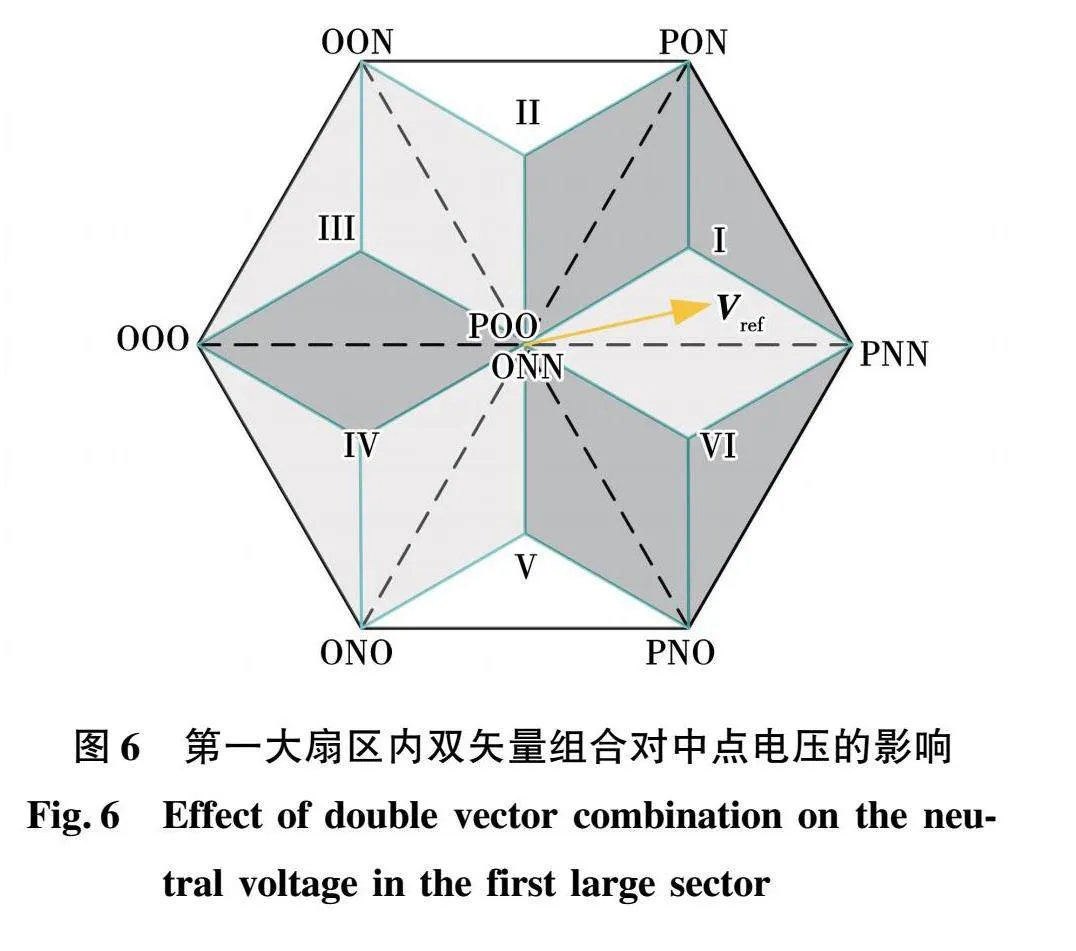
根据2.2节的描述可知，当中矢量和小矢量作用时，直流侧的中点电压会产生波动。为了研究双矢量组合限定后，中点电压的振荡趋势，本节将所提双矢量组合对中点电压的影响进行详细分析。以第一大扇区为例，第一大扇区内包含的双矢量组合对中点电压的影响如图6所示，其中深色区域作用的矢量组合使得中点电压增大，浅色区域作用的矢量组合使得中点电压减小，白色区域作用的矢量组合包含一个中矢量和一个非冗余小矢量，控制周期结束时对中点电压的影响与2个矢量的作用时间相关。

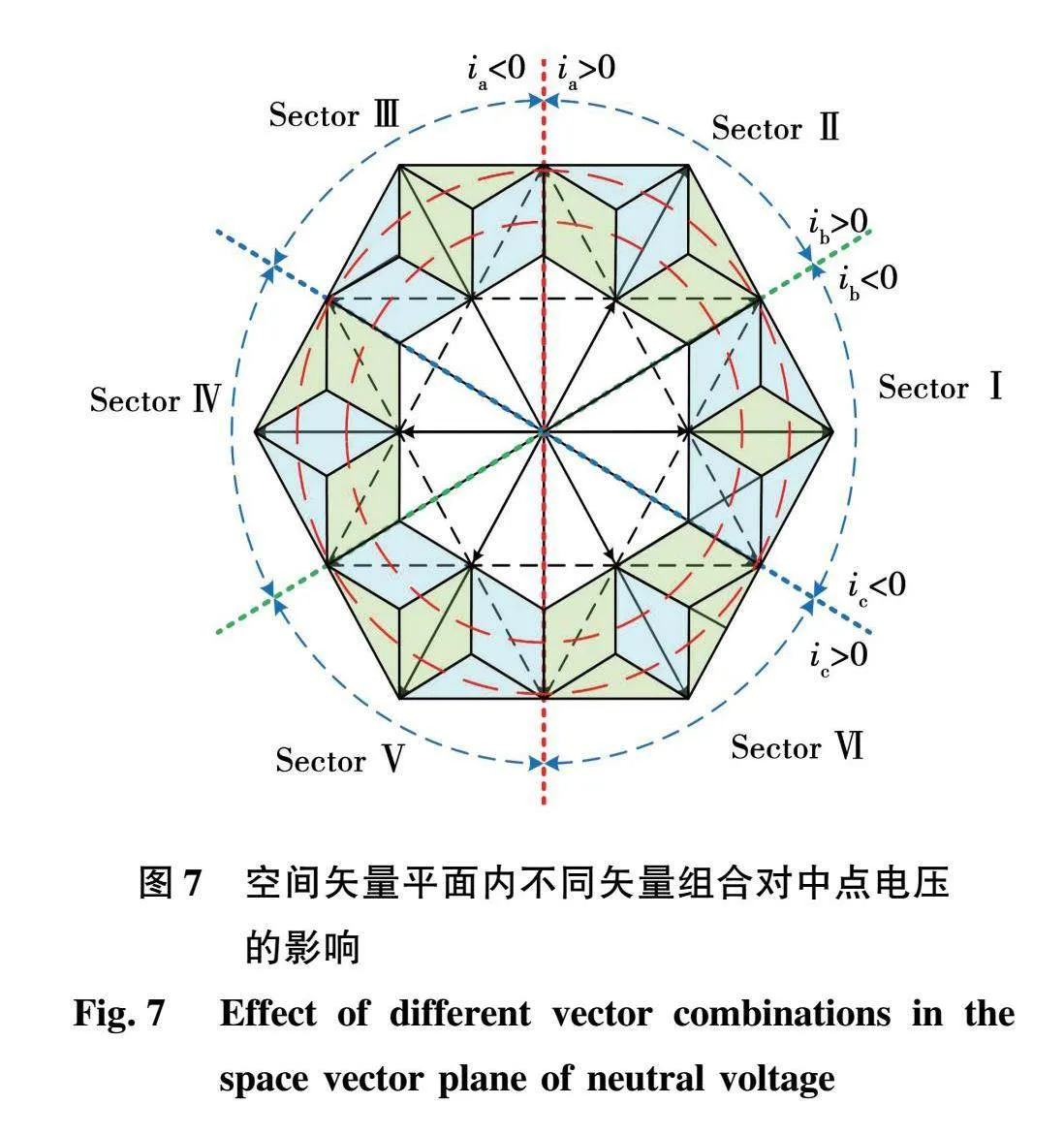
空间矢量平面内不同矢量组合对中点电压的影响如图7所示。假设整流器直流侧输出电压的幅值一定，参考电压矢量在整个空间矢量平面的轨迹位于图7正六边形内的两个圆形轨迹之间。从图7可以看出，限定后的每一对双矢量组合都对直流侧中点电压产生影响，且对中点电压具有相反影响的矢量组合个数相同。当参考电压矢量按照一定的轨迹在空间矢量平面逆时针旋转时，中点电压就能够被不同的矢量组合所调节。

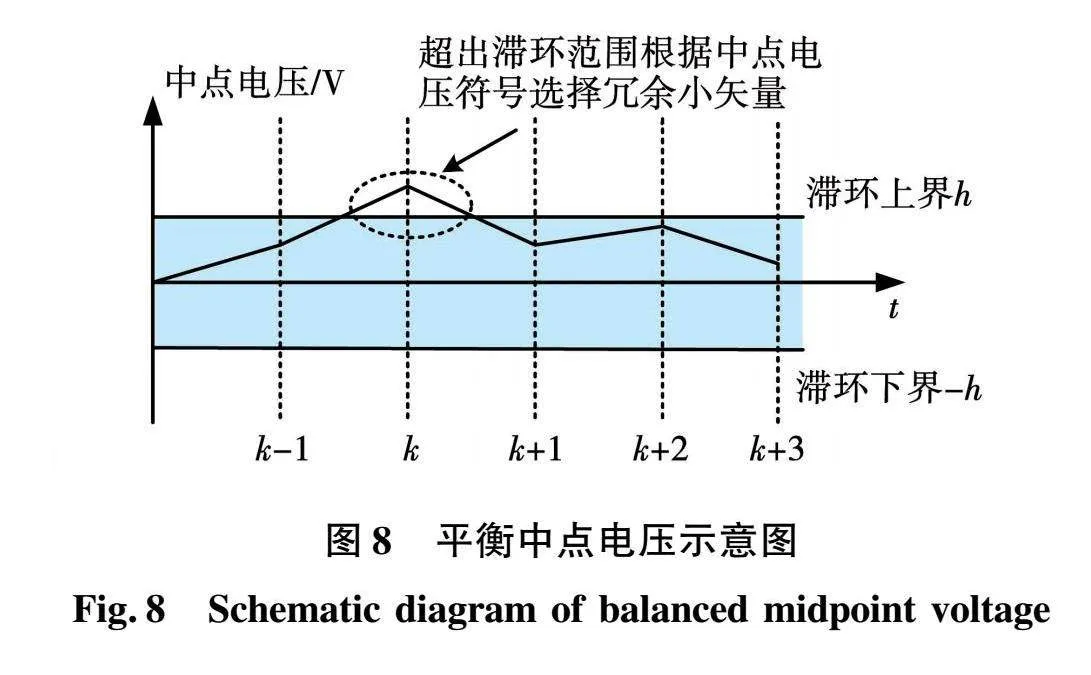
在实际的控制系统中，由于采样频率和开关频率的限制，参考电压矢量的轨迹存在波动，不同矢量组合跟踪参考电压矢量的作用时间无法精确控制，直流侧中点电压会产生波动。为此，本文在平衡中点电压时引入滞环环节，图8为引入滞环后中点电压平衡的示意图。当中点电压位于滞环内，输出2.3节所提双矢量组合平衡中点电压；当中点电压位于滞环外，依据2.2节所述，按照中点电压的正负选择冗余小矢量平衡中点电压。

2.5 相邻控制周期矢量作用顺序的调整

在控制周期进行切换时，会出现桥臂开关3次或者开关2次的情况。例如在图6所示的第一大扇区中，当参考电压矢量以逆时针方向从增大中点电压的区域到减小中点电压的区域时，矢量组合从k时刻的[ONN]和[PNN]，变为k+1时刻的[POO]和[PON]或[PNN]和[PON]，此时桥臂的开关次数如表2所示。

为了减小控制周期切换时功率器件的开关次数，本文定义控制周期切换时关于桥臂开关次数的函数为

N=|Sa（k+1）－Sa（k）|+|Sb（k+1）－Sb（k）|+|Sc（k+1）－Sc（k）|。（18）

式中：S（x）（k）（x=a，b，c）为k时刻第二个矢量作用时三相桥臂的开关状态；S（x）（k+1）为k+1时刻第一个矢量作用时三相桥臂的开关状态。在控制周期切换时，将桥臂开关次数少的矢量作为第一个矢量输出。

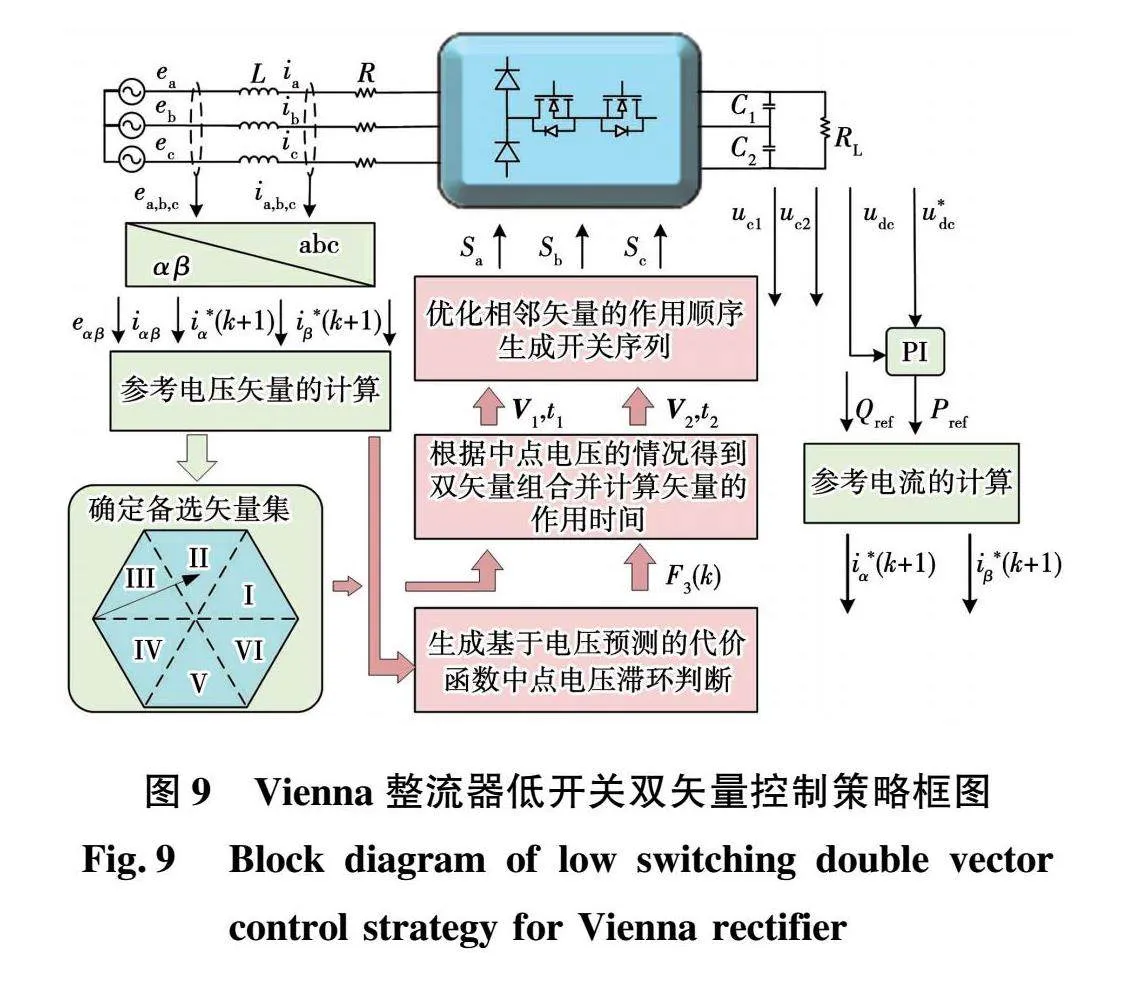
综上所述，本文提出的Vienna整流器低开关频率双矢量模型预测控制策略的控制框图如图9所示。

3 仿真分析

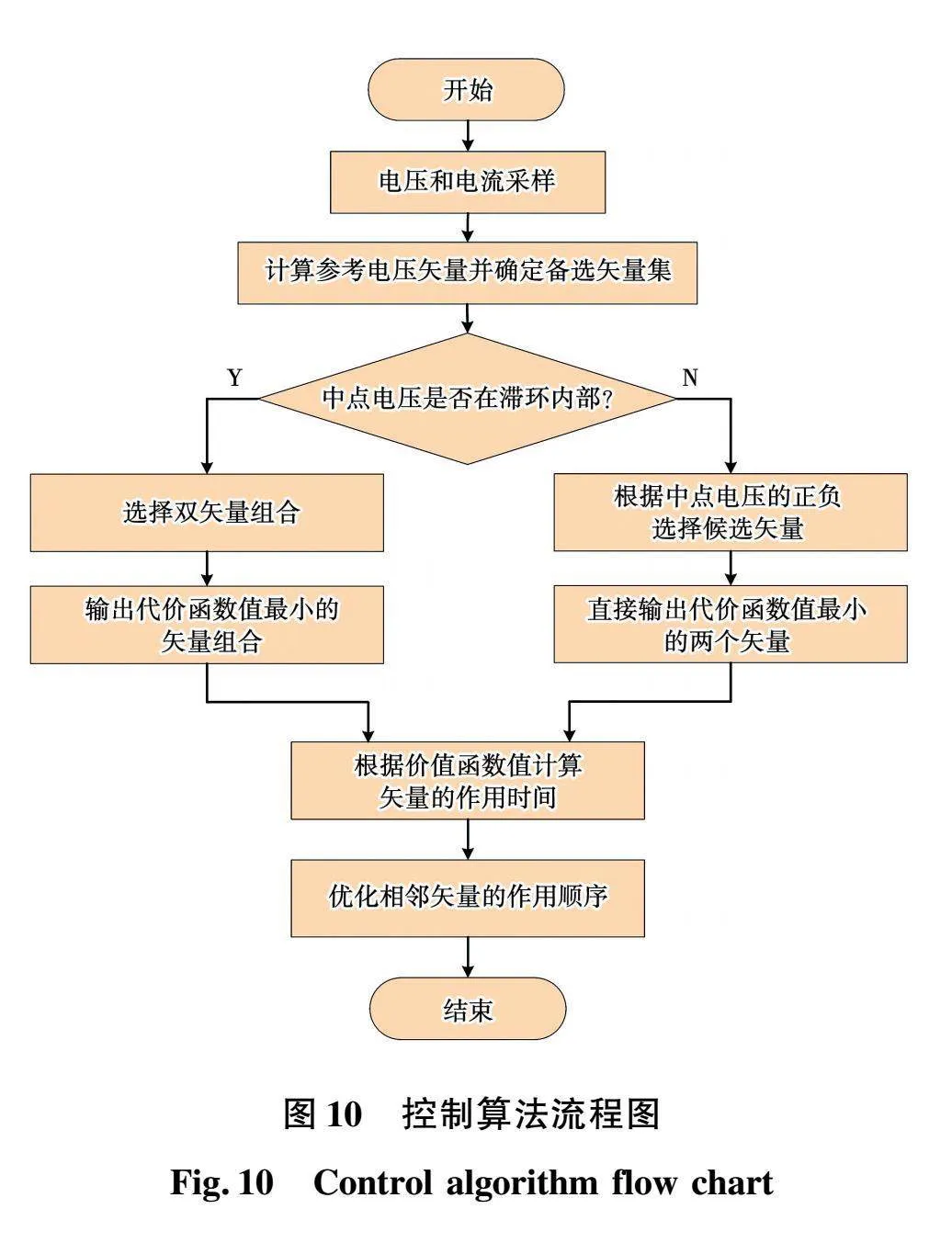
为了验证本文所提出控制方法的有效性，搭建基于MATLAB/Simulink的仿真模型，对以式（10）为代价函数的传统FCS-MPC策略和本文所提出的LD-MPC策略进行仿真和对比分析，主要的仿真参数如表3所示。仿真中FCS-MPC的采样频率为20 kHz，LD-MPC的采样频率为10 kHz。所提出LD-MPC策略的算法流程图如图10所示。

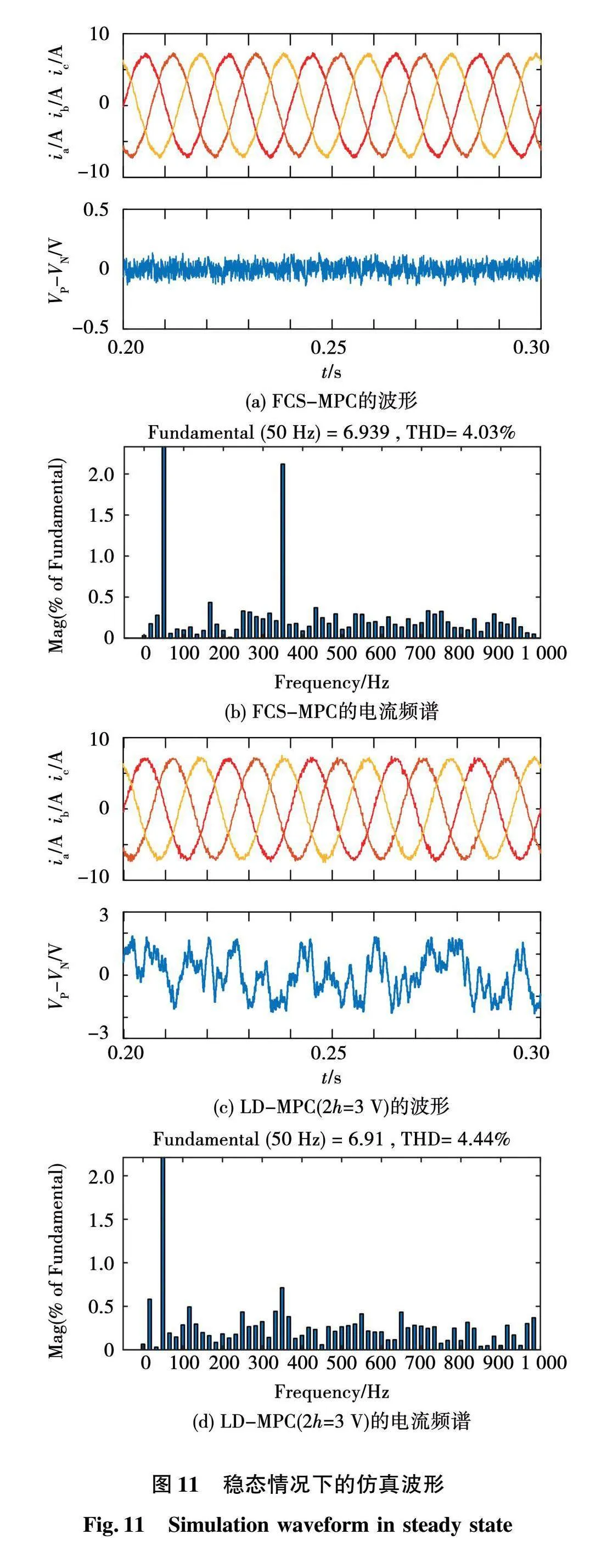
图11给出了FCS-MPC和本文所提LD-MPC设置中点电压滞环宽度为3 V时，三相输入电流及其谐波分析和直流侧中点电压的稳态仿真波形，2种控制策略的负载均为50 Ω。

从图11可以看出，FCS-MPC和LD-MPC均能保证Vienna整流器的稳定运行。采用FCS-MPC策略时输入电流的谐波畸变率为4.03%，中点电压波动的峰峰值在0.3 V左右，采用LD-MPC策略并设置中点电压滞环宽度为3 V时输入电流的谐波畸变率为4.44%，中点电压波动的峰峰值在3.9 V左右，可以看出在中点电压引入滞环后，输入电流没有发生剧烈的畸变，这证明本文所提出的控制策略具有良好的稳态性能。

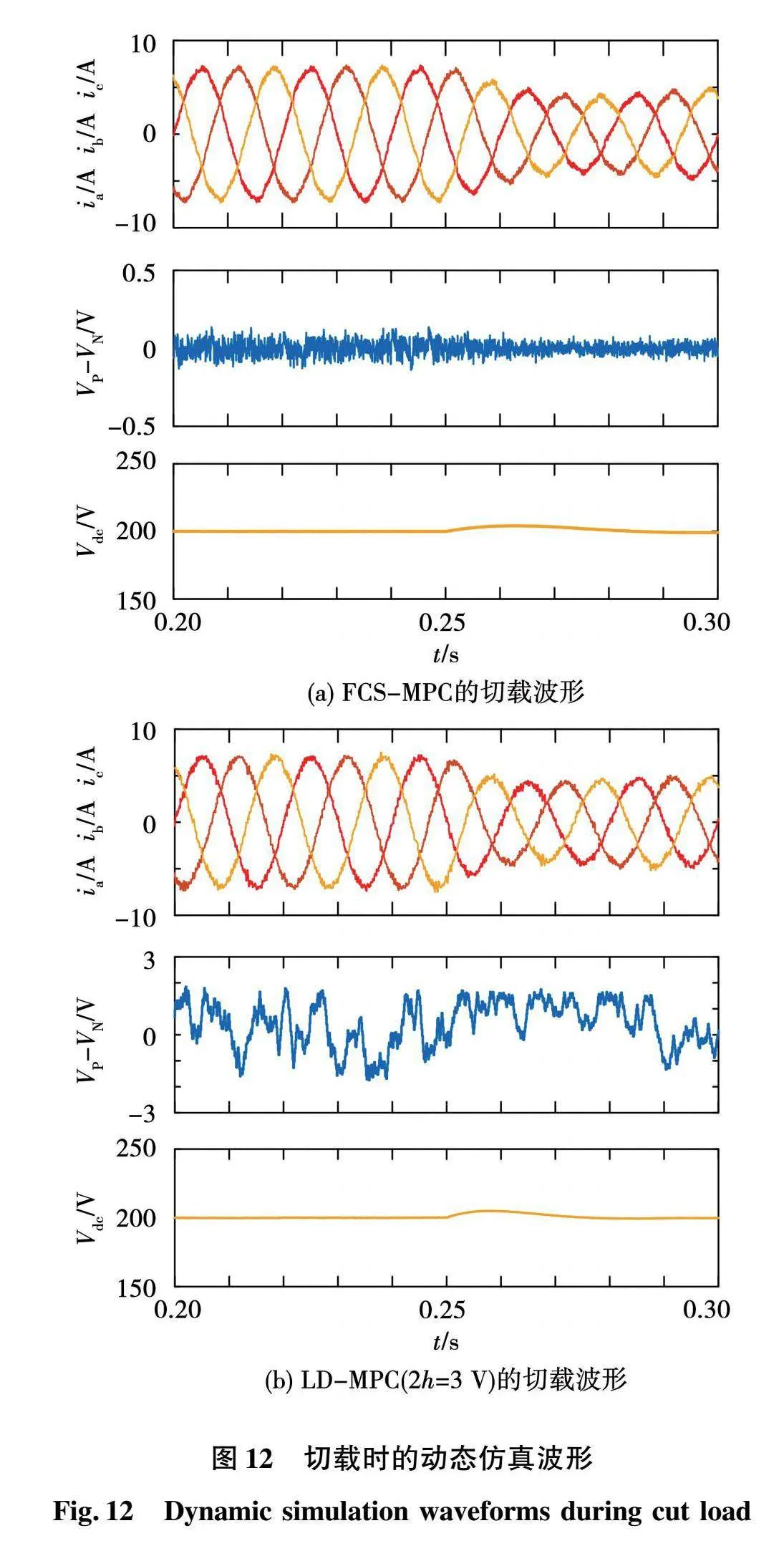
为了验证所提出控制方法的动态性能，图12给出了FCS-MPC和所提出LD-MPC设置中点电压滞环宽度为3 V时负载从50 Ω切换到75 Ω的动态仿真波形。从图12可以看出，两种方法在切载后都能够正常工作，输入电流没有发生严重畸变，直流侧输出电压超调小，证明2种控制策略都具有较好的动态响应能力。所提出LD-MPC策略在切载后中点电压没有失控，证明所提中点电压平衡策略是有效的。

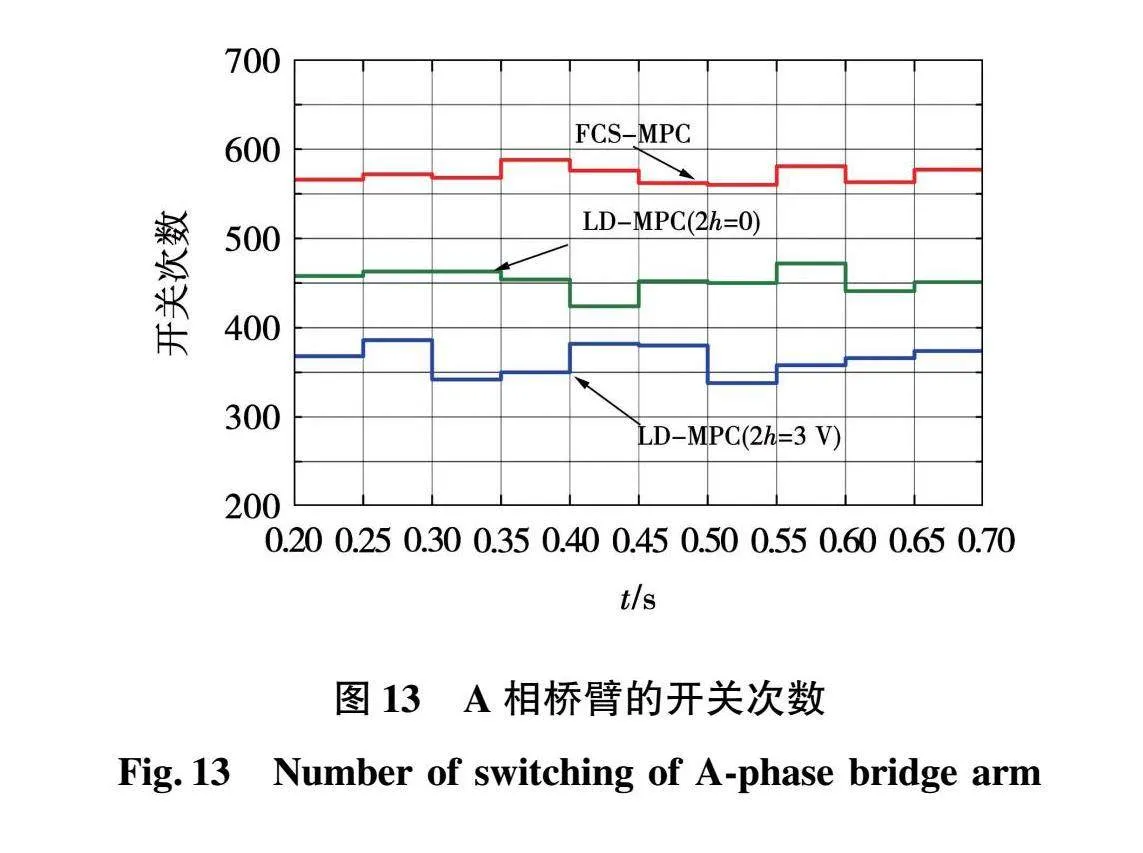
通过仿真对比可知，LD-MPC策略在10 kHz采样频率下能够获得与传统FCS-MPC策略在20 kHz采样频率下相媲美的性能。此外LD-MPC策略通过限制控制周期内部的矢量组合，优化相邻控制周期作用矢量的开关关系，减小了控制系统的开关频率。由于2种策略的开关频率都不固定，所以为了获得相对平均的开关次数，本文每隔0.05 s统计一次桥臂的开关次数，统计10个时间间隔的开关次数计算得到平均开关次数，再将平均开关次数乘以20得到等效开关频率。以A相桥臂为例，图13为采用FCS-MPC和LD-MPC策略时，在稳态情况下A相桥臂平均开关次数的示意图。从图13可以看出，FCS-MPC在0.05 s内的平均开关次数为515.3次，等效平均开关频率为10.306 kHz，LD-MPC设置中点电压滞环宽度为0时，0.05 s内的平均开关次数为452.8次，等效平均开关频率为9.056 kHz，LD-MPC在设置中点电压滞环宽度为3 V时，0.05 s内的平均开关次数为364.4次，等效平均开关频率为7.288 kHz。综上所述，本文所提LD-MPC策略能够在保证控制精度的前提下有效降低功率器件的开关次数，减小控制系统的开关损耗。

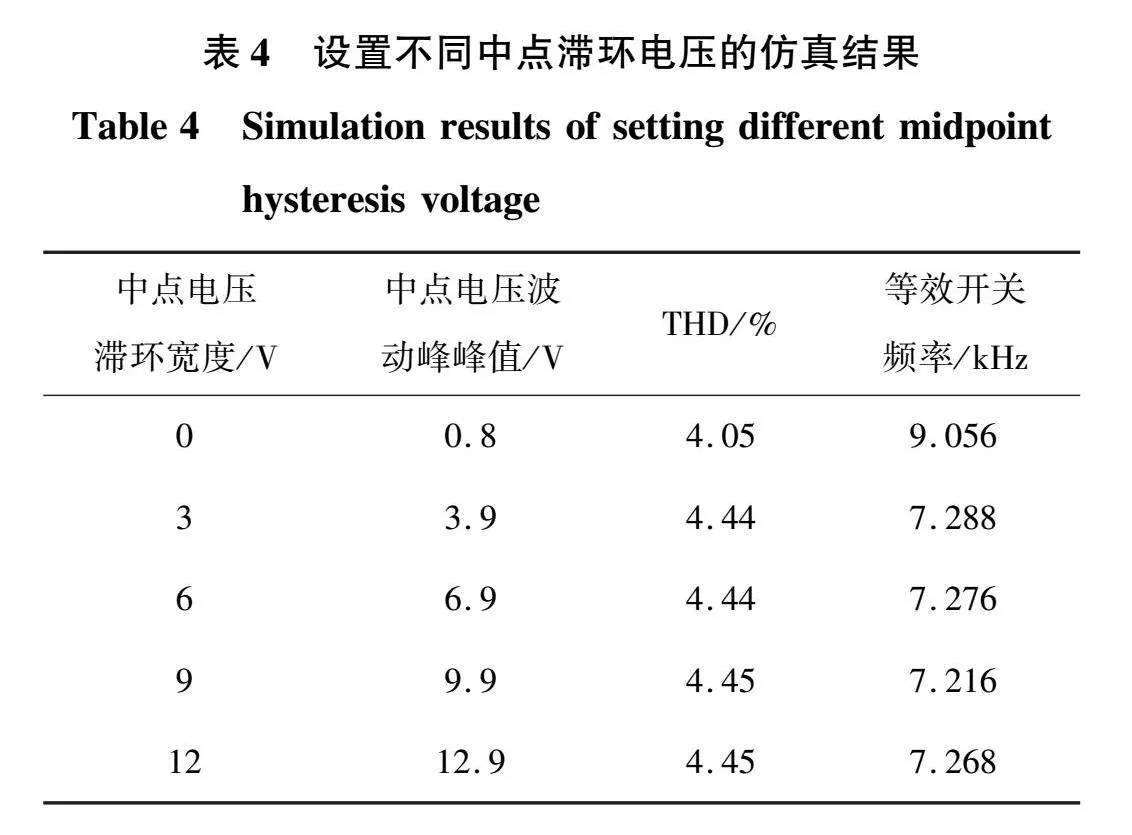
为了分析中点电压滞环宽度对控制系统性能的影响，表4给出了本文所提LD-MPC策略在设置直流侧输出电压为200 V时，输入电流谐波畸变率、中点电压振荡峰峰值、A相桥臂等效开关频率关于中点电压滞环宽度的仿真结果。

从表4可以看出，当设置不同的滞环宽度时，输入电流谐波畸变率和等效开关频率会发生变化，当滞环宽度达到一定限度时这种变化会趋于稳定。

4 实验验证

为了验证所提LD-MPC策略的有效性，搭建基于DSPACE的三相Vienna整流器半实物实验平台，如图14所示。实验平台由Vienna整流器主电路、DSPACE控制器、三相调压器、示波器、辅助电源等组成。在实验中传统FCS-MPC的采样频率为20 kHz，LD-MPC的采样频率为10 kHz，主电路的相关参数如表3所示。

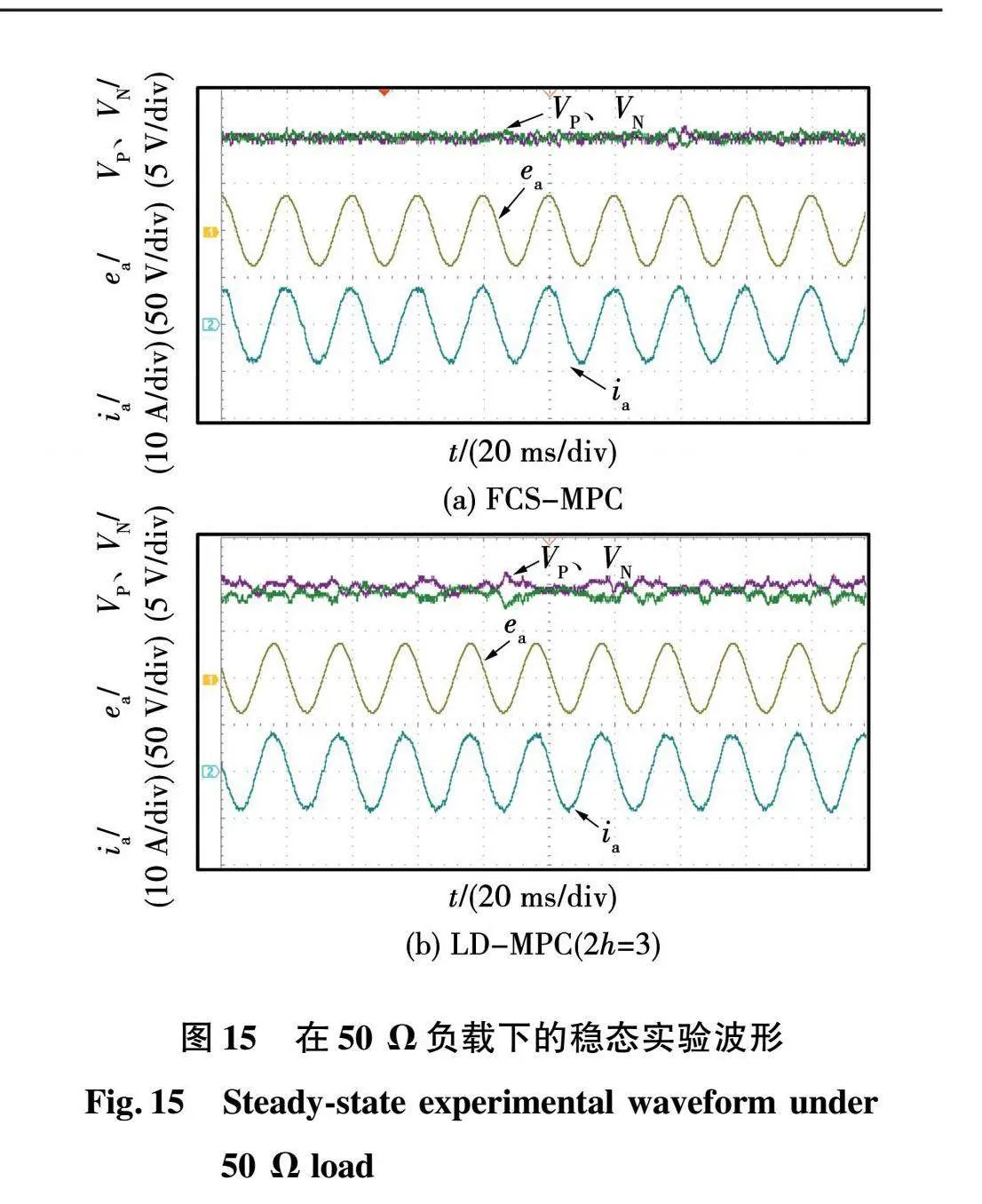
图15为传统FCS-MPC和LD-MPC策略的稳态实验波形，可以看出，2种方法的输入电流和输入电压同相位，输入电流没有发生剧烈的畸变；当设置LD-MPC的中点电压滞环宽度为3 V时，中点电压波动的峰峰值在3.5 V左右，并且与FCS-MPC策略相比，输入电流没有发生较大的畸变，证明所提LD-MPC策略具有良好的稳态控制性能，能够有效减轻FCS-MPC策略对采样频率的依赖。

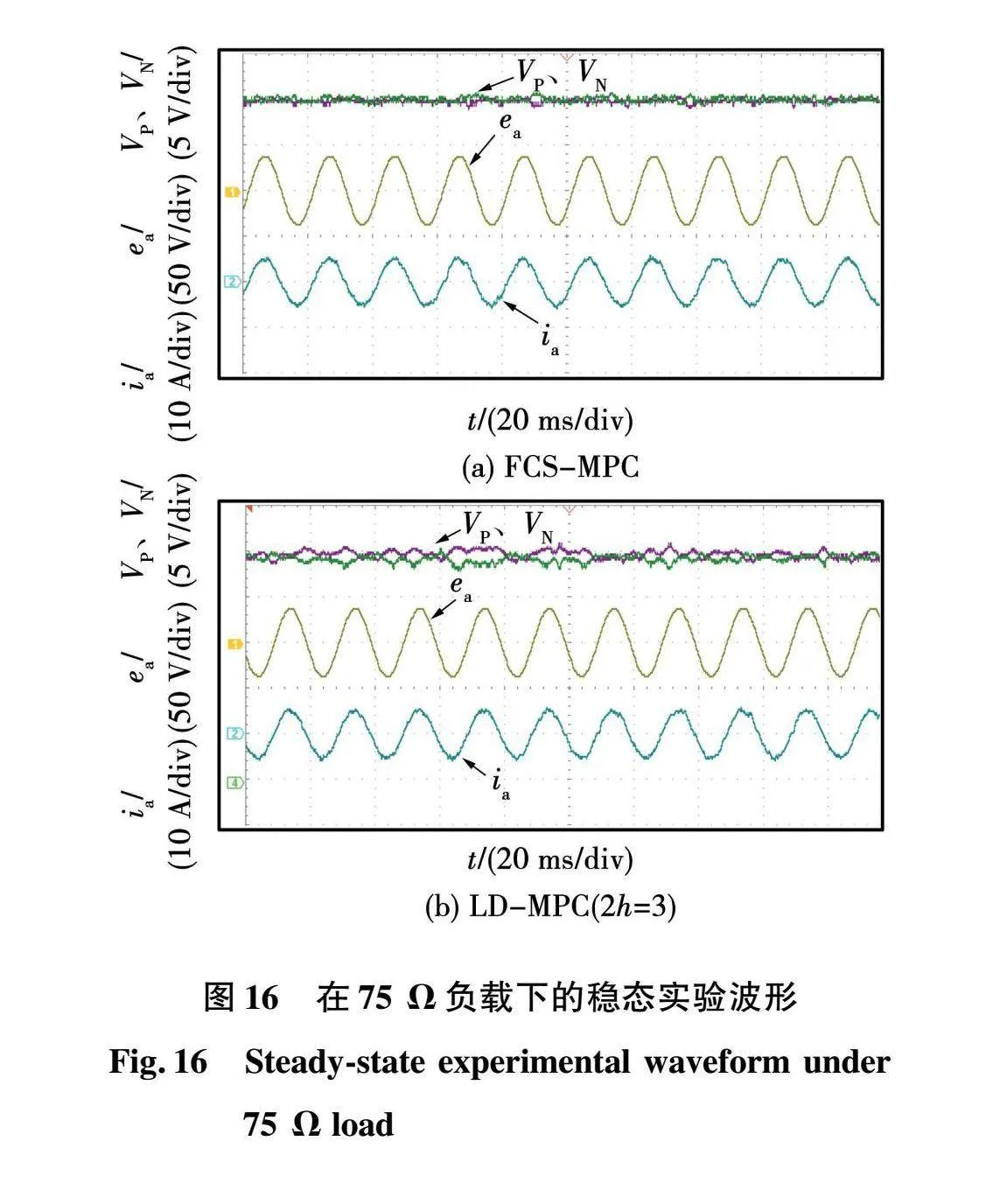
图16为设置直流侧负载为75 Ω时，FCS-MPC和LD-MPC设置中点电压滞环宽度为3 V的实验波形。可以看出，在75 Ω的负载下，2种控制方法均能稳定运行，LD-MPC策略下的中点电压在一定范围内波动，没有发生失控，证明所提LD-MPC策略在不同的负载下都能稳定运行。

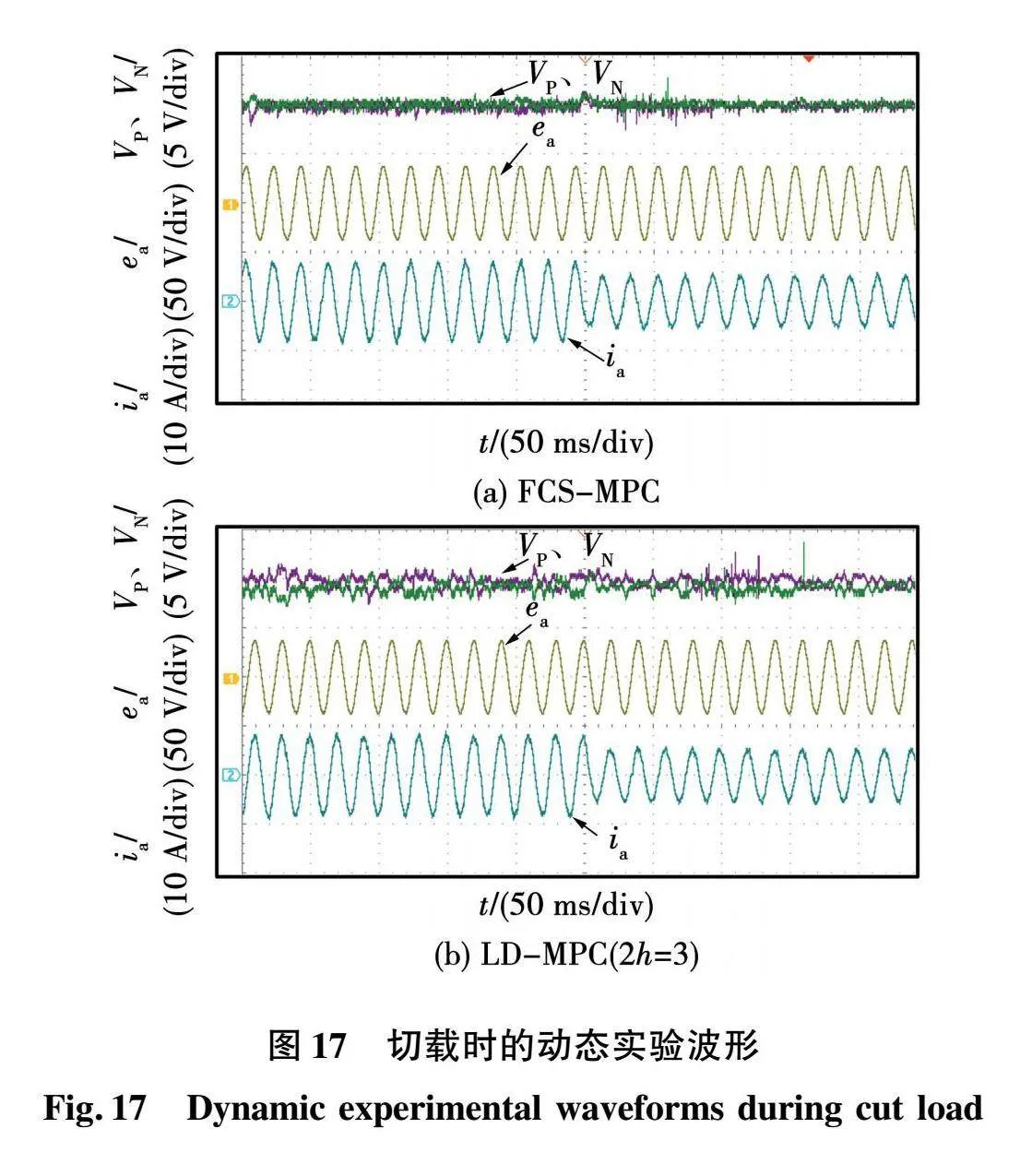
为了验证所提LD-MPC策略的动态性能，图17为FCS-MPC和LD-MPC设置中点电压滞环宽度为3 V时负载从50 Ω到75 Ω的动态切载波形。可以看出，LD-MPC在切载后输入电流没有发生明显的畸变，直流侧的电容电压没有发生剧烈超调并且能够迅速回到参考值，证明所提控制策略能够快速跟踪系统的功率变化，具有良好的动态响应能力。

算法的计算量是模型预测控制需要重点关注的指标之一。为了证明所提LD-MPC策略的优越性，表5给出了传统FCS-MPC策略和所提LD-MPC策略的算法执行时间、切载后系统调节时间和输入电流畸变率的对比。算法执行时间通过DSPACE控制器得到，包括预测控制的计算时间和参数采样时间，在同一套控制系统下可认为参数采样时间相同。从表5可以看出，本文所提LD-MPC策略与传统FCS-MPC相比所占用的计算资源更少，切载后系统调节时间更短。LD-MPC策略在10 kHz采样频率下的稳态性能够媲美FCS-MPC在20 kHz采样频率下的稳态性能，并具有更快的动态调节能力。

5 结 论

本文在三相Vienna整流器传统FCS-MPC策略的基础上提出一种LD-MPC策略，通过仿真和实验验证了所提控制策略的正确性和可行性，并得出以下结论：

1）与传统FCS-MPC的单矢量跟踪方式相比，所提LD-MPC策略在控制周期内输出的双矢量组合提高了对参考矢量的跟踪精度，减轻了控制系统对采样频率的依赖。

2）通过定位参考电压矢量所在的位置，减少了参与在线寻优的矢量个数，减轻了控制器的计算负担。

3）通过建立矢量组合表并优化相邻控制周期的开关顺序，在中点电压不失控的前提下，有效降低功率器件的开关频率。

参 考 文 献：

［1］ RAJAEI A， MOHAMADIAN M， YAZDIAN VARJANI A. Vienna-rectifier-based direct torque control of PMSG for wind energy application[J]. IEEE Transactions on Industrial Electronics， 2013， 60（7）： 2919.

［2］ KOLAR J W， ZACH F C. A novel three-phase utility interface minimizing line current harmonics of high-power telecommunications rectifier modules[J]. IEEE Transactions on Industrial Electronics， 1997， 44（4）： 456.

［3］ 李春杰， 黄文新， 卜飞飞， 等. 电动汽车充电与驱动集成化拓扑[J]. 电工技术学报， 2017， 32（12）： 138.

LI Chunjie， HUANG Wenxin， BU Feifei， et al. The integrated topology of charging and drive for electric vehicles[J]. Transactions of China Electrotechnical Society， 2017， 32（12）： 138.

［4］ 郝振洋， 徐子梁， 陈宇， 等. 航空Vienna整流器故障诊断与容错控制[J]. 电工技术学报， 2020， 35（24）： 5152.

HAO Zhenyang， XU Ziliang， CHEN Yu， et al. Fault diagnosis and fault tolerant control for aviation Vienna rectifier[J]. Transactions of China Electrotechnical Society， 2020， 35（24） ： 5152.

［5］ HE Z， DING H， CHEN Z， et al. A novel method to evaluate the influence of Vienna rectifier neutral-point voltage fluctuation on input current quality[J]. IEEE Transactions on Power Electronics， 2021，36（7）： 8347.

［6］ ZHU W， CHEN C， DUAN S， et al. A carrier-based discontinuous PWM method with varying clamped area for Vienna rectifier[J]. IEEE Transactions on Industrial Electronics， 2019，66（9）： 7177.

［7］ XING X， LI X， QIN C， et al. Two-layer pulse width modulation strategy for common-mode voltage and current harmonic distortion reduction in Vienna rectifier[J]. IEEE Transactions on Industrial Electronics， 2020， 67（9）： 7470.

［8］ HANG L， LI B， ZHANG M， et al. Equivalence of SVM and carrier-based PWM in three-phase/wire/level Vienna rectifier and capability of unbalanced-load control[J]. IEEE Transactions on Industrial Electronics， 2013，61（1）： 20.

［9］ LI X， HAN J， SUN Y， et al. A generalized design framework for neutral point voltage balance of three-phase Vienna rectifiers[J]. IEEE Transactions on Power Electronics， 2019， 34（10）： 10221.

［10］ 王金平， 季圣植， 姜卫东， 等. 一种实现Vienna整流器开关损耗降低和中点电压平衡的新型不连续PWM策略[J]. 中国电机工程学报， 2022， 42（11）： 4125.

WANG Jinping， JI Shengzhi， JIANG Weidong， et al. A novel discontinuous PWM strategy to achieve switching loss reduction and neutral point voltage balance for Vienna rectifier[J]. Proceedings of the CSEE， 2022，42（11）： 4125.

［11］ 邹宇航， 张犁， 赵瑞， 等. 三相Vienna整流器的不连续空间矢量脉宽调制及电压谐波分析方法[J]. 中国电机工程学报， 2020， 40（24）： 8123.

ZOU Yuhang， ZHANG Li， ZHAO Rui， et al. Discontinuous pulse width modulation and voltage harmonic analysis method for three-phase Vienna-type rectifiers[J]. Proceedings of the CSEE， 2020， 40（24）： 8123.

［12］ 柳志飞， 杜贵平， 杜发达. 有限集模型预测控制在电力电子系统中的研究现状和发展趋势[J].电工技术学报，2017，32（22）： 58.

LIU Zhifei， DU Guiping， DU Fada. Research status anddevelopment trend of finite control set model predictive control in power electronics[J]. Transactions of China Electrotechnical Society， 2017， 32（22）： 58.

［13］ DAVARI S A， NEKOUKAR V， GARCIA C， et al. Online weighting factor optimization by simplified simulated annealing for finite set predictive control[J]. IEEE Transactions on Industrial Informatics， 2021，17（1）： 31.

［14］ LI X， SUN Y， WANG H， et al. A hybrid control scheme for three-phase Vienna rectifiers[J]. IEEE Transactions on Power Electronics， 2018，33（1）： 629.

［15］ NAIR H S， LAKSHMINARASAMMA N. An improved FS-MPC algorithm for Vienna rectifier based EV chargers[C]// IEEE Transportation Electrification Conference amp; Expo， June 24-26， 2020， Chicago， Illinois， USA.2020：1103-1108.

［16］ LEE J S， LEE K B. Predictive control of Vienna rectifiers for PMSG systems[J]. IEEE Transactions on Industrial Electronics， 2017，64（4）： 2580.

［17］ 周运红， 张爱民， 黄晶晶， 等. 基于动态事件触发的Vienna整流器模型预测控制[J]. 电工技术学报， 2022， 37（8）： 2040.

ZHOU Yunhong， ZHANG Aimin， HUANG Jingjing， et al. Dynamic event-triggered model predictive control for Vienna rectifier[J]. Transactions of China Electrotechnical Society， 2022， 37（8）：2040.

［18］ SONG W， YANG Y， JIAO Z， et al. Simplified model predictive current control based on fast vector selection method in a Vienna rectifier[J]. IET Power Electronics， 2022， 16（3）： 436.

［19］ LEE J S， LEE K B， BLAABJERG F. Predictive control with discrete space-vector modulation of Vienna rectifier for driving PMSG of wind turbine systems[J]. IEEE Transactions on Power Electronics， 2019， 34（12）： 12368.

［20］ 朱文杰， 陈昌松， 段善旭. 一种基于离散空间矢量调制的Vienna整流器模型预测控制方法[J]. 中国电机工程学报， 2019， 39（20）： 6008.

ZHU Wenjie， CHEN Changsong， DUAN Shanxu. A model predictive control method with discrete space vector modulation of Vienna rectifier[J]. Proceedings of the CSEE， 2019， 39（20）： 6008.

［21］ ZHANG Y， YANG H. Model predictive torque control of induction motor drives with optimal duty cycle control[J]. IEEE Transactions on Power Electronics， 2014， 29（12）： 6593.

［22］ YU F， LIU X， ZHANG X， et al. Model predictive virtual-flux control of three-phase Vienna rectifier without voltage sensors[J]. IEEE Access， 2019， 7： 169338.

［23］ 党超亮， 王飞， 穆晓宇， 等. 引入电感参数辨识的Vienna整流器双矢量预测恒频控制[J].中国电机工程学报， 2022， 42（S1）： 246.

DANG Chaoliang， WANG Fei，MU Xiaoyu， et al. Sliding mode predictive control of Vienna rectifier based on optimal vector synthesis[J]. Proceedings of the CSEE， 2022， 42（S1）： 246.

［24］ ZHANG H， ZHANG C， XING X， et al. Three-layer double-vector model predictive control strategy for current harmonic reduction and neutral-point voltage balance in Vienna rectifier[J]. IEEE Transactions on Transportation Electrification， 2022，8（1）： 251.

（编辑：邱赫男）