基于代理模型的永磁直线同步电机多目标优化

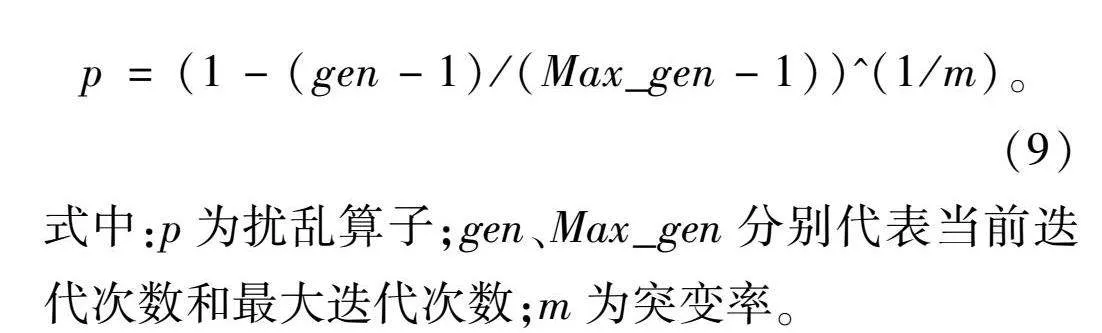
摘 要：针对传统值解析法、有限元等作为分析模型进行电机多目标优化设计，存在建模难度大、时间成本高的问题，提出一种基于代理模型的电机优化设计框架，该框架由遗传算法优化的极限学习机（GA-ELM）以及多目标粒子群优化（MOPSO）算法组成，并用于一台永磁直线同步电机（PMLSM）的结构优化。基于单变量扫描、主效应分析以及试验设计（DOE）的方法建立了模型训练样本库，在保证样本质量的同时降低了样本容量、节约了建模时间；采用GA-ELM搭建了电机的代理模型，进一步提高了原模型精度；基于MOPSO优化算法引入扰乱子完成对模型的多目标寻优，获得了三维Pareto最优前沿解集。最后依据优化结果加工样机，实验验证了该优化设计框架所得优化结果的正确性，且结果表明优化后的电机平均推力提高了11.19%，推力波动降低了21.95%。

关键词：永磁直线同步电机；优化设计框架；多目标优化；代理模型；极限学习机；多目标粒子群优化

DOI：10.15938/j.emc.2024.11.013

中图分类号：TM359.4

文献标志码：A

文章编号：1007-449X（2024）11-0139-12

Multi-objective optimization of permanent magnet linear synchronous motor based on surrogate model

XU Xiaozhuo， GUO Guobin， FENG Haichao， DU Baoyu， ZHAO Yunji

（School of Engineering and Automation， Henan Polytechnic University， Jiaozuo 454003， China）

Abstract：Aiming at the problems of difficult modeling and high time cost in traditional multi-objective optimization design of motors with analysis method and finite element as analysis models， a motor optimization design framework based on surrogate model was proposed. The framework consists of a genetic algorithm extreme learning machine （GA-ELM） and a multiple objective particle swarm optimization （MOPSO） and is used for structural optimization of a permanent magnet linear synchronous motor （PMLSM）. Based on univariate scanning， main effect analysis and design of experiment （DOE）， a model training sample library was established， which reduces the sample size and saves the modeling time while ensuring the sample quality; The surrogate model built using GA-ELM further improves the accuracy of the original model. Using MOPSO as an optimization algorithm， a multi-objective optimization of the model was conducted， and a three-dimensional Pareto optimal frontier solution set was obtained. Finally， the prototype was processed according to the optimization results. The experiment verifies the correctness of the optimization results obtained by the optimization design framework. The results show that the average thrust of the optimized motor is increased by 11.19%， and the thrust ripple is reduced by 21.95%.

Keywords：permanent magnet linear synchronous motor; framework for motor optimization design; multi-objective optimization; surrogate model; extreme learning machine; multiple objective particle swarm optimization

0 引 言

由直线电机直接驱动的直驱无绳提升系统，能够实现无配重、无提升高度限制、无提升速度限制、无中间传动机构、无曳引钢绳的“五无”提升模式，永磁直线同步电机（permanent magnet linear synchronous motor， PMLSM）具有推力密度大、响应速度快、加工装配简单等优点，使得PMLSM驱动的无绳提升系统在近年来得到了快速发展^[1-]。

随着直驱无绳提升系统对电机成本、推力密度等要求的不断提高，高性能PMLSM的设计结构也变得复杂多样，在进行电机优化设计时，复杂的电机结构一方面增加了精确解析模型的建模难度；另一方面大量的结构参数使得有限元计算时间成本激增，导致传统的基于解析法、有限元等作为分析模型进行的多目标优化变得困难^[4-6]。因此，如何在降低优化模型建模难度的同时提高电机优化效率已成为电机设计领域关注的热点问题^[7-9]。

文献[10]利用响应面建立了管状直线感应电机关于电机重量和推力的解析模型，并采用遗传算法作为搜索工具对该电机进行优化设计，极大地缩短了电机优化周期。文献[11]将反向传播（back propagation，BP）神经网络引入到电机机壳拉伸成型质量的预测代理模型中，结合电机壳体拉伸成形实验验证了该代理模型的精度。文献[12]为了进一步提高BP神经网络的建模效率，提出了一种基于数据预处理的建模方法，与传统BP网络相比有效减少了网络节点数量、增强了网络泛化能力，但在训练过程中仍需不断反向调整网络权值和阈值。文献[1]提出了基于Kriging代理模型的考虑精度和计算时间的两步优化设计方法。通过所提出的流程设计的超高速表贴永磁同步电机与初始模型相比，在满足电气规格的同时，减小了尺寸，提高了效率。文献[14]基于深度学习算法并以纯数据驱动的方式构建了永磁同步电机的温度预测模型，数据驱动的特点极大地降低了模型的构造难度，但是，更多的数据需求无疑增加了前期建模成本。

ELM由于良好的学习能力，近年来引起了国内外学者的关注，对模型的研究主要集中在改进算法本身、拓展ELM应用领域两方面，前者包括自适应差分进化极限学习机（SaDE-ELM）、粒子群优化的极限学习机（PSO-ELM）、卷积神经网络极限学习机（CNN-ELM）等^[15-17]，后者极限学习机的应用大多使用其分类功能^[18]，利用其预测功能应用于工程问题的实例较少，多集中于流量、速度、效率、寿命等方面的预测。

对于电气工程领域，尤其是电机设计中，怎样利用ELM的预测功能，建立较为准确、快速、便捷的代理模型，完成对电机的应力分析、温度预测、多目标优化等工作，具有很大的研究空间。文献[19]对一台变压器的杂质损耗进行了研究，并在此基础上加装了磁屏蔽结构，最后基于ELM以及PSO算法，以总损耗为优化目标，对该结构的两个设计参数进行了单目标优化，优化后屏蔽结构的性能指标得到提高，但研究内容多集中在损耗的分析及抑制上，且工程设计中多为多目标优化问题。在电机多目标优化中，文献[20]采用了ELM来建立电机的优化模型，并基于灰狼算法完成了一台PMLSM的优化，结果表明ELM具有比SVM更高的精度且得到了电机最佳的优化参数，尽管构建样本库时有限元采用2D进行求解，但是全因子的实验设计方法需要至少5⁴=625个样本数据，造成样本库过于庞大，增加了建模时间成本。

为了进一步探究ELM在电机设计中的应用，提高代理模型精度和泛化能力、降低建模时间成本和构造难度，本文提出一种遗传算法优化的极限学习机（genetic algorithm extreme learning machine，GA-ELM）作为代理模型，多目标粒子群优化（multiple objective particle swarm optimization，MOPSO）作为优化算法的电机优化设计框架。首先，通过关键参数的选取、敏感性分析以及合理的实验设计（design of experiment，DOE）选择来构建模型训练样本库；其次，基于GA-ELM神经网络搭建了三目标代理模型，并基于MOPSO算法引入扰乱算子完成对代理模型的多目标寻优，将优化前、后的数据、模型进行对比；最后，制作样机进行实验验证。

1 电机结构与工作原理

1.1 电机结构及参数定义

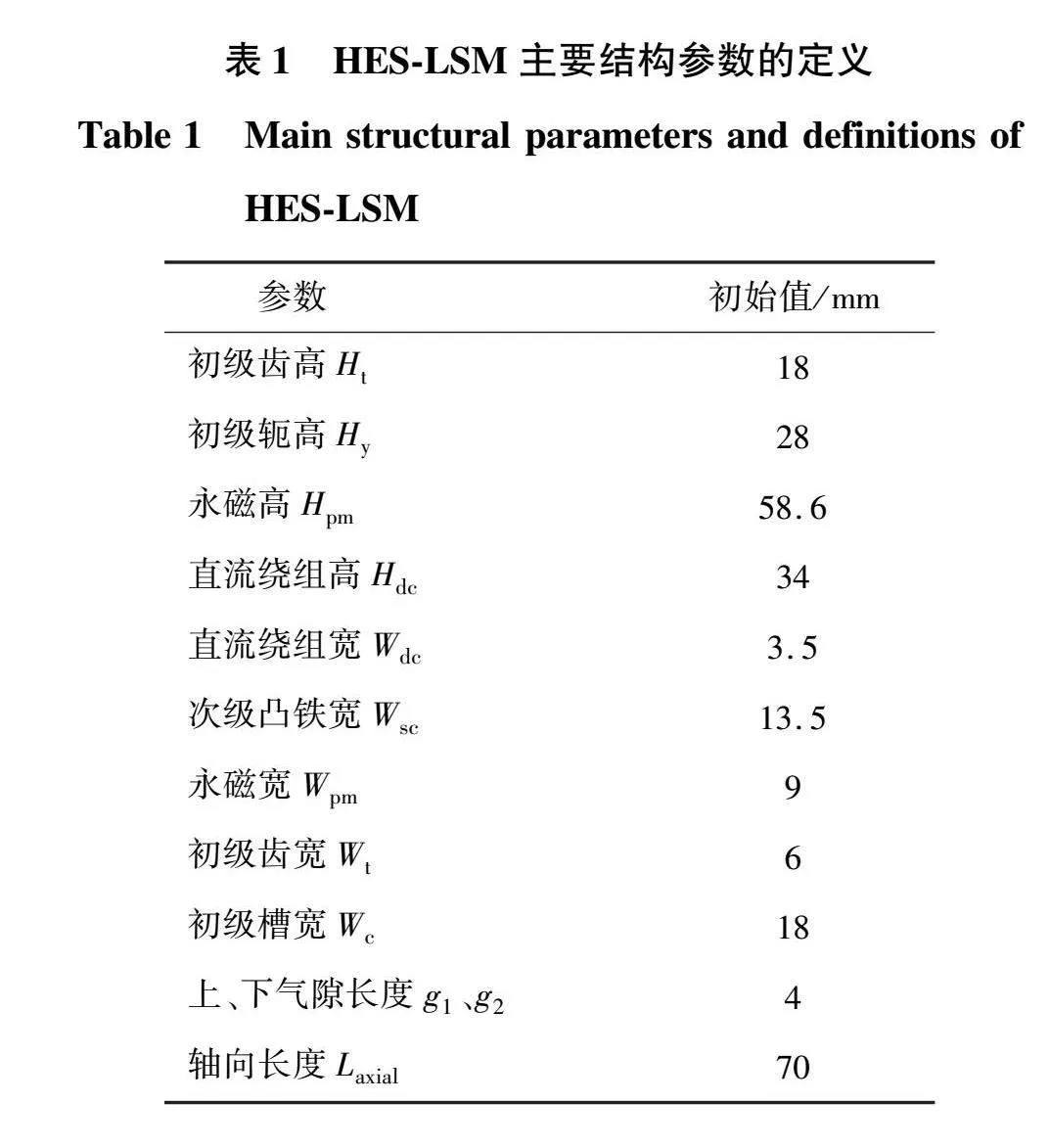
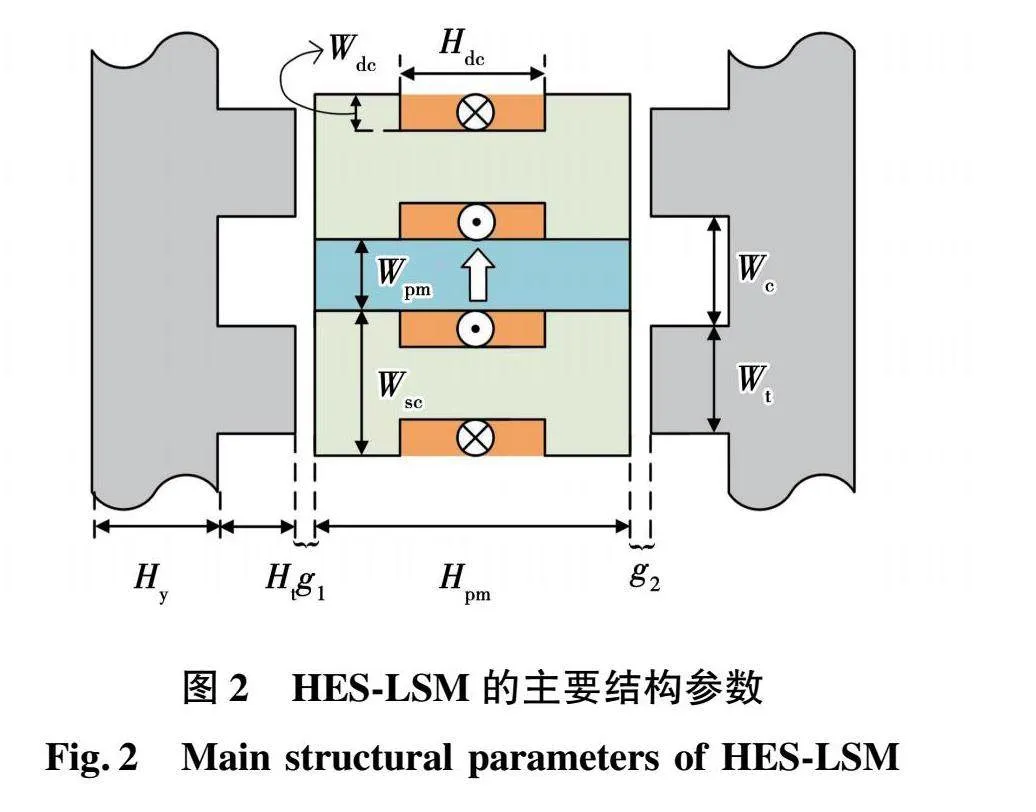
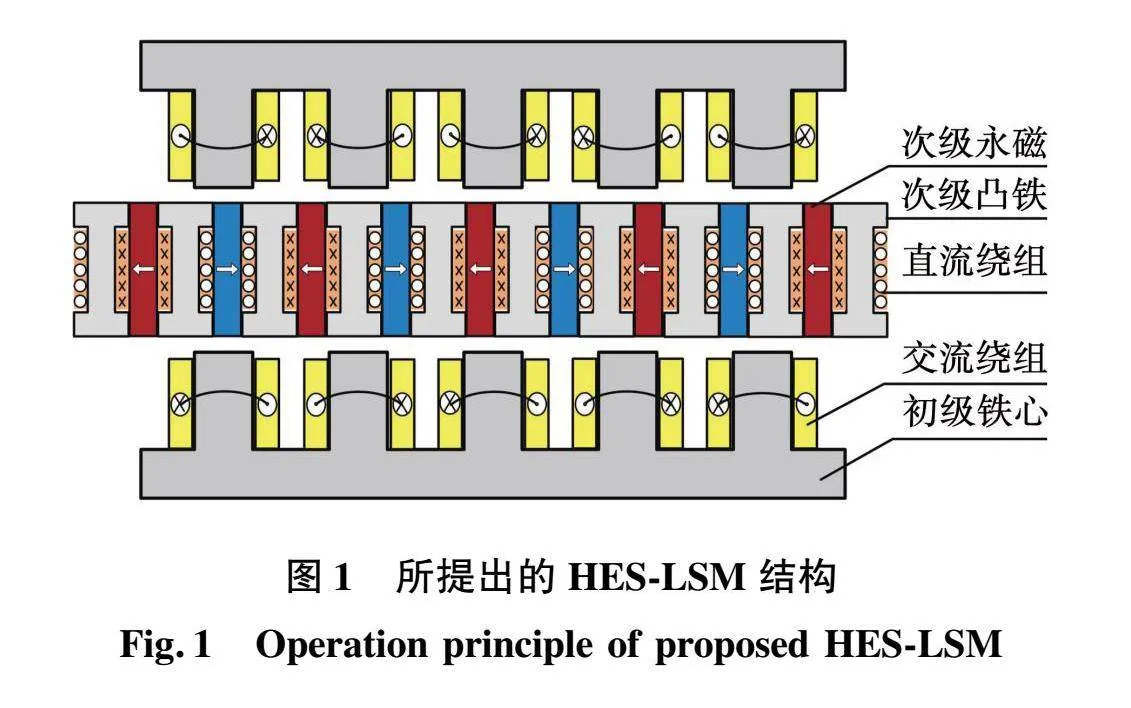
本文针对直驱无绳提升系统用的混合励磁凸极直线同步电机（hybrid excited salient-pole linear synchronous motor，HES-LSM）开展多目标优化研究。其结构如图1所示，由双边初级和一个次级组成，初级由三相交流励磁绕组和铁心组成，交流绕组采用双层分数槽集中绕组结构，次级绕组由永磁体、凸铁和直流励磁绕组组成。该结构利用次级凸铁作为电励磁磁通路径，通过直流励磁调节双边气隙均衡，实现电机无接触运行。表1和图2给出了电机的主要结构参数。

1.2 工作原理

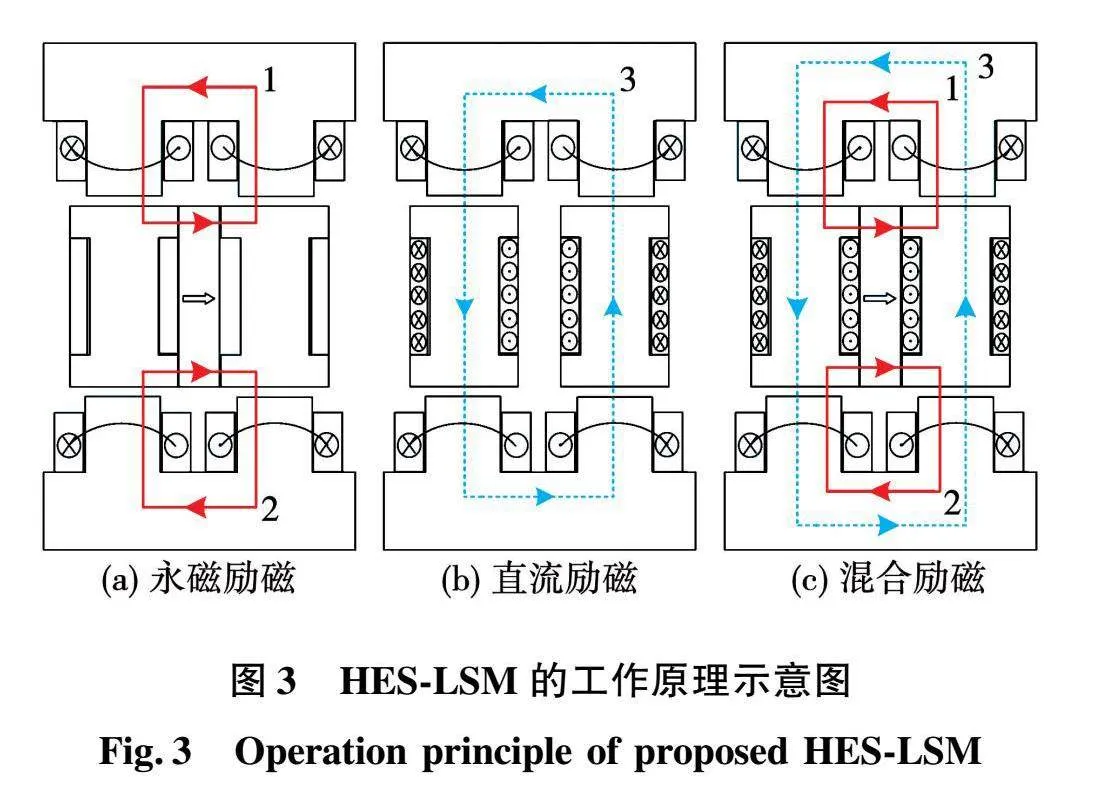
HES-LSM的运行原理与传统PMLSM相同，初级三相绕组通电后产生行波磁场与永磁磁场相互作用而产生推力，该电机的法向力调节功能通过混合励磁结构实现。为了便于阐明其运行原理，忽略初次级铁心磁阻和漏磁磁阻的影响，简化为线性等效磁路，分别对混合励磁次级的永磁体和直流励磁绕组两个磁势源进行单独分析，然后通过磁场叠加的方法获得两者共同作用时的磁场分布情况。

图3所示依次为仅永磁励磁，仅直流绕组励磁，永磁和直流绕组共同励磁时的主磁通路径。次级永磁体磁势源形成两个并联磁路，如图3 （a）中实线1、2所示，其中每个分支主磁通从永磁体出发依次经过单侧初级铁心、单侧气隙和次级两个相邻凸铁，形成小循环磁通路径。

图3（b）虚线3所示为不考虑永磁体，仅有次级直流励磁源作用时的直流励磁磁路图。直流励磁磁通形成贯穿两侧初级铁心和次级凸铁的串联磁路，该磁通不经过永磁体本身，两者仅在双侧气隙中相互作用，永磁体无退磁风险。

图3（c）为永磁体和直流励磁共同作用时的磁路图，此时，在上侧气隙中永磁磁场和直流励磁磁场方向相同，上气隙处于增磁状态，下侧气隙中永磁磁场和直流励磁磁场方向相反，下气隙磁场处于去磁状态，反之亦然。对于推力来说，上初级的推力随气隙磁场增强而变大，下初级的推力随气隙磁场减弱而减小，二者作用方向相同，合力基本不变。

可见，次级直流励磁对电机具有较好的磁场调节能力，能够调节双边气隙均衡而推力基本不变，为无接触直驱无绳提升系统提供新的参考。

2 代理模型建模

关键参数的选取是高精度代理模型的前提，其中包括参数的遴选及敏感性分析；关键参数确定后，需要选择合理的实验设计并结合有限元模型建立起训练样本库；最后依据GA-ELM建模流程构建代理模型，引入MSE和R²来评价模型精度。

2.1 关键参数的选取及实验设计的选择

理论上，电机的任何一个尺寸参数都可以作为优化设计的变量，但这显然是不可能的，不仅消耗大量的人力、物力，而且优化的计算成本是相当巨大的，尤其是对于HES-LSM来说，在优化中不可能将众多的设计参数都一一考虑。一般来说，选取关键参数遵循以下原则：

1）所选关键参数对有优化目标和约束性能有较大的影响；

2）所选关键参数之间应该互相独立，且能够确定其他参数；

3）所选关键参数不宜过多，否则影响优化效率，延长优化周期。

为了保证优化结果的有效性，保持初级齿距、次级极距、永磁体用量以及导线材料不变，该约束条件可表示为：

τp=Wt+Wc；

τs=Wsc+Wpm；

C=WpmHpmLaxial。 （1）

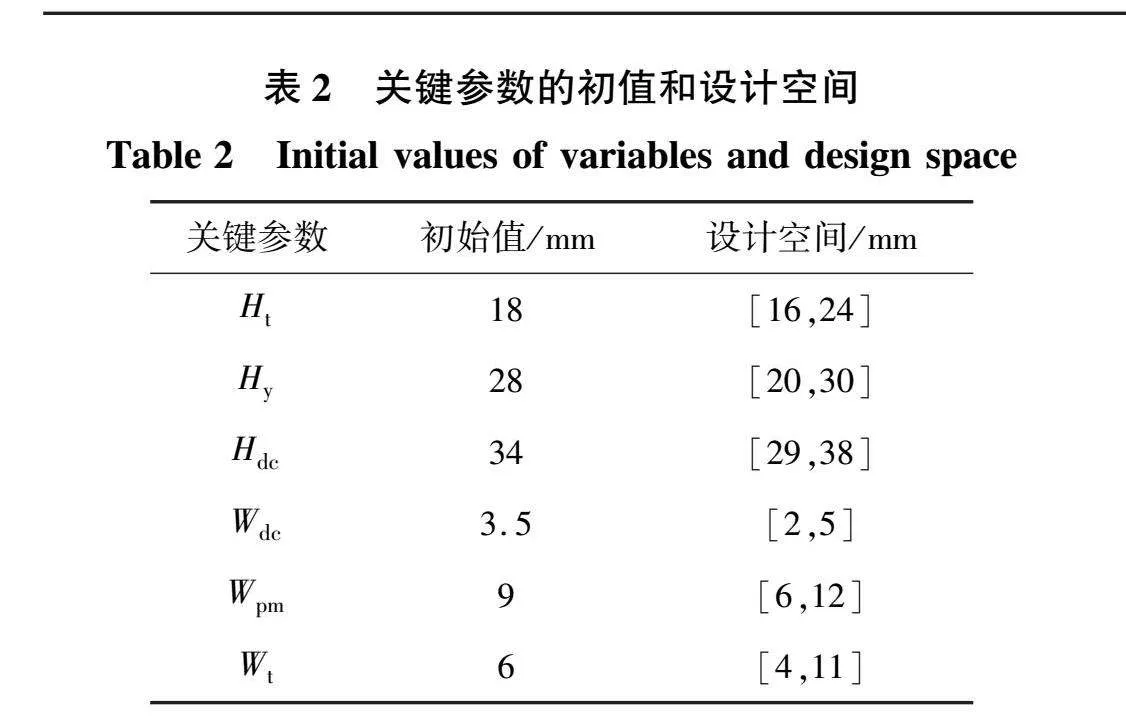
基于上述理论，主要结构参数的初步选取见表2，并以平均推力 Favg 、推力波动Frip 和推力密度Td做为优化目标。

平均推力定义为

Favg=∑Ni=1FiN。（2）

式中：Favg为平均推力；Fi为极距下得到的推力值；N为推力值的个数。

推力波动定义为

Frip=Fmax－Fmin。（3）

式中Fmax、Fmin分别为电机稳定运行时的推力最大值与最小值。

推力密度定义为

Td=FavgV。（4）

式中：Td、V分别为电机推力密度，电磁耦合体积。

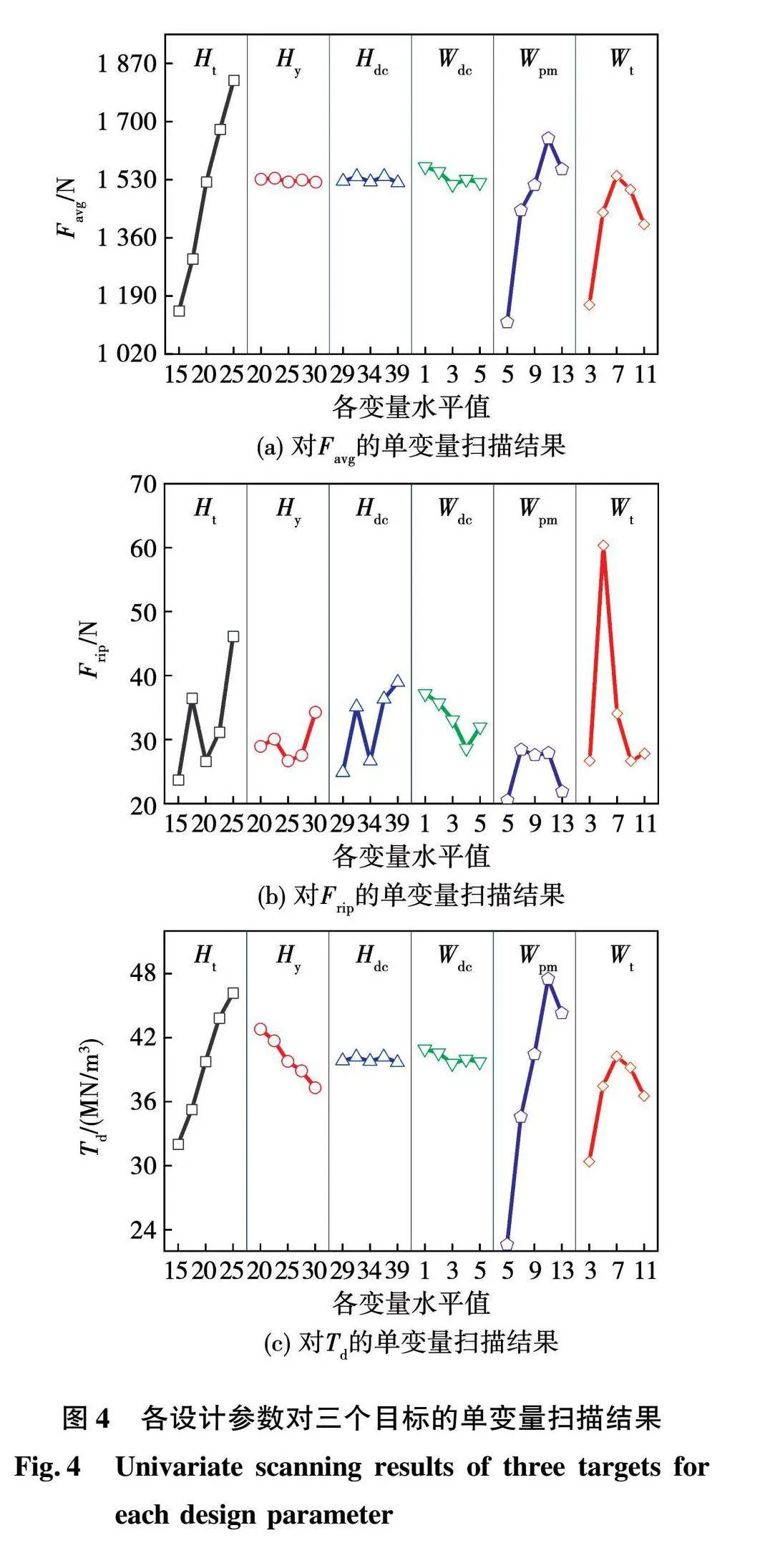
合理的关键参数选择、科学的设计空间定义是参数敏感性分析以及多目标优化的前提。为了获得各参数相应的设计空间，分别对其进行单变量扫描，依据扫描结果，选取各参数对3个目标影响较大的区域作为设计空间。扫描结果如图4所示，关键参数的初始值和设计空间如表2所示。

试验设计包括全因子设计和部分因子设计，一方面，全因子设计会带来巨大的计算成本；另一方面，神经网络数据驱动的特点又不得不要求样本库应当具备较好的均匀性。基于空间填充技术的最优拉丁超立方（OLHD）实验设计满足投影特性，能够实现样本点在设计变量空间内每一维上的投影都是均匀分布的，即可以在降低样本容量的同时保障样本点的质量。因此本文采用OLHD进行实验设计，其所需最少样本点个数为

ns=（nv+1）（nv+2）2。（5）

式中nv为设计空间的维数。

2.2 参数敏感性分析及样本库的建立

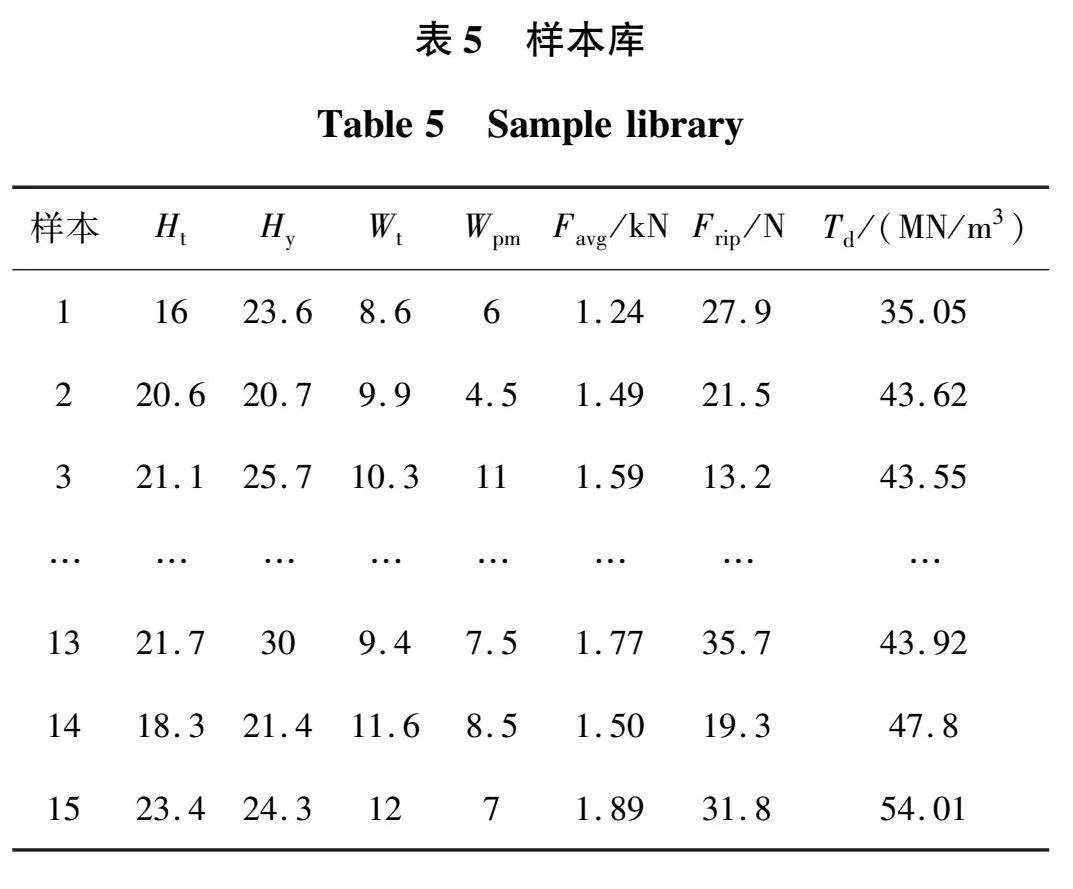
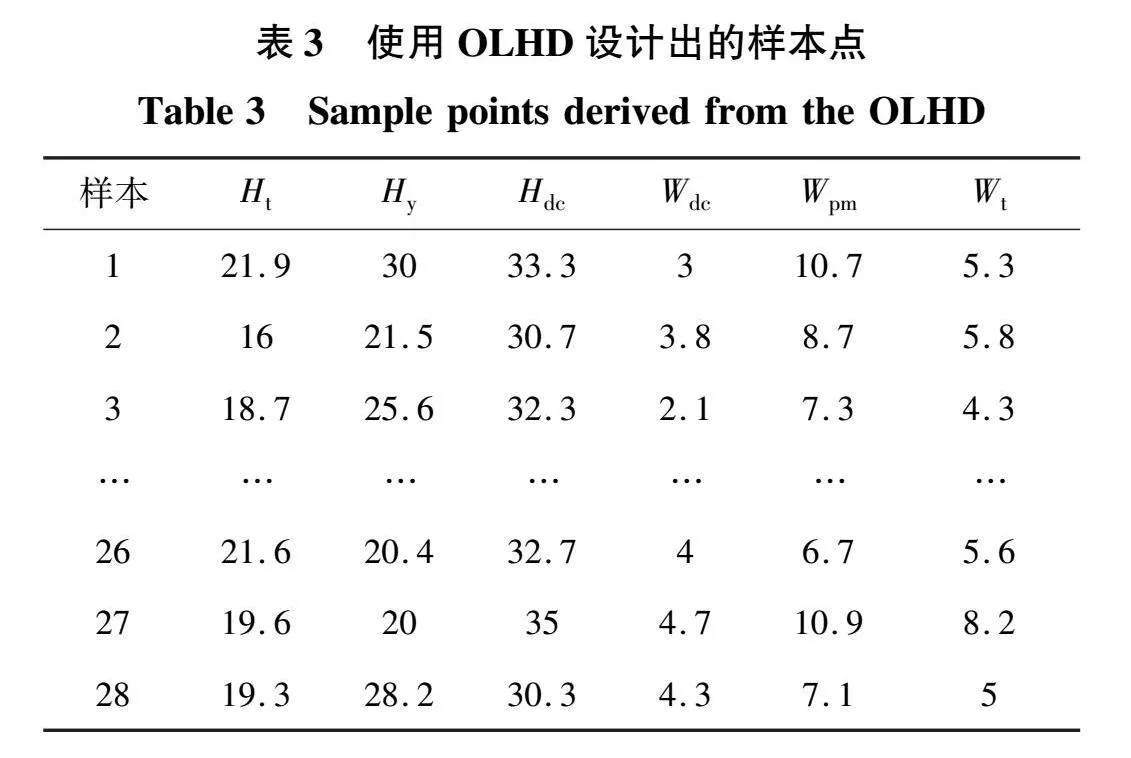
关键参数的设计空间确定后，采用OLHD进行实验设计进而对其进行敏感性分析并建立模型训练样本库。根据式（5）可知，选取的6维变量进行抽样所需的最少样本点数为28个，选取的部分样本点如表3所示，其对应的有限元计算结果见表4。其中，为了保证样本的可信度，有限元模型采用统一建模原则，包括：各有限元模型的网格采用相同剖分原则、相同的电流驱动源以及相同的边界条件等。

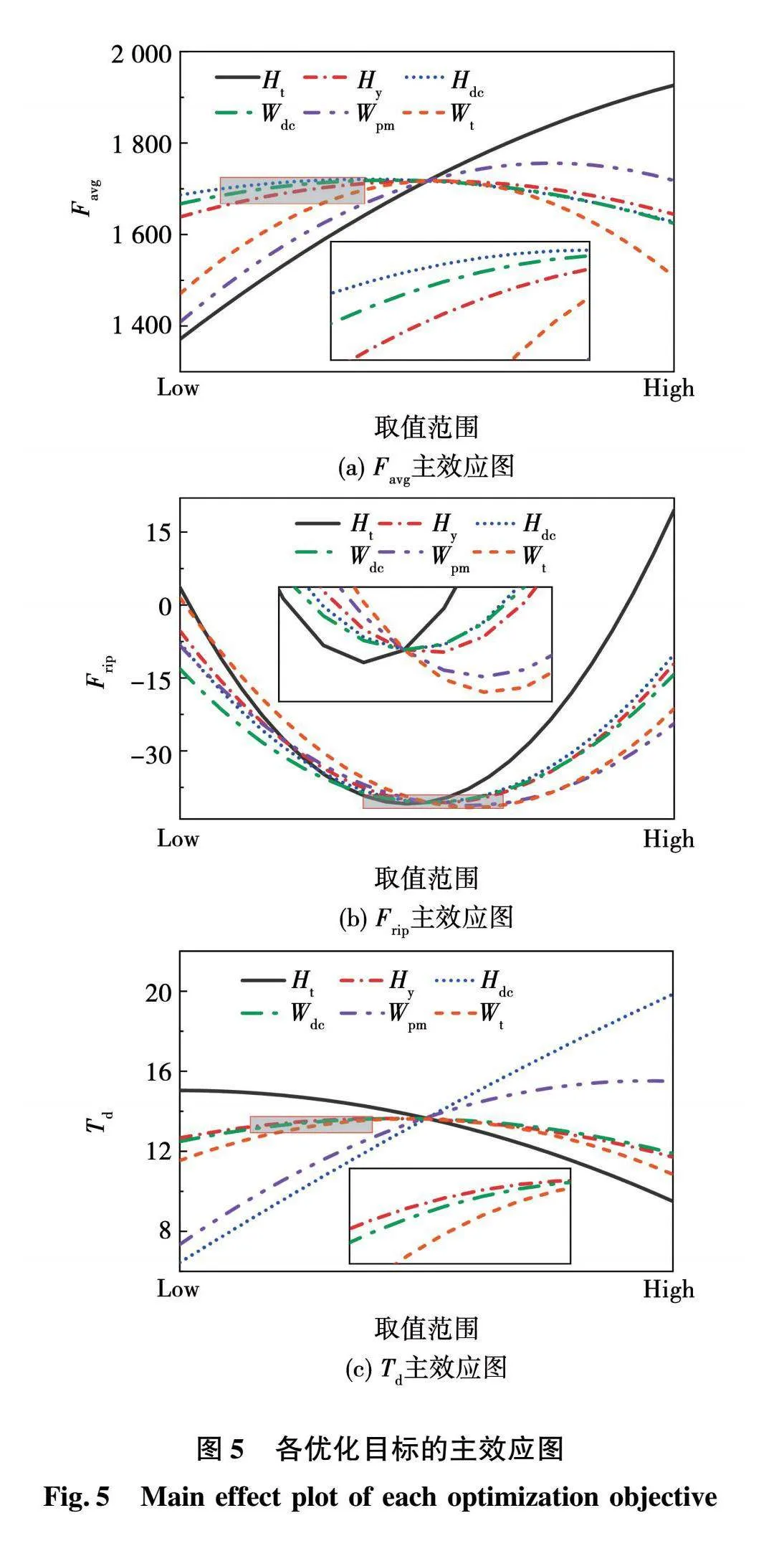
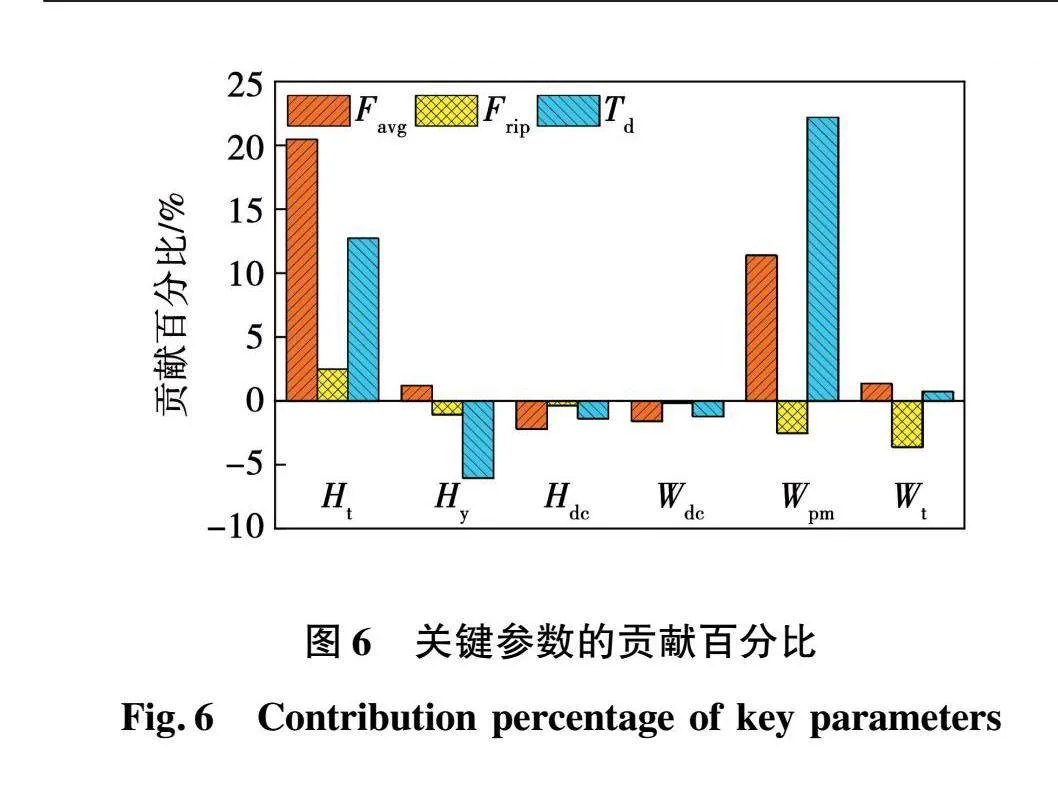
各响应的主效应图如图5所示，图中通过斜率的大小和正负分别反映了各因子对各响应的贡献排序和正、反效应之分，为便于直观分辨各因子对每个响应的影响程度，基于极差分析原理，以百分比的形式制于图6。

结合图5、图6可知，尽管直流绕组的高、宽对三个目标会产生一定程度的影响，但总体而言对模型贡献度占比较小，因此，确定最终优化设计参数为：初级齿高Ht、初级轭高Hy、永磁宽Wpm、初级齿宽Wt。随后更新关键参数并建立训练样本库如表5所示。

2.3 GA-ELM代理模型的构建

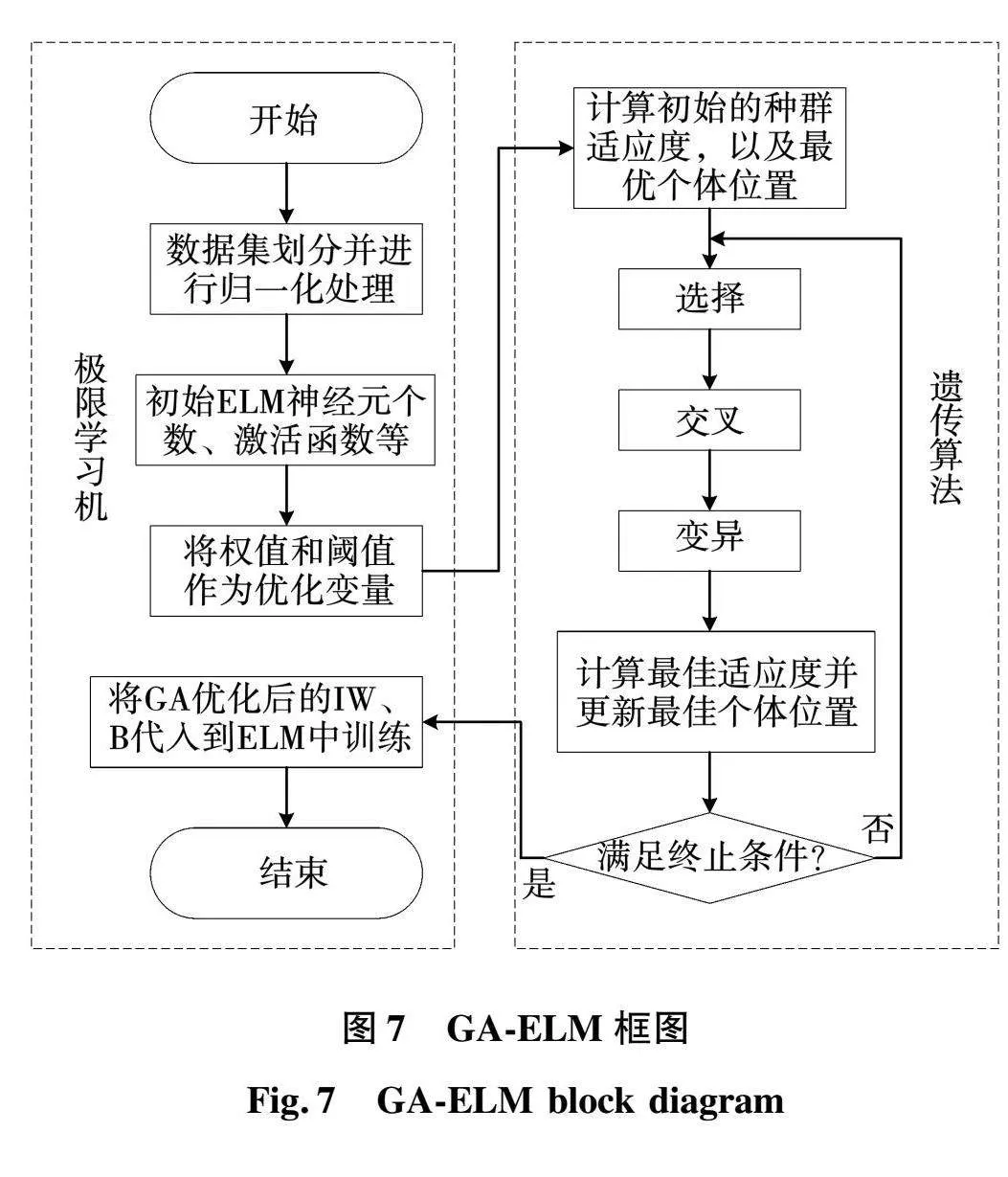
ELM随机产生输入层与隐含层间的连接权值（IW）及隐含层神经元的阈值（B），且在训练过程中无需调整，只需设置隐含层神经元的个数，便可获得唯一的最优解，相比传统的BP神经网络，没有负反馈多层迭代的大量数学计算，极大地减少了算法运算时间的同时又满足了隐藏层进行非线性运算的需求。由于IW和B是随机产生的且取值直接决定了ELM模型的精确度，所以本文采用遗传算法（GA）对IW和B进行优化，优化流程图如图7所示。

采用均方正则误差（MSE）以及决定系数（R²）来描述模型预测值和实际值之间得差异，进而间接验证模型得精度。MSE如下式所示，其值越小说明预测模型拟合效果更好：

MSE=1n∑ni=1（yi－y^i）2，∈［0，+∞）。（6）

R²如下式所示，其值越接近于1则表明预测值越接近真实样本值：

R2=1-∑ni=1（y^i－y-）2∑ni=1（yi－y-）2，∈［0，1］。（7）

式中：n表示测试样本数量；yi表示第i个样本的真实值；y^i表示第i个样本的预测值；y-表示真实值的平均值。

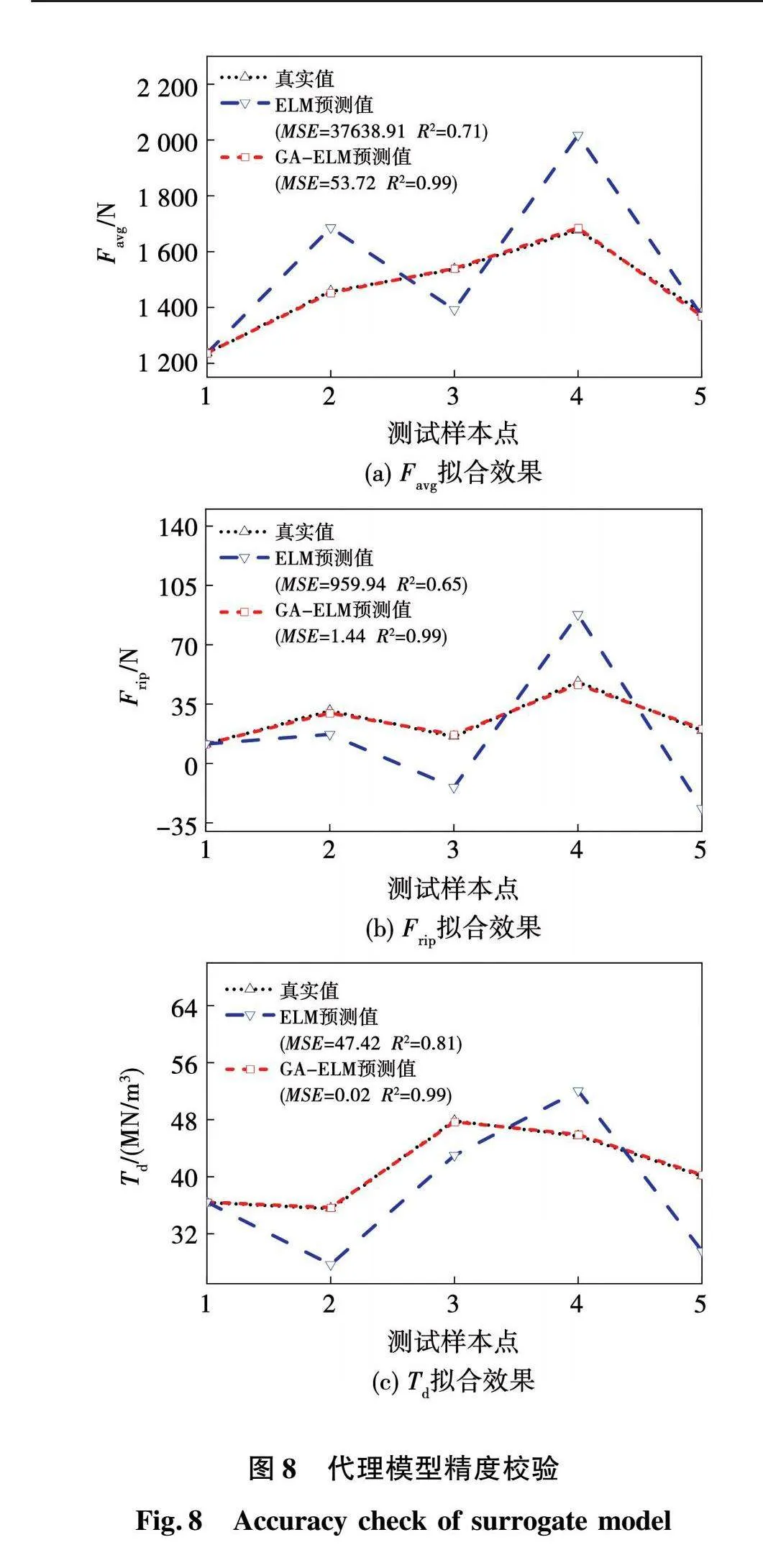
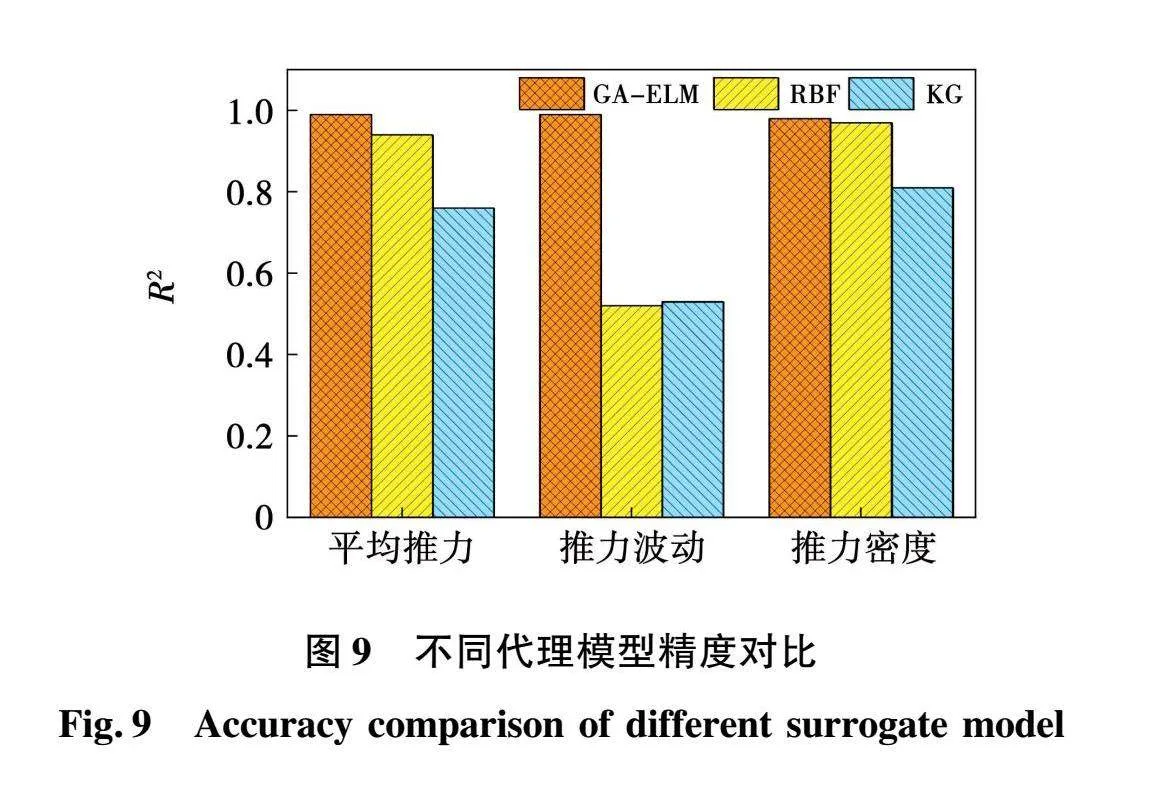
图8、图9分别给出了GA-ELM模型优化前后的预测结果对比以及GA-ELM与RBF、KG代理模型的对比，从图中可以看出：

1）经过GA优化ELM权值和阈值后能够极大改善网络性能，提高网络精度；

2）与GA-ELM相比，RBF和KG需调试参数众多，训练难度较大；

3）GA-ELM自适应能力强，具有比RBF和KG强的泛化能力，可以为后续多目标优化提供精确的快速计算模型。

3 基于代理模型的多目标优化

基于代理模型的优化设计利用代理模型拟合目标值与输入变量的数学关系，再借助适合的寻优算法多次迭代，从而快速寻找到全局最优值。

3.1 多目标粒子群优化算法

MOPSO是一种经典的仿生算法，属于启发式算法的一种。该算法通过模拟鸟集群飞行觅食的行为，鸟之间通过集体的协作使群体达到最优目的。它的核心思想是利用群体中的个体对信息的共享使整个群体的运动在问题求解空间中产生从无序到有序的演化过程，从而获得问题的可行解。

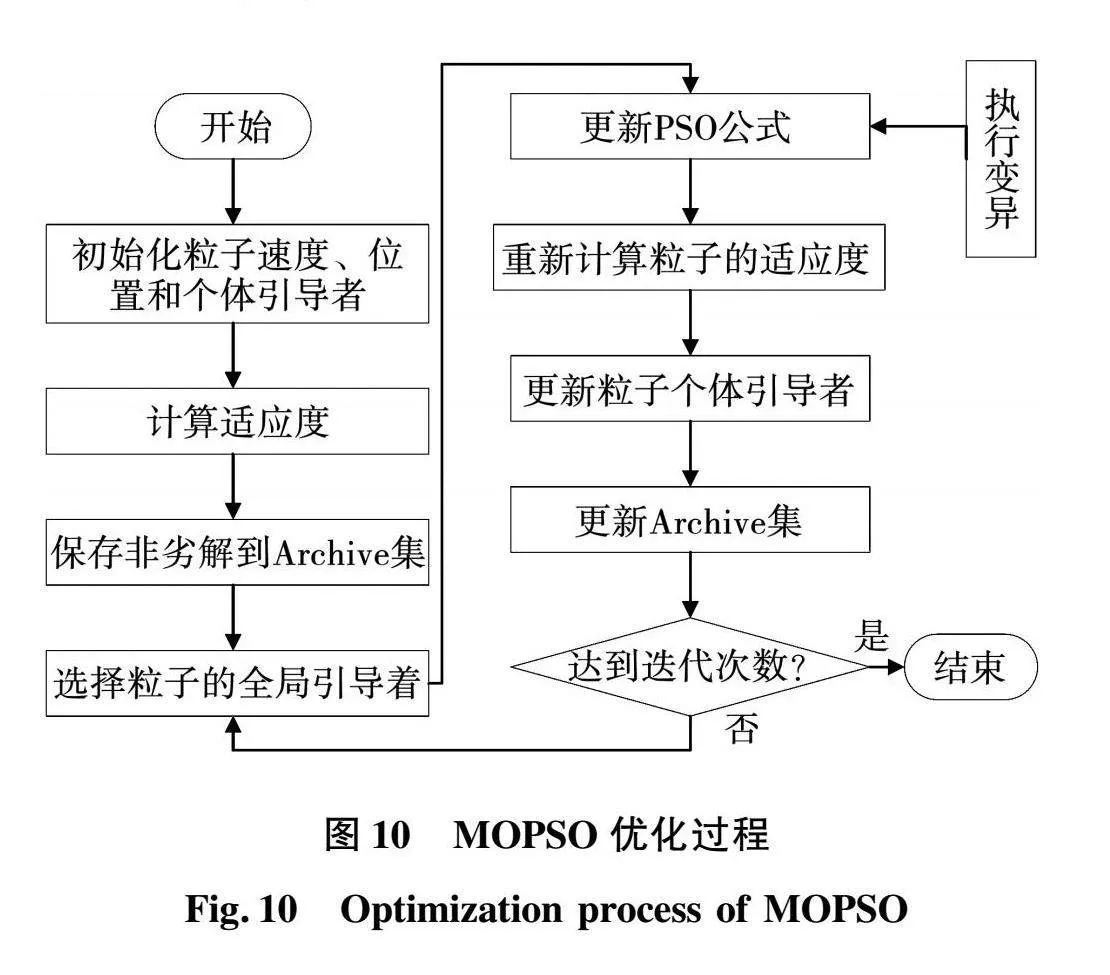
MOPSO算法是在PSO算法的基础上拓展而来，其具体过程如图10所示。通过增加外部储备集Archive保存算法迭代过程中出现的非劣解，依据Archive集中粒子的密度信息选择Gi，在每一次迭代过程中都需要更新粒子的速度和位置，并计算适应值更新Archive集。粒子速度和位置更新公式为：

V′id=WiVid+c1r1（Pid－Xid）+c2r2（Gid－Xid）；

X′id=Xid+V′id。（8）

式中：Vid、Xid分别代表第i个粒子在d维空间中的速度和位置；V′id、X′id分别代表粒子更新后的速度和位置；d为粒子飞行空间的维数；Wi为惯性权重；c1、c2为加速系数（学习因子）；r1、r2为[0，1]之间的随机数；Pi、Gi分别为个体最优解和全局最优解。

此外，为了确保种群的多样性，解决PSO易陷入局部最优解的问题，在MOPSO中加入变异，引入扰乱算子，其表达式为

p=（1－（gen－1）/（Max_gen－1））＾（1/m）。（9）

式中：p为扰乱算子；gen、Max_gen分别代表当前迭代次数和最大迭代次数；m为突变率。

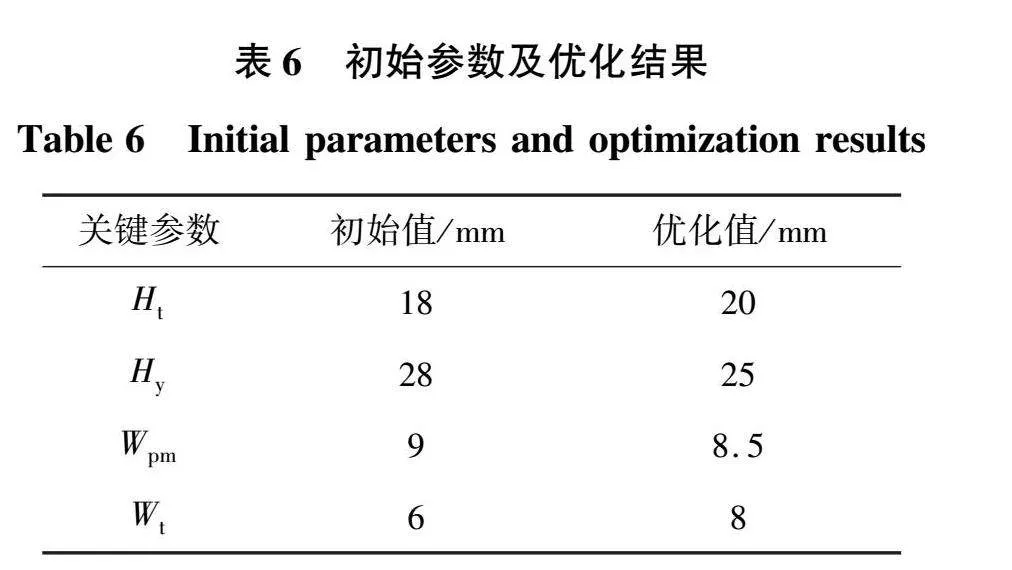
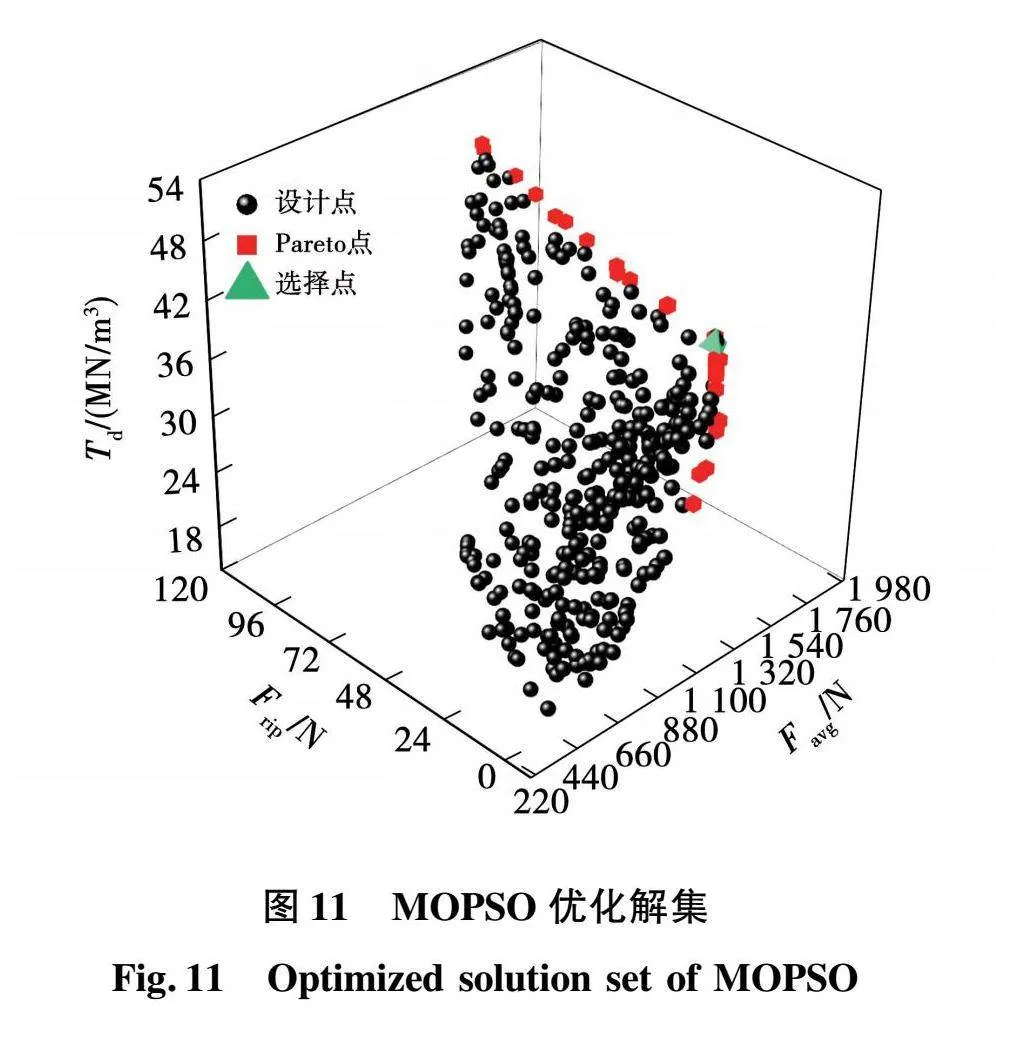
优化后的解集如图11所示。每个最优解确保至少有一项结构参数被优化，确保了解集的多样性。为进一步验证解集的有效性，选择一个最优解作为最终优化结果。初始方案和优化方案的结构参数见表6。

3.2 优化前后对比分析

优化前后电机性能对比如图12至图15所示，其中空载反电动势以单侧A相绕组为例，进而对其进行傅里叶分解，并计算其总谐波畸变率（total harmonic distortion，THD）。THD计算公式为

THD=E22+E23+…+E210E1×100%。（10）

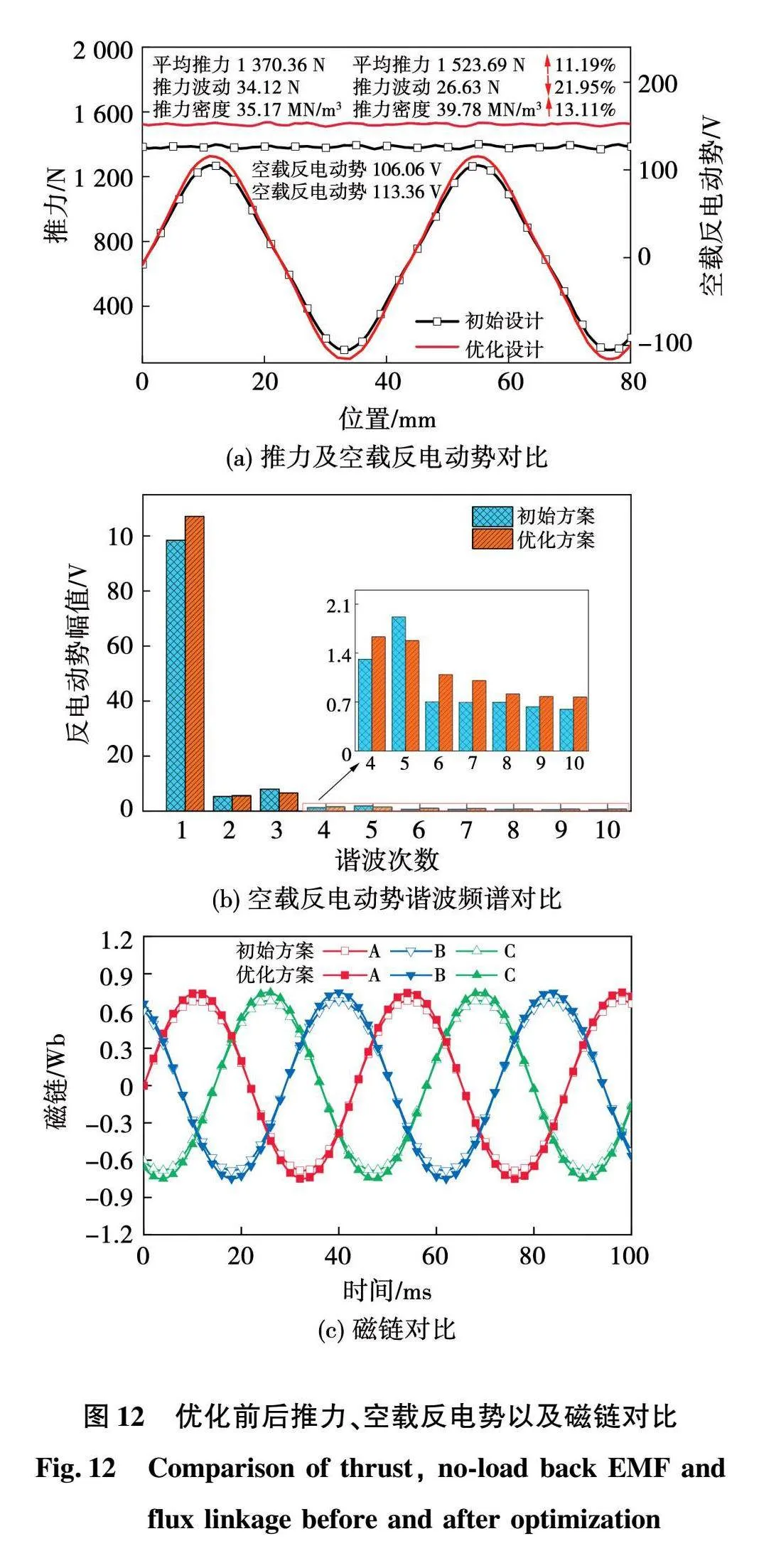
空载反电动势、推力波形以及磁链波形如图12所示，HES-LSM优化前后的平均推力分别为1 370.36、1 523.69 N，提高11.19%；推力波动分别为34.12、26.63 N，降低21.95%；推力密度分别为35.17、39.78 MN/m3，提高13.11%；空载反电势分别为106.06、113.36 V，提高9.71%；磁链分别为0.68、0.75 Wb，提高10.29%。

分析上述效果产生的原因如下：

1）由式（10）计算可得优化前后的THD分别为10.22%和8.66%，首先优化后空载反电动势的谐波畸变率显著降低，且基波幅值明显增加，进而提高了空载反电动势；其次，高次谐波中，3次和5次谐波是影响波形正弦度的主谐波，优化后二者均有所降低，使得反电动势波形得到改善。

2）从结构上看，优化后初级齿与次级凸铁的增大使得有效磁通路径面积变大，电机初次级之间的电磁耦合面积随之增大，这有助于电机推力的增加，且优化后空载反电动势以及磁链均增大，进而电机推力得到提升。

3）从幅值上来看，电机优化前后的推力波动峰峰值分别为34.12、26.63 N，相较于平均推力1 370.36、1523.69 N而言较小，当推力波动峰峰值略有降低且平均推力提高时，推力波动在平均推力中的占比将显著降低。其次，理想边界条件下，推力波动产生的原因包括齿槽力、初次级之间耦合作用对电机气隙磁场的影响等等，随着电机齿槽尺寸以及次级凸极尺寸的改变，均会对气隙磁场产生一定作用，进而对电机推力波动产生影响。

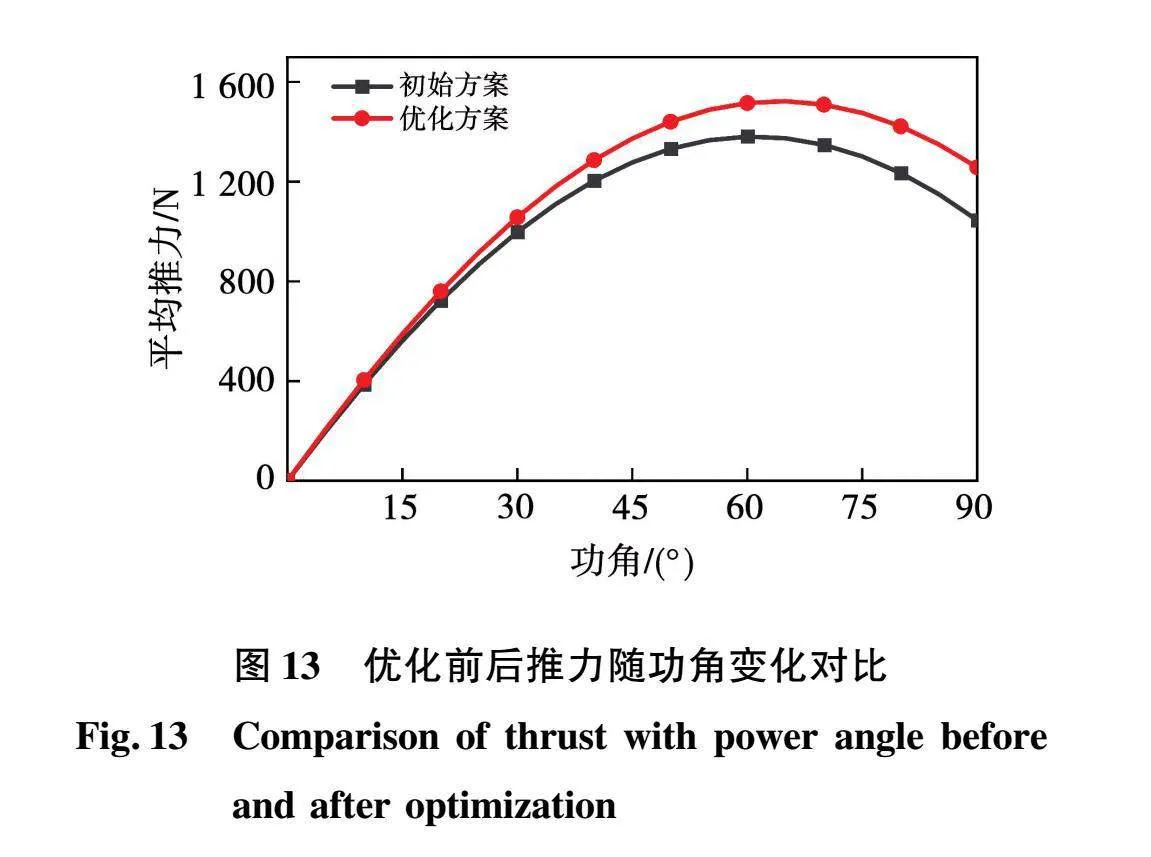
电压激励下电机推力随功角变化的曲线如图13所示，优化后电机的推力得到提升，以额定推力点为例，与优化前结构相比推力提升约10.8%，与电流激励下提升11.19%相比误差较小。优化后电机在不同激励下的初级绕组电流对比如图14所示，不同激励下电机的稳态电流幅值基本相同，电压激励下的电流波形正弦度较差，对电压激励下的初级绕组电流进行傅里叶分解，并计算谐波畸变率为11.5%，其中高次谐波中2次和3次谐波占比较大。

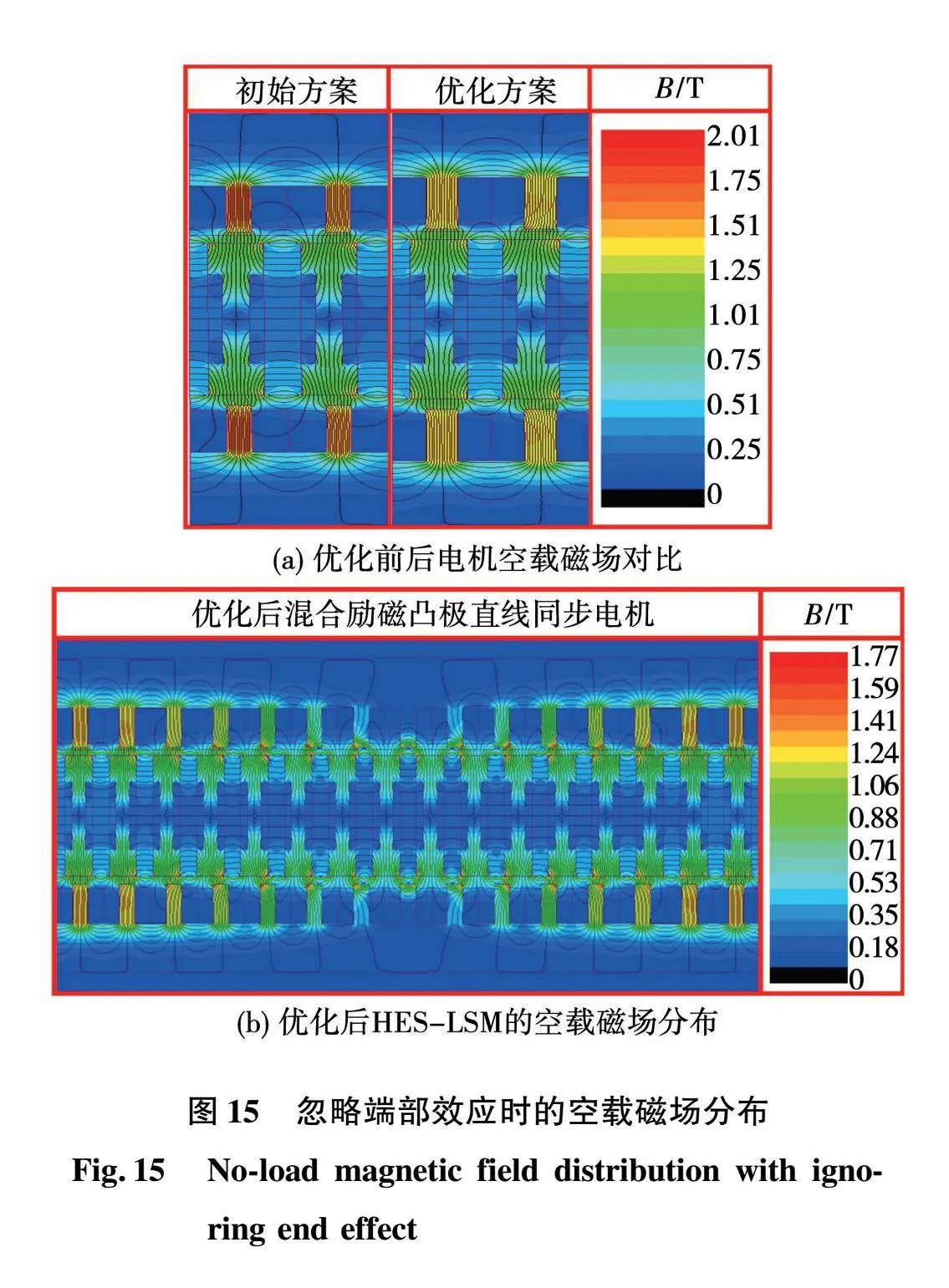
此外，为了验证优化后的电机静态性能的优越性和合理性。对优化前后电机的永磁磁场分布进行分析，如图15所示，图15（a）给出了初始方案和优化方案的磁场分布图，从结构上看，优化后，次级永磁宽的减小使得次级凸铁宽增大，同时初级齿变宽，二者综合作用使得有效磁通路径增大。从数值上看，初始方案局部位置的磁场发生畸变，磁场强度最高为2.01 T，而优化后该现象得以改善，磁场强度最高区域为1.77 T，最大磁通密度减小。图15（b）中，磁力线呈偶对称边界条件连续分布，即忽略端部效应的影响，初级齿与次级凸铁相对应的位置磁力线分布很密，为磁场强度最高区域，最大磁通密度为1.77 T。

4 实验验证

4.1 样机及测试平台搭建

依据优化结果制作样机，电机的初级结构和混合励磁次级结构分别如图16（a）和图16（b）所示。电机初级铁心由硅钢片叠压而成，嵌入绕组后采用环氧树脂封装。电机次级凸铁极由整块电工铁加工而成，槽内嵌入直流励磁绕组；永磁体双面涂专用胶，用夹具将其压入两凸铁极之间固定。

电机整体采用3段次级单元连续安装在定子侧，动子为双边初级模块结构，在初级模块与背板之间装设轮辐式拉压力传感器，并在电机初级四个角沿法向安装微动滑块，如图17所示，保证动子初级模块在法向偏移的自由度。添加另外一套双边隐极式直线电机作为基准电机，本文的混合励磁凸极电机作为被测电机，基准电机动子和被测电机动子之间设置拉/压力传感器，通过法兰刚性连接成一体。利用磁栅位移传感器高精度检测两台电机的位置和速度，磁栅尺沿定子底板安装，读数头及配套的数据处理单元分别装在两台电机动子上。整体测试平台如图18所示。

4.2 空载反电势测试

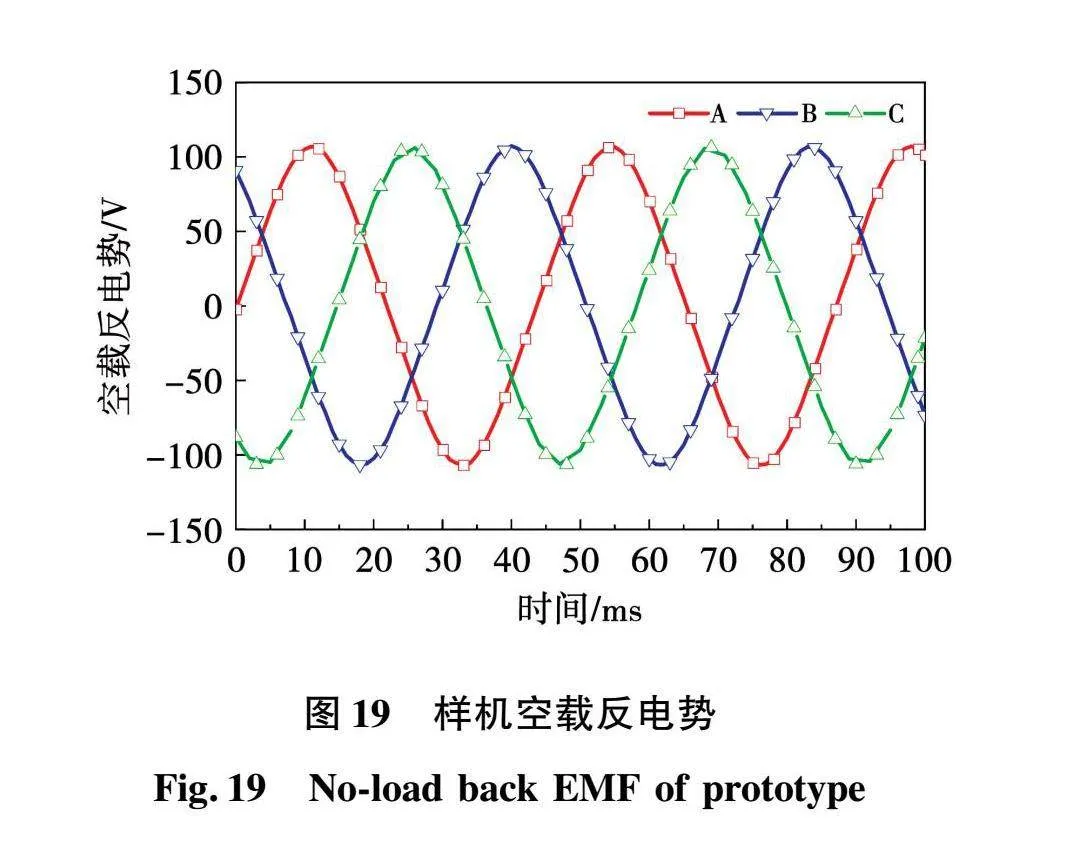
HES-LSM被测电机的绕组开路，基准电机通入23 Hz电源并带动实验样机初级以1.035 m/s的速度沿直线方向匀速运动，测得样机单侧反电势波形如图19所示，从波形上可以看出，三相反电势波形正弦度较好，相位互差120°。从数值上看，三相反电势幅值基本相等，反电势幅值为106.79 V，略低于有限元仿真值113.36 V，误差为5.8%。

4.3 静推力及推力测试

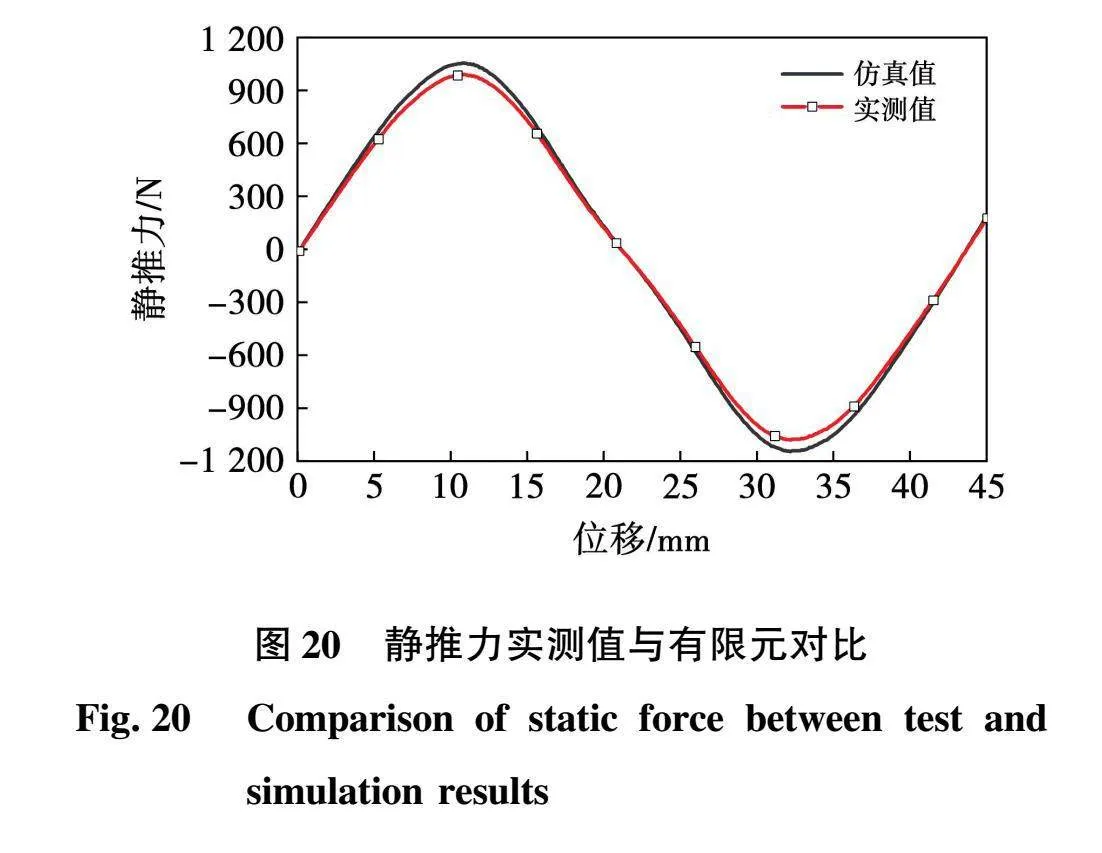
为了更好地测试该电机的性能，对其进行静推力测试。将双侧A相绕组通入5A直流电，同时利用基准电机带动丝杆拉动样机初级沿直线方向做匀速运动，图20给出了拉力传感器检测该电机在不同位置时静推力变化特性，静推力实测波形与有限元仿真波形变化趋势基本保持一致，并且以两倍极距为周期。其中，静推力实测值为990.75 N，略小于有限元仿真值1 055.87 N，误差为6.17%。

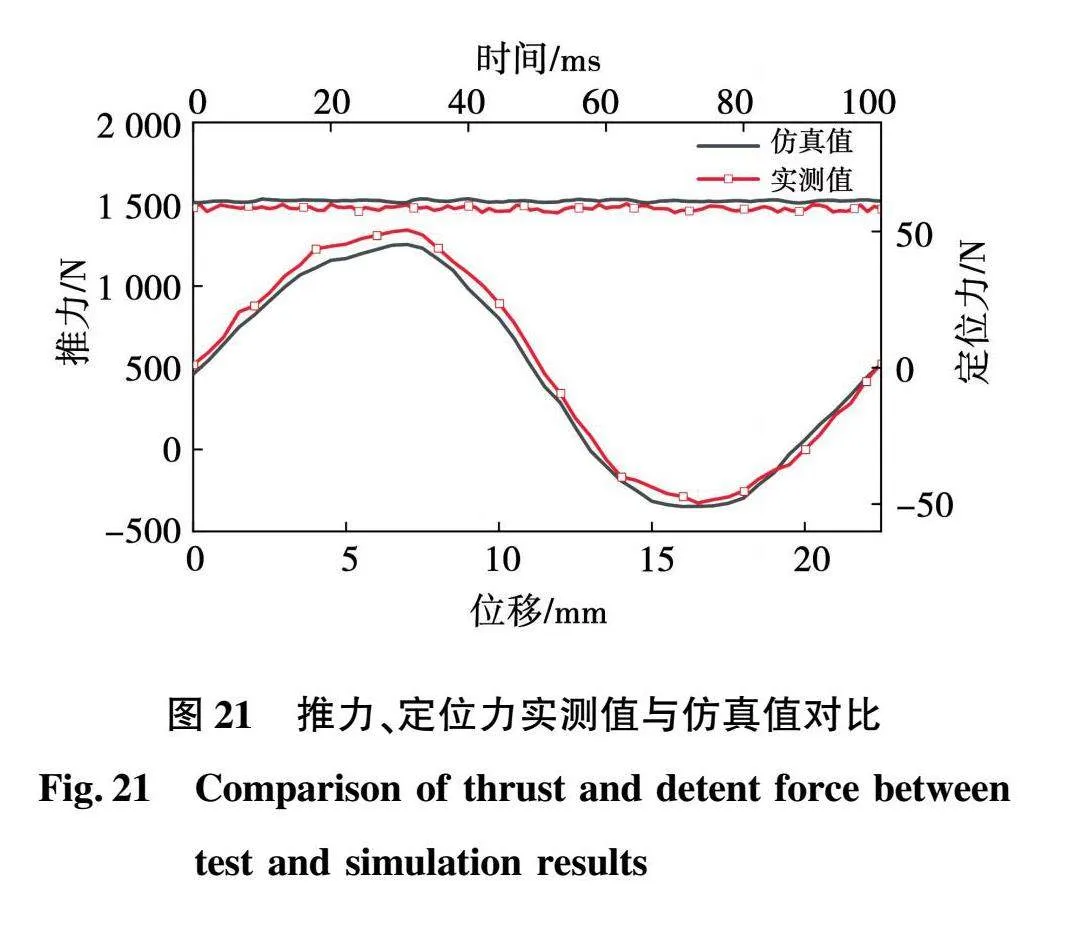
图21给出了电机推力、定位力的测试值与仿真值波形对比。从数值上看，实验结果与仿真结果的趋势基本吻合，平均推力测试值与仿真值的最大误差为3.2%，定位力实测值与仿真值的最大误差为9.2%。

从波形上看，推力实测的波动与电压激励下仿真的波动相比较大，这是由于仿真是在初级铁心无限长的前提下进行，即忽略了端部力的影响，分数槽集中绕组又很好地削弱了齿槽力的大小，而为了清晰地展示样机的混合励磁结构，实测样机设置为短初级、长次级结构，受端部力的影响，导致推力实测波形中波动较大，定位力的测试结果再次验证了定位力对推力波动的影响。

5 结 论

本文提出一种适用于电机优化设计的优化框架，该框架通过搭建电机的GA-ELM代理模型，进而引入MOPSO算法获得多目标最优解，最后成功地将该优化框架应用于一台HES-LSM的结构优化，并制作样机，完成了实验验证，得出如下结论：

1）GA优化后的ELM网络具有更高的拟合精度，且无需设置网络权值、阈值等参数便可得到精确的代理模型，在一定程度上降低了建模难度。

2）所提出的优化框架能够同时利用ELM模型的计算速度、有限元模型的分析准确度以及MOPSO算法的全局寻优能力，在保证模型精度的前提下，显著减少有限元样本个数，缩短优化周期。

3）优化结果与初始方案对比，电机平均推力提高了11.19%、推力波动降低了21.95%、推力密度提高了13.11%，电机性得到改善。通过修改约束条件和设计参数，该框架可应用于其他电机的优化设计。

参 考 文 献：

［1］ 蒋钱， 卢琴芬， 李焱鑫. 双三相永磁直线同步电机的推力波动及抑制[J].电工技术学报， 2021， 36（5）： 883.

JIANG Qian， LU Qinfen， LI Yanxin. Thrust ripple and depression method of dual three phase permanent magnet linear synchronous motors[J]. Transactions of China Electrotechnical Society， 2021， 36（5）： 883.

［2］ ZHANG Zijiao， LUO Meizhu， DUAN Jian， et al. Design and modeling of a novel permanent magnet width modulation secondary for permanent magnet linear synchronous motor[J]. IEEE Transactions on Industrial Electronics，2022，69（3）：2749.

［3］ BODUROGLU A， DEMIR Y， CUMHUR B， et al. A novel track structure of double sided linear PM synchronous motor for low cost and high force density applications[J]. IEEE Transactions on Magnetics，2021，57（2）：1.

［4］ JIAO Zongxia， WANG Tianyi， YAN Liang. Design of a tubular linear oscillating motor with a novel compound Halbach magnet array[J]. IEEE/ASME Transactions on Mechatronics： A joint publication of the IEEE Industrial Electronics Society and the ASME Dynamic Systems and Control Division，2017，22（1）：498.

［5］ HIRAYAMA T， YAMASHITA S， KAWABATA S. Design and analysis of linear switched reluctance motor with coreless HTS excitation windings for ropeless elevator[C]//2018 21st International Conference on Electrical Machines and Systems （ICEMS）， October 7-10，2018， Jeju， Korea. 2018：1879-1884

［6］ FAN Hua， CHAU K T， LIU Chunhua， et al. Quantitative comparison of novel dual-PM linear motors for ropeless elevator system[J]. IEEE Transactions on Magnetics， 2018， 54（11）： 1.

［7］ 谢冰川， 张岳， 徐振耀， 等. 基于代理模型的电机多学科优化关键技术综述[J].电工技术学报，2022，37（20）：5117.

XIE Bingchuan， ZHANG Yue， XU Zhenyao， et al. Review on multidisciplinary optimization key technology of electrical machine based on surrogate models[J]. Transactions of China Electrotechnical Society， 2022， 37（20）： 5117.

［8］ 杨巧玲，宋柏良，郭生辉，等.基于RSM-正交法的磁障式直线永磁游标电机的设计与优化[J].电机与控制学报， 2024， 28（3）： 179.

YANG Qiaoling， SONG Bailiang， GUO Shenghui， et al. Design and optimization of magnetic barrier linear permanent magnet vernier motor based on RSM orthogonal method[J]. Electric Machines and Control， 2024， 28（3）： 179.

［9］ 樊英， 陈秋蒴， 陈俊磊， 等. 基于无人配送车辆运行工况的交替极游标轮毂电机优化设计[J].电工技术学报，2023，38（19）：5141.

FAN Ying， CHEN Qiushuo， CHEN Junlei， et al. Optimization design of consequent pole vernier wheel motor based on operating conditions of unmanned delivery vehicles[J]. Transactions of China Electrotechnical Society， 2023，38（19）：5141.

［10］ GIURGEA Stefan， FODOREAN Daniel， CIRRINCIONE Giansalvo， et al. Multimodel optimization based on the response surface of the reduced FEM simulation model with application to a PMSM[J]. IEEE Transactions on Magnetics， 2008， 44（9）： 2153.

［11］ 杨树财， 王贤良， 杨松涛. 基于BP网络模型的电机壳加工工艺参数优化[J].航空精密制造技术，2018，54（5）： 19.

YANG Shucai， WANG Xianliang， YANG Songtao. Optimization of machining parameters for motor shell based on BP network model[J]. Aviation Precision Manufacturing Technology， 2018， 54（5）： 19.

［12］ 孙利宏， 赵永生， 李存贺， 等. 基于预处理BP神经网络的开关磁阻电机建模[J].电机与控制应用，2019，46（3）： 64.

SUN Lihong， ZHAO Yongsheng， LI Cunhe， et al. Modeling of switched reluctance motor based on pretreatment BP neural network[J]. Electric Machines amp; Control Application， 2019， 46（3）： 64.

［13］ IM S Y， LEE S G， KIM D M， et al. Kriging surrogate model-based design of anultra-high-speed surface-mounted permanent-magnet synchronous motor considering stator iron loss and rotor eddy current loss[J]. IEEE Transactions on Magnetics， 2022， 58（2）： 1.

［14］ HOSSEINI S， SHAHBANDEGAN A， AKILAN T. Deep neural network modeling for accurate electric motor temperature prediction[C]//IEEE Canadian Conference on Electrical and Computer Engineering （CCECE）， September 18-20，2022， Halifax， NS， Canada. 2022： 170-175.

［15］ CAO Jiuwen， LIN Zhiping， HUANG Guangbin. Self-adaptive evolutionary extreme learning machine[J]. Neural Processing Letters， 2012， 36（3）： 285-305.

［16］ YOU X， YANG S. Evolutionary extreme learning machine based on particle swarm optimization[C]//3rd International Symposium on Neural Networks （ISNN）， May 28-31， 2006， Chengdu， China. 2006： 644-652.

［17］ ZENG Yujun， XU Xin， SHEN Dayong， et al. Traffic sign recognition using kernel extreme learning machines with deep perceptual features[J]. IEEE Transactions on Intelligent Transportation Systems，2017，18（6）： 1647.

［18］ HUANG Guangbin， ZHOU Hongming， DING Xiaojian， et al. Extreme learning machine for regression and multiclass classification[J]. IEEE Transactions on Systems Man and Cybernetics Part B-Cybernetics， 2012， 42（2）： 513.

［19］ ZHU Lijun， HUANG Tianyu， REN Ziyan， et al. Optimal design of power transformer magnetic shielding utilizing extreme learning machine and particle swarm optimization[C]//2022 25th International Conferenceon Electrical Machines and Systems （ICEMS）， November 29-December 2，2022， Chiang Mai， Thailand. 2022： 1-5.

［20］ SONG Juncai， DONG Fei， ZHAO Jiwen， et al. An efficient multiobjective design optimization method for a PMSLM based on an extreme learning machine[J]. IEEE Transactions on Industrial Electronics， 2019， 66（2）： 1001.

（编辑：刘素菊）