非对称占空比调制下DAB损耗方差优化策略

摘 要：非对称占空比调制（ADM）策略可以解决双有源桥变换器（DAB）轻载时系统效率低的问题，但是，ADM方式会造成DAB开关管损耗分布差异大、热应力高危及系统可靠性的问题。为了解决上述问题，提出一种基于开关管损耗方差最小的非对称占空比调制优化策略，分析ADM各模式的功率传输和软开关范围，建立ADM方法下的器件损耗模型，以DAB开关管损耗方差最小为优化目标，采用粒子群优化算法获得最优控制组合。最后，针对一台容量1.6 kW采用SiC MOSFET的DAB样机进行实验，以器件温度峰值和方差作为评价指标，验证所提优化调制方法的可行性和有效性，在330 W和500 W的轻载工况下，所提优化方案的器件温度方差分别降低了43%和21.5%，温度峰值分别降低了2.8 ℃和0.6 ℃，系统效率分别提高了1.2%和0.5%。

关键词：双有源桥变换器；非对称占空比调制；粒子群算法；损耗分布；系统可靠性

DOI：10.15938/j.emc.2024.11.012

中图分类号：TM46

文献标志码：A

文章编号：1007-449X（2024）11-0127-12

Power switch loss variance based optimization scheme for DAB converter with asymmetric duty cycle modulation

ZHANG Fan¹， LI Xinghao¹， ZHANG Yao¹， ZONG Jiaxing¹， WEI Yuqi²

（1.School of Electric and Engineering， Hangzhou Dianzi University， Hangzhou 310018， China;

2.School of Electric and Engineering， Xi’an Jiaotong University， Xi’an 710049， China）

Abstract：The asymmetric duty cycle modulation （ADM） strategy can solve the problem of low system efficiency in dual active bridge （DAB） under light load conditions. However， ADM can cause large difference of DAB switch loss distribution， high risk of thermal stress and system reliability. To solve the above-mentioned problems， an asymmetric duty cycle modulation optimization strategy based on minimal variance of switch loss was proposed. The power transmission and soft switching range of ADM were analyzed， and the device loss model under ADM was established， with minimal variance of DAB switch loss as the optimization target， and optimal control combinations were obtained using particle swarm optimization algorithm. Finally， a DAB prototype with 1.6 kW capacity and SiC MOSFET was tested. The feasibility and validity of the optimized modulation method were verified by taking the peak and variance of device temperature as evaluation index. Under the light load conditions of 330 W and 500 W， the device temperature variance of the optimized scheme is reduced by 43% and 21.5%， the peak temperature is reduced by 2.8 ℃ and 0.6 ℃， and the system efficiency is improved by 1.2% and 0.5%， respectively.

Keywords：dual active bridge converter; asymmetric duty cycle modulation; particle swarm algorithm; loss distribution; system reliability

0 引 言

双有源桥（dual active bridge，DAB）变换器具有拓扑结构简单、功率双向传输和电气隔离等优点，在交直流微电网、固态变压器、电动汽车以及储能等领域的应用越来越广泛^[1-4]。

单移相（single phase shift，SPS）^[5]控制是DAB变换器最基本的控制方式，通过调整2个全桥输出电压之间的相位就可以对DAB变换器的功率大小以及传输方向进行调整。但是，在轻载或电压不匹配时，SPS控制方式容易丢失软开关，使得电感电流应力、回流功率以及开关损耗增大，导致系统效率降低。为了解决SPS控制方式存在的问题，拓展移相（extended phase shift，EPS）^[6]、两重移相（double phase shift，DPS）^[7]、三重移相（triple phase shift，TPS）^[8]等多自由度的调制方式相继被提出，同时衍生出一系列以电感电流应力、回流功率和电流有效值等为优化目标的控制策略^[9-11]，但他们只能在一定程度上减小器件的导通损耗和关断损耗。上述调制方式的驱动信号占空比都是50%（忽略死区时间），在一个开关周期内前半段和后半段的电压电流绝对值相同，符号相反，都属于对称占空比调制（symmetric duty modulation，SDM）方式。

为了进一步提升DAB变换器性能，突破对称占空比限制的非对称占空比调制（asymmetric duty modulation，ADM）方式被提出^[12-16]，其驱动信号占空比不再受限于50%，因此具有更多的优化空间。与SDM方式类似，基于ADM衍生出一系列以电流应力、电流峰峰值和电流有效值等为优化目标的控制策略，与传统SDM方式相比，ADM方式在轻载时具有更好的软开关性能，提高了系统效率。

功率半导体器件是电力电子变换器中最容易失效的部件^[17]，功率半导体器件的可靠性关系到系统的整体可靠性。导致功率半导体器件失效的主要因素是热应力，然而，功率半导体器件的热应力与器件损耗有关，因此可以通过优化器件损耗提升系统的可靠性^[18]。目前关于DAB损耗优化的文献较多，主要集中于SDM方式下总损耗最小为优化目标的效率最大化研究^[19-21]，但是关于ADM损耗分布差异的均衡方法鲜有报导。由于ADM在SDM的基础上引入了新的控制变量-占空比，流过各开关管的电流有效值和同一桥臂上的开关管关断时的瞬态电压电流不相同，易造成各开关管的损耗分布差异增加，从而导致开关管热应力过高，使系统的整体可靠性降低，因此有必要对ADM方式下的损耗分布优化进行深入研究。

文献[14]提出的ADM方法在SPS基础上增加了一个控制自由度-占空比，极大地提高了系统轻载时的效率，但未对各开关管的损耗分布差异进行分析和优化。为了减小ADM方式下各开关管的损耗分布差异，提高系统的整体可靠性，本文在文献[14]所述ADM方法基础上提出一种以各开关管损耗方差最小为优化目标的优化调制策略。首先分析ADM方式下各模式的功率传输范围和软开关工作范围，然后建立ADM方式下的器件损耗模型，而后以各开关管损耗方差最小为优化目标，采用粒子群优化算法获得其最优控制组合，最后通过实验验证理论分析的正确性和所提调制方法的有效性。

1 ADM调制策略分析

1.1 工作原理

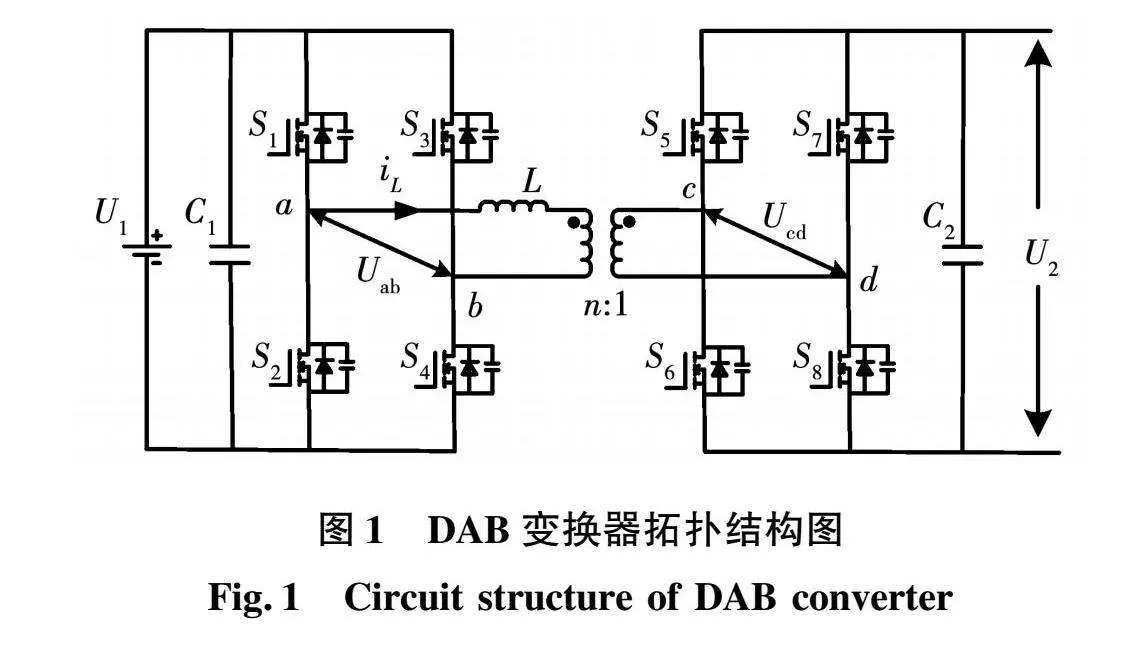
图1是DAB变换器的拓扑结构图，由2个全桥、1个高频变压器和一个等效电感L组成，等效电感L包含变压器漏感和外部辅助电感，主要用于传递能量；C1和C2为滤波电容；U1、U2分别表示DAB原副边电压，高频变压器原副边匝比为n∶1；Uab和Ucd分别表示原边侧和副边侧的H桥输出电压；iL为电感电流。

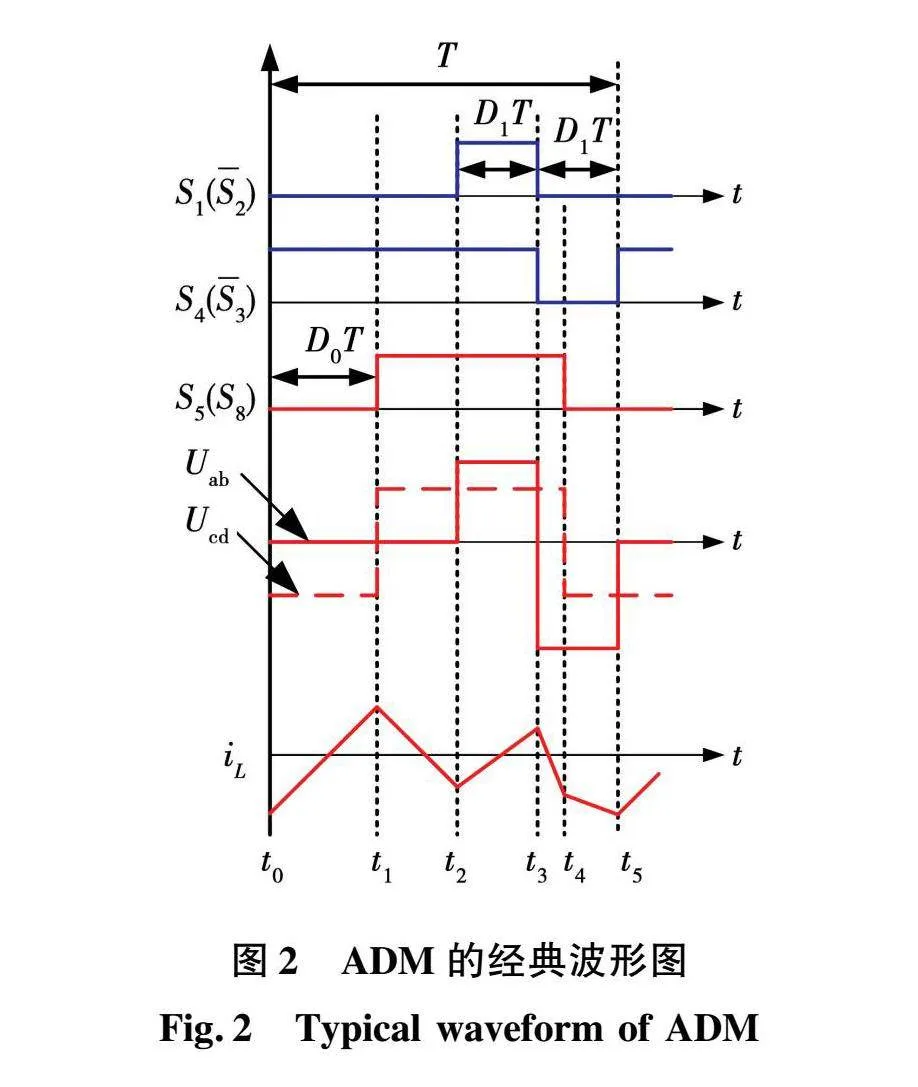
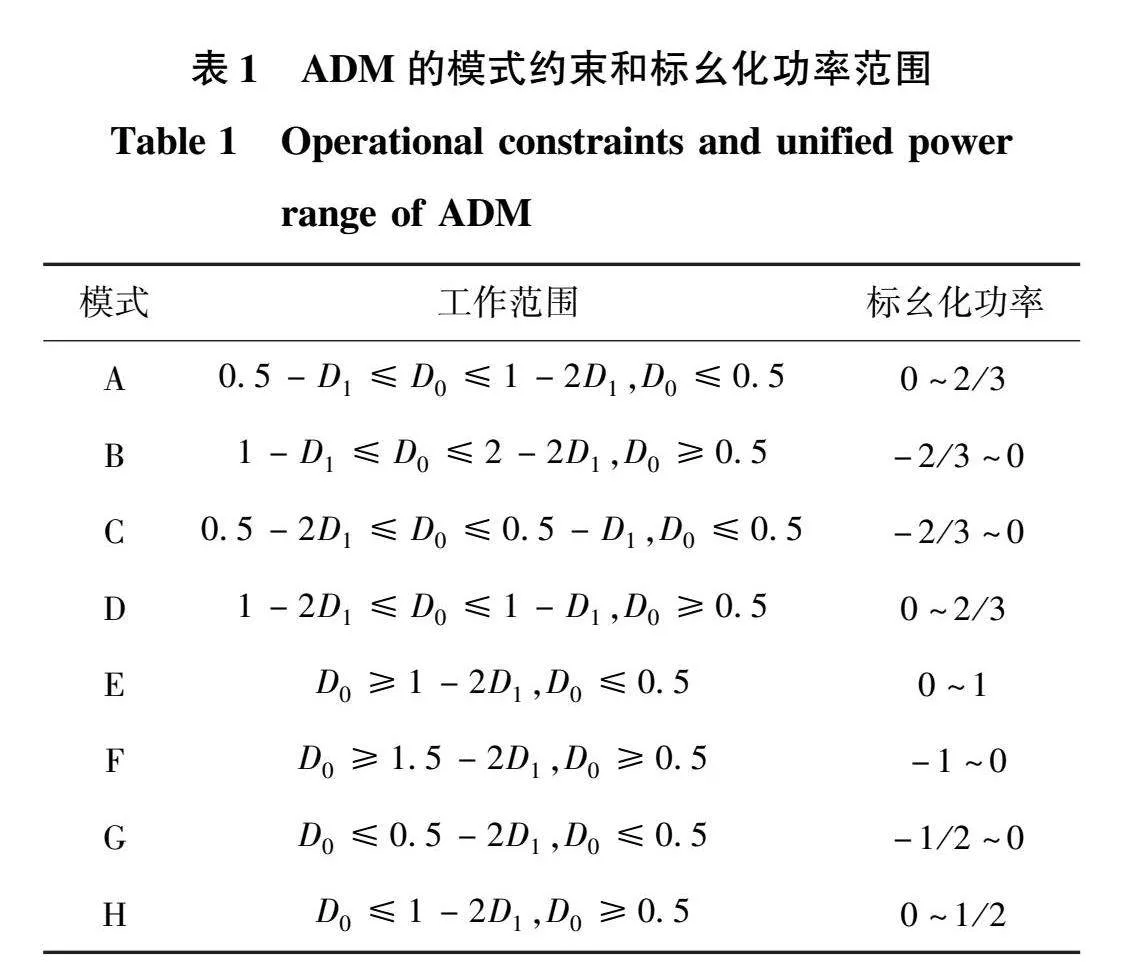
图2展示了ADM方式下DAB变换器的典型稳态工作波形，S1、S4、S5和S8与S2、S3、S6和S7的驱动波形互补，T为一个开关周期，D0∈［0，1］表示Uab和Ucd之间的移相比，D1∈［0，0.5］表示开关管S1和S3驱动信号的占空比，S1和S4驱动信号的下降沿在同一时刻，副边侧的占空比固定为50%。根据D0和D1的不同组合，可以将ADM方式分为8种不同的工作模式，不同模式之间的区域划分如表1所示。

1.2 传输功率

图2为模式A的典型稳态工作波形，由于Uab和Ucd的变化使得不同时间段内电感电流的变化趋势不一致，模式A可以进一步细分为5种模态：模态1为t0～t1 ，模态2为t1～t2，模态3为t2～t3，模态4为t3～t4，模态5为t4～t5，其中t0=0，t1=D0T，t2=（1-2D1）T，t3=（1-D1）T，t4=（0.5+D0）T，t5=T。各模态的电感电流时域方程为：

iL（t）=iL（t0）+nU2L（t－t0），t（t0～t1）；

iL（t）=iL（t1）－nU2L（t－t1），t（t1～t2）；

iL（t）=iL（t2）+U1－nU2L（t－t2），t（t2～t3）；

iL（t）=iL（t3）+－U1－nU2L（t－t3），t（t3～t4）；

iL（t）=iL（t4）+－U1+nU2L（t－t4），t（t4～t5）。（1）

根据开关周期内电流的安秒平衡原理，在稳态时电感电流在一个开关周期内的积分值为0，结合式（1）可以得到模式A在各时间节点的电感电流表达式为：

iL（t0）=iN（－4D21k－4D0+1）；

iL（t1）=iN（－4D21k+1）；

iL（t2）=iN（－4D21k+4D0+8D1－3）；

iL（t3）=iN［（－4D21+4D1）k+4D0+4D1－3］；

iL（t4）=iN［（－4D0－4D21+2）－1］；

iL（t5）=iL（t0）。（2）

式中：k=U1/（nU2）；iN=nU2/（4Lfs），fs表示开关频率。

t0时刻的电感电流瞬时值与t5时刻一致，除t1时刻的电感电流瞬时值仅与D1相关，其它时刻的电感电流瞬时值均与D0和D1两个控制量相关。

模式A的传输功率可以表示为

PA=1T∫T0U1iL（t）dt=PN（8D0－8D20+8D21－2）。（3）

式中PN=nU1U2/（8Lfs），则模式A的标幺化功率可以表示为

PU_A=PAPN=8D0－8D20+8D21－2。（4）

模式B～H的推导类似于模式A，表1给出了各模式标幺化功率传输范围，其中模式A、D、E和H属于正功率传输，模式B、C、F和G属于负功率传输，其中模式E的功率传输范围为[0，1]，模式A和模式D的功率传输范围一致均为[0，2/]，模式H的功率传输范围最小，其最大标幺化功率仅为0.5。本文将以正向功率传输的模式A、D、E和H对后续内容展开分析，负向功率传输的模式依此类推。

1.3 软开关分析

为了提升硬件拓扑的功率密度等级，DAB变换器的工作频率一般都在几十千赫兹及以上，功率开关器件的暂态损耗在总损耗中的占比很大，应尽可能让DAB变换器的各个开关管都工作在零电压开通（zero voltage switching，ZVS）状态，以此来减小开关器件的暂态损耗。为了简便分析，本文以开关管开通时刻的电感电流方向作为ZVS的判断依据。

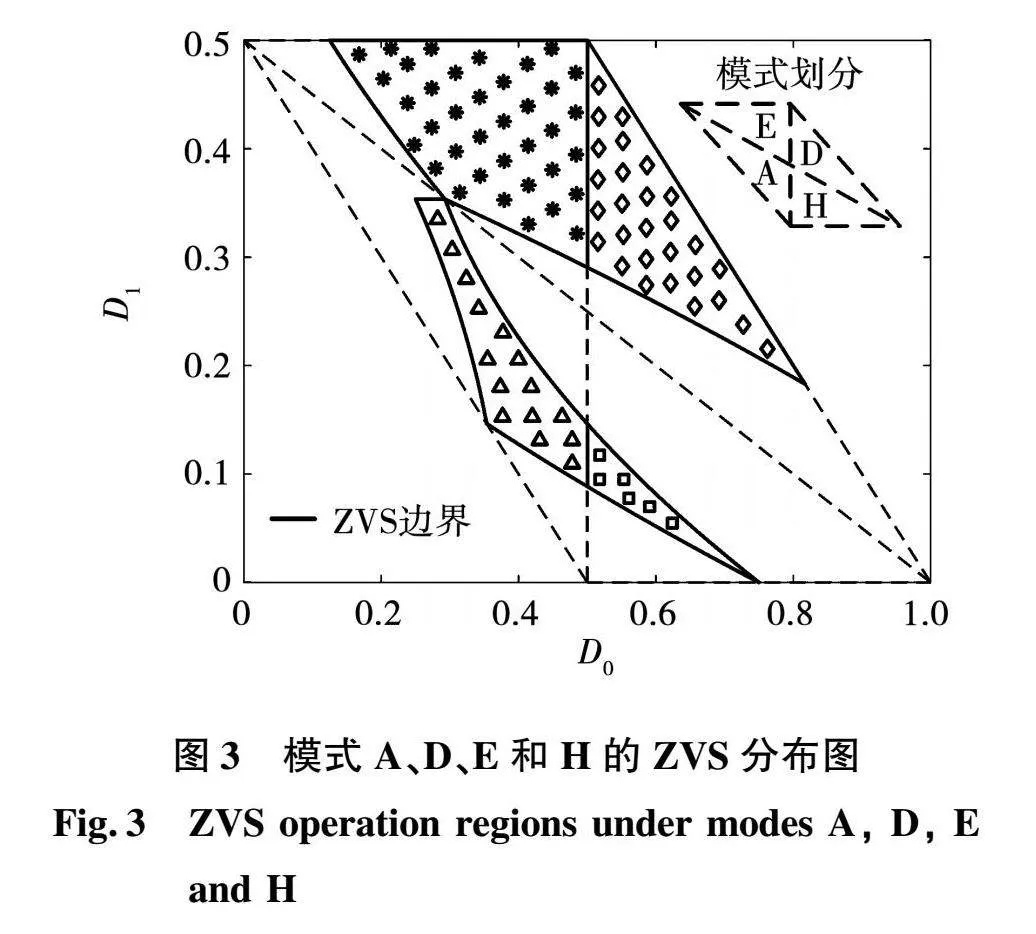
以模式A为例，开关管S1的驱动信号上升沿在t2时刻到来，此时流过电感的电流应小于0才能保证S1实现软开关。尽管S2的驱动信号与S1互补，但由于占空比不等于50%，电感电流波形不对称，必须满足t3时刻电感电流值大于0才能保证S2实现软开关。同理可以推导出模式A下其他开关管的ZVS条件，模式D、E和H的ZVS条件推导与模式A类似。如图3所示为模式A、D、E和H的操作边界以及ZVS边界，实线表示ZVS边界线，虚线表示模式边界线。

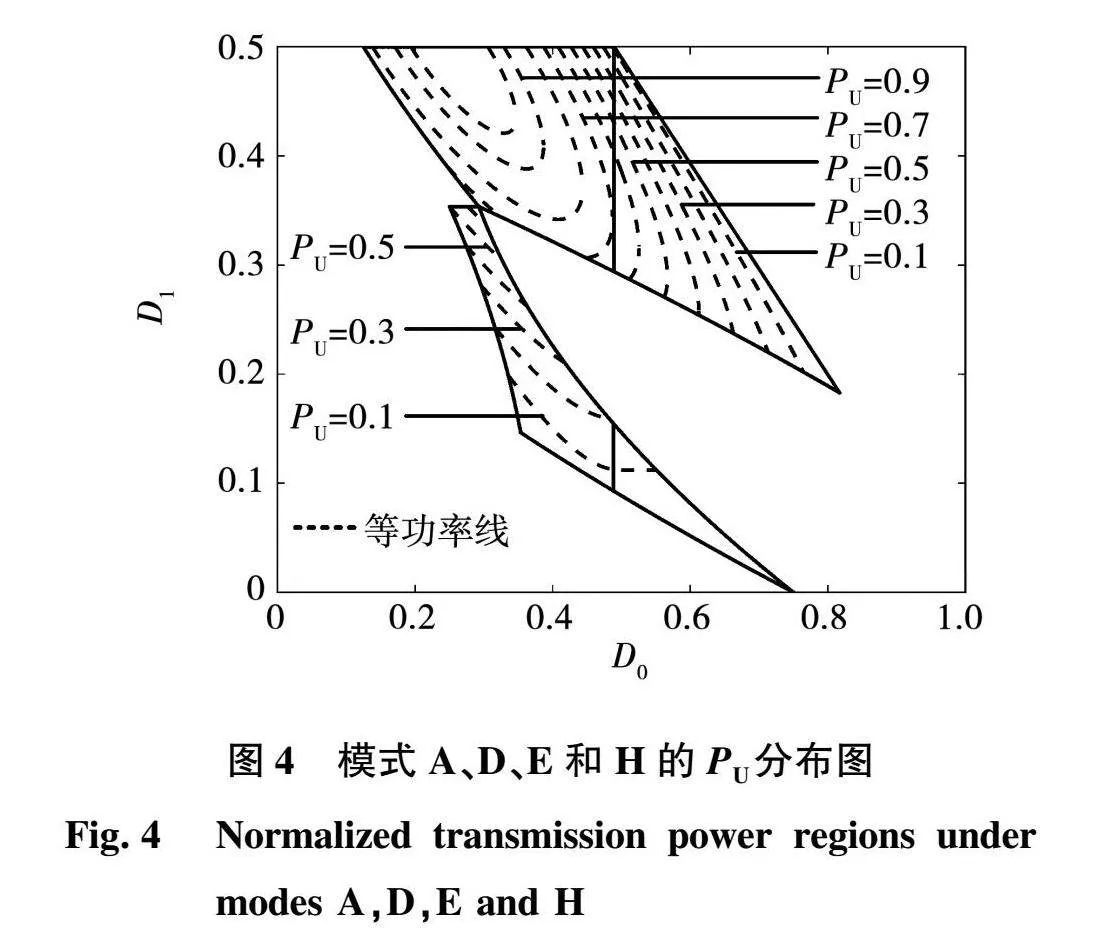
图4所示为模式A、D、E和H在ZVS区域内的标幺化功率PU分布图，实线表示各模式的ZVS边界线，虚线表示等标幺化功率线。结合表1和图4可知，模式A、E和D在ZVS条件限制下的标幺化功率传输范围没有缩小，模式H的标幺化传输功率上限由0.5降低至0.2以下。

2 开关器件损耗模型

本文以各开关管损耗方差最小为优化目标，因此将对ADM方式下的DAB变换器开关器件进行损耗建模，主要包括通态损耗和暂态损耗两部分，然后基于所建损耗模型分析ADM方式下DAB变换器原边侧全桥开关管的损耗峰值和损耗方差分布。考虑到可以通过合理设置死区时间来减小其对ZVS实现的影响^[26-27]，为了简化分析，本文在损耗建模过程中忽略了死区时间。

2.1 功率开关器件通态损耗

功率开关器件的导通电阻RDS（on）在不同工况下会随着栅源极电压VGS，漏源极电流ID以及节温Tj等因素的影响而发生变化^[22]，其函数表达式为

RDS（on）=f（Tj，VGS，ID）。（5）

功率开关器件的通态损耗计算模型Pcond为

Pcond=1T∫T0VDSIDdt=I2rmsRDS（on）。（6）

由于ADM方式的电感电流波形不对称，原边侧全桥4个功率开关管的导通时间和实际电流大小不一致，导致4个开关管的通态损耗不同，因此需要确定每个开关管开通的时间以及各开关管在一个开关周期内的电流有效值。以模式A为例，S1在t2～t3时间段内导通，S2在t0～t2和t3～t5时间段内导通，S3在t3～t5时间段内导通，S4在t0～t3时间段内导通，原边侧各开关管电流有效值为：

Irms_S1=1T∫^t3t2iL（t）2dt；

Irms_S2=1T［∫^t1t0iL（t）2dt+∫^t2t1iL（t）2dt+∫^t4t3iL（t）2dt+∫^t5t4iL（t）2dt］；

Irms_S3=1T［∫^t4t3iL（t）2dt+∫^t5t4iL（t）2dt］；

Irms_S4=1T［∫^t1t0iL（t）2dt+∫^t2t1iL（t）2dt+∫^t3t2iL（t）2dt］。（7）

原边侧各开关管一个周期内的通态损耗为

Pcond_Si=I2rms_SiRDS（on），i=1，2，3，4。（8）

式中Pcond_Si表示第Si个功率开关管的通态损耗。

由式（8）可知，电感电流有效值与功率开关器件的通态损耗成正相关，以电流有效值最小为优化目标的方案可以一定程度上降低功率开关器件的损耗，但功率开关器件的损耗不仅包含通态损耗，还有暂态损耗需要考虑。

2.2 功率开关器件暂态损耗

功率开关器件的暂态损耗主要由开通损耗和关断损耗两部分组成。功率开关管的暂态损耗与漏源极电压VDS，漏源极电流ID以及节温Tj等相关，其函数表达式为

Eon/off=f（Tj，VDS，ID）。（9）

式中：Eon表示开通损耗的能量；Eoff表示关断损耗的能量。

考虑到暂态损耗数值主要与开关动作时刻的功率成正比^[2]，因此功率开关管的开通和关断时刻所消耗的能量Eon和Eoff表示如下：

Eon=Um（a1I3on+a2I2on+a3Ion+a4）；

Eoff=Um（b1I3off+b2I2off+b3Ioff+b4）。（10）

式中：Um为开通或关断时刻开关管所承受的电压与参考电压的比值；Ion和Ioff分别为开关管开通和关断时刻的电流瞬时值。

为了减小暂态损耗，开关管通常工作在ZVS或零电流开通（zero current switching，ZCS）状态，在计算暂态损耗时仅需考虑功率器件的关断损耗。在kgt;1的情况下，当iL（t1）≥0、iL （t2）≤0、iL （t3）≥0、iL（t4）≤0时，模式A工作在软开关状态下，各开关管的暂态损耗为：

Etran_S1=Eoff_S1=Um（a1I33+a2I23+a3I3+a4）；

Etran_S2=Eoff_S2=Um（a1I32+a2I22+a3I2+a4）；

Etran_S3=Eoff_S3=Um（a1I30+a2I20+a3I0+a4）；

Etran_S4=Eoff_S4=Um（a1I33+a2I23+a3I3+a4）。（11）

式中：Etran_S1～Etran_S4表示S1～S4的暂态损耗；Ii表示ti时刻（i=0，1，2，3，4，5）的电流瞬时值的绝对值。

原边侧各开关管的总损耗Ploss_Si（i=1，2，3，4）可以表示为

Ploss_Si=Pcond_Si+Etran_Si/T。（12）

2.3 原边侧开关管损耗方差和损耗峰值

针对本文所涉及的ADM方式，其原边侧开关管的驱动信号占空比可变，一个周期内各开关管关断时刻的瞬态电流不一致，导致原边侧4个开关管损耗存在差异；而副边侧开关管的驱动信号占空比一直保持50%且没有发生内移相，副边侧全桥的两桥臂之间的对管具有相同的开关损耗，即开关管S5与S8损耗相同，S6和S7损耗相同，本文将针对损耗分布差异较大的原边侧各开关管进行展开分析。

2.3.1 原边侧开关管损耗峰值

原边侧开关管损耗峰值表示如下：

Ploss_max=max（Ploss_Si），i=1，2，3，4。（13）

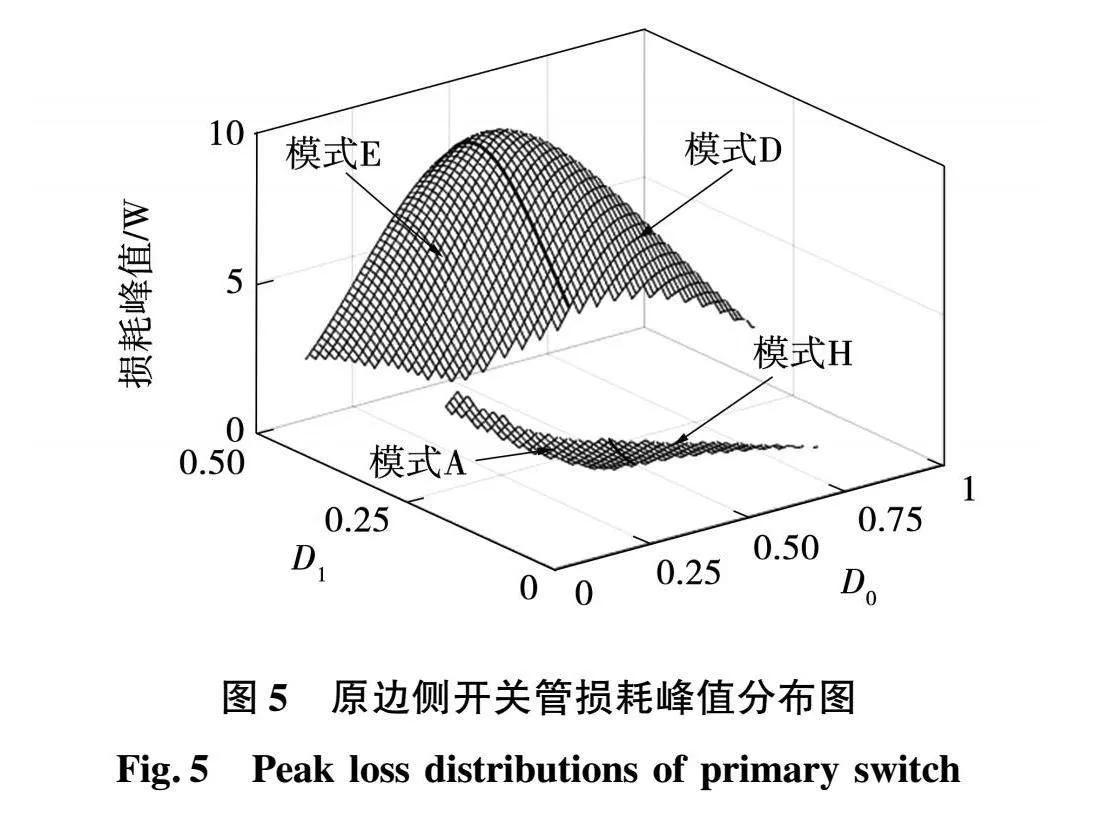
图5给出了模式A、D、E和H在ZVS条件下原边侧开关管损耗峰值分布三维图，图中黑色实线表示模式边界线。

结合图4和图5可知，在模式A传输功率范围内，模式A和H原边侧开关管损耗峰值较低，但模式H在ZVS条件约束下功率传输范围变窄；模式A和模式E的边界即模式A的传输功率上限，在模式A软开关条件下的传输功率范围内，其原边侧开关管损耗峰值要低于模式E，超出模式A的传输功率上限时，可以直接过渡到模式E。

2.3.2 原边侧开关管损耗方差

原边侧开关管方差表示为

Ploss_ss=14∑4i=1（Ploss_Si－Ploss_ave）2。（14）

式中Ploss_ave表示原边侧开关管的损耗平均值。

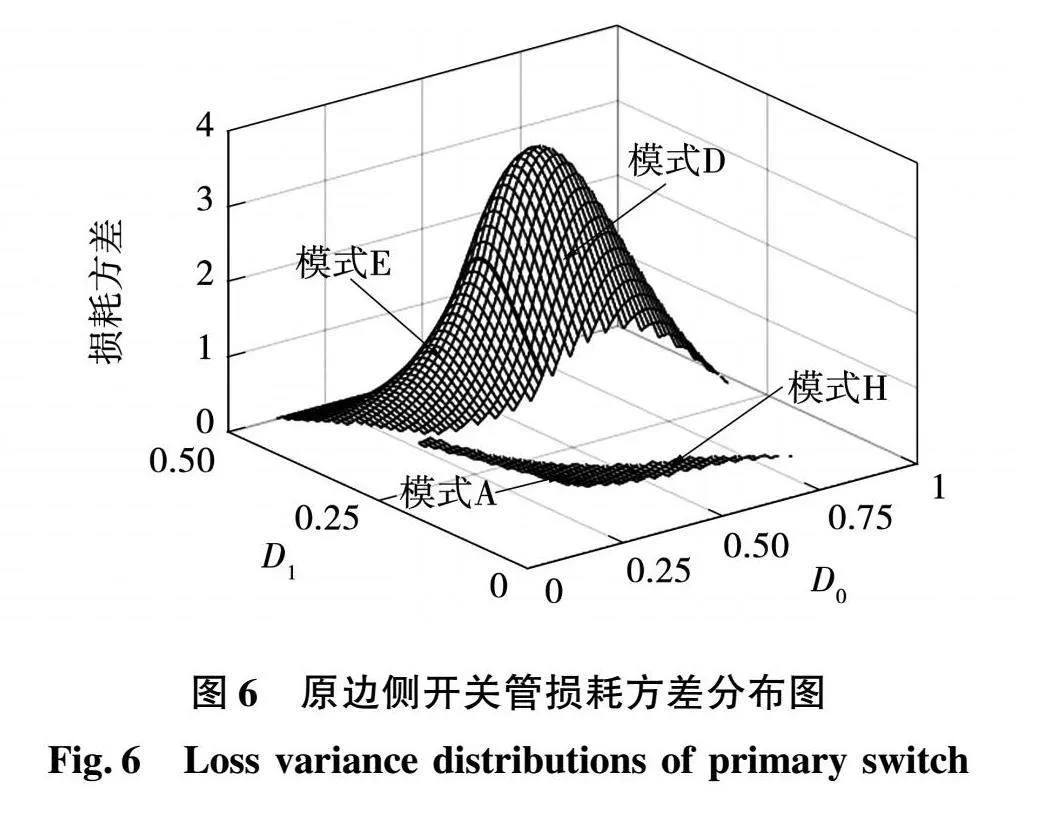
图6给出了模式A、D、E和H在ZVS条件下原边侧开关管损耗方差分布三维图，图中黑色实线表示模式边界。与损耗峰值的分析过程类似，结合图4和图6可知，选择模式A和E可以保证全功率范围内各开关管损耗方差最小。

传统ADM方案具有2个调制自由度D0和D1，D0和D1的定义和约束与本文一致，传统ADM方案基于最小电感电流有效值离散拟合的结果，选择ZVS的边界条件来确定D0和D1。以模式A为例，传统ADM方案的部分优化解为：

D0=－D21－1/（4k）+1/2；

D1=［2k+2k（2k－PU_Ak－2）－1］/2k。（15）

D0=1/2－2［－（PU_Ak－2）/k］/4；D1=1/4k。（16）

式（15）和式（16）对应的标幺化功率范围分别为（0，（2k-2）/k²）和（（2k-2）/k²，8/k^1/2-6/k-2）。

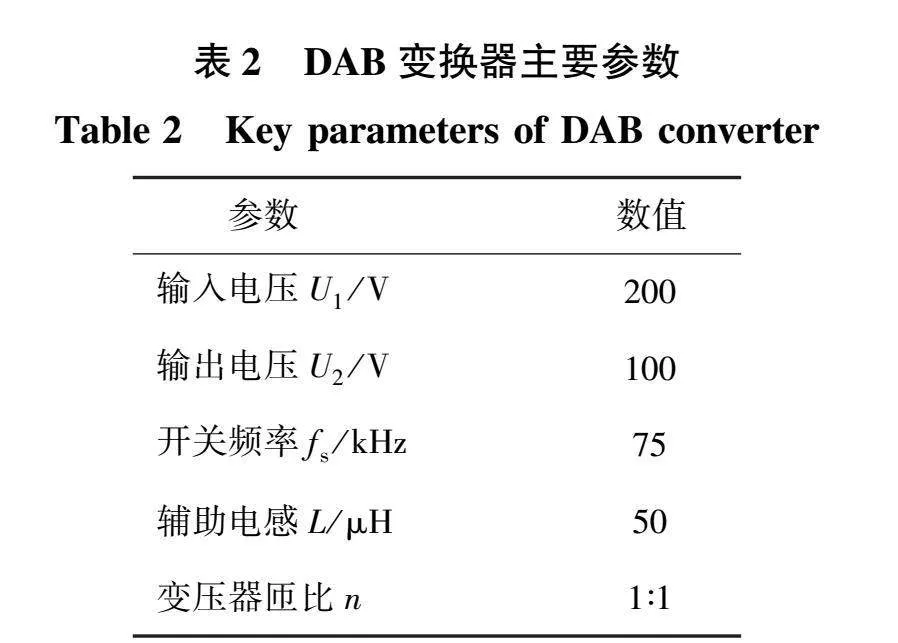
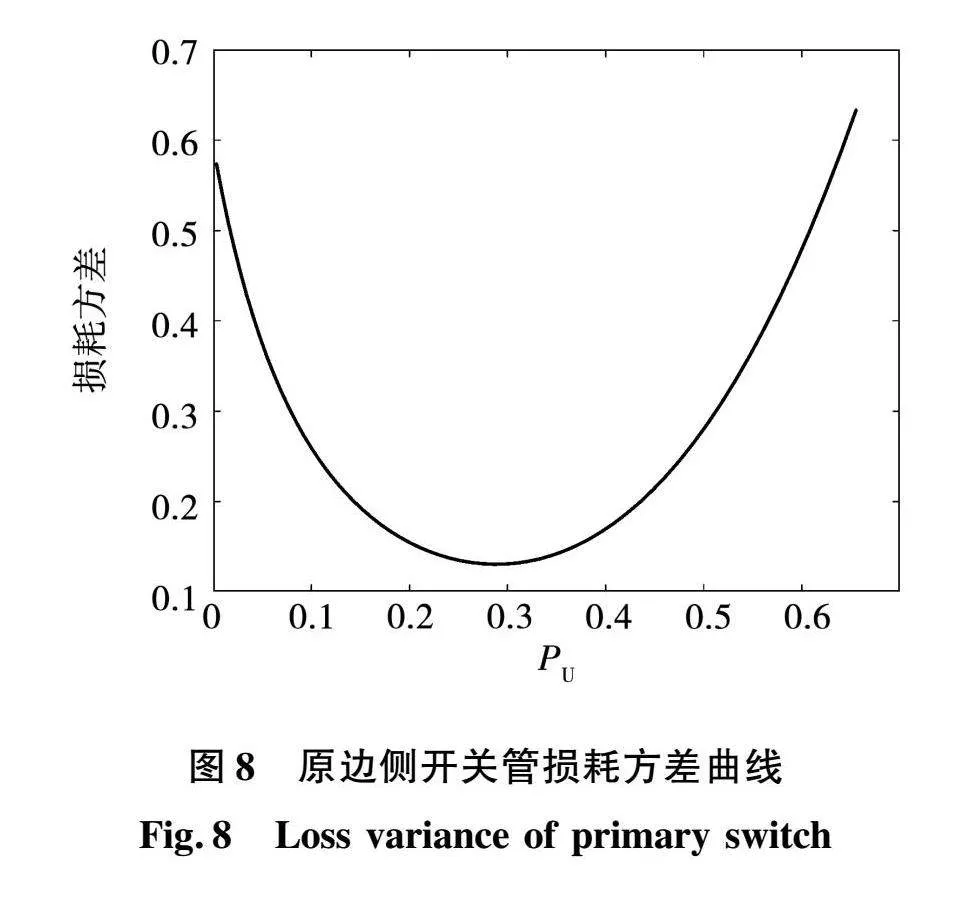
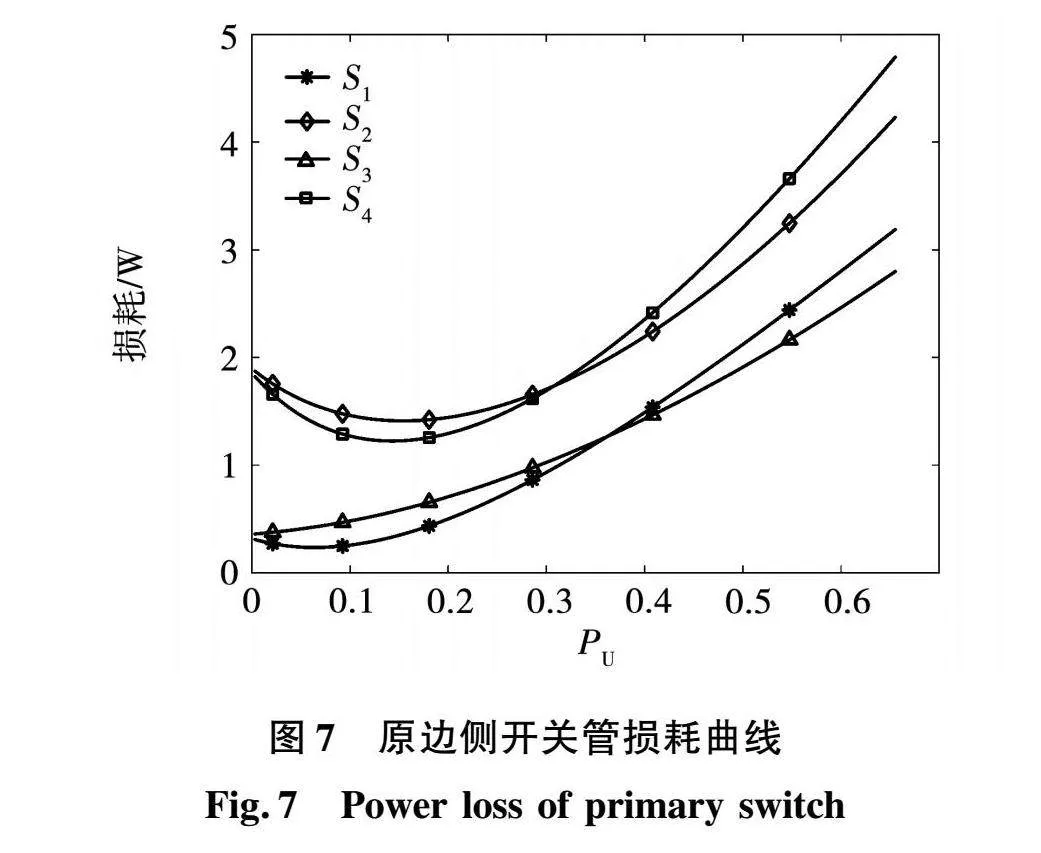
根据传统ADM方案的优化解，结合表2中DAB变换器的主要电路参数以及式（12）和式（14），在模式A下计算了开关管S1～S4的损耗并绘制了其随标幺化功率的变化曲线以及损耗方差曲线，分别如图7和图8所示。

由图8可知，原边侧各开关管的损耗差异呈现出中间低两边高的趋势，损耗差异较大可能会导致某个开关管热应力过高，使该开关管性能下降，从而影响系统的整体可靠性，因此有必要寻找一种均衡各开关管损耗分布的优化方案，以此来提高系统整体的可靠性。

3 损耗方差最小优化方案

在ADM方式DAB变换器的功率开关管器件损耗模型基础上，选择各开关管损耗方差作为优化目标，以给定的传输功率、控制量边界等作为约束条件，进一步提高系统可靠性。

优化目标：Ploss_ss（D0，D1）最小。

约束条件：P（D0，D1）－P*=0；0≤D0≤0.5，0≤D1≤0.5；0.5－D1≤D0≤1－2D1；ZVS条件。（17）

在式（17）中等式约束是功率约束，在给定的传输功率P^*下求解目标函数的最优解。不等式约束包括控制变量的边界条件以及模式划分的边界条件。由于目标函数涉及器件损耗模型，无法得到解析解，将采用粒子群优化（particle swarm optimization，PSO）算法进行优化求解。

3.1 基于PSO算法的损耗方差最小优化方案

PSO算法的核心思想是将群体中的个体视作粒子，根据制定的规则让粒子群在空间中进行动态调整，不断迭代更新粒子和粒子群的历史最优位置，从而获得解决问题的可行解方案^[24-25]。PSO算法的迭代更新公式如下：

V^m+1id=［ωVmid+c1r1（Xmid_best－Xmid）+c2r2（Xmgd_best－Xmid）］;

X^m+1id=Xmid+Vmid。（18）

式中：Vid表示第i个粒子的第d维速度；Xid表示第i个粒子的第d维位置；m是迭代指数；ω是值为非负的惯性因子，通常在0.5到1之间，其值越大越适合全局寻优，其值越小越适合局部寻优；c1和c2分别表示个体学习因子和群体学习因子，通常取0到4之间，他们分别反映了粒子接近个体历史最优位置和群体历史最优位置的趋势；r1和r2是0到1之间的随机数。

本文基于PSO数值求解方法提出一种以各开关管损耗方差最小为优化目标的ADM调制策略，通过降低各开关管损耗分布差异，提高系统的整体可靠性。首先初始化粒子群参数（粒子数量、迭代次数、粒子群初始位置和速度等），然后根据约束条件规定粒子的运动空间，以损耗方差作为适应度函数，计算每个粒子的适应度，更新个体和群体历史最优适应度和位置，而后根据式（18）更新所有粒子的位置和速度，直至达到结束条件。

3.2 基于PSO算法的损耗方差最小方案实例

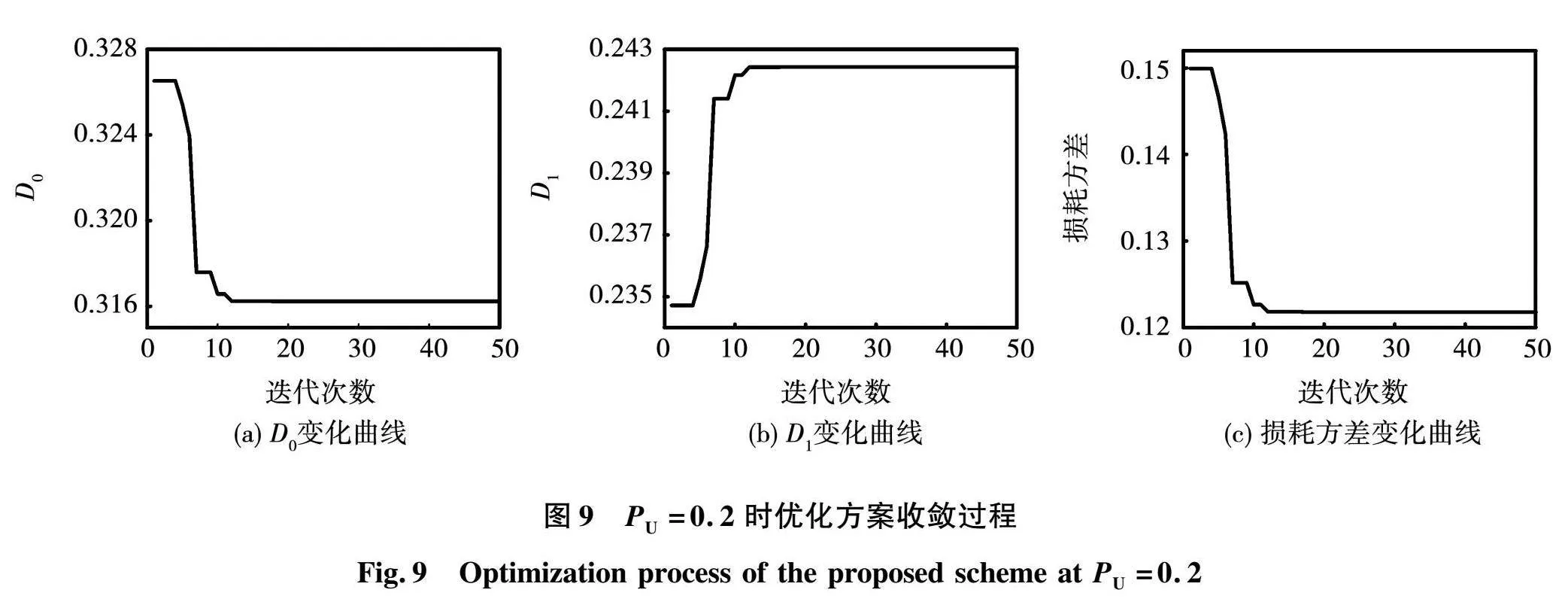
选用型号为SCT2080KE的SiC开关管，结合表2中的DAB变换器参数，以标幺化功率PU=0.2为例绘制了基于PSO算法的损耗方差最小方案的寻优过程曲线，如图9所示。图9（a）和图9（b）分别表示控制变量D0和D1随迭代次数增加的变化曲线，图9（c）表示各开关管损耗方差的收敛过程。

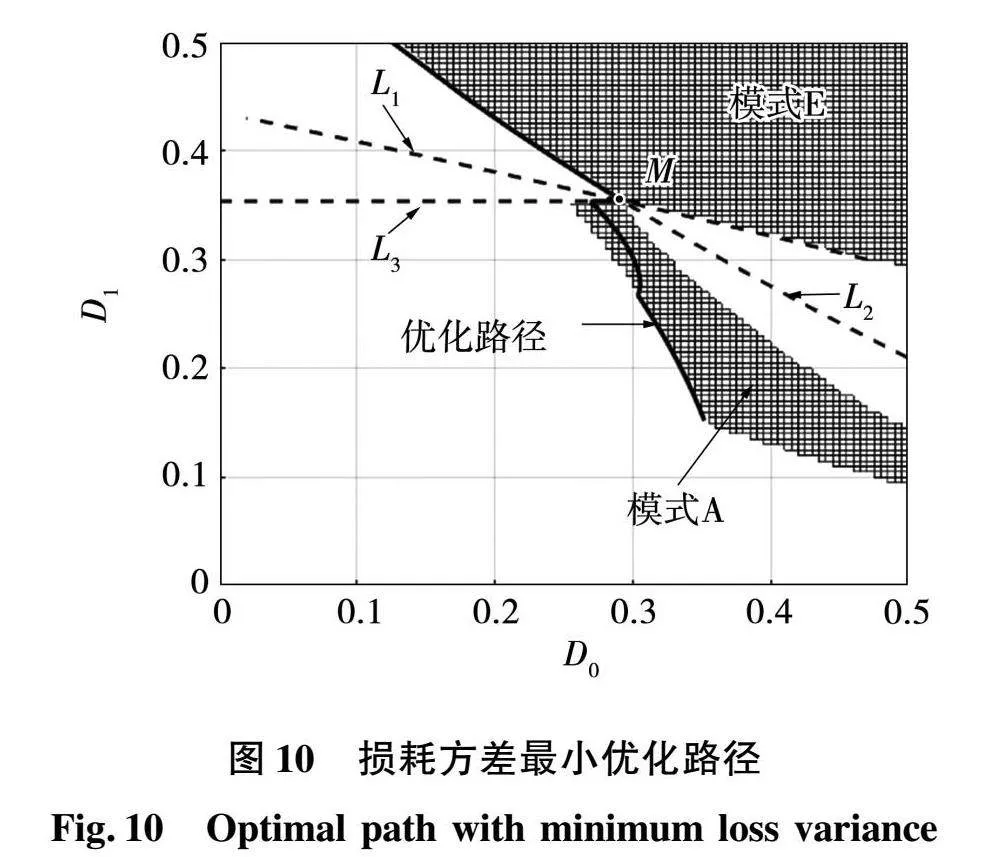
对不同标幺化功率点进行优化求解，得到在ZVS条件下全功率范围内各开关管损耗方差最小的优化路径，如图10所示。L1和L2为模式E的ZVS边界，L3为模式A的ZVS边界，L1、L2和L3的表达式为：

L1∶D0=D21－2D1+1－14k；

L2∶D0=－D21k－2D1+54；

L3∶D1=14k。（19）

L1、L2和L3的交点即为模式A与模式E的交接点M。大于M点功率时变换器工作在模式E，小于M点功率时变换器工作在模式A的工作范围，当标幺化功率接近1时，控制变量D1恒等于0.5，此时模式E等效为SPS调制方式，原边侧各开关管的损耗相等，损耗方差为0。

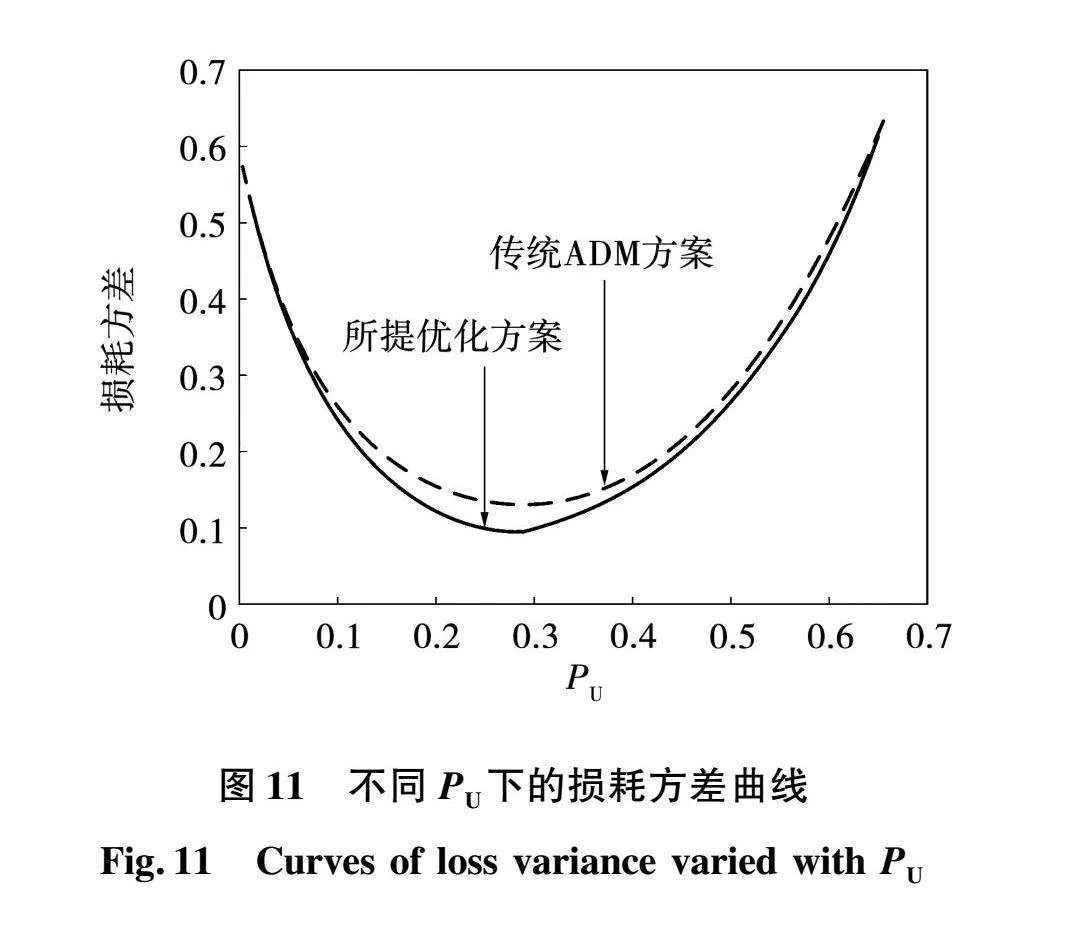
以模式A为例，将传统ADM方式下原边侧各开关管损耗方差和损耗峰值与本文所提优化方案进行对比，结果分别如图11和图12所示。

图11所示为2种方案的损耗方差随标幺化功率PU的变化曲线，实线和虚线分别表示本文所提优化方案和传统ADM方案的损耗方差。由图11可知，本文所提优化方案的损耗方差与传统ADM方案相比有所降低，PU=0.1～0.4时效果比较明显。

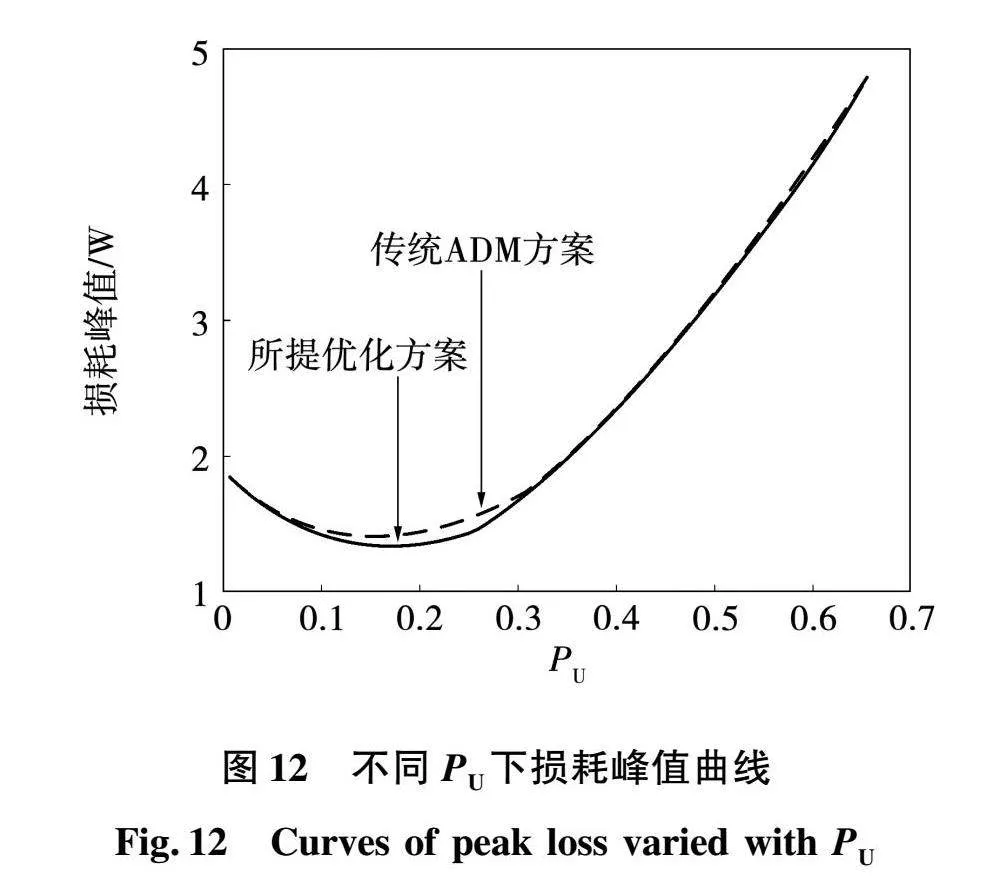
图12所示为2种方案的损耗峰值随标幺化功率的变化曲线，实线和虚线分别表示本文所提方案和传统ADM方案的损耗峰值。由图12可知，在轻载（PU=0.1～0.3）时本文所提优化方案的损耗峰值与传统ADM方案相比有明显降低。结合图11和图12分析可知，在轻载时本文所提优化方案有效降低了各开关管的损耗方差，同时降低了开关管损耗峰值，减小了各开关管损耗分布差异，提高了系统的整体可靠性；此外，随着PU的增大，2种方案下的各开关管损耗峰值和方差趋于相等。

3.3 闭环控制方案

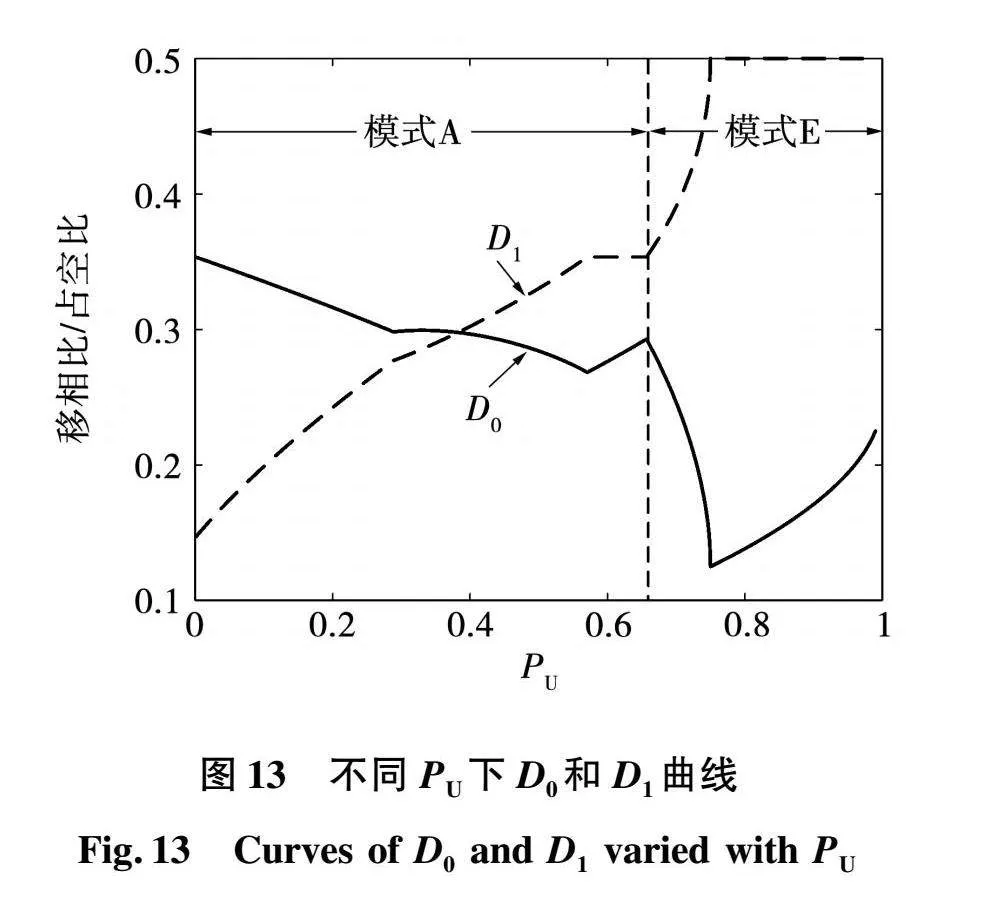
将图10所示的优化路径转化为单个变量随标幺化功率PU变化的曲线图，如图13所示，其中，实线和虚线分别表示移相比D0和占空比D1，根据图13可绘制PSO离线数据表。为了提高离线表的精度，根据厂商提供的开关管模型，基于LTspice仿真平台进行双脉冲测试获取不同工况下开关管的通态损耗和暂态损耗数据，并对每个工况都进行多次测试并取平均值。

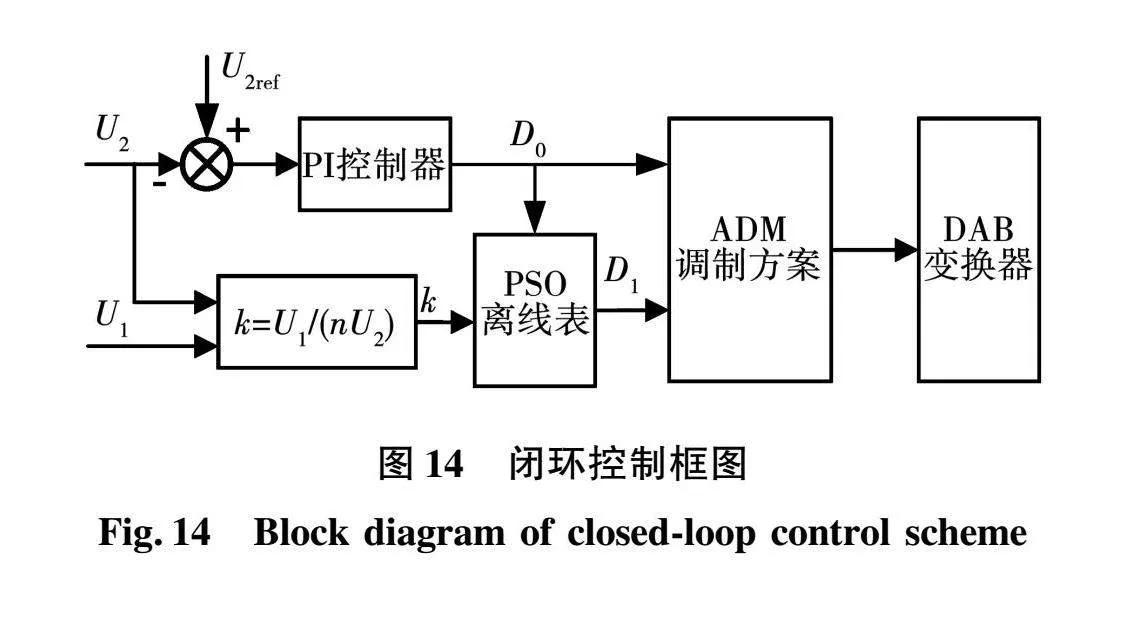
图14表示本文所提优化方案的闭环控制框图，其中控制变量D0是实际输出电压和参考电压的误差通过PI变换器得到的，D1则是由输入输出电压先计算出电压调节比k，然后查表获得。在模式A和模式E下D1都存在一段恒定值，因此不适合用作闭环参数，D0在2种模式下并不是完全单调递增或单调递减，但可以根据D1的阈值和模式边界调整PI变换器的控制参数，从而实现分段闭环控制。

4 实验验证

为验证本文所提的损耗方差最小优化方案，搭建了如图15所示的硬件实验平台，主要电路参数如表2所示。

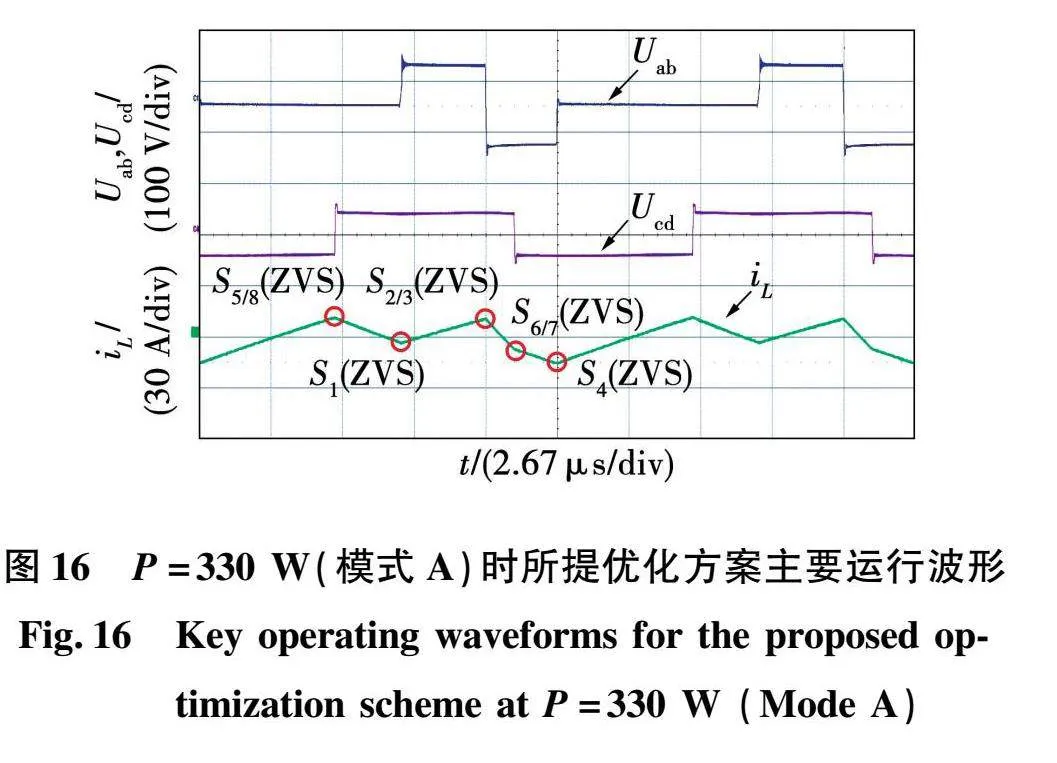
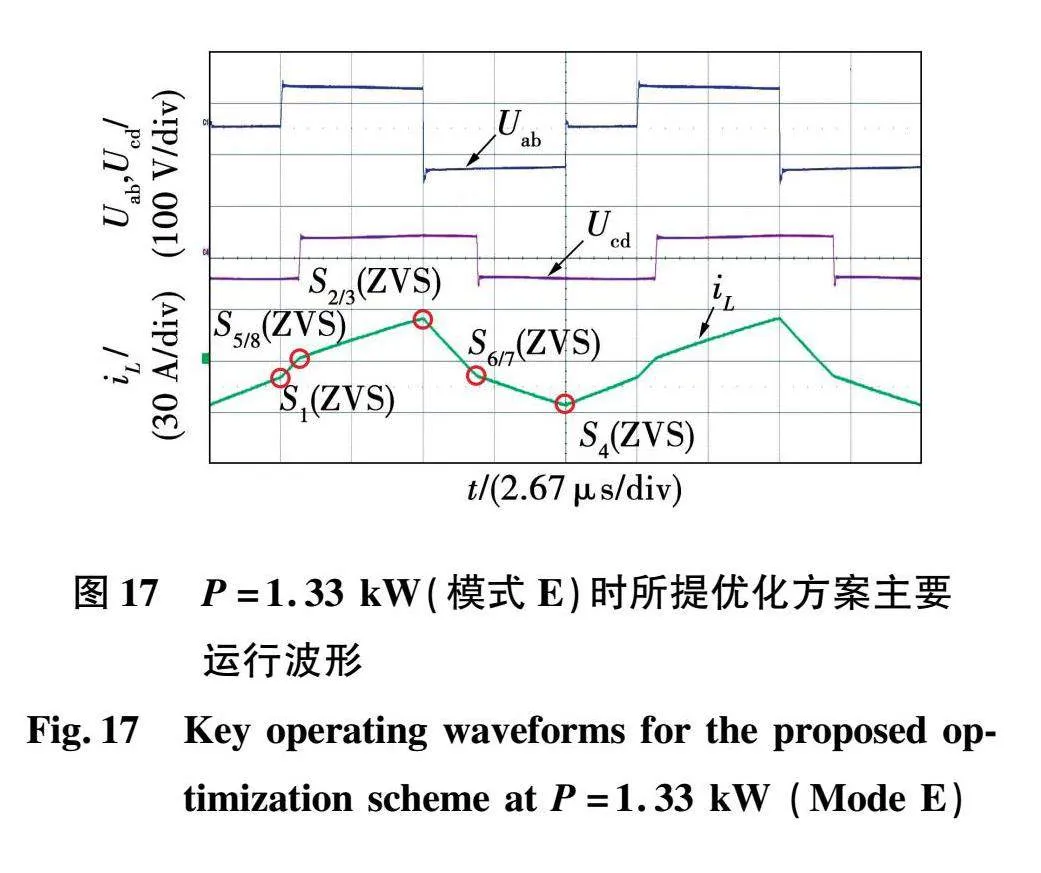
图16和图17分别表示DAB变换器在模式A和模式E状态下的主要运行波形，图16中输出功率P=330 W，变换器工作在模式A，图17中输出功率P=1.33 kW，变换器工作在模式E。

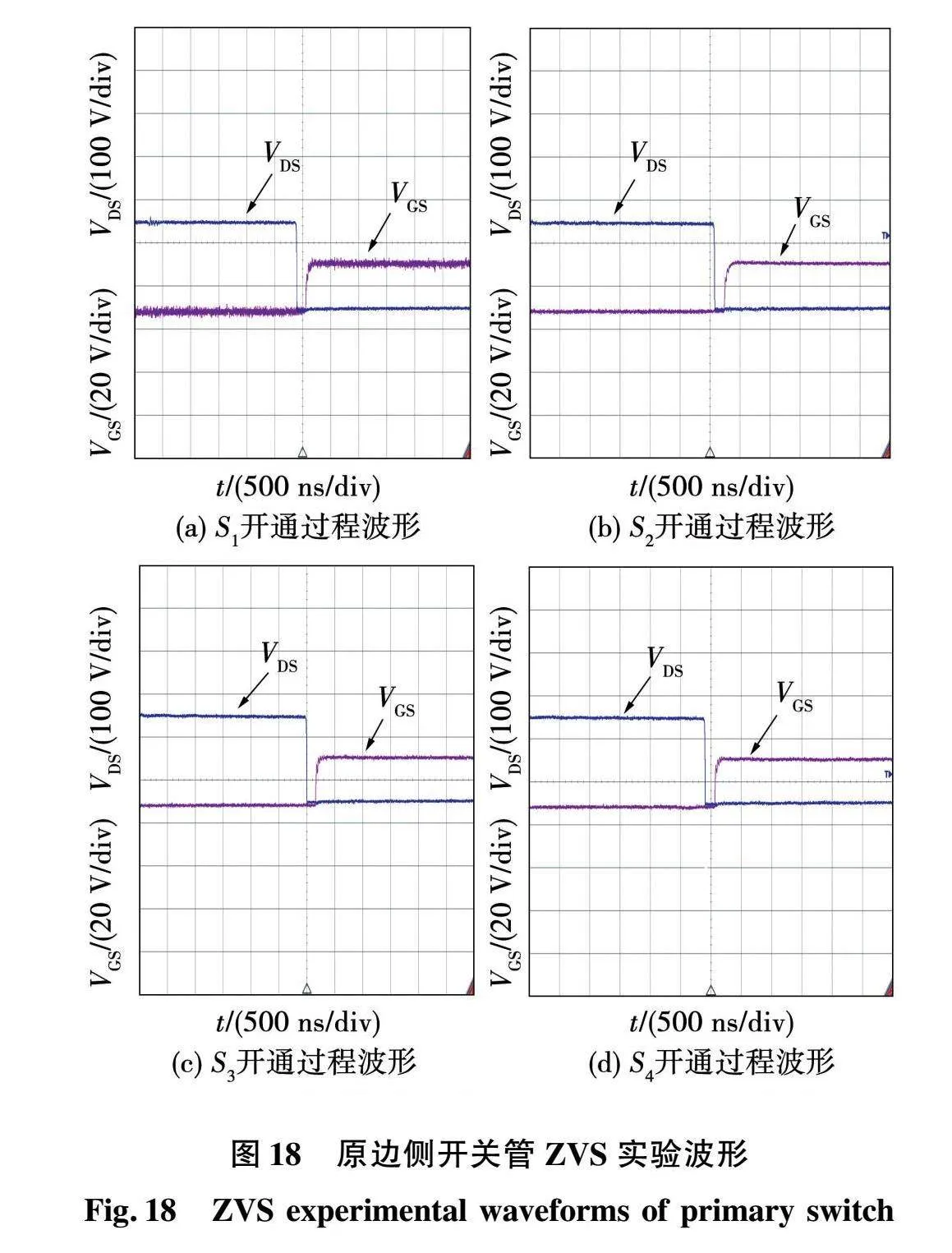
图18表示输出功率P=330 W时DAB变换器原边侧开关管的开关动作，VDS表示漏源极电压，VGS表示驱动信号。开关管S1～S4的VDS在VGS到来之前下降到0，均可以实现ZVS。

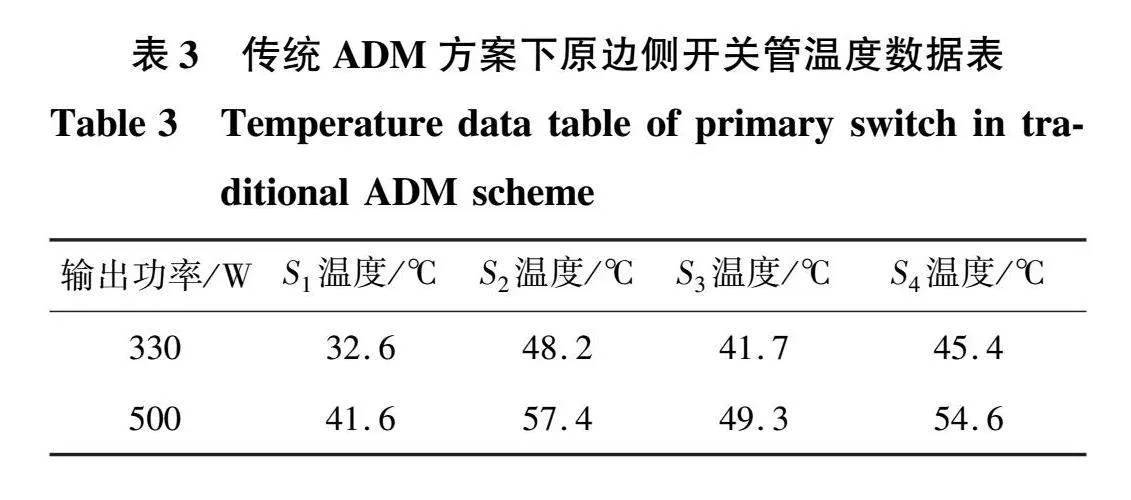
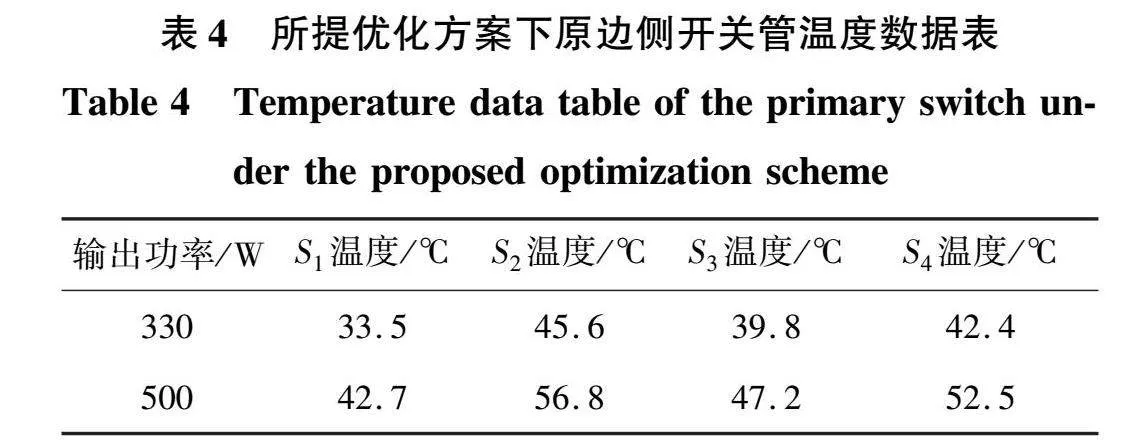
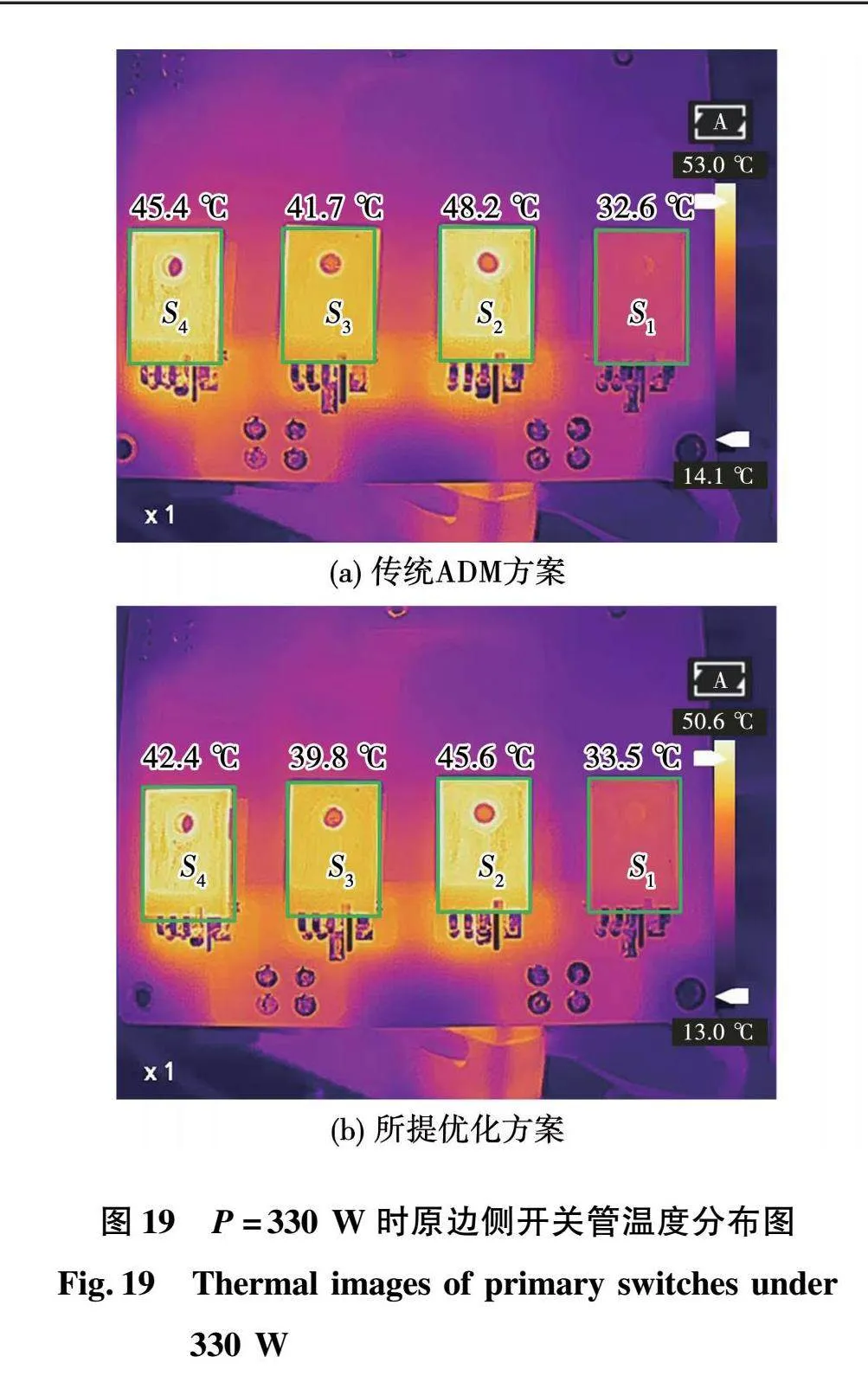
由于开关器件的损耗很难通过直接测量进行定量分析，通常采用开关器件的温度作为器件损耗的评估指标。在稳态工作情况下，通过测量开关器件达到热平衡后的器件温度分布代替开关器件的损耗分布，以温度间接代替损耗进行方案验证。本文采用艾睿公司生产的天璇M300F手持热像仪测量功率开关器件的运行温度，传统ADM方案与本文所提损耗方差最小优化方案在输出功率P=330 W和P=500 W工况下稳态运行30分钟后的温度分布分别如图19和图20所示，在2种方案下各开关管的温度分别如表3和表4所示。

传统ADM方案在P=330 W和P=500 W时的温度峰值分别为48.2 ℃和57.4 ℃，温度方差分别为34.6和36.2。本文所提损耗方差最小优化方案在P=330 W和P=500 W时的温度峰值分别为45.6 ℃和56.8 ℃，温度方差分别为19.7和28.4，与传统ADM方案相比器件温度峰值和温度方差均有所下降，验证了本文所提优化方案的有效性和可行性。

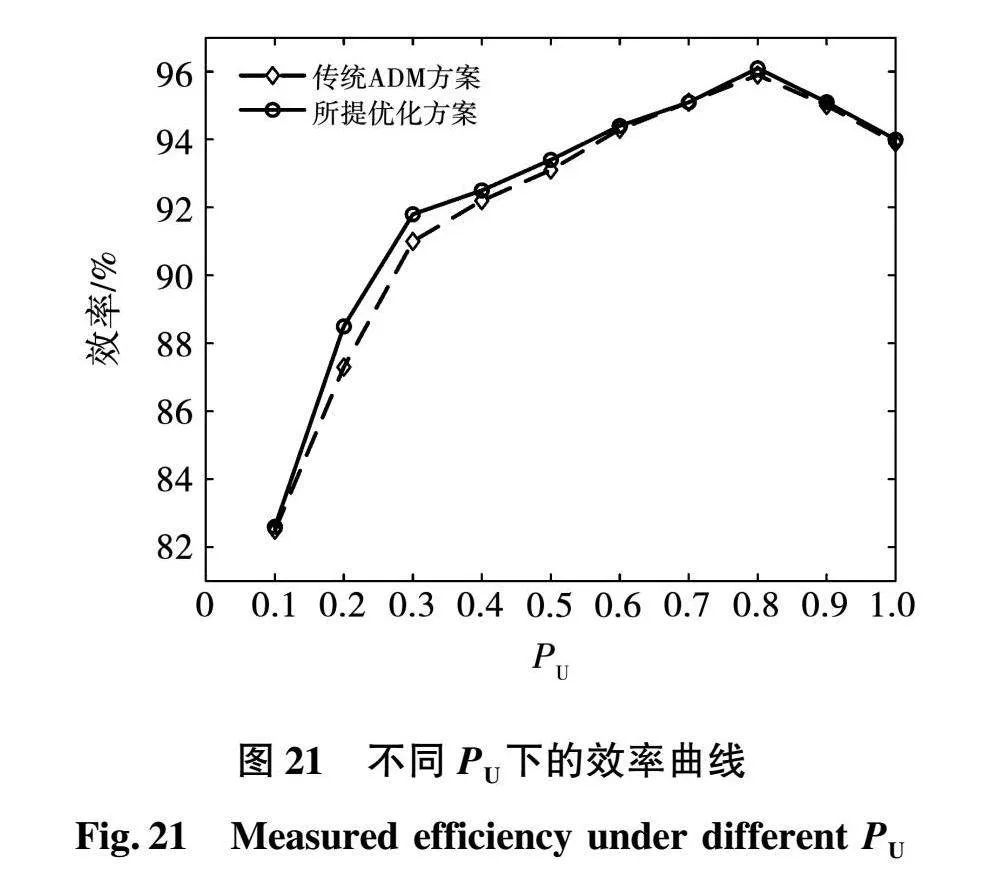
图21是传统ADM方案和本文所提损耗方差最小优化方案随标幺化功率变化的效率测试曲线，由图21可知，在轻载时本文所提损耗方差最小方案的效率比传统ADM方案高，在330 W和500 W的轻载工况下，所提优化方案的系统效率分别提高了1.2%和0.5%；在中高功率段时，由于D1趋于0.5，此时的ADM方式类似于SPS方式，DAB变换器原边侧H桥中4个开关管损耗几乎一致，损耗方差趋于0，因此在中高功率段时2种方案效率基本相同。

5 结 论

针对DAB变换器在ADM调制策略下各开关管损耗分布差异大导致系统的整体可靠性下降的问题，提出一种以各开关管损耗方差最小为优化目标的ADM调制策略。在相同工况下，通过仿真和实验对比了传统ADM方案和所提损耗方差最小优化方案，仿真分析结果与实验结果基本一致。所提优化方案不仅降低了ADM方式下DAB变换器中各开关管的损耗方差，在轻载时还有效降低了损耗峰值，减小了ADM方式下各开关管的损耗分布差异和损耗峰值。在330 W和500 W的轻载工况下，所提损耗方差最小优化方案的各开关管温度方差分别降低了43%和21.5%，温度峰值分别降低2.8 ℃和0.6 ℃，系统效率分别提高了1.2%和0.5%，提高了系统的可靠性和效率。

参 考 文 献：

［1］ ZHAO Biao， SONG Qiang， LIU Wenhua， et al， Next-generation multi-functional modular intelligent UPS system for smart grid[J]. IEEE Transactions on Industrial Electronics，2013， 9（60）：3602.

［2］ XUE Liangxiao， SHEN Zhiyu， BOROYEVICH D， et al， Dual active bridge-based battery charger for plug-in hybrid electric vehicle with charging current containing low frequency ripple[J]. IEEE Transactions on Power Electronics，2015， 12（30）：7299.

［3］ KARTHIKEYAN V， GUPTA R. Multiple-input configuration of isolated bidirectional DC-DC converter for power flow control in combinational battery storage[J]. IEEE Transactions on Industrial Informatics， 2018， 1（14）：2.

［4］ GORLA N B Y， KOLLURI S， CHAI M， et al. A comprehensive harmonic analysis and control strategy for improved input power quality in a cascaded modular solid state transformer[J]. IEEE Transactions on Power Electronics，2019， 7（34）： 6219.

［5］ DONCKER R W D， DIVAN D M， KHERALUWALA M H， et al. A three-phase soft-switched high-power-density DC/DC converter for high-power applications[J]. IEEE Transactions on Industry Applications，1991，27（1）： 63.

［6］ ZHAO Biao， YU Qingguang， SUN Weixin， et al. Extended-phase-shift control of isolated bidirectional DC-DC converter for power distribution in microgrid[J]. IEEE Transactions on Power Electronics， 2012， 27（11）： 4667.

［7］ LIU Xu. Novel dual-phase-shift control with bidirectional inner phase shifts for a dual-active-bridge converter having low surge current and stable power control[J]. IEEE Transactions on Power Electronics， 2017， 32（5）： 4095.

［8］ HUANG Jun， WANG Yue， LI Zhuoqiang， et al. Unified triple-phase-shift control to minimize current stress and achieve full soft-switching of isolated bidirectional DC-DC converter[J]. IEEE Transactions on Industrial Electronics， 2016， 63（7）： 4169.

［9］ HOU Nie， SONG Wensheng， WU Mingyi， et al. Minimum-current-stress scheme of dual active bridge DC-DC converter with unified phase-shift control[J]. IEEE Transactions on Power Electronics， 2016， 31（12）： 8552.

［10］ SHI Haochen， WEN Huiqing， CHEN Jie， et al. Minimum-reactive-power scheme of dual-active-bridge DC-DC converter with three-level modulated phase-shift control[J]. IEEE Transactions on Industry Applications， 2017， 53（6）： 5573.

［11］ TONG Anping， HANG Lijun， LI Guojie， et al. Modeling and analysis of a dual-active-bridge-isolated bidirectional DC/DC converter to minimize RMS current with whole operating range[J]. IEEE Transactions on Power Electronics，2018，33（6）：5302.

［12］ HU Song， LI Xiaodong， BHAT A K S， et al. Operation of a bidirectional series-resonant converter with minimized tank current and wide ZVS range[J]. IEEE Transactions on Power Electronics，2018，34（1）：904.

［13］ MOU Di. Optimal asymmetric duty modulation to minimize inductor peak-to-peak current for dual active bridge DC-DC converter[J].IEEE Transactions on Power Electronics，2021，36（4）：4572.

［14］ CHEN Gen， CHEN Zhangyong， CHEN Yong， et al. Asymmetric phase-shift modulation strategy of DAB converters for improved light-load efficiency[J]. IEEE Transactions on Power Electronics，2022，37（8）：9104.

［15］ WANG Mixin， WEI Shusheng， MOU Di， et al. Research on efficient single-sided asymmetric modulation strategy for dual active bridge converters in wide voltage range[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics，2022，10（5）：5738.

［16］ CUI Xinyu， ZHENG Zhi， TIAN Jiachen， et al. A novel asymmetric duty modulation control of dual-active-bridge for LVDC applications[C]//IEEE/IAS Industrial and Commercial Power System Asia，July 18-21，2021，Chengdu，China.2021：110-117.

［17］ YANG Shaoyong， BRYANT A， MAWBY P， et al. An industry-based survey of reliability in power electronic converters[J]. IEEE Transactions on Industry Applications，2011，47（3）：1441.

［18］ 雷万钧，刘进军，吕高泰，等.大容量电力电子装备关键器件及系统可靠性综合分析与评估方法综述[J].高电压技术，2020，46（10）：3353.

LEI Wanjun， LIU Jinjun， L Gaotai， et al. Review of reliability comprehensive analysis and evaluation methods for key components and system of large capacity power electronic equipment[J]. High Voltage Engineering，2020，46（10）：3353.

［19］ 谷庆，袁立强，赵争鸣，等.基于三重移相控制的双有源桥DC-DC变换器性能综合优化[J].清华大学学报（自然科学版），2019，59（10）：785.

GU Qing， YUAN Liqiang， ZHAO Zhengming， et al. Performance comprehensive optimization of dual active bridge DC-DC converter based on triple phase shift control[J]. Journal of Tsinghua University（Science and Technology），2019，59（10）：785.

［20］ 陈晓楠，王明才，李驰，等.基于综合损耗最优的双有源桥式变换器调制方法[J].电气工程学报，2022，17（2）：49.

CHEN Xiaonan， WANG Mingcai， LI Chi， et al. Optimum total losses orientated modulation strategy for dual active bridge[J]. Journal of Electrical Engineering，2022，17（2）：49.

［21］ GOU Yating， XIA Binbing， ZHUO Fang， et al. Thermal stress distribution analysis of SiC power modules in DAB converter within the whole operating range[C]//IEEE International Power Electronics and Application Conference and Exposition （PEAC）， December 16-19， 2022， Guangdong， China. 2022：594-598.

［22］ GLITZE S， ORDONEZ M. MOSFET power loss estimation in LLC resonant converters： time interval analysis[J]. IEEE Transactions on Power Electronics，2019，34（12）：11964.

［23］ 李婧，袁立强，谷庆，等.一种基于损耗模型的双有源桥DC-DC变换器效率优化方法[J].电工技术学报，2017，32（14）：66.

LI Jing， YUAN Liqiang， GU Qing， et al. An efficiency optimization method in dual active bridge DC-DC converter based on loss model[J]. Transactions of China Electrotechnical Society，2017，32（14）：66.

［24］ LI Jia， LUO Quanming， LUO Ting， et al. Efficiency optimization scheme for isolated triple active bridge DC-DC converter with full soft-switching and minimized RMS current[J]. IEEE Transactions on Power Electronics， 2022， 37（8）： 9114.

［25］ MOU Di. Modeling and analysis of hybrid dual active bridge converter to optimize efficiency over whole operating range[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics， 2023， 11（1）： 432.

［26］ SHI Haochen， WEN Huiqing， HU Yihua， et al. Deadband effect and accurate ZVS boundaries of gan-based dual-active-bridge converters with multiple-phase-shift control[J]. IEEE Transactions on Power Electronics， 2020， 35（9）： 9886.

［27］ LI Jia， LUO Quanming， MOU Di， et al. Comprehensive optimization modulation scheme of low current level and wide ZVS range for dual active bridge converter with dead-zone control[J]. IEEE Transactions on Power Electronics， 2022， 37（3）： 2731.

（编辑：刘琳琳）