基于判别信息极限学习机的高光谱遥感图像分类

杨伊+闫德勤+张海英+楚永贺

摘要摘要：极限学习机（ELM）以其高效、快速和良好的泛化性能在模式识别领域得到广泛应用，然而在高光谱遥感图像分类中，极限学习机算法不能较好地利用数据蕴含的判别信息，限制了ELM的分類性能。为此，提出一种基于判别信息极限学习机（IELM），IELM继承了极限学习机的优势，并在一定程度上解决了极限学习机在有限高光谱遥感图像数据样本中学习不充分的问题。高光谱遥感图像分类实验结果表明，该算法具有较好的分类效果。

关键词关键词：极限学习机；模式识别；高光谱遥感图像；判别信息

DOIDOI：10.11907/rjdk.162600

中图分类号：TP317.4文献标识码：A文章编号文章编号：16727800（2017）001016105

对于连续狭窄的光谱带，高光谱成像传感器能够捕获详细和丰富的光谱信息。近年来，随着图像处理技术的发展，高光谱图像得到广泛应用，在高光谱图像应用中最重要的任务是对图像进行分类。然而，在高光谱遥感图像分类问题中存在一些挑战。例如有限训练样本之间的不平衡和高维度，高光谱遥感图像几何形状复杂，高光谱遥感图像分类计算复杂度高。为使高光谱遥感图像分类取得良好效果，近年来，机器学习方法在高光谱图像分类中得到广泛应用，例如人工神经网络（Artificial neural networks，ANNs）[1]、支持向量机（Support vector machine，SVM）[2]、多项逻辑回归（Multinomial logistic regression，MLR）[3]、主动学习（Active learning，AL）[4]等，其它方法如利用稀疏表示[5]以及谱聚类[6]对高光谱进行分离也得到广泛应用。然而，由于高光谱遥感图像具有髙维度以及复杂性，通过机器学习算法寻找最优的参数来进行分类通常非常困难，并且耗时，实现高光谱遥感图像高效快速分类已成为遥感图像领域的重要问题。

近年来，Huang等[7]基于单隐层前馈神经网络（Single-hidden layer feedforward networks，SLFNs）结构提出了极限学习机（Extreme learning machine，ELM）。ELM随机产生隐层节点的输入权值和偏置值，所有参数中仅有输出权值经过分析确定。ELM将传统神经网络的求解过程转化为一个线性模型，ELM随机选择输入权值和分析确定SLFNs的输出权值，避免了传统神经网络学习方法收敛速度慢及陷入局部极小解的可能，具有更好的泛化能力和更快的学习速度。文献[7]指出ELM通过随机产生隐层节点的输入权值和偏置值分析确定输出权值，保持了SLFNs的通用逼近能力，同时能够得到一个全局最优解。由于ELM良好的泛化能力，使得ELM应用在不同的领域中。在高光谱遥感图像领域，Pal等[8]将ELM应用到土地覆盖分类中，与BP[9]神经网络和支持向量机相比，ELM取得了更好的分类效果，并且ELM算法的计算复杂度远远小于BP和支持向量机。Bazi等[10]利用差分进化方法优化核ELM算法的参数，提高了高光谱遥感图像的分类效果。为了提高ELM算法在高光谱遥感图像分类中的稳定性，Samat等[11]基于Bagging 和 AdaBoost算法提出了集成的极限学习机算法（Ensemble extreme learning machine，E2LM）。

虽然针对高光谱遥感图像分类问题，研究人员在ELM算法的基础上提出了改进，然而 ELM及其改进算法并未充分考虑数据样本间的几何特征和数据蕴含的判别信息。知道样本之间具有某些相似的属性和分布特征，样本之间的相似属性和分布特征能够弥补ELM学习不够充分的问题，进而可以提高ELM的泛化能力，因而数据样本的几何特征和数据蕴含的判别信息对ELM的分类性能具有重要作用。

基于以上分析，本文提出一种基于判别信息极端学习机（Discriminative information regularized extreme learning machine，IELM），对于分类问题，IELM同时考虑到数据样本的几何特征和数据蕴含的判别信息，通过最大化异类离散度和最小化同类离散度，优化极端学习机的输出权值，从而在一定程度上提高ELM的分类性能和泛化能力。IELM方法的优势在于：①继承了ELM的优点，在一定程度上避免了ELM学习不充分的问题；②将异类离散度和同类离散度引入到ELM中，充分利用数据样本的判别信息；③利用MMC[12]方法有效解决最大化异类离散度和最小化同类离散度矩阵奇异问题。

为评价和验证本文提出的基于判别信息极端学习机的高光谱遥感图像分类方法，实验使用Indian Pines，Salinas scene两个高光谱遥感图像数据，将本文所提出的方法与ELM、支持向量机（Support vector machine，SVM）、最近邻分类器协作表示（Collaborative representation nearest neighbor classifier，CRNN）[13]进行对比，实验结果表明本文提出的算法能够取得较好的分类效果。

实验环境为惠普工作站处理器：Intel（R）Xeon（R） CPU E5-1603 0 @2.80 GHz，安装内存：8.00GB ，系统类型：64位操作系统，版本：win7，语言开发环境采用 Matlab 2010b。

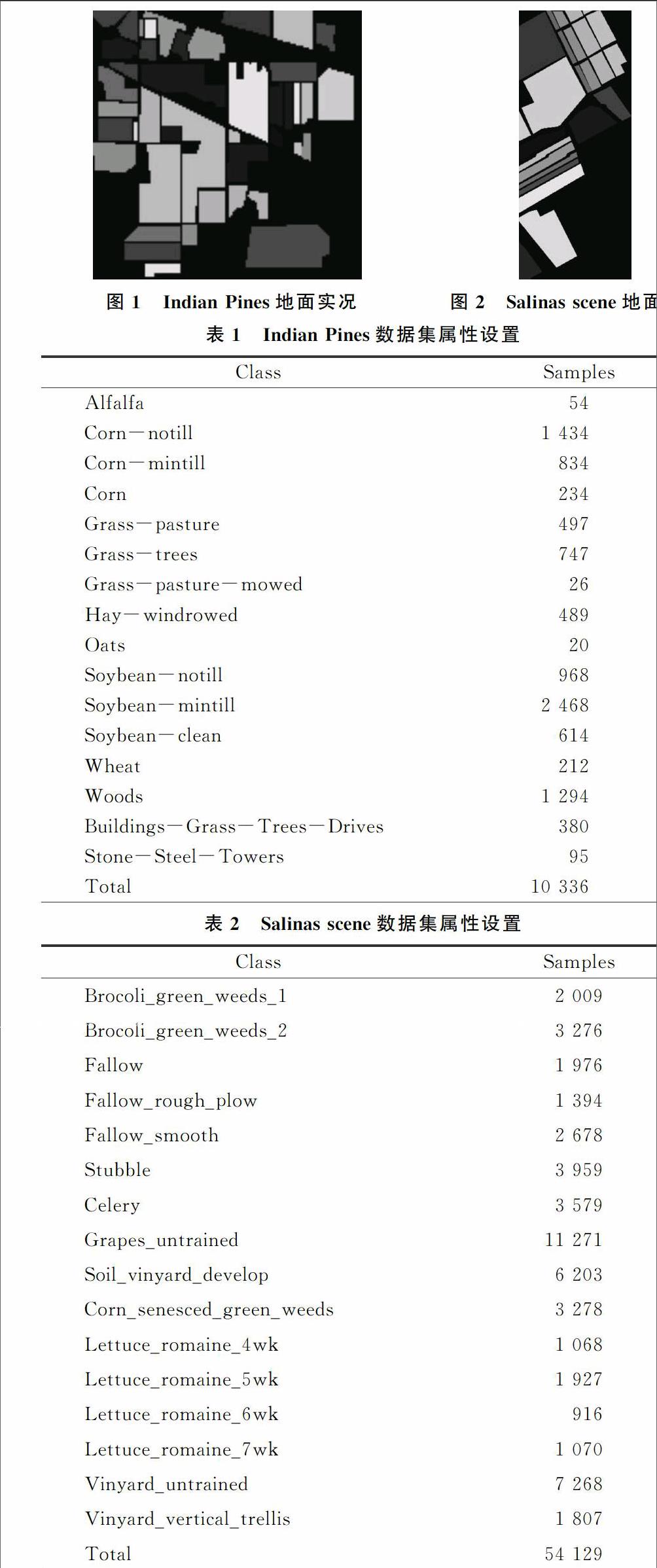
第一组实验数据为Indian Pines遥感图像数据，Indian Pines数据是AVIRIS传感器在萨利纳斯山谷收集的数据，该图像包含200个波段，图像大小为145×145，地表真实分类如图1所示，Indian Pines数据集属性设置如表1所示。

第二组实验数据为Salinas scene遥感图像数据，Salinas scene数据是AVIRIS传感器在萨利纳斯山谷收集的数据，该图像包含204个波段，图像大小为512×217，地表真实分类如图2所示， Salinas scene数据集属性设置如表2所示。

实验中，对于Indian Pines和Salinas scene图像数据，随机选取1%的数据样本作为训练集，剩下部分为测试集，使用总体精度（OA），Kappa系数，平均准确率（AA）衡量不同算法的性能。

（1）總体精度。总体精度（overall accuracy，OA）是对分类结果质量的总体评价，等于被正确分类的像素总和除 以总的像素个数。被正确分类的像素沿着混淆矩阵的对角线分布，它显示了被正确分类到真实分类中的像元数。根据混淆矩阵可得OA的计算式为：p=∑ci=1miiN（21）其中，c表示类别数目，mii表示混淆矩阵对角线上的元素，N=∑ci=1∑cj=1mij表示测试样本的总数。

（2）Kappa系数。Kappa系数采用一种多元离散分析技术，反映分类结果与参考数据之间的吻合程度，它考虑了混淆矩阵的所有因子，是一种更为客观的评价指标，其定义为：k=N∑ci=1mii-∑ci=1（mi+m+i）N2-∑ci=1（mi+m+i）（22）其中，mi+，m+i分别表示混淆矩阵第i行的总和、第i列的总和，c表示类别数目，N为测试样本总数，mii表示混淆矩阵对角线上的元素，Kappa系数越大分类精度越高。

（3）平均精度。平均精度（average accuracy，AA）定义为每类分类准确率相加除以类别总数。AA=∑ci=1accic（23）其中，c表示类别数目，acci表示每类的分类准确率。

4.2实验结果及分析

将IELM与ELM，SVM，CRNN进行对比，SVM采用libsvm工具箱，核函数采用径向基核函数（Radial basis function，RBF），惩罚参数c=0.02，核函数参数g=0.02，IELM与ELM均采用Sigmoid函数作为激活函数，隐层节点个数设置为500，惩罚参数c=20。

5结语

本文提出了一种基于判别信息极端学习机的高光谱遥感图像分类方法，创新之外在于考虑到光谱遥感图像数据的联系和差异信息。IELM引入同类离散度和异类离散度的概念，体现了输入空间数据的判别信息，通过最大化异类离散度和最小化同类离散度，优化极端学习机的输出权值。与NN，SVM， ELM算法的对比实验表明，本文所提出方法的分类效果优于NN，SVM，ELM算法。

参考文献：

[1]Q SAMI UL HAQ，L TAO.Neural network based adaboosting approach for hyperspectral data classication[J].International Conference on Computer Science and Network Technology（ICCSNT），2011：241245.

[2]J A GUALTI，R F CROMP.Support vector machines for hyperspectral remote sensing classification[J].in Proc.SPIE 27th AIPR Workshop：Adv.Comput.Assisted Recognit.Int.Soc.Opt.Photonics，Washington，DC，USA，1999：221232.

[3]J Li，J BIOUCASDIAS，A.PLAZA.Semisupervised hyperspectral image classification using soft sparse multinomial logistic regression[J].IEEE Geosci.Remote Sens.Lett，2013，10（2）：318322.

[4]W DI，MM CRAWFORD.Active learning via multiview and local proximity coregularization for hyperspectral image classification[J].IEEE Journal of Selected Topics in Signal Processing，2011，5（3）：618628.

[5]J BIOUCASDIAS，M A T.FIGUEIREDO.Alternating direction algorithms for constrained sparse regression：application to hyperspectral unmixing[J].Hyperspectral Image and Signal Processing：Evolution in Remote Sensing （WHISPERS），2010：14.

[6]Y TARABALKA，J A BENEDIKTSSON，J CHANUSSOT.Spectralspatial classification of hyperspectral imagery based on partitional clustering techniques[J].IEEE Transactions on Geoscience and Remote Sensing，2009，47（8）：29732987.

[7]GB HUANG，H ZHOU，X DING，et al.Extreme learning machine for regression and multiclass classification[J].IEEE Trans.Syst Man Cybern B，2012，42（2）：51329.

[8]M PAL，A E MAXWELL，T A WARNER.Kernelbased extreme learning machine for remotesensing image classification[J].Remote Sens.Lett，2013，4（9）：853862.

[9]D RUMELHART，G HINTON，R WILLIAMS.Learning by backpropagating errors[J].Nature，1986，323（6088）：533536.

[10]Y BAZI.Differential evolution extreme learning machine for the classification of hyperspectral images[J].IEEE Geosci.Remote Sens.Lett，2014，11（6）：10661070.

[11]A SAMAT，P DU，S LIU，et al.E2LMs：ensemble extreme learning machines for hyperspectral image classification[J].IEEE J.Sel.Topics Appl.Earth Observ.Remote Sens，2014，7（4）：10601069.

[12]H LI，T JIANG，K ZHANG.Efficient robust feature extraction by maximum margin criterion[J].IEEE Transactions on Neural Networks ，2006，17（1）：157165.

[13]W LI，Q DU，F ZHANG.Collaborativerepresentationbased nearest neighbor classifier for hyperspectral imagery[J].IEEE Geoscience and Remote Sensing Letters ，2015，12（2）：389393.

[14]G B HUANG.An insight into extreme learning machines：random neurons，random features and kernels[J].Cognitive Computation，2014，6（3）：376390.

责任编辑（责任编辑：陈福时）