基于短路电流法的永磁同步电机速度及转子角度计算方法
2024-01-26袁小平张庆华孙祺明甘亚楼
袁小平,彭 洵,张庆华,孙祺明,罗 松,甘亚楼
(1.中煤科工集团重庆研究院有限公司,重庆 400039;2.中冶南方(武汉)自动化有限公司,武汉 430205)
0 引 言
永磁同步电机由于具有体积小、效率高,响应速度快、精度控制高等优点,在冶金、陶瓷、橡胶、石油、纺织等行业的中、低压电动机中得到了广泛应用[1]。在实际应用中,电机所处的环境易对电机的初始状态造成影响[2-3]。永磁同步电机起动瞬间,可能会处于一种带速状态,其转子位置或转速无法确定,同时电机转子安装了永磁材料,转子带速起动时会在定子绕组中产生反电动势。若盲目起动电机,则可能会给定子绕组带来较大电流,导致过流等问题[4-6],严重时甚至损坏定子绕组。因此,在永磁同步电机起动瞬间,状态信息未知情况下,如何保证可靠安全起动,需要进行深入探索。
针对电机存在带转工况的应用场合,为确保带转工况到电动工况的成功切换,需准确获取带速状态下电机转子位置、转速和转向数据[7]。本文通过对控制永磁同步电机的逆变器桥臂进行两次短路,在电机定子绕组中获得因转子转速不为零产生的感应电动势形成的短路电流[8-9],进而分析该电流,实现对断电重投时电机的转子位置和转速的观测,从而实现带速起动控制[10]。
1 短路电流检测及矢量解析
在电机起动前,短暂闭合IGBT的上桥臂(此时下桥臂关断),如图1所示,此时带速状态下的电机会出现瞬时的三相短路电流。

图1 上桥臂短路时拓扑图
短路电流检测的具体操作步骤如下:
(1)电机的定子电流已经衰减为0;
(2)打开逆变器上(或者下)桥臂,并持续时间ton后关断,如图2所示;
(3)桥臂关断时间为toff;
(4)再次打开IGBT上(或者下)桥臂,持续时间ton后关闭,在三相绕组阻抗作用下,绕组中的电流会逐步减小至0,此时可以重新起动电机。

图2 短路法驱动信号
逆变器未启动时,IGBT全部关断。当电机即将结束空载状态时,给IGBT发出脉冲信号,使IGBT的上桥臂V1、V3、V5导通,保持ton后关断短路信号。在间隔时间为toff后,再次将IGBT的上桥臂导通,并保持ton时间后再关断。为确保不发生逆变器桥臂被贯穿短路,在这个过程中需关闭IGBT所有下桥臂V2、V4、V6。通过分析这两次短路电流矢量,来预估电机转子位置及转速。
在电机处于转动且逆变器未启动时,对逆变器上桥臂的进行两次短路,并计算分析得到短路后的电流,分别为iT1、iT2。短路电流矢量的空间矢量如图3和图4所示。

图3 电机正向运行时空间矢量图
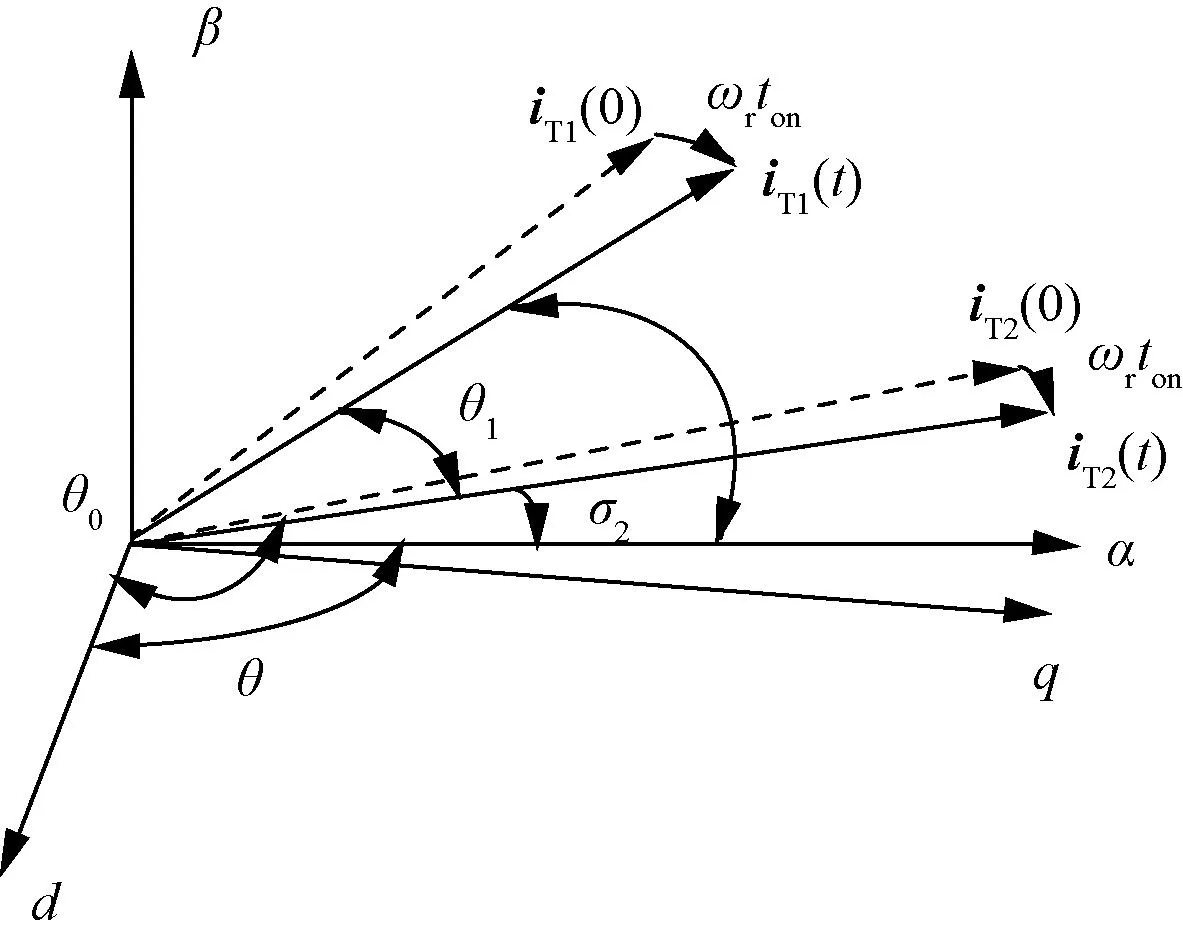
图4 电机反向运行时空间矢量图
iT1为第一次短路电流矢量,iT2为第二次短路电流矢量。σ1为iT1(t)到α轴的夹角,σ2为iT2(t)到α轴的夹角,θ0为iT2(t)到d轴的夹角。θ1为iT2(t)到iT1(t)的夹角。
在三相坐标系中,电压方程:
us=Rsis+P(Lsis)+P(ψf)
(1)

P(Lsis)+P(ψf)=0
(2)
由此得到电流矢量:
(3)
2 电机转子角速度估算
由于短路得到的电流矢量包含转子角度信息,通过坐标解析可以得到电机转子角度。由式(3)可以得到电流在a-b-c三相静止坐标系下的关系:
(4)
在两相静止坐标中,的电流关系如下:
(5)
任意时刻的电流iT与α轴的夹角θ1:
(6)
假设第一次短路以及第二次短路的时间间隔toff较小,在此过程中电机的转速为同一定值,转子转过的角度一致。此时电机转子的角速度:
(7)
3 电机转向估计
利用两次短路时电流矢量与α轴的夹角的差值Δθ=σ2-σ1与π的大小判断出此时电机的转向。

永磁同步电机三相绕组短路,电机内部产生三相感应电流。当逆变器上半桥全部关断时,电机内部线圈电感的储能效应,电流会维持一段时间,流经续流二极管将能量送入电容中。短路时间ton过长会造成系统过压或者过流,因此应当考虑使桥臂短路时间比较短,同时为排除短路后的二极管续流的电流对第二次桥臂短路电流的影响,应当使两次短路的时间间隔toff相对较大。
4 电机转子位置估算
由电机的转速可以计算出电机转子与α轴的夹角θ。d,q旋转坐标系下的电压关系如下:
(8)
在上桥臂短路的情况下,ud=0,uq=0,Rs可以忽略。由式(8)得:
(9)
在时域下,由式(9)可得:
(10)
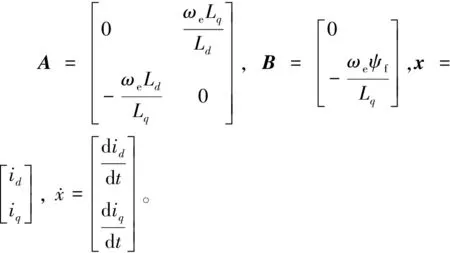
由式(10)可得:
(11)
由式(11)得:
(12)
由式(12)得:
(13)
由此可知,时域下的电流:
(14)
由于在桥臂开始短路瞬间电流均为0即x(0)=0且u(t-τ)=1,故由式(14)得:
(15)
由式(15)可得电流iT与d轴的夹角θ0:
(16)
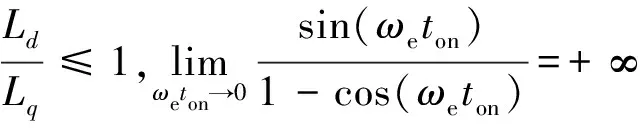
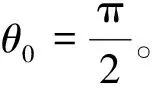
从图3可知,当电机处于正向转动时,d轴到α轴的夹角,即转子到α轴的夹角θ:
由图4可知,当电机处于反向转动时,d轴到α轴的夹角,即转子到α轴的夹角θ:
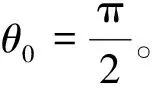
5 短路法转速跟踪仿真分析
根据上述理论分析,基于滑模观测器的短路法转速跟踪的模型如图5所示。

图5 短路法转速跟踪的模型
基于该模型进行仿真分析,仿真条件:电机给定转速为1 000 r/min,短路时间为1 ms,两次短路间隔时间为0.3 ms。图6为实际电机转速与短路法计算得到速度,两者误差为0.102%。

图6 速度误差
通过将实际计算得到的转速给速度环,得到的角度给电流坐标变换,能够得到电机运行时的三相电流等波形,同时发现速度环误差及角度误差均较小,说明了该方法的可行性。如图7、图8所示。

图7 速度环波形
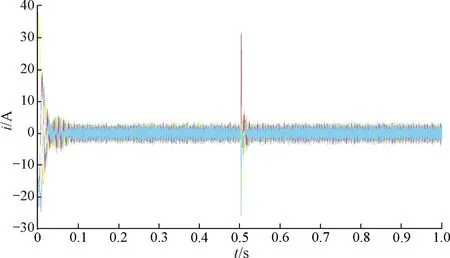
图8 三相电流波形
6 结 语
本文介绍了一种基于短路电流法的永磁同步电机速度及转子角度计算方法,通过理论分析及仿真分析,验证了该方案的可行性及准确性,为实现永磁同步电机转速跟踪功能起到重要作用。
