无铁心轴向磁通永磁电机的磁场解析计算
2024-01-26王斗勇
王斗勇,彭 兵
(沈阳工业大学 电气工程学院, 沈阳 110870)
0 引 言
传统永磁电机的定子由硅钢片叠压而成,由于齿槽的存在,电机在运行时会产生转矩脉动,运行不稳定。此外,定子铁心产生的铁耗占总损耗的20%~30%[1],不仅质量大而且效率低。轴向永磁电机具有结构简单、质量轻、维修方便、尺寸灵活多样和无级调速等优点,相对于传统电机,轴向永磁电机的气隙为与磁力线垂直的二维平面沿磁力线方向延伸所得到的,可以设计成具有较大功率密度的电机。无铁心永磁电机没有铁心中的铁耗,效率高,节能效果显著,在众多领域都有广泛的应用前景[2]。
对于永磁电机的磁场计算方法主要有有限元法和解析法[3],有限元法分析磁场更加准确,但是当电机的几何模型和相关参数发生变化时,都需要重新仿真计算,十分耗时。为了克服这个问题,很多学者提出了用解析方法计算电机磁场,于慎波教授采用了等效磁网络模型来计算电机的漏磁系数和空载气隙磁密,其是将电机中的磁路问题转化为电路问题来进行分析的方法,可以较大提高电机磁场的计算速度。文献[4]用保角变换法对电机的空载气隙磁场进行计算,该方法考虑了定子的开槽效应对磁场的影响,并与有限元法进行对比,证明该方法对于分析电机磁场的准确性。文献[5]通过将永磁体和电枢绕组等效为电流片来计算电机的磁场,将解析结果与二维和三维有限元分析结果继续比较,其偏差在5%以内,准确性很高。文献[6]通过建立轴向磁通永磁电机的准三维分析模型,通过求解圆柱坐标系下矢量势的广义泊松方程,计算了轴向磁通永磁电机的空载磁场,该方法考虑了磁场的边缘效应,求解准确性很高。
本文通过建立无铁心轴向磁通永磁电机的三维多截面解析模型,推导电机的空载气隙磁密、电枢反应气隙磁密、空载反电动势和负载电磁转矩的建立过程和数学表达式,最后用有限元仿真软件建立无铁心轴向磁通永磁电机的三维仿真模型,计算气隙磁场、空载反电动势和电磁转矩,与解析结果相比较,验证解析模型的可行性。
1 多截面三维建模
通过将电机沿径向进行多截面处理,可以对轴向磁通电机的磁场计算进行降维处理,提高磁场计算的速度。图1为将轴向磁通电机进行多截面处理的电机三维图。多截面如图1所示,然后将电机沿圆环展开,如图2所示,轴向磁通电机等效为ng个无边缘效应的直线电机的组合体,从而实现三维磁场到二维磁场的降维计算。
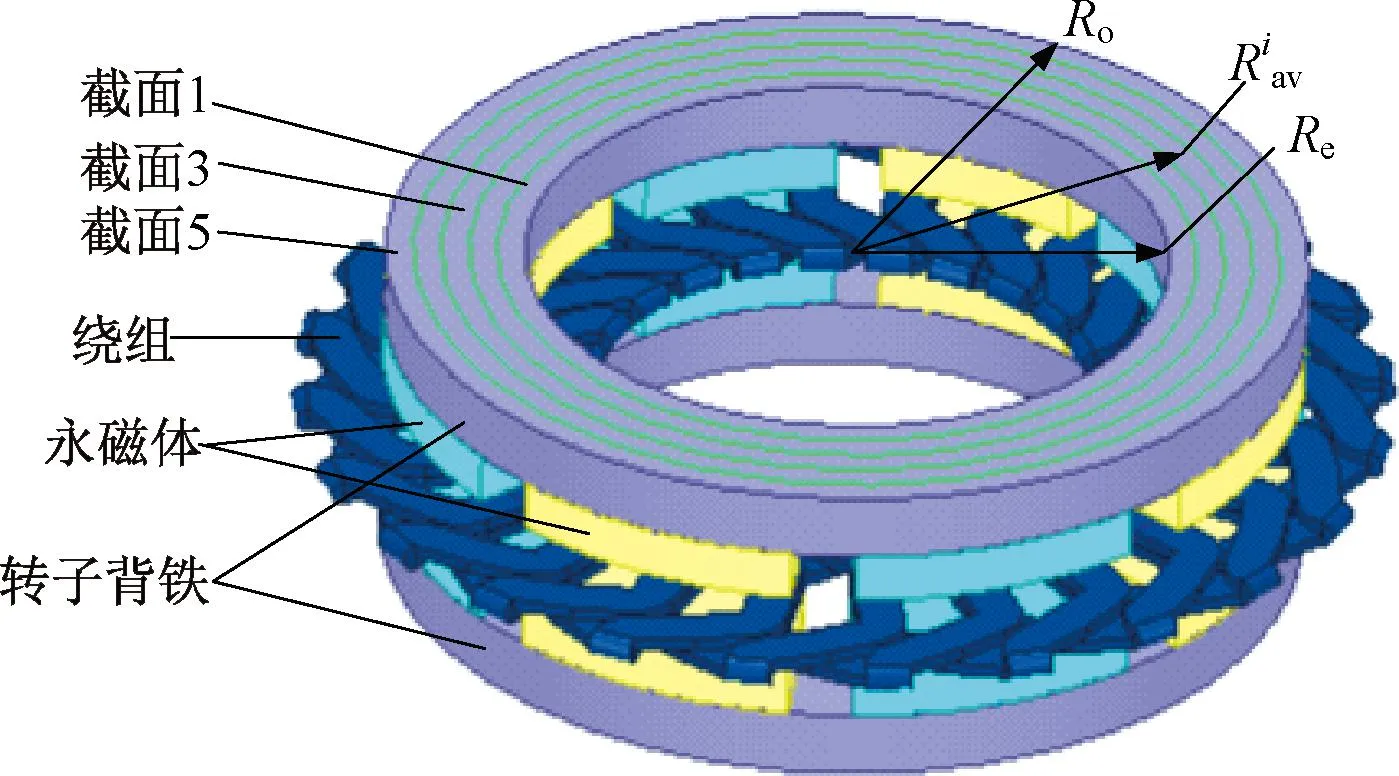
图1 无铁心轴向磁通电机多截面准三维模型
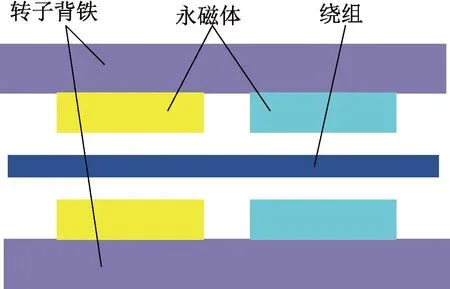
图2 第i个截面的等效直线电机模型
(1)
式中:Ro和Re分别为电机的外、内径;ng为截面的选取数量,ng一般为5~6,本文选取ng=5。
电机的主要参数如表1所示。
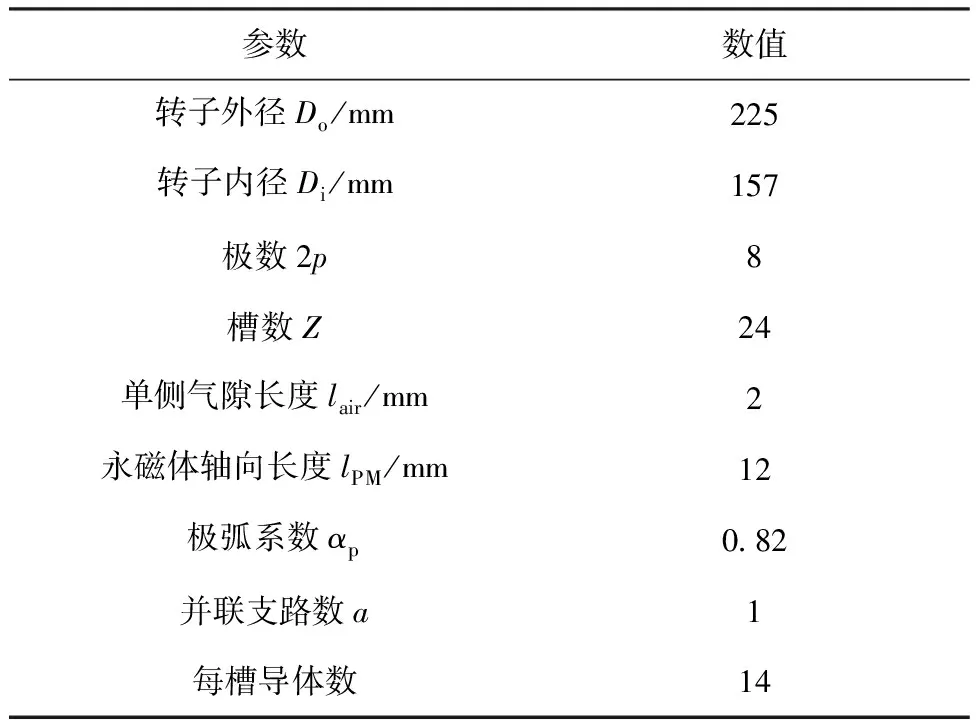
表1 电机主要参数
2 空载磁场解析计算
为了简化计算,做如下假设[3]:永磁体的退磁曲线为直线;永磁体均匀充磁,材料各向同性;不考虑边缘效应。
将电机分为两个求解域,分别为气隙区域和永磁体区域,考虑到电机为双转子中间定子轴向磁通电机,可以将电机沿轴向分两部分,只考虑一侧转子计算空载磁场,建立如图3所示的求解模型。

图3 空载磁场求解模型
求解域Ⅰ和Ⅱ内磁感应强度B和磁场强度H的关系:
(2)
式中:μ0为真空磁导率;μr为永磁体相对磁导率;M为永磁体剩余磁化强度。
由文献[4]可知,剩余磁化强度M仅含有轴向分量,在直角坐标系下,剩余磁化强度可用傅里叶级数展开:
(3)
式中:Kn=nπ/p,p为电机极对数。
式中:Br为永磁体剩磁;αp为永磁体极弧系数。
采用矢量磁位A进行求解,其在求解域中满足拉普拉斯方程:
(4)
磁场强度H和矢量磁位A的关系:
(5)
在求解域Ⅰ和Ⅱ内,采用分离变量法,可求得其通解:
(6)
式中:a1~a4为待定系数。
求解域的边界条件:
(7)
式中:hm为永磁体厚度;g为气隙长度。
将式(7)代入式(6),可求得求解域Ⅰ的磁密:
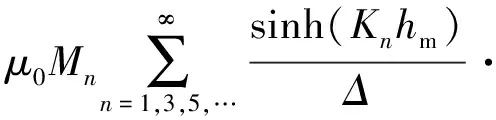
(8)
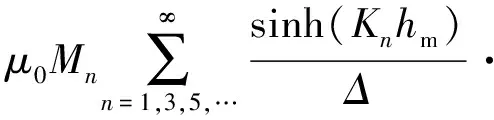
(9)
求解域Ⅱ内的磁密:
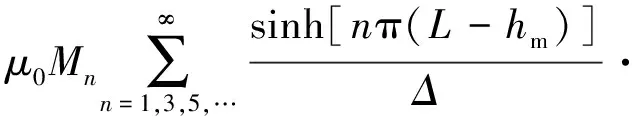
(10)
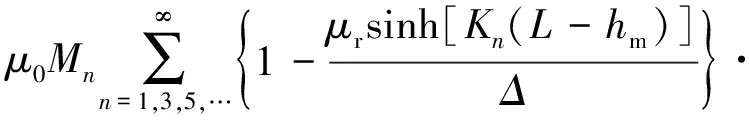
(11)
式中:L=hm+g/2。
Δ=μrcosh(Knhm)sinh[Kn(L-hm)+sinh(Knhm)cosh[Kn(L-hm)]
电机沿圆周选取1 012个计算点,磁密选取100个奇数次谐波,首先对电机截面1、截面3和截面5且在气隙轴向中心处的气隙磁密的轴向分量和周向分量进行计算,其结果如图4~图6所示。
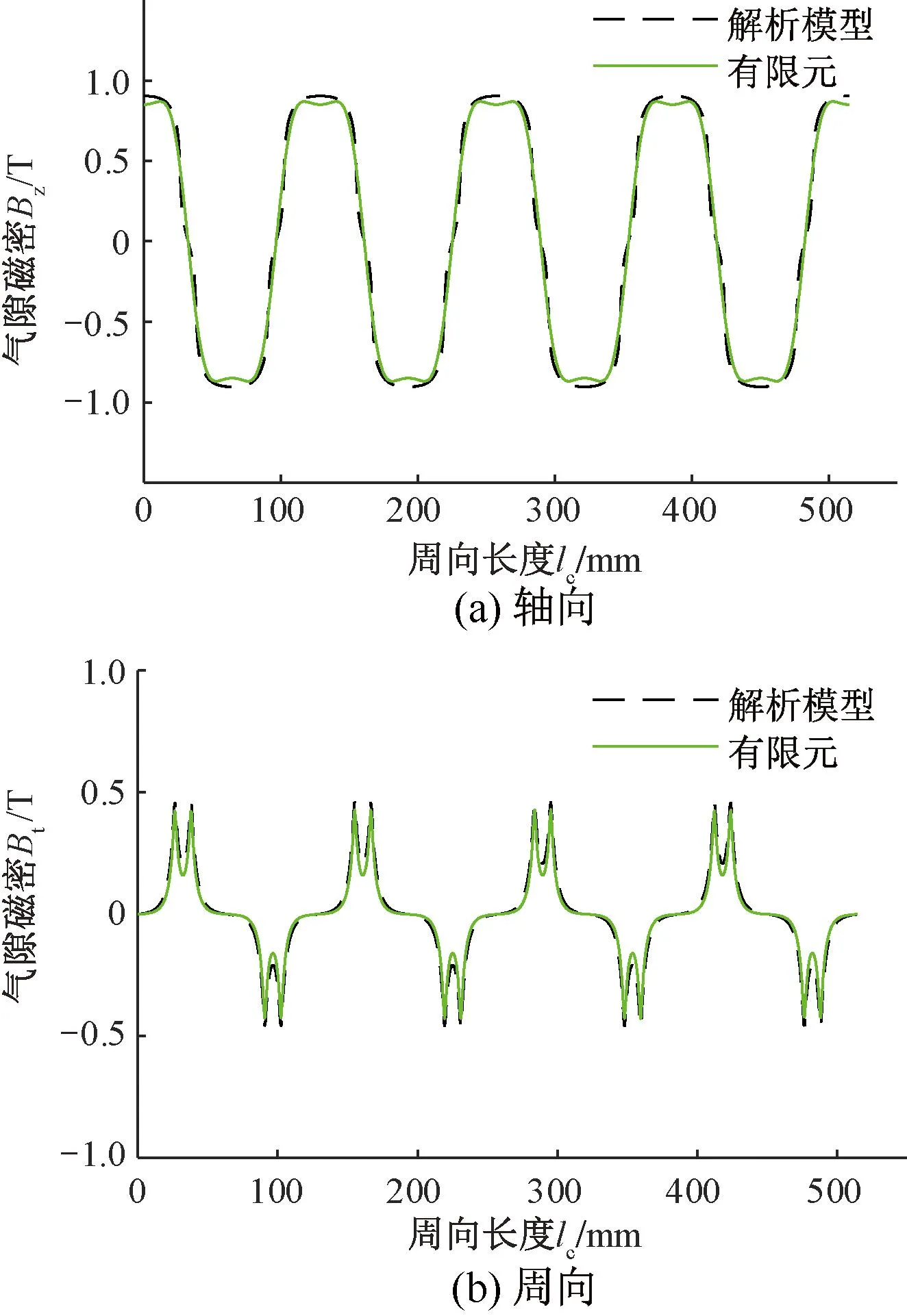
图4 截面1气隙中心处气隙磁密波形

图5 截面3气隙中心处气隙磁密波形
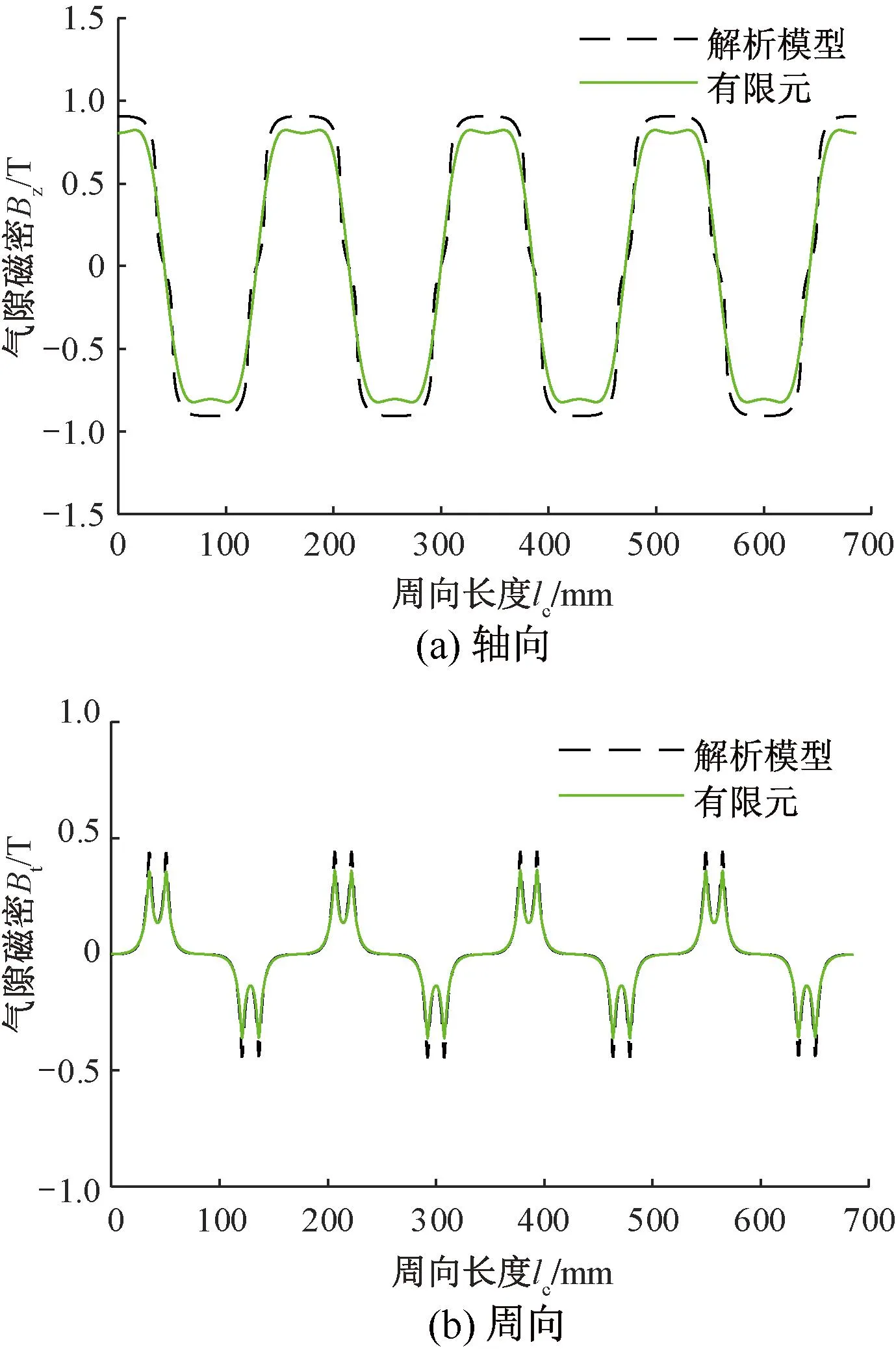
图6 截面5处的气隙磁密波形
从图4~图6和表2可看出,解析法与有限元仿真的s差值较小,电机截面1气隙处和截面5气隙处的磁密值均小于截面3气隙处的磁密值,说明永磁磁场沿径向气隙分布的磁密不相等。
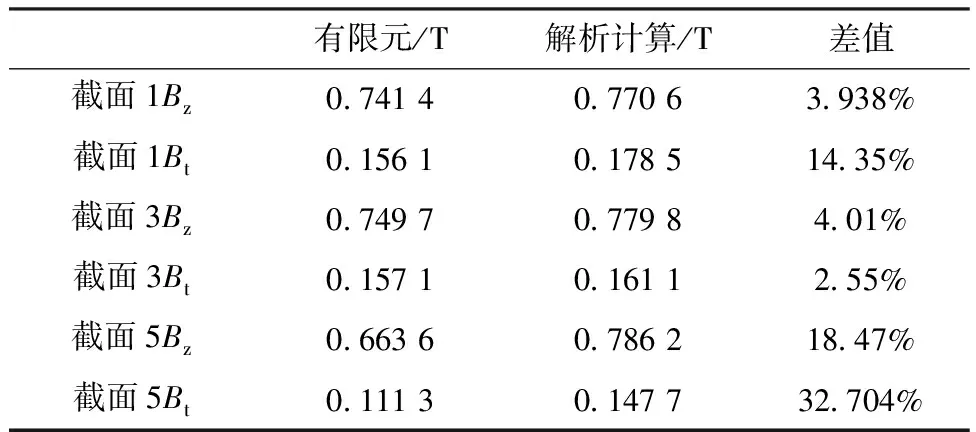
表2 解析计算与有限元计算的空载气隙磁密有效值对比
3 电枢反应磁场解析计算
由于本电机绕组为双层绕组,所以可建立一侧绕组来等效计算电枢反应磁场。将电枢绕组等效为电流片,电流片的长度t1为线圈边的宽度,电流片沿绕组纵向均匀分布,建立如图7所示的电枢反应磁场求解模型。
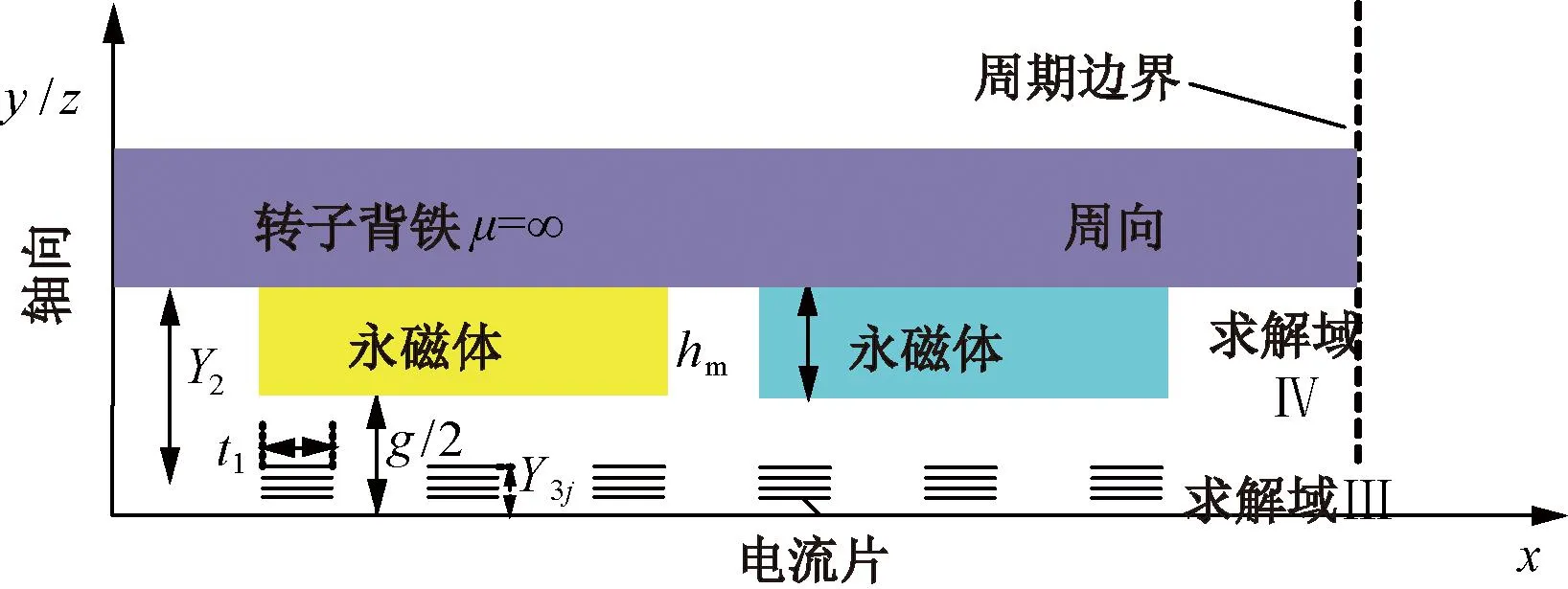
图7 电枢磁场求解模型
每一片电流片的电流密度J可表示为Nci/(t1j)的磁化强度,Nc为线圈匝数,当电机极对数p=1,每极每相槽数q=1时,每一相每一层电流片所产生的电流密度可表示[8]:
(12)
式中:j为电流片的层数;τ为极距。
通过将每一相每一层电流密度所产生的磁场进行求和,即可得到电机三相电流所产生的电枢反应磁场。
当电流为下式时:
(13)
一相中一层电流片所产生的电流密度波形可表示:

(14)

一相一层电流片的电流密度的基波幅值:
(15)
(16)
式中:ke1为基波电流密度的系数。
当p=1,每极每相有q个线圈时,一相一层电流片的电流密度基波为q个电流密度的基波的叠加,于是,其电流密度基波幅值:
(17)
(18)
式中:kq1为基波电流密度的分布系数;α1为槽距电角。
当电机的极对数p为任意整数时,其一相一层电流片的电流密度的基波幅值:
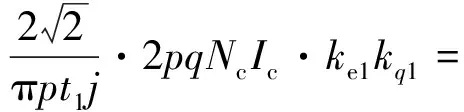
(19)
式中:a为并联支路数;Ic为线圈电流;I为每相电流;N为每相串联匝数。其中:
kN1=ke1kq1
I=aIc
一相一层电流片所产生的第n次谐波电流密度幅值:
(20)
其中:
kNn=kenkqn
一相一层电流片的电流密度的傅里叶级数表达式:
(21)
电机的三相电流:
(22)
于是,三相电机每相每层电流片所产生的n次电流密度:
(23)
其三相每层电流片的合成电流密度:
Jn(t,θ)=JAn+JBn+JCn
(24)
将其在空间上进行傅里叶分解:
(25)
式中:Un2=2nπ/(2τ),边界条件:
通过将每层电流片数值叠加,可得区域Ⅲ内的由电枢磁场产生的磁场强度:
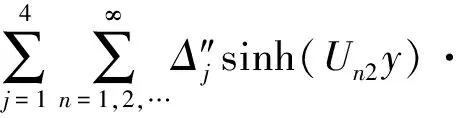
(26)
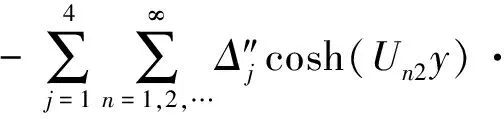
(27)
区域Ⅳ内的磁场强度:
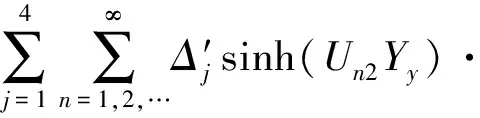
(28)

(29)
式中:Yy=Y2-y;j为电流片的层数;
当相电流为9 A时,首先对电机截面1、截面3和截面5,且在气隙轴向中心处的磁密的轴向分量和周向分量进行计算,其结果如图8~图10所示。
从图8~图10和表3可看出,解析法与有限元仿真的差值较小。由表3可知,电枢磁场径向分布的气隙磁密不相等,因为电枢绕组有端部效应,所以使得靠近绕组端部的磁密更大一点。
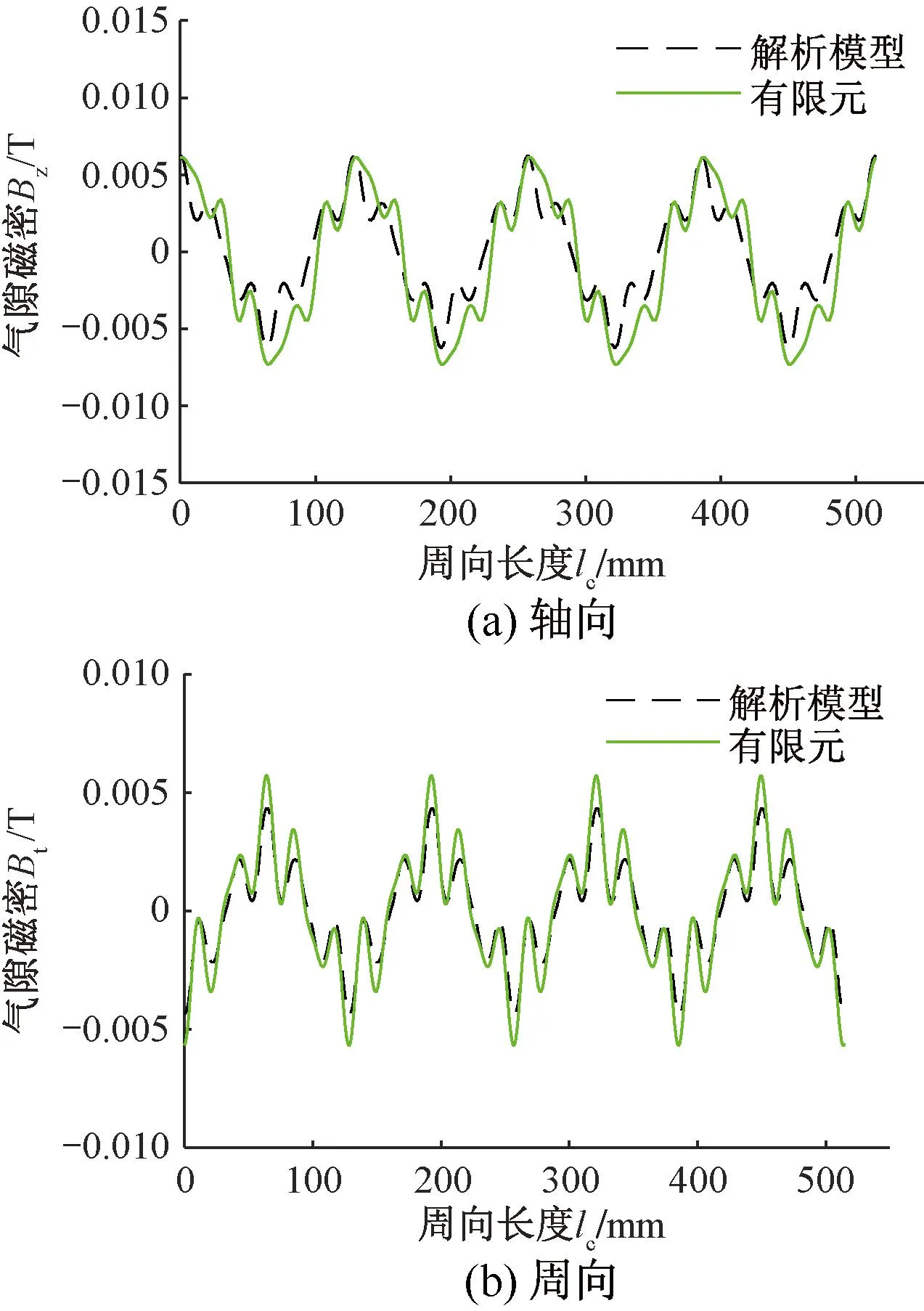
图8 截面1气隙中心处磁密波形
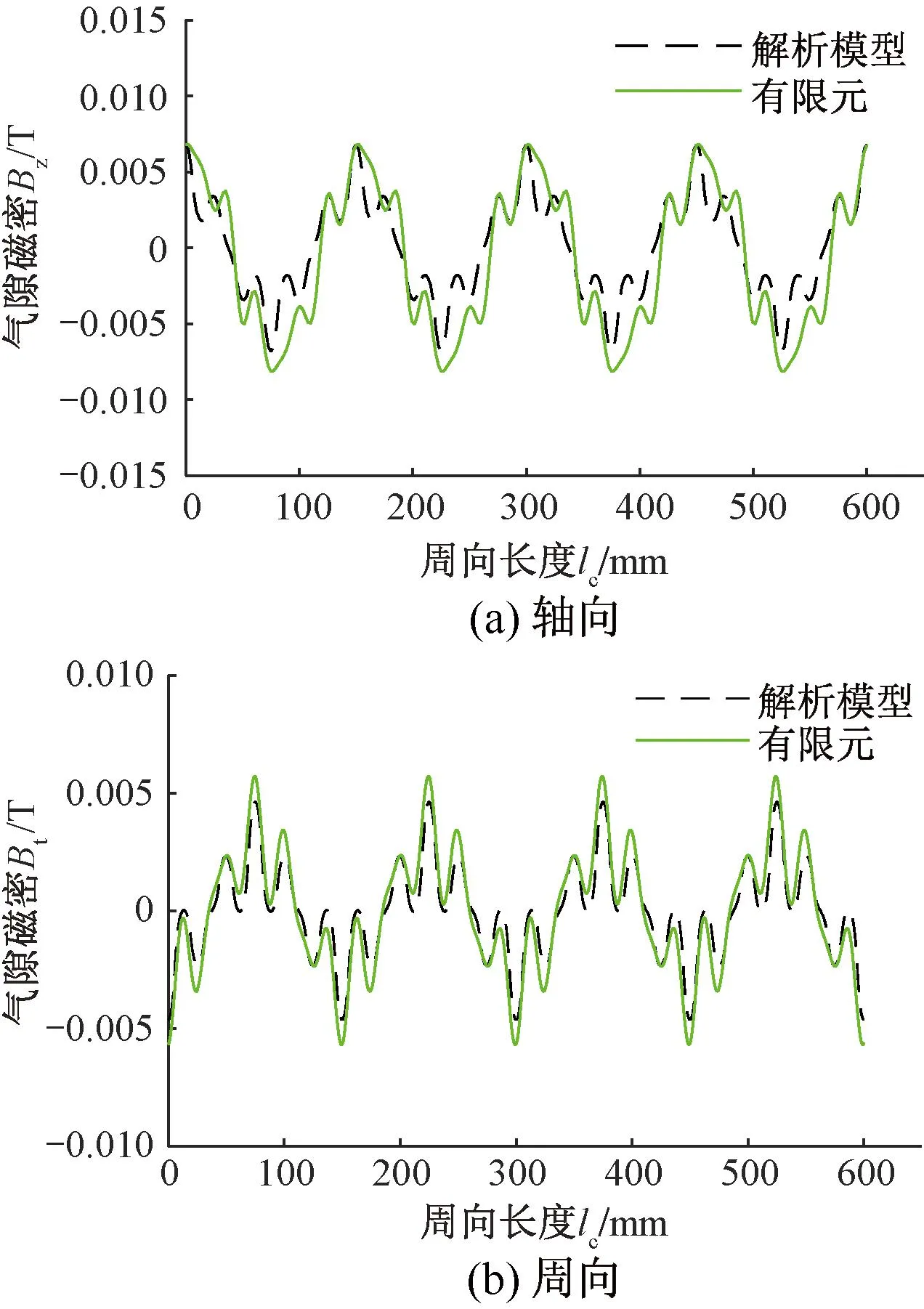
图9 截面3气隙中心处磁密波形
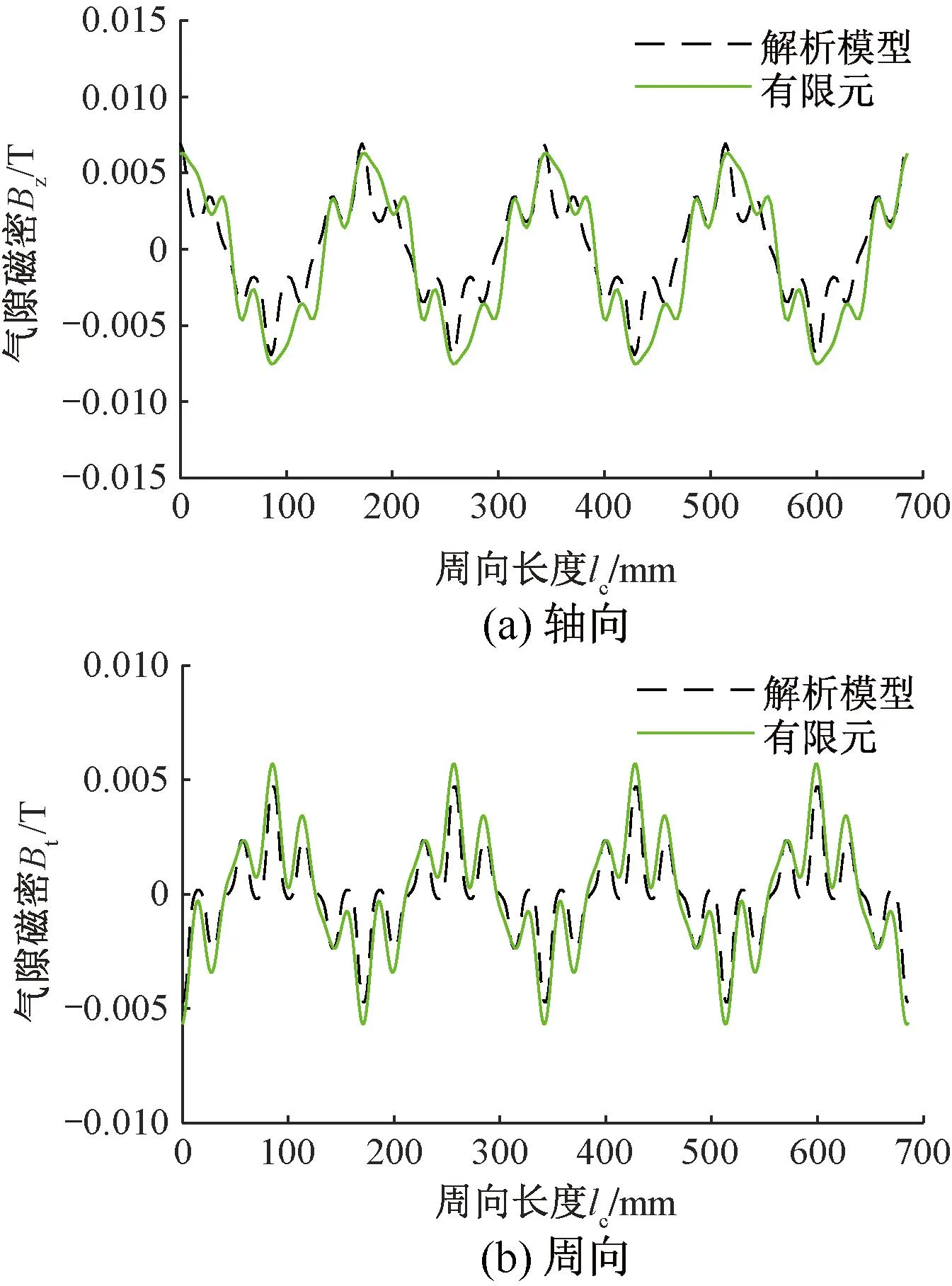
图10 截面5处的气隙磁密波形
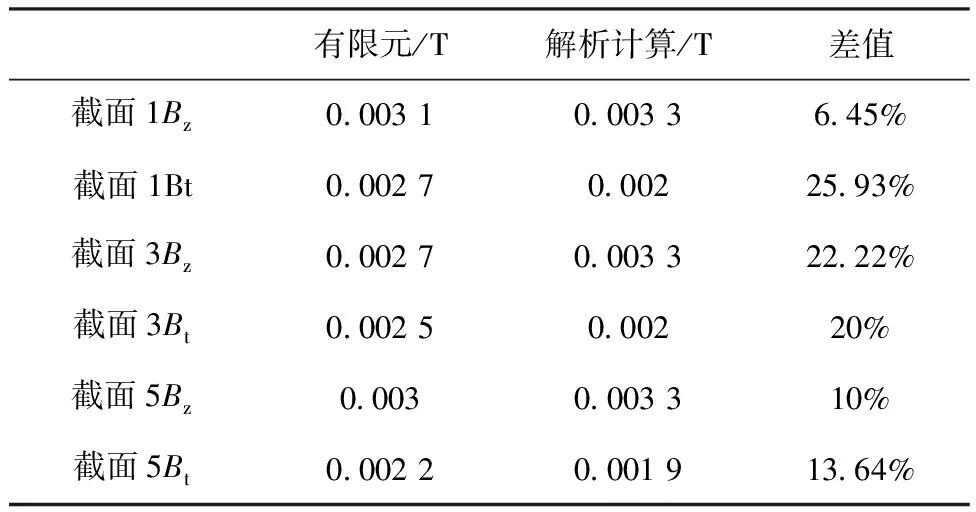
表3 解析计算与有限元计算的电枢反应气隙磁密有效值对比
4 空载反电动势和电磁转矩的计算
电机第i个截面的线圈反电动势[9]:
(30)
式中:ψc,i,s,j为第i个截面第s个线圈的第j个电流片处的磁链,s=1,2,…Z/(3a)。
(31)
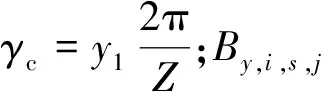
A相绕组的每个截面中的线圈反电动势:
(32)
A相绕组的反电动势:
(33)
图11和表4为用解析方法和有限元仿真求出的A相反电动势波形及有效值对比。可看出,解析方法求出的反电动势有效值比有限元结果大,这是由于解析法没有考虑端部漏磁,使得结果偏大。
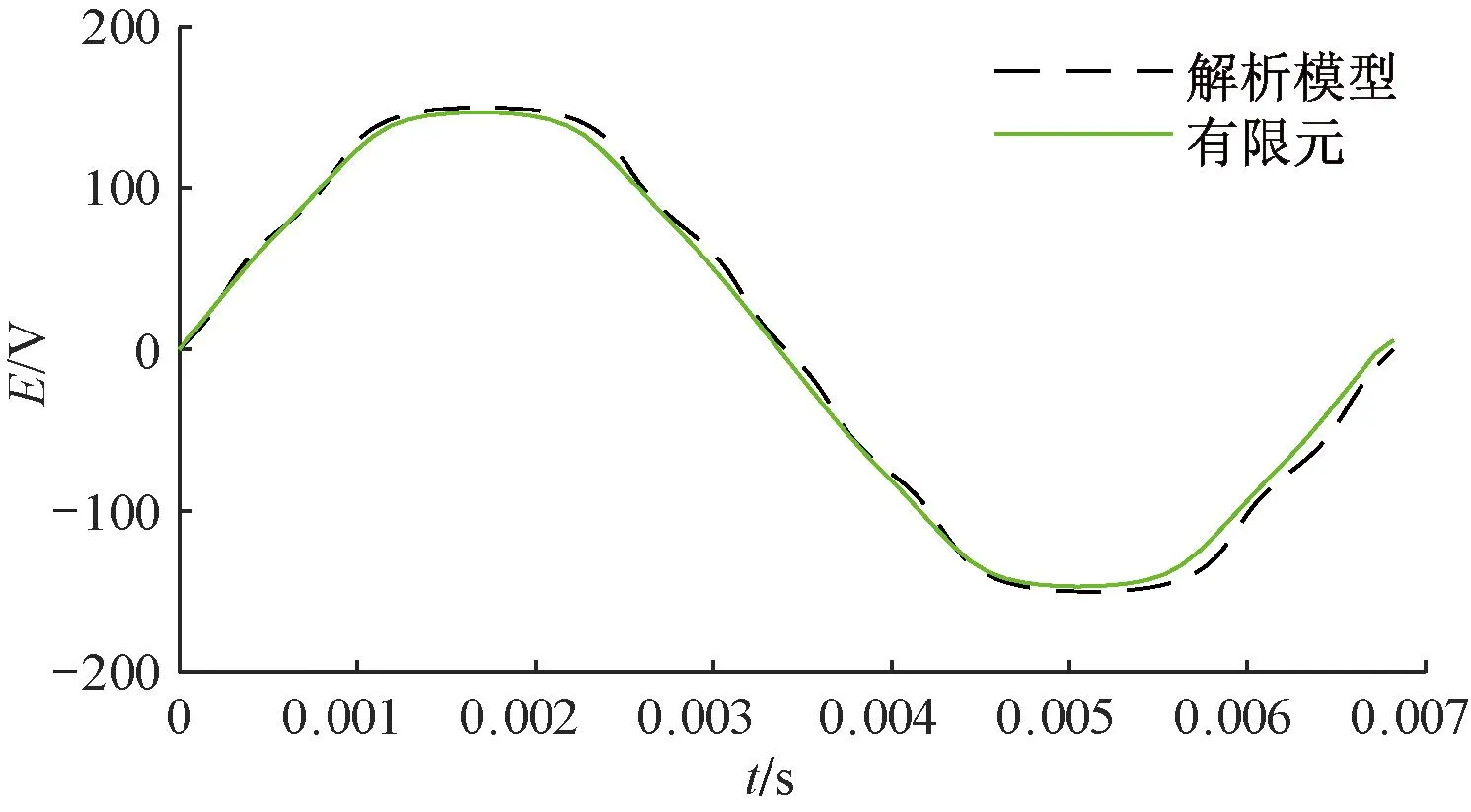
图11 A相绕组反电动势波形

表4 解析计算与有限元计算的A相反电动势有效值对比
通过文献[10]可知,将空载磁密和电枢反应磁密的轴向和周向分量分别叠加代入到麦克斯韦张量方程中,可得电机电磁转矩表达式:
(34)
式中:BRθ为电机空载磁密的切向分量;BRy为电机的空载磁密的轴向分量;BSθj为第j层电流片所产生的电枢反应磁密的切向分量;BSyj为第j层电流片所产生的电枢反应磁密的轴向分量。
通过将每个截面所产生的电磁转矩进行叠加,即可得电机电磁转矩的解析计算结果,如图12所示。

图12 电磁转矩
表5为解析计算与有限元结果的平均值对比。

表5 解析计算与有限元计算的电磁转矩平均值对比
由图12、表5可以看出,解析计算结果与有限元波形吻合较好;电磁转矩的计算精度较高,计算时间较短。
5 结 语
本文对电机进行多截面等效处理,采用解析法计算无铁心轴向磁通永磁电机的空载磁场、电枢反应磁场、空载反电动势和电磁转矩,得出以下结论:
1)对电机进行多截面等效处理后,可将复杂的三维电机等效为多个二维直线电机的组合体,简化了电机模型;
2)解析法可对无铁心轴向磁通电机的磁场进行解析计算,提高了电机初始设计的速度;
3)采用解析法计算电机空载反电动势和电磁转矩,其误差小,分别为3.46%和3.856%,验证了解析法法的准确性。
