机泵一体外转子潜油永磁同步电机设计与优化

谭利萍,王俞聪,肖文生,崔俊国,周于富,任承桢,郭嘉祥,甄东芳

(1.中国石油大学(华东)机电工程学院,青岛 266580; 2.海洋物探及勘探开发装备国家工程研究中心,青岛 266580;3.潍坊市工业和信息化局,潍坊 261061; 4.中海油田服务股份有限公司,天津 300450)

0 引 言

近年来,我国高黏度稠油、高含沙蜡油地开发需求逐步增加,螺杆泵因其在采油时不会产生困油、卡泵、乳化等问题,经常被用来开采稠油和含砂原油[1]。目前应用较为广泛的是井下潜油电机直驱螺杆泵采油系统,其井下机组结构从下到上由潜油电机、电机保护器、减速器、减速器保护器、柔性轴连接器、单螺杆泵组成[2]。应用该种驱动方式的抽油系统传动链较长、效率较低、故障点增加、系统可靠性降低,并且在通过水平井的造斜段时机组容易发生弯曲变形[3]。

利用直驱螺杆泵与低速大扭矩永磁同步电机在井下油液中进行采油的系统逐渐用在油田中。因其动力源为低速大扭矩永磁同步电机,不需要减速器对电机主轴进行减速,其结构省去了齿轮减速器及其保护器,有效缩短了长度,一定程度提高了井下通过性[4-5]。该系统虽较传统潜油电机直驱螺杆泵采油系统传动结构简单,长度变短,但仍采用永磁同步电机通过传动轴与螺杆泵进行串接的传动方式,整机尺寸仍较长,通过性较差,故在水平井的应用仍受到限制。

针对此问题,本文设计机泵一体外转子潜油永磁同步电机,将螺杆泵镶嵌到电机内部,组成机泵一体式采油系统,将机组长度缩短约一半,大大提高其井下通过性。该机组在水平井、定向井以及高粘稠井的油田开发环境中有更好的适应性,对于发展一体化和小型化的石油开采装备具有重要指导意义。

电机优化设计方法通常有全局优化和局部优化两种[6]。全局优化算法建立目标函数较为复杂,且求解周期较长,很难实现电机的快速优化。本文采用计算周期短并能对多个目标进行优化设计的局部优化方法,即田口法,对外转子永磁同步电机的齿槽转矩、转矩、转矩脉动和效率4个性能指标进行优化,缩小优化参数范围,然后采用遗传算法对转矩脉动进一步优化,并对优化后的电机进行电磁性能仿真分析,验证该电机设计的合理性[7]。

1 机泵一体外转子潜油永磁电机设计

一体式外转子永磁同步电机螺杆泵采油系统采用的方案是将电机设计为外转子电机,将螺杆泵内嵌于电机内部,外转子通过转动转换装置带动螺杆泵的转子转动,设计方案如图1所示。

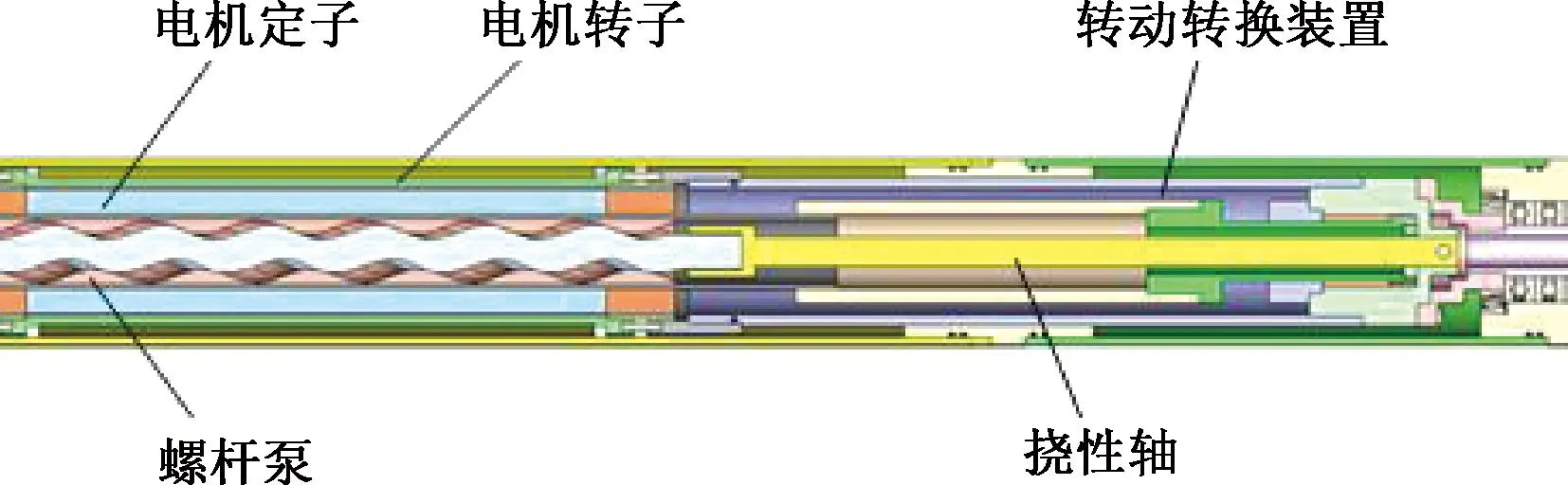
图1 一体式外转子永磁同步电机螺杆泵采油系统

1.1 电机额定参数

首先根据油井的理论排量、扬程等要求确定螺杆泵的基本参数,然后确定电机的额定数据[8]。其中电机外壳采用较为通用的外径143 mm,电机额定数据如表1所示。

表1 电机额定数据

1.2 电机主要尺寸设计

电负荷A对电机尺寸的影响起到了关键作用,其计算式:

(1)

式中:m为电机相数;W为每相串联导体数;IN为绕组电流;D为电枢直径。

表贴式永磁电机的气隙磁密计算公式可表示:

(2)

式中:Br为剩磁密度;μr为永磁体相对磁导率;σ为漏磁系数;ks为主磁路饱和系数;kδ为气隙系数;δ为气隙长度。

外转子永磁同步电机定子外径及其长度可以表示:

(3)

式中:Dil为电枢外径;Lef为电枢铁心计算长度;Pem为计算功率;α′p为计算极弧系数,取0.7;Bδ为气隙磁通密度,取0.85;

电机电枢直径和长度有如下关系:

Lef=λDil

(4)

气隙长度主要受机械制约,其取值和异步电机相似,可由下式计算:

(5)

式中:P为电机功率;

1.3 电机转子设计

对于外转子永磁同步电机,永磁体贴在转子内表面,定子外径与外转子内径D1的关系[9]:

D1=D+2(hm+δ)

(6)

式中:D为定子外径;hm为永磁体磁化方向厚度;δ为气隙长度。

考虑到制造的成本问题,选择表贴式转子结构。永磁体磁化长度及宽度公式由下式确定:

(7)

bm=αpτ

(8)

式中:μr为相对回复磁导率;δ为气隙长度;Br为永磁体剩磁密度;Bδ为气隙磁密;αp为极弧系数;τ为极距。

1.4 电机定子设计

潜油永磁同步电机受套管限制,外径较小,为保证电机定子的机械强度,采用平底梯形槽,同时考虑制造过程嵌线的要求,最终选择半闭口平底梯形槽,如图2所示。

图2 定子槽型

分数槽电机由于绕组端部小、制造加工难度低和转矩脉动小等优点被广泛应用于低速潜油永磁同步电机设计。电机采用双层绕组时,可通过短距来改善绕组电动势和磁动势的波形,且短距还可节省端部铜用量,故本文采用分数槽双层绕组[10]。

永磁同步电机转速计算公式:

(9)

式中:n为转速;f为频率;p为极对数。

电路的频率会影响电机的磁滞损耗,电路频率越大磁滞损耗越大,在电机设计时尽可能使电源频率小,以减小磁滞损耗。通过式(9)可知,极数和三相电源频率成正比,应尽量选择更少的极数。

定子绕组的谐波次数取决于定子槽数,若槽数设置不合理,会导致电机气隙磁密谐波畸变,从而产生谐波转矩导致起动转矩变小,严重时会影响到电机正常起动。同时空载反电动势含有谐波分量会引起电机的损耗和振动。因此,综合考虑空载气隙磁密和空载反电动势的谐波畸变率,最终选用10极18槽配合[8]。

2 电磁参数优化设计

电机优化设计是对已经初步设计的电机,在满足设计要求的前提下,通过优化方法寻找到使得电机性能最佳或者是某一个性能达到最优的方案。

2.1 田口法优化

结合ANSYS Electronics Desktop 中Rmxprt参数化仿真的结果,选择电机的槽开口宽度、定子槽顶宽度、永磁体厚度、气隙长度以及极弧系数5个电机电磁结构参数作为影响因子,以转矩脉动,齿槽转矩,电机效率和额定转矩作为优化目标进行优化。

根据电机参数化分析选取5个水准,不同影响因子在不同水准下的取值,如表2所示。根据田口法可以得出如表3所示的实验计划正交表。利用ANSYS Electronics Desktop中Maxwell 2D模块对各个实验进行仿真分析,得到如表4所示的仿真实验数据。

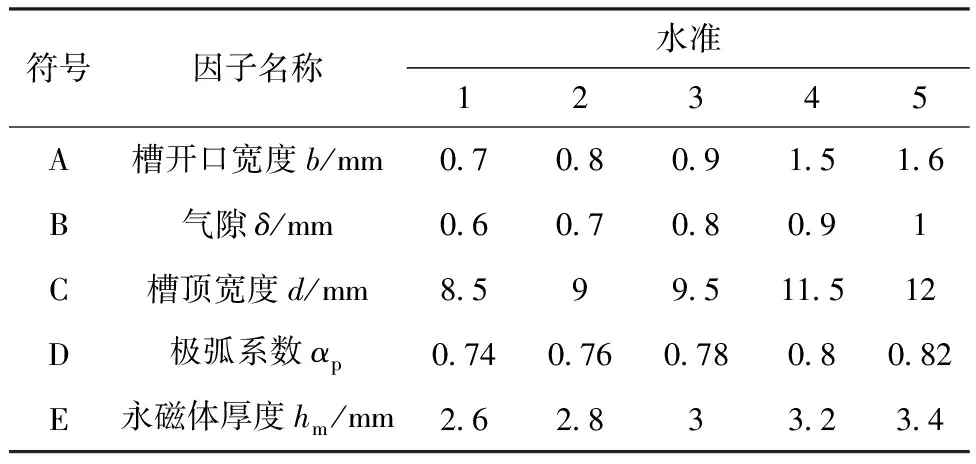
表2 不同影响因子及其不同水准值(田口法)

表3 实验计划正交表(田口法)

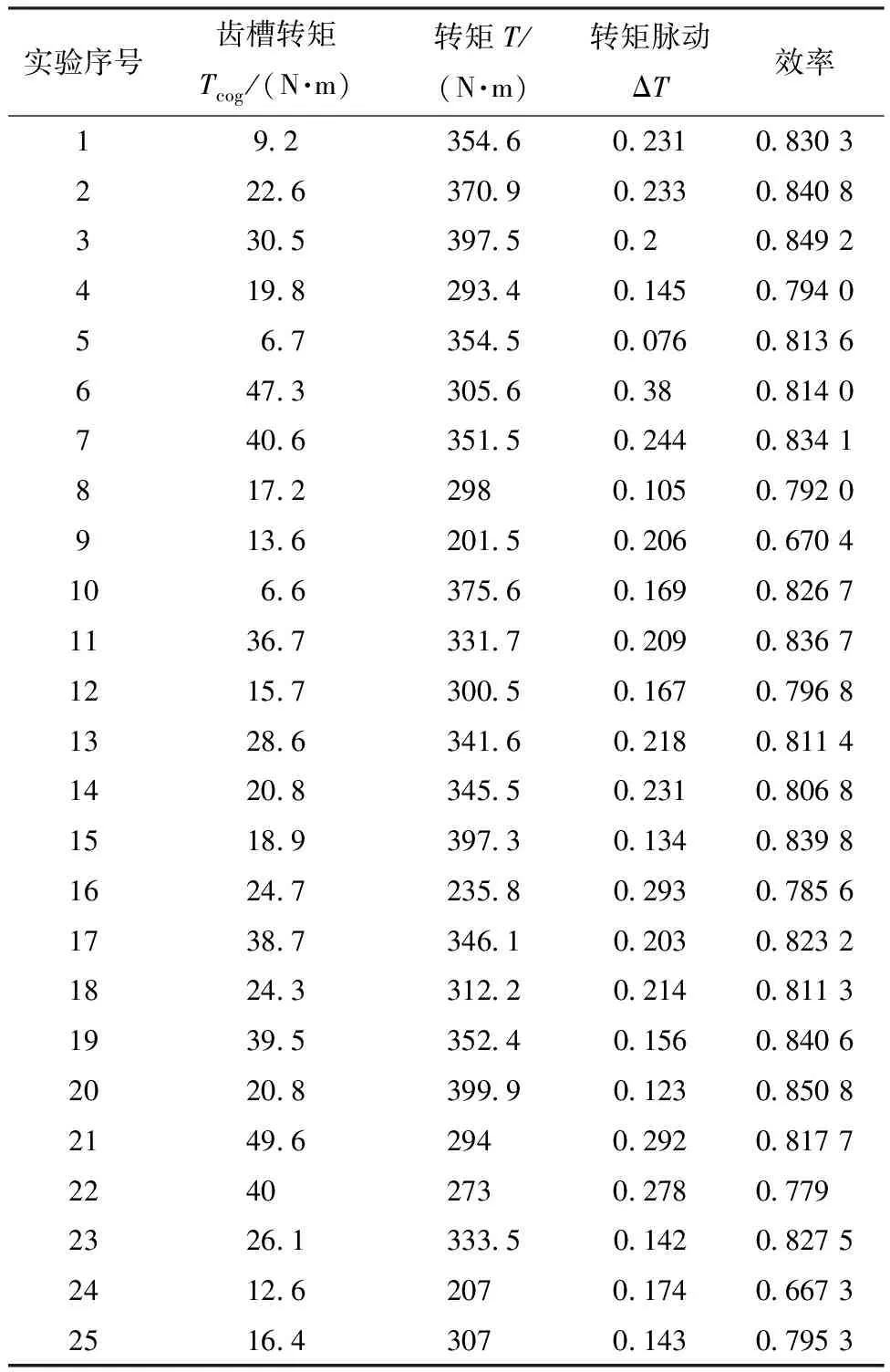
表4 有限元仿真实验数据(田口法)

田口法可以分析不同优化参数对电机性能的影响程度。首先需要获得全部有限元仿真结果的平均值;然后计算各电机参数下不同水准数的仿真实验结果的平均值,得到不同电机参数对不同性能指标的效应图如图3所示,进而对电机参数进行分类,找出最佳组合如表5所示;最后通过计算不同电机参数下不同电机性能仿真结果的方差,分析该优化参数对该电机性能的影响比重如表6所示。

表5 电机各性能的最佳组合(田口法)

表6 不同参数对电机各性能的影响比重(田口法)

考虑到正交有限元仿真中,平均额定转矩可以满足电机驱动螺杆泵的转矩要求,所以本田口法优化设计主要为提高电机效率的前提下,减小电机的转矩脉动和齿槽转矩,以此来减弱电机运行时产生的振动,提高电机运行时稳定性。综合以上分析,选择齿槽转矩和转矩脉动最低的参数组合,优化后的参数组合为槽开口宽度0.7 mm、气隙1 mm、槽顶宽度8.5 mm、极弧系数0.74,永磁体厚度2.6 mm。仿真得到优化后参数组合的电机性能如表7所示,齿槽转矩降低了66.57%,转矩提升了16.91%,转矩脉动降低了19.91%,效率提升了2.51%。

表7 优化前后电机性能指标对比(田口法)

2.2 田口迭代法优化

田口法优化受到单一控制变量参数化分析的影响,且水准值间隔较大。为增大优化设计准确度,改进田口法,提出田口迭代法即针对需要优化的电机性能,去除对其影响最小的参数,选取间隔更小的水准值,进行迭代优化, 直到某个目标电机性能已无法优化,迭代结束。

本次优化的主要目标是,保证转矩大于驱动螺杆泵转动的扭矩之上,且在保持或者增加效率的基础上,进一步降低转矩脉动和齿槽转矩。4因子5水准的参数表如表8所示。

利用田口法可得出正交实验表,同时仿真之后可以得到正交实验表以及仿真结果,如表9所示。参考第一次田口法的处理方式,计算得到不同参数在不同水准数下的性能平均值,然后得出各个参数对电机不同性能的效应图如图4所示。

表8 不同影响因子及其不同水准值(田口迭代法)

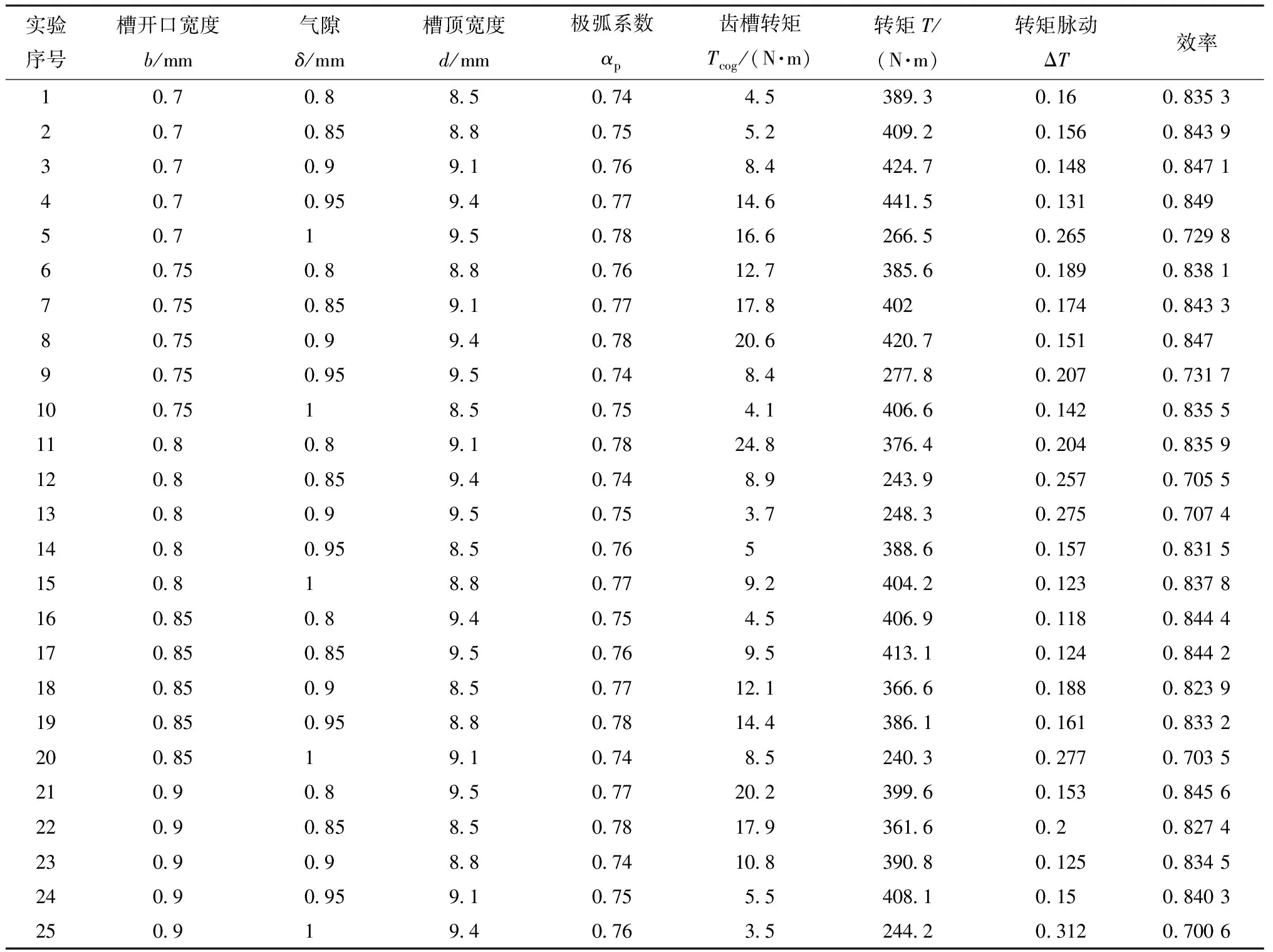
表9 正交实验表及仿真数据(田口迭代法)

图4 各目标性能效应图(田口迭代法)

分析各个效应图可以得到每个性能的最佳组合如表10所示。本次优化各参数对电机性能影响的比重如表11所示,第二次田口法中永磁体极弧系数对齿槽转矩、转矩、转矩脉动、效率的影响占比都比较大,而槽开口宽度对各个电机性能影响占比均最小。

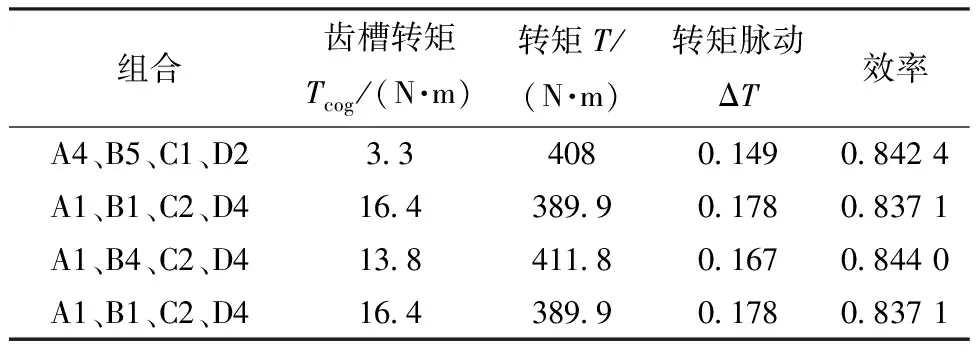
表10 电机各性能的最佳组合(田口迭代法)

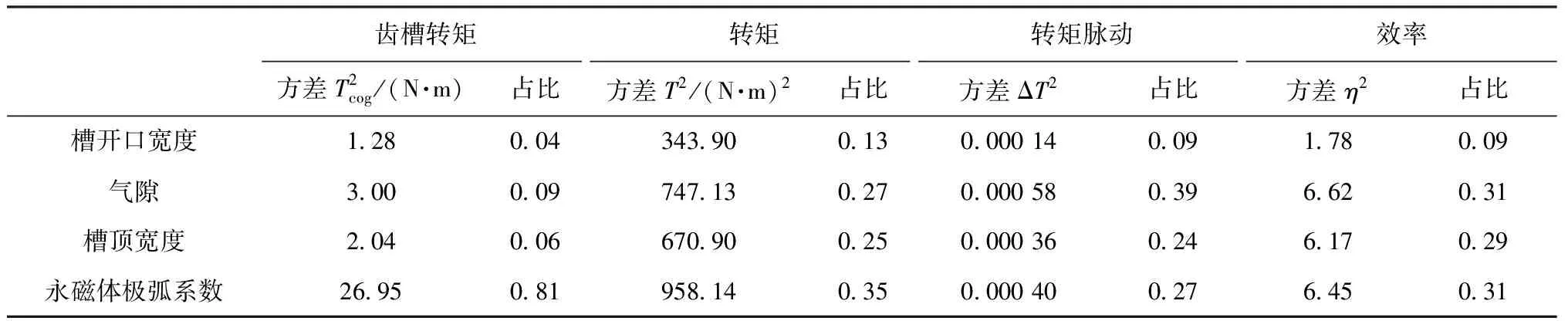
表11 不同参数对电机各性能的影响比重(田口迭代法)

在不降低效率的前提下,进一步降低齿槽转矩和转矩脉动,选择组合:槽开口宽度0.7 mm、气隙长度1 mm、槽顶宽度8.8 mm、极弧系数0.75。仿真后得到第二次优化结果,与第一次田口法优化结果对比如表12所示,齿槽转矩降低70.6%,转矩提升7.3%,转矩脉动降低20.7%,效率提升0.58%。

表12 优化前后电机性能指标对比(田口迭代法)

第二次优化得到的槽开口宽度对电机各项性能的影响比重都很小,因此在进行第三次优化时,将槽开口宽度定为0.7 mm,在第二次优化结果的基础上,进一步降低转矩脉动。本次优化的影响因子及水准值,如表13所示。

表13 不同影响因子及其不同水准值(田口迭代法)

正交实验及其仿真实验结果如表14所示。由表14可知,第三次优化后,齿槽转矩、转矩、转矩脉动、效率4个电机性能均稳定了在一个较小的范围内,可以推断此次优化已达到了瓶颈。有少数几个参数组合比第二次迭代后的转矩脉动略低,但齿槽转矩大很多。故得出结论,第二次优化之后的参数组合已达到最优。

表14 正交实验及其仿真结果(田口迭代法,槽口宽度0.7 mm)

2.3 基于遗传算法的转矩脉动优化

田口迭代法优化后,电机转矩脉动偏大,故利用遗传算法优化转矩脉动。为使遗传算法能以较少的迭代次数快速搜索优化,分析田口迭代法优化时的数据,得到遗传算法参数优化范围如表15所示。

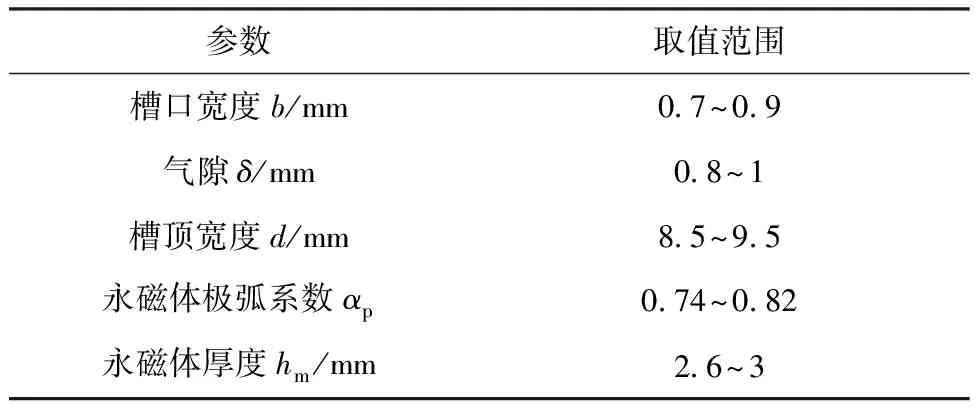
表15 遗传算法优化参数取值范围

遗传算法中成本函数的最小值点就是遗传算法搜索的优化目标的最优解。本遗传算法优化目标为电机的转矩脉动、效率和电机永磁体体积。

式中:Gtotal为总成本函数;n为优化目标的个数;Wi为第i个优化目标的权重系数;Gi(x)为i个优化目标的成本函数。

设定转矩脉动和效率的成本函数的权重系数为2,永磁体成本的权重系数为1,故本次遗传算法优化的优化总目标函数:

G(x)=2G1(x)2+G2(x)2+2G3(x)2

确定目标函数后,对遗传算法的各因子进行设置,启动算法优化器,搜索到总目标函数G(x)的最小值,即为此次优化的最优值。遗传算法优化之后电机最优组合如表16所示。

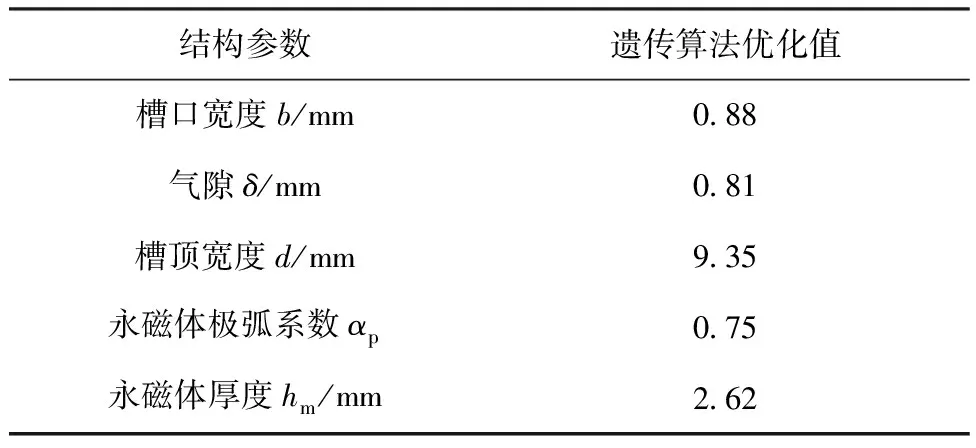
表16 遗传算法优化后电机参数最优组合

根据优化后的参数,开展电磁场有限元仿真分析,并将三种优化方法的转矩和齿槽转矩分别对比,如图5、图6。

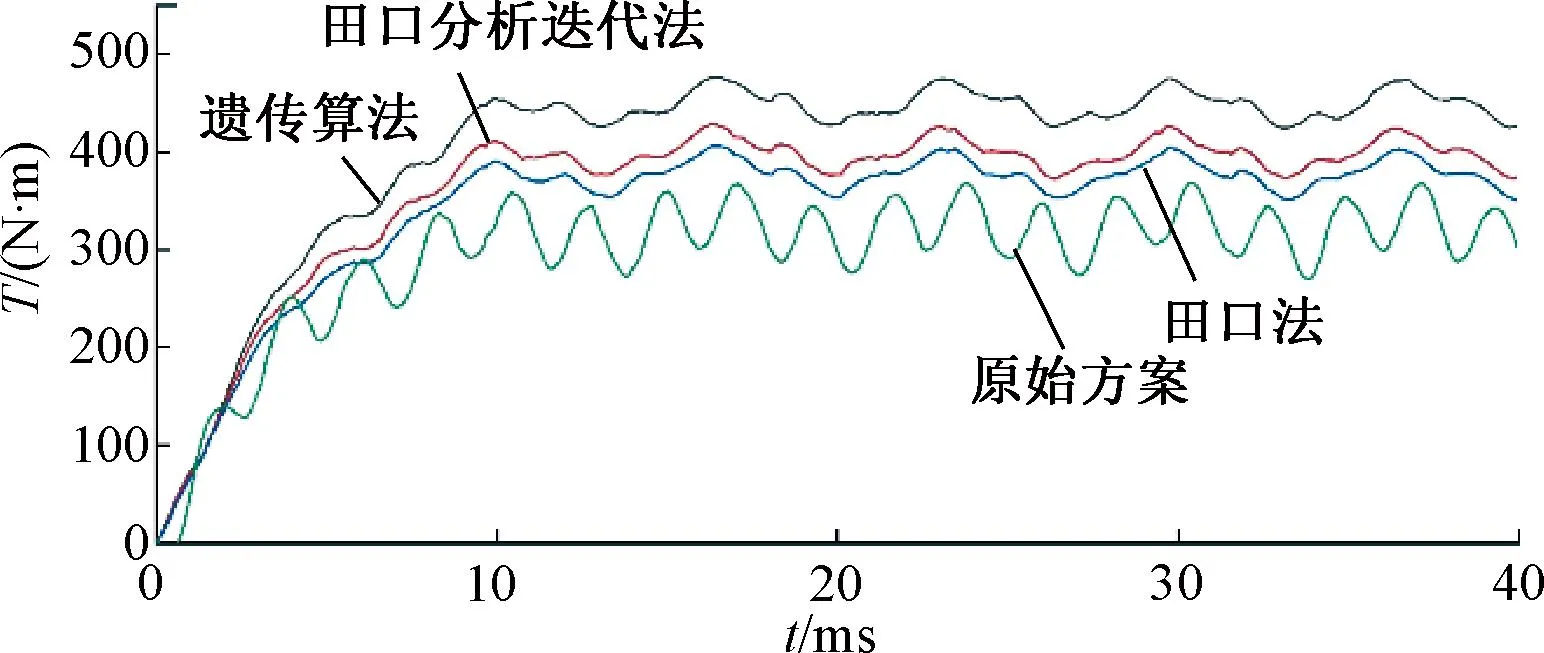
图5 转矩优化对比图

图6 齿槽转矩优化对比图

由图5可知,经过田口法、田口迭代法或者遗传算法优化之后,电机转矩均有所提升,且优化之前永磁体厚度为3.4 mm,优化之后为2.6 mm,更具经济性。由图6可知,使用田口法、田口迭代法或者遗传算法优化之后,齿槽转矩明显减小。

表17为遗传算法、田口法、田口迭代法和原始方案的电机性能对比。三种方法优化后,电机性能均有一定幅度提升。其中,遗传算法与田口迭代法相比,转矩提升7.6%,转矩脉动降低14.9%,齿槽转矩降低8.5%,效率提高0.047%。

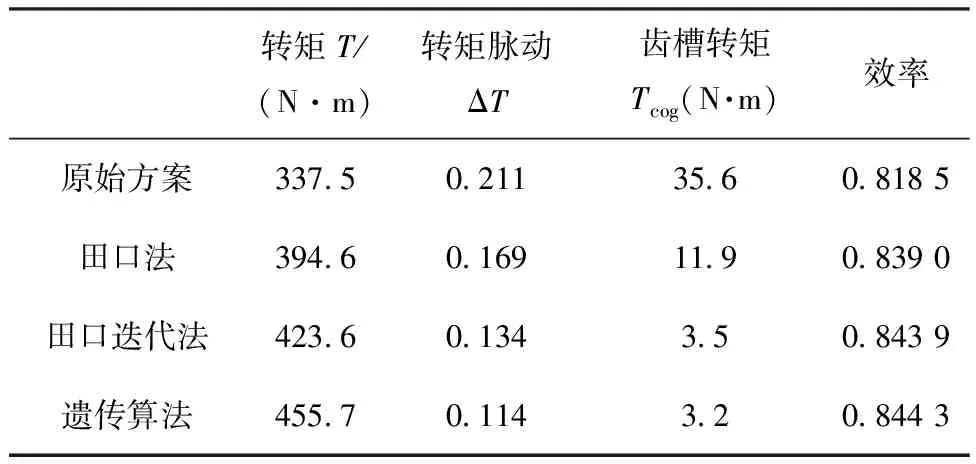
表17 各优化方法性能

通过对三种优化方法的优化效果对比,可以发现,首先,田口迭代法优化后的结果更接近于遗传算法优化后的结果,说明田口迭代法能够使得传统田口法优化得到局部最优解的可能性降低,提高优化的精确度和准确度。其次,在实验设计过程中,田口法较遗传算法简单。田口法通过正交实验,分离参数性能选择最优组合,而遗传算法则需要构建成本函数。最后,田口法仿真实验次数较少,本文的三次田口法优化共66次仿真实验,而遗传算法共进行了420次实验,且本文遗传算法是在前文田口法基础上缩小了搜索范围,若直接开展遗传算法优化,仿真实验次数将大量增加。综上分析,田口迭代法与遗传算法相比,可节约大量仿真时间,大大提高效率;与原始田口法相比,可有效避免产生局部最优解的问题,大大提高优化精确度和准确度。通过以上研究,验证了田口迭代法作为永磁同步电机快速、准确的设计优化方法的合理性。

3 有限元分析

在前文参数优化基础上,利用ANSYS Electronics Desktop中的RMxprt模块和Maxwell 2 D模块建立电机的电磁场二维模型进行空载及负载有限元仿真。Maxwell 2D有限元仿真分析电机的二维模型采用RMxprt导入,如图7所示。

图7 1/2电机二维模型

3.1 空载仿真分析

优化后的电机,空载仿真分析结果如图8～图12所示。从图8、图9及图10可知,磁力线分布整体较均匀,仅在永磁体空隙对应的定子齿部表面存在少量漏磁,故在磁密云图中,漏磁部位有较大的磁通密度,同时在对应部位产生了少量的局部磁饱和,但对电机的性能影响不大。从磁密云图来看,定子

图8 0 s和18 s空载磁力线分布图

图9 0 s和18 s空载磁密矢量图

图10 0 s和18 s空载磁密云图

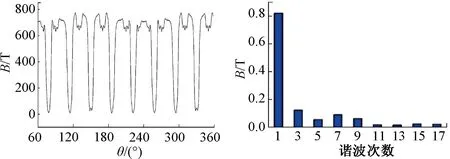
图11 空载气隙磁密及其傅里叶分解

图12 空载反电动势及其A相傅里叶分解

齿部磁密基本处于2.0 T以下,定子轭部磁密处于1.4 T左右,满足电机设计要求。

由图11可以看出,气隙径向磁密基波幅值约0.82 T。除基波外,主要含3、5、7、9次谐波,其中3次和7次谐波含量较多,分别占比基波幅值15.01%和10.91%,11次及大于11次的谐波含量较少,空载径向磁密谐波畸变率为21.65%。

由图12可知,反电动势波形变化稳定,呈现周期性变化,对称性较好,定子绕组空载反电动势幅值约为292 V,有效值约为206 V,A相的反电动势谐波分解后的空载反电动势基波幅值为264.3 V,3次谐波幅值为25.3 V,3次以上谐波含量较低。

3.2 负载仿真分析

电机负载运行时,由于绕组磁场对永磁体磁场产生影响,使电机气隙磁密发生变化[3],进而影响电机的其他性能。因此进一步对外转子潜油永磁同步电机进行负载瞬态仿真分析。

由图13～图15可知,定子槽开口两侧磁密较高,局部最高值达到了2.18 T,但齿部磁密在2.0 T以下,轭部磁密在1.4 T以下,未达到磁饱和,满足电机设计要求。负载反电动势和三相电流如图16所示,负载时反电动势峰值不超过300 V,有效值约为186 V;负载三相电流有效值约为24 A,反电动势和电流均符合电机设计要求。由图17可知,平均转矩为455.7 N,转矩脉动为0.114,转矩较设计目标高出30.2%,大于设计目标的转矩可以有效防止起动时螺杆泵需要较大扭矩而出现无法起动的问题。负载气隙磁密如图19所示,电机工作在额定工况下时,永磁体产生的磁场和电枢绕组产生的磁场叠加在一起使电机气隙合成的磁场波形畸变增大,与理论分析一致。

图13 0和0.02 s负载磁力线分布图

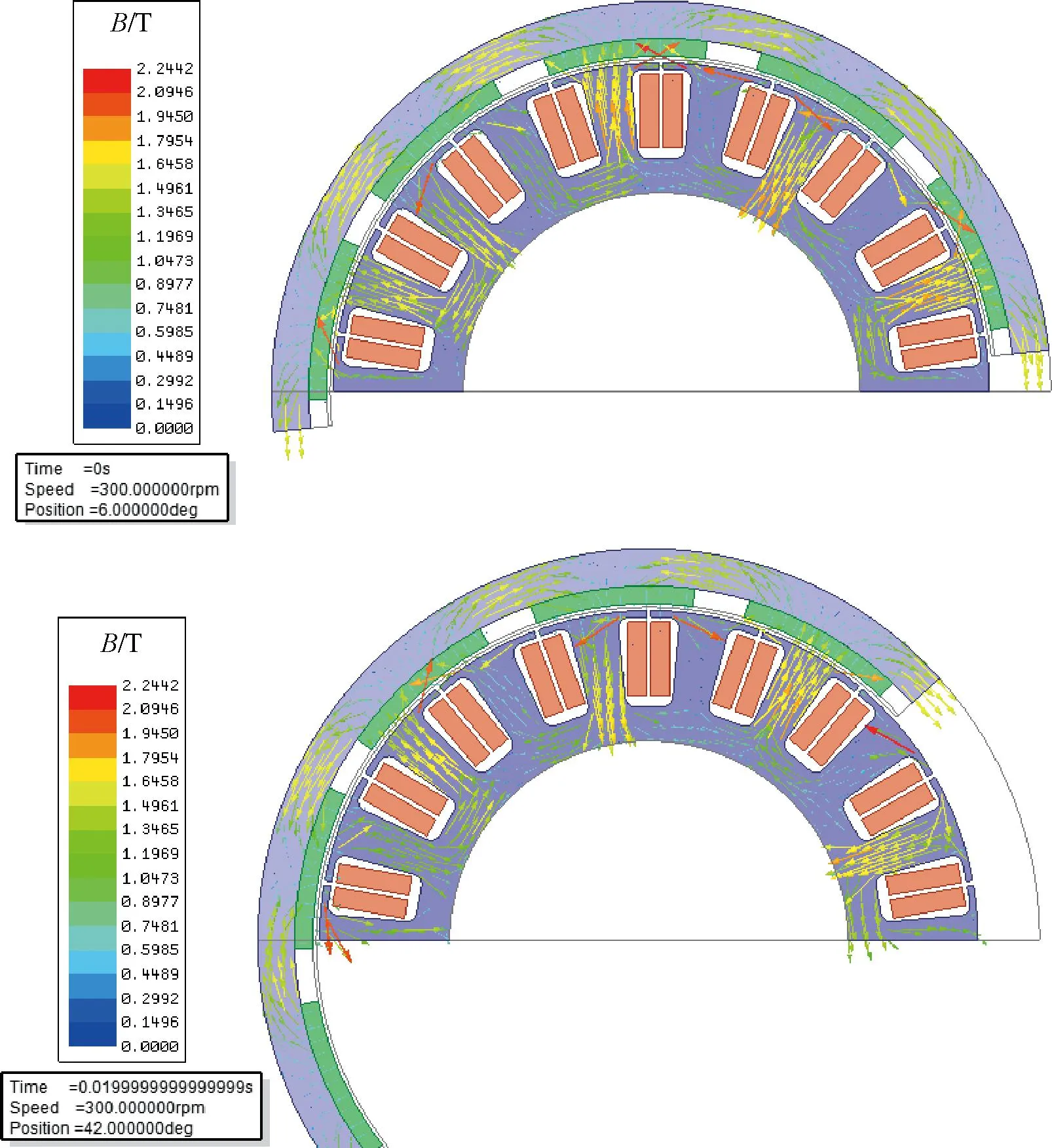
图14 0和0.02 s负载磁密矢量分布图

图15 0和0.02 s负载磁密云图

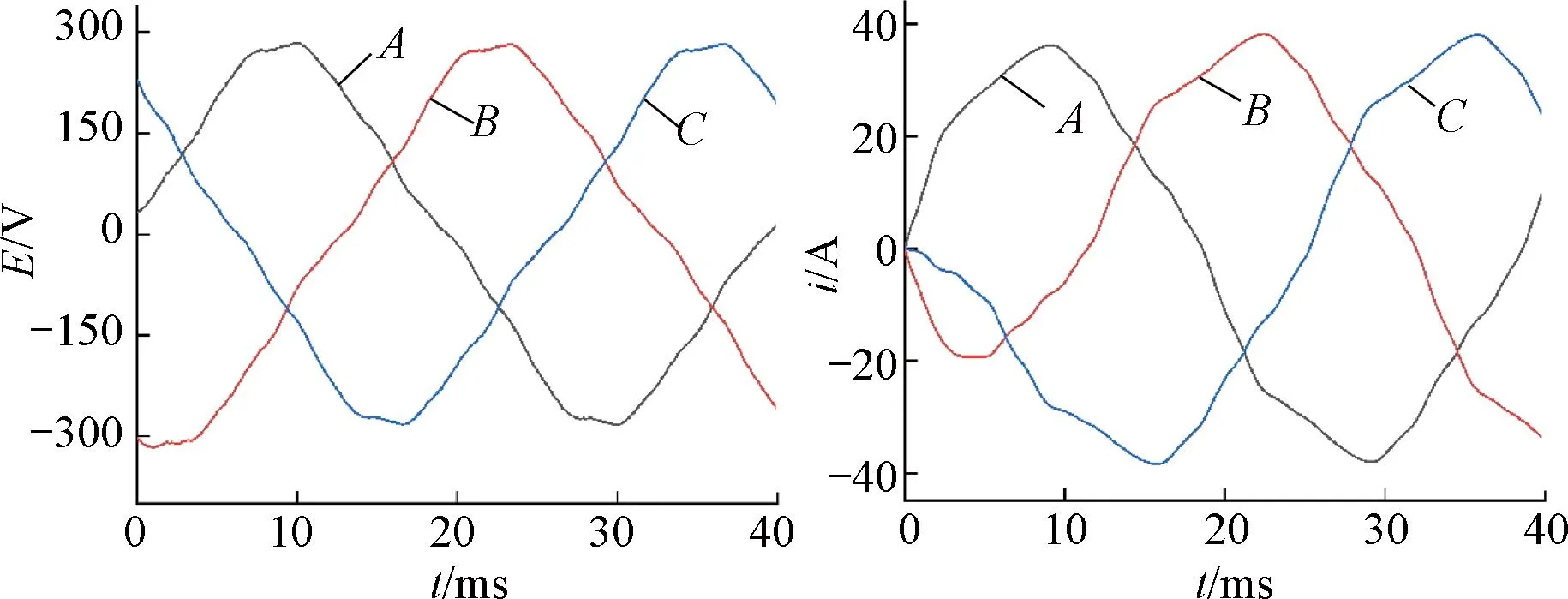
图16 负载反电动势和三相电流

图17 转矩曲线

图18 负载气隙磁密

4 结 语

确定螺杆泵嵌入到外转子永磁同步电机内部的一体化方案,提出一体式外转子潜油永磁同步电机,并开展电磁方案设计。通过对螺杆泵的扭矩分析得到电机额定参数。利用电机学原理设计电机电枢尺寸、气隙、永磁体尺寸等电磁参数。

开展基于田口法和遗传算法的电机电磁参数优化,并改进传统田口法,提出田口迭代法。将原始方案和通过田口法、田口迭代法及遗传算法优化后的电机性能进行对比分析,发现田口迭代法优化结果与遗传算法优化结果相近,验证田口迭代法作为永磁同步电机快速、准确的设计优化方法的合理性,能够用较少的正交实验获得与遗传算法全局寻优接近的优化效果,使电机某一个性能快速达到最优,节省电机参数优化设计的时间,提高效率。

利用RMxprt和Maxwell 2D对优化后的电机进行电磁性能仿真分析,获得其空、负载下的磁力线分布、磁密分布、齿槽转矩和负载转矩等曲线,分析仿真结果,验证机泵一体外转子潜油永磁同步电机的性能符合设计要求。