无刷同步发电机电枢绕组温升分析的分段磁热耦合法

2024-01-26薛敬业陈志辉茆林仪

微特电机 2023年12期

薛敬业,陈志辉,茆林仪

(南京航空航天大学自动化学院,南京 211100)

0 引言

无刷同步发电机在航空发电机领域得到了长期应用,目前多数飞机的航空发电系统均采用了无刷同步发电机[1]。无刷同步发电机具有功率密度高的特点,在运行过程中会带来较多的热问题,如果超温运行,会引起电机绕组绝缘材料的损坏,直接影响电机使用寿命。温升是电机设计优化需要关注的关键问题,而温升最高点通常出现在电枢绕组处,所以研究无刷同步发电机中电枢绕组的温升情况具有重要意义。

随着计算机技术的发展,计算流体力学(以下简称CFD)方法成为了研究多物理场耦合问题的重要手段。文献[2-7]采用CFD方法计算了高铁异步牵引电机、发电机组、轴向磁通永磁电机、永磁发电机、双定子开关磁阻电机和无刷直流电机的温度场特性。文献[8]以风冷永磁电机为对象,研究了电机整体流体域的速度分布,并以此对电机温升进行估计。文献[9]采用流固共轭传热数值计算方法对永磁电机的散热性能进行了仿真计算,并通过温升测试验证了仿真结果。文献[10]提出了一种基于磁-热-流体的多物理场模拟方法,对高速永磁同步电机进行了热分析。文献[11]采用对称性方法建立凸极风力发电机模型,并进行了温度场分析,优化了冷却结构。文献[12]仿真计算了各种工况下永磁同步电机的转子温升,并采用温度传感器的测量实验方案验证了计算结果,转子的仿真计算结果和温升实验结果存在13%的误差。文献[13]利用CFD方法,重点分析了转速和转子表面粗糙度对空气摩擦损耗的影响规律。

由于现有计算方法存在较大的温升误差,为了更准确得到电枢绕组的温升,本文采用CFD方法,借助热仿真工具研究30 kVA无刷同步发电机的电枢绕组温升,得到了额定负载情况下电枢绕组温度分布,并采用整体绕组分析法和绕组分段分析法这两种磁热耦合的迭代方法计算电枢绕组温升。根据温升测试结果,采用绕组分段方法可以提高电枢绕组温升分析的精度,同时也为准确研究电机的散热情况提供了方法。

1 无刷同步发电机参数及模型

本文以采用自通风冷却方式的无刷同步发电机为研究对象,发电机绝缘等级为C级,主要参数如表1所示。

无刷同步发电机本身是一个强耦合的模型,所以考虑流固耦合的因素来建立等效的流固实体区域。由于无法考虑电枢绕组的股线绝缘、槽绝缘和层间绝缘,因而对定子槽内及绕组端部的计算区域采用等效绝缘体的方法进行处理,并对定子槽作如下假设:

a) 电机浸漆状态良好,浸渍漆填充均匀;

b) 铜线的绝缘漆均匀分布;

c) 忽略股线间绝缘漆膜存在所造成的温差;

d) 认为定子槽内绕组的发热情况相同,忽略绕组的集肤效应。

根据以上假设将股线绝缘、层间绝缘以及槽绝缘等效为一个绝缘实体。其示意图如图1所示。

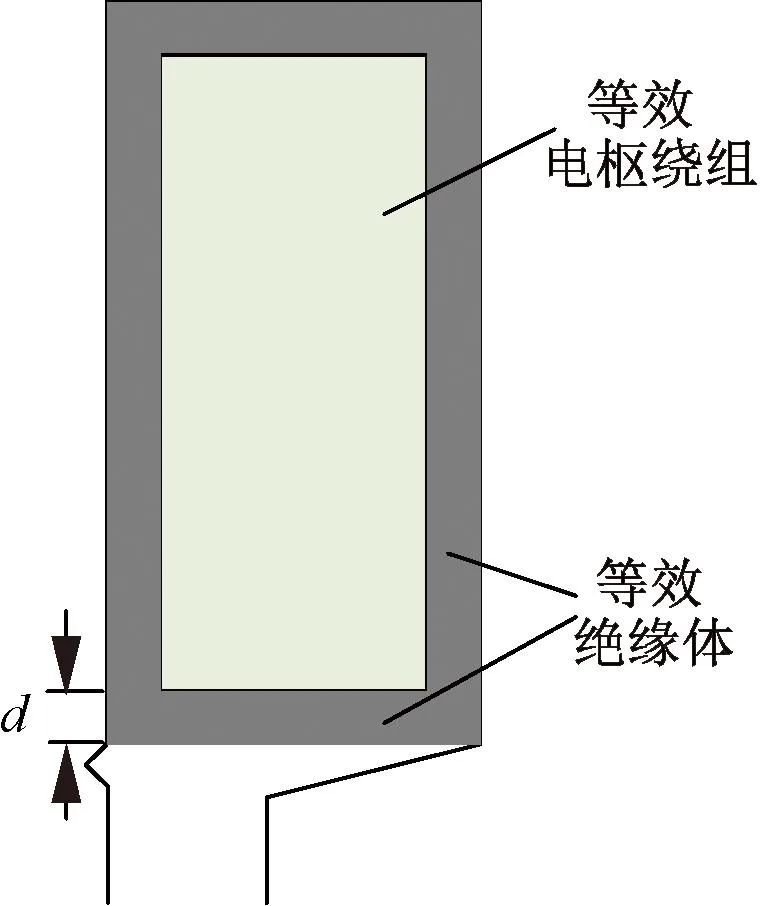
图1 定子槽截面

图1中,用槽面积减去裸导线面积得到等效绝缘体的总面积,再除以等效绝缘体的槽周长即可得到它的厚度d。电枢绕组采用一个整体紧密排列的铜线进行等效。

电机热稳定的过程是周期对称的,为提高网格剖分的质量,减少计算资源的浪费,取发电机圆周的1/4区域作为CFD数值计算域,建立1/4的固体模型,如图2所示。

图2 1/4固体区域模型

由图2可以看出,发电机主要由定子、转子、电枢绕组、励磁绕组、压块以及其他固定部件组成。

电机采用自通风的冷却方式,流体主要通过定子通风道和转子通风道与发电机进行对流换热,从而对电机进行散热。发电机的1/4流体区域示意图如图3所示,主要包括定子通风道流体、转子通风道流体、气隙流体和外部流体4个部分。

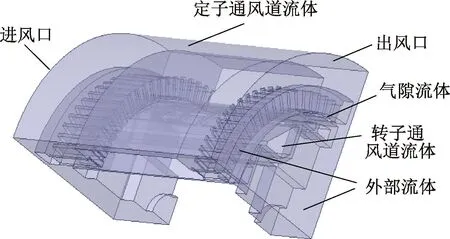
图3 1/4流体区域模型

2 热仿真分析

2.1 数学模型

本文对无刷同步发电机额定负载状态下的稳态温度场进行数值计算,热量传递主要以热传导和热对流的形式进行,不考虑热辐射的影响。由于电机内部流体雷诺数大,流动速度远小于声速,所以将流动状态假设为湍流流动,湍流模型选择k-omega SST。

依据模型的简化和求解模型,仿真过程中涉及到的k-omega SST控制方程如下:

(1)

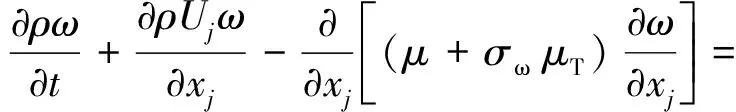
(2)

式中:Uj是j方向的速度分量;xj是j方向上的坐标分量;μ是流体黏度系数;μt是涡流运动黏度系数;k是湍流动能;τij是雷诺应力;ω是湍流动能耗散率;F1是混合函数;σk,β*,σω,γ,vT,β,σω2为模型系数。

以上控制方程是x,y平面下k方程和omega方程的对应形式,x,z和y,z平面下的方程只要在该方程的基础上更改成对应的坐标分量和速度分量。最终的空间变量由三个方程的分量合成得到。

2.2 网格剖分

本文采用多面体和六面体混合的网格剖分,边界层网格采用多面体网格,其余部分采用六面体网格。与四面体网格相比,同样条件下网格数量少,网格节点之间的过渡性好,计算精度高。网格剖分结果如图4所示。

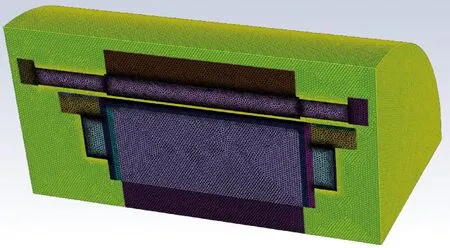
图4 网格剖分结果

2.3 边界条件

1) 固体

定子和电枢绕组采用静止坐标系,转子、励磁绕组及转子上的部件采用固体运动,转速为12 000 r/min。固体部分的材料属性如表2所示。

表2 材料属性

2) 流体

流体模型为理想气体,采用旋转参考坐标系,转速12 000 r/min,进风口为速度入口,通过实验测得入口速度6.7 m/s,出风口为压力出口,出口表压为1个大气压,流固接触壁面为耦合壁面,环境温度设为20 ℃。

2.4 热源分布

电机各部分的损耗是计算温度场的热源,损耗计算完成之后,在热仿真工具中转换为单位体积的热生成率,即可进行热计算。无刷同步发电机的总损耗主要由电枢铜损、励磁铜损、阻尼铜损和定转子铁损组成。电枢铜损和励磁铜损由式(5)计算,其余部分的损耗由有限元仿真计算,20 ℃下各部分损耗如表3所示。

表3 电机损耗

2.5 电枢绕组温度结果

利用分离求解器SIMPLE对流固模型进行计算,得到电枢绕组的温度分布,如图5所示。为了能够对电枢绕组的温度进行实时测量,样机加工过程中在电枢绕组上埋设了两处测温电阻,测温点位置如图5中所示。

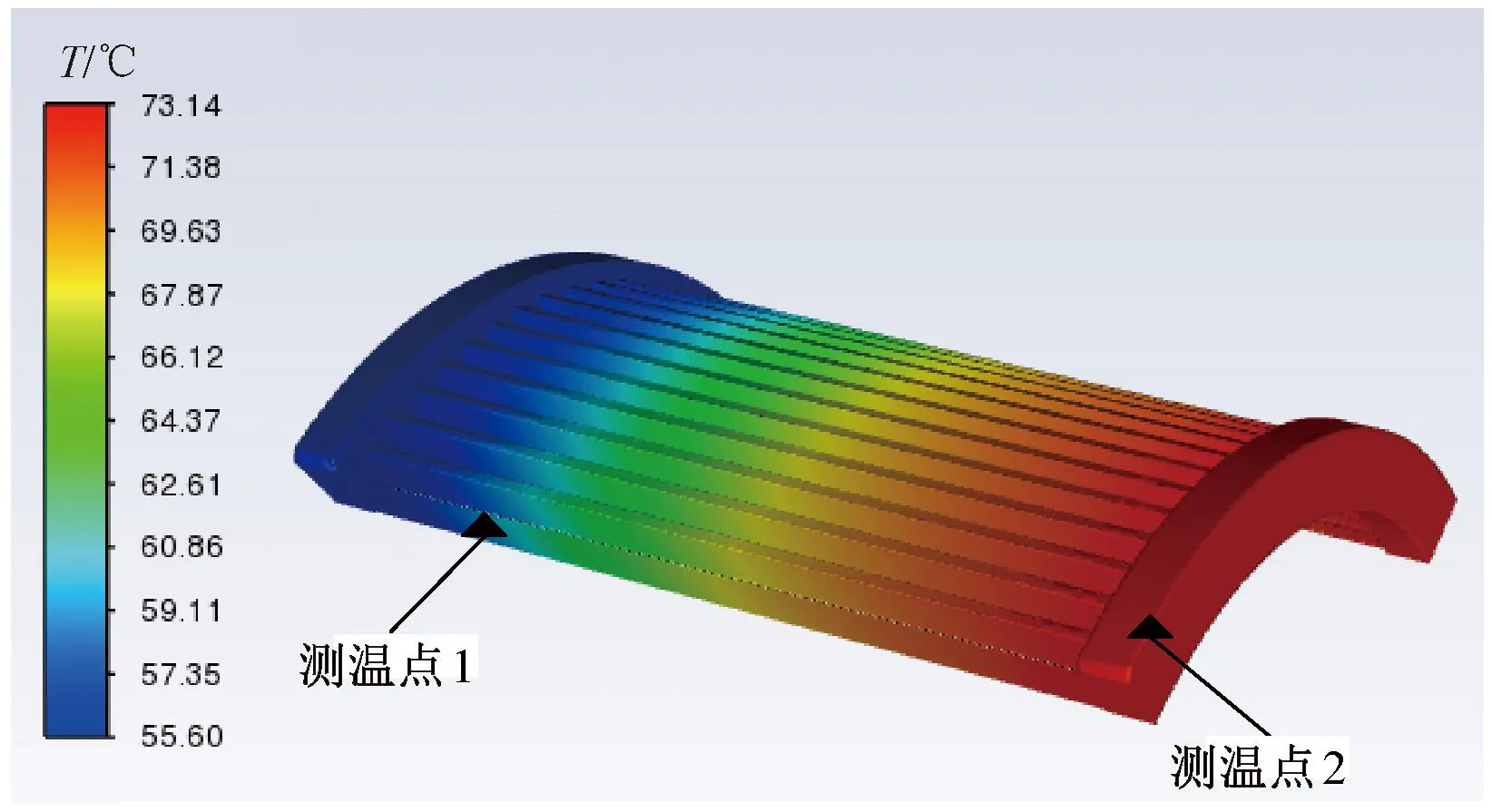
图5 电枢绕组温度结果

发电机进风口侧的温度较低,测温点1处的温度58.49 ℃,出风口侧温度较高,测温点2处的温度73.14 ℃。

3 磁热耦合法

采用磁热耦合法对电枢绕组温升分析时,进行如下假设:

a) 电枢电流有效值不变,励磁电流不变,忽略定转子铁损的变化;

b) 励磁绕组与电枢绕组不直接换热,励磁绕组的温升对电枢绕组温升影响较小,忽略励磁绕组铜损的变化;

c) 忽略空气摩擦损耗。

根据以上假设,只考虑电枢绕组电阻随温度的变化对电枢绕组温升的影响。由于电枢绕组电阻随温度的升高而增大,电枢铜损增加,电枢绕组的温升也会变化,所以初始条件下计算的电枢绕组温升会与实际运行过程中有较大的差异。本文提出磁热耦合方法,通过迭代对电枢绕组温升进行计算。磁热耦合法流程图如图6所示。

图6 磁热耦合法流程图

首先确定20 ℃下电枢绕组的电阻和铜损,进行仿真,根据温度结果,由积分求得电枢绕组平均温度,再计算此温度下电枢绕组的电阻和铜损,迭代求解,直到电枢铜损和温升之间达到平衡,输出温升结果。

电枢绕组铜线电阻率和温度的关系式:

ρT=ρT0[α(T-T0)+1]

(3)

式中:ρT为温度T时的电阻率;ρT0为温度T0时的电阻率。当T0=20 ℃时,ρ20=1.72×10-8Ω·m;α=4.27×10-3K-1为温度系数。

由式(3)可推出电枢绕组电阻计算公式:

R1=R2[α(T1-T2)+1]

(4)

式中:R1为温度为T1时的电阻;R2为温度为T2时的电阻。

电枢铜损的计算公式:

pCu=mIR2

(5)

式中:pCu是电枢铜损;m是发电机相数;I为相电流有效值;R是相绕组电阻。

20 ℃下电枢绕组的相电阻为0.019 Ω,相电流有效值87 A,图5是以此条件的仿真结果。随着电枢绕组温度的升高,电阻增大,电枢铜损增加,又会影响电枢绕组温升。采用迭代计算的方法,由式(4)、式(5)求得平均温度下电枢绕组的电阻和铜损,将每次的结果作为热源条件再次计算,最终得到电枢绕组温升。

本文重点对整体绕组分析法和绕组分段分析法进行研究。

3.1 整体绕组分析法

根据20 ℃环境温度下热仿真数值计算结果,求得整体电枢绕组上的平均温度,以此求出该温度下电枢绕组的电阻值。

根据积分求得整体绕组上平均温度65.60 ℃,电枢绕组相电阻变为0.023 6 Ω,电枢铜损变为535.89 W。以此铜损作为热源条件,迭代计算,得到电枢绕组的温度分布如图7所示。

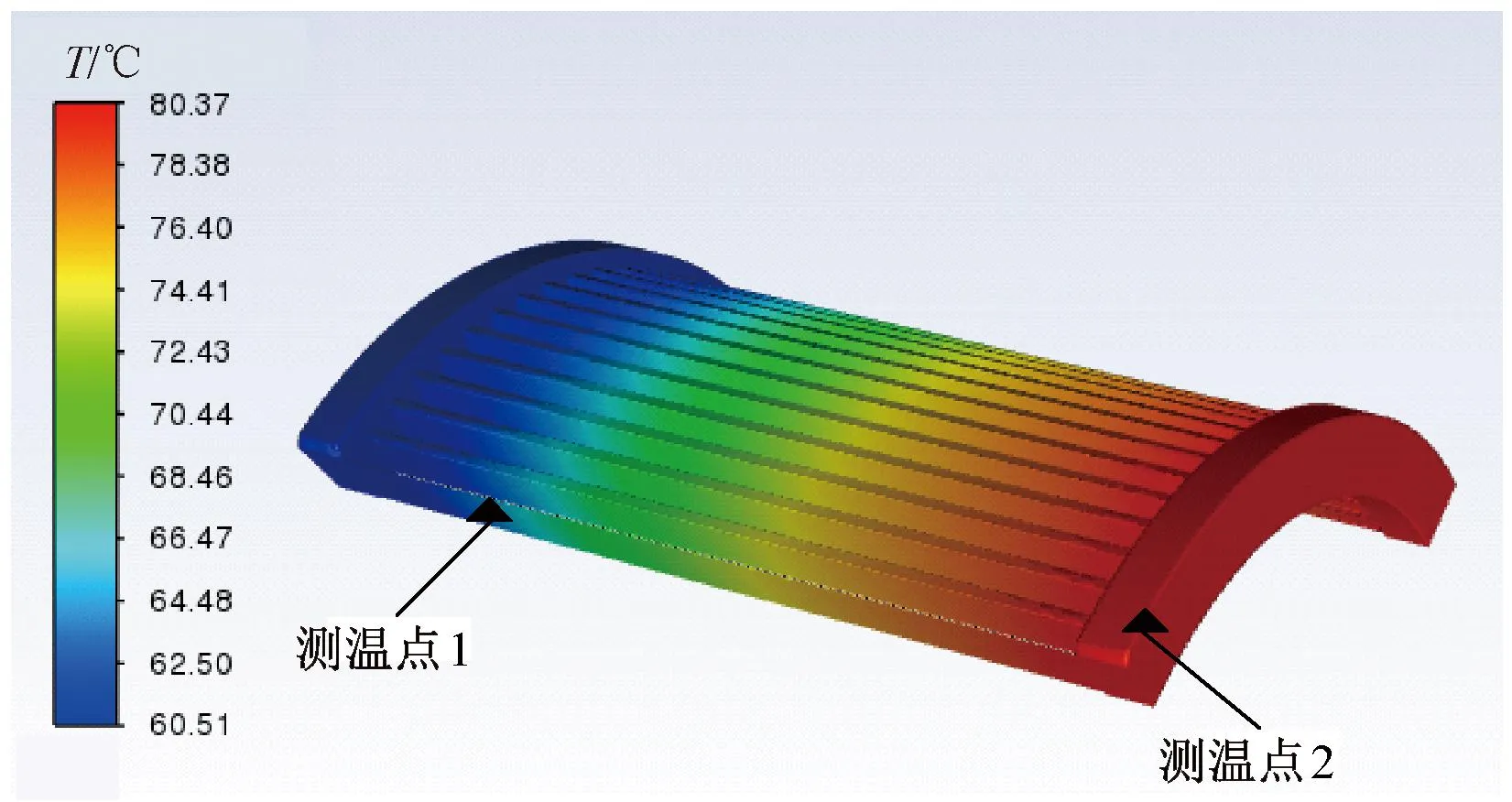
图7 整体绕组分析法第一次迭代温度结果

测温点1处的温度64.90 ℃,测温点2处的温度80.37 ℃,积分求得电枢绕组平均温度为72.15 ℃,相电阻为0.024 4 Ω,电枢铜损为544.05 W,进行第二次迭代计算。

第二次迭代得到测温点1处的温度66.59 ℃,测温点2处的温度82.44 ℃。平均温度73.68 ℃,此时电枢铜损和平均温度72.15 ℃时相差不大,达到磁热平衡的状态。三次计算的温升结果如表4所示。

表4 整体绕组分析法温升结果

若采用热仿真工具进行迭代计算,最终可以得到稳态时电枢绕组温升,但这种方法的计算周期太长。采用拟合的方法,对得到的测温点1、2处的温升结果与计算次数的关系进行拟合,拟合出的函数关系如下:

ΔT1=47.20-23.79·e-1.23n

(6)

ΔT2=63.27-35.38·e-1.25n

(7)

式中:ΔT1,ΔT2为测温点1、2处的温升;n为计算次数。拟合出的关系曲线如图8所示。

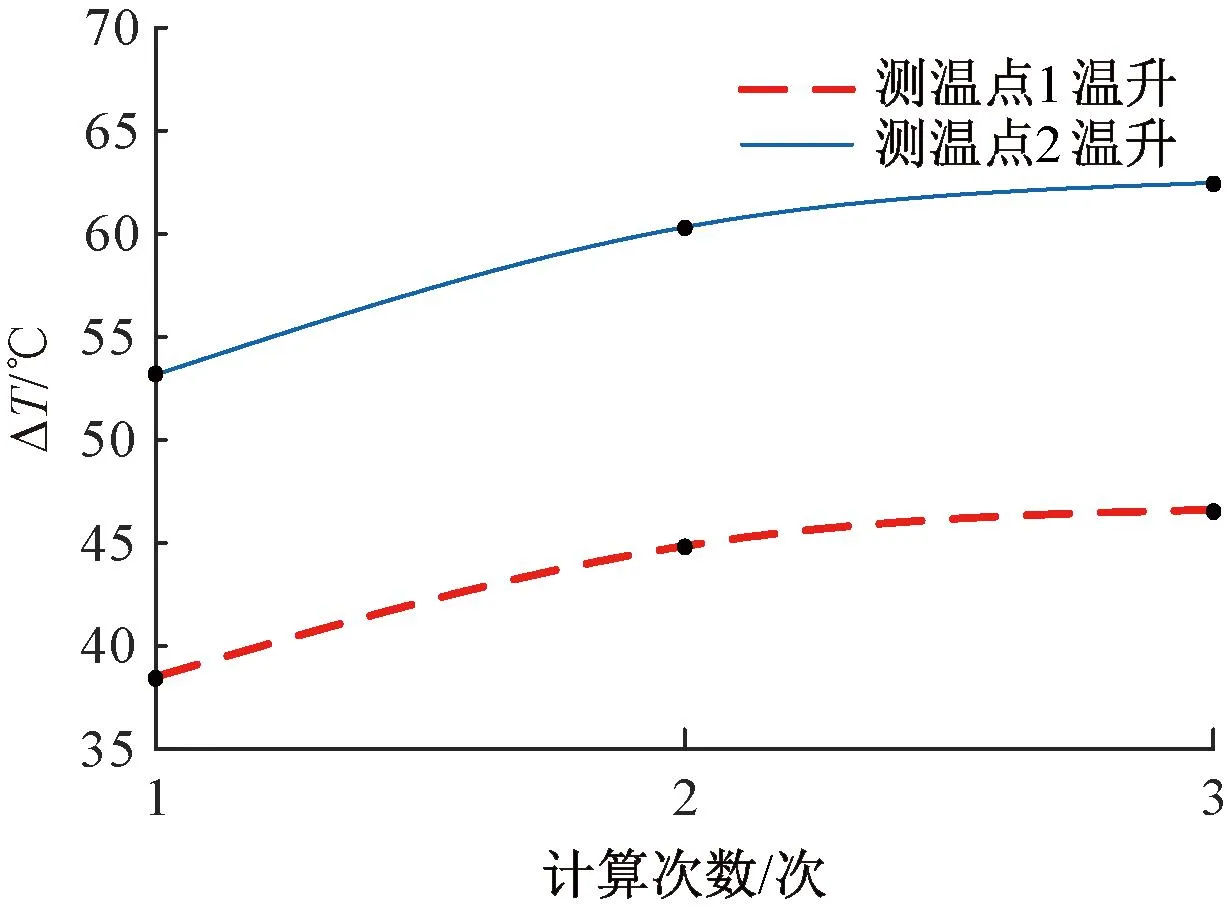
图8 温升和计算次数关系曲线

当计算次数为4时,由上式得测温点1处的温升47.03 ℃,测温点2处的温升63.03 ℃。将第二次迭代计算的结果继续进行仿真,得到测温点1处的温升46.86 ℃,测温点2处的温升62.77 ℃。仿真计算结果和函数计算结果基本一致,验证了拟合函数关系的正确性。即采用上式得到稳态时测温点1处的温升47.20 ℃,测温点2处的温升63.27 ℃。

3.2 绕组分段分析法

电枢绕组端部的温度与平均温度的差值较大,采用整体绕组分析法求得的平均温度来代替绕组各部分的温度,进而求解的电枢铜损会有较大的偏差。为了更准确计算电枢绕组温升,采用绕组分段分析法进行计算,将电枢绕组分两段,对每段绕组分别求平均温度,以此温度来计算每段绕组的电阻和电枢铜损,再进行迭代计算。

绕组分两段的示意图如图9所示,在定子轴向中线的位置进行分段。在截面位置只对电枢绕组进行分段,其他部位并未进行分段,对分段后的模型采用相同的方法进行网格剖分,并在分段位置添加两层边界层网格。仿真计算时,将分段位置电枢绕组截面设置为耦合传热壁面,其余求解域采用的边界条件和整体绕组分析法相同。

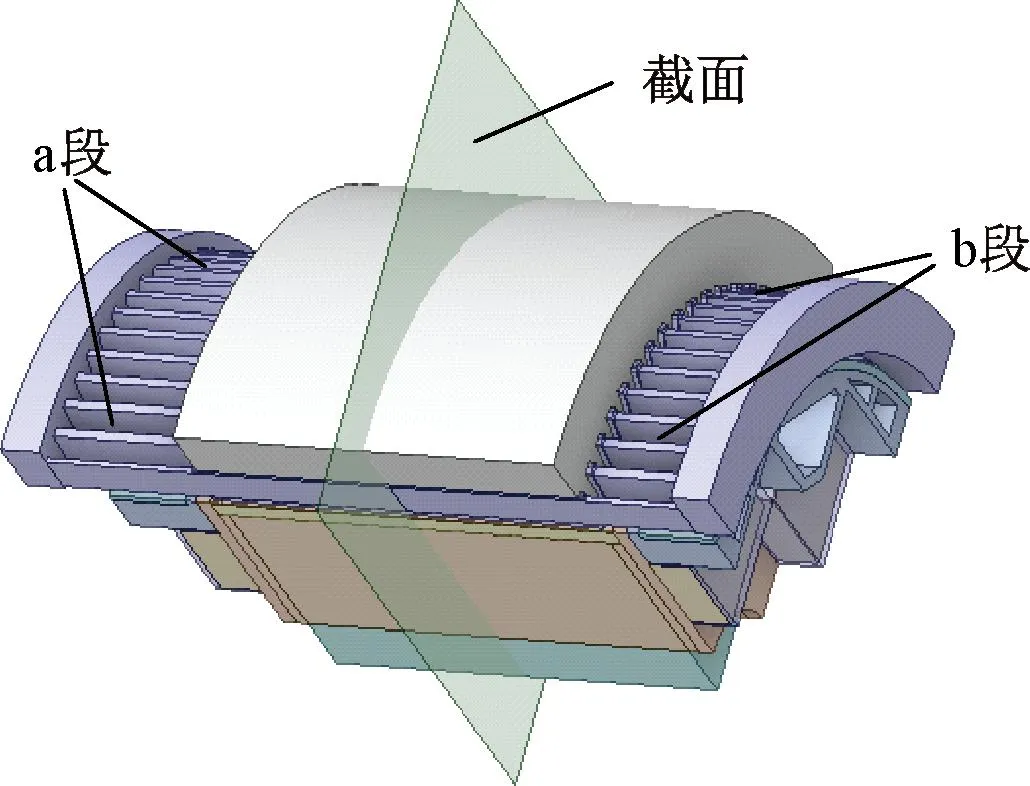
图9 绕组分两段示意图

如图9,根据a段和b段的长度比,求得20 ℃下a段的相电阻为0.009 67 Ω,b段的相电阻为0.009 33 Ω,a段电枢铜损219.58 W,b段电枢铜损211.86 W,其余损耗不变,采用相同的边界条件,得到a段和b段绕组温度分布如图10所示。

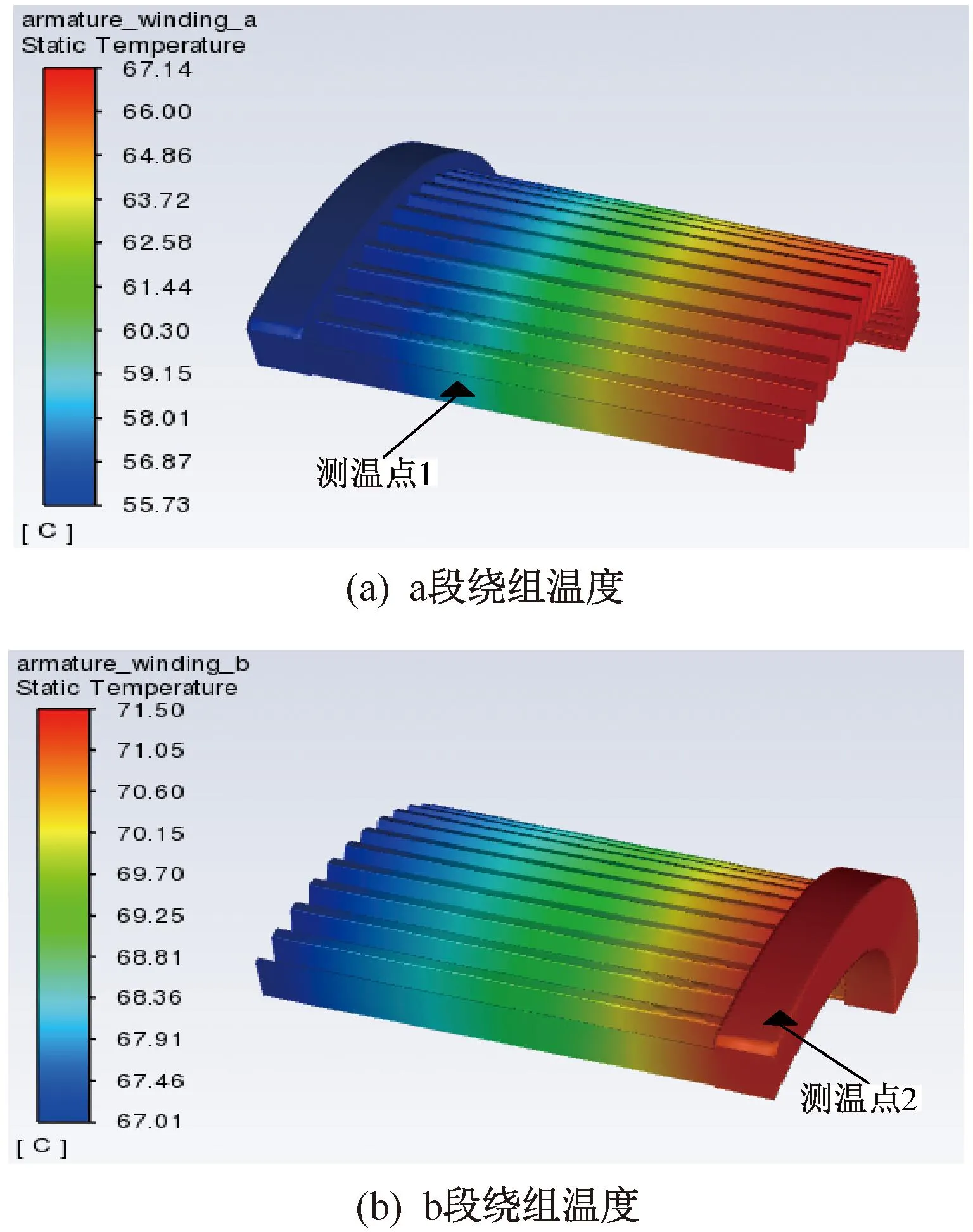
图10 绕组分两段温度结果

测温点1处的温度59.13 ℃,测温点2处的温度71.50 ℃。求得两段平均温度,即得到a段电枢铜损变为266.13 W;b段电枢铜损变为268.40 W。进行再次计算,得到a、b段绕组的温度分布情况。

迭代计算后,测温点1处的温度65.24 ℃,测温点2处的温度79.21 ℃。根据求得每段的平均温度,a段电枢铜损变为273.85 W,b段电枢铜损变为278.39 W,此时电枢铜损和温升之间还未完全达到平衡,需要再次计算。

第二次迭代计算后,测温点1处的温度67.57 ℃,测温点2处的温度80.52 ℃,和第一次迭代的计算结果相比,a段和b段的平均温度基本相同,即此时发电机磁热已经平衡。

三次计算的温升结果如表5所示。

表5 绕组分两段的温升结果

和整体绕组分析法相同,对测温点1、2处的温升结果和计算次数进行拟合,拟合得到的函数关系式如下:

ΔT1=49.00-25.90·e-0.97n

(8)

ΔT2=60.79-54.67·e-1.77n

(9)

由上式可得,采用绕组分两段的分析方法,得到稳态时测温点1处的温升49.00 ℃,测温点2处的温升60.79 ℃。

若电枢绕组的分段越细,每段温度就越接近求得的平均温度,即计算的电阻值和电枢铜损误差也会越小。为了研究电枢绕组的分段数对温升的影响,对电枢绕组进行分四段处理,分四段示意图如图11所示。和绕组分两段的方法相同,在对分段模型进行网格剖分时,在分段位置分别添加两层边界层网格,求解时分段截面设置为耦合传热壁面,其余边界条件保持不变。

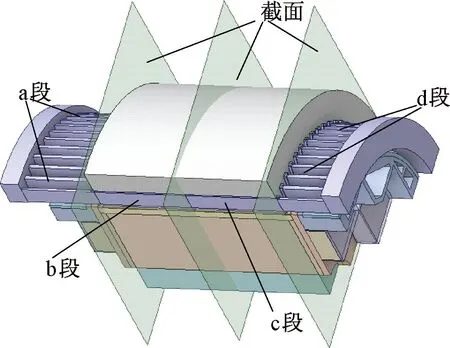
图11 绕组分四段示意图

计算每段的电阻和电枢铜损,添加热源,以相同的条件进行计算,得到每段的平均温度,进行迭代。同样经过3次计算后,每段的平均温度和电枢铜损基本不变化,已经达到磁热平衡的状态。电枢绕组分四段的温升结果如表6所示。

表6 绕组分四段的温升结果

采用相同的方法进行拟合,拟合的测温点1、2处的温升和计算次数的函数关系如下:

ΔT1=49.25-21.58·e-0.96n

(10)

ΔT2=60.48-60.88·e-1.84n

(11)

由上式可得,绕组分四段,稳态时测温点1处的温升49.25 ℃,测温点2处的温升60.48 ℃。电枢绕组分两段时,测温点1处的温升49.00 ℃,测温点2处的温升60.79 ℃。依据实验结果,电枢绕组分四段得到的温升,更接近实验测得的温升。因为分段越细,求得的平均温度来代替每段的温度产生的误差也就越小,计算的电枢铜损也更准确,从而温升也更接近实际运行中的温升。

同时,电枢绕组分两段的结果和分四段的结果比较相近,温升误差没有大幅降低。而且增加电枢绕组的分段数,模型的复杂度会提高,计算所消耗的时间和资源也会更多。因此在温升误差允许的范围内,对电枢绕组分两段处理,经过3次计算,通过拟合的函数关系式即可得到稳态时电枢绕组温升。

4 实验验证

实验平台如图12所示,主要由原动机、齿轮箱、无刷同步发电机和负载箱组成。由原动机经过齿轮箱,拖动无刷同步发电机运行至额定转速,完成额定阻性负载状态下电枢绕组温升测试实验。

图12 实验平台

为避免温度过高对电机部件造成损坏,无刷同步发电机电枢绕组的进风口端部和出风口端部分别埋设了铂电阻(Pt100)作为传感器测量电枢绕组温度,埋设位置图如图13所示。温度传感器的引线通过位于机壳内的钻孔引出到电机外部,然后将引出线接至温度显示仪,可以实时显示电枢绕组的温度。

无刷同步发电机进行温升测试时,发电机外接额定阻性负载,由原动机拖动至额定转速,运行至热稳定的状态,同时记录下测温点1和测温点2处的温度。温升实验总共进行30 min,由于后期6分钟内温升小于0.1 ℃,即认为电机已经达到该工况下的稳态温度。其中1组实验结果如图14所示。

图13 测温位置图

图14 实验结果

进行3组测量后取平均值,实验数据如表7所示。

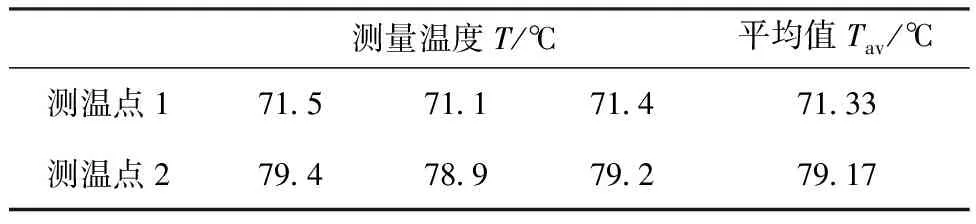
表7 温升实验结果

由表7看出,实测的测温点1和2每次的温度基本一致,实验环境温度20 ℃,实验得到测温点1处温升51.33 ℃,测温点2处温升59.17 ℃。额定负载情况下电枢绕组温升最高59.17 ℃,电机的绝缘等级为C级,有较强的过载能力,可以在恶劣的环境下应用。

采用三种方法的温升误差分析结果如表8所示。

表8 温升误差分析

温升误差是通过拟合预测的温升和实验测量温升之间的误差。由表8可得,采用整体绕组分析法对电枢绕组温升计算后,测温点1处的温升误差8.05%,测温点2处的温升误差6.93%,较为准确度地计算了电枢绕组温升。

采用绕组分段分析法计算后,对电枢绕组分两段,得到测温点1处的温升误差4.54%,测温点2处的温升误差2.74%。比较整体绕组分析法,两个测温点的温升误差大幅减小,准确度相对更高,仿真计算结果也更接近同步发电机运行过程中的温升。对电枢绕组分四段进行计算,测温点1处的温升误差4.05%,测温点2处的温升误差2.21%,经过比较,温升误差结果和分两段的结果基本一致。