基于拟合优先搜索的多场景自适应改进A*算法*

沈克宇,游志宇,刘永鑫

(西南民族大学电气工程学院,四川 成都 610225)

1 引言

近年来,移动机器人技术已经逐渐替代传统人工作业,被广泛应用到工业、服务业、城市安全和空间探测等领域。路径规划是移动机器人任务管理系统的关键技术之一,是指在有障碍物的工作环境中规划出一条从起始节点到目标节点的无碰撞路径,并使规划路径满足某些优化原则(如搜索速度更快、路径距离更短等)成为最优路径[1]。根据对场景地图信息掌握的程度,无人驾驶机器人路径规划可分为局部路径规划和全局路径规划[2,3]。局部路径规划需要硬件设备能实时采集周围场景地图信息,对环境误差和噪声有较高的鲁棒性。全局路径规划基于先验全局地图信息,规划出的路径精度取决于获取的场景地图信息的准确度。

在全局路径规划算法中,基于启发式搜索的A*算法[4,5]拥有出色的路径最优性、寻路完备性和搜索高效性,多被应用于静态场景地图的路径规划中,一直是研究人员研究改进的重点。文献[6]通过改变距离计算方式与函数权重来缩短寻路时间、减少冗余节点数量。文献[7]将切比雪夫距离作为启发式函数因子,同时引入父节点增强其影响力,使得搜索速度极大提升。文献[8]通过扩展到20搜索邻域,并设置了安全距离,使规划出的路径更平滑且距离更短。文献[9]设计了新型距离计算方式,使得最终规划出的路径距离更短。文献[10]针对复杂场景地图引入安全因子使路径尽量避开危险区域,适用于机器人运行。文献[11,12]都采用双向搜索方式以增强算法实时性,文献[12]还引入了扇形邻域扩展,使搜索更有导向性。文献[13]利用模拟退火法取代传统算法的距离判断方式,使得搜索更快地向目标节点进行。文献[14]通过引进时间因子对估价函数进行改进,使得改进算法可以节约规划时间、降低路程成本。文献[15]在传统A*算法中引入动态窗口法,提升路径平滑处理的灵活性并满足移动机器人非完整性约束条件。

从上述文献中可以看出,对A*算法的改进主要包括优化距离计算函数、扩展邻域以及与其它智能算法相结合,但这些改进的普适性和鲁棒性较弱,且部分对计算机性能要求较高。本文针对部分文献中的改进A*算法存在鲁棒性差、遍历节点数多、路径转折角度较大和搜索速度较慢的问题,基于传统A*算法,在二维静态环境下以移动机器人为载体,提出一种兼顾算法鲁棒性和普适性且计算效率较高的基于拟合优先搜索的多场景自适应改进A*算法。首先,通过自适应控制机制实现启发式搜索,根据地图变化适时调整权重。其次,引入拟合优先搜索,增强算法的启发性。接着,通过路径剪枝和冗余节点删除机制,对路径进行导向规划和平滑处理。在相同栅格场景地图中,传统A*算法与本文改进A*算法的仿真结果表明,本文改进A*算法在路径规划时遍历节点更少、路径更平滑、搜索速度更快,对多场景地图具有更强的鲁棒性和普适性。

2 传统A*算法

A*算法是由Hart等人[4]提出的,在Dijkstra算法基础上发展而来。它根据定义的代价函数在静态环境中寻找一条从起始位置到目标位置的最小移动距离路径,其代价函数表达式如式(1)所示:

f(n)=g(n)+h(n)

(1)

其中,n表示当前节点所在位置;f(n)表示从起始节点位置到当前节点位置的代价函数;g(n)表示移动机器人从起始节点位置到当前节点位置的实际移动代价;h(n)表示从当前节点位置到目标节点位置的预估移动代价,称为启发式函数。在路径规划时,若h(n)远小于g(n),此时A*算法近似于Dijkstra算法,遍历节点会增多,搜索速度将大大降低;若h(n)远大于g(n),此时A*算法约等于最佳优先搜索算法,搜索速度提高,但容易出现局部最优解。因此,选择合适的启发式函数h(n)将会影响A*算法的规划性能。

常用的h(n)计算方法有欧几里得距离(Euclidean Distance)、曼哈顿距离(Manhattan Distance)和对角线距离(Diagonal Distance)。假设起点坐标为(s1,s2),终点坐标为(g1,g2),则欧几里得距离的计算公式如式(2)所示:

(2)

曼哈顿距离的计算公式如式(3)所示:

h=|s1-g1|+|s2-g2|

(3)

对角线距离的计算公式如式(4)所示:

h=1.4×Diagonal+(Straight-2×Diagonal)

(4)

其中,Diagonal=min(|s1-g1|,|s2-g2|),Straight=|s1-g1|+|s2-g2|。

由于欧几里得距离的计算精度高于曼哈顿距离和对角线距离的,得出最优路径的可能性更大,故A*算法选取欧几里得距离进行移动代价预估。

3 改进A*算法

传统A*算法在进行路径规划时,需要遍历的节点数较多、搜索速度慢、鲁棒性较差,而且规划出的路径存在许多冗余节点,路径总转折角过大而不适合移动机器人运动学原理,这些不足都限制了A*算法的应用。

本文从自适应权重调整、拟合优先搜索以及局部剪枝与冗余节点删除这3个方面对传统A*算法进行改进,以保证改进后算法最终规划出的路径相对最优,增强鲁棒性和搜索效率,减少遍历节点数和总转折角度,从而缓解移动机器人的存储压力,降低能源损耗。

3.1 自适应权重调整

传统A*算法在遍历节点时存在循环访问判断的情况,搜索效率较低。因此,本文引入父节点并增强其启发能力,以减少遍历节点数,同时提高搜索速度。为了增强算法的鲁棒性和普适性,同时避免因启发函数过强导致规划出的路径出现更多局部最优解,本文设计了能随场景地图变换的自适应权重W,如式(5)所示:

(5)

在规划之前先量化标定障碍物所在栅格,将栅格地图中可通行节点总数记作Sum0,障碍物节点总数记作Sum1,则式(5)中的P表示起始节点到目标节点所围地图的障碍物分布率,其计算如式(6)所示:

(6)

在场景地图发生变化时,障碍物分布率P也会变化,此时自适应权重W会随P的改变而自适应地调整,使之能适应多种场景地图,此时能够进行自适应权重调整的启发式函数h′(n)如式(7)所示:

h′(n)=W×[h(n)+h(n-1)]

(7)

其中,(n-1)表示当前节点位置n的父节点所在位置。

为了验证增加了自适应权重调整的启发式函数在遍历节点和搜索速度上的性能,在图1所示30×30栅格地图中进行对比测试,相关结果如表1所示。

Figure 1 Comparison of traditional A* algorithm and the algorithm with adaptive weight adjustment图1 传统A*算法与增加自适应权重调整的A*算法对比

Table 1 Results comparison of traditional A* algorithm and the algorithm with adaptive weight adjustment

图1中,圆形为起始节点,五角星为目标节点,黑色为障碍物,灰色节点为遍历且收录的节点,浅灰色为在判断后丢弃的节点,黑色实线为最终路径。

根据图1和表1的数据可知,增加自适应权重调整的A*算法所遍历的节点数远少于传统A*算法的,且寻路时间更短。

3.2 拟合优先搜索

传统A*算法的搜索范围为4邻域或图2a中的8邻域。研究人员针对搜索邻域的扩增与缩减展开研究,当邻域增大为16邻域甚至无穷大时,能保证寻路最优,但搜索速度变慢;当缩减邻域到3邻域甚至单向搜索时,搜索速度提高但无法保证寻路最优,且可能搜索失败。由此可见,无论是扩大邻域还是缩减邻域,都有一定的局限性,故本文并没有针对可扩展邻域的数量进行改进,而是重新设计传统8邻域中的动态规划矩阵Motion。

记(dx,dy)为当前节点与邻接节点之间横纵坐标的变化数值,S(i)为从当前节点到邻接节点的单步移动距离,此时的动态规划矩阵如式(8)所示:

Motion=[dx,dy,S(i)]

(8)

Figure 2 Traditional 8 neighborhoods search and its limitations图2 传统8邻域搜索与其局限性

如图2b所示,以目标节点为中心,向外画圆时,搜索过程中会出现h(n)相等的情况。由于A*算法是基于最小移动距离原理进行路径搜索,所以当h(n)相等时,g(n)将占据算法的主导位置,起到引导搜索方向的决定性作用。故本文提出拟合优先搜索策略,通过对搜索邻域分配优先级,以增强g(n)的搜索启发性,如图3所示。当移动方向靠近搜索方向时,实际移动距离变小,此时寻优路径向最优方向拟合,搜索速度得到提升。图3中,黑色虚线表示从起始节点(父节点)到目标节点的搜索向量,黑色实线为从起始节点向子节点的移动向量,向量间的夹角记作θ。

Figure 3 Vector angle representation图3 向量夹角表示

记a=(ax,ay),b=(bx,by),向量间夹角θ的余弦如式(9)所示:

(9)

根据搜索向量与移动向量的位置关系,本文对传统8邻域的动态规划矩阵Motion进行设计。由式(9)可知,向量间夹角θ越小,其移动方向与最优搜索方向越拟合,故设计关于cosθ的函数作为搜索邻域时单步移动距离S(i)的权重,确保在寻路过程中优先选择与搜索向量拟合的邻域,从而增强g(n)的启发性和导向性,提高搜索速度。但该函数取值应该适中,若是过大则无法用于复杂地图环境,若是过小则路径优化不够明显。

改进后的S′(i)如式(10)所示:

S′(i)=[(1-cosθ)/8+1]×S(i)=

(10)

此时扩展邻域并分配优先级的g(n)动态规划矩阵如式(11)所示:

Motion=[dx,dy,S′(i)]

(11)

由式(1)及A*算法寻路原理可得拟合优先搜索f(n)如式(12)所示:

(12)

在图1的场景地图中进行验证,测试结果如图4所示。图4中黑色实线为在自适应权重调整基础上增加拟合优先搜索策略后规划出的路径。与图1b对比,图4中灰色栅格覆盖面积更少,可以看出路径向目标节点拟合程度较高。结果表明,遍历节点数比表1中自适应权重调整算法的减少10个,寻路时间由表1中的0.161 s减少到0.142 s,此时算法搜索效率更高。可见在自适应权重调整算法的基础上对其进行优先拟合搜索使得改进A*算法的性能更为优越。

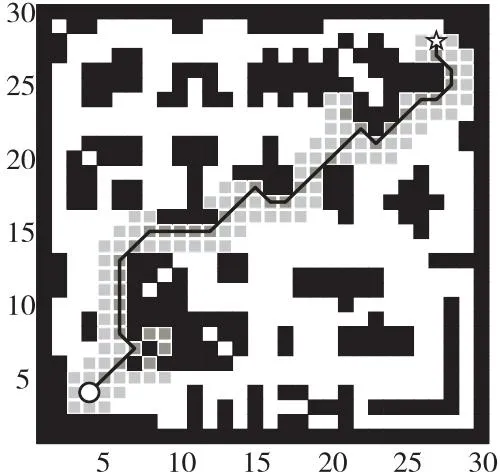
Figure 4 Test result of algorithm introducing fitting-first search图4 引入拟合优先搜索的算法测试结果

3.3 局部剪枝与冗余节点删除

从图4中可以明显看到,路径存在局部最优解,而且经过了大量的冗余节点,故还需要对之前规划出的路径进行平滑处理。首先通过局部剪枝去除路径上的局部最优解,之后再删除路径上的冗余节点,以保证最终规划出的路径经过的节点数更少且路径更为平滑。

3.3.1 局部剪枝

因为场景地图中存在多种障碍物分布情况以及8邻域搜索的角度局限性,故可能出现三角形和梯形局部冗余。即使是更复杂的局部冗余路径,也可以先将三角形剪枝为梯形,再对梯形剪枝,从而形成平滑路径。

图5a所示为三角形局部冗余路径,图5b为梯形局部冗余路径。其中,灰色圆球代表的a、b、c、d均是路径上相邻的节点,黑色为障碍物。图5a中若需要从a点到达c点,可以直接从a到c,并不需要经过中间节点b。图5b中若需要从a点到达d点,可以直接从a到d,并不需要经过中间节点b和c。图5的三角形和梯形路径存在局部最优解,导致全局路径无法最优,因此需要对局部冗余路径进行剪枝处理,以避免出现局部最优。 记4个相邻节点a、b、c、d的坐标分别为(a1,a2),(b1,b2),(c1,c2)和(d1,d2)。

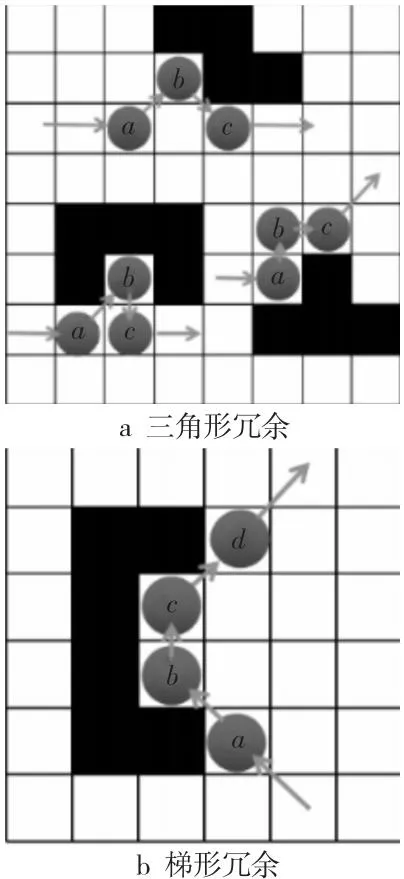
Figure 5 Schematic of local redundant paths图5 局部冗余路径示意图

对于图5a的三角形局部冗余路径,将从a到b的向量记作AB,将从b到c的向量记作BC,将从a到c的向量记作AC。本文采用8搜索邻域进行路径规划,一旦路径出现三角形局部最优的情况,该三角形一定是等腰直角三角形,此时可以通过坐标位置关系或向量垂直原理进行判断。

向量垂直判断函数如式(13)所示:

Judge_Tri=

(AB·BC)×(AC·BC)×(AC·AB)

(13)

若Judge_Tri为0,表示此时路径可能存在三角形局部冗余,需要对路径进行判断:若对局部最优路径剪枝后经过障碍物,不处理;若a与c可直连且未经障碍物,可以直接沿着从a到c的方向剪枝。

剪枝完三角形局部冗余后,再对梯形冗余进行剪枝操作。记从a到d的向量AD=(d1-a1,d2-a2),从b到c的向量记作BC=(c1-b1,c2-b2)。通过向量平行原理判断路径中的梯形冗余,其判断函数如式(14)所示:

Judge_Tra=(d1-a1)×(c2-b2)-

(d2-a2)×(c1-b1)

(14)

若Judge_Tra为0,说明此时局部路径呈梯形,需要对从a到d的节点进行判断。若经过障碍物不处理,否则直接对路径剪枝。

Figure 6 Path pruning demonstration图6 路径剪枝演示

为验证路径剪枝的有效性,针对图1所示地图进行剪枝处理仿真测试,测试结果如图6所示。其中虚线为原始路径,实线为剪枝后路径。从图6中可知,剪枝可以有效解决复杂地图中出现的局部最优路径的问题。

3.3.2 冗余节点删除

剪枝完成后,还需要对路径上的冗余节点进行处理,从而减少路径经过的节点数,使得最终路径更平滑。首先,计算初始路径中邻近3个节点间的位置关系,通过向量共线原理判断并存储路径中的拐点;接着,依次判断邻近4个拐点是否可以直连,直连后若未经过障碍物且总距离最短,则记录该拐点位置,并删除初始路径中位于直连拐点之间的冗余节点;随后,以记录拐点为起点,再与随后3个邻近拐点进行直连判断,直到目标节点为止。更新路径节点作为新规划路径,再次循环判断,直到路径上没有冗余节点,此时得到的路径即为最终路径。

冗余节点删除原理示意图如图7a所示,图中A→B→C→D为规划出的路径。假设A→D、A→C和B→D均未经过障碍物,可直接得出A→D为最优路径。若A→D经过障碍物,再比较A→C→D与A→B→D这2条路径的总距离,距离最小的为最优路径。

为验证路径剪枝和冗余节点删除策略的有效性,在图4场景中进行路径规划测试,结果如图7b所示。其中,虚线为初始路径,实线为经过路径剪枝与冗余节点删除之后的路径,深灰色方格表示最终经过的节点。

从图7b中可知,删除冗余节点后的规划路径需要存储的遍历节点数大大减少,路径更为平滑,经过的节点数也更少。此时仅需要记忆几个拐点就可以规划出完整的路径,有效缓解了移动机器人的存储压力。

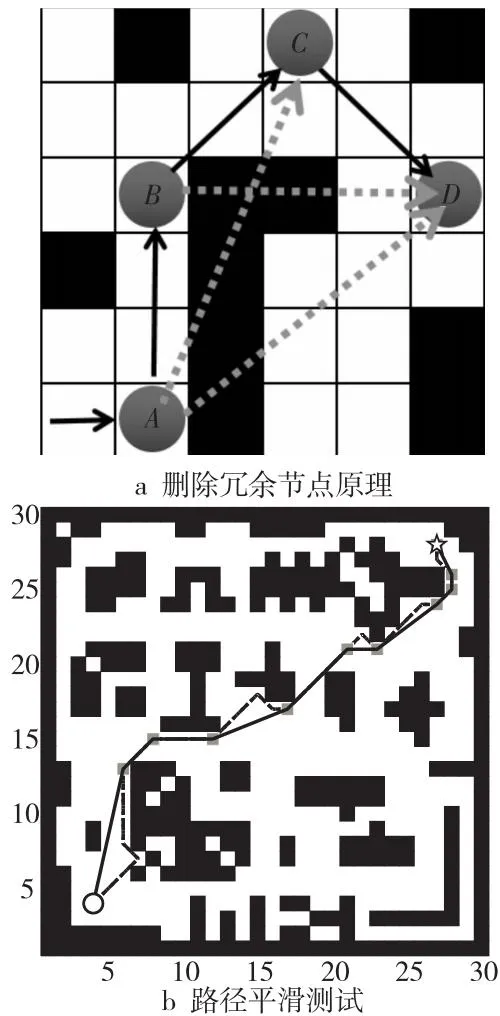
Figure 7 Removing redundant node principle and path smoothing test图7 删除冗余节点原理与路径平滑测试

4 实验仿真

为了验证本文改进A*算法的优越性,在Intel®CoreTMi5-7300HQ CPU @ 2.50 GHz计算机上利用MATLAB 2020b对传统A*算法和本文改进A*算法进行仿真测试。

在图8所示的3种场景中进行路径规划,图中黑色虚线表示传统A*算法规划出的路径,黑色实线为本文改进A*算法规划出的路径。相关仿真实验结果如表2所示。

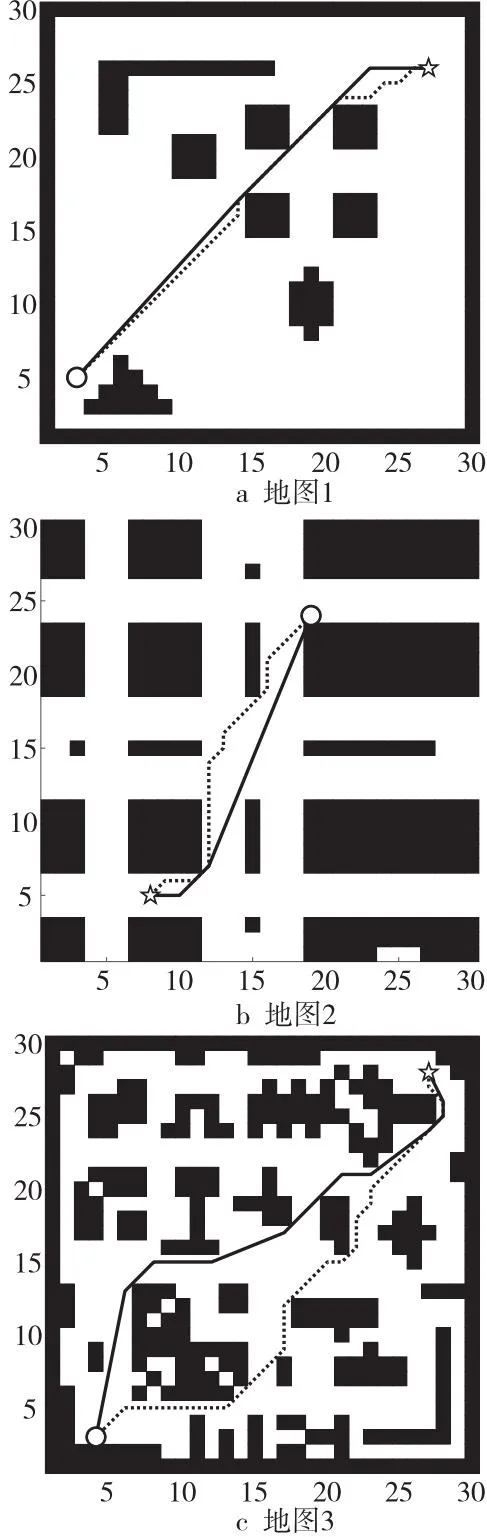
Figure 8 Test results of the proposed improved A* algorithm in different maps图8 本文改进A*算法在不同场景地图中的测试结果

Table 2 Experimental results of path planning in figure 8

从本文改进A*算法与传统A*算法在以上3种不同场景地图中的规划路线和表2中相关数据可知,本文改进A*算法鲁棒性和实时性更强,能适应多种场景地图,且规划出的路径更优。

为了进一步论述本文改进A*算法的优越性和稳定性,在模仿小区环境构建的50×50栅格地图中选取5组不同起始节点和目标节点进行测试,分别为[ (7,7),(42,43)],[(7,47),(47,7)],[(37,33),(14,13)],[(26,25),(7,18)],[(49,7),(13,47)]。

以第1组起始节点与目标节点为例,分别使用传统A*算法、文献[6]改进A*算法和本文改进A*算法进行路径搜索,最终规划出的路径如图9所示。5组不同起始节点和目标节点测试的相关结果如表3所示。

根据表3可知,本文改进A*算法与传统A*算法和文献[6]改进A*算法相比,遍历节点数平均减少了72.19%和28.36%,在删除冗余节点后极大缓解了计算机存储压力;总转折角度平均减少了64.33%和28.59%,规划出的路径更为平滑,降低了移动机器人与障碍物发生碰撞的几率;寻路时间平均减少了68.51%和27.15%,实时性更强,搜索速度更快,一定程度上解决了机器人在转弯时额外产生的能源损耗和时间等待问题。

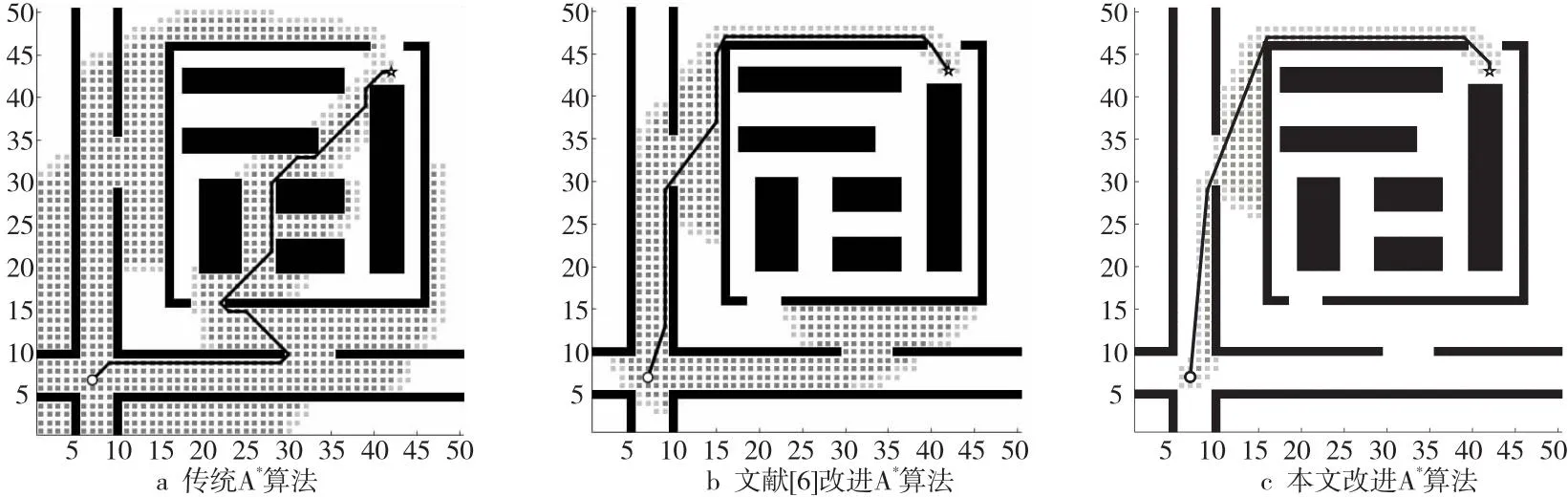
Figure 9 Test results of different path planning algorithms图9 不同路径规划算法测试结果

Table 3 Testing results of five different starting and target nodes

5 结束语

本文针对传统A*算法存在遍历节点数较多、总转折角度过大和搜索速度较慢等不足,提出了基于拟合优先搜索的多场景自适应改进A*算法。首先,引入父节点的启发距离,设计能自适应地图变化的启发式搜索权重,以减少遍历的节点数,提高搜索速度;然后,引入拟合优先搜索进一步增强算法启发性;最后,对初步规划出的路径进行局部剪枝并删除冗余节点,最后得出最终路径。仿真测试结果表明,本文提出的改进A*算法的鲁棒性更强,遍历节点数更少,路径更平滑,搜索速度更快,更适用于移动机器人的日常工作。