动车组空心车轴应力强度因子研究

2024-01-22余海峰吴兴文梁树林池茂儒

机械科学与技术 2024年1期

余海峰,吴兴文,梁树林,池茂儒

(1. 西南交通大学牵引动力国家重点实验室,成都 610031; 2. 西南交通大学机械工程学院,成都 610031)

车轴作为动车组走行部中及其重要的部件,承受着各种复杂载荷,当车轴表面出现裂纹后,有必要采用基于断裂力学的损伤容限方法评估其剩余寿命。在进行断裂安全分析时,应力强度因子是一个重要的指标,它是判断裂纹体在载荷作用下裂纹扩展规律和断裂破坏的主要参数。因此,对于车轴剩余寿命的安全评估,应力强度因子的求解极为重要。

目前针对三维应力强度因子的求解,主要方法有实验法、权函数法、解析法和有限元法等。赵大华等[1]和李相麟等[2]采用三维光弹性应力冻结法对带环形裂纹的圆轴进行了实验分析,利用双参数法测定I型应力强度因子,切片逐次削去法测定III型应力强度因子,取得了较好的结果。Wang等[3]和Jin等[4]针对有限厚度板中的半椭圆形表面裂纹,采用权函数法计算任意一维以及二维应力场作用下的应力强度因子,并将计算结果与有限元法对比,验证了方法的有效性。周素霞等[5-6]通过对弯曲载荷下实心轴表面裂纹应力强度因子解析式进行修正,得出空心轴表面裂纹应力强度因子,并将解析式计算结果与有限元法进行比较,发现结果非常相近。

以上几种方法中,实验法受到实验设备和条件的制约,权函数法对于车轴这种复杂结构难于实施,解析法只能针对简单垂向弯曲载荷下的计算,而有限元法以其强大的模拟和数值计算功能已被广泛用于应力强度因子的计算。一种常见的方法是通过有限元法来计算裂纹体裂纹尖端附近的位移场和应力场,然后通过位移外推法或应力外推法来计算应力强度因子[7-9]。另外一种方法,更常见于有限元软件中,是通过J积分或I积分等,利用能量与应力强度因子之间的关系来计算应力强度因子[10-12]。其中,第一种方法是通过将节点断开来模拟裂纹,需要在裂纹尖端设置足够密集的网格才能够精确地模拟裂纹尖端附近的位移场或应力场;第二种方法是通过特殊的建模手段,在裂纹尖端设置奇异单元来模拟裂纹,虽然其对网格的精度没有太高的要求(由于J积分与路径无关),但是在模拟多个不同裂纹形状的裂纹时,需要大量的网格划分工作。

综上,虽然有限元法能够很好地求解车轴的应力强度因子,但由于裂纹形状的演变,需要建立多组含裂纹车轴有限元模型来进行不同载荷下的单个应力强度因子求解。其中,Madia等[13-14]以表格的形式给出了指定裂纹深度下的形状因子以求解车轴应力强度因子;Pokorny等[15]针对车轴的不同裂纹深度,基于应力强度因子解析式的一般形式,采用多项式对形状因子函数进行拟合。总体来说,目前对于车轴整个裂纹演变周期内的任意裂纹深度的应力强度因子的研究较少。为此,本文基于车轴应力强度因子的一般解析式,根据有限元法中位移外推法的计算结果,使用五次多项式对形状因子函数进行拟合,在给定裂纹形状演变特性和载荷的情况下,推导出同一载荷模式下任意载荷大小和裂纹深度的应力强度因子的解析式,并验证了形状因子函数和解析式的适用性。

1 有限元法求解应力强度因子的原理

对于车轴来说,其主要受载为垂向载荷、压装配合载荷和横向载荷,在运动时受到旋转弯曲的作用,加速、制动产生的扭转载荷占少数[16]。并且有实验证明,对动车组动车空心车轴进行动应力测试,在两种编组运行工况下,车轴的弯曲应力远远大于车轴的扭转应力[17-18]。在这种受载情况下,裂纹面受到拉应力作用会张开,因此这里主要研究车轴的I型裂纹。同时许多研究表明,沿裂纹前缘绝大部分范围为平面应变状态,平面应力状态只在紧靠自由表面的一个很小的区域内存在[17-18],因此,假设车轴裂纹前沿平面内的应力分布为平面应变状态,便可以将三维裂纹简化为二维模型来求解。

如图1所示,考虑嵌入线弹性材料中的裂纹,对于沿三维裂纹前沿的给定位置,引入垂直于裂纹前沿的二维平面。

图1 二维平面内裂纹尖端坐标系的定义Fig. 1 Definition of coordinate systems at crack tip in a two-dimensional plane

在二维平面内,从裂纹尖端点引入两个坐标系,一个为xyz直角坐标系,一个为rθ极坐标系。选取一个距离裂纹尖端很近,极坐标为(r,θ)的节点,根据线弹性断裂力学理论,可以推得裂纹尖端的应力表达式为

(1)

进一步,可以得到裂纹尖端的位移表达式为

(2)

式中:σx、σy和τxy分别为正应力和切应力分量;ux、uy分别为x和y方向上的位移分量;KI为I型应力强度因子;E为弹性模量;υ为泊松比。

一般来说,σy和uy会使裂纹张开,因此是裂纹前沿最重要的变量。在裂纹面上,取θ=0,由式(1)可得

(3)

取θ=π,由式(2)可得

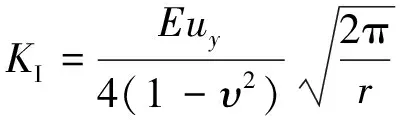
(4)

因此,裂纹尖端点的应力强度因子KI,tip为

(5)

或

(6)

由于数值计算不可能得到r→0的应力和位移,一般需要在裂纹尖端前取几个距尖端很近的点,利用式(3)、式(4)计算这些点的应力强度因子,然后通过外推获得尖端点的应力强度因子。

值得注意的是,由式(2)可知当r→0时,uy=0,即假设裂纹尖端点的位移值为0。而在实际加载中,裂纹尖端点的位移不为0,即裂纹场产生了刚体位移,那么实际上裂纹前沿的位移场uy,real应该为有限元计算出来的位移值uy,FEM减去裂纹尖端点的位移值uy,tip,即

uy,real=uy,FEM-uy,tip

(7)

所以,采用位移外推法时,裂纹尖端点的应力强度因子KI,tip为

(8)

2 车轴应力强度因子计算模型

在给定车轴材料属性(弹性模量和泊松比)的情况下,车轴的应力强度因子与以下3个变量有关:初始裂纹的位置、初始裂纹形状及其演变特性和车轴所受载荷。本文首先通过无裂纹车轴有限元计算结果确定了初始裂纹位置,接着给定了初始裂纹形状及其演变特性,然后确定采用叠加法计算垂向载荷和压装配合载荷下的应力强度因子,最后建立含裂纹车轴有限元模型,进行应力强度因子的计算。

2.1 初始裂纹位置的确定

计算应力强度因子的第一步是要确定初始裂纹的位置。通常在确定车轴剩余寿命时,所考虑的初始裂纹位置位于可能导致车轴最早疲劳失效的地方,由于此处研究的是I型裂纹,轴向主应力对其裂纹扩展起决定性作用,因此本文以车轴最大轴向主应力为判据来确定初始裂纹的位置。为此首先建立了无裂纹车轴有限元模型,来计算车轴在垂向载荷和压装配合载荷下的应力分布。

轮对模型如图2所示,包括空心车轴、车轮和齿轮箱。

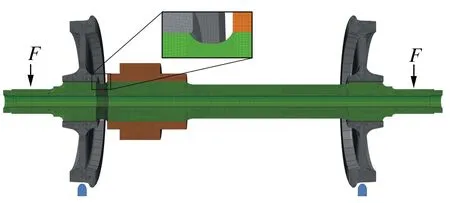
图2 无裂纹车轴有限元模型Fig. 2 Finite element model of a crack-free axle

由于几何和载荷的对称性,使用ABAQUS建模时仅建立轮对一半的结构,网格类型使用C3D8三维线性六面体单元。设置车轴为线弹性体,其材料的弹性模量为206 GPa,泊松比为0.3。加载设置如下:

1) 第一个载荷步,压装配合工况,一侧轴端全约束,选取齿轮箱和车轮内表面为主面,空心车轴外表面为从面,设置摩擦因数为0.6,过盈量为0.28 mm,以逐渐递增的方式分多个载荷子步施加,保证接触的良好收敛。

2) 第二个载荷步,垂向载荷工况,车轮与钢轨接触部分全约束,在车轴两侧轴肩轴承安装处施加垂向载荷(F=34 kN模拟车辆静载荷,该载荷为车轴受到的主要载荷68 kN的一半)。

在施加过盈接触载荷和垂向载荷后,计算的有限元结果如图3所示,车轴的轴向主应力在轮座和齿轮箱座之间的过渡槽(S型过渡槽)处达到最大。分析原因: 1) 由于S型过渡槽处存在缺口效应,导致此处容易产生应力集中; 2) 由于此处垂向载荷产生的弯曲应力较大; 3) 由于车轮、齿轮箱与车轴的压装配合,改变了此处的应力比,使得车轴轮座和齿轮箱座表面处受到残余压应力,而S型过渡槽表面处受到残余拉应力。考虑轴向拉应力对I型裂纹的扩展起主要作用,因此将初始裂纹位置确定为S型过渡槽处。

图3 有限元计算结果Fig. 3 Calculation results of finite element model

2.2 初始裂纹形状及其演变特性

影响车轴应力强度因子的另一个重要因素是裂纹前沿的形状,即初始裂纹形状及其演变特性。文献中通常使用半椭圆形表面裂纹来描述车轴的裂纹形貌[15-16,19],椭圆轴之间的比率在裂纹扩展过程中不断变化,符合车轴真实裂纹前沿的演变过程。因此,本文采用半椭圆形裂纹,用于车轴的裂纹扩展仿真。

根据经验和文献[20],疲劳裂纹垂直于最大主应力扩展,而最大主应力的方向几乎与轴向主应力相同,因此,可以假设疲劳裂纹垂直于车轴扩展。由于文献[21]模拟的车轴裂纹初始位置以及考虑的载荷种类均与本文一致,因此本文引用文献中的裂纹形状演变曲线来进行应力强度因子的计算。如图4所示,考虑无损探伤的精度,设置初始裂纹深度为1 mm,裂纹深度a从1、1.5、2、2.5、3、4、5、6.5、9、12、15、20、25、32、38、45、55 mm逐渐递增,裂纹形状比a/c的比率随着裂纹深度a的增长从0.814逐渐减小到0.281。

图4 裂纹形状演变曲线Fig. 4 Evolution curve of crack shape

2.3 叠加法求解不同载荷下的应力强度因子

裂纹萌生位置是靠近轮轴压装配合的S型过渡槽处,而该处的载荷主要来源于压装配合载荷和垂向载荷。对于车轴的给定位置,压装配合载荷在车轴装配时已经确定,仅与过盈量和摩擦因数有关,在整个服役周期内基本保持不变。而垂向载荷会由于列车的不同运行状态(通过曲线、道岔等)而发生改变。针对垂向载荷,可通过试验或仿真获得车轴在服役期间的载荷,再通过雨流计数法将其转变成不同等级的载荷谱。

由于应力强度因子的概念是建立在线弹性断裂力学基础上的,由式(3)可得应力强度因子与裂纹尖端附近的应力呈线性关系,那么在相同几何形状(包括裂纹几何形状)的前提下,可以采用叠加原理,将复杂载荷下的应力强度因子求解转变为单个载荷下的应力强度因子的求解,然后叠加求和。

因此,有

KTol=KBending+KPF

(9)

式中:KTol为垂向载荷和压装配合载荷共同作用下的应力强度因子;KBending为垂向载荷作用下的应力强度因子;KPF为压装配合载荷作用下的应力强度因子。

为了验证叠加法求解应力强度因子的可行性,本文比较了2种情况下无裂纹车轴S型过渡槽处沿厚度方向上的应力结果:1) 同时施加压装配合载荷和垂向载荷;2) 分别单独施加压装配合载荷(车轴与车轮及齿轮箱设置过盈接触,过盈量为0.28 mm,摩擦因数为0.6)和垂向载荷(F=34 kN,此时不考虑过盈配合,车轴与车轮及齿轮箱共节点),然后叠加。

应力计算结果如图5所示,从图5中可以看出两种方法得到的应力结果没有明显差异,而采用叠加法计算应力强度因子不仅能够将恒定的压装配合载荷和变化的垂向载荷(载荷谱中不同的载荷等级)分开,方便计算应力强度因子,还能够显著降低计算时间,提高计算效率,因此本文采用叠加法计算应力强度因子。

图5 两种情况下沿厚度方向上的轴向主应力比较Fig. 5 Comparison of axial principal stress along the thickness direction in two cases

2.4 含裂纹车轴有限元模型建模

在应力强度因子的计算过程中,若裂纹深度发生改变,只需要将裂纹截面附近的网格重构,以实现不同裂纹形状的模拟,上述部分称为裂纹模块。此外,车轴其它部分的网格保持不变,使用Tie绑定功能将裂纹模块与车轴剩余部分网格进行连接,以保持应力应变传递的准确性。为了保证应力强度因子的计算精度,裂纹前沿的网格尺寸应当足够小以保证应力外推或位移外推的准确性,文献[19]采用应力外推法,将裂纹前沿网格尺寸设置为裂纹深度a的10%。本文经过多次仿真,设置不同的裂纹前沿网格尺寸来计算对应的应力强度因子,发现当网格尺寸取为裂纹深度的4%时,应力强度因子的计算趋于收敛,因此将裂纹前沿网格尺寸设置为裂纹深度a的4%,具体模型如图6所示。

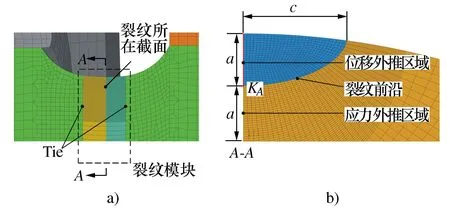
图6 裂纹模块示意图Fig. 6 Schematic diagram of crack module

对于给定裂纹形状的车轴模型,由于采用叠加法求解应力强度因子,根据载荷的不同设置2组模型:1) 考虑裂纹(使用Tie绑定),不考虑过盈配合载荷(车轴与车轮及齿轮箱共节点),施加垂向力载荷F=34 kN; 2) 考虑裂纹(使用Tie绑定),施加压装配合载荷(车轴与车轮及齿轮箱设置过盈接触,过盈量为0.28 mm,摩擦因数为0.6)。

3 计算结果分析

依据2.4节含裂纹车轴建模方法,建立了不同裂纹形状的车轴有限元模型,进而求解给定载荷下的应力强度因子。本节首先设置裂纹形状比a/c=0.5,裂纹相对深度a/T=0.102,即a=6.426 mm,c=12.852 mm的裂纹,采用位移外推法和应力外推法计算垂向载荷和压装配合载荷下的应力强度因子KBending和KPF;然后将计算结果与文献[13-14]对比,验证了模型和方法的有效性;接着根据2.2节设置的裂纹形状演变曲线,采用位移外推法计算出随着裂纹深度变化的应力强度因子,基于应力强度因子解析式的一般形式,使用五次多项式来拟合给定载荷下的形状因子函数;最后设置不同裂纹深度及载荷,将该解析式计算结果与位移外推法比较,验证了形状因子函数与载荷的无关性。

3.1 位移外推法及应力外推法计算结果

位移外推法拟合曲线如图7所示,应力外推法拟合曲线如图8所示。

图7 位移外推法拟合曲线Fig. 7 Fitted curve by using displacement extrapolation method

图8 应力外推法拟合曲线Fig. 8 Fitted curve by using stress extrapolation method

由于靠近裂纹尖端的计算结果误差较大,故舍弃靠近裂纹尖端较近的几个点,位移外推法从第5个点开始外推,应力外推法从第6个点开始外推,采用最小二乘法进行外推,得到直线方程,其截距即为计算得到的应力强度因子,如表1所示。

表1 应力强度因子计算结果Tab. 1 Calculation results of stress intensity factors

3.2 计算结果验证与对比

文献[13-14]给出了裂纹位于S型过渡槽处的A点应力强度因子表达式,将其变形如下

(10)

式中:YA,Bending和YA,PF为垂向载荷和压装配合载荷作用下的形状因子,与裂纹深度a以及裂纹形状比a/c有关,可通过查表得到;σBending和σPF为无裂纹车轴垂向载荷和压装配合载荷作用下外表面的轴向主应力,计算得σBending为22.27 MPa,σPF为66.33 MPa;θ为车轴旋转角度。

根据文献[14]查表可得a/c为0.5,a/T为0.102时的形状因子YA,Bending为0.98,YA,PF为0.629。取θ=0,带入式(10)可得KA,Bending为3.100 86 MPa·m0.5,KA,PF为5.928 25 MPa·m0.5,KA,Tol为9.029 11 MPa·m0.5,将位移外推法与应力外推法的计算结果和文献[13-14]所提方法进行对比,结果如图9所示。

图9 应力强度因子计算结果对比Fig. 9 Comparison of stress intensity factor calculation results

从图9中可以看出,基于位移外推法和应力外推法计算得到的KA,Tol,和通过文献形状因子公式推导出的结果相比差别不大,其相对误差分别为2.92%、-6.26%,验证了方法和模型的有效性。从中还可以看出基于位移外推法的应力强度因子具有更高的精度,这是由于在有限元中,一般是先通过刚度矩阵求解得到位移值,再通过偏导求解得到应力值,同时应力值对网格大小有很强的敏感性,所以应力值通常不如位移值精确[7]。

3.3 形状因子函数及应力强度因子拟合

基于2.2节的裂纹形状演变曲线,采用精度更高的位移外推法计算了随裂纹深度a变化的应力强度因子值。应力强度因子的一般解析式为:

(11)

(12)

根据计算结果,采用五次多项式来拟合形状因子函数,即:

(13)

(14)

式中:a为裂纹深度;YA,Bending(a)和YA,PF(a)为垂向载荷和压装配合载荷作用下的形状因子函数;pi和qi为五次多项式拟合常数(i=0～5)。

将拟合的形状因子函数代入到式(11)、式(12)中,可求得任意裂纹深度下的应力强度因子,形状因子函数拟合常数如表2所示。

表2 形状因子函数拟合常数Tab. 2 Constants for fitting the shape factor function

形状因子函数拟合结果如图10所示,应力强度因子拟合结果如图11所示。

图10 形状因子函数拟合曲线Fig. 10 Fitted curve of shape factor function

图11 应力强度因子拟合曲线Fig. 11 Fitted curve of stress intensity factors

3.4 形状因子函数验证

一般来说,裂纹深度和载荷大小都对应力强度因子的计算有重大影响,而式(11)与式(12)的优点在于将裂纹深度和载荷这两项影响因素分隔开。

在给定裂纹形状演变曲线的基础上,保持载荷不变(垂向载荷F=34 kN,过盈量为0.28 mm),依次增大裂纹深度,推导出了随裂纹深度变化的形状因子函数。理论上,形状因子函数与载荷值无关,即对于不同大小的载荷,式(11)、式(12)依然适用,仅需要变动与载荷有关的变量σBending和σPF,为了验证形状因子函数的适用性,保持裂纹形状演变曲线不变,设置垂向载荷为F=41 kN,过盈量为0.30 mm,分别使用式(11)、式(12)和位移外推法计算裂纹深度a为3 mm和9 mm下的应力强度因子,计算结果如图12所示。