结合Cokriging模型和单目标函数的随机模型修正

彭珍瑞,张雪萍,张亚峰

(兰州交通大学 机电工程学院,兰州 730070)

近年来,有限元模型修正技术发展迅速,逐渐成为结构动力学领域的热门研究方向。模型修正的本质是利用实测响应来调整、优化有限元模型参数,包括材料参数、几何尺寸以及约束条件等,使修正后的有限元模型能够更好地反映实际结构的动力学行为[1-2]。

当下,绝大多数模型修正方法局限于确定性领域,确定性方法认为结构参数及响应均为定值,导致修正后的有限元模型只能重现某一特定情形下的动力学行为[3-5]。然而,不确定性方法通过引入概率统计来量化模型修正过程中的不确定性,对于结构模型修正具有重要研究意义[6-7]。国内外学者在不确定模型修正领域开展研究,取得了一定的研究成果。宗周红等[8]采用蒙特卡洛模拟来量化分析模型修正中的不确定性,同时评价修正后模型的预测精度,并成功地对连续刚构桥有限元模型进行了修正。Hua等[9]引入计算效率较高的改进摄动法,利用随机实测响应修正了桁架有限元模型,并获得了结构参数的统计特征。Fang等[10]基于Hermite多项式混沌展开理论,建立了模型修正的随机反问题,有效修正了结构参数的均值和标准差等统计特征。陈炉云等[11]基于多类型响应和多层次理论,建立了考虑多响应的结构动力学修正归一化模型,并对一船舰底座模进行了修正。陈辉等[12]通过多变量非正交多项式展开式来表示结构的待修正参数,构造了结构响应与待修正参数之间的随机修正方程,并引入混合摄动-伽辽金方法求解得到了结构参数的统计特征。秦仙蓉等[13]将不确定性模型修正问题转化为一系列确定性模型修正问题,采用多目标遗传算法进行求解,并对一岸桥模型进行了修正。

采用上述方法进行随机模型修正时,通常需要建立多个目标函数进行求解。在利用智能优化算法进行多目标优化的过程中,通常不能保证所有子目标函数同时获得最优值[14]。针对随机模型修正中计算成本较高的问题,本文将Cokriging代理模型技术和单目标函数进行结合,提出了一种随机模型修正方法。首先,利用训练集样本和对应的有限元计算响应来构造满足精度要求的Cokriging模型;然后,基于有限元模型计算响应和试验响应的统计特征值,建立加权残差之和目标函数;最后,引入土狼优化算法获得待修正参数的最优均值和标准差,并通过二维桁架与三维桁架结构验证本文方法的有效性。

1 Cokriging模型构造

Cokriging模型将主变量的自相关性和主变量与协变量的交叉相关性结合进行估计。理论上Cokriging方法比Kriging方法更好。采用Cokriging法构造的修正模型[15]可表示为

(1)

式中:μ(xi)为x的多项式函数;z(xi)为服从正态分布N(0,σ2)且协方差不为0的随机分布。

初始待修正参数由拉丁超立方方法抽样,样本区间为待修正参数的±20%,计算样本响应值,将样本与所对应的响应值分为训练集和测试集,训练集构建Cokriging模型,由均方根误差(RMSE)值检验模型精度,RMSE越小,表明Cokriging模型的预测精度越高。RMSE表示为

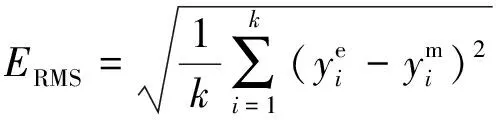
(2)

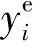
2 目标函数构造

随机有限元模型修正中往往需要建立随机参数的均值和标准差的多个目标函数进行多目标优化。目标函数可表示为:

(3)

(4)

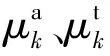
两个目标函数往往相互矛盾,有时候很难同时达到最优,考虑转化为单目标优化问题,简化修正过程,提高计算效率,其目标函数为

(5)

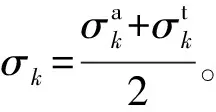
3 模型修正过程

3.1 土狼优化算法

土狼优化算法是基于土狼对环境的适应行为提出的一种新型群智能全局优化算法[16],该算法具有种群多样性强、收敛速度快等优点。土狼优化算法步骤如下:

1) 土狼群初始化。土狼划分Np组,每组Nc只土狼,土狼的社会条件socj为

socj=lbj+randj(ubj-lbj)

(6)

式中:ubj和lbj分别为参数上、下界;randj为[0,1]区间的随机数,j=1,2,…,D,D为优化问题决策变量数量。

2) 土狼组内文化互动。土狼在群体影响(δ1)和最优狼影响(δ2)下产生组内族群间文化互动,即形成新的社会条件,可表示为

socnew=soc+r1δ1+r2δ2

(7)

式中:r1和r2为[0,1]中的随机数。

3) 新土狼诞生。考虑出生和死亡为生命中的主要事件,在环境影响和遗传因子共同作用下,新土狼的诞生公式为

(8)

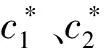
ps=1/D,pa=(1-ps)/2

(9)

3.2 模型修正过程

在Cokriging模型作为代理模型参与迭代计算的过程中,参数样本和结构响应需要相对应,难以直接获得响应的标准差,因此本文在每次迭代过程中随机抽取2 000个服从正态分布的样本;然后,利用Cokriging模型计算随机样本的响应,进而得到响应的统计特征值;最后,采用土狼优化算法求解目标函数obj3,得到待修正参数的均值和标准差。模型修正流程如图1所示。

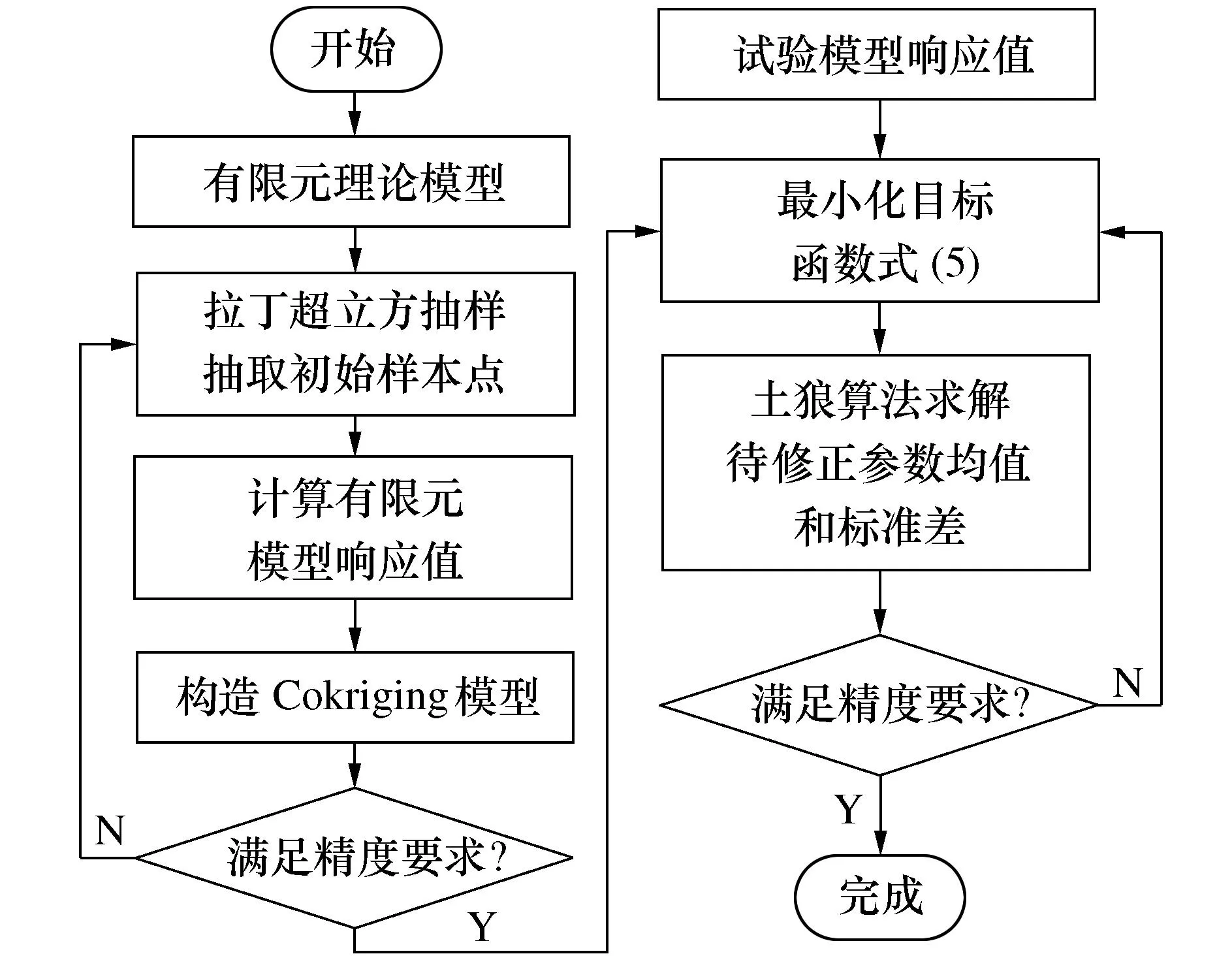
图1 模型修正流程图Fig. 1 Flow chart of model updating

4 数值算例

4.1 二维桁架

二维桁架结构如图2所示,其由16个节点和29个自由度组成。将杆单元分为斜杆和剩余杆两组,弹性模量分别为E1和E2,所有杆单元的质量密度为d。选取上述材料参数的均值和标准差作为待修正参数,假设有限元模型的E1、E2及d的试验均值分别为190 GPa、210 GPa和7 800 kg/m3,标准差为2.5、2.2和25。同时,初始均值和试验均值的相对误差为±10%,则待修正参数的初始均值分别为209 GPa、231 GPa和7 020 kg/m3。

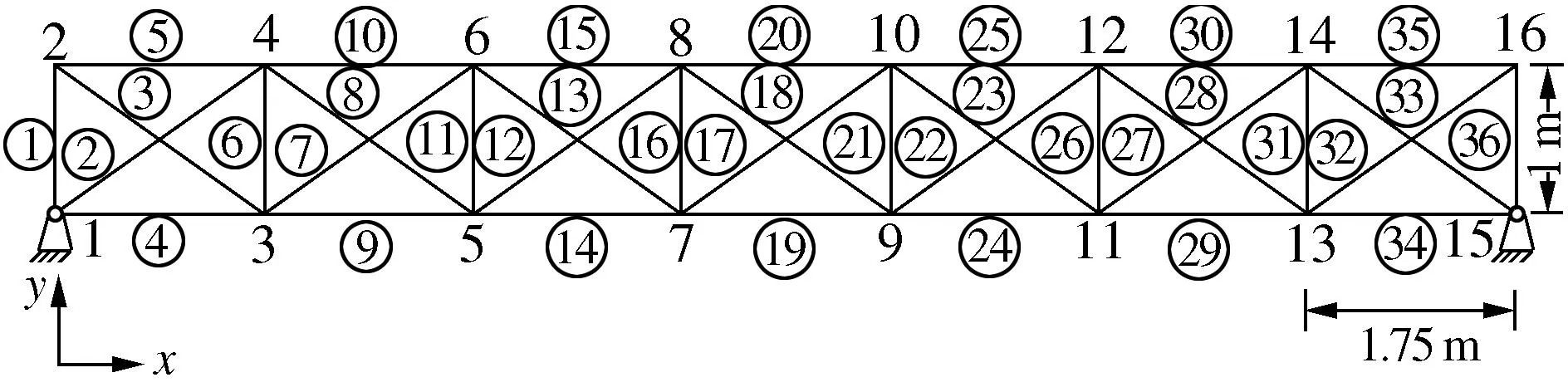
图2 二维桁架模型Fig. 2 Two dimensional truss structure

采用拉丁超立方抽样在待修正参数范围内抽取550组样本,其中,将前450组样本作为训练集,前10阶模态频率和第3节点的前4阶模态振型作为响应来构造Cokriging模型,后100组样本作为测试集来检验所构造Cokriging模型的预测精度。计算得到RMSE为1.09×10-5,说明模型精度满足要求。为进一步验证预测精度,分别利用有限元模型和Cokriging模型计算第6阶频率和第2阶振型,如图3和图4所示。可以看出,Cokriging模型的预测值和有限元模型计算值基本重合,表明所构造的Cokriging模型具有较高的预测精度。

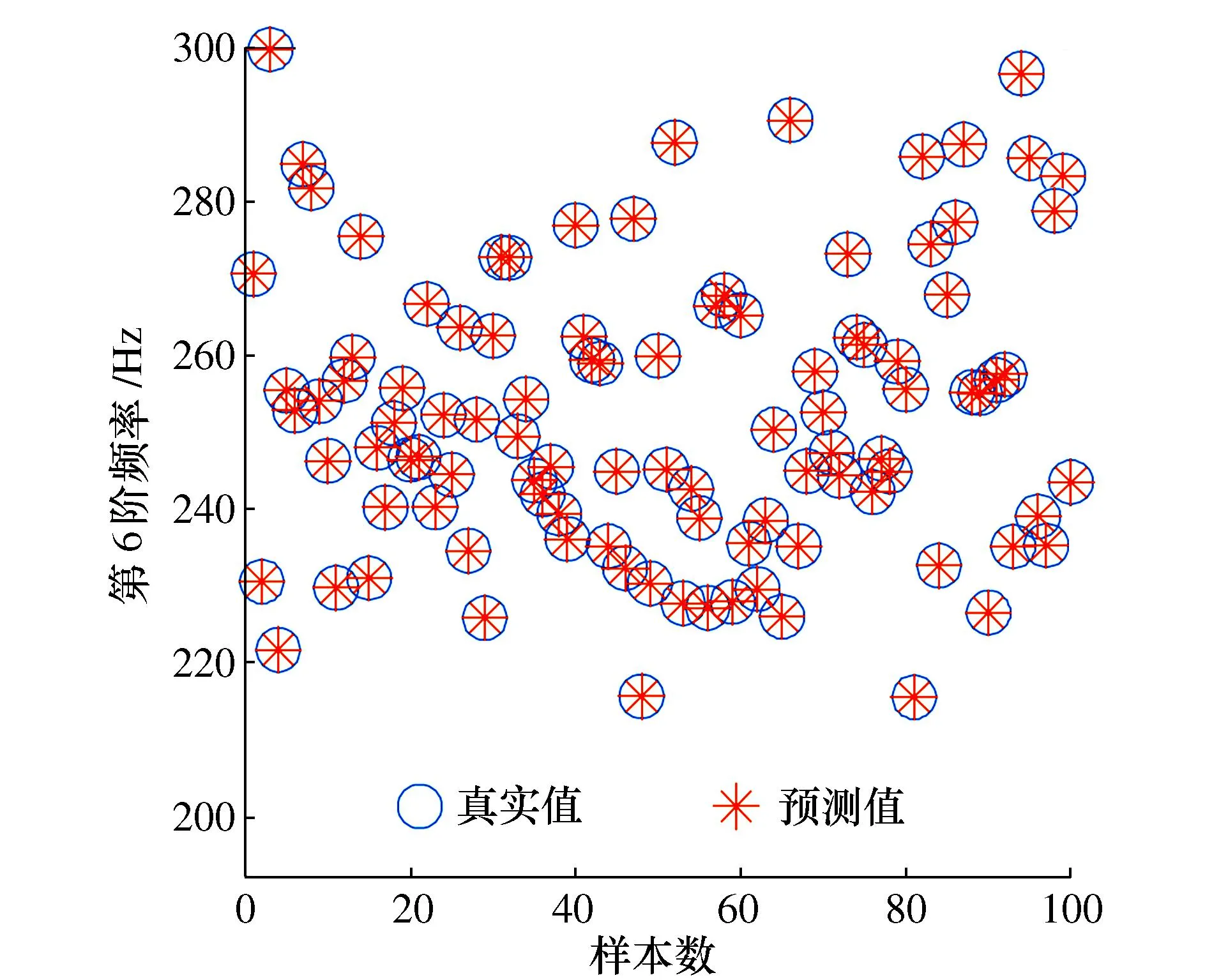
图3 频率的预测值和真实值Fig. 3 Predicted and true values of frequency

由于在实际工程中难以获得大样本试验数据,因此本文采用半实验样本数据,即随机抽取500组服从试验高斯分布的参数样本,将样本代入有限元模型,计算得到前10阶频率和第3节点前4阶振型作为试验响应。然后,设定土狼优化算法中的相关参数,分别为:Np=10,Nc=10,进化次数为500。求解待修正参数的均值与标准差,多次试验得到ω1=0.605、ω2=0.155。为了验证本文方法的优势,在相同条件下,利用土狼优化算法分别求解多目标函数和单目标函数,获得待修正参数的统计特征值,如表1所示。可以看出,经多目标函数修正方法修正后的有限元模型,其结构参数的均值和标准差的相对误差小于5%,而经本文所提单目标函数修正方法修正后的相对误差均能保持在3.5%以内,本文方法具有更高的修正精度。

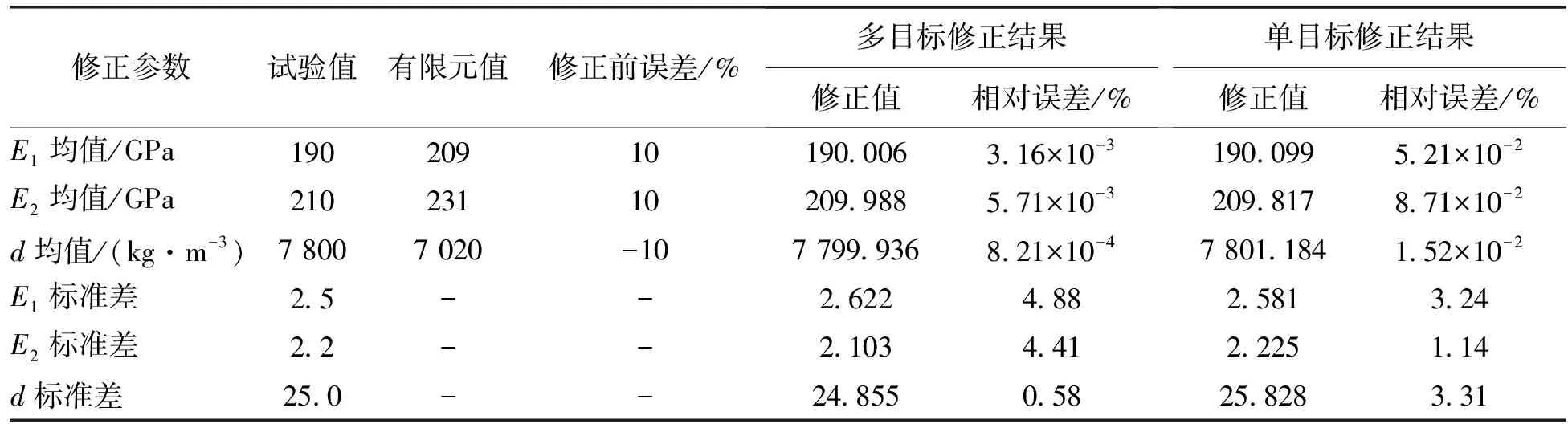
表1 修正前后结构参数均值与标准差(二维桁架)Tab. 1 The means and standard deviations of structural parameters before and after updating(2D truss)

图5和图6分别为利用本文所提方法修正前后的模态频率和振型的对比图,可以看出,经本文方法修正后模态响应的均值与试验响应的均值能够充分接近。

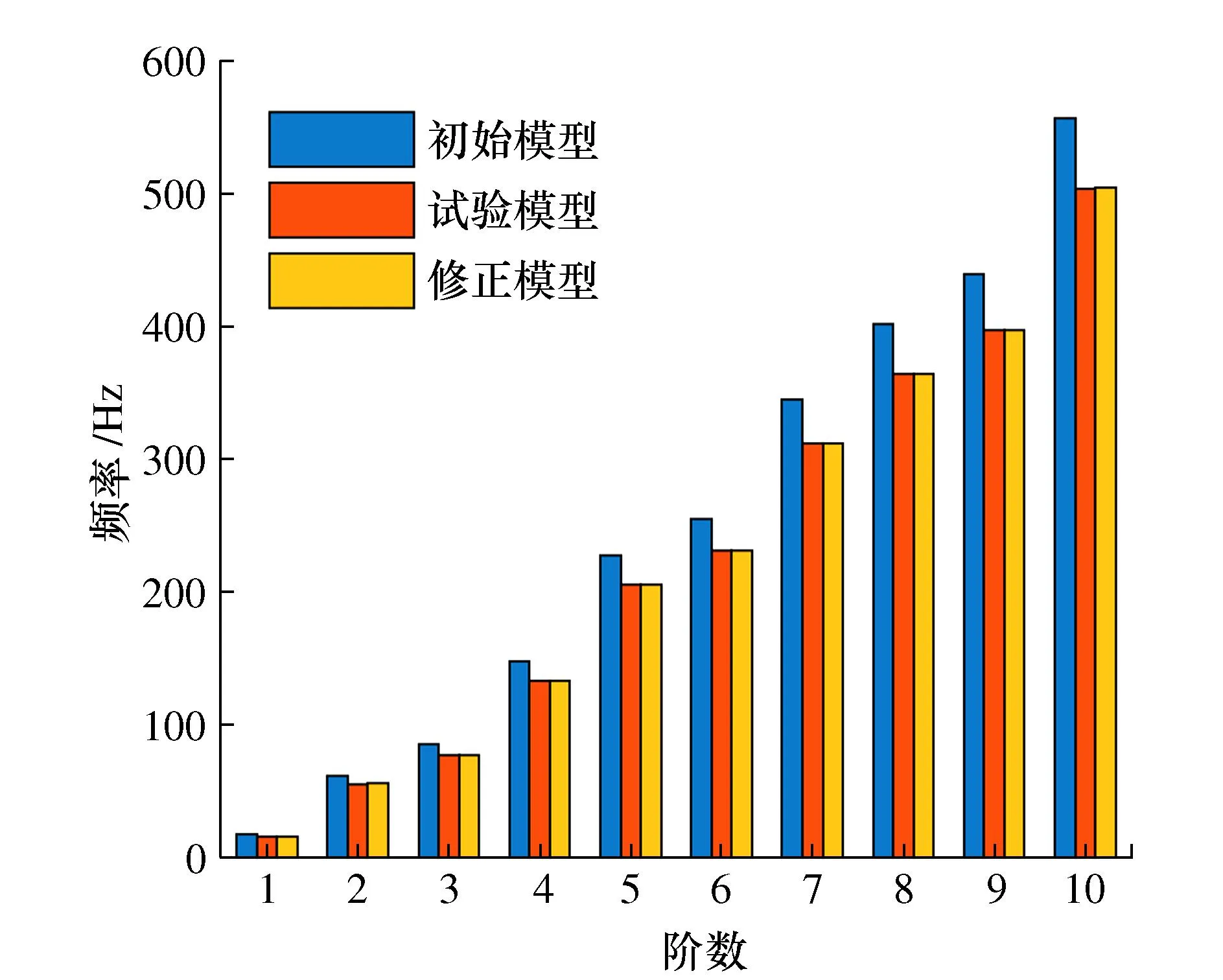
图5 频率对比Fig. 5 Frequencies comparison

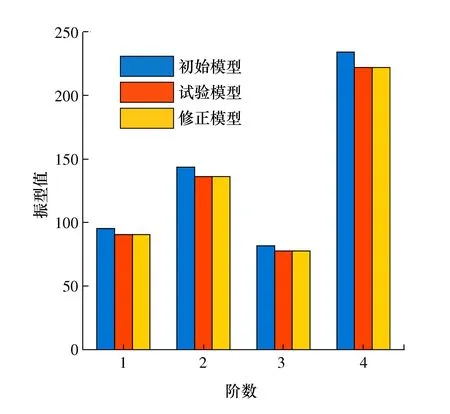
图6 振型对比Fig. 6 Shapes comparison

为进一步验证本文方法的有效性,在表1修正值所对应的高斯分布内,随机抽取300组样本,代入修正后有限元模型中计算频率来得到概率密度函数。修正后模型和试验模型的第1、2、5、10阶模态频率的概率密度函数曲线如图7所示,可以看出修正后频率的概率密度曲线与试验结果基本重合。

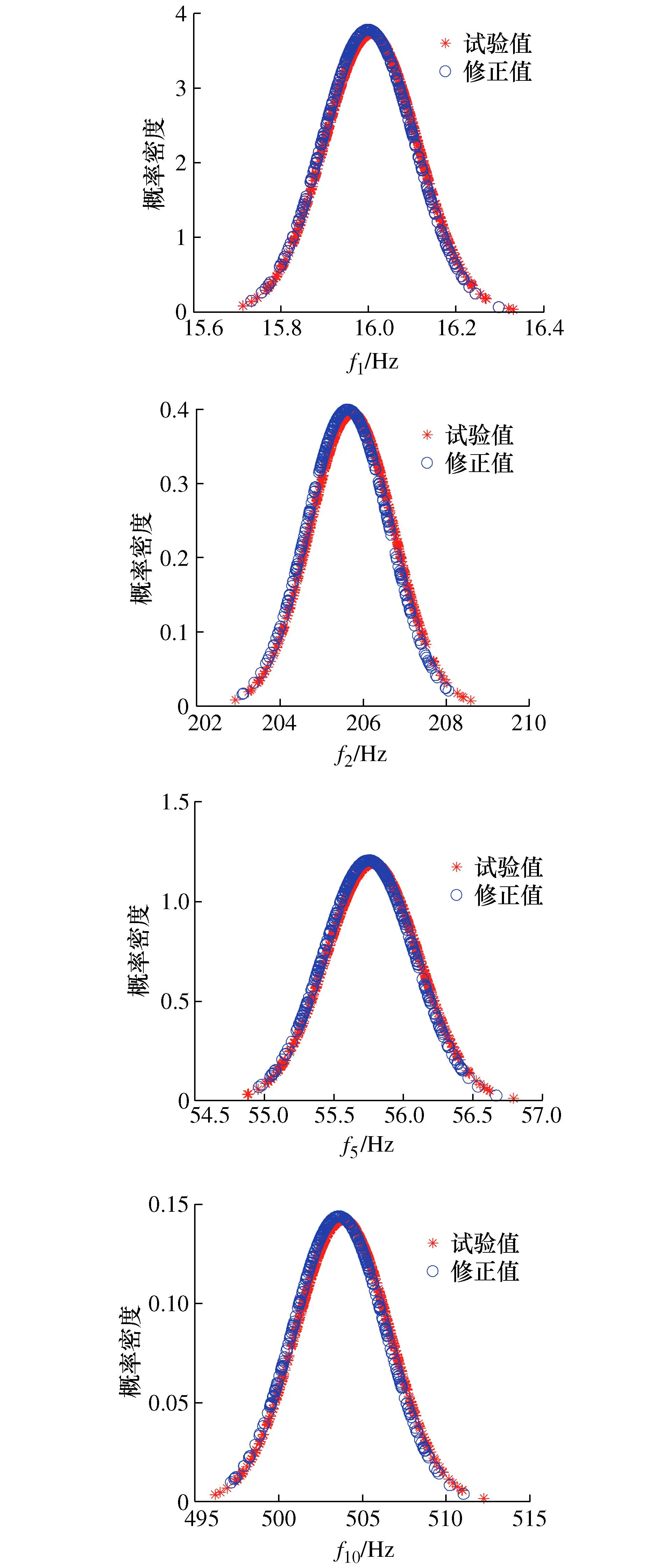
图7 修正后频率的概率密度函数曲线Fig. 7 Updated frequency probability density function curves

对修正后的模态响应进行归一化处理,第5阶与第6阶模态频率、第7阶与第8阶模态频率、第1阶与第3阶模态振型的分布及95%置信椭圆如图8所示。由图8可以看出:修正后的模态响应大部分位于置信椭圆内的高概率区域内,且修正后模型响应和试验响应的置信椭圆基本一致。

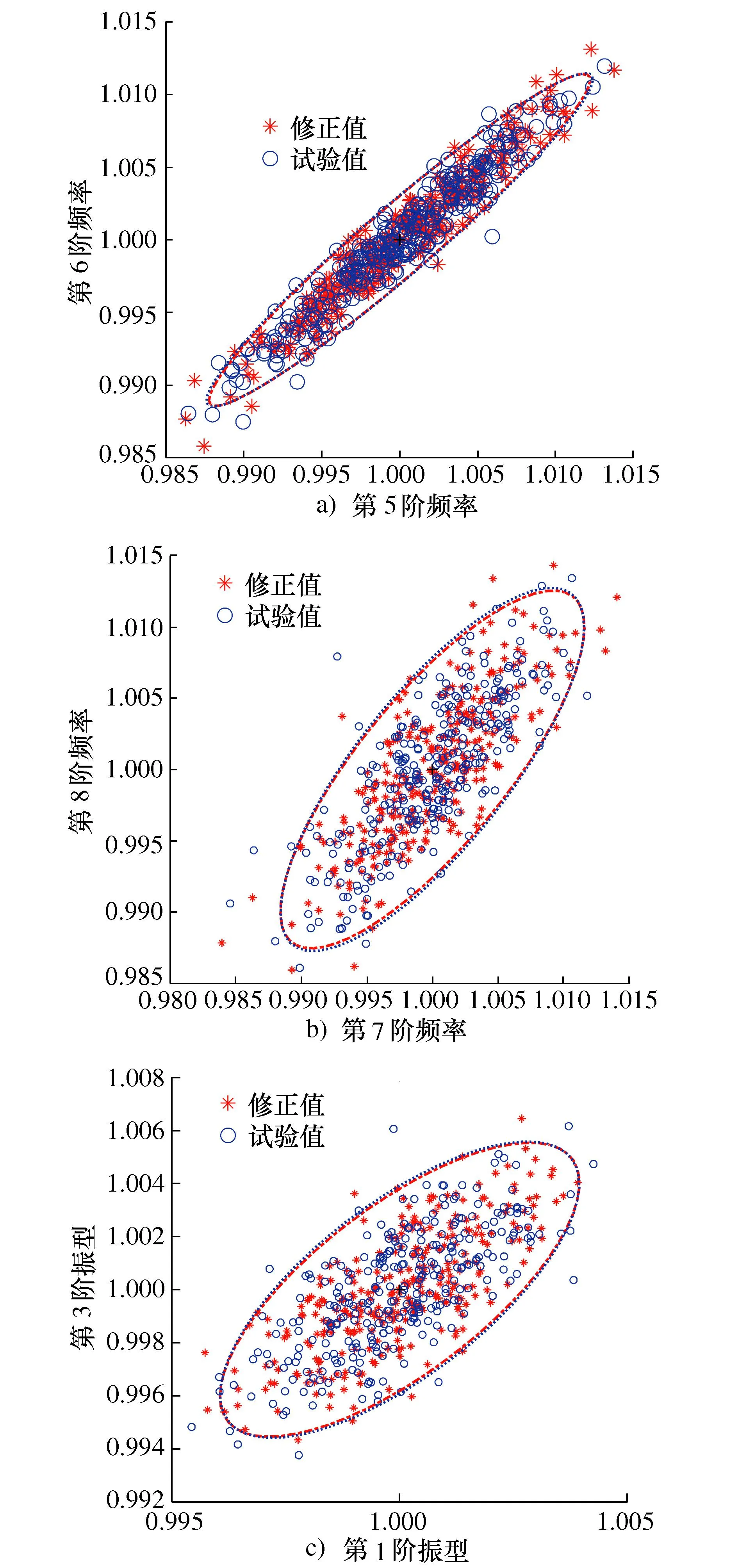
图8 修正后参数响应的分布及置信椭圆Fig. 8 The distributions and confidence ellipses of the updated parameter response

4.2 三维桁架

三维桁架结构如图9所示,基本属性参数如表2所示。将杆单元分为两组,分别为各主桁杆单元和上、下平纵联各杆单元。两组杆单元的弹性模量分别为E1和E2,各杆单元的质量密度均为d。选取待修正参数为E1、E2及d的均值和标准差,假设试验均值分别为230 GPa、210 GPa和7 300 kg/m3,标准差分别为3.0、2.0和20,同时,初始均值分别为253 GPa、189 GPa和8 030 kg/m3。

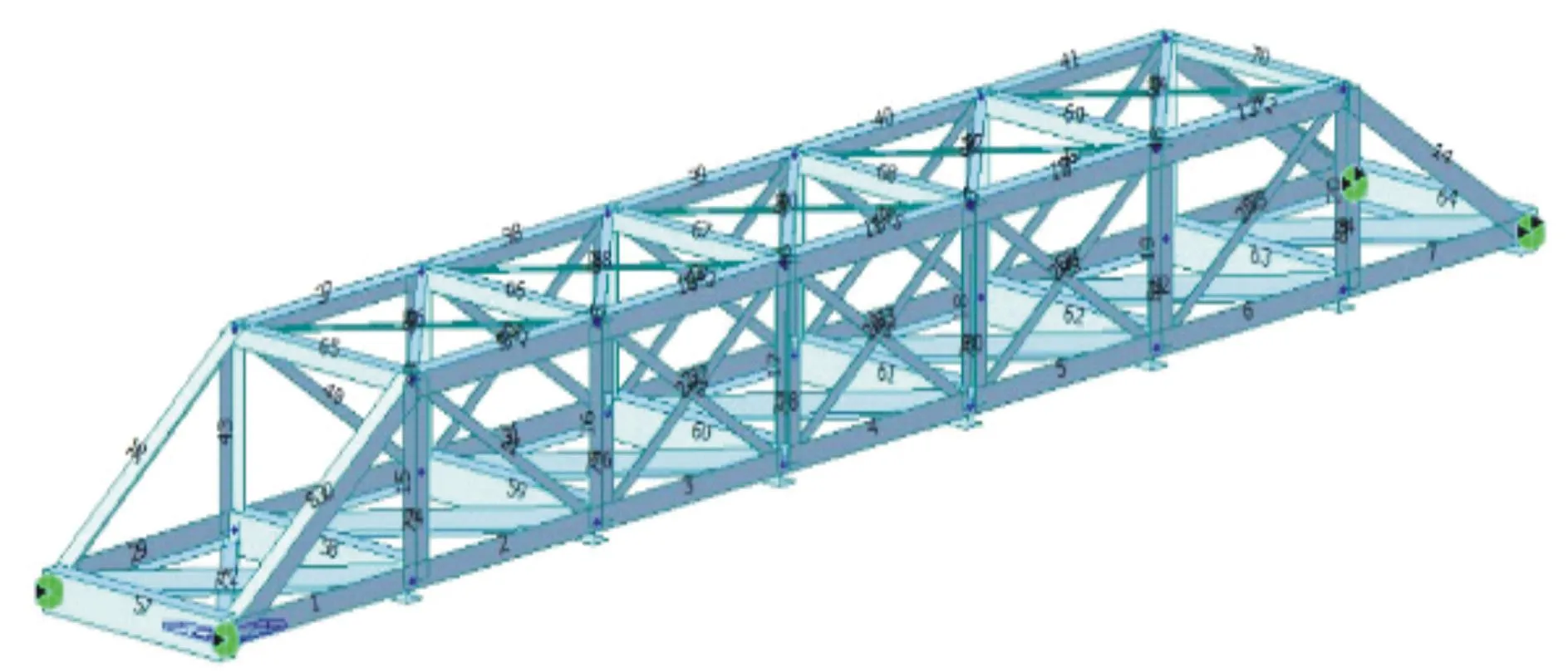
图9 三维桁架模型Fig. 9 Three dimensional truss model

表2 三维桁架模型属性Tab. 2 Properties of 3D truss model

选取前4阶频率和第6节点前4阶振型作为响应,采用4.1节方法构造训练集和测试集样本,计算相应的结构响应来构建Cokriging模型。计算得到RMSE为1.43×10-5,表明所构造的Cokriging模型精度满足要求。图10为第1阶频率的预测值和有限元模型计算值,可以看出预测值与有限元模型计算值几乎重合,表明所构造的Cokriging模型的预测精度满足要求。

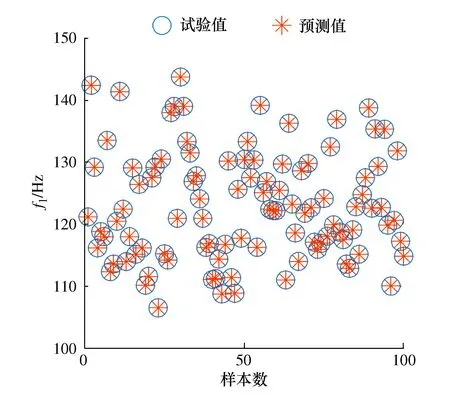
图10 第1阶频率的预测值和真实值Fig. 10 Predicted value and true value of first order frequencies

同样采用半实验样本数据,计算有限元模型的前4阶频率和第4节点的前4阶振型作为试验响应,得到ω1=0.605、ω2=0.155及多目标和单目标函数下的参数修正结果,如表3所示。

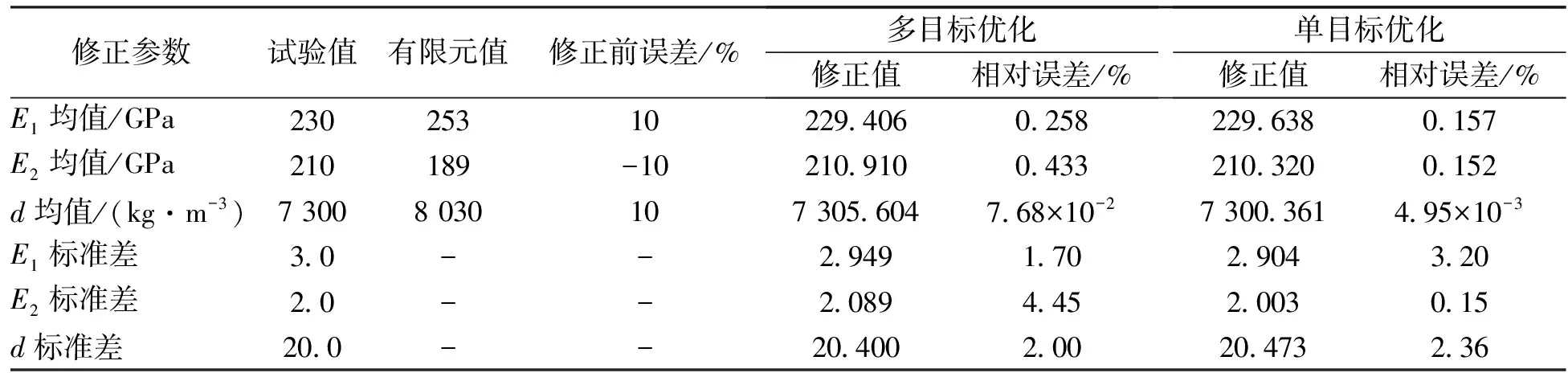
表3 修正前后结构参数均值与标准差(三维桁架)Tab. 3 The means and standard deviations of structural parameters before and after updating(3D truss)

由表3可以看出:本文单目标函数修正后的参数均值与标准差的相对误差小于3.2%,小于多目标函数修正方法的4.5%。频率和振型的修正结果如图11和图12所示,可看出修正前频率和振型的均值与试验模态响应均值相差较大,经所提方法修正后,两者的均值接近。由表3还可以看出,经多目标函数修正方法修正后的有限元模型,其结构参数的均值和标准差的相对误差在4.5%以内,而经本文所提单目标函数修正方法修正后的相对误差均能保持在3.2%以内,所提方法具有更高的修正精度。

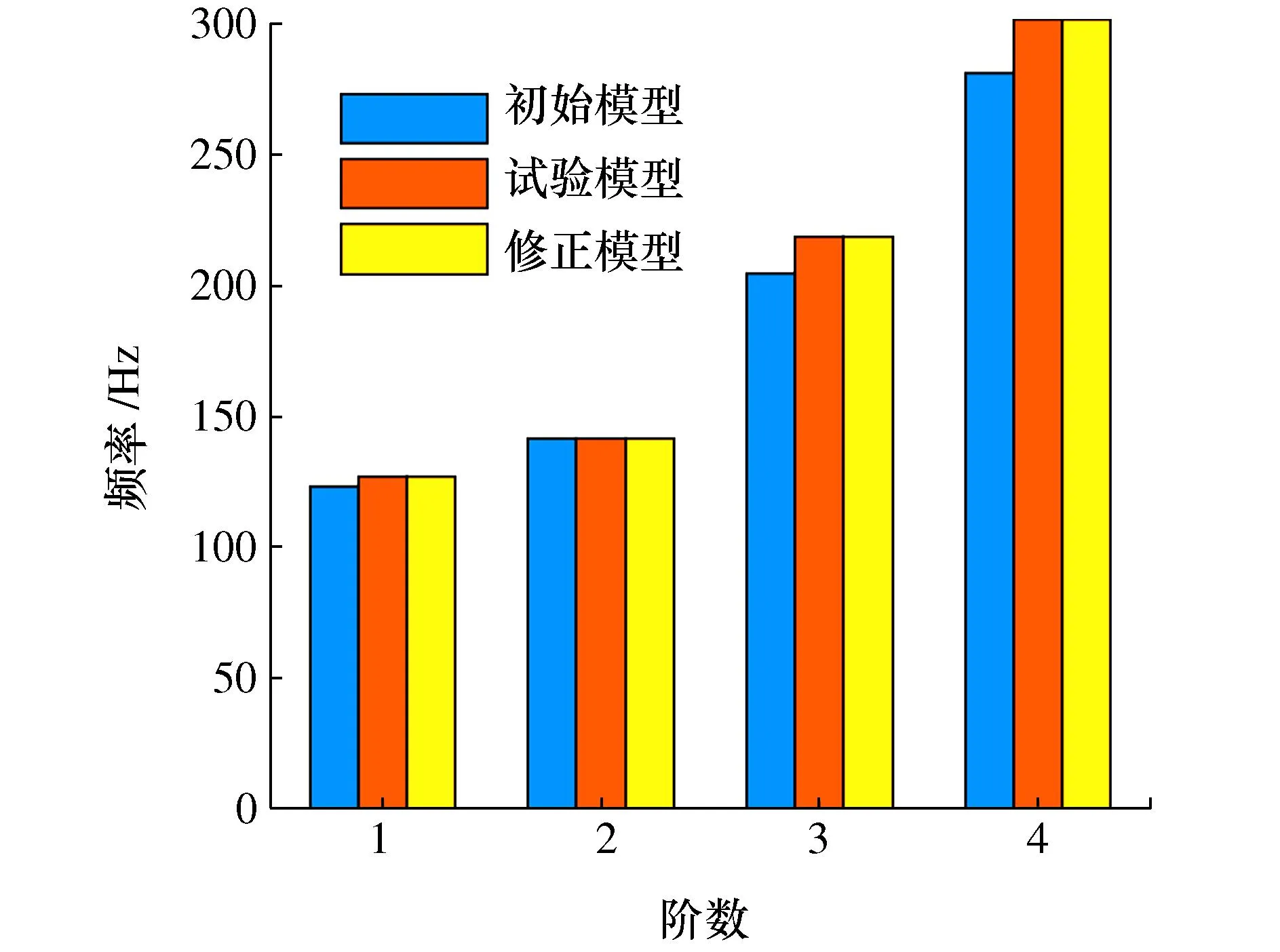
图11 频率对比Fig. 11 Frequencies comparison

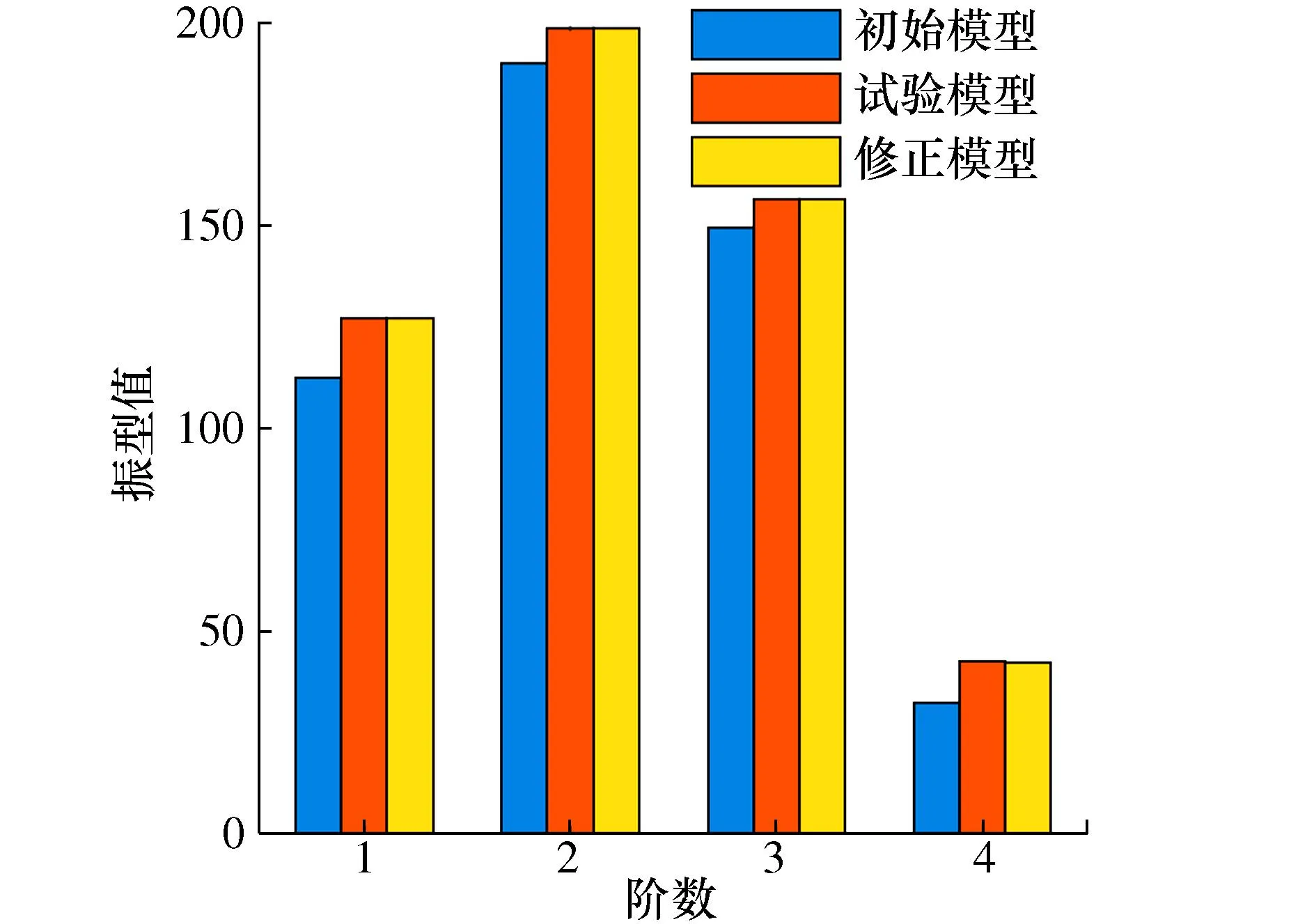
图12 振型对比Fig. 12 Shapes comparison

图11和图12分别为修正前后模态频率和振型的对比图,可以看出,经所提方法修正后的模态响应均值能够充分接近于试验响应均值。

为进一步验证本文方法的修正效果,同4.1节计算修正后模型和试验模型的概率密度函数,如图13所示,可以看出修正后频率的概率密度曲线向试验结果充分靠拢。进而对修正后的模态响应进行归一化处理,第1阶与第3阶模态频率、第2阶与第4阶模态频率、第1阶与第3阶模态振型的分布及置信椭圆如图14所示。由图14可以看出:修正后的修正后模型响应和试验响应的置信椭圆基本重合,进一步验证了所提方法的可行性和有效性。

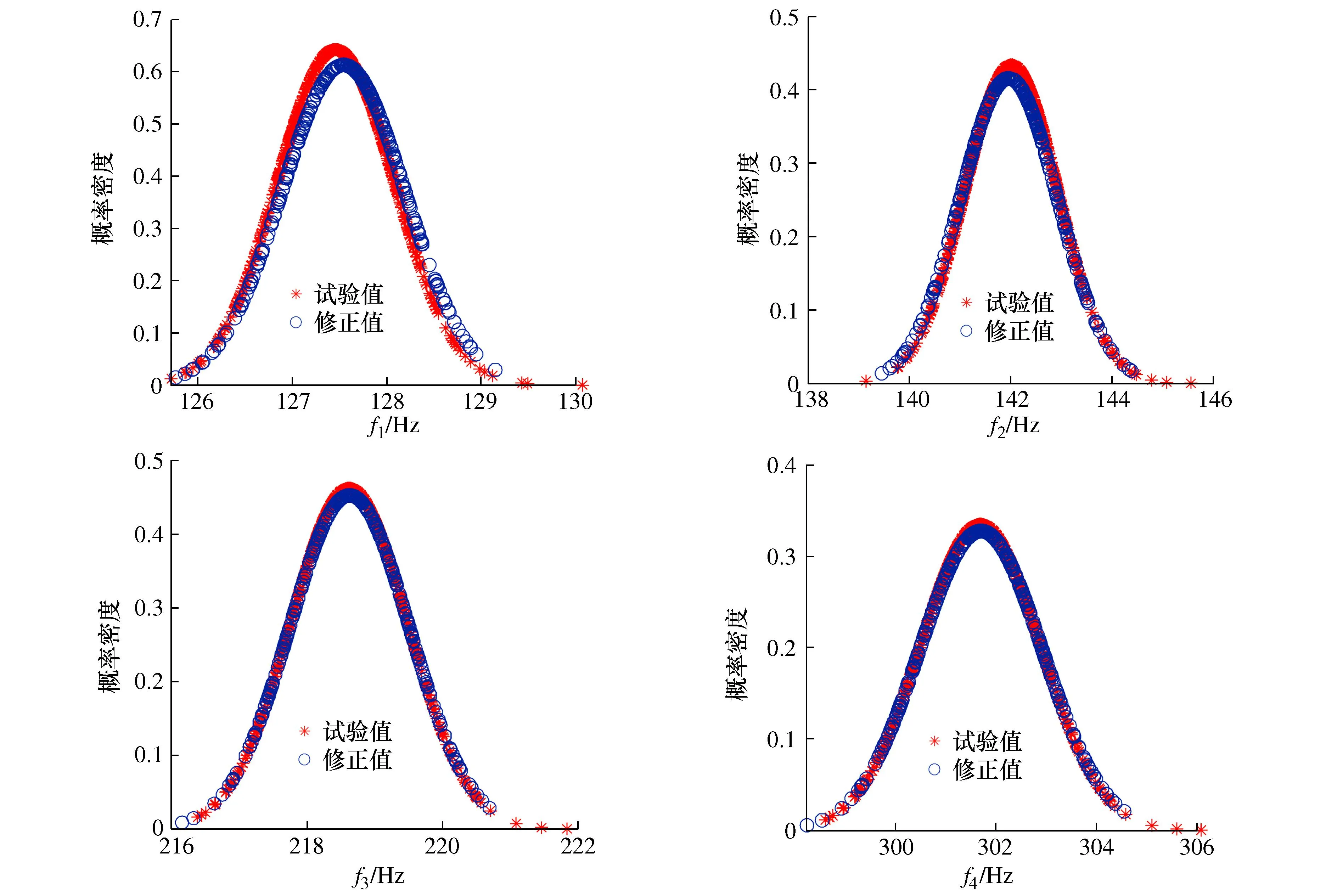
图13 修正后频率的概率密度函数曲线Fig. 13 Updated frequency probability density function curves

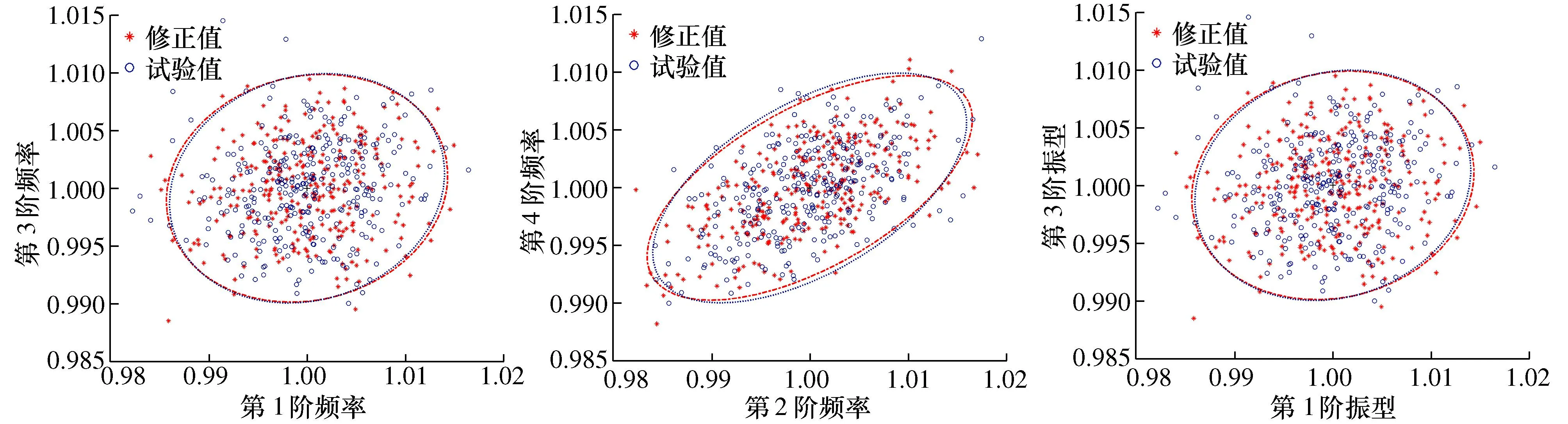
图14 修正后参数响应的分布及置信椭圆Fig. 14 The distributions and confidence ellipses of the updated parameter response

5 结论

1) 将随机模型修正问题简化为修正结构参数的统计特征值,直接求解加权残差目标函数得到参数的统计特征,提高了随机模型修正的效率。

2) 建立的单目标函数能够较好地度量两个概率分布之间的差异,为解决多目标优化中的各子目标函数相互制约的问题提供了一定的借鉴。

3) 通过Cokriging模型技术拟合待修正参数与响应之间的复杂关系,进而替代有限元模型参与迭代计算,降低了模型修正的计算成本。