面向电流信息与模态分析的工业机器人关节振动求解研究
2024-01-22赖泽浪王之海柳小勤李佳慧冯正江
赖泽浪,王之海,柳小勤,李佳慧,冯正江
(1. 昆明理工大学 机电工程学院,昆明 650500; 2. 云南省先进装备智能制造技术重点实验室,昆明 650500)
工业机器人末端执行器的精度由各关节健康状态决定,为获取充分的工业机器人关节状态信息,目前常采用如温度、振动、声发射等多类或同类多枚传感器开展测试工作[1-4],采集数据量大,算法复杂,传感器布置繁琐,获取数据成本高,同时关节处布放振动传感器的额外质量也可能对工业机器人关节性能退化的计算结果产生影响。对于传感器布放空间有限的机器人,可能会由于获取的关节状态信息不完整导致计算结果失真。在测试时,机器人需停机布放传感器对各关节开展独立测试与分析,生产效率与诊断效率均受到影响。因此,对可高效获取完整关节状态信息的方法研究将具有重要意义与应用价值。
刘颖[3]提出一种基于电流信号的工业机器人关节故障快速诊断方法,有效的提取了关节电流信号微弱特征,实现关节螺栓松动和传动皮带松动故障的识别。Li等[4]采用电流信号和深度神经网络算法对行星齿轮进行故障诊断,在不同负载与健康状况下与其他方法进行了对比。
以上研究表明,通过电流数据可获取机器人关节状态信息,但仅可解决关节简单故障问题,而基于人工智能的电流诊断算法复杂,中间层特征物理意义不明确,且模型泛化能力不足,难以推广应用。
模态分析是研究结构动力特性的重要方法,通过获取结构各阶主要模态特性,就可预测结构在各种激振力下的振动响应。郭闯强等[5]设计了一种轮辐式力矩传感器,利用机械臂反作用于关节的扭转力矩直接获得关节振动信息。强艳辉[6]提出一种新的两脉冲输入整形器参数学习策略,利用工业机器人关节力矩获取关节振动幅值。Kvrgic等[7]考虑了电机的力/力矩饱和,提出了一种基于正向动力学的关节加速度计算算法。
以上研究表明,由关节力矩可获取关节振动信息,该方法便捷、直观,但力矩传感器价格高昂,且由正向动力学计算关节加速度的算法复杂。
综上,为避免因采用振动传感器对机器人各关节逐一检测而引起测试成本剧增问题。本文提出一种基于电流信息与模态分析的工业机器人关节振动求解方法,该方法可直接从关节电流有效获取关节振动信息。
1 工业机器人振动模型
1.1 多自由度串联机器人系统振动模型
n自由度经典阻尼振动系统运动方程[8]为
(1)
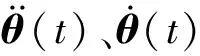
阻尼矩阵C[9]可表示为
C=αM+βK
(2)
其中:
(3)
式中:α、β为比例系数;ωi与ωj为机器人第i阶与第j阶模态频率;ζi与ζj为机器人第i阶与第j阶模态阻尼比,i≤n,j≤n,i≠j,n为机器人总关节数。
利用模态矩阵对式(1)进行解耦,当结构的阻尼为比例阻尼时,可用实模态计算,由下式方程组可求解模态矩阵[10]:
(4)
式中:ki和mi为第i关节刚度和质量;λi为特征值;∧为特征值矩阵,∧=diag(λi);Φ为各阶模态向量组成的n×n阶模态矩阵。
经模态空间变换[10],通过Mr=ΦTMΦ、Cr=ΦTCΦ、Kr=ΦTKΦ和Pr=ΦTF(t),式(1)可转换为
(5)
1.2 引入电流信息的工业机器人关节振动数值求解
1.2.1 机器人关节电流-振动模型
若可从关节电流转化为关节驱动力矩,则既可降低采用价格高昂力矩传感器带来的测试成本,又可避免采用振动传感器由于布放不佳或传感器自身额外质量带来的测量误差。
本文研究对象钱江QJR6-1型工业机器人关节均采用伺服控制,理想条件下,在关节系统中,关节驱动力矩向量τ(t)[11]可表示为
τ(t)=DtIη
(6)
式中:I=[I1,I2,…,I6]T,Ii为第i关节电流;η=[η1,η2,…,η6]T,ηi为第i关节减速器的减速比;Dt为关节转矩常数。
由式(5)与式(6)可得方程组:
(7)
式中:mri、cri和kri分别为第i关节模态质量、模态阻尼和模态刚度;Pr(t)=[pr1,pr2,…,pr6]T=ΦTτ(t)。
1.2.2 关节振动求解
对式(7),采用4阶变步长自适应Runge-Kutta数值积分方法进行求解[12-13],可引入状态变量
X=[x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12]T=
(8)
先定义ui=pri为输入,取Y=[x1,x3,…,x11]T为输出,本文以第一关节计算为例,式(7)第一个方程的状态方程为:
(9)
关节输出为
y1=x1
(10)
将式(9)、式(10)整理成矢量形式,即:
(11)
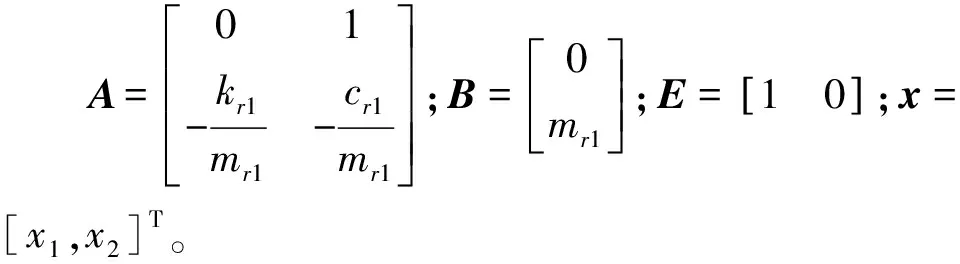
由4阶Runge-Kutta数值求解式(11)得到模态空间下第一关节角位移响应y1,4阶Runge-Kutta数值求解算法如下:
(12)
式中h为迭代步长。
以上述第一关节求解为例,将式(7)中6个2阶微分方程写为12个一阶微分方程,并用Runge-Kutta数值法求解,最后得到模态空间下各关节角位移响应Y=[y1,y2,…,y6]T,通过θ(t)=ΦY得到机器人关节在物理空间的角位移响应θ(t)。

(13)
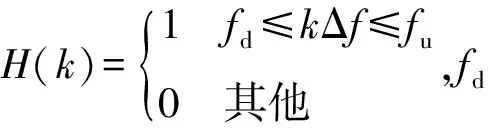
2 工业机器人测点优化及结构模态参数获取
本文采用模态试验获取工业机器人振动模型的质量、刚度等模态参数进行关节角加速度的求解,在模态试验中,激励点的选择不仅决定着能否完全激发出所关注的模态,还关系到测试结果精度[15]。为避免测点不佳而导致模态不明显甚至丢失的情况,本文基于有限元法优化模态试验测点布置。模态试验使用比利时LMS公司的Test Lab采集数据并分析。
2.1 有限元法测点优化
本文研究对象为钱江QJR6-1型6自由度工业机器人,如图1所示。机器人各关节均为电伺服驱动。

图1 钱江QJR6-1型机器人Fig. 1 Qianjiang QJR6-1 robot
首先,通过Solidworks建立工业机器人三维模型,随后导入Ansys-Workbench进行有限元模态分析。由于机器人三维模型实体结构复杂,零件、连接方式较多,为防止不规则的实体模型在网格划分时引起仿真精度降低[16],对分析对象进行了适当简化与等效处理[17],其中包括移除螺栓与垫圈,对电机等部件结构进行实体等配重处理等,然后进行模型材料设定和模型网格划分[18-19]。
模态仿真采用结构静力学分析和模态分析顺序分析的方法,利用结构静力学的边界条件作为模态分析的初始条件,以确保模态分析的结果与实际情况具有较好的一致性。将模型底座底面设为固定支撑,对机器人施加重力加载,然后进行结构静力学与模态分析。
经计算得机器人前6阶振型(见图2)与模态参数(见表1)。
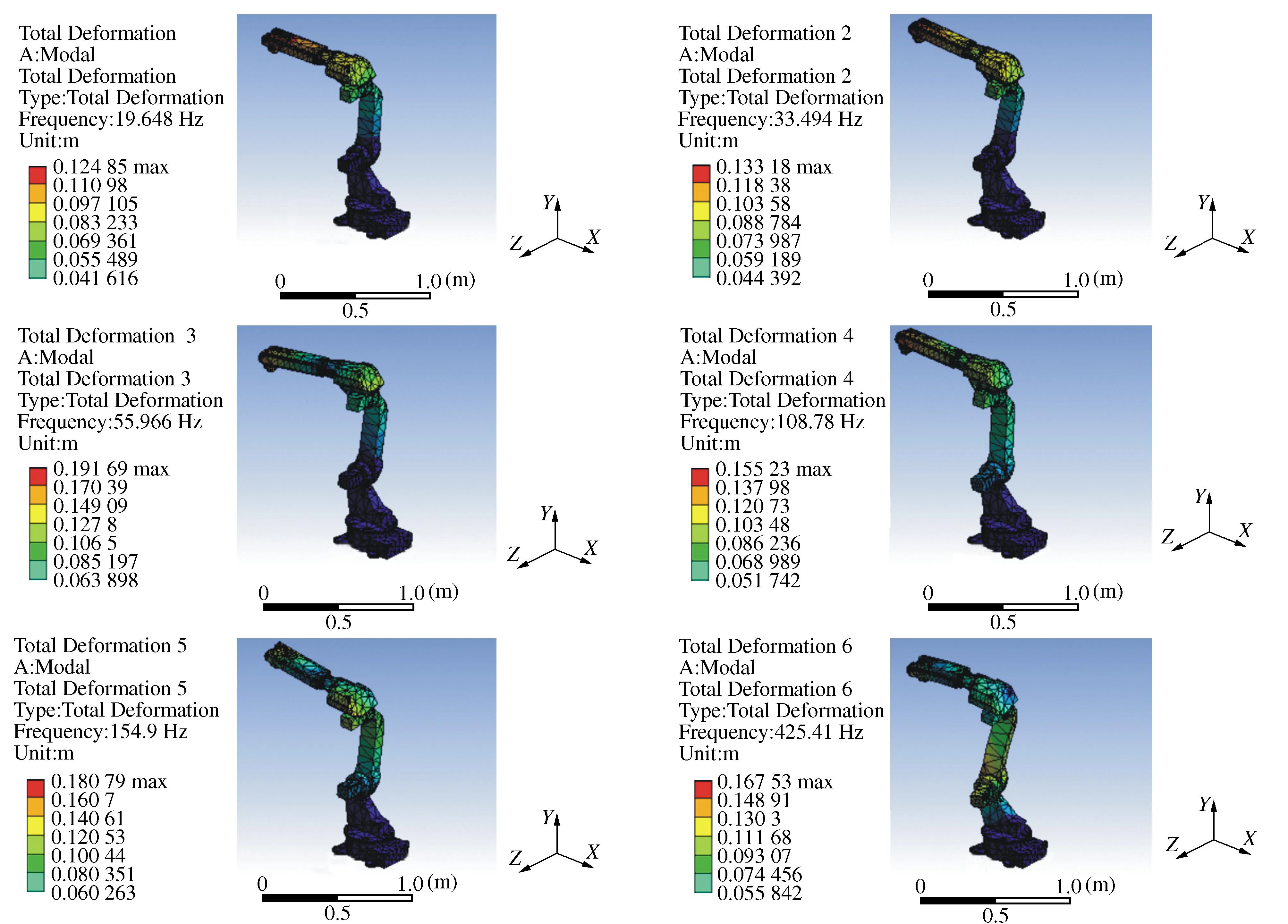
图2 机器人前6阶振型Fig. 2 The first 6th order shape of the robot
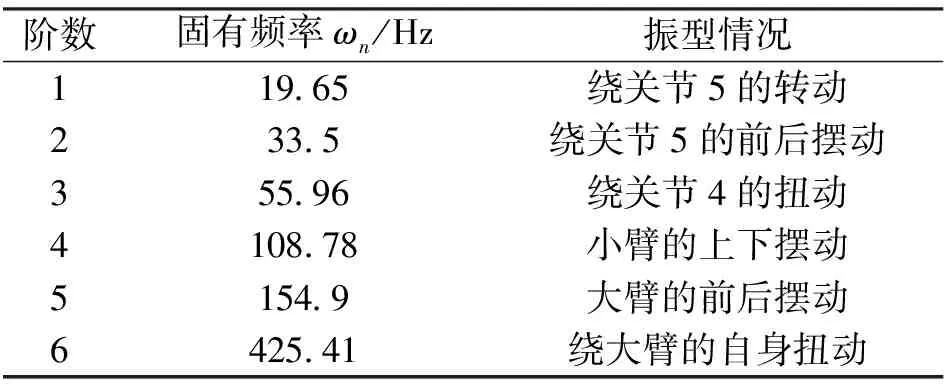
表1 机器人前6阶仿真模态分析Tab. 1 Mode analysis of the first 6 stages of robot simulation
结合图2仿真结果可知,工业机器人的前6阶固有频率分布于19.65~425.41 Hz之间。
由图2,根据机器人仿真振型变形幅值和激励点要反应机器人结构特点的基本原则,沿机器人机体布置66个激励点,并在机器人关节附近振型变形幅值大的6个区域优化测点布置[15],如图3所示。
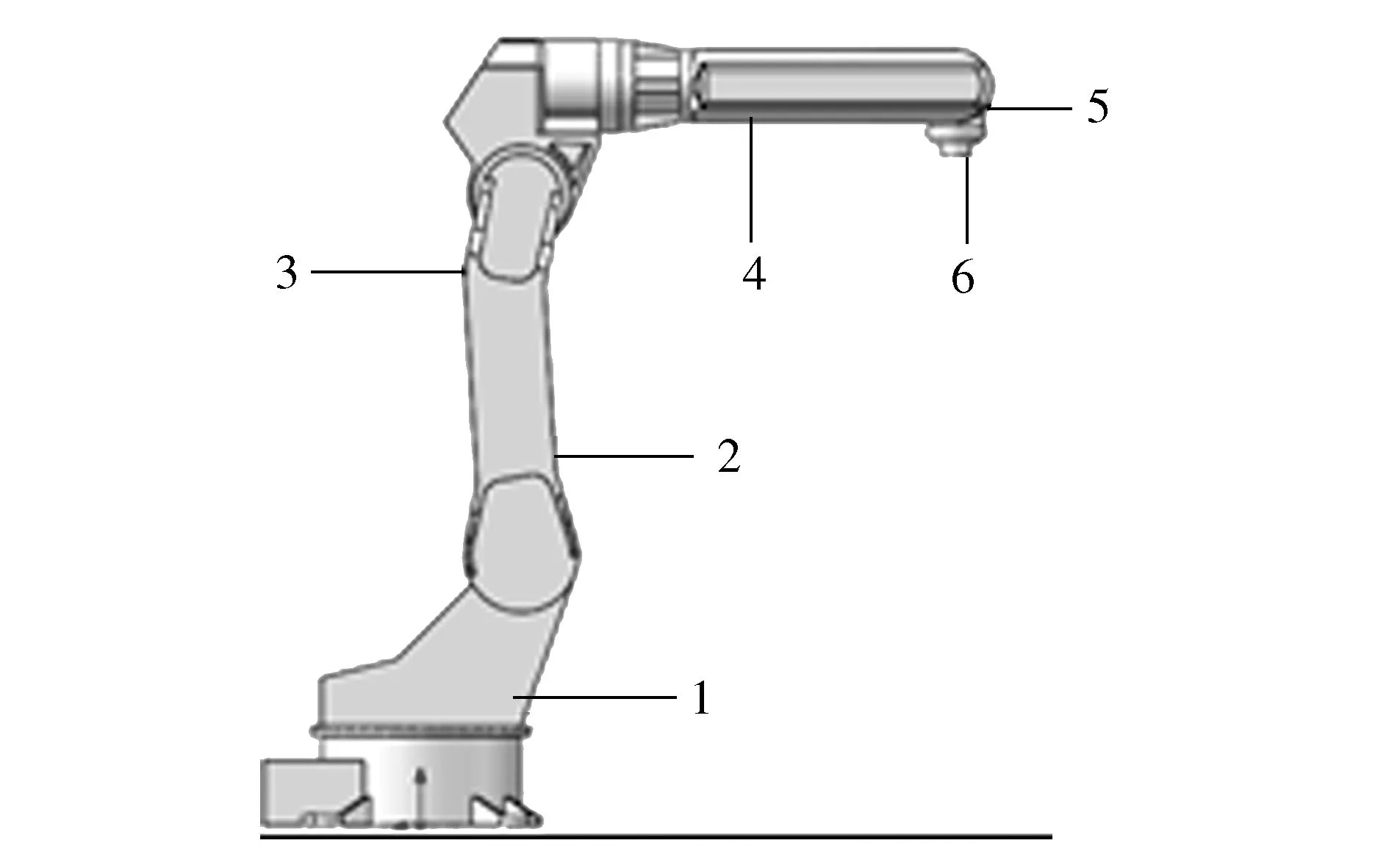
图3 模态测试关键测点优化布置区域Fig. 3 Optimal layout of key modal measurement points
2.2 工业机器人测点优化及模态试验
2.2.1 模态测试系统与测试方案
模态测试系统主要由激励子系统、振动响应拾取子系统、传递函数测量与模态参数识别子系统组成[20],如图4所示。
1) 激励子系统:由YDL-C-2型模态力锤和配套的DHF-0866B型电荷放大变换器组成。
2) 振动响应拾取子系统:主要由356A16 ICP三向加速度传感器和LMS-SCM05数据采集器组成。
3) 传递函数测量及模态参数识别子系统:主要包括LMS的Impact Testing和Modal Analysis模块。
由于机器人结构复杂,本文采取单输入多输出(SIMO)测量方式,即移动力锤进行多次单点激励且多点布置传感器拾振的方式进行试验,根据2.1节测点优化,沿机器人空间坐标系的X、Y和Z轴3个方向,在机器人的大臂、小臂上沿各关节周向同时布置加速度传感器。为了提高信噪比,依次对66个激励点进行5次力锤激励取平均,通过力锤激励与关节振动响应得到机器人系统传递函数,再进行曲线拟合得到所需模态参数。
综上,模态测试方案流程为:
首先,按有限元法优化测点布置并安装振动传感器。然后,连接好测试设备并设置好包括通道设置、锤击示波和锤击设置,锤击设置包含触发设置、带宽设置、加窗设置和驱动点设置等参数,并开始模态测试。最后,测试结束后,在数据验证模块中检查是否有遗漏,如有激励点遗漏应补齐,如数据完整,则完成测试。
2.2.2 模态测试结果与分析
根据上述模态试验流程,模态参数分析结果如表2所示。
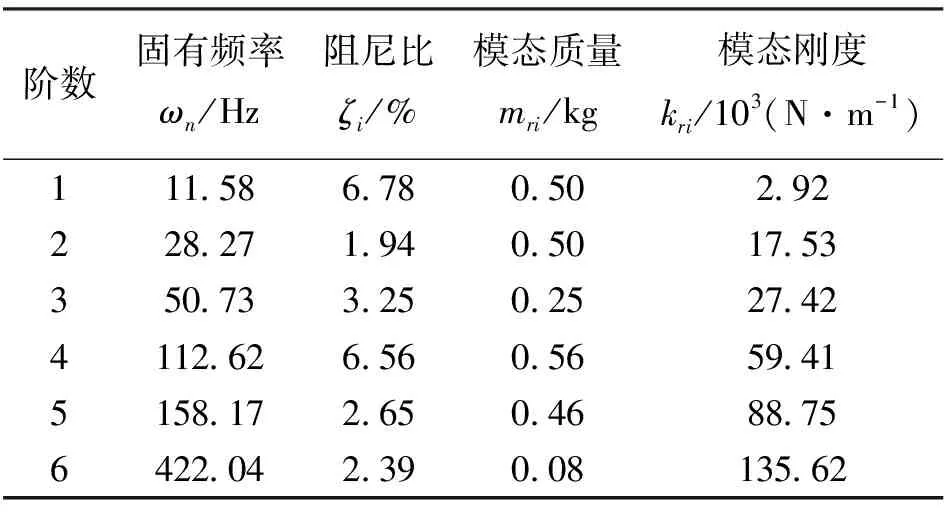
表2 机器人模态试验前6阶模态参数Tab. 2 The first six-order modal parameters before the robot modal test
由表1与表2对比可知:机器人有限元仿真模态分析与模态试验所得前6阶固有频率较为接近,第1阶固有频率偏差较大的原因可能在于仿真时对具有复杂结构机器人模型的简化与网格划分所引入的误差。
3 实验验证
3.1 工业机器人路径规划与关节数据采集
为检验所提关节振动求解方法的有效性,本文规划了机器人单关节运动和多关节联动两种指定路径。单关节运动时,利用示教器程序每次只定义一个关节运动,而多关节运动时则同时定义6个关节运动,机器人关节转角设置如表3所示。

表3 工业机器人路径规划Tab. 3 Path planning of industrial robot
机器人运动时,同时采集参与运动关节的电流与振动数据,采集系统由LabVIEW开发,具有采集、显示及存储数据等功能,数据采集设备如表4所示。

表4 机器人关节数据采集设备Tab. 4 Robot joint data acquisition equipment
本文在两种规划路径下,分别对各路径下用电流互感器对机器人关节伺服驱动器电流采集。因机器人启动和停止两个阶段电流会有微小波动而影响分析结果,故将这两个阶段剔除后的完整周期进行分析。
关节振动响应除了与关节振动系统的质量、刚度等参数有关,还主要受关节驱动力矩的影响[21],故关节运动时,其主要振动方向沿关节旋转运动的周向,如图5所示。

图5 关节振动物理模型Fig. 5 Physical model of joint vibration
根据图5所示的模型,本文在关节旋转运动周向布置单向加速度传感器以拾取各关节振动信号。
关节振动测试现场如图6所示,中间为机器人和相关采集设备,左侧两图分别为关节2振动传感器安装位置(左上)和机器人示教器(左下),右侧两图分别为关节1振动传感器安装位置(右上)和NI9234采集卡(右下)。首先根据表3定义各关节转角,振动信号采样频率设置为25.6 kHz,然后采集各关节至少包含一个完整周期的加速度信号。

图6 机器人关节振动试验现场Fig. 6 Robot joint vibration test site
3.2 关节周向加速度求解
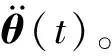
(14)

(15)
最后所求理论周向加速度与实测关节周向加速度均为关节扭转振动,可进行后续方法结果对比验证。
3.3 实验验证
本文以工业机器人前2个关节的实测加速度信号对所提方法进行验证。在表3的2种机器人规划路径条件下,将式(15)的转换加速度和实测关节周向加速度经滤波和归一化处理后,单关节1与单关节2的理论与实测振动对比结果如图7所示。
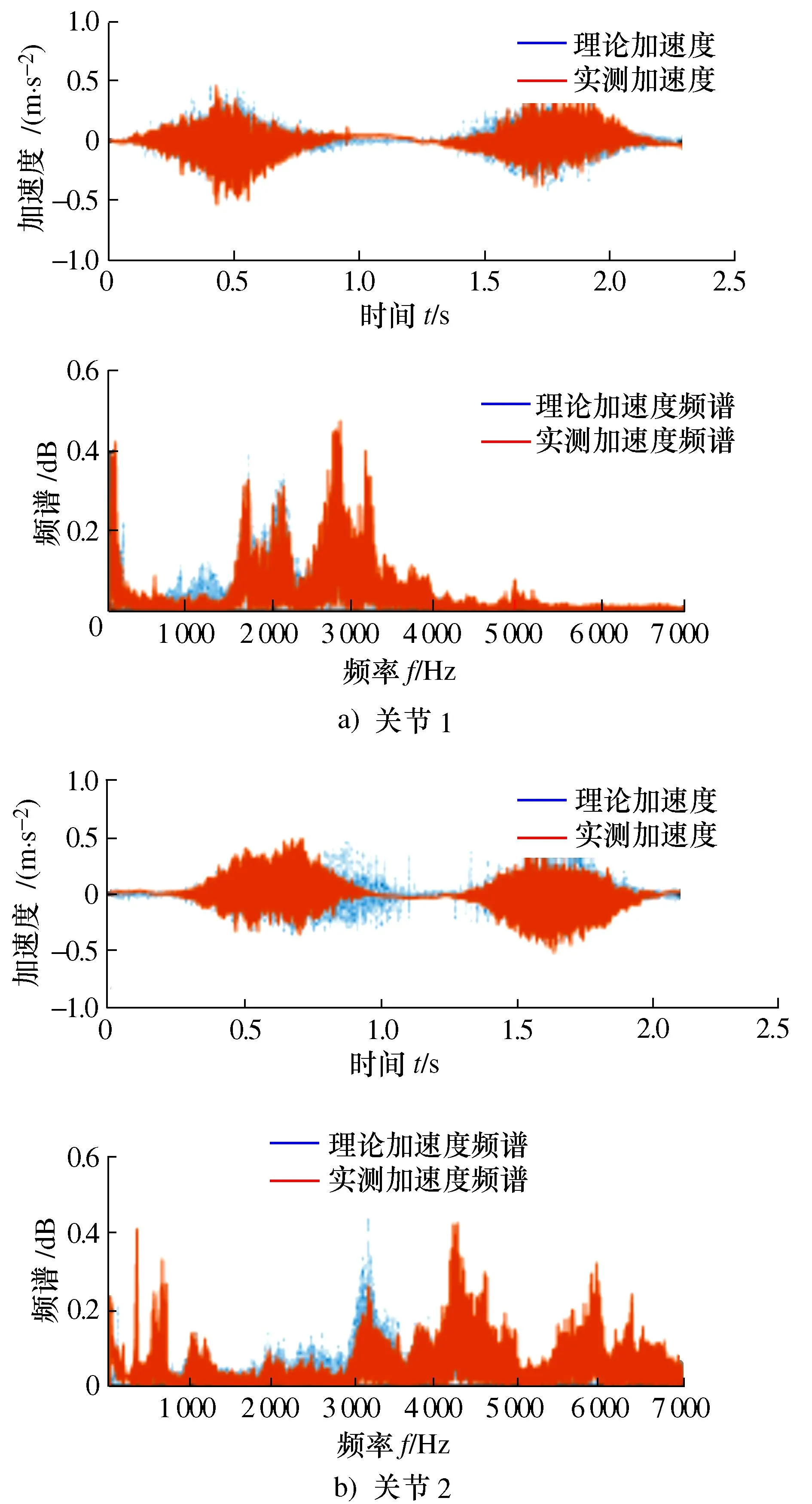
图7 单关节运动理论与实测振动时频域对比Fig. 7 Comparison of single-joint motion theory and measured vibration in the time-frequency domain
从单关节运动对比结果来看,工业机器人关节理论振动求解和关节实测振动结果在时域、频域上基本吻合。为量化理论求解与实际数据的差异,采用均方误差MSE(记为EMS)反映真实值与理论预测值的偏离程度,即
(16)
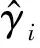
MSE值越小表示偏离程度越小。本文也对多关节联动时关节1、关节2的理论和实测振动频域偏差进行了MSE量化。由表5可知:无论时域或频域,各关节的MSE值均在0.01数量级以下,采用本文方法求解关节振动结果较理想。理论求解结果和实测结果间存在的微小差异可能是由于关节力矩与电流不是完全正比关系而带来的误差。
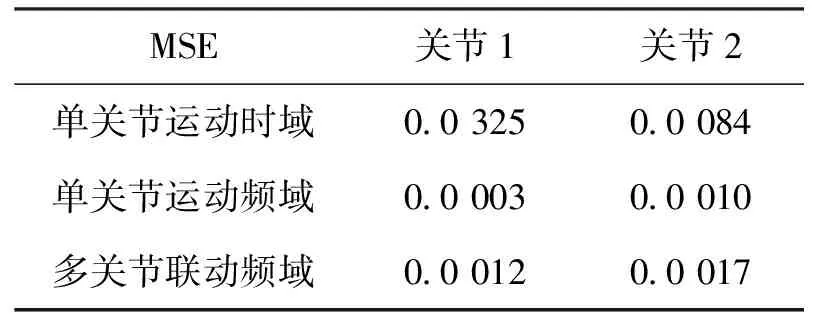
表5 机器人关节运动的理论与实测振动MSETab. 5 Theoretical and measured vibration MSE of robot joint motion
因全部关节联动时比单关节运动时的电流、振动周期长很多,且运动时的电流耦合导致难以从时域对比观察,故多关节联动仅从频域对比。由图8可知,从关节1与关节2的理论与实测振动对比来看,所提的振动求解方法与实测结果基本吻合,求解结果较理想。
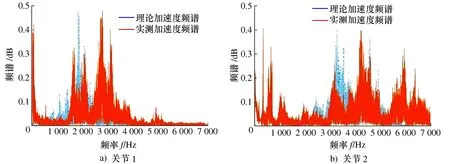
图8 多关节联动理论与实测振动频域对比Fig. 8 Comparison of multi-joint linkage theory and measured vibration frequency domain
表5中多关节联动时的MSE比机器人单关节运动时略大,产生此结果的原因除了可能来自工业机器人振动系统模型参数之外,还可能因为关节联动时各关节电流存在耦合所致。
4 结论
1) 通过有限元模态仿真优化模态试验测点布置,可以为建立工业机器人关节振动模型获取较精确的模态参数;
2) 在理想伺服控制条件下,可直接利用关节转矩常数与减速比将关节电流信息转化为关节驱动力矩,避免了高昂价格购买力矩传感器,且而从关节驱动力矩求解关节振动响应,避免了采用振动传感器对机器人各关节逐一检测而引起测试成本剧增。
本文所提出的方法为工业机器人状态监测与故障诊断提供了新的思路。
