一种S型加减速组合的速度规划算法

李甍材,赵东标,冯胜利

(南京航空航天大学 机电学院,南京 210016)

NURBS曲线拥有良好的局部控制能力和形状表达性能,被广泛用于自由曲线和曲面的构造中。国内外许多学者对NURBS曲线插补进行了大量研究,其中一个主要方向是插补中的加减速规划问题。

常见的加减速模型有直线型、三角函数型、指数型和S型。其中,S型加减速以其良好的柔性在NURBS曲线插补中被广泛运用[1-2]。从本质上讲,S型加减速是一种多项式方程的加减速,因此可以通过改进速度方程得到效率或柔性等方面更优的改进S型加减速模型。例如,Luo等[3]设计了一种加加速度连续且正负上限不同的改进S型加减速模型以提高柔性;赵国勇等[4]设计了一种使加加速度连续的七段式三次多项式速度方程;冷洪滨等[5]、Zhang等[6]等简化S型加减速,设计了另一种三段式三次多项式的速度方程,在保证加速度曲线连续的同时以最大加加速度值开始与结束加减速,减少计算量并缩短了加工时间;Zhu等[7]提出一种分数幂多项式的速度控制策略来实现加加速度连续;王允森等[8]设计了四次多项式的速度方程更柔性地实现加加速度连续,缓解高速加工中的冲击;Li等[9]在四次多项式速度规划基础上加入滤波器进一步实现了加速度、加加速度的平滑和冲击的减小。石川等[10]根据加减速轨迹段的特征归纳了8种S型曲线加减速形式,潘海鸿等[11]则更细致全面地分为17种加减速类型。

因为加加速度的连续和加工效率的提高往往存在冲突,单独一种改进的S型加减速只能做到一个方面的优化。因此,本文设计了一种兼顾加加速度连续和加工效率提高的新改进S型加减速模型,再通过与另外两种分别在加工柔性或加工效率上改进的S型加减速灵活组合,最大程度地发挥3种改进S型加减速的优点,实现加加速度连续的同时提高加工效率。同时,因为通过速度敏感点分段规划的加减速算法往往疏于对段间过渡的优化,本文设计了一种分段间速度平滑算法。先将加减速状态类型简化为4种,再根据不同加减速类型适当合并前后段曲线一起进行速度规划,最终减小了速度曲线的波动,极大地提高了合并前因分段距离限制的加工速度,实现加工柔性与加工效率的进一步提升。

1 速度规划预处理

1.1 自适应速度规划

为保证加工质量,先求取自适应速度作为后续速度规划的最大速度上限,使得任意点处速度值满足最大弓高误差emax、最大进给速度Vmax、最大法向加速度ANmax以及最大加加速度Jmax的约束[12-13]。

(1)

1.2 根据速度敏感点划分NURBS曲线

式(1)中的曲率半径ρi与曲率k(ui)成反比,因此可知在曲率极大值处自适应速度需要减小。但是一条NURBS曲线往往有多个曲率极大值点,并不是所有曲率极大值点处的最终自适应速度都是由曲率决定。例如曲率极大值点的曲率值很小时,它的自适应速度是由最大进给速度来约束的。因此本文通过式(2)筛选出真正由曲率决定自适应速度的曲率极大值点,称为速度敏感点[14],并以速度敏感点为界将NURBS曲线进行分段加减速规划[15-16]。

(2)

以图1为例,A、F为曲线首末两点,速度为0。以B、C、D、E这4个速度敏感点为界,曲线分为5段。为保证加工质量,应在速度敏感点前减速以满足自适应速度要求;为提高加工效率,则需在速度敏感点后尽可能地加速。因此对于单独一段曲线,往往由加速和减速两个过程组成,但有时由于曲线段长度限制可能出现纯加速和纯减速的情况,此时应根据实际情况调整速度敏感点处的速度。本文的加减速算法将基于此曲线分段方式进行。

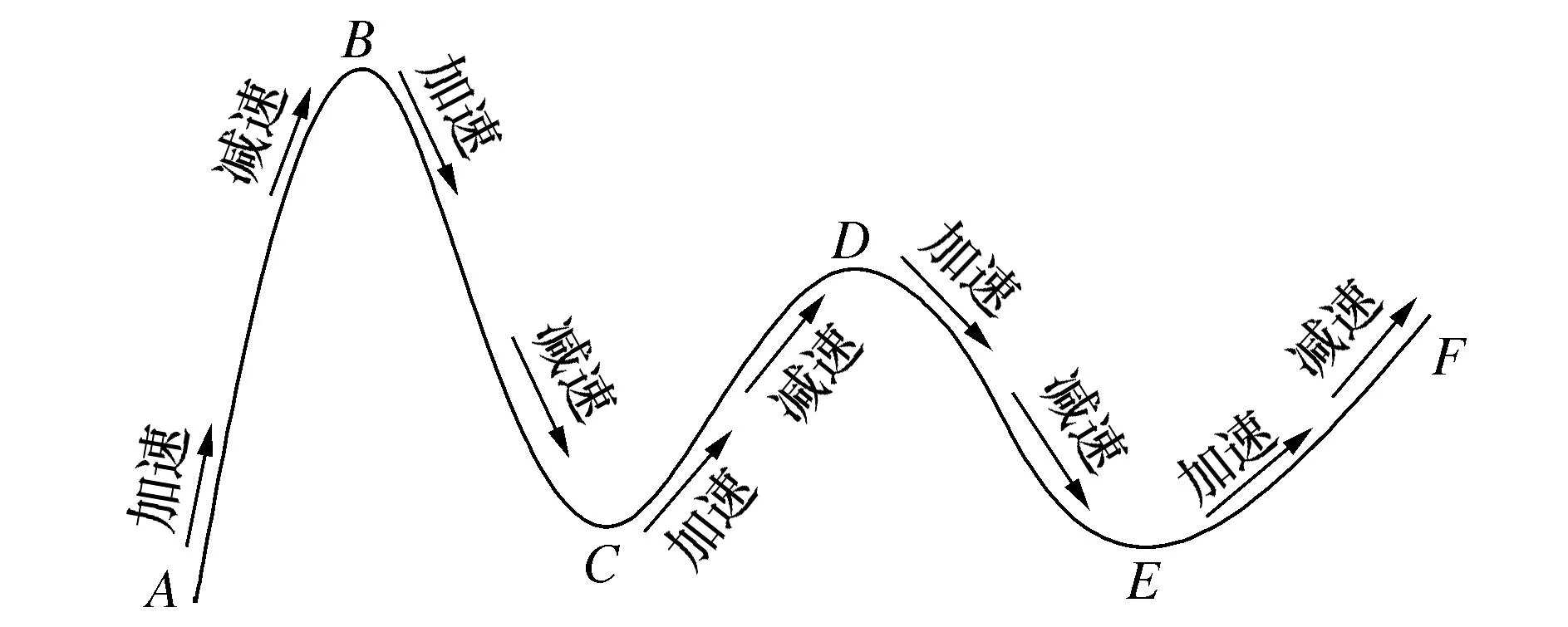
图1 基于速度敏感点的NURBS曲线分段加减速Fig. 1 Segmental acceleration and deceleration of NUBRS curve based on velocity sensitive points

2 3种S型加减速组合的加减速规划

2.1 一种新改进S型加减速模型

为了兼顾加加速度连续和加工效率,本文构造了一种新的S型加减速模型,如图2所示。该加减速模型保持加加速度连续,并通过在加减速中以最大加加速度起始与结束的方式实现加工效率的提高。

图2 改进S型加减速模型Fig. 2 Improved S-type acceleration and deceleration model

该模型加减速公式的推导如下:

以加速段为例,将减速段视为反向加速。加加速度曲线有两个要求:一是以最大加加速度开始并以0加加速度结束使得加加速度能在匀速时保持连续;二是加速段的加加速度积分最终为0以保证加速度在加速结束时重新归0。于是加速段的加加速度曲线如图3所示,分为一段加加速和两段加减速。

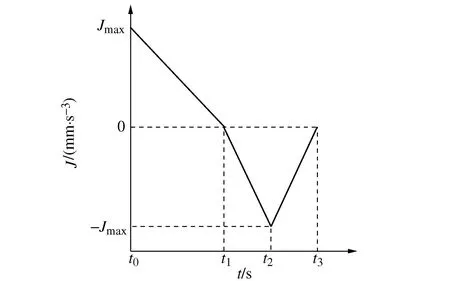
图3 加速段的加加速度曲线Fig. 3 Jerk curve of acceleration section

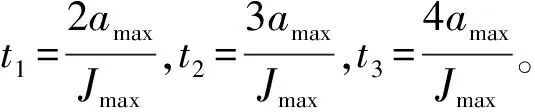
(3)

(4)

V(t)=

(5)

2.2 组合中的3种S型加减速模型

单独一种改进S型加减速无法同时在柔性和效率的提升上都做到最优。因此需要结合其他的改进S型加减速模型分情况使用来突出各自的优点。

本文选择了两种已有的改进S型加减速与上节本文设计的改进S型加减速模型进行组合。一种是由文献[4]简化得来的三段式加减速,它具有连续的加加速度,但是加工效率有所减低;另一种是文献[5-6]中的三段式加减速,它以最大加加速度起始与结束,提高了加工效率,但在匀速时出现加加速度的跃变。如图4所示,为区分这3种加减速,根据它们加加速度曲线的形状,分别称它们为W型、N型与V型加减速。且以加速段为例,可以将3种模型加速前后速度和位移的变化总结如表1所示。

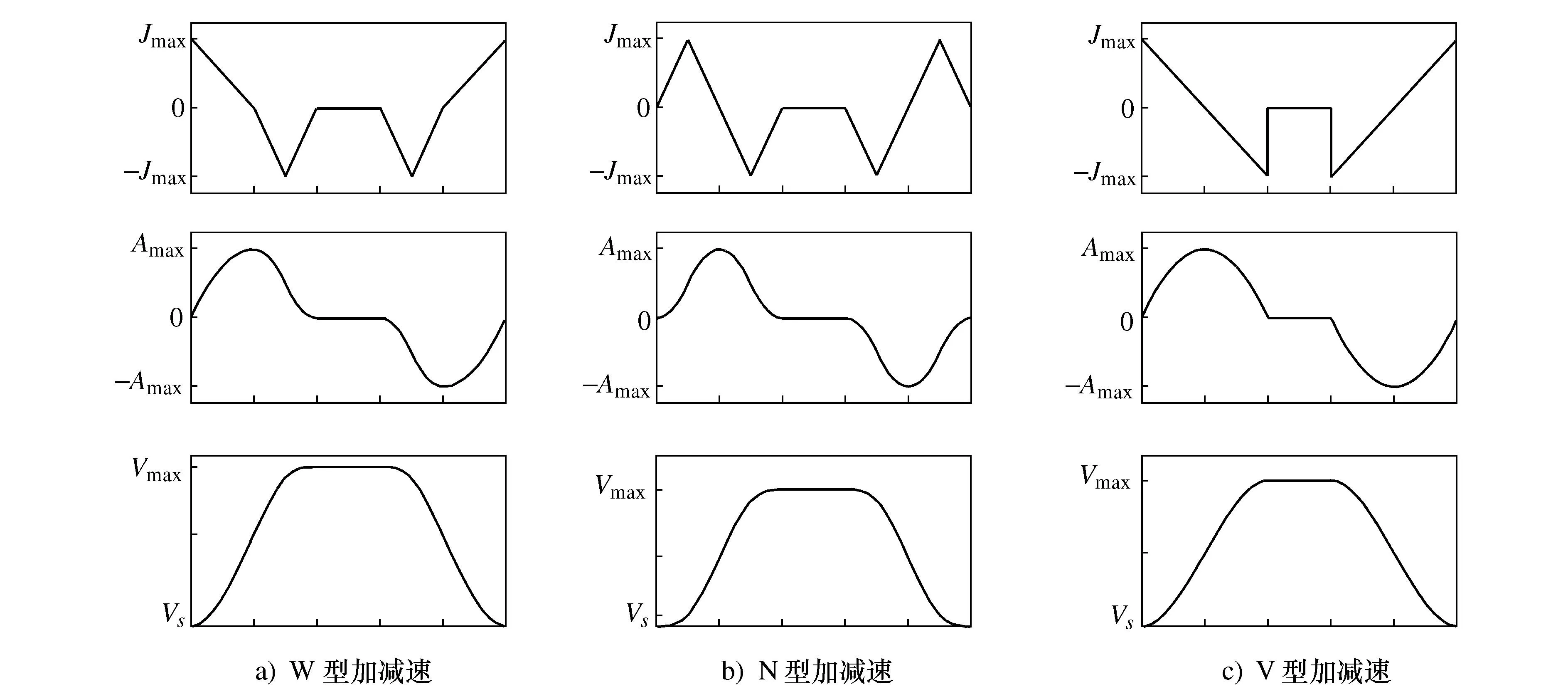
图4 3种S型加减速模型Fig. 4 Three S-shaped acceleration and deceleration models

表1 3种S型加减速模型加速段结束时的速度位移变化Tab. 1 The velocity and displacement changes at the end of the acceleration segment for the three models

2.3 3种S型加减速的组合策略

基于预处理的结果,NURBS曲线被速度敏感点分成了许多段。本文将每一段曲线加减速过程分为:加速段、匀速段和减速段,并根据加减速过程中这3部分的缺失情况将每段加减速形式分为4种类型:加速减速型、加速匀速减速型、纯加速型和纯减速型。

根据表1可知:V型加减速加工效率最高,但匀速时出现加加速度阶跃;W型加工效率次之,但能在匀速时保证加加速度连续;N型首末加加速度为0,加工效率最差,但能实现纯加、减速前后的柔性过渡。因此在保证加加速度连续的前提下,速度规划在曲线分段未出现匀速时使用V型;当出现匀速或纯加速、纯减速时使用W型;而N型加工效率低,只用在纯加速后一分段的加速段或纯减速前一分段的减速段中,以保证前后分段的加加速度连续。

基于以上加减速策略,从加减速状态判断和速度修正两部分对一段曲线加减速规划的具体推导如下:

1) 加减速状态判断。因为V型加减速效率最高,优先使用,所以每次加减速模型都从V型加减速开始判断。下面以加速段和减速段模型均是V型加减速为例,设曲线长度为L,首末速度为vs和ve,最大速度为vmax。由表1中V型加减速的速度变化得

(6)

同理,将ve替换成vmax或将vs替换成vmax可分别得到a+max与a-max,其中,“+”为加速度,“-”为减速度。再根据表1中V型加减速的位移变化,求得V型加减速模型下4种加减速状态的判断依据如下:

(1) 纯加速型

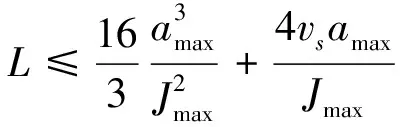
(2) 纯减速型

(3) 加速减速型

(4) 加速匀速减速型

若加减速模型不为V型,也可以类比上面方法根据表1数据进行加减速状态的判断。

2) 速度修正。根据曲线段的以下3种不同加减速状态类型对速度进行修正。

(1) 纯加速或纯减速型。先将加减速模型修正为W型。加减速状态若为纯加速型,需要修改末尾速度;若为纯减速型则修改起始速度。

以纯加速为例,根据表1中W型加减速的速度位移变化,利用vs和L可以求出ve。将位移公式化简可得

(7)

令

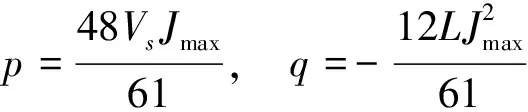
(8)

根据Cardan公式可解得

(9)

因此求得

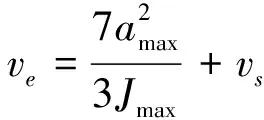
(10)

此时应更新后一段的起始速度并将它的加速段模型修正为N型。同理,当加减速状态为纯减速型时,则更新前一段的末尾速度并将减速段加减速模型修正为N型,此时因为改变了前一段速度规划的末尾速度参数,还需要进行回溯规划。

(2) 加速减速型。因加减速距离限制,最大速度达不到自适应预处理的vmax,所以通过二分法求取新的速度最大值。

(3) 加速匀速减速型。由于匀速段出现,若加速或减速段模型为V型则需要改为W型重新进行加减速状态判断,然后根据新的加减速状态调整速度。若加、减速段模型皆不为V型则直接按照相应模型进行速度计算。

基于3种S型加减速组合的加减速规划流程如图5所示。

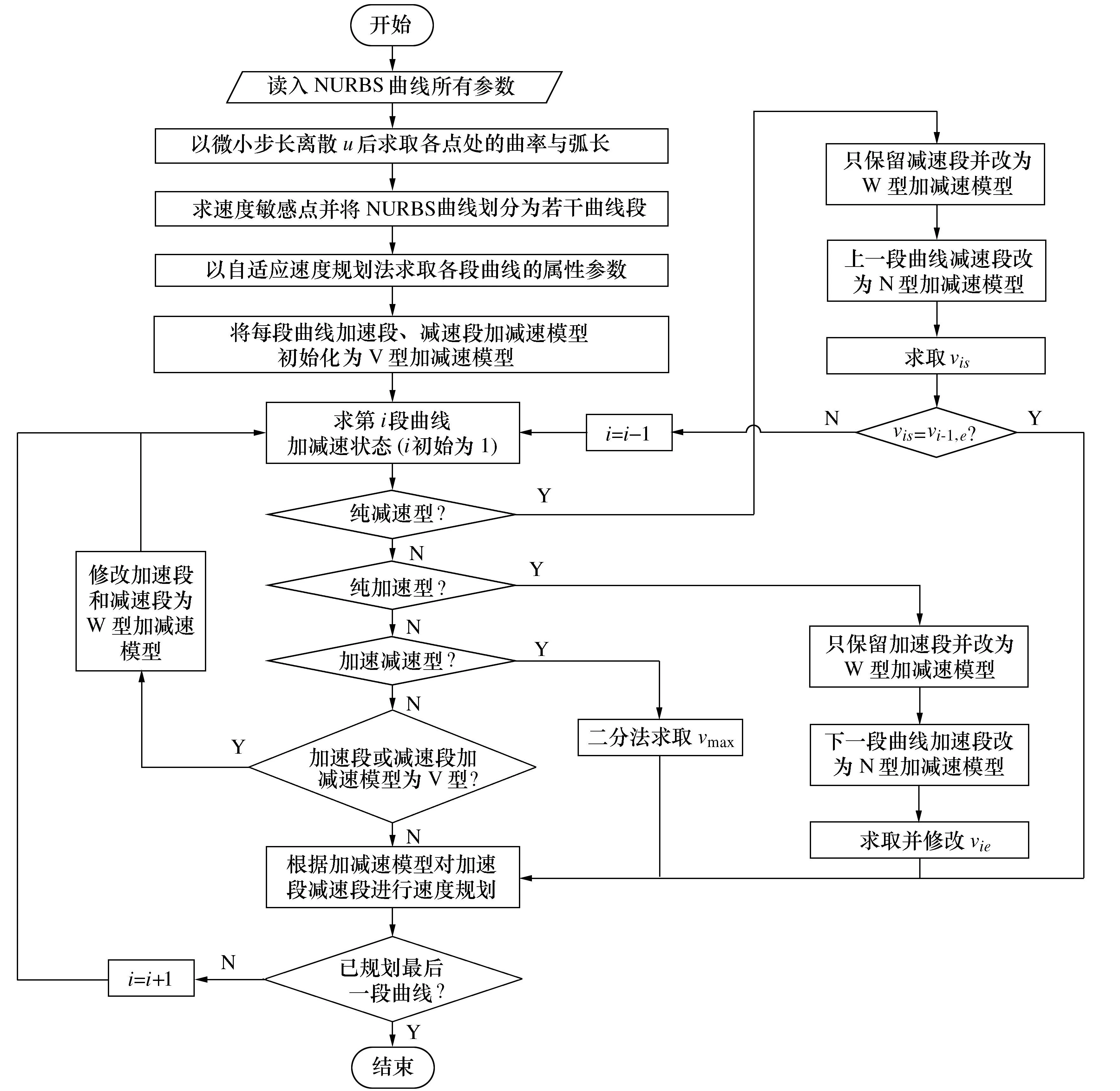
图5 基于3种S型加减速组合的加减速规划流程图Fig. 5 Acceleration and deceleration planning flow chart based on three S-type acceleration and deceleration combinations

3 曲线段间的加减速规划

3.1 曲线段间的速度平滑

以往分段规划的加减速算法,往往只注重分段内部的加减速设计,忽视了曲线分段数过多,加速减速频繁的问题。特别是曲线曲率变化趋势频繁改变处容易出现许多细小弧长的加减速分段,不仅降低了加工效率而且增大加工时对机床的冲击。为此本文针对加减速分段过多,对分段间连接进行速度平滑规划,采用一定算法适当地合并前后段曲线后,再一起进行速度规划,可以有效地减小微小分段数量,提高加工效率和柔性。

4种加减速状态中,因加工长度受限导致的纯加速、纯减速,是影响加减速平滑的最主要因素,因此本文针对纯加速、纯减速段从以下3种情形进行分析处理,最终实现曲线段间加减速的平滑。

1) 连续出现纯加速或纯减速

将连续的纯加速段或纯减速段合并为一段曲线,一起进行速度规划。因为曲线分段减少,不需要频繁多段地加速或减速,速度曲线得到平滑且能提高合并前因分段距离限制的加工速度。以连续纯加速为例,平滑示意图如图6a)所示。

2) 纯加速紧接纯减速

合并这两段曲线,归做加速减速形式处理,这样可以将合并前纯加、减速的W型模型修改为V型模型,提高加工效率,平滑后如图6b)所示。

3) 单独的纯加速或纯减速

对于单独的纯加速或纯减速(可以是情形一合并得到的),可以尝试将纯加速合并到后一段曲线的加速段中,或将纯减速合并到前一段曲线的减速段中来一起进行速度规划。如图6c)所示,纯加速、加速匀速减速和纯减速组成的3段曲线被合并为一段。

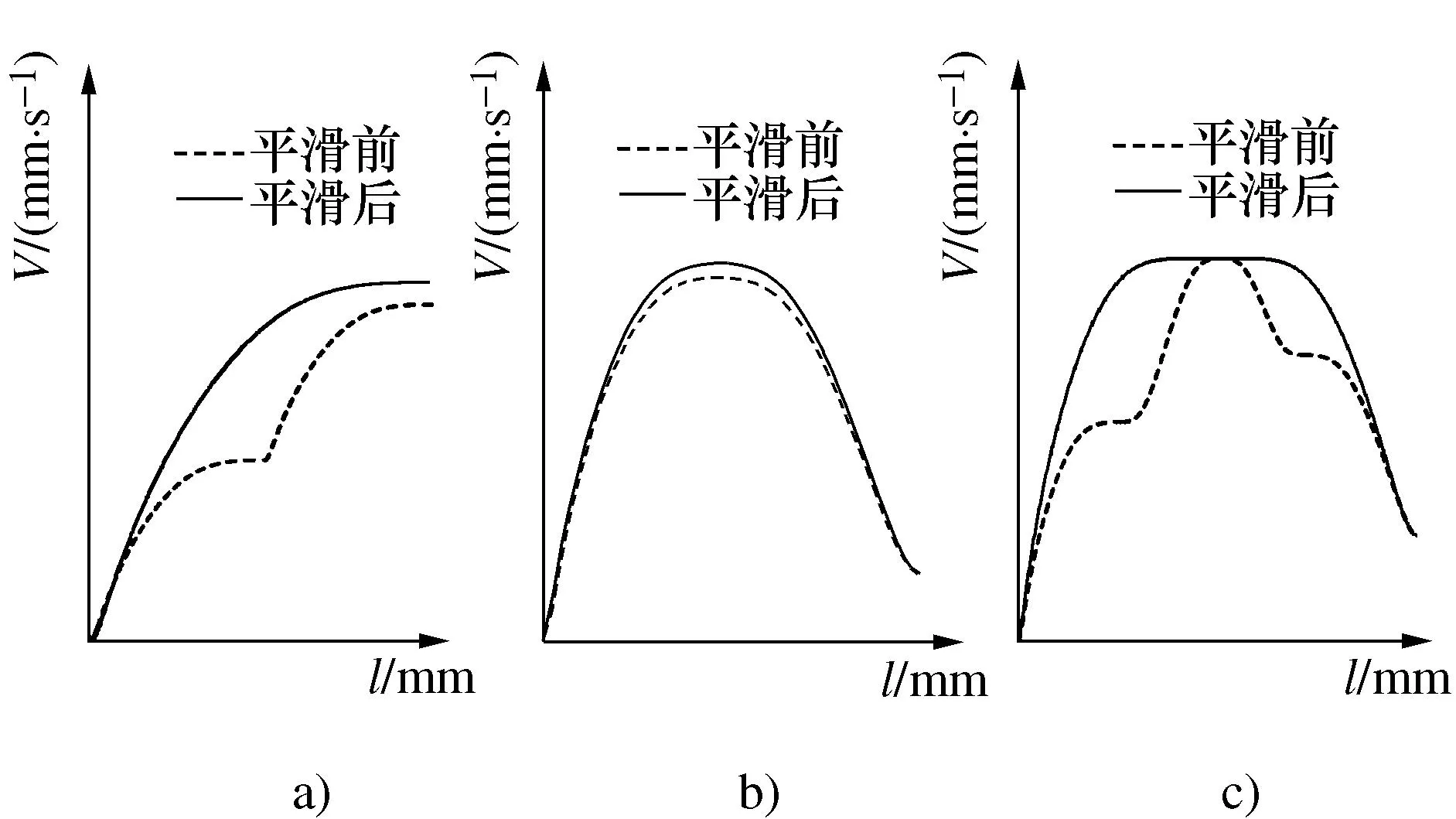
图6 平滑前后的速度位移曲线Fig. 6 Smoothed velocity displacement curve

合并曲线规划能提高因分段距离限制的速度,但也可能导致速度超限的情况出现。如图7所示,本文以自适应速度作为速度上限,合并平滑后在圆圈处出现了速度超限的情况。

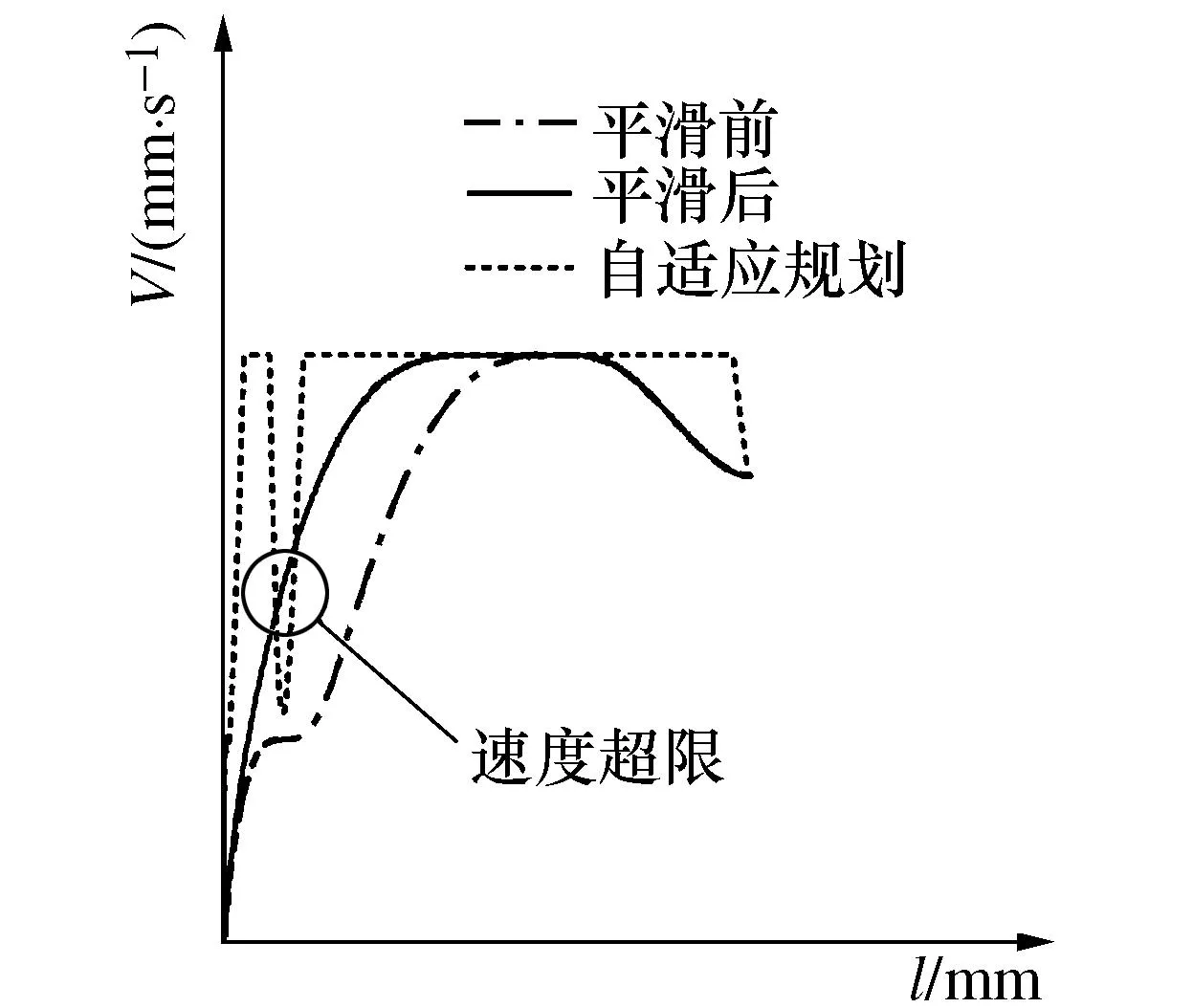
图7 合并曲线段后的速度超限Fig. 7 Speed overrun after merging curve segments

因此每次合并都需要记录下曲线段分段处即速度敏感点的位置及自适应速度,并在合并速度规划中,判断各个速度敏感处是否出现速度超限。

若出现速度超限,对于情形一,通过二分法求取合适的最大速度vmax来满足每个速度敏感点处的速度限制。对于情形二,因为需要减小最大速度,所以会出现匀速段,加减速模型又修改回W型,因此取消合并重新各自进行速度规划。情形三比较特殊,分两种情况讨论:①若合并后是加速减速形式,先判断是否需要修改加减速模型,最后以二分法找出合适的最大速度,以满足合并前所有速度敏感点处的速度限制。②若合并后是加速匀速减速型,此时若为满足所有速度敏感点处的速度限制,修正后的匀速段速度将远比合并前小,极大增大了加工时长,因此取消合并重新各自进行速度规划。

合并后判断各速度敏感点速度是否超限的具体方法如下:

首先根据加减速模型和表1数据,判断速度敏感点位置Lcheck在速度规划中属于加速、匀速还是减速阶段。若为匀速段,直接比较速度敏感点限制速度vcheck与vmax来进行速度超限判断;若不为匀速段,先根据表1和表2数据判断vcheck在实际加减速规划中属于加速段或减速段中的哪一细分阶段;再通过Cardan公式求取vcheck在实际加减速规划中对应的位置Lreal,比较Lcheck与Lreal即可判断在速度敏感点处是否超限。W型和N型加减速加速段的3个细分阶段速度变化Δv与位移变化ΔL,如表2所示。

表2 W型和N型加减速各加速阶段的速度与位移变化Tab. 2 Velocity and displacement changes in each acceleration phase of W type and N type acceleration and deceleration

以加速、减速段皆为W型加减速模型和加速匀速减速的加减速状态为例,对一个速度敏感点的处理给出数学推导:

设加速、减速段最大加速度分别为a+max,a-max,曲线段首末速度分别为vs,ve,最大加加速度为Jmax,vcheck、Lcheck分别为速度敏感点的速度上限和位置。根据表1可得速度敏感点Lcheck所处的加减速阶段,即:

(11)

假设处于加速阶段,则根据表2的数据进一步判断vcheck在加速阶段中的具体阶段,即:

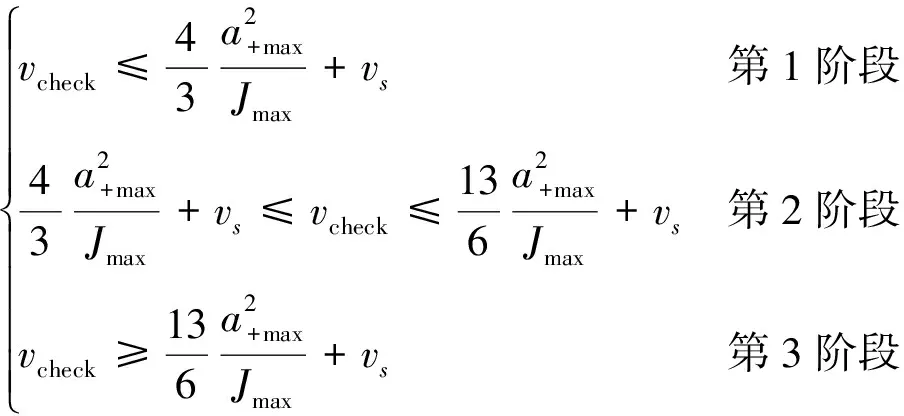
(12)

假设处于第1阶段,则通过Cardan公式计算出加速过程中达到vcheck时的Lreal。若Lcheck≤Lreal,则速度在Lcheck处未出现速度超限;若Lcheck>Lreal,则出现速度超限。其他处于匀速或减速各阶段的超限判断可以根据上述方法进行类推。V型加减速加速段只有一个阶段,它的速度位移变化如表1所示。而3种模型的减速段速度位移变化则可以视为反向加速来计算。

3.2 仿真与实验

将曲线段间的速度平滑与基于3种S型加减速组合的加减速规划结合得到了本文完整的速度规划算法。为验证算法的有效性,选取蝴蝶型NURBS曲线进行仿真加工[16]。其中插补周期为1ms,最大速度240mm/s,最大法向加速度4 900mm/s2,最大加加速度48 000mm/s3,最大弓高误差0.001mm。

如图8所示,在蝴蝶的头尾部和翅膀的下方存在许多曲率突变的微小弧段,这些地方加减速时极易出现纯加速或纯减速,而本文速度规划算法中的速度平滑部分即在这些地方发挥作用。本文基于3种S型加减速组合的改进S型加减速在加入段间平滑前后对比如图9和图10所示。

图8 蝴蝶型NURBS曲线Fig. 8 Butterfly-shaped NURBS curve

图9 有无段间平滑的改进S型加减速速度位移曲线Fig. 9 Improved S-shaped acceleration and deceleration velocity displacement curves with and without inter-segment smoothing

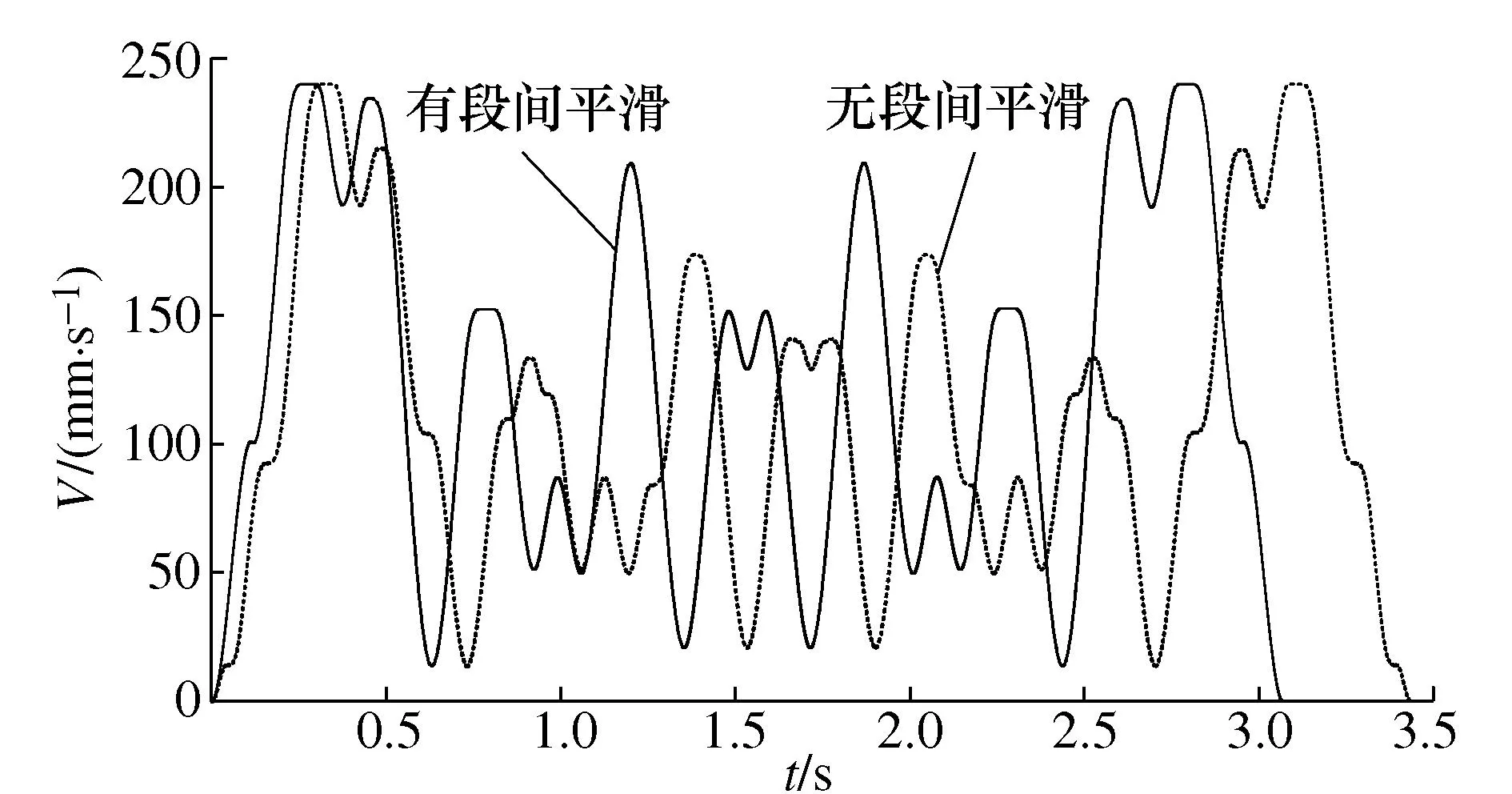
图10 有无段间平滑的改进S型加减速速度时间曲线Fig. 10 Improved S-shaped acceleration and deceleration speed time curves with and without inter-segment smoothing

由图9可知:基于3种S型加减速组合的加减速算法在加入分段间速度平滑后,消除了许多微小弧段的加速减速波动,且没有出现速度超限的情况。曲线分段由原来的26段变为14段,因此整体速度曲线更加平滑。由图10可知:曲线段合并后一起进行速度规划使得合并处的速度相比原来有所提升,最终缩短了整体的加工时间。加工时间由原来的3.435 8s缩减到3.068 7s,加工效率提高了10.68%。

3种S型加减速组合的加减速算法与分段间速度平滑结合得到本文完整的速度规划算法。将其与S型加减速算法进行仿真比较。

如图11所示,与S型加减速相比,本文算法在加加速度上,保证了加加速度连续不阶跃;在加速度方面,本文算法波动幅度明显小于S型加减速,且因合并曲线段使得整体波动频率有所降低,从26段减少为14段;从速度曲线还可以看出本文算法的加工时间与S型加减速相差甚小。本文算法为3.068 7s,S型加减速为3.033 7s。若对V型和N型加减速进行同样仿真可得:V型加减速3.322 9s,N型加减速3.562 1s。相比其他3种加减速,本文算法在加工效率上明显优于V型和N型算法,几乎追平S型加减速。此外本文算法整体的速度曲线更加平滑,没有许多微小的波动。提高加工效率的同时拥有更好的加工柔性。

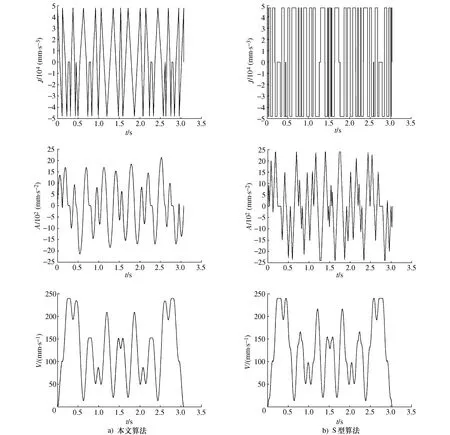
图11 加减速仿真比较图Fig. 11 Comparison of acceleration and deceleration simulation

除了加工效率,加工精度也是评价速度规划算法好坏的一个重要指标。在实际NURBS曲线插补过程中是以微直线代替曲线所以存在弓高误差。此外,步长与参数u没有直接的计算关系,速度规划的速度只能作为理想速度来进行参数预估,且插补周期是固定离散的,使得实际步长与理想步长存在偏差,用速度波动率来表示。因此,本文对速度波动率和弓高误差这两个精度指标进行插补实验比较。

由图12和图13可知:本文算法的弓高误差与S型算法变化趋势相似但处处小于S型算法,速度波动率则明显小于S型算法。将相关参数进行统计处理可得表3,通过对比可知本文算法在加工精度上要明显优于S型算法。

图12 弓高误差图Fig. 12 Diagram of arch height error

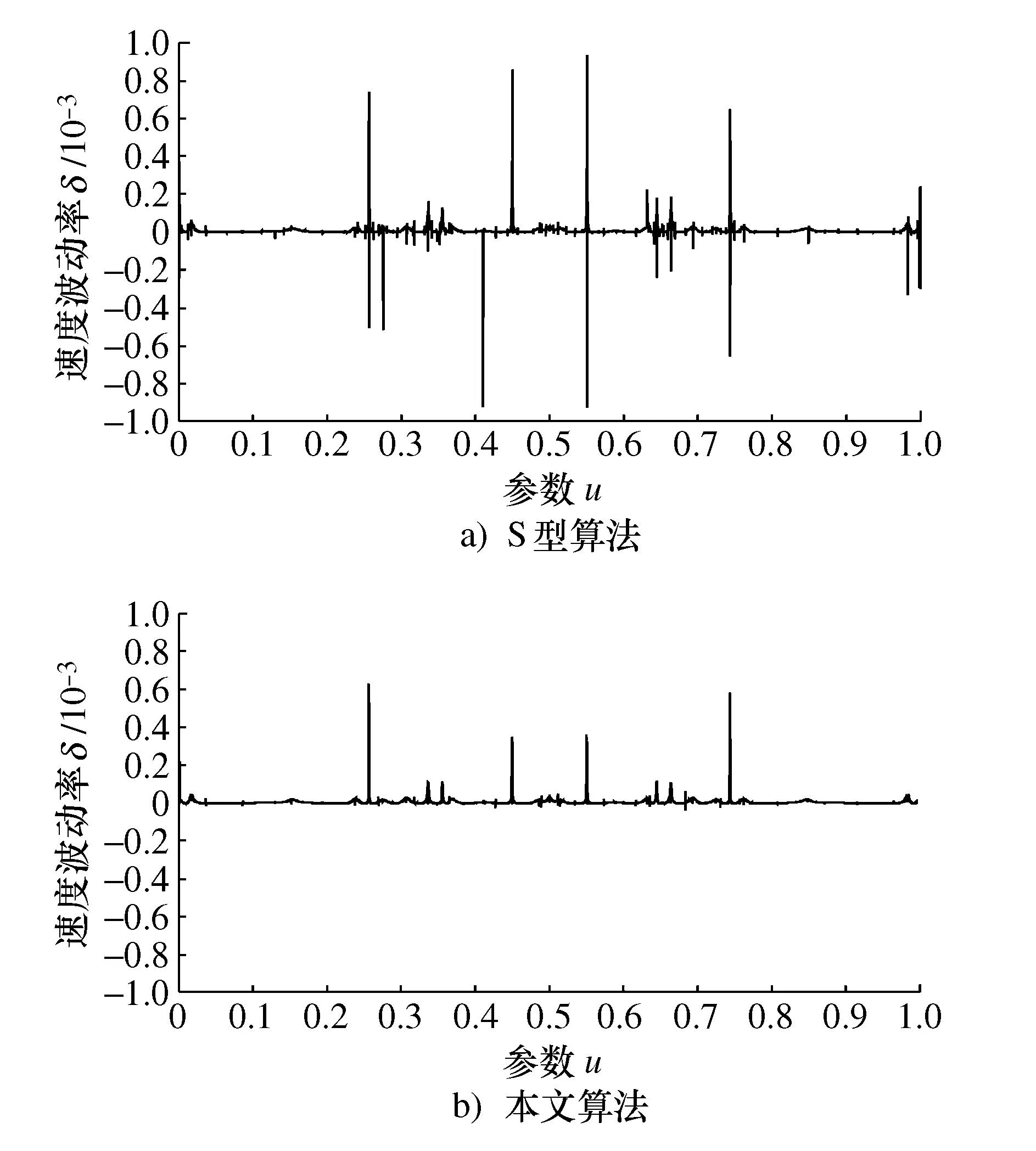
图13 速度波动率Fig. 13 Volatility of velocity

表3 弓高误差和速度波动率统计表Tab. 3 Chord error and speed fluctuation statistical table

总体上,相关结果表明了本文速度规划算法能在加工中全程保持加加速度连续,并通过合并微小分段,提升加工速度的同时减少速度的频繁波动。相比传统S型加减速,本文速度规划算法同时兼顾了加工柔性和加工效率,且加工精度有所提高。

4 结论

1) 本文设计了一种兼顾加加速度连续和加工效率提高的新改进S型加减速模型,并选取了另外两种分别在这两方面进行单一改进的S型加减速模型。针对纯加速、纯减速、加速减速和加速匀速减速4种不同的加减速状态,通过3种加减速模型的合理组合,发挥各自优点,在保持加加速度连续的同时尽可能地提高加工效率,使得加减速综合性能获得提升。

2) 针对大部分基于曲线分段规划的加减速算法缺少对曲线分段间连接优化的问题,设计了一种分段间的速度平滑算法。将其与本文设计的S型加减速组合算法相结合再运用到速度规划中。通过合并纯加速、纯减速段到前后曲线段,再对合并曲线进行速度规划,使得整体曲线分段减少,加减速更加平滑、加工效率明显提高。最后验证了本文算法能兼顾加工柔性和加工效率且在加工精度上具有一定的优越性。