部分接入电池储能系统的模块化多电平换流器控制方法

韩 雪，贺荣栋，凌志斌

（上海交通大学电力传输与功率变换控制教育部重点实验室，上海市 200240）

0 引言

大容量储能可以抑制新能源发电波动性、随机性和反调峰特性对电网的不利影响。基于模块化多电平换流器（modular multilevel converter，MMC）的电池储能系统以其模块化、分散化和高压大容量的优势得到越来越多的研究［1-3］。

现有研究多集中在每个子模块都接入储能电池的MMC 电池储能系统（MMC based battery energy storage system，MMC-BESS）上。MMC-BESS 作为一个三端系统，可以方便地实现交直流系统的互联和解耦，同时发挥电池的储能作用来实现功率的平抑及缓冲［4］。其基本控制策略为外环控制得到电流dq轴参考值，再由内环控制实现电流的快速响应，实现有功无功功率的解耦控制［5］。研究重点多为储能电池的管理，文献［6］提出一种离散时域电池荷电状态的功率预测模型进行实时动态控制，系统响应速度快且电流追踪准确。现有运行控制均针对所有子模块都接入储能电池的拓扑，多采用传统的双闭环控制。整个系统电池数量多、体积庞大、造价昂贵，在储能需求不是很大的情况下会造成电池容量的浪费。

电池储能系统主要由电池组、电池管理系统、能量管理系统、储能变流器以及其他电气设备构成［7］。减小每个子模块储能电池的容量可以一定程度上缩减成本，但二者并不成正比，即成本降低比例会小于电池容量减小比例，且所需电池管理系统并不会减少。因此，国内外少数学者开始研究部分接入电池储能系统的MMC （MMC with partly integrated BESS，MMC-PBESS），能够在满足储能配比要求的前提下有效降低储能成本。此外，MMC-PBESS可以为电力电子化程度逐步加深的电网提供惯量，在一次调频、黑启动等储能容量要求不是很大的辅助服务方面也有良好应用前景［8］。现已有MMCBESS 工程项目在建，故在MMC-BESS 基础上减少电池数量的MMC-PBESS 同样有应用前景和价值，其相应消防等配套措施在现有储能电站、MMC 换流站中已有研究应用。

MMC-PBESS 具体可以分为部分子模块储能、电池堆平行支路储能、电感平行支路储能这3 种拓扑［9-12］，其中，第1 种拓扑不改变MMC-BESS 原有结构，且有半数子模块接入储能、某相接入储能、某桥臂接入储能等不同实现形式。现有研究均通过注入环流来解决部分储能导致的系统内部不平衡问题，即通过环流直流分量来实现相间能量平衡、交流分量来实现相内能量平衡，但是环流计算烦琐且注入环流增加了系统控制的复杂性，各桥臂控制策略是耦合的，缺乏各拓扑形式的针对性［13-15］。文献［13］基于某相接入储能的MMC-PBESS 提出了电池或电网控制方法，通过改变电池电流给定值来实现电池均衡，但是储能子模块中电池通过斩波电路接入，控制复杂。文献［16］研究了电容电压平衡及调制范围约束下储能电池接入比和调制比、并网功率因数之间的关系，但没有进一步对其控制策略做出优化改进。上述关于MMC-PBESS 的文献，虽然拓扑结构与传统的MMC 不同，但其电容部分的电容电压均衡策略与传统MMC 的电容电压均衡策略相同。基于载波移相调制的桥臂电容电压均值和子模块电容电压的策略通过比例-积分（PI）控制改变调制波波形来实现电容电压均衡；基于最近电平逼近的闭环排序算法根据最近电平逼近确定需要投入的子模块数，在对子模块充电时投入相应个数电压最低的子模块，放电时投入相应个数电压最高的子模块，从而实现电容电压均衡；电容电压外环控制策略以桥臂总的子模块电容电压为控制目标生成电流内环的参考值，桥臂内部电容电压均衡仍需要另外采取措施，如排序均衡算法；还有附加子模块、投切矩阵自平衡、环流注入等控制策略［17-18］。

本文针对下桥臂接入储能电池的MMCPBESS 做了分析及控制方法研究。半数子模块储能不仅可以降低储能成本，还可以在交流侧短路的情况下支撑直流电压，该控制方法同样适用于上桥臂接入储能电池的拓扑。每相均匀接入电池也可以实现半数子模块储能，但是其控制策略需要考虑调制波分配等因素，更加复杂，且已有学者进行了研究。本文第1 章介绍了下桥臂接入储能电池的MMC-PBESS 拓扑及其数学和电路模型；第2 章给出了MMC-PBESS 的控制策略和运行边界；第3 章对比分析了MMC-PBESS 在MATLAB/Simulink平台上的仿真结果；第4 章给出了研究结论。

1 下桥臂接入电池的MMC-PBESS 建模

下桥臂接入储能电池的MMC-PBESS 拓扑如图1（a）所示。该拓扑和传统MMC 拓扑结构类似，由三相6 个桥臂组成。每个桥臂由N个电容子模块（SMC）或电池子模块（SMB）和一个桥臂电感La串联组成，子模块均为半桥子模块。其中，ij(j=a，b，c)为j相交流母线电流；ipj、inj分别为j相上、下桥臂电流；Idc为直流母线电流；ugj为j相交流侧并网电压；Udc为直流电压；UB为子模块电池电压；Lg为交流侧并网电感；C为电容子模块的电容；C0为电池子模块中电池并联的电容。

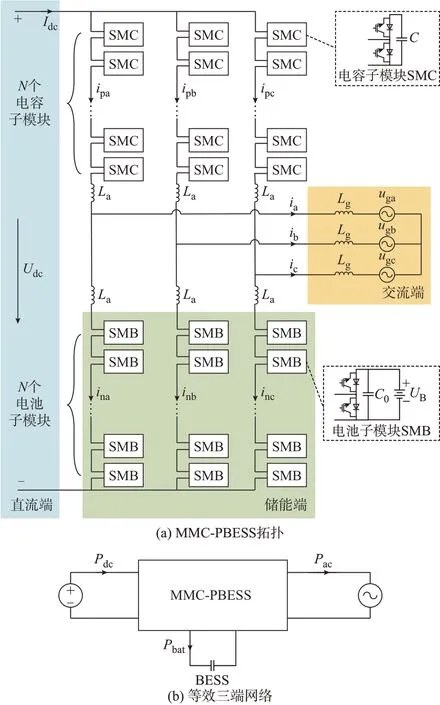
图1 下桥臂接入储能电池的MMC-PBESSFig.1 MMC-PBESS with lower bridge arm connected to energy storage battery

不同的是，该拓扑每相下桥臂子模块均接入储能电池，将传统MMC 拓展为一个三端口网络，如图1（b）所示，可以实现直流端、交流端和储能端的功率交换。其中，Pdc、Pac和Pbat分别为MMC-PBESS 的直流、交流和储能功率，箭头所指方向为正方向，忽略电路损耗，三者满足约束Pdc-Pac=Pbat。

1.1 MMC-PBESS 直流侧模型

直流母线电流在三相中均分：

式中：idcj为j相上、下桥臂电流中的直流分量。

令unj、upj分别为j相下、上桥臂子模块总的等效电压，可以列出MMC-PBESS 的直流侧的基尔霍夫电压定律方程：

式（2）即为MMC-PBESS 的直流侧数学模型。另外，下桥臂子模块电池电压和直流母线电压间存在如下约束。

1.2 MMC-PBESS 交流侧模型

上下桥臂和交流母线之间存在如下电压电流关系。

MMC-PBESS 上、下桥臂不对称，故交流母线电流无法和传统MMC-BESS 一样在两桥臂间均分。设j相上桥臂电流中的交流分量为ip，ac，j，其占交流母线电流的比例为η∈(0，1)；j相下桥臂电流中的交流分量为in，ac，j，其占交流母线电流的比例为1-η，即：

以A 相为例，由拓扑图可以得到上、下桥臂回路的基尔霍夫电压定律（KVL）方程：

式中：t为时间变量。

式（10）和式（11）即为MMC-PBESS 的交流侧数学模型。可以得到该拓扑A 相上、下桥臂交流侧等效电路分别如图2（a）、（b）所示。

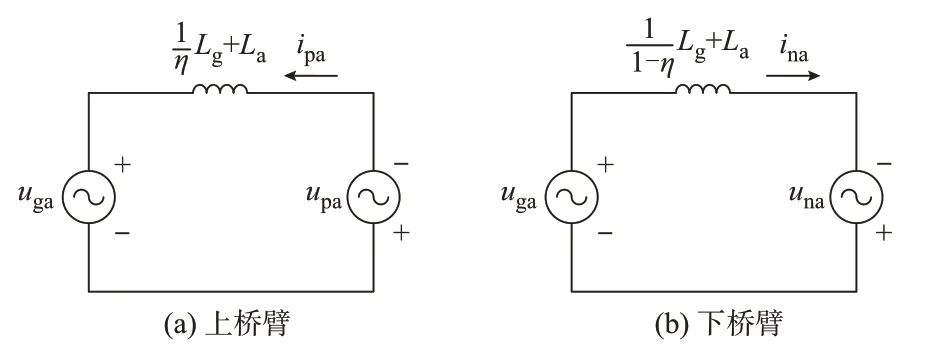
图2 A 相上、下桥臂交流等效电路Fig.2 AC equivalent circuits of A-phase upper and lower bridge arms

2 下桥臂接入电池的MMC-PBESS 分控控制方法

2.1 子模块电容电压均衡控制

系统运行中，交直流侧功率不能时刻保持平衡，且各子模块电容相互独立，各开关管的开关情况也不可能完全一致，电容子模块可能发生过充或过放现象，且不同子模块间会出现电容电压不平衡问题。

因此，需要对子模块电容电压进行均衡控制，即根据子模块电容电压相对参考值的偏差情况对直流或交流电流做出调整，来实时保持电容桥臂的充放电平衡。本文研究拟在实验中验证，故电压等级不是很高，桥臂子模块数较少。因此，采用载波移相调制，输出波形谐波特性更好。下述电容电压均衡控制本质上改变了载波移相调制的调制波［19］。

2.1.1 电容电压平衡原理

以a 相为例，忽略二倍频及更高频率环流，上桥臂电流及电压可以表达为：

式中：Im、Um分别为交流并网电流、电压幅值；ω为工频角频率。

将式（12）和式（13）同侧相乘可以得到上桥臂功率的直流分量为UdcIdc/6-ηImUm/2，则电容电压平衡的条件为该直流分量为零，也可表示为：

式中：Pacp、Pdcp分别为三相上桥臂所承担的交、直流功率。即只有上桥臂回路直流功率和交流功率相等时，上桥臂功率没有直流分量，电容电压可以实现平衡。

2.1.2 桥臂平均电压控制

桥臂电流中的直流分量在子模块投入运行时对子模块电容进行充电。因此，调整该直流分量的值就可以对子模块电容进行充电控制。

具体地，以A 相为例，定义A 相上桥臂电容平均电压ua，p，av为：

式中：uapi为A 相上桥臂第i个子模块的电容电压值。以ua，p，av维持在电容电压设定值uc，ref为控制目标，将uc，ref和ua，p，av作差后通过PI 控制器，输出添加到直流控制桥臂电流直流分量的参考值中。

当桥臂平均电压小于电容电压设定值时，桥臂电流直流成分参考值增大，闭环控制下桥臂电流实际直流分量增大，子模块电容进行充电，桥臂平均电压上升，从而实现了桥臂平均电容电压的控制。

2.1.3 子模块电容电压控制

桥臂内子模块间的电容电压也可能不平衡，因此需要独立对每个子模块的电容电压做进一步的均衡控制。

桥臂电流为正时，如果子模块电容电压偏小，则延长其投入时间；如果子模块电容电压偏大，则缩减其投入时间，反之亦然。投入时间的改变由子模块独立的调制波大小决定，即可以通过改变子模块的调制波来控制其电容电压大小。

桥臂电流为正时，将uc，ref和uapi作差后通过PI控制器，输出叠加到子模块调制波中；桥臂电流为负时，将uc，ref和uapi作差后取反通过PI 控制器，输出叠加到子模块调制波中。

2.2 上、下桥臂分控控制策略

图1 所示拓扑三相相间对称，从直流侧看直流母线电流在三相中均分，其直流侧控制策略和应用于MMC 的传统策略无异，通过给定直流功率Pdc计算得到直流母线电流参考值，再由内环控制实现快速响应。

传统策略控制交流母线电流，从交流侧看上下桥臂并联，由于MMC 上下桥臂对称，母线电流在两桥臂间自然均分。与MMC 不同的是，本文拓扑上下桥臂子模块不同。因此，上下桥臂不对称，交流母线电流不能在两桥臂间均分，采用传统策略会导致环流中有基频分量。

拓扑中电池的存在使得交直流侧控制可以解耦，即交直流功率可以不等。当系统交直流功率不等时，需要电池来发挥储能作用。应用于MMC 的传统策略交直流不解耦，无法发挥电池的储能作用。因此，需要对上、下桥臂电流分别进行独立控制，本文定义该独立控制策略为分控控制策略，可以在满足上桥臂电容电压平衡的基础上发挥下桥臂电池的充放电功能。

分别对图2 所示三相上、下桥臂两个回路做dq轴变换，采用双闭环控制。外环为定功率控制，由交流功率参考值Pac和交流并网电压幅值Um可以计算得到交流母线总的d轴分量参考值ID。

内环为桥臂电流控制，采用交流并网电压前馈以及dq轴解耦控制，等效电感为Lg/η+La或Lg/(1-η)+La，实现上、下桥臂电流的快速响应。假设功率因数为1，分控控制策略的重点为桥臂电流d轴参考值的选取。

式中：IDp为j相上桥臂电流ipj的d轴分量参考值；IDn为j相下桥臂电流inj的d轴分量参考值。

底层调制策略选用载波移相调制，在子模块开关频率较低的情况下可以得到较高的等效开关频率，适用于MMC-PBESS。上、下桥臂调制波ump、umn由直流成分umdc和交流成分umac，p、umac，n构成：

式中：umdc为桥臂调制波的直流成分；umac，p、umac，n分别为上、下桥臂调制波的交流成分。umdc、umac，p和umac，n分别由直流侧控制和交流侧分控控制产生。

由式（14）可知，为了保证上桥臂电容电压平衡，上桥臂电流交流分量幅值ηIm为定值，转换到dq轴即参考电流IDp为定值。 考虑调制比m=2Um/Udc≈1 的情况，上桥臂控制产生的umac，p约等于umdc/2。半桥子模块无法输出负电压，为了保证下桥臂半桥子模块在正常调制范围内，umac，n必须小于等于umdc/2，即小于等于umac，p，下桥臂IDn的选取须满足如下约束。

IDp和IDn的具体取值和系统交直流功率的比值有关，令k为系统交直流功率的比值，考虑Pac=kPdc(Pdc≥0)的情况，即直流侧向MMC-PBESS 输送功率，MMC-PBESS 工作在逆变模式。定义下桥臂所承担的交直流功率分别为Pacn和Pdcn，则交直流功率间存在如下关系：

以维持上桥臂子模块电容电压平衡为目标，上桥臂交直流功率间存在如下约束：

由此可以得到：

k=0 时，交流侧短路，直流侧全部功率被储能电池吸收。此时，上桥臂短路，下桥臂电池子模块全部投入，支撑直流侧电压。

k≠0 时，由式（24）和式（25）可得：

1）k＜0

交直流侧都向MMC-PBESS 输入功率，此时ID＜0。

不满足式（20）的约束，半桥子模块系统无法正常运行。此时，为了使下桥臂子模块可以工作在负电压状态，可以将半桥子模块改为全桥子模块［20-21］，但是功率器件数增加，成本上升，本文不予考虑。

2）0 ＜k＜0.5

交流功率小于直流功率的一半，IDp＞ID＞0，IDn＞0，上桥臂传输的多余交流功率被下桥臂电池吸收。

3）0.5 ≤k＜1

交流功率大于等于直流功率的一半，0 ＜IDp＜ID，-ID＜IDn＜0，下桥臂电池提供少部分交流功率。

4）k=1

交直流功率相等，电池不发挥储能作用，整个系统发挥传统MMC 的作用，实现交直流功率的转换。

可见，上、下桥臂电流的基频分量被强制取为交流母线电流的一半，消除了环流基频成分。

5）k＞1

交流功率大于直流功率，此时：

不满足式（20）的约束，半桥子模块系统无法正常运行。

综上所述，当Pac=kPdc(Pdc≥0)时，半桥子模块MMC-PBESS 的正常运行范围为0 ＜k≤1，IDp和IDn的选取规则如图3 所示。

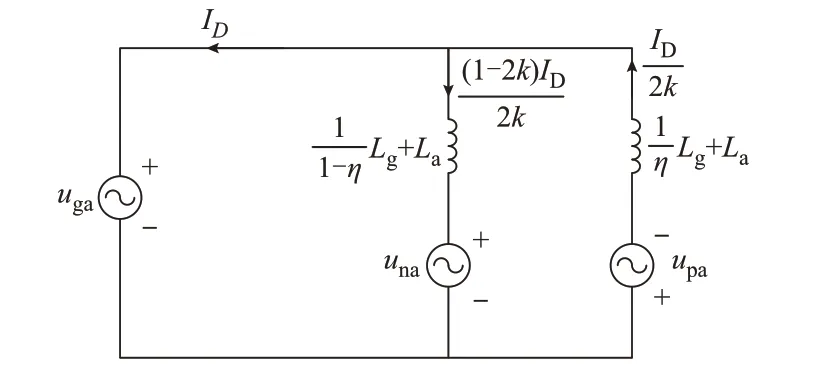
图3 A 相上、下桥臂交流回路电流给定值Fig.3 Given values of current of AC circuit for a-phase upper and lower bridge arms

本文所提MMC-PBESS 及其控制策略可以实现类似静止同步补偿器的分相控制。不过本文中MMC-PBESS 的三相交流等效电路为两个星形电路的并联，三相虽然可以分相控制，但三者之间存在约束和耦合，即无论三相电压分别为多大，需时刻保持总的三相输出端口电压不变。

上述分控控制策略也可以应用在MMCPBESS 交流侧故障时实现低电压穿越。假设正常运行时Pac=kPdc(Pdc≥0，0 ＜k≤1)，令μ为故障时交流侧电压与正常运行时交流侧电压的比值，则故障时交流侧电压跌至μUm(0.2 ≤μ＜1)。为了保持交流母线电流不变，实现低电压穿越，故障发生后更改上、下桥臂电流d轴分量参考值为：

式中：I'Dp、I'Dn分别为故障发生后系统上、下桥臂电流的d轴分量参考值。

故障发生后更改桥臂电流参考值可以发挥储能电池充电功能，吸收直流侧盈余功率，实现MMCPBESS 交流侧低电压穿越。当然，也可采用传统MMC 的交流故障穿越方法。针对直流侧故障，本文拓扑中的半桥子模块没有直流故障穿越能力，直流侧故障处理方法和传统半桥子模块MMC 的处理方法一样，即可以通过故障后快速将限流电阻、电感串联接入直流电流的流通路径来限流或者在子模块两端并联晶闸管来限流［22］。交直流故障处理内容复杂且已有大量文献对此进行研究，本文不再进行详述。

3 仿真验证

为了验证上述分析的正确性，在MATLAB/Simulink 平台上搭建一个桥臂子模块数N=16 的MMC-PBESS，其三相的上桥臂子模块均接入电容C，下桥臂子模块均接入储能电池。系统参数如表1所示。

表1 系统参数Table 1 System parameters

3.1 电容电压均衡验证

设置系统交直流功率相等，不采取任何电容电压均衡措施，三相上桥臂电容电压平均值的仿真结果如图4（a）所示，可见由于系统内部等效电阻消耗了部分直流功率，使得上桥臂子模块电容存在过放现象，系统不能稳定运行。

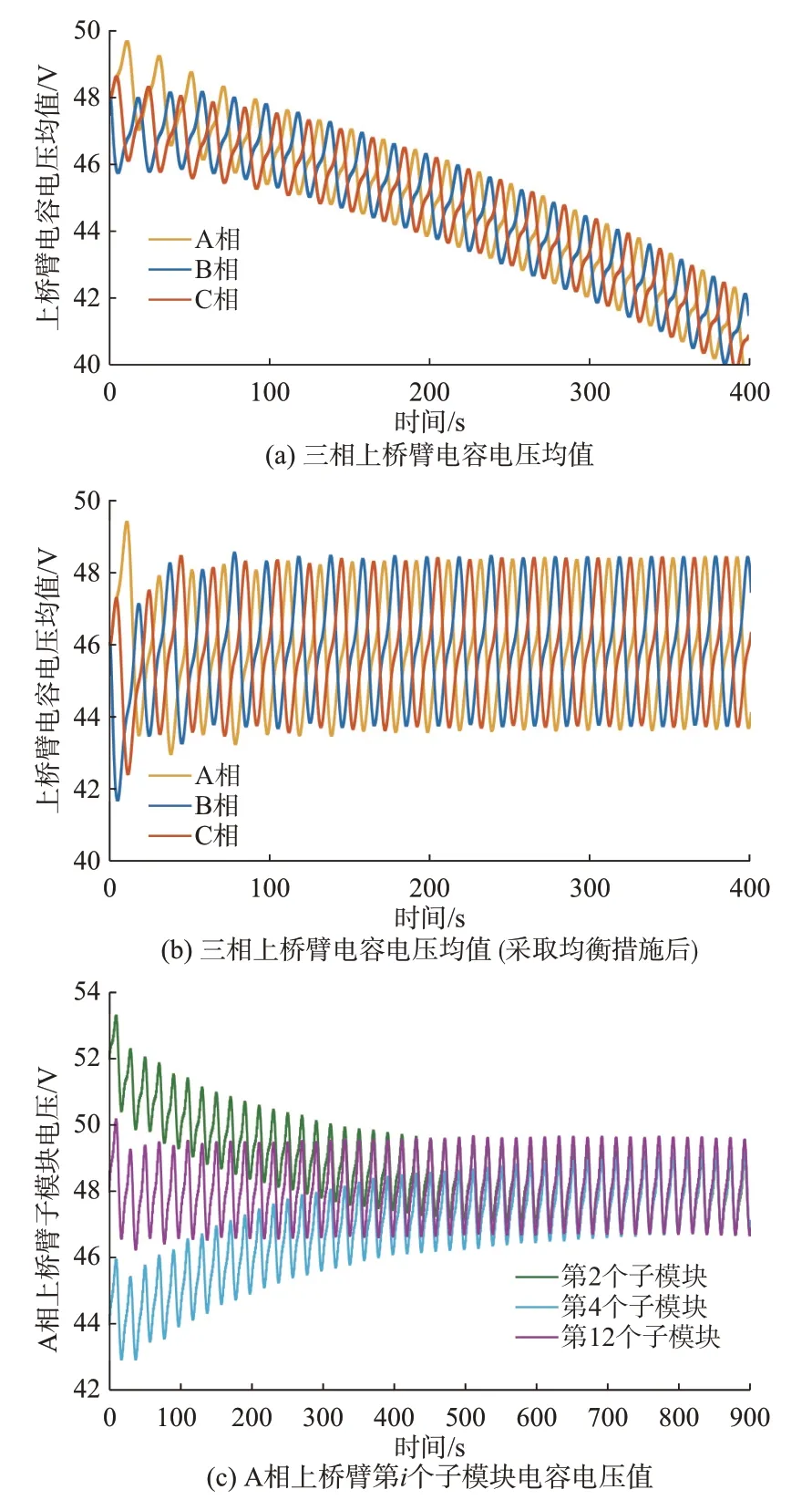
图4 电容电压均衡控制仿真结果Fig.4 Simulation results of balancing control for capacitor voltage

3.1.1 桥臂平均电压控制验证

首先，验证桥臂平均电压的控制效果，电容电压参考值为48 V，仿真结果如图4（b）所示。可以看到大约在4 个工频周期（0.08 s）后桥臂电容电压平均值稳定在48 V 左右，即电容不再过放，电容电压波动幅值约为2.4 V，主要以基频频率为主。

3.1.2 子模块电容电压控制验证

其次，验证子模块电容电压的控制效果。设置A 相上桥臂第2 个子模块电容电压初始值为52 V，第4 个子模块电容电压初始值为44 V，第12 个子模块电容值设置为其他子模块电容值的80%（即8 mF），其仿真结果如图4（c）所示。第2 个子模块的电容电压逐渐降低，在0.7 s 后稳定在48 V 左右；第4 个子模块的电容电压逐渐升高，在0.7 s 后稳定在48 V 左右；第12 个子模块在0.08 s 后稳定在48 V左右，电容电压波动幅值大约为2.9 V，可见电容值越小，电容电压波动越大。

3.2 上、下桥臂分控控制验证

令Pdc=10 kW，算得Idc=Pdc/Udc≈13.33 A，idcj=Idc/3 ≈4.44 A。首先，仿真0 ＜k＜0.5 的情况，取k=0.4，此时交直流母线电流、A 相桥臂电流的仿真结果如图5（a）所示。可见，交流母线电流幅值被较好地控制在Im=2Pac/(3Um)≈8.6 A，直流母线电流在电容电压均衡控制下稳定在14 A 附近，略大于理论值13.33 A。由式（26）计算得到IDp=1.25ID，上桥臂电流交流分量的幅值为1.25Im=10.75 A；由式（27）计算得到IDn=0.25ID，下桥臂电流交流分量的幅值为0.25Im=2.15 A。上、下桥臂电流交流分量同向，交流母线电流Im=IDp-IDn=8.6 A。图5（a）展示了系统0.06 s 即3 个工频周期的仿真结果，和计算结果一致，桥臂电流在14/3 ≈4.67 A 左右直流分量的基础上叠加各自的交流分量，交流母线电流为上下桥臂电流之差。

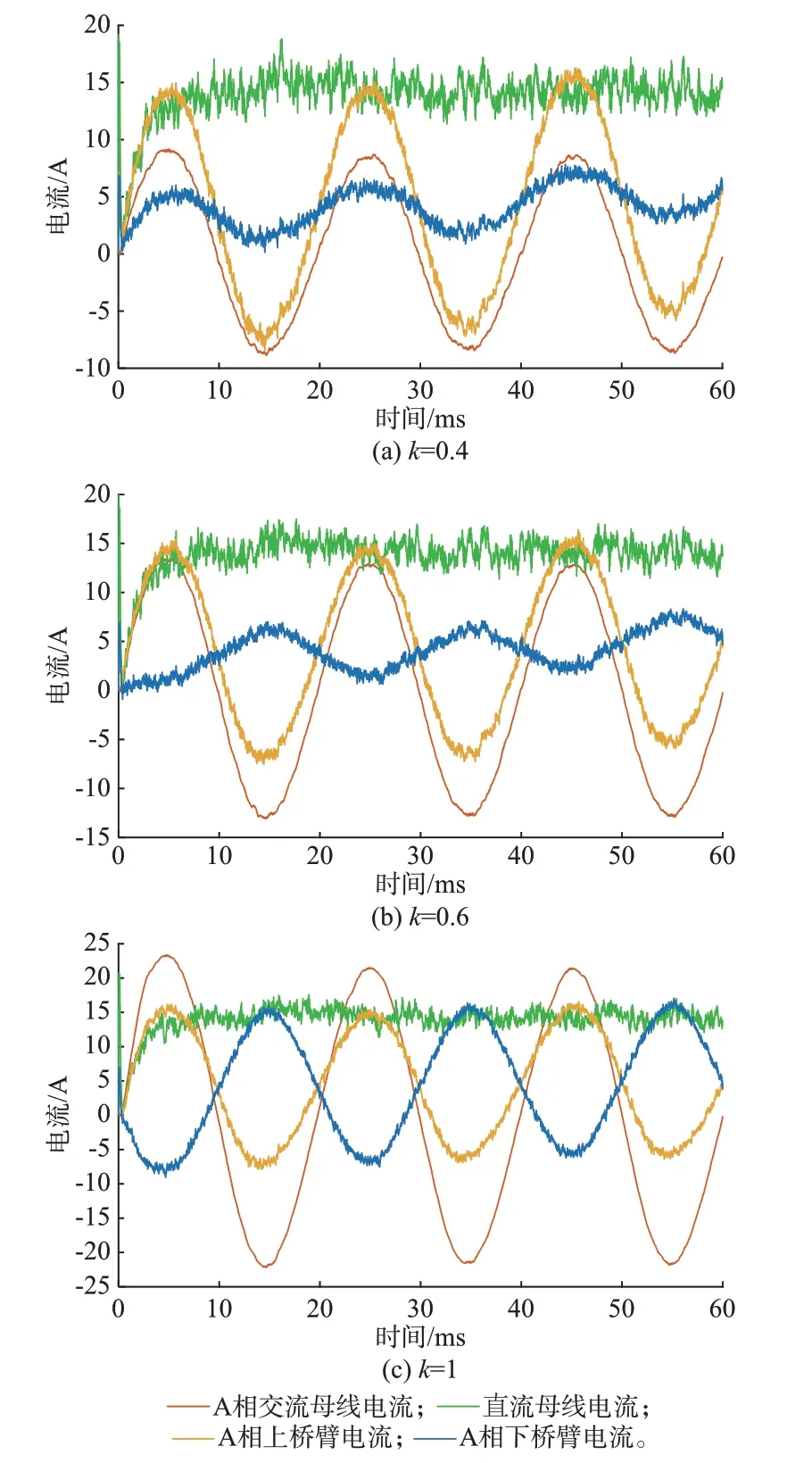
图5 上、下桥臂分控控制仿真结果Fig.5 Simulation results for separate control of upper and lower bridge arms

接着，仿真0.5 ≤k＜1 的情况，取k=0.6。此时，交直流母线电流、A 相桥臂电流的仿真结果如图5（b）所示。可见，交流母线电流幅值被较好地控制在Im=2Pac/(3Um)≈12.86 A，直流母线电流在电容电压均衡控制下稳定在14 A 附近。由式（26）计算得到IDp=0.83ID，上桥臂电流交流分量的幅值为0.83Im=10.67 A；由式（27）计算得到IDn=-0.17ID，下桥臂电流交流分量的幅值为0.17Im=2.19 A。上、下桥臂电流交流分量反相，交流母线电流Im=IDp-IDn=12.86 A。图5（b）展示了系统0.06 s 即3 个工频周期的仿真结果，和计算结果一致，桥臂电流在4.67 A 左右直流分量的基础上叠加各自的交流分量，交流母线电流为上下桥臂电流之差。

最后，仿真k=1 的情况，此时交直流母线电流、A 相桥臂电流的仿真结果如图5（c）所示。可见，交流母线电流幅值被较好地控制在Im=2Pac/(3Um)≈21.44 A，直流母线电流在电容电压均衡控制下稳定在14 A 附近。由式（26）计算得到IDp=0.5ID，上桥臂电流交流分量的幅值为0.5Im=10.72 A；由式（27）计算得到IDn=-0.5ID，下桥臂电流交流分量的幅值为0.5Im=10.72 A。上、下桥臂电流交流分量反相，交流母线电流Im=IDp-IDn=21.44 A。图5（c）展示了系统0.06 s 即3 个工频周期的仿真结果，和计算结果一致，桥臂电流在约4.67 A直流分量的基础上叠加各自的交流分量，交流母线电流为上下桥臂电流之差。

通过上述分析可以发现，无论交直流功率的比例如何，上桥臂电流的波形保持不变，其直流分量代表上桥臂承担的直流功率，交流分量代表上桥臂承担的交流功率，二者耦合，因此在直流功率固定的情况下交流分量也是定值。下桥臂电流的交流分量随k值变化，代表储能电池发挥充电功能，当其相位和上桥臂电流相反时，电池充电吸收下桥臂部分直流功率；当其相位和上桥臂电流相同时，电池充电吸收下桥臂全部直流功率和上桥臂部分交流功率。环流大小等于1/2 上、下桥臂电流之和，当0 ＜k＜0.5 时上、下桥臂电流同向，此时环流最大，需要采取额外的环流抑制措施。

4 结语

本文针对下桥臂接入电池的MMC-PBESS 拓扑进行了数学建模及上、下桥臂交流回路电路分析，在MATLAB/Simulink 平台上验证了电容电压均衡策略及所提的上、下桥臂分控控制策略的有效性。该控制策略可以在系统交直流功率相等时抑制环流基频分量，在系统交直流功率不等时发挥电池的充电功能，同样适用于上桥臂接入电池的MMCPBESS 拓扑，在更高电压等级采用最近电平逼近调制的情况下也适用。和现有的环流注入方法相比，实现了上、下桥臂的解耦控制，方便电容、电池子模块的独立控制和管理，更加简单。该策略在直流功率为正时的适用条件为交流功率大于零且小于等于直流功率，即半桥子模块MMC-PBESS 可以实现灵活逆变，在维持电容电压均衡的前提下实现直流端功率向储能端、交流端流动。

本文所提控制策略只适用于直流侧功率流入的上/下桥臂储能的半桥子模块MMC-PBESS，且没有考虑电池荷电均衡和功率器件应力问题，后续研究将对此进行扩展。