基于灵敏度协同的多馈入新能源集群最大容量优化分配方法

姜颢宇，齐 磊，孙孝峰，赵 巍，李 昕，翟燕飞

（1.燕山大学电气工程学院，河北省秦皇岛市 066004；2.国网冀北电力有限公司秦皇岛供电公司，河北省秦皇岛市 066099）

0 引言

在能源结构转型背景下，新能源主导新型电力系统呈现电力电子化、高随机性、低惯性等特征［1-2］。为此，考虑局部电网运行约束，合理评价电力系统对可再生能源的承载能力，是统筹规划新能源装机容量和上网电量的重要依据［3-4］。

考虑线路容量约束，文献［5］对分布式能源接入电力系统的布局和规划评估进行了综述，为处理多目标约束的复杂工程问题提供了指导；文献［6］将过载风险作为光伏接入容量的限制，结合供电线路提出了最大光伏接入容量规划方法。考虑电压频率稳定，文献［7］对比了几种典型的光伏承载能力量化方法的应用场景和优缺点；文献［8］研究了高渗透率对配电系统的电压调节动态特性和暂态特性的影响，评估了节点电压达到临界时系统承载容量的上限；文献［9］综合节点电压上升与电压谐波畸变限值，确定系统的最大光伏接入量。

此外，新能源接入比例的提升导致电网不断变弱、振荡频发、电能质量变差，进而引发逆变器并网电压及电流超出额定值，导致逆变器开关管电压、电流应力增加，存在炸机风险。同时，振荡过流可能会触发继电保护装置，造成新能源脱网。上述非正常并网现象会反向制约渗透率的继续提升，如沽源地区因电流谐振导致风机脱网事故［10-13］。基于阻抗分析法，目前已有较多振荡机理分析的相关研究［14-17］。对于射线型配电网，文献［18］应用模态分析法分析了控制参数、LCL 滤波器参数变化对系统振荡的影响。文献［19］提出当逆变器并网容量增加时，组串式光伏逆变器的共模电路会产生共模谐振。文献［20］提出，当逆变器并网台数增加时，随着新旧集电线路长度的接近，系统容易失稳。因此，振荡问题逐渐成为限制电网新能源渗透率提升的关键因素之一。

对于系统允许接入的最大新能源容量评估问题，考虑过载风险、电压稳定限制等已有较多研究［5-9］。同时，考虑振荡频发这一新型小信号稳定性约束下的新能源最大接入容量评估问题，已有相关前瞻性研究［21-23］。文献［21］提出用于复杂多馈入系统小信号稳定评估的广义短路比指标。进一步地，文献［22］考虑小干扰同步稳定约束，构建了广义短路比约束下的新能源最大接入容量评估模型，并提出了半定规划模型转化方法，实现了固定接入节点场景下新能源容量最优分配比例的高效求解。同时，考虑构网型逆变器的额外接入场景，文献［22］还开展了面向新能源接入容量最大化的新能源最优落点评估。该研究对高比例新能源系统的渗透率提升及规划具有重要意义。

未来，将有更多的分布式发电（distributed generation，DG）单元接入配电网，复杂的多馈入系统及多变的运行环境还会诱发中高频谐振问题，制约新能源渗透率的提高。为此，本文以逆变器容量变化下变流器与电网快速交互造成的数百赫兹中高频谐振为约束，探索多馈入新能源集群最大容量协同分配方法。首先，建立新能源集群多馈入系统复矢量形式的阻抗模型；然后，基于灵敏度协同原则，提供求解局部微网中接入可再生能源总容量上限及各集群分容量优化分配的方法；最后，以IEEE 9 节点和IEEE 33 节点系统为算例，通过硬件在环半实物仿真测试系统验证了所提理论的可行性。

1 新能源多馈入系统稳定性评估模型

图1 所示广义多馈入系统指的是供电网络连接形式随意（并非仅含有单一环型、射线型连接形式）、馈入节点随机的多节点分布式新能源馈入局部电网。该新能源多馈入系统可划分为新能源侧和电网侧两部分。新能源侧定义为所分析系统中可再生能源转化为电能的环节，也是易受外界影响的可控部分，即多个新能源DG 集群；电网侧定义为等效无穷大电网和相应的连接网络。通过对新能源侧建立模型，对电网侧等效化简，可以将二者聚合分析，进而解决系统的稳定性问题。

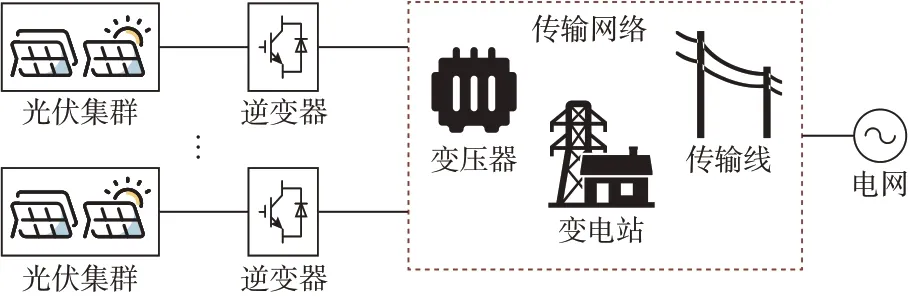
图1 广义多馈入系统示意图Fig.1 Schematic diagram of generalized multi-infeed system

1.1 并网逆变器的阻抗模型

电流源型逆变器（current source inverter，CSI）的主电路及控制环路如附录A 图A1 所示。图中：Lf为逆变器滤波电感；Cf为滤波电容；Rf为滤波电容串联电阻；Lt为网侧电感；io为输出电流；vo为输出电压；Vdc为直流侧电压；PWM 表示脉宽调制；Gc为电流比例-积分（PI）控制器；PLL 为锁相环控制器；θPLL为锁相角度；iod和ioq分别为输出电流的d、q轴分量；iodref和ioqref分别为输出电流参考值的d、q轴分量；vod和voq分别为输出电压的d、q轴分量；kv为电压前馈增益。控制方式采用在dq坐标系下，基于电网电压前馈的单电流环控制方案。

本文聚焦研究中高频谐振约束下多馈入系统集群工作点的最优分配问题，考虑传统abc 坐标系下阻抗建模不含额定工作点的缺陷及稳定裕度方便量化评估的需求，采用文献［24］中涵盖完整环路的基于自导纳和伴随导纳的阻抗推导方法进行建模。假设本文研究附录A 图A1 所示逆变器直流侧前级保持稳定且具有较大的母线电容，同时电流环控制器参数均一致且锁相环控制带宽为50 Hz，因此，次超同步频段的频率耦合效应并不明显［25-26］。考虑本文所关注的中高频谐振问题，对文献［24］的复矢量形式阻抗模型进行简化，仅采用该模型的自导纳（阻抗）部分进行稳定性判断。阻抗推导中，下标p 表示含工作点变量，上标s 表示系统变量，上标c 表示控制变量。

1）主电路模型

将拉氏变换改写为复矢量形式，并将工作点引入输出电压、输出电流和占空比，建立主电路的小信号模型如下：

式中：Δvpo、Δipo、Δdp分别为含工作点的输出电压、电流和占空比的复矢量形式小信号扰动量；Gid为电流I与占空比的传递函数；为并网逆变器开环阻抗；系数G1、G2、G3的具体含义及计算过程详见附录A。

2）锁相环模型

复矢量形式锁相环小信号模型为：

式中：Δθp为含工作点的相角差；上标“*”表示共轭运算；Tpll为锁相环控制器传递函数，计算过程及表达式详见附录A。

对逆变器输出电压施加小信号扰动，可得逆变器输出电压复矢量小信号表达式为：

将式（2）代入式（3），可得：

式中：Gpllv为锁相环环节对电压影响的传递函数为系统输出电压。

类比电压扰动的引入，考虑电流扰动、占空比扰动的小信号表达式如下：

式中：Gplli、Gplld分别为锁相环环节对电流和占空比影响的传递函数；分别为系统输出电流和占空比；为输出控制用占空比的小信号扰动。

上述公式的计算过程详见附录A。

3）控制环路模型

CSI 控制环路小信号表达式为：

根据小信号表达式（4）至式（7），绘制CSI 闭环小信号控制框图如附录A 图A2 所示，则含工作点的CSI 闭环阻抗Zoi为：

1.2 基于电网络理论的系统聚合模型

实际应用的电力系统的电网侧通常为射线型和环网型结构混合应用，在统计负载端阻抗时，无法清晰有效地计算分析。根据电网络理论，高于3 阶的角形网络支路数多于星形网络，角形网络可以变换为星形网络。因此，面对高阶复杂的配点网侧，需要应用广义星角变换理论进行化简分析［27-28］。多角形电路等效为星形电路的各支路阻抗表达式具体推导详见附录B，其中，多角形电路等效为星形电路的各支路阻抗为：

式中：Zi和yi分别为节点i与新建立的中心节点之间的等效阻抗和导纳；yij为节点i和j间导纳；n为星形电路的支路个数。

广义多馈入配电系统阻抗结构如图2（a）所示，集群都采用电流源型并网逆变器。应用电网络变换，对于每个新能源集群所在区域进行聚合处理，通过广义星角变换对每个集群所在馈线拓扑进行化简整合，聚合新能源侧和电网侧，将复杂的电力系统拓扑转化为图2（b）所示的射线型结构。图中：ZlineA-a为线路A 与逆变器a 之间的线路阻抗。

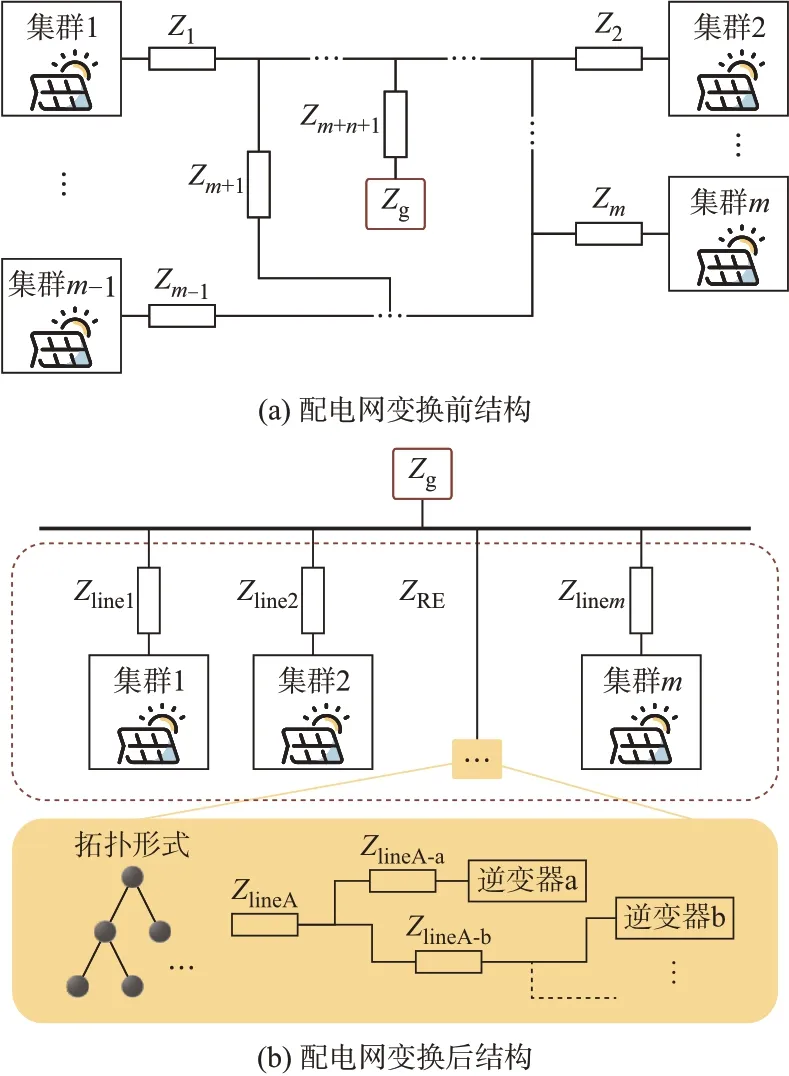
图2 配电网广义星角变换示意图Fig.2 Schematic diagram of generalized star-delta transformation in distribution network

根据简化后的射线型系统结构，可以计算所在区域线路和集群的总阻抗。电网侧等效阻抗为Zg，根据式（8）所示单机逆变器阻抗Zoi，集群m的阻抗ZΣm推导如下：

式中：Zlinem为集群m连接线路等效阻抗；jm为集群m中接入的CSI 台数。

新能源集群侧整体等效阻抗ZRE为：

根据阻抗分析法，逆变器阻抗与电网阻抗共同构成了并网系统的开环外特性。在此基础上，利用该闭环系统的开环外特性，即通过判断源网阻抗比的开环稳定性来间接评估闭环系统运行状态［29］。其源网侧阻抗比F可表示如下：

1.3 多馈入系统稳定性评估指标

基于前文获得的多馈入系统源网阻抗比，为了更清晰获得该并网系统的稳定性评价指标，进一步利用基于Bode 图的阻抗判据进行稳定性分析，即基于源网阻抗Bode 图的网侧阻抗与逆变器阻抗幅值交叉点处的相角裕度预判系统稳定性［24］。Bode 图判据的阻抗相位裕度具体获得过程如下：

1）求取网侧阻抗与逆变器阻抗幅值交叉点处的交截频率fc。

传递函数F的幅度分贝通常由20 lg|F|定义，故阻抗比的幅频特性为：

式中：Re 表示复变量实部；Im 表示复变量虚部。

当以dB 为单位标定时，幅度为1 表示0 dB，故令|F(fc)|dB=0 dB，可以求解Bode 图中网侧阻抗与逆变器阻抗幅值交叉点处的交截频率fc。

2）求取源网阻抗幅值交叉点处的相角裕度。阻抗比的相频特性为：

根据前述所求的交截频率fc，将其代入式（15）中，计算出源网阻抗交截频率处的相位裕度φPM：

基于阻抗分析理论，当系统电网阻抗幅值和逆变器阻抗幅值交点频率处的相角裕度为正时，系统处于稳定状态，否则反之。

1.4 工作点变化对系统谐振频段影响分析

由式（8）推导的逆变器阻抗模型可知，模型中包含工作点即并网电流信息，逆变器工作点变化由锁相环动态等效环节Gplli引入，可能影响系统稳定性。因此，综合考虑逆变器的完整控制环路，进一步探究工作点变化对逆变器具体阻抗频段影响。本文通过分析用于系统稳定性判断的阻抗比对工作点的变化率，判断运行工作点变化对系统潜在振荡频段的影响［30-31］。

阻抗比幅值或相角变化率的通用表达式定义如下：

式中：p为影响参数；Δp为参数变化量；Z为并网系统阻抗比的幅值或相角。

阻抗比变化率反映了某一参数变化对系统阻抗比即系统稳定性的影响，某频段内变化率数值越大，表征参数变化对该频段内的阻抗比影响越大；变化率数值越小，表征参数变化对该频段内的阻抗比影响不明显。

以射线型多机同构逆变器并入弱电网场景为例，当并网工作点即并网电流变化时，并网系统阻抗比Bode 图及阻抗比变化率如附录C 图C1 所示。随着工作点的变化，阻抗比的变化率在100～1 000 Hz频段内变化较大，且在200～400 Hz 频段内变化率较高，通过阻抗比Bode 图及其变化率分析可知，逆变器工作点变化对系统阻抗比的中高频段影响较大。

同时，在Simulink 中搭建射线型多机同构逆变器并入弱电网的仿真模型，验证工作点变化下系统的运行情况。典型工作点下的并网波形如附录C 图C2 所示。进一步对上述典型工况的并网波形进行总谐波畸变率(total harmonics distortion,THD)分析，谐振频率如附录C 图C3 所示。通过快速傅里叶变换（fast Fourier transform，FFT）分析可以发现，当并网容量越限后，失稳波形中的谐波频段集中在300～400 Hz 附近，与理论分析基本相符。上述算例分析说明工作点的变化将主要在系统中引入中高频谐振。

2 灵敏度协同的集群最大容量优化分配

2.1 新能源集群最大容量评估

考虑谐振约束，系统的稳定性取决于等效系统的阻抗相角裕度。在工程实践中，微网各接入节点的网侧等效阻抗不一定相同，系统不同的接入总容量和集群间不同的容量配比都会计算出不同的相角裕度，考虑其中高频谐振约束的系统新能源承载能力也会有差异。但随着局部微网的各集群接入容量增加，多机交互易出现谐振现象，考虑其约束特性，亟须分析得出系统允许接入的容量最大值和不同集群的最优容量配比，提升新能源集群对电网的支撑能力。

多馈入系统的相角裕度随新能源集群接入容量的变化而变化。但系统阻抗稳定裕度关于并网容量的表达式具有高阶、强耦合特性，难以解析。为实现集群接入容量增量一定情况下的阻抗裕度变化量评估，本文基于特征变量一阶灵敏度线性插值方法［32-35］，实现接入容量增加后阻抗裕度变化量的表达式构建：

式中：Idsum为系统接入的新能源总容量；上标“1”表示当前值，上标“0”表示初始值；Idi为集群i中逆变器单机接入容量；ni为集群i接入的逆变器个数；Δni为集群i接入的逆变器个数变化量；g为集群个数；∂φPMi()/()为集群i的相角裕度对集群容量nIdi的灵敏度，即δPMi。

为保证集群具有最优的运行性能，需保证集群接入容量增量一定的情况下，系统阻抗裕度变化量ΔφPM最小。故定义目标函数和约束条件如下：

式中：ΔIdsum为各集群逆变器接入容量变化总和；和分别为集群中逆变器单机允许接入容量的上限和下限。

其中，基于含并网电流工作点的逆变器阻抗模型及网侧等效模型以谐振为约束，可获得单机逆变器接入供电网络单馈入工况下的最大允许接入容量Id，max1。综合考虑用户并网输出电流的最大期望值Id，max2，综合系统与用户的上限制约，即min(Id，max1，Id，max2)作为单机变换器稳态工作点上限约束。根据用户并网输出电流的最小期望值，确定单机变换器稳态工作点下限约束。

2.2 集群阻抗裕度灵敏度协同原则

在求解目标函数受单一条件约束的多元函数最优问题时，可采用拉格朗日乘数法。本文引入拉格朗日乘子λ，式（18）所示目标函数和约束条件构造的拉格朗日函数如下：

令拉格朗日函数对变量Idi的一阶偏导数等于零，求解得出目标函数在此约束条件下的极值点，展开如下：

由于不同集群逆变器个数不同，在分析时将式（20）中的个数ni和单机容量Idi相乘即可获得集群i的容量，故等式（20）约束可以改写为：

集群间在稳定的前提下容量最优分配的条件是各集群的裕度灵敏度相等。在工程实际中，不同集群的灵敏度各异，提出灵敏度协同原则如下：新能源集群多馈入配电系统在保持稳定的前提下维持各集群灵敏度标准差达到规定范围以内，此时的系统稳定裕度最高，可以实现各集群间容量的最优分配。

2.3 基于灵敏度协同的容量优化分配方法

在评估系统能够接入的可再生能源最大容量时，通常需要遍历每个总容量下的所有集群容量配比，通过计算所有配比情况下的稳定裕度，比较分析得出每个总容量下稳定性最好的配比，进而获得总容量的上限。但是这种方法没有考虑到每个集群容量对系统整体稳定性的影响度，经常在遍历过程中产生无效的求解。

由此，本文提出一种基于灵敏度协同的新能源最大容量评估方法，主要包括快速探限和细化配置两个部分。对应的整体求解流程详见附录D 图D1（a）。主要的实现步骤如下：

步骤1：确定接入新能源集群的节点，通过广义星角变换，快速聚合原有系统的新能源侧和电网侧，建立线路聚合阻抗。

步骤2：设定当前系统接入新能源的总容量和不同集群的配比，求解当前配比方案下的稳定裕度及不同集群的灵敏度。

步骤3：当各集群间的灵敏度标准差较小时，保存当前容量前提下的集群配比方案；当各集群间的灵敏度标准差较大时，通过调整灵敏度偏移较大的集群容量，改善系统的稳定裕度。

步骤4：设定逆变器单机的容量变化调节尺度为大步长，以此大幅度地增加系统接入的新能源总容量，并循环执行步骤2 和步骤3，直到系统的稳定裕度接近边界，由此使系统接入的新能源总容量达到上限的附近，则进入步骤5。

步骤5：设定逆变器单机的容量变化调节尺度为小步长，以此精细化地调整灵敏度偏移较明显的集群容量，并循环执行步骤2 和步骤3，直至系统的稳定裕度达到边界，由此使系统接入的新能源总容量达到精确上限，并通过各集群的全局灵敏度一致性，实现系统总容量达到最大值时的集群容量优化配置。

考虑工程应用实际，在集群出力调节过程中，下发的集群调节指令实际为对集群逆变器点对点的指令，以直接实现逆变器控制及群控群调。基于以上考虑，在步骤4、5 的具体实施中对逆变器单机容量进行了寻优及输出。

综上，当系统需要评估定点接入新能源集群的总容量及具体配置时，应用上述求解流程即可快速获得不同集群间的新能源最优配比及系统允许接入的新能源最大容量。该方法仅需简单迭代寻优，且容量分配原则清晰，易于工程指导。

2.4 容量分配方法复杂度对比

2.4.1 时间复杂度定义

时间复杂度用来反映算法流程在应用运算时的工作量度，展现了执行时间随输入数据的增加而增加的数量级增速关系，在一定程度上可以对比算法的优越性和局限性。整个算法的耗时与算法中每个步骤执行的时间和次数正相关，算法预解决的问题规模为O，当O不断变化时，它所呈现的规律即为时间复杂度。时间复杂度通常只关注最高数量级，与系数没有关系，渐进上界常用O表示。通常一个算法由控制结构和固有操作构成，算法时间取决于两者的综合效率。

常见算法的时间复杂度由小到大依次为：O（1）＜O(logo)＜O(o)＜O(ologo)＜O(o2)＜O(2o)。随着问题规模o的不断增大，时间复杂度不断增大，算法的执行效率越低。计算机科学的数据结构指出，遍历求解的时间复杂度为O（o），冒泡排序的时间复杂度为O（o），二分求解的时间复杂度为O（logo）。

2.4.2 不同方法实现复杂度讨论

常规的容量求解方法侧重于通过遍历获取所有可行的方案。针对相同容量下所有配比方案进行统计研究，通过横向对照获得最优配比，并以此为基础获得最大容量，求解流程详见附录D 图D1（b）。但是稳定裕度与新能源容量呈非线性关系，随着组网结构的复杂化及组网单元的增加，在该非线性约束条件下，采用简单算法，短时直接获得优化模型中的最优解较为困难，工程指导意义较差。

常规求解方法需要不断遍历求解每个总容量下各集群所有容量配比结果的裕度并排序比较，其寻优过程较为繁复；而本文则引入灵敏度协同理论进行求解，通过求解寻优过程中各集群的灵敏度，避免了求解偏移优化路径的无效集群容量配比下的相角裕度，从而有效减少了求解一定总容量下各集群容量优化配比的计算耗时，实现了集群容量阈值和优化配比的快速求解。

附录D 表D1 对图D1 中所提两种求解方法的各个求解阶段进行了描述，并对典型步骤的时间复杂度进行了标注。由附录D 表D1 可知，优化求解方法与常规求解方法预处理阶段和外层阶段步骤相同，但内层及中层算法不同，优化方法内层及中层采用基于本文提出的阻抗灵敏度协同原则实现二分求解，整体时间复杂度为O（logo）；而常规方法内层及中层采用遍历求解冒泡排序的方法，整体时间复杂度为O（o2）。

时间复杂度对比如附录D 图D2 所示，通过观察对比两种方法的时间复杂度可以发现，随着系统中可再生能源集群数量的增加和整体规模的增大，采用基于灵敏度协同的容量优化分配方法的时间效率显著优于常规求解方法。

3 算例分析

为验证所研究方法在新能源多馈入系统下的渗透率提升效果，本文设计了两种算例，其场景定位为业主指定或者经过初步选址后的具有固定接入节点的多馈入工业园区配电网。其中，算例1 是以IEEE 9 节点系统模拟较为简单的环形配电系统，定位为小型厂区系统；算例2 是以IEEE 33 节点系统模拟接入线路结构更为复杂的配电系统，定位为大型厂区系统。

在此基础上，本文基于附录E 图E1 所示的实时数字仿真系统（RTDS）硬件在环实验平台搭建系统，并进行验证实验。实验参数设定如附录E 表E1所示。其中，RTDS 的控制端安装在计算机中，基于图形化界面搭建实验模型，通过即时通信将模型与RTDS 系统平台内部同步，并实时观测RTDS 中实验结果。其中，RTDS 实验平台内部包含GTAO、GTDI、DSP 等硬件设备，可以方便地进行设计和测试多种实验工况。

3.1 IEEE 9 节点系统

3.1.1 IEEE 9 节点系统线路化简与优化求解

IEEE 9 节点系统中集群接入点的位置如附录E 图E2（a）所示，逆变器假设采用组串式结构，每个集群配置的逆变器台数各异：节点3 为集群1 接入节点，节点1 为集群2 接入节点。其中，集群1 接入2 台逆变器，集群2 接入3 台逆变器。

为了对多馈入系统进行稳定性分析，建立集群1 和集群2 的阻抗模型，并基于电网络理论对线路聚合分析。首先，针对环网7-8-9 进行三角形-星形变换；其次，对集群1 和集群2 所在的线路阻抗进行分类叠加；最后，对网侧阻抗进行聚合计算，由此完成IEEE 9 节点系统的线路化简，过程详见附录E图E2。

对系统接入的可再生能源容量上限和各集群容量分配进行分析时，采用基于灵敏度协同的容量优化分配方法，依照总容量一定时各集群灵敏度的标准差最小，以此容量配比建立一组优化递增序列。同时建立对照组，依照总容量一定时各集群中的逆变器单机容量相等，以此容量配比建立一组平均递增序列。在生成以上序列的过程中，逆变器单机容量最小单位为1 A，系统接入的总容量以25 A 为步长增加。

对上述两种序列进行汇总对比，在平行坐标系中记录每一次系统总容量增加时，二者集群中逆变器单机容量、相角裕度、各集群的灵敏度和灵敏度总标准差，如图3 所示。图中实线是采用优化分配策略的选择；虚线是采用平均分配策略的选择；折线颜色从绿色过渡为红色时，其系统的稳定裕度也从正变为负。

由图3 可知，当前系统能够接入的可再生能源总容量阈值为355 A，此时优化的集群容量配比为集群1 的逆变器单机容量77 A、集群2 的逆变器单机容量67 A。通过对比可以发现，采用优化递增序列时，灵敏度的一致性较好。针对小型厂区系统，与其他分配策略相比，优化递增序列在总容量相同时，系统的稳定裕度更大；在稳定裕度相同时，系统的接入总容量更高。

为了验证获得的系统可再生能源总容量阈值和各集群容量配比的准确性，在系统接入总容量达到阈值附近时，以优化递增序列和平均递增序列为基础，选取一些典型容量分配的工况，如表1 所示。

表1 IEEE 9 节点系统总容量在阈值附近的典型容量分配Table 1 Typical capacity allocation of IEEE 9-bus system when total capacity reaches threshold

当各集群容量配比采用优化分配时，灵敏度的标准差最小，根据系统的相角裕度判据判定系统稳定；当各集群容量配比采用平均分配时，灵敏度标准差居中，根据系统的相角裕度判据判定系统稳定；当各集群容量配比采用随机分配时，灵敏度标准差较大，根据系统的相角裕度判据判定系统不稳定。

为了观察系统总容量阈值边界的稳定性趋势，对阈值附近的工况进行稳定性分析时绘制的Bode图如图4 所示。

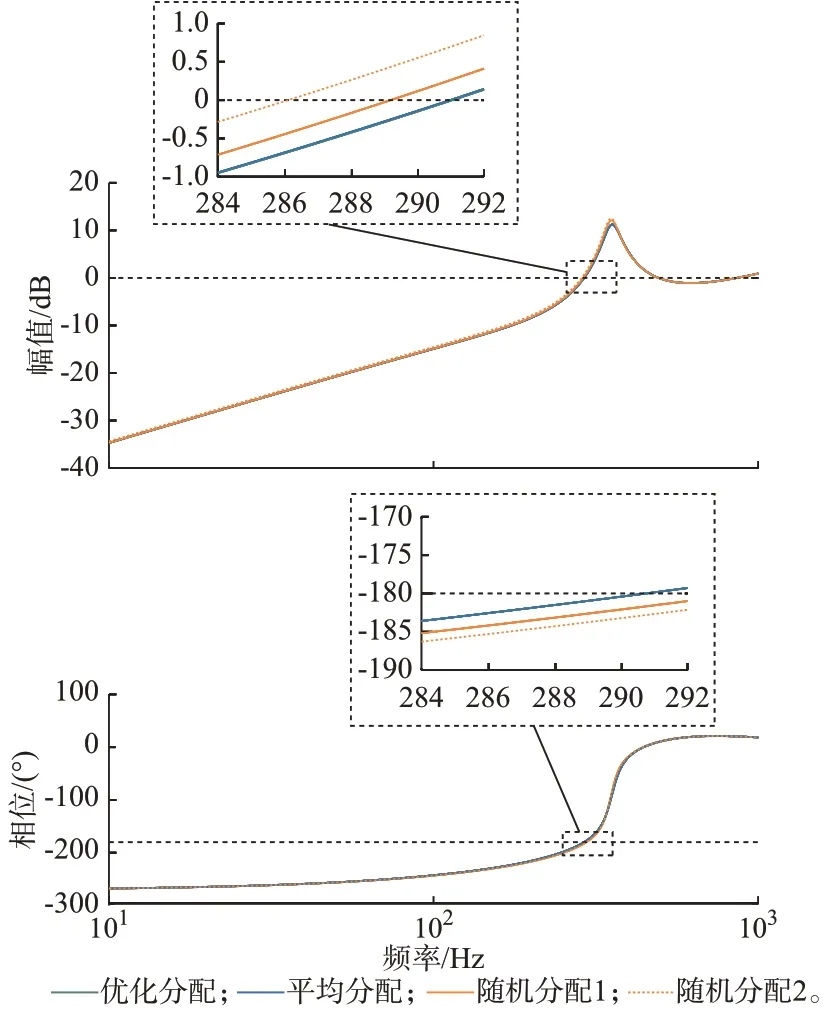
图4 IEEE 9 节点系统总容量在阈值附近的Bode 图Fig.4 Bode diagram of IEEE 9-bus system when total capacity reaches threshold

图4 中：橙色虚线为总容量超过阈值时的随机分配；橙色实线为总容量达到阈值时的随机分配；蓝色实线为总容量达到阈值时的平均分配；绿色实线为总容量达到阈值时的优化分配。

通过分析求解系统在阈值周围的稳定裕度可以得出如下结论：当总容量相同时，不同集群的新能源接入容量不同会导致系统的稳定性发生改变，在阈值附近采用基于灵敏度协同的容量优化分配方法可以有效地维持系统的稳定性。

3.1.2 IEEE 9 节点系统工况验证

为实现小型厂区系统场景模拟，在RTDS 中搭建IEEE 9 节点系统。其中，逆变器采用组串式结构，集群接入节点和逆变器个数与前文一致。

当系统接入容量在阈值附近时，采用表1 中的不同容量分配方案时，各集群并网输出电压、输出电流和各工况的THD 如图5 所示。

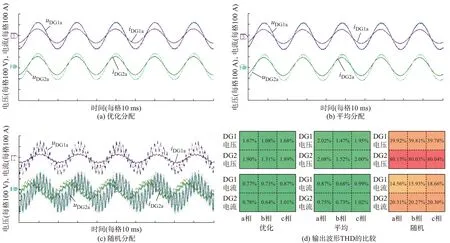
图5 IEEE 9 节点系统总容量在阈值附近的输出波形和THD 对比Fig.5 Output waveforms and THD comparison of IEEE 9-bus system when total capacity reaches threshold

图5 波形中的u和i分别为各集群总输出电压和电流，下标DG1 表示集群1，下标a 表示a 相。由图5（a）和图5（b）可知，当系统采用各集群容量优化分配和平均分配的方案时，集群1 和集群2 的并网电流幅值均稳定在额定值，并网电流波形顺滑且正弦性良好，说明此时并网系统运行稳定；由图5（c）可知，当系统采用各集群容量随机分配的方案时，各集群的并网电压和并网电流波形有明显的谐振现象，说明此时并网系统运行不稳定。

同时通过对比分析图5（d）可以看出，优化分配的工况下THD 值均在5%以内，符合并网要求，而平均分配的工况下THD 值较工况1 有所增加，但也在5%以内，符合并网要求。这是因为灵敏度标准差距离过小，故优化分配和平均分配之间稳定性并无明显区别。随机分配工况下的THD 值显著增加，均在5%以外，不符合并网要求。由此可知，在小型厂区系统的容量达到上限时，采用灵敏度协同原则的最优分配方案稳定性优于其他分配方式。

3.2 IEEE 33 节点系统

3.2.1 IEEE 33 节点系统线路化简与优化求解

IEEE 33 节点系统中集群接入点的位置如附录E 图E3（a）所示。在该大型厂区中，为便于安装及管理逆变器，假设采用集中式结构，每个集群配置单台逆变器：节点21 为集群1 接入节点，节点28 为集群2 接入节点，节点15 为集群3 接入节点。其中，每个集群分别接入1 台集中式逆变器。

为了对多馈入系统进行稳定性分析，建立各集群的阻抗模型，并基于电网络理论对线路聚合分析。首先，针对环网5-15-28 进行三角形-星形变换，获取中性点A；其次，针对环网2-A-28 进行三角形-星形变换，获取中性点B；然后，对集群1 和集群2、3所在的线路阻抗进行分类叠加；最后，对网侧阻抗进行聚合计算，由此完成IEEE 33 节点系统的线路化简，线路化简过程详见附录E 图E3。

与前文类似，建立两种序列，在生成序列的过程中，逆变器单机容量最小单位为5 A，系统接入的总容量以50 A 为步长增加在平行坐标系中，记录每一次系统总容量增加时，二者集群中逆变器单机容量、相角裕度、各集群的灵敏度和灵敏度总标准差。总容量每次递增时，各个集群的变化情况详见附录E图E4。图中实线表示最优递增序列，虚线表示平均递增序列。由图E4 知，当前系统能够接入的可再生能源总容量阈值为300 A，此时优化的集群容量配比为集群1 的逆变器单机容量95 A、集群2 的逆变器单机容量160 A、集群3 的逆变器单机容量45 A。通过对比可以发现，采用优化递增序列时，灵敏度的一致性较好。针对大型厂区系统，与其他分配策略相比，优化递增序列在总容量相同时，系统的稳定裕度更大；在稳定裕度相同时，系统的接入总容量更高。

为了验证获得的系统可再生能源总容量阈值和各集群容量配比的准确性，在系统接入总容量达到阈值附近时，以优化递增序列和平均递增序列为基础，选取典型容量分配的工况，详见附录F 表F1。

当各集群容量配比采用优化分配时，灵敏度的标准差最小，根据系统的相角裕度判据判定系统稳定；当各集群容量配比采用平均分配时，灵敏度标准差居中，根据系统的相角裕度判据判定系统稳定；当各集群容量配比采用随机分配时，灵敏度标准差较大，根据系统的相角裕度判据判定系统不稳定。

为了观察系统总容量阈值边界的稳定性趋势，将阈值附近的工况进行稳定性分析时绘制的Bode图堆叠对比，详见附录F 图F1。

通过分析求解系统的稳定裕度可以得出如下结论：在总容量相同时，优化分配方案的灵敏度一致性较好，在系统的总容量达到上限时，采用优化分配的系统相角裕度最高，相比等额分配等其他方案具有更好的系统稳定性。

3.2.2 IEEE 33 节点系统工况验证

为实现大型厂区系统场景模拟，在RTDS 中搭建IEEE 33 节点系统。其中，逆变器采用集中式结构，集群接入节点和逆变器个数与前文一致。

当系统接入容量达到阈值时，采用附录F 表F1中的不同容量分配方案时，各集群并网输出电压和输出电流并总结各工况的THD 如附录F 图F2所示。

由附录F 图F2 可知，当系统采用各集群容量优化分配的方案时，集群1 和集群2 的并网电流幅值均稳定在额定值，并网电流波形顺滑且正弦性良好，说明此时并网系统运行稳定；当系统采用各集群容量平均分配的方案时，各集群并网电流波形振荡明显，说明此时并网系统运行不稳定；当系统采用各集群容量随机分配的方案时，所有接入集群均产生剧烈谐振现象，说明此时并网系统运行不稳定。

同时通过对比分析THD 可以看出，优化分配的工况下THD 值均在5%以内，符合并网要求，而平均分配的工况下THD 值较工况1 有所增加，集群2 和集群3 的并网电压THD 和集群3 的并网电流THD 均超5%，不符合并网要求。随机分配的工况下THD 值进一步显著增加，均远超5%，同样不符合并网要求。由此，在大型厂区系统的容量达到上限时，采用灵敏度协同原则构建的最优分配方案相较无优化的等额分配方案和随机分配方案具有更加优异的稳定性。

3.3 方法性能对比分析

针对新能源集群最大接入容量评估应用场景，进一步对所提优化求解方法和常规求解方法进行求解性能对比。在相同工况下，两种方法在IEEE 9 节点和IEEE 33 节点系统中的求解计算耗时可利用MATLAB 函数计时功能探查。两种方法不同场景下的算力数据对比见附录F 表F2 和图F3。

综合附录F 表F2 和图F3 可知：优化求解算法在两种场景下对系统接入的新能源容量上限和节点配比的计算耗时均远小于常规求解算法，所提的基于灵敏度协同的优化求解方法可以大幅提高集群容量阈值和优化配比的构建效率。

上述不同方法求解结果存在差异性的主要原因是：常规求解方法需要不断遍历求解每个总容量下各集群所有容量配比结果的裕度并排序比较，其寻优过程较为繁复；而本文则引入灵敏度协同理论进行求解，通过求解寻优过程中各集群的灵敏度，避免了求解偏移优化路径的无效集群容量配比下的相角裕度，从而有效减少了求解一定总容量下各集群容量优化配比的计算耗时，实现了集群容量阈值和优化配比的快速求解。

4 结语

针对谐振发生导致新能源上网容量受限问题，本文开展了基于灵敏度协同的多馈入新能源集群最大容量优化分配方法研究，主要结论如下：

1）基于并网逆变器单机阻抗模型，应用电网络变换理论的线路拓扑化简方法，构建了新能源多馈入系统的稳定性评估模型。

2）建立了稳定裕度关于集群容量的目标函数，通过拉格朗日乘数法获得了灵敏度协同的极值条件，即集群阻抗裕度的灵敏度一致时，固定容量下系统具有最优的稳定裕度。

3）面向评估系统允许接入最大容量的需求，以灵敏度协同为核心步骤，提出基于灵敏度协同原则的容量优化分配方法。该方法以最优稳定裕度集群分配为增量调节的输出结果，迭代过程中的容量分配原则清晰、易于工程指导，仅需简单迭代可实现梯度最速寻优。

目前，本文仅从谐振约束角度研究了多馈入新能源集群最大容量优化分配方法。下一步工作将研究考虑线路容量、电压频率稳定等多维约束下灵敏度协同的异构控制、异构参数下的新能源多馈入系统接入容量优化分配方案。此外，现有模型基础采用的是容量相关的阻抗建模及裕度评估，下一步工作将融合并网容量与短路比评价指标，形成更系统的评价及调控机制。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。