电能型-功率型混合储能日前-日内协同滚动调度策略
2024-01-19吴永飞包宇庆
吴永飞,包宇庆
(南京师范大学南瑞电气与自动化学院,江苏省南京市 210046)
0 引言
近年来,各种类型的储能被运用到电力系统中。储能作为一种重要的柔性资源,可有效平抑风电波动,重塑负荷分布。因此,对含有风电和不同储能资源的电网系统进行优化调度,已成为高比例风电并网下电网系统亟待解决的问题[1-3]。
储能系统具有快速的双向调节能力,配置一定容量的储能系统可以有效应对风电随机波动[4]。文献[5]提出一种基于预测控制的风电场调度方法,有效提升电池储能系统(battery energy storage system,BESS)性能。文献[6]从发电侧和电网侧的角度,提出一种高比例风电并网下考虑储能参与的互联电网调度模型。文献[7]针对可再生能源在储能调度中的不确定问题,采用随机对偶动态规划的方法,建立多阶段随机规划模型。文献[8]考虑风电接入下储能的闲置时段和容量,提出储能运行的协同策略,实现最大程度消纳风电。文献[9]提出一种风电-电池储能-蓄热电锅炉的调度模型,充分考虑电池特性以及电、热系统互补的物理特性。文献[10]提出一种考虑BESS 和超级电容(supercapacitor,SC)的随机优化调控模型,采用概率预测与自适应模态分解相结合的方法,有效平抑风电波动。文献[11]以系统风险、煤耗量、弃风量为目标,建立一种风-储联合的多目标优化调度系统。
利用持续更新的预测信息进行滚动调度可有效提升电网风电消纳能力[12]。文献[13]采用协调调度和多目标决策的方法,建立了风-储联合系统的滚动优化模型。 文献[14]将需求响应(demand response,DR)资源和实际储能视为广义储能,实现火电机组与广义储能联合滚动调度。文献[15]使用BESS 与抽水蓄能储能系统组成混合储能系统(hybrid energy storage system,HESS),结合DR 资源建立了多时间尺度调度模型。文献[16]采用卡尔曼滤波算法,提出一种增强超短期预测与超前滚动优化组合的风储系统调度策略。文献[17]建立了基于机会约束目标规划的火-储滚动调度模型,提升调度计划的全局最优性。文献[18]建立了考虑多类型火电机组及储能的两阶段滚动调度模型,提出一种截断滚动优化的方法。文献[19]考虑可平移负荷的能量特性,将日内滚动周期拓展到日内剩余时间,提出一种全周期的滚动调度模型。
上述文献分别从日前及日内优化方法、各类资源出力特性的角度提出创新,建立了滚动调度模型。目前,围绕含储能装置的滚动调度研究中,电能型储能资源在优化调度中主要依靠其电能存储的优势实现削峰填谷;而功率型储能资源在优化调度中主要依靠其大功率快充快放的优势,平抑风电波动[20-22]。然而,传统调度策略在处理由电能型和功率型储能资源组成的HESS 时,存在以下两点不足:
1)较短的日内滚动时间窗会影响电能型储能资源的长期调度效果,这种调度策略在处理电能型储能资源时只考虑局部的调度范围,不能反映当天全局调度目标,无法充分发挥其削峰填谷的能力,导致电能型储能资源调度的“近视”问题。
2)较长的日前时间窗会影响功率型储能资源的短期调度效果,这种调度策略会导致功率型储能资源过度参与削峰填谷,无法发挥其快速充放电的优势,造成功率型储能资源调度的“远视”问题。
为解决上述问题,本文在已有研究的基础上,提出一种同时考虑电能型和功率型储能的日前-日内协同滚动调度模型。为解决电能型储能的“近视”问题,提出电能型储能的变周期调度策略,将滚动周期分为时间分辨率不同的两部分,并动态调整滚动周期长度,提升模型的求解效率;为解决功率型储能的“远视”问题,对风电波动量的极值进行统计分析,提出功率型储能资源的有限时间窗电量约束策略,实现其大功率快速充放电,有效平抑风电波动。最后,构建混合整数线性规划模型进行求解,结合算例验证模型的有效性。
1 滚动调度模型的基本框架
1.1 整体架构
风电的不确定性和波动性给电力系统的调度带来了新的挑战:一方面,目前风电预测还存在一定误差,其精度与时间尺度强相关;另一方面,系统中各调度资源存在多时间尺度的特性,只采用日前调度难以满足各类资源的运行特性[23]。同时,电能型和功率型储能资源因传统调度策略中调度时间窗的限制而无法充分发挥其在电量和功率上的调度潜力。
基于上述因素,针对不同时间尺度的风电预测数据和各类调度资源,本文建立了一种同时考虑电能型和功率型储能资源的日前-日内协同滚动调度模型,有效降低并网风电给系统带来的影响,提高系统运行的经济性与可靠性。模型中考虑以下调度资源:
1)火电机组资源:在日前调度中确定火电机组启停状态,在日内调度中确定火电机组出力;
2)风电机组资源:在日前调度确定预测误差较大条件下的消纳情况,在日内调度中确定预测误差较小条件下的消纳情况;
3)BESS:在日内调度中,确定BESS 的充放电功率;
4)SC:在日内调度中,确定SC 的充放电功率。
滚动调度模型流程如图1 所示。通过本文提出的功率型储能的有限时间窗电量约束策略,有效解决了功率型储能资源调度的“远视”问题;通过提出的电能型储能的变周期调度策略,有效解决了电能型储能资源调度的“近视”问题。
1.2 功率型储能的有限时间窗电量约束策略
SC 具有快速充放电的特性,响应较为迅速,可以在调度周期内频繁切换充放电状态,起到平抑风电波动的作用。然而,SC 的能量密度较小,需要构建SC 的有限时间窗电量约束策略来保证其不会长期处于单一的充/放电状态中。对于SC 的电量约束时间窗Tsc(SC 的单次充放电循环周期)求解过程如附录A 图A1 所示。
高频风电波动很大程度上决定了SC 的电量约束时间窗Tsc。确定Tsc的过程如表1 所示。首先,对日内风电曲线进行短期预测,得到原始日内风电预测数据Pw,利用滤波器设置通带频率得到高频风电功率Pwh;其次,对高频风电电量Ewh的极值点、和其出现时间进行统计分析,得到高频风电的峰值电量波动及其出现时间;最后,取峰值电量波动的平均时间间隔,即可得到SC的电量约束时间窗Tsc。SC 在单个时间窗内完成一次充放电循环,从而构建了SC 的有限时间窗电量约束策略,避免因过度参与削峰填谷而导致无法快速充放电,解决功率型储能资源调度的“远视”问题。
1.3 电能型储能的变周期调度策略
为实现火电、风电、混合储能资源调度的协同配合,本文提出电能型储能的变周期调度策略。该策略将日内短周期的局部调度转变为日内变周期的全局调度,通过动态调整日内滚动周期范围及对应的分辨率,调度结果可以反映全局调度目标。滚动调度模型的基本结构如图2 所示。
日前调度计划调度周期为24 h,分辨率为1 h,SC 不参与日前调度。日内调度计划单次滚动调度周期为日内剩余时间,分辨率为5 min 和1 h 两部分,每5 min 向前滚动优化一次,对日内调度结果进行更新。以10:00—11:00 为例,图2 展示了日内调度范围和长度的变化。随着时间推移,模型周期呈现阶段1 到阶段12 的状态。为避免电能型储能资源调度的“近视”问题,同时提高计算效率,该方法将调度周期分为两段,即初始段Ω5min和剩余段Ω1h,具体过程如表2 所示。初始段Ω5min从当前时刻开始,到第3 个整点时刻结束,分辨率为5 min,考虑SC 的有限时间窗电量约束,每个时间窗内完成单次充放电循环;剩余段Ω1h为剩余时间,从整点时刻开始到一天的结束时刻,分辨率为1 h。
2 滚动调度模型的建立
确定滚动模型的整体架构后,对日前、日内调度计划进行建模。
2.1 日前调度模型
2.1.1 日前调度模型目标函数
日前调度模型的目标函数是最小化成本函数CDA,如式(1)所示。
2.1.2 日前调度模型主要约束条件
1)有功功率平衡约束
式中:Pd,t,s为第s个场景下第d个节点在t时段的负荷量。
2)弃风约束
3)失负荷约束
4)火电机组开停机状态约束
式中:ug,t为第g台火电机组在t时段的开停机状态,为1 时表示机组处于开机状态,为0 时表示机组处于停机状态。
5)火电机组出力上下限约束
6)火电机组爬坡约束
式中:Dg为第g台火电机组爬坡的功率限制。
7)BESS 充放电功率约束
8)BESS 电量约束

2.1.3 目前调度模型优化结果
日前调度采用基于场景的随机规划,对日前调度模型进行求解,确定火电机组的启停状态ug,t,求解结果作为已知量代入日内调度模型中。
2.2 日内调度模型
2.2.1 日内调度模型目标函数
日内调度模型的目标函数是最小化成本函数CID,如式(10)所示。

2.2.2 日内调度模型主要约束条件
1)有功功率平衡约束
2)弃风约束
3)失负荷约束
4)火电机组出力上下限约束
5)火电机组爬坡约束
6)BESS 充放电功率约束
7)BESS 电量约束
8)SC 充放电功率约束
9)SC 电量约束

10)系统旋转备用约束
式中:ε为设置的置信度,本文取值为0.95;Φ-1为正态分布概率密度函数的反函数;δD为负荷预测的标准差;δW为风电预测的标准差。
2.2.3 日内调度模型优化结果
日内调度采用本文提出的电能型储能的变周期调度策略和功率型储能的有限时间窗电量约束策略,对日内调度模型进行求解。

3 算例分析
3.1 算例参数
本文基于PJM-5 系统对所提出的调度模型进行验证。该系统由5 台火电机组、2 个储能单元和1 个风电场构成。系统的5 个节点分别接入1 台火电机组,总装机容量为1 530 MW,火电机组的具体参数如表3 所示,其中,csh均为0 元。同时,在节点4接入1 个装机容量为600 MW 的风电场,系统的风电渗透率约为35%。
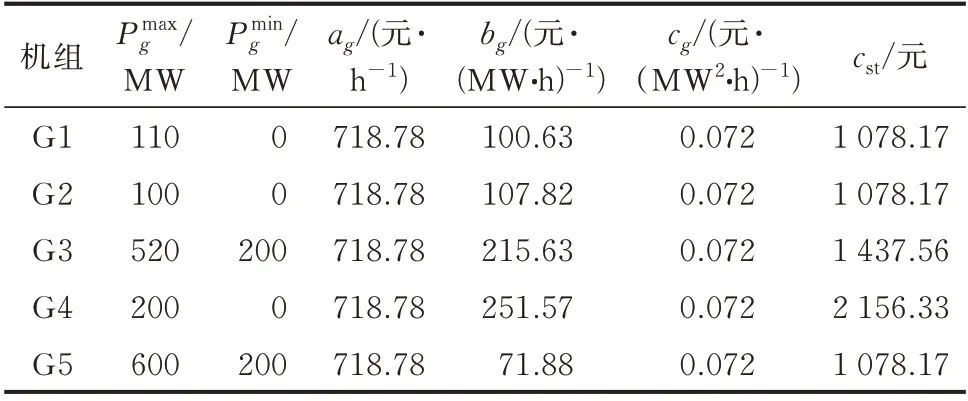
表3 火电机组参数Table 3 Parameters of thermal power units
该系统包含两种储能设备,在节点1 接入1 个功率为70 MW、容量为280 MW·h 的BESS,同时在节点2 接入1 个功率为20 MW、容量为5 MW·h 的SC,系统的总储能容量占比约为17%。储能设备参数参考文献[24],具体参数见表4 所示。
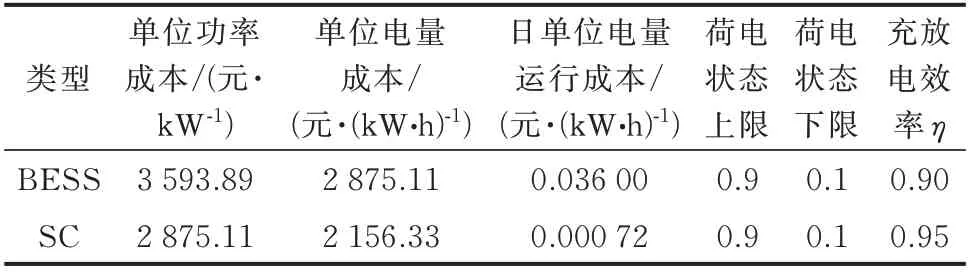
表4 HESS 参数Table 4 Parameters of HESS
本文风电和负荷预测曲线及预测误差如附录A图A2 所示,根据该曲线执行滚动调度。可以明显看出,与日前曲线相比,日内曲线精确度更高。
日前调度采用基于场景的随机规划。首先,通过对实际曲线添加扰动来获得日前风电预测曲线,生成全部风电场景数设置为200 个;然后,采用kmeans 算法对生成的全部风电场景进行聚类[25],获得3 类典型场景,各类典型场景的个数在全部风电场景中的占比即为典型风电场景的概率πs;最后,使各典型场景曲线的加权平均等于实际曲线,即可得到本文中的场景1、场景2 及场景3 下的日前风电预测曲线。附录A 图A3 为日前调度中生成的典型风电出力场景,各场景的发生概率分别为0.300、0.295、0.405。
3.2 算例结果分析
为了研究一天中发电侧资源、储能资源的调度情况,本文以系统运行总成本最低为目标,对所提出的调度模型进行求解,得到一天24 h 的滚动调度结果及相应的成本。此时,火电机组、风电机组、储能装置的调度出力情况如附录A 图A4 及图3 所示。
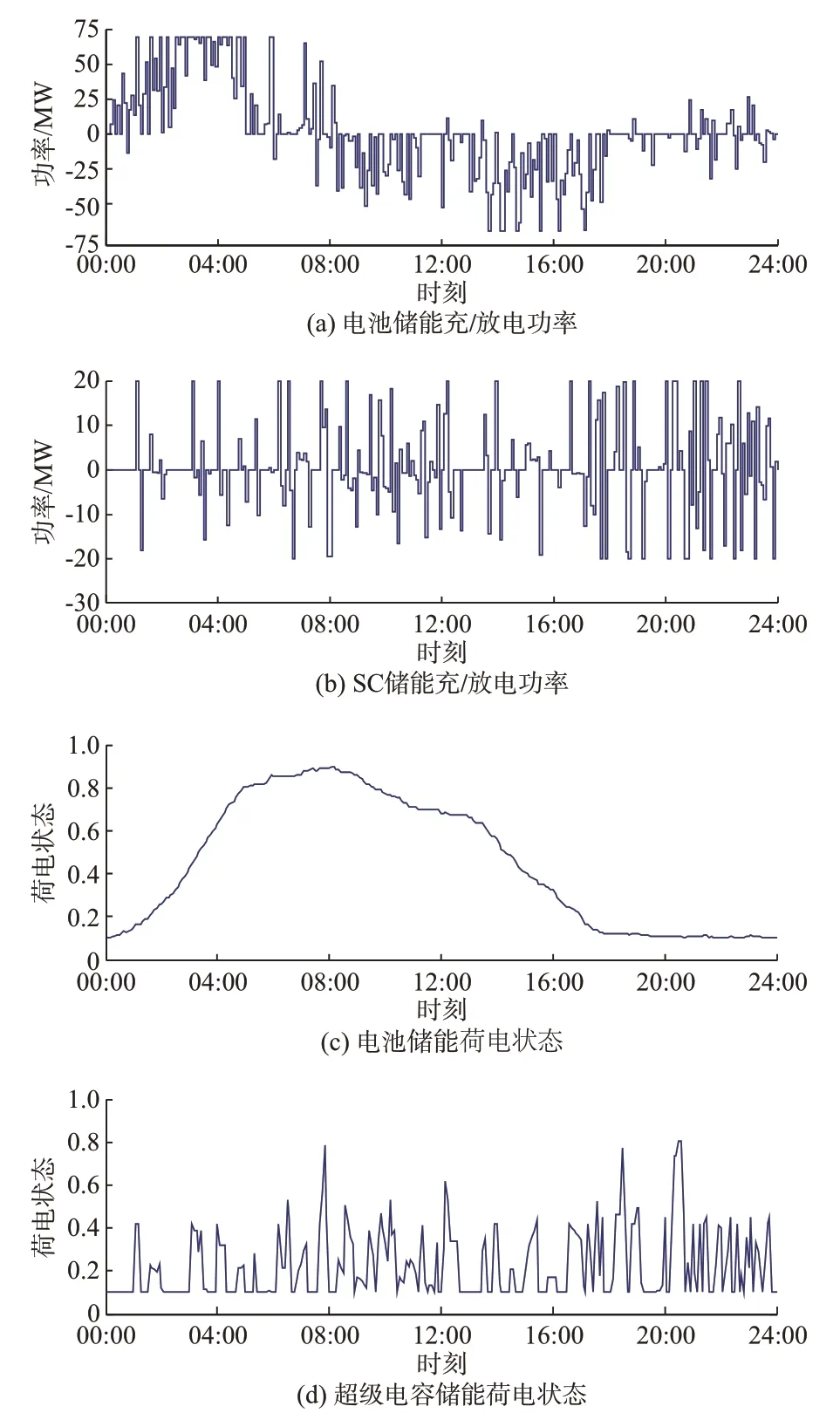
图3 HESS 功率及荷电状态Fig.3 Power and state of charge of HESS
附录A 图A4 中,蓝色曲线代表预测负荷曲线,绿色曲线表示调度结果,在系统调度过程中实现了高峰负荷的转移。风电出力处于高峰阶段(00:00—08:00 和19:00—24:00 时段)时,在储能装置的作用下,有效实现系统对风电的消纳,对保障电网安全运行具有重要意义。
同时,由图3 可以看出,BESS 起到了削峰填谷的作用,在夜间(00:00—08:00 时段)进行充电,在白天(08:00—20:00 时段)进行放电。在夜间风电出力高峰阶段(00:00—08:00 时段),由于BESS 处于充电状态,风电波动基本由BESS 与火电机组共同承担,SC 响应频率较低。在08:00—20:00 时段,BESS 电量饱和,处于放电状态,同时因火电机组功率变化受到爬坡约束,SC 处于快速充放电的状态,有效平抑了风电波动,充分发挥了HESS 的调度潜力。
在日内调度中,风电和负荷的预测精度较高,需要调整日前阶段确定的各资源调度结果,以获取更新后的结果。附录A 图A5 给出了日前调度与日内调度阶段火电机组、BESS、SC 功率的调整量。其中,火电机组承担了大部分的功率调整量,BESS 起到削峰填谷的作用,SC 承担了一部分变化较为剧烈的功率调整量,起到了平抑风电波动的作用,对维持系统功率平衡具有重要意义。
3.3 与其他调度方法对比分析
为了体现本文所提出的调度模型对实现风电消纳、充分发挥HESS 调度潜力的作用,在接下来的算例中,本文设置了4 种其他调度模型来进行对比。各调度策略如附录A 图A6 所示。
调度模型1:日前调度模型。仅采用日前调度模型,考虑BESS 与SC 这2 种储能装置。
调度模型2:单一时间尺度滚动调度模型。日内调度的滚动周期为2 h,分辨率为5 min。
调度模型3:变周期滚动调度模型。日内调度的滚动周期为日内剩余时间,分辨率为5 min 和1 h,不考虑功率型储能的有限时间窗电量约束策略。
调度模型4:全周期滚动调度模型。日内调度的滚动周期为日内剩余时间,分辨率为5 min。考虑功率型储能的有限时间窗电量约束策略。
调度模型5:本文所提出的调度模型。日内调度的滚动周期为日内剩余时间,分辨率为5 min 和1 h,考虑功率型储能的有限时间窗电量约束策略。
不同调度模型的调度结果如图4 所示。不同调度模型的储能调度结果如图5 所示。
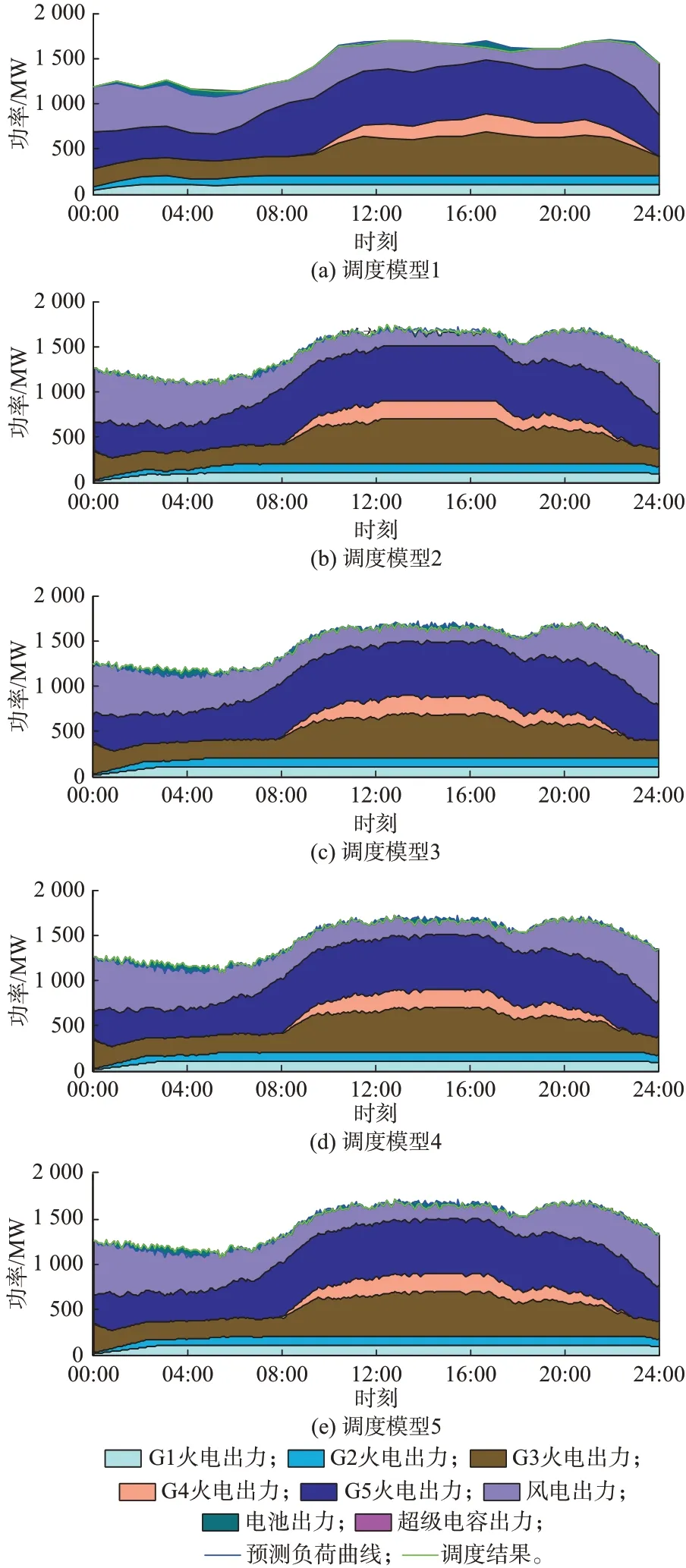
图4 不同调度模型的调度结果Fig.4 Scheduling results of different scheduling models
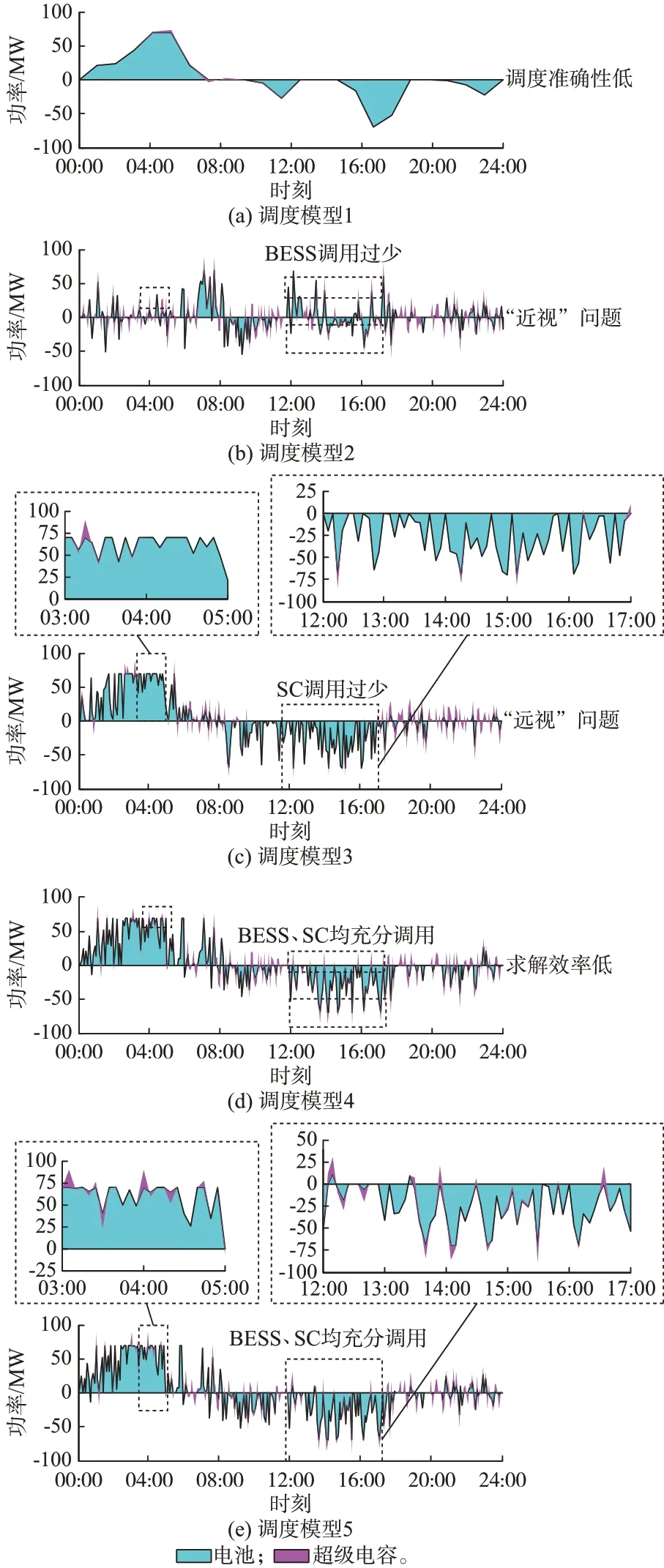
图5 不同调度模型的储能调度结果Fig.5 Scheduling results of energy storage with different scheduling models
从图4 和图5 可以看出,调度模型1 可以成功对各类资源进行调用,但是相比于滚动调度模型,其调度结果不能根据最新的负荷及风电预测信息进行更新。24 h 内SC 充放电循环仅2 次,无法有效平抑风电波动。
调度模型2 的日内单次滚动周期为2 h,每5 min 向前滚动一次。从图5 中可以看出,调度结果仅考虑接下来的2 h,而忽略了整个调度周期的资源安排,从而导致电能型储能资源调度的“近视”问题。具体到本文算例而言,则为模型2 中BESS 因过度考虑短期的调度收益,无法起到长期的削峰填谷的效果,在负荷低谷期及高峰期调用过少,其调用量明显少于其他调度方法,转移峰值负荷的性能最差。同时,调度结果中还存在一定失负荷情况(13:00—17:00 时段),总失负荷电量为51.53 MW·h。因此,调度模型2 的总运行成本显著高于其他调度模型。
调度模型3 的日内单次滚动周期为日内剩余时间,但未考虑功率型储能的有限时间窗电量约束策略。具体到本文算例而言,则为模型3 中SC 因过度考虑长期的调度收益,无法起到短期的快速充放电效果,在负荷低谷期及高峰调用过少。在负荷高峰阶段(12:00—17:00 时段),SC 过度参与削峰填谷而导致电量不足,无法有效平抑这一时段的风电波动,从而导致功率型储能资源调度的“远视”问题。
调度模型4 和调度模型5 均可以实现BESS 和SC 的充分利用,各火电机组出力及储能资源调用的幅值和变化趋势基本相同。区别在于本文提出的模型5 通过动态调整滚动周期的范围及对应的分辨率,相比于模型4 减少了求解混合整数线性规划模型的决策变量数量,有效提升了求解效率。在模型5 中,通过构建电能型储能的变周期调度策略及功率型储能的有限时间窗电量约束策略,充分发挥了电能型、功率型储能资源的调度潜力,对比模型2 和模型3,分别解决了电能型储能的“近视”问题及功率型储能的“远视”问题,在负荷低谷期、高峰期BESS 及SC 均充分调用。
表5 给出的总运行成本是基于式(10)构建的日内调度最小成本函数CID,通过MATLAB 中的YALMIP 工具箱构建混合整数线性规划模型,采用CPLEX 商业优化软件进行求解。表5 中对各模型的成本和计算时间进行了比较,从数据中可以看出,模型5 的计算效率比模型4 提高了22.19%,但总成本几乎一致。
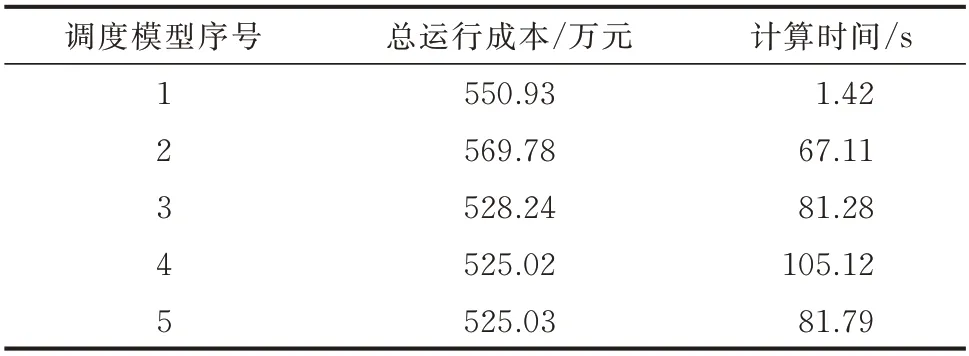
表5 不同调度模型的总运行成本及计算时间Table 5 Total operation costs and computation time of different scheduling models
4 结语
为解决电能型储能资源调度的“近视”问题,以及功率型储能资源调度的“远视”问题,本文提出一种同时考虑电能型和功率型储能资源的日前-日内协同滚动调度策略。结果表明:
1)滚动调度模型可以充分利用日内风电、负荷的预测结果进行更新,提高调度计划的准确性。
2)较短的日内滚动时间窗会影响电能型储能资源的长期调度效果,通过构建电能型储能资源的变周期调度策略,避免其因“近视”问题而导致其削峰填谷能力受限,同时提升了模型的求解效率。
3)较长的日前时间窗会影响功率型储能资源的短期调度效果,通过构建功率型储能资源的有限时间窗电量约束策略,避免其因“远视”问题而影响其平抑风电波动的能力,实现功率型储能资源的快速充放电。
本文提出的同时考虑电能型和功率型储能资源的协同滚动调度模型,可以充分发挥不同储能资源在电量和功率上的调度潜力,有效提升电网对风电消纳的能力。后续将针对日前-日内-实时的多时间尺度及多类型储能的协同滚动调度开展进一步研究。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。
