考虑热舒适度的居民空调负荷调控潜力差异化评估

金 旭，张远实，李 明，窦晓波，阮文骏，段梅梅

（1.东南大学电气工程学院，江苏省南京市 210096；2.国家电网有限公司，北京市 100031；3.国网江苏省电力有限公司，江苏省南京市 210000）

0 引言

为了应对日益严重的能源紧缺和环境污染问题，中国计划在2030 年前实现“碳达峰”，争取在2060 年前实现“碳中和”［1］。随着“双碳”目标的提出，电力系统可再生能源渗透率不断提升［2-4］。由于可再生能源具有间歇性和随机性，电力系统面临巨大的供需平衡压力［5］，仅依靠发电侧的调节能力难以实现系统的安全经济运行。相比之下，负荷侧的调节潜力可观且成本较低，已受到广泛关注［6-9］。

作为负荷侧的重要组成部分，空调负荷可占部分地区夏季高峰负荷的50%［10-11］，且空调负荷具有响应速度快、调控方式多样等特征［12-14］。因此，高效管理空调负荷有助于保障电力供需平衡，促进可再生能源消纳，而评估空调负荷调控潜力则是实现这一目标的重要前提条件。

掌握居民空调负荷的调控潜力可以辅助负荷管理者设计最优激励方案和控制策略［15-17］。目前，国内外学者对居民空调负荷调控潜力评估开展了一些研究。 文献［18］采用等效热参数（equivalent thermal parameter，ETP）模型对居民空调热动力学建模，揭示了空调负荷聚合后具有提供小时内负荷平衡服务的调控潜力。文献［19］基于一阶ETP 模型进一步分析了室外温度、空调设定温度及聚合数量等因素对居民空调负荷调控潜力的影响。考虑到频繁启停空调将降低其使用寿命，文献［20］在基于空调热动力学模型评估空调负荷调控潜力时增加了启停转换间隔时长约束，提高了潜力评估结果的可靠性。考虑到居民用户对调控指令的响应具有不确定性，文献［21］基于概率论评估了不同设定温度调整量下空调负荷的调控潜力及其分布特性，丰富了负荷管理者的决策依据。文献［22］将空调热动力学模型和储能模型结合，建立了空调负荷的虚拟储能模型，在此基础上有效评估了空调负荷的聚合调控潜力。然而，上述研究大多选取典型参数值建立空调热动力学模型，未能有效考虑不同居民空调状态及参数的差异性，因而限制了不同居民空调负荷调控潜力的差异化评估，实际应用中不利于负荷管理者有针对性地选择参与用户。

为了差异化评估不同居民的空调负荷调控潜力，需要辨识其空调状态及参数。文献［23］利用空调的运行信息（功率、室内温度、室外温度）数据，基于遗传算法实现了空调热动力学模型参数辨识。为了满足在线实时应用的需要，文献［24］在实时监测空调负荷数据及环境数据的基础上，通过粒子群优化算法对空调热动力学模型参数进行了在线辨识。以上辨识方法的实施需要获取居民空调负荷数据，而受成本、数据存储和隐私保护等因素制约，目前居民家中安装的智能电表普遍仅能提供全屋总负荷数据［25］。在仅使用总负荷和室外温度数据的基础上，文献［26］依据空调负荷的温敏特性对居民空调的状态及参数进行辨识，然后评估了不同居民空调负荷的调控潜力。文献［27］通过线性回归和无监督分类算法辨识了不同居民空调的状态及参数，然后计算了调高空调设定温度可提供的稳态和暂态负荷削减量。文献［28］依据回归分析从总负荷数据中提取出空调负荷数据，然后辨识了空调热动力学模型参数，并实现了对不同居民空调负荷调控潜力的评估。考虑到居民对空调的使用具有不确定性，文献［29］利用从总负荷中分解出的空调负荷数据计算了不同小时、不同居民空调处于开机状态的概率和相应的调控潜力。然而，上述研究未能量化考虑居民热舒适度，所评估的空调负荷调控潜力对应的室内温度变化可能不满足居民热舒适度要求，影响居民对空调负荷管理的参与意愿。

针对上述问题，为了兼顾调控潜力差异性和热舒适度，本文提出一种考虑热舒适度的居民空调负荷调控潜力差异化评估方法。首先，构建居民热舒适度模型和空调热动力学模型，提取模型中的关键参数。然后，考虑不同居民空调负荷调控潜力的差异性，基于隐马尔可夫模型（hidden Markov model，HMM）估计不同居民的空调模型参数，并利用维特比算法解码不同居民的空调状态时间序列。在此基础上，考虑居民的热舒适度要求，差异化评估不同居民热舒适度可接受范围内的空调负荷调控潜力。最后，基于真实居民负荷数据开展算例分析，结果验证了所提方法的有效性。

1 居民热舒适度模型及空调热动力学模型

1.1 居民热舒适度模型

根据文献［30］，居民热舒适度可以通过计算预测平均投票（predicted mean vote，PMV）指数衡量。PMV 指数等于0 表明居民感觉舒适；PMV 指数大于0 表示居民感觉偏热，PMV 指数越大意味着居民感觉越热；PMV 指数小于0 表示居民感觉偏冷，PMV 指数越小意味着居民感觉越冷。PMV 指数IPMV的计算公式如下：

式中：M为人体代谢率；W为人体活动产生的机械功率，对于大多数活动可忽略不计；pa为水蒸气分压；Tin为室内温度；fcl为着装系数；Tcl为服装表面温度；Tˉr为平均辐射温度，通常比室内温度高2.8 ℃；hc为对流换热系数。

pa、fcl、Tcl和hc的计算公式如下：

式中：rh为相对湿度；var为空气流速；Icl为服装热阻，可依据06：00 的室外温度Tout，6计算，如式（6）所示。

由式（1）—式（6）可知，影响居民热舒适度的参数主要有人体代谢率、室内温度、相对湿度、空气流速以及室外温度。

1.2 空调热动力学模型

基于一阶ETP 模型，可以建立居民空调机组的热动力学模型［31］。以空调运行在制冷状态为例，其功率与室内外温度关系如下：

式中：C为等效比热容；Q=ηPac为制冷量，其中，η为空调能效比，Pac为空调额定功率；Tout为室外温度；R为等效热阻。

与电力系统调度周期相比，空调的热力学动态过程较为短暂，调整设定温度后将快速运行至新稳态。依据式（7）可知，热稳态下空调运行使室内温度保持在设定温度Tset，则dTin/dt=0，其消耗功率Pacs为：

式中：α=1/ηR为温度响应率，体现了空调负荷的温敏特性。本文后续评估不同小时居民空调负荷调控潜力时，为了降低模型复杂度，忽略了空调的热力学动态过程，基于空调的热力学稳态模型展开研究。

由式（8）可知，影响稳态居民空调负荷的参数有温度响应率、设定温度和室外温度。其中，设定温度与室内温度相等。

2 空调状态及参数辨识方法

受自然环境和居民用能习惯影响，不同时间、不同居民的空调状态及参数存在区别，导致其空调负荷调控潜力存在差异。因此，本章实施居民空调状态及参数辨识，其方法框架如附录A 图A1 所示。首先，输入小时级全屋总负荷和室外温度数据，基于HMM 估计居民空调在不同状态下的模型参数。然后，利用维特比算法解码居民空调状态的时间序列，为差异化评估居民空调负荷的调控潜力建立基础。

2.1 空调模型参数估计

HMM 是一种统计模型，常用于建立隐藏状态和可观测变量之间的联系［32］。实际上，受资金成本、数据存储和隐私保护等问题限制，居民空调状态无法通过计量设备直接测量，属于隐藏状态；而与空调状态有关的室外温度和全屋总负荷可分别由气象监测设备和智能电表直接测量，属于可观测变量。因此，利用易获得的小时级全屋总负荷和室外温度数据，本节构建用于辨识空调状态及参数的HMM，结构如图1 所示。图中：Tout，t和Pt分别为t时段室外温度和总负荷；St为t时段的空调状态；蓝色箭头表示总负荷输出过程，即当前时段的总负荷与该时段的室外温度和空调状态有关，用总负荷输出概率矩阵表示；红色箭头表示空调状态转移过程，即当前时段的空调状态受上一时段的室外温度和空调状态影响，用空调状态转移概率矩阵表示。

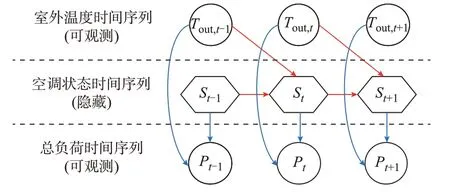
图1 用于辨识空调状态及参数的HMM 结构Fig.1 HMM structure employed for identifying air conditioning states and parameters

下面将具体介绍空调状态种类、总负荷输出概率矩阵以及空调状态转移概率矩阵。

所有的空调状态由状态集合s={s1，s2，…，sk}表示，其中，k为空调状态数量。依据空调热动力学模型可知，空调运行时将电功率转化为冷（热）量以改变室内温度。一般地，为保持自身舒适，当温度较低、居民感觉偏冷时会开启空调制热，使室内温度上升；当温度较高、居民感觉偏热时会开启空调制冷，使室内温度下降；当温度适宜，居民基本不使用空调。因此，本文假设空调状态有3 种：制冷状态s1、制热状态s2以及关机状态s3，则k=3。

在t时段处于第m种空调状态sm时，总负荷的输出概率po为：

式中：Bm为空调状态sm时全屋总负荷中的非空调负荷，Bm≥0；αm为空调状态sm时的温度响应率，其中，制冷状态下温度响应率α1＞0，制热状态下温度响应率α2＜0，关机状态下温度响应率α3=0；Tset，m和σm分别为空调状态sm时的设定温度和标准差。

基于式（9），t时段总负荷的输出概率矩阵po为：

从t时段到t+1 时段，空调状态从si转变为sj的概率ps为：

式中：bi，j表示非温度因素对空调状态si至sj转移的影响；ai，j表示温度因素对空调状态si至sj转移的影响。

基于式（11），从t时段到t+1 时段，空调状态的转移概率矩阵ps为：

依据总负荷输出概率矩阵和空调状态转移概率矩 阵 ， 给 定 总 负 荷 时 间 序 列P={P1，P2，…，Pt，…，Ph} 和室外温度时间序列T={Tout，1，Tout，2，…，Tout，t，…，Tout，h}，所构建HMM 的似然函数L(θ)为：

式中：ps（S1）为初始时段空调状态的概率向量；h为时段数量；θ为参数向量，包括Bm、αm、Tset，m、σm、bi，j和ai，j（m，i，j=1，2，…，k）。

根据极大似然估计法获得参数估计值θ̂：

2.2 空调状态时间序列解码

维特比算法是一种动态规划算法，常用于HMM 中隐藏状态时间序列的解码［33］。因此，在获得模型参数估计值后，本节利用维特比算法解码总负荷时间序列对应的空调状态时间序列，详细步骤如算法1 所示。

算法1：空调状态时间序列解码算法1）输入总负荷时间序列P={ P1,P2,…,Ph}、室外温度时间序列T={Tout,1,Tout,2,…,Tout,h}、空调状态集合s={ s1,s2,…,sk}、状态转移概率矩阵ps、总负荷输出概率矩阵po、空调状态初始概率向量ps(S1)；2）对i ∈[1,k]；3）计算初始时段空调状态si 时输出总负荷的概率u(si,1)为ps(si) po(P1|si,Tout,1)，并保存对应空调状态至v(si,1)；4）步骤2）循环结束；5）对t ∈[2,h]；6）对i ∈[1,k]；7）计算t 时段空调状态si 时输出总负荷最优路径的概率u(si,t)为max(u(sj,t-1) ps(si|sj,Tout,t-1) po(Pt|si,Tout,t)), 其中，sj=s1,s2,…,sk,并保存对应t-1 时段的空调状态至v(si,t)；8）步骤6）循环结束；9）步骤5）循环结束；10)选择最终时段输出总负荷最优路径概率最大的空调状态作为最终时段的空调状态Sh；11)对t ∈[1,h-1]；12)逆向回溯计算t 时段的空调状态St为v(St+1,t+1)；13)步骤11）循环结束；14)输出空调状态时间序列S={S1,S2,…,Sh}。

算法流程解释如下：

1）初始化。在初始时段t=1，根据空调每个状态的初始概率ps(si)和对应的总负荷输出概率po(P1|si，Tout，1)，计算每个空调状态下输出总负荷的概率u(si，1)，并保存该状态。

2）递推计算。对于剩余时段t=2，3，…，h，利用t-1 时段每个空调状态下输出总负荷最优路径的概率u(sj，t-1)，计算t时段每个空调状态下输出总负荷最优路径的概率u(si，t)，并保存相应的t-1时段的空调状态v(si，t)。

3）回溯计算。在最终时段t=h，选择输出总负荷最优路径概率最大的空调状态作为最终时段的空调状态Sh。然后，逆向回溯（t=h-1，h-2，…，1），根据t+1 时段的空调状态确定t时段的空调状态St。

3 空调负荷调控潜力评估模型

在获得不同居民的空调状态时间序列、设定温度和温度响应率的基础上，根据居民热舒适度模型及空调热动力学模型可以差异化评估不同居民热舒适度可接受范围内的空调负荷调控潜力。

3.1 单个居民空调负荷调控潜力评估

考虑热舒适度限制的单个居民空调负荷调控潜力评估方法如附录A 图A2 所示。

具体实施步骤如下：

1）判断居民空调是否处于关机状态，若是，则该空调无法参与负荷管理，其调控潜力为0；否则，收集居民热舒适度模型及空调热动力学模型关键参数的数据，构建调控潜力评估方法的输入数据集。其中，设定温度和温度响应率由第2 章介绍的空调模型参数估计方法得到。通过微气象监测设备，可以获得室外温度、空气流速和相对湿度数据。人体代谢率与人体活动有关，不易直接测量，由于居民使用空调是为了保持自身的热舒适度，未调控空调时居民的PMV 指数可假设为0，进而计算出人体代谢率为：

2）调整设定温度。由于实际中大部分空调设定温度的单位调整量为0.5 ℃，本文以0.5 ℃为步长调整设定温度。接着，利用式（1）计算PMV 指数，判断设定温度调整后居民的热舒适度是否会越限。若没有，继续调整设定温度，重新计算PMV 指数并判断；反之，输出居民热舒适度可接受范围内设定温度的最大调整量。根据ISO 7730 标准，居民可接受的热舒适度范围为IPMV∈[-0.5，0.5]。考虑不同居民热感觉存在差异，可假设不同居民热舒适度上限的PMV 指数服从均值为0.5、标准差为0.1 的正态分布；热舒适下限的PMV 指数服从均值为-0.5、标准差为0.1 的正态分布。

3）利用设定温度的最大调整量ΔTms和温度响应率α，计算满足居民热舒适度要求的空调负荷调控潜力ΔPac：

3.2 多个居民空调负荷聚合调控潜力评估

基于不同居民热舒适度可接受范围内的空调负荷调控潜力的差异化评估结果，可以进一步评估满足多个居民热舒适度要求的空调负荷聚合调控潜力ΔPA：

式中：n为参与空调负荷管理的居民数量；ΔPac，r为第r个居民热舒适度可接受范围内的空调负荷调控潜力；αr和ΔTms，r分别为第r个居民的空调温度响应率和热舒适度限制下空调设定温度的最大调整量。

4 算例分析

4.1 算例说明

本文采用Pecan Street 公司提供的44 个美国居民负荷数据集［34］和SoDa 记录的气象数据［35］实施算例分析，每个居民负荷数据集包含全年小时级总负荷和空调负荷数据。其中，空调负荷数据仅用于检验空调状态辨识结果的准确性，总负荷和气象数据则用作所提方法的输入数据。

按全年总负荷的升序对居民进行编号，44 个居民的全年总负荷、全年空调负荷及空调负荷占比如附录B 图B1 所示。空调负荷占比平均为32%，最高可达51%。附录B 图B2 展示了全年小时级的室外温度数据。可以看出，室外温度在-8～40 ℃之间变化，平均值为20 ℃。

4.2 空调状态辨识结果

基于所构建的HMM 和维特比算法，输入每个居民的全年小时级总负荷和室外温度数据，可辨识其全年小时级空调状态。附录B 图B3 展示了利用真实和辨识空调状态数据计算的不同居民空调全年分别处于制冷状态、关机状态以及制热状态的比例。其中，21 号和35 号居民空调状态与室外温度的映射关系如附录B 图B4 所示。

分析附录B 图B3 和图B4 可知：1）辨识的空调状态比例与真实的空调状态比例相似，表明空调状态辨识结果较为准确；2）空调运行在制热状态时室外温度普遍较低，空调运行在制冷状态时室外温度普遍较高，而空调关机状态则可能出现在任意室外温度下；3）所有居民空调全年运行在制冷状态的比例都高于运行在制热状态的比例，这是由于美国居民冬季主要采用燃气锅炉采暖，空调只是辅助制热设备，而夏季则主要采用空调制冷降温。此外，结合附录B 图B1 不难发现，空调关机状态比例较高的居民的总负荷普遍较低，空调关机状态比例较低的居民的总负荷普遍较高，这体现了空调属于居民家中主要用电设备，其使用程度对居民总负荷水平具有一定影响。

为检验空调状态辨识结果的准确度，引入多分类问题中常用的评价指标MicroF1［36］。MicroF1 考虑了分类模型的查准率和召回率，对每个类别的分类结果进行量化评估，因而能够衡量模型对所有类别样本的综合性能，不会受到少数类别样本数量较少的影响。MicroF1 值RMF的计算公式如下：

式中：RP为整体查准率，衡量了模型在整个分类任务中的辨识精确性；RE为整体召回率，衡量了模型对所有类别实际样本的捕捉能力；Etp，i为辨识状态为i、真实状态为i的样本个数；Efp，i为辨识状态为i、真实状态不为i的样本个数；Efn，i为真实状态为i、辨识状态不为i的样本个数。辨识状态与真实状态一致的样本数量越多，RMF越趋近于1，表明辨识结果的准确度越高；相反，RMF越趋近于0，表明辨识结果的准确度越低。

图2 展示了不同居民空调状态辨识结果的MicroF1 值的频数分布和概率密度分布。从图中可以看出，MicroF1 的平均值为0.82，所有MicroF1 值都大于0.4 且主要分布在0.8～0.9，这表明本文提出的居民空调状态辨识方法具有一定准确性和鲁棒性。

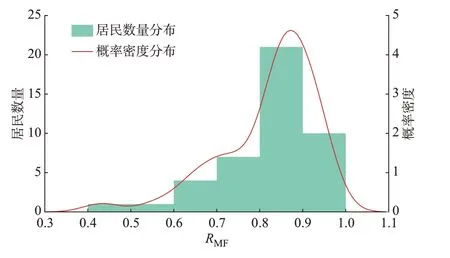
图2 空调状态辨识结果的MicroF1 值的分布Fig.2 MicroF1 value distribution of air conditioning state identification results

4.3 空调负荷调控潜力评估结果

基于空调状态辨识结果，可评估居民热舒适度可接受范围内的空调负荷调控潜力。图3 展示了2018 年8 月1 日36 号居民空调在不同小时及设定温度调整量下的负荷调控潜力。图中：红色球体表示满足热舒适度要求的空调设定温度最大调整量及对应负荷调控潜力。附录B 图B5 给出了空调运行时不同设定温度调整量下36 号居民PMV 指数的计算结果。

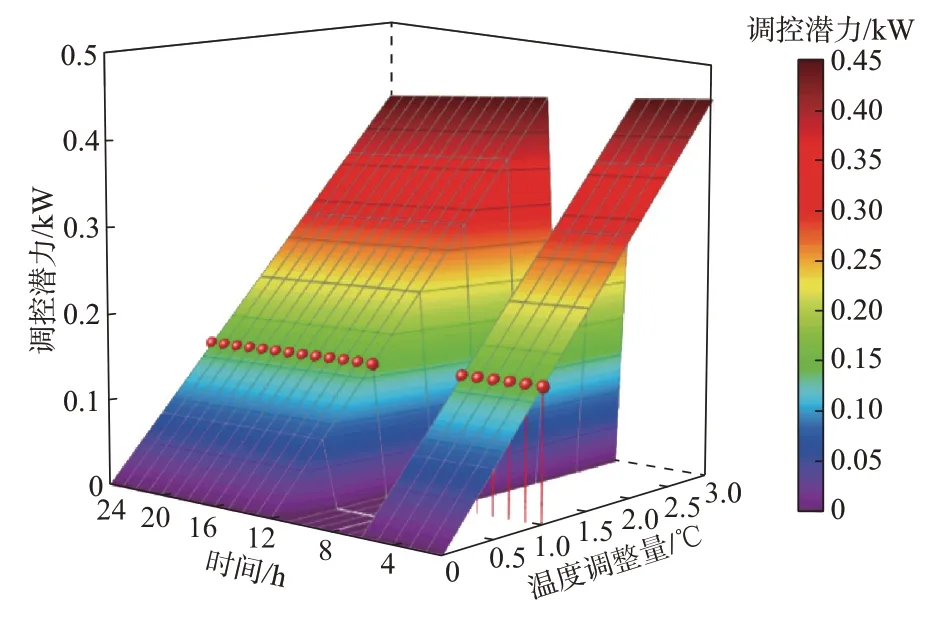
图3 36 号居民空调负荷调控潜力评估结果Fig.3 Evaluation results of air conditioning load regulation potential of resident 36

图3 中，对于大部分时段（1～6 h、12～24 h），该居民空调负荷的调控潜力随着设定温度调整量的上升而增加；在相同设定温度调整量条件下，不同小时居民空调负荷的调控潜力保持不变。但还有部分时段（7～11 h），不论设定温度调整量如何变化，空调负荷的调控潜力始终为0，这是由于这些时段内该居民的空调处于停机状态，无法提供负荷削减服务。此外，该居民热舒适度上限的PMV 指数为0.55，当空调设定温度调整量为1 ℃时，不同小时该居民的PMV 指数均小于0.55，相应负荷调控潜力为0.15 kW。虽然继续增大设定温度调整量会得到更高的调控潜力评估值，但同时PMV 指数也在不断增加，意味着更高空调负荷调控潜力的获得需要牺牲居民的热舒适性。因此，设定温度调整1 ℃时的负荷削减量可作为该居民热舒适度可接受范围内的空调负荷调控潜力。

与系统负荷缺额相比，单个居民空调负荷的调控潜力有限，无法直接参与负荷管理，一般通过聚合参与调控。考虑到成本问题，需要在空调聚合数量有限的条件下最大化其调控潜力。因此，基于优先选择调控潜力大的用户原则，评估了满足居民热舒适要求的空调负荷聚合调控潜力。图4 所示为2018 年8 月1 日的聚合调控潜力评估结果。可以看出，随着空调聚合数量的增加，空调负荷聚合调控潜力先增加后趋于饱和，这是因为优先选择调控潜力大的用户参与聚合，故前期增加聚合数量所增加的调控潜力大，后期继续增加聚合数量所增加的调控潜力有限。并且，由于单个居民空调负荷的调控潜力并不始终相同，导致不同小时的空调负荷聚合调控潜力存在差异。

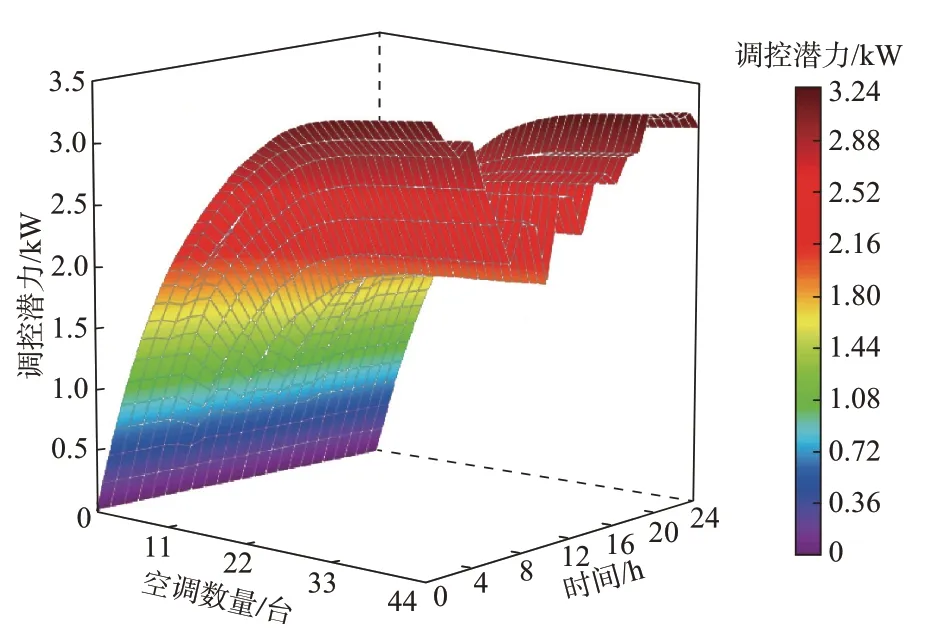
图4 考虑热舒适度的空调负荷聚合调控潜力评估结果Fig.4 Evaluation results of air conditioning load aggregation regulation potential considering thermal comfort

4.4 不同方法下潜力评估结果对比

为了检验所提方法的有效性，本文还采用了其他3 种方法来评估居民空调负荷聚合调控潜力。其中，对比方法Ⅰ不考虑不同居民空调负荷调控潜力的差异性，随机选择用户参与空调负荷聚合调控；对比方法Ⅱ不考虑居民的热舒适度要求，按照所有居民空调设定温度均调高1 ℃来评估空调负荷聚合调控潜力；对比方法Ⅲ不考虑居民的热舒适度要求，按照所有居民空调设定温度均调高2 ℃来评估空调负荷聚合调控潜力。图5 为上午08：00、下午14：00、傍晚19：00 以及夜间23：00 的不同方法的居民空调负荷聚合调控潜力评估结果。表1 和表2 分别给出了不同方法的居民空调负荷聚合调控潜力的最大评估值及对应的居民PMV 指数越限比例。

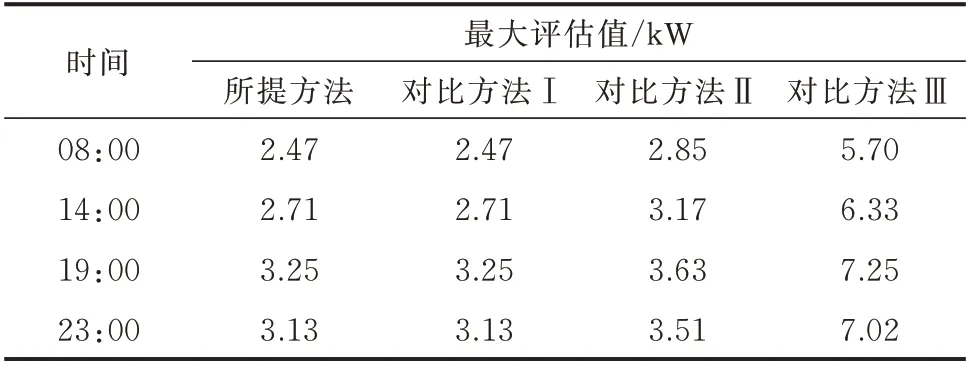
表1 居民空调负荷聚合调控潜力的最大评估值Table 1 Maximum evaluation value of residential air conditioning load aggregation regulation potential

表2 最大潜力评估值下居民PMV 指数的越限比例Table 2 Exceedance ratio of resident PMV indices corresponding to maximum potential evaluation value

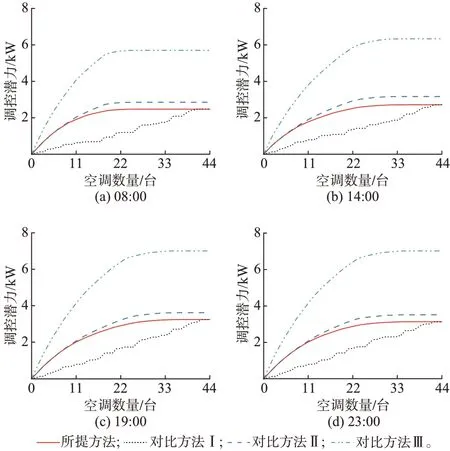
图5 居民空调负荷聚合调控潜力评估结果对比Fig.5 Comparison of evaluation results of residential air conditioning load aggregation regulation potential

从图5 可以看出，与所提方法相比，对比方法Ⅰ的空调负荷聚合调控潜力评估值普遍较低，这是由于后者未考虑不同居民空调负荷调控潜力的差异性，聚合时可能优先选择调控潜力小的用户，导致无法充分挖掘居民空调负荷的聚合调控潜力。因此，通过考虑不同居民空调负荷调控潜力的差异性，所提方法有利于辅助负荷管理者有针对性地选择参与用户以实现最优调控。

此外，值得注意的是，虽然对比方法Ⅱ和Ⅲ的空调负荷聚合调控潜力评估值高于所提方法的空调负荷聚合调控潜力评估值，但是结合表2 不难发现，所提方法完全满足居民的热舒适度要求，而对比方法Ⅱ和Ⅲ却产生了不同程度的居民热舒适度越限。具体来说，所提方法的居民空调负荷聚合调控潜力最大评估值的居民PMV 指数越限比例为0，可作为居民热舒适度可接受范围内的最大空调负荷聚合调控潜力。相比之下，对比方法Ⅱ的最大潜力评估值平均增加了14%，相应的居民PMV 指数越限比例平均为22%；对比方法Ⅲ的最大潜力评估值平均增加了128%，相应的居民PMV 指数越限比例达到了100%。可见，忽视居民的热舒适度要求将导致居民空调负荷聚合调控潜力评估值偏高，若参考该潜力评估值实施空调负荷管理，将影响居民的热舒适性，降低其参与意愿。因此，为提升居民空调负荷管理的实施效率，管理者以所提方法的空调负荷聚合调控潜力评估值作为决策参考更合理。

5 结语

本文提出一种考虑居民热舒适度的空调负荷调控潜力差异化评估方法。利用易于获取的小时级智能电表数据和气象数据，基于HMM 和维特比算法准确地辨识了空调状态及参数，然后根据热舒适度和空调热动力学模型差异化地评估了满足不同居民热舒适度要求的空调负荷调控潜力。通过真实居民负荷数据集开展算例分析，验证了所提方法的有效性。主要结论如下：

1）所提方法的不同居民空调状态辨识结果的平均MicroF1 值为0.82，因而具有一定准确性和鲁棒性。利用居民空调状态及参数辨识结果，可以差异化评估居民空调负荷的调控潜力，为负荷管理者合理选择参与用户提供决策支撑。

2）相比于未考虑居民热舒适度的方法，所提方法的空调负荷调控潜力评估值100%满足居民的热舒适度要求，避免了因忽视居民的热舒适度而过高地估计居民空调负荷调控潜力，有助于提升空调负荷管理的实施效率。

本文所提方法兼顾了居民空调负荷调控潜力差异性和热舒适度，对于高效管理居民空调负荷具有重要意义。但在研究过程中采用PMV 指数衡量居民的热舒适度，由于居民的热舒适度较为主观，后续研究将收集不同环境下的居民热感受评价数据，以检验PMV 指数的准确性，提升所提方法的有效性。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。