面向广义能量品质分析的多能耦合流集线器建模

王 丹，李宜哲，贾宏杰，周天烁，曹逸滔，张 帅，刘佳委

（1.智能电网教育部重点实验室（天津大学），天津市 300072；2.天津市智慧能源与信息技术重点实验室（天津大学），天津市 300072）

0 引言

综合能源系统（integrated energy system，IES）能够实现多种能源形式的转化与供给，是提高系统整体能效和促进可再生能源利用的有效途径［1-2］。为了应对传统多能利用方式和引入可再生能源所带来的诸多挑战，学者们开始关注诸如能量品级［3-4］、碳排放［5-7］和可再生能源不确定性［8-9］等关键问题。部分研究针对能量［10-11］、有效能［12-13］、能量无序性程度［14-16］和环境影响［17-19］等能量介质自身和附加的属性，对IES 供能水平进行分析和评价，推动了IES 能量流［10］、㶲流［20］、熵增流［14］、碳排放流［19］等能源系统“流”建模理论的发展。为实现IES 在有效能（㶲）、无序性（熵）、环境影响（碳）等广义能量品质视角下的能量供应，需要在量质协同多维评价体系下，对IES 系统形态、能量管理、调度运行等方面做出科学决策。

多能耦合环节决定着不同品质能量（本文简称“异质能”）的转化与分配，充当着IES 能量数量和品质“调节者”的角色。由于各类“流”的传播、转化和分配特性存在一定差异，为了准确描述异质能的品质变化规律，需要采用广义能量品质分析要素的建模理论。本文梳理了多能耦合环节能量流、㶲流、熵增流、碳排放流的建模方法，并总结了各类模型的区别与特点。

随着IES 中多能耦合环节的数量和复杂性的增加，需要一种方法系统地描述异质能及其品质要素的多种“流”足迹。本文在统一精细化、抽象化的模型架构下，给出多能耦合环节“流”通用元件的定义，提出基于标准化矩阵框架的流集线器（flow hub，FH）模型，该模型可针对多种广义能量品质分析要素进行建模与计算，根据关系矩阵判定参数对不可行条件进行合理化修正，从而保证FH 存在唯一运行状态。最后，通过算例验证了FH 的有效性及适用性，并展望了该模型的应用前景。

1 多能耦合环节多样化建模理论

一个具有较高广义能量品质的供能系统应具备高效、低耗、有序、低碳等特征，本文以“流”模型的流率数值对广义能量品质进行衡量。IES 广义能量品质的相关研究中，具有代表性的流模型主要包括：能量流、㶲流、熵增流、碳排放流。IES 多能耦合环节多样化建模理论能够在一定程度上涵盖上述流理论的不同内涵与传播机理，但存在精细化、抽象化不足等问题。

1.1 IES 典型流模型

IES 能量流模型是基于不同介质的传播机理和能量属性，考虑多能耦合因素而构建的统一量纲能源系统模型，可实现多能流的联合求解［10，22］，是IES规划、运行优化和安全性等课题的理论依据［11］。

IES 㶲流模型将能量流中能够有效转化为功的部分被定义为IES 㶲流［23］，量化分析㶲的传播、转化和分配情况，实现能源系统的量质协同分析［24］，能够刻画IES 的有效能层面的整体或局部广义能量品质［25］，对于实现高㶲转型、增效提质具有重要意义。

IES 熵增流模型采用“熵增”这一概念描述㶲损和源荷不确定性导致的能量无序性增长，反映系统各环节能量品质退化情况［26］。深度分析IES 熵增机理与熵态分布，研究供能造成的品质流失，可为进一步提升IES 无序性层面的广义能量品质提供理论依据［14］。

IES 碳排放流模型通过量化分析能源网络中能量生产、传输、转换和利用等各环节对应的碳排放量［27］，从而准确描述系统供能的碳排放水平［19］，刻画IES 环境影响层面的广义能量品质，有助于科学衡量各方的碳排放责任，促进IES 合理低碳转型。

1.2 多能耦合环节典型流模型

1.2.1 多能耦合环节典型流模型的研究意义

上述IES 流模型中，均采用了某种网络流描述能量介质的某种属性，以流的分布和数值情况刻画系统各个环节的“量”与“质”。各类流在网络中的传播机理不同，形成了各具特色的流机理模型和相应的求解方法，从而使多能耦合环节的多流计算变得丰富且复杂。

为了系统分析典型流的特性，根据其与介质流的数量关系，可将能量流、㶲流、熵增流、碳排放流划分为两大类：物理流与虚拟流。当确定了能量传输介质的数量和状态时，便可确定介质中的能量和有效能的对应关系，能量流和㶲流反映的是介质实体对应能量和有效能在系统中的分布，因此，二者属于物理流；碳排放流与熵增流依附于物理流存在，反映物理流在传播时空进程中对系统品质造成的影响，具有独特的流动性质，因此，属于虚拟流。

物理流与虚拟流比较重要的共性特征为：在能量品质不发生改变的分配环节，无论是物理流还是虚拟流，都均匀分散在介质流中。因此，各类流的分配比例与介质流是一致的。表1 展示了能量流、㶲流、熵增流、碳排放流的主要特征与共性。

表1 能量流、㶲流、熵增流、碳排放流的主要特征与共性Table 1 Main features and commonalities of energy flow, exergy flow, entropy increase flow,and carbon emission flow

相较于物理流，虚拟流会受到特殊因素的制约，例如可再生能源出力的观测时空区间、机组碳排放特性等对熵增流、碳排放流会造成影响。

物理流和虚拟流伴随着介质流，具有各自独特的转化和分配过程，多能耦合环节多样化模型能够较为精确地描述多种流的转化与分配特性，下面以较为典型模型为例进行介绍。

1.2.2 多能耦合环节的能量流模型

基于标准化矩阵的多能耦合环节能量流模型如式（1）所示。基于图论原理，可将多能耦合环节视为输入与输出端口组成的系统，通过输入与输出的能量流进行向量化处理。根据内部设备能量转化效率形成耦合关系式矩阵，在关系式矩阵中引入调度因子可表达对内部能流的分布控制作用［28］。

式中：V和V分别为输出和输入能量流列向量；Ven为内部支路能量流列向量；Xen为能量输入耦合矩阵；Yen为能量输出耦合矩阵；Zen为能量转换特征耦合矩阵，Zen中的主要构成元素为各设备能量转换效率系数和调度因子。

1.2.3 多能耦合环节的㶲流模型

多能耦合环节㶲流模型能够量化各转化环节的有效能传播和损失，可根据㶲效率系数进行运算。能质系数（energy quality coefficient，EQC）可以描述能量介质中的能量与㶲的数量关系，如式（2）所示［13］。

式中：eex为能量介质的㶲；Pex为能量介质包含的能量；λex为该能量介质的EQC。

以某能量转化设备为例，该设备将能量介质a中的能量转化为介质b中的能量，设该过程的能量转化效率系数为η，介质a与介质b对应的EQC、㶲、能量分别为λ和λ、e和、P和P，则该转化环节㶲效率系数η-b的计算方法为：

根据上述㶲效率系数转化方法，替换基于标准化矩阵的能量流模型中的对应参数，形成标准化矩阵的㶲流模型，如式（4）所示［29］。

式中：eex为内部支路㶲流列向量；Xex和Yex分别为㶲流输入和输出耦合矩阵；eexin和eexout分别为标准化的输入和输出矩阵；Zex为㶲转换特征耦合矩阵，Zex中的主要构成元素为各设备㶲效率系数和调度因子。

1.2.4 多能耦合环节的熵增流模型

多能耦合环节熵增流模型将多能耦合环节内部所有设备产生的熵增合并为一个等效熵增源，输入熵增流经输入节点注入，经等效熵增源产生增量叠加后，由输出节点流向负荷侧，输出的熵增流在输出节点处满足节点㶲流分配率［14］。

该模型在网络中体现为两个等效节点和节点间的支路，对网络中其他部分的影响表现为一个广义的“大节点”，也被称为大节点熵态模型［14］。大节点熵态模型高度抽象化内部结构，但计及了内部设备熵增叠加和熵增流分配特性，简化了建模的复杂度。大节点熵态模型示意图如图1 所示。能源站包括热电联产(combined heat and power,CHP)机组、电锅炉（electric boiler，EB）、燃气锅炉（gas boiler，GB）和变压器。

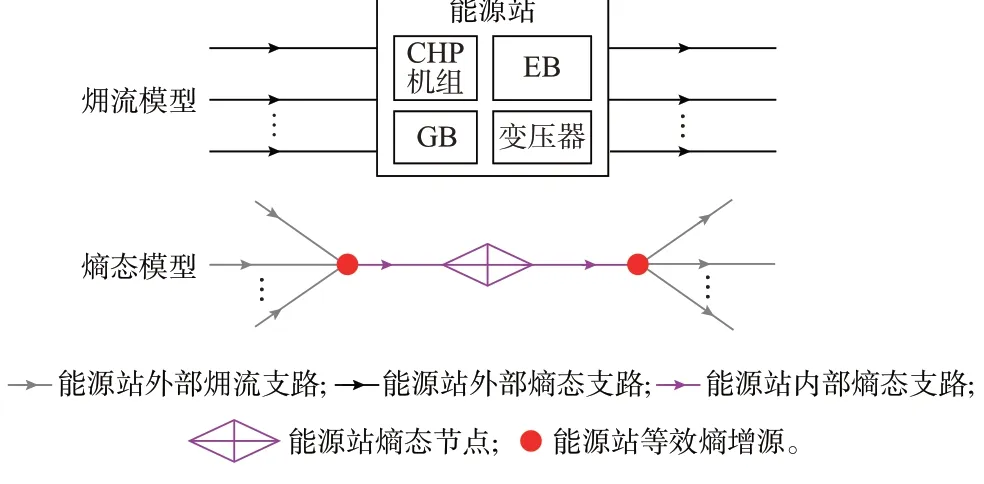
图1 大节点熵态模型示意图Fig.1 Schematic diagram of big node entropy state model

在输出节点处的熵增流遵循节点㶲流分配率，即输出支路o中的熵增流ΔSf，o与节点输出熵增流总和∑ΔSout之比等于支路㶲流eo与节点㶲流总和∑eout之比，如式（5）所示［14］。

等效熵增源ΔShub包含两部分：能量转化设备产生的传统热力学熵增ΔShub，th和可再生能源设备处理不确定性产生的信息学等效热力学熵增ΔShub，info。ΔShub计算方法如式（6）所示［14］。

式中：z为能量转化设备编号；ψ为能量转化设备z的集 合；Δez和ΔSth，z分 别 为 能 量 转 化 设 备z产 生 的 㶲损和传统热力学熵增；y为可再生能源设备编号；ξ为 可 再 生 能 源 设 备y的 集 合；py、fy和ΔSinfo，y分 别 为可再生能源设备y产生的信息势、信息流和信息学等效热力学熵增；Ta为环境温度。

1.2.5 多能耦合环节的碳排放流模型

多能耦合环节碳排放流模型将多能耦合环节视为特殊负荷，碳排放责任由能量转化设备的能量损耗对应的碳排放量衡量。同时，多输出的转化设备会对碳排放流进行分配，精细化计算内部能量损耗以及输出能量的碳排放强度，有助于科学量化能量供应者和使用者的碳排放责任［19］。能量转化设备的碳排放流转化规律遵循碳势比例分摊原则［30］，根据碳势转化系数λc与能量转化系数ηen可计算碳排放流转化系数ηc。以某能量转化设备为例，该设备将能量介质a中的能量转化为介质b和介质c中的能量，两个转化过程的能量转化效率系数分别为ηb和ηc，则介质a至b转化过程的碳排放流转化系数ηb为：

基于ηc可构建矩阵化输入、输出碳排放流关系式，即碳排放流模型，如式（8）所示［31］。

式中：Pin和Pout分别为输入、输出能量流对角矩阵；Ein和Eout分别为输入、输出碳势对角矩阵；R为碳排放流耦合矩阵，R中的主要构成元素为各设备碳排放流转化系数。

1.2.6 多能耦合环节多样化建模的弊端

多能耦合环节能量流、㶲流、熵增流、碳排放流模型具有各具特色的模型结构，但存在以下弊端：

1）内部环节的抽象化程度存在差异，导致描述内部多流分布特征的精细化程度不统一，求解精度也难以统一；

2）模型架构差别较大，数学上的变量形式、种类、数量不同；

3）多种流在具体设备处的转化和分配特性存在差异。

从上述分析可以看出，各自为营的多样化建模方法难以统一标准评估多能耦合环节对系统广义能量品质的影响情况。多种流均依托介质流进行传播，需要挖掘流的传播规律，形成通用模型以减少冗余建模过程。本文在统一精细化、抽象化的模型架构下，提出基于标准化框架的FH，针对多种广义能量品质分析要素进行建模与计算。

2 流集线器建模

多流统一建模的整体思路是将多能耦合环节物理结构与图论概念相结合，在统一拓扑结构下描述能量转换设备、内部互联结构和内部支路流的关系，以及设备与节点对多种流的分配作用。考虑到不同的流在转化环节遵循各自的规律，本文提出了广义源阻的概念，以统一表达式描述能量转化设备的多流转化与分配特性。

2.1 流集线器方程

构建输入流与输出流之间的关系式，称为流集线器方程，如式（9）所示。附录A 详述其具体构建方法。

式 中：XU为设备-支路关联矩阵；XI和XO分别为输入和输出端口-支路关联矩阵；XN为联络节点-支路关联矩阵；VB为内部支路流列向量；VU为广义源阻列向量；VI和VO分别为输入和输出流列向量；VN为联络节点注入流列向量。

通过矩阵变换可得流集线器方程的计算式（10）与式（11），推导过程详见附录B。

式中：I为单位矩阵；Qin、Pin、Rin、Qout、Pout、Rout均为计算中间量，如附录B 式（B3）—式（B5）和式（B9）—式（B11）所示。

2.2 可解性判定及合理化修正

形成式（10）与式（11）的前提条件为Qin或Qout可逆，二者蕴含着拓扑关系、能源设备流转化特征及调度信息等约束条件。附录C 探讨了多能耦合环节约束条件与方程的可解性的关系，以及借助方程可解性判定等式（12）与式（13）获悉方程可解性的方法。已知ES 输入流时，应采用式(10)求解内部支路流和输出流，并根据式(12)判定模型是否可解；对于已知输出流求解输入流的情况，即采用式(11)时，需根据式(13)判定模型是否可解。本文简称为“判定等式”，其中的参数称为“判定参数”。

式中：nN，eqn和nU，eqn分别为XN和XU的行数；nN，in为注入节点的支路数；nN，out为流出节点的支路数；nU，in为注入广义源阻的支路数；nU，out为流出广义源阻的支路数。

当判定参数不满足判定等式时，将导致流集线器方程不存在唯一解，尽管可通过最小二乘等方法获取最优近似值［32］，但是出现该现象的本质为系统存在不符合实际或违背可行性的设想条件，应当首先合理化修正条件集，使方程具有唯一解。

引入更多的约束条件或适度放宽工程设计灵活度，增加或减少子方程，从而改变XU与XN的维数，判定参数随之而变。当判定等式得以满足，流集线器方程便具有唯一解。例如，对于某联络节点，决策者考虑设置以下两种约束条件：1）精确配置该节点各输出端口分配系数；2）赋予该节点一定的灵活度，无须按指定比例分配输出流。这两种约束条件对应的方程数是不同的，即XN的行数不同，导致两种条件集的判定参数nN，eqn不同，可在校验模型的过程中酌情加以调整，使方程存在唯一解。

3 算例分析

3.1 算例介绍

本文以3 种多能耦合环节作为研究对象，求解能量流、㶲流、熵增流、碳排放流的分布和流动情况，用以验证FH 的正确性和有效性，探讨当约束条件过多和过少时，合理化修正条件集的方法。

算例1 的多能耦合环节结构如图2 所示。其中，能量转化设备包括变压器、CHP 机组、GB 和EB。输入天然气按一定比例分配至CHP 机组和GB，转化为电能和热能，GB 的热能转化效率为η=0.85。该CHP 机组可以在可变热电比工况下运行，热电比范围为1.4～14.0。此时，整体能量效率为η=0.7［33］。假设输入电能经由变压器流向输出侧，其中一部分电能被分配至EB 转化为热能，与CHP 机组和GB 共同支持负荷的热需求，变压器的电能转化效率为η=0.98，EB 的热能转化效率为η=0.95［34］。电能的EQC 为1.000 0，天然气化学能的EQC 为0.701 3，热能EQC 为0.185 3［13］。可以看出，由于需要分析能量流、㶲流、熵增流、碳排放流的不同场景，算例相关参数设置相比于传统能量流分析更为复杂。

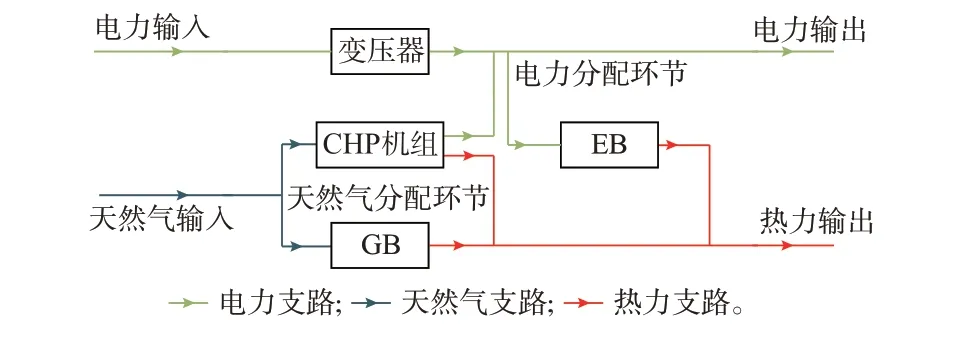
图2 算例1 的多能耦合环节结构示意图Fig.2 Schematic diagram of structure of multi-energy coupled link in case 1

算例2 的多能耦合环节结构如图3 所示，在算例1 的基础上增设了一条支路承载输入热源，在CHP 机组和GB 的出口处汇合。算例3 的结构如图4 所示。在算例1 的基础上，不考虑电能输入并去除了变压器，仅考虑天然气输入。

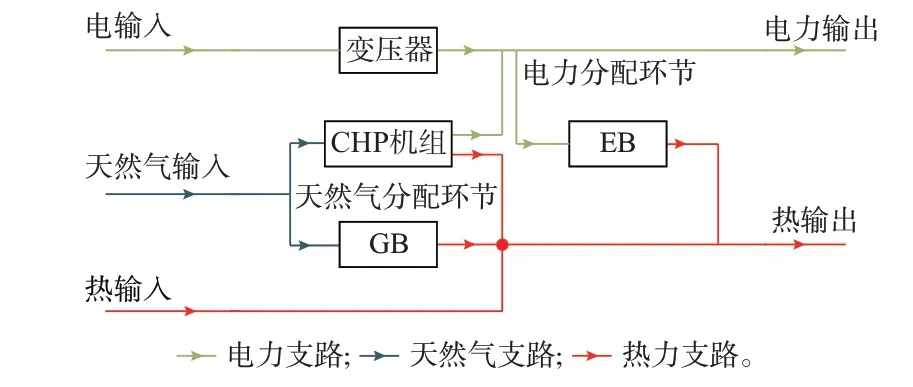
图3 算例2 的多能耦合环节结构示意图Fig.3 Schematic diagram of structure of multi-energy coupled link in case 2

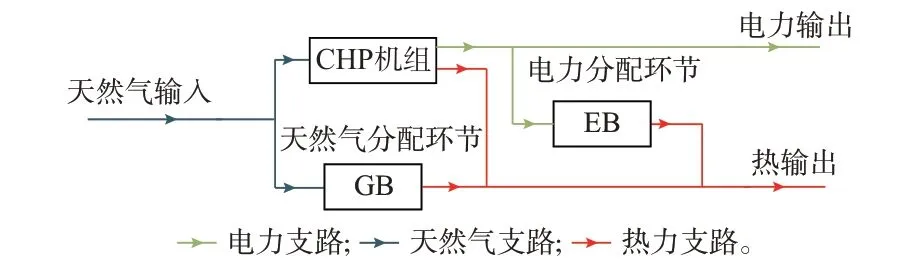
图4 算例3 的多能耦合环节结构示意图Fig.4 Schematic diagram of structure of multi-energy coupled link in case 3

为了进行有效对比，3 个算例中的电力、热力负荷能量需求均分别设置为2 554 kW 和4 782 kW，电、气、热输入熵增流为3.000 0 kW/K，电输入碳势为500 tCO2/h，气输入碳势为400 tCO2/h，热输入碳势为300 tCO2/h。

3.2 算例分析：可解性判定

为了分析约束条件对可解性的影响，假定3 个算例的预设常规运行模式，称为“条件集1”。

1）预设CHP 机组的热电比为1.333，此时，电、热转化效率分别为η=0.3、η=0.4。

2）预设EB 电力分配系数为0.1；

3）预设CHP 机组与GB 天然气分配系数均为0.5。

在构建FH 的方程之前，可根据条件集和多能耦合环节内部结构，统计判定参数，判断是否存在不合理条件。在条件集1 下，本文设置的3 个算例中，算例1 的流集线器方程存在唯一解；算例2 存在亚定关系，还需补充约束条件；算例3 存在超定关系，需酌情放宽条件。具体判定过程如下。

图5 至图7 为3 个算例对应的FH 拓扑结构的示意图，结合条件集1 的内容，可以在构建模型方程前直接统计各方程的判定参数。

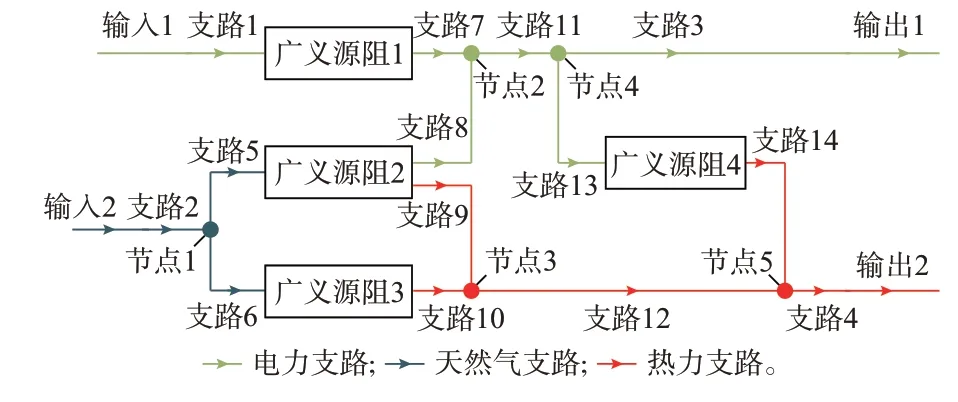
图5 算例1 的FH 模型结构示意图Fig.5 Schematic diagram of structure of FH model in case 1

图6 算例2 的FH 模型结构示意图Fig.6 Schematic diagram of structure of FH model in case 2

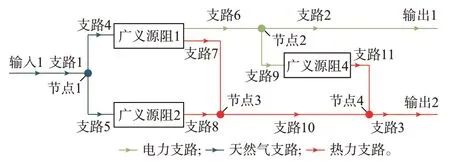
图7 算例3 的FH 模型结构示意图Fig.7 Schematic diagram of structure of FH model in case 3

以算例1 为例，统计判定参数，如表2 和表3 所示。节点与广义源阻的输入与输出支路如图5 所示，统 计 得 到nN，in=8、nN，out=7、nU，in=4、nU，out=5。对于条件集1 相关的判定参数，经分析可知nU，eqn=5、nN，eqn=7。

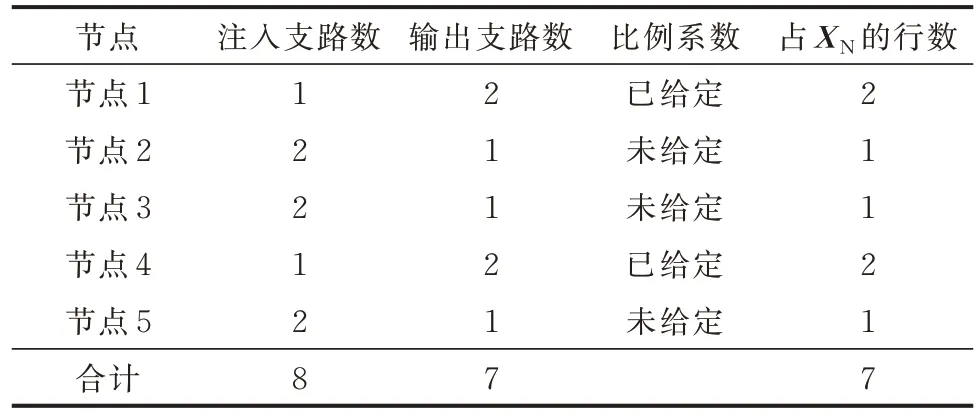
表3 算例1 的节点判定参数统计结果Table 3 Statistical results of judgment parameters of nodes in case 1

nU，eqn的统计范围包括：

1）GB、EB、变压器为单输入、单输出广义源阻元件，在XU中各占据1 行，共3 行；

2）按照条件集1 要求，CHP 在定热电比的工况下运行，电输出与热输出分别对应0.3 和0.4 的能量效率，因此在XU中占2 行。

nN，eqn的统计范围包括：

1）节点2、3、5 未被指定分配系数，XN仅描述广义基尔霍夫电流定律，各占1 行，共3 行；

2）按照条件集1 要求，节点1 的两个输出端口均按比例系数为0.5 进行分配，因此在XN中占2 行；

3）节点4 的2 个输出端口分别按0.9 和0.1 的比例系数进行分配，在XN中占2 行。

由于求解熵增流和碳排放流需优先求解能量流和㶲流，且本文算例均设置为输出能流已知，应当采用式（11）根据输出能流计算输入能流。此时，必须先行判断Qout是否可逆，等价于判断判定参数是否满足式（13）。采用判定等式对3 个算例的合理性进行判断，采用与算例1 相同方法，对算例2、算例3 能流方程对应的判定参数进行统计，如表4 所示。

表4 条件集1 下算例的能流和㶲流判定参数Table 4 Judgement parameters for energy flow and exergy flow in cases under condition set 1

可知在条件集1 下，有如下结论：

1）算例1 的判定参数满足式（13），判定为正定关系，因此存在唯一解；

2）算例2 判定参数nN，in+nU，in大于nU，eqn+nN，eqn，判定为亚定关系，存在无穷多的解，可知条件集1 欠缺某约束条件；

3）算 例3 的 判 定 参 数nN，in+nU，in小 于nU，eqn+nN，eqn，判定为超定关系，可知条件集1 须减少某约束条件。

3.3 算例分析：合理化修正

算例2 合理化修正：需要对节点或设备的参数进行补充描述或引入约束，假设经支路15 注入的外部采购热源不易管控，选取该支路作为补充固定流率约束条件的对象。

为算例2 制定条件集2。在条件集1 的基础上，将支路15 的能流设为1 000 kW（㶲流为185.3 kW）。新的能流方程组将增加1 个子方程，XU维数由11 升至12，此时方程判定等式参数（nU，eqn+nN，eqn=13）满足判定等式（12），方程存在唯一解。

算例3 合理化修正须减少约束，该算例可选择的有：1）舍弃节点1 的输出端口分配系数；2）舍弃节点2 的输出端口分配系数；3）将CHP 调整为可变电热比工况。舍弃上述约束之一均可使XU或XN维数下降（本文选择舍弃约束条件1）。

为算例3 制定条件集3。在条件集1 的基础上，不再指定节点1 天然气输出端口的分配系数。此时，算例3 流集线器方程的合理性判定参数nU，eqn+nN，eqn由10 降为9，满足式（12）存在唯一解的条件。

3.4 算例分析：修正后求解与分析

首先，根据条件集1 和已知参数，可构建算例1的FH 能量流、㶲流方程组中的XU、XI、XO、XN，VU、VN为零向量。

本文算例已知输出电、热能量需求，可直接构成能量流方程的VO，同时，可根据式（2）计算输出电、热㶲，构成㶲流方程的VO。视VI为待求量，便可构建能流方程和㶲流方程。根据式（11）可计算输出能流、㶲流列向量VI，根据附录B 式（B7）可计算内部支路能流、㶲流列向量VB，从而获得全部能流、㶲流分布。

其次，FH 的熵增流、碳排放流方程的已知量包含了能量流、㶲流方程的部分结果。根据㶲流模型可计算各广义源阻传统热力学熵增ΔSth，进而构成熵增流方程的VU，若存在可再生能源设备的信息学等效热力学熵增源，将其视为单端口的广义源阻。根据给定的输入端口碳势，可由输入能量流计算各输入端口碳流列向量VI。视VO为待求量，便可构建FH 的熵增流方程和碳排放流方程。

条件集1 下的算例1、条件集2 下的算例2、条件集3 下的算例3 的FH 计算结果如表5 至表7 所示。在输出能量需求完全一致的前提下，内部结构将对输出能量的品质产生影响，内部4 种流的分布规律不同，各设备产生的能损、㶲损、熵增、碳损表现出不同分布特点，输入能量形式也会影响输出能量的品质。

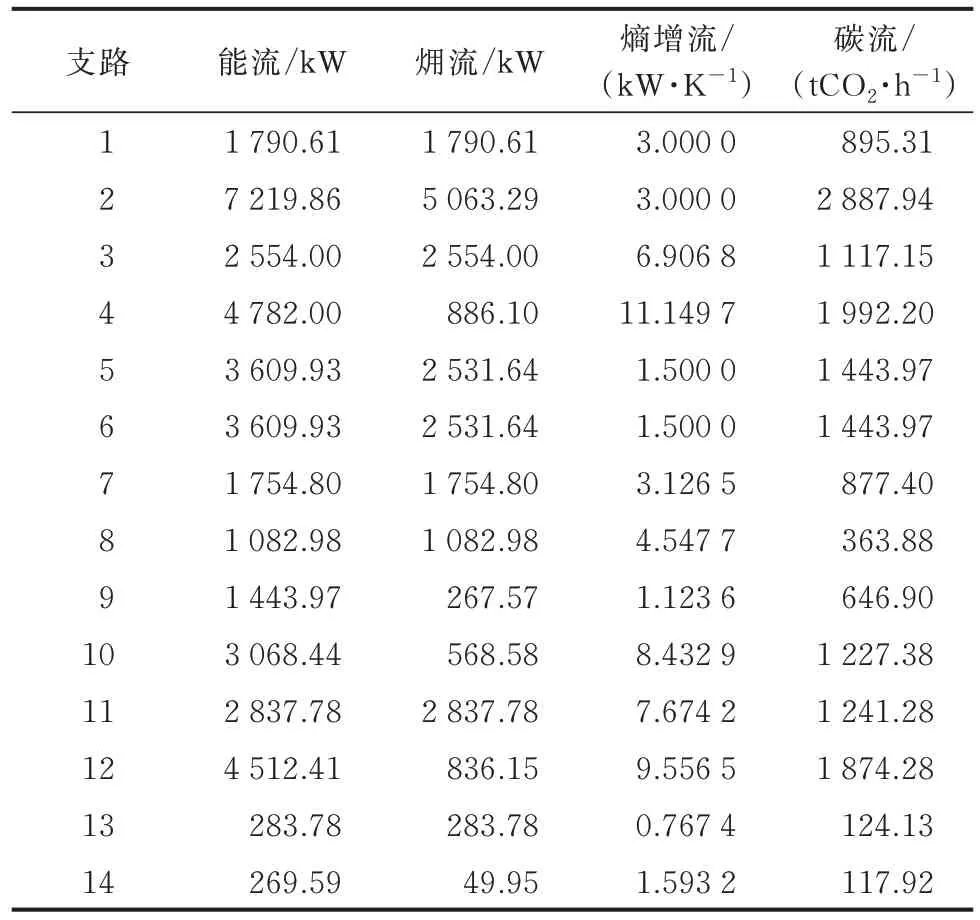
表5 条件集1 下算例1 的FH 计算结果Table 5 Calculation results of FH in case 1 under condition set 1

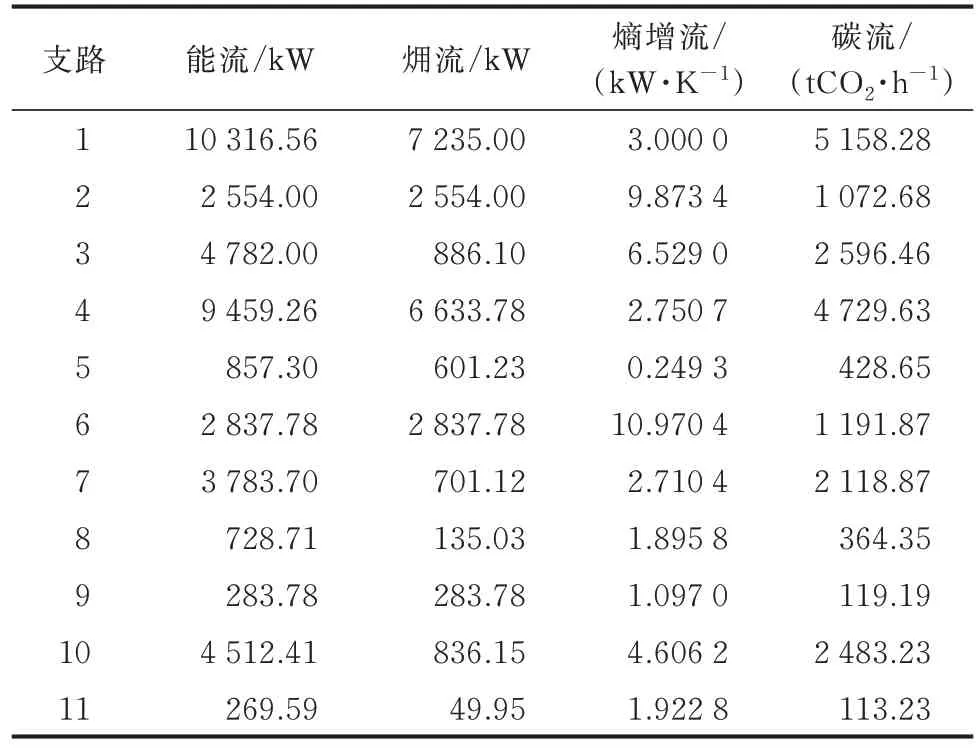
表7 条件集3 下算例3 的FH 计算结果Table 7 Calculation results of FH in case 3 under condition set 3

FH 可计算多种流的分布情况，由于不同流的内涵各异、传播规律也不尽相同，因此，它们的分布呈现出多样化特征。即使运行状态并未发生任何变化，只要在不同评价视角下观测多能耦合环节对多种广义能量品质分布情况，得到的结果具有多样性，了解其分布规律具有一定的研究价值。例如：在有效能视角下，电能具有优于天然气的做功能力。因此，表5 中CHP 机组的电输出（支路8）的㶲流大于热输出（支路9）的㶲流。CHP 机组由气转电的过程具有大量的有效能损失，CHP 机组的气转热属于能量的梯级利用，有效能损失较少，因此，CHP 机组电输出的熵增流较少。

在输出侧能量需求不变的情况下，3 个算例向负荷侧输送的能量也具有不同的广义能量品质。如表8 所示，输出能量流、㶲流不变的情况下，算例3 的热输出熵增流与电输出熵增流，不同于另外两个算例，主要原因是算例3 对CHP 机组的利用最大，而CHP 机组产生的电能相比高比例可再生能源出力的电网具有更高的熵增流，而CHP 机组产生的热能具有较低的熵增流，相比外部输入热能或EB 生产的热能，CHP 机组产生的热无序性层面上的广义能量品质更高。

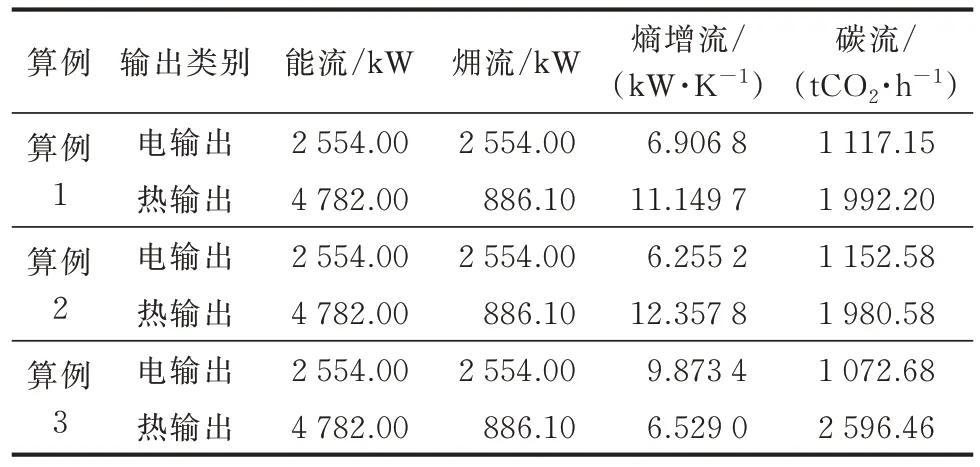
表8 合理化修正后算例的输出流结果Table 8 Results of output flow of case after rationalization correction

多能耦合环节内部结构的差异使多流分布具有多样性，辨识高损与高增环节对提升供能品质具有一定意义，表9 展示了算例中各设备的多流损耗与增量，可见在算例中给定负荷侧能量需求的基础上，算例1、2 中，CHP 机组均为最高能损、熵增、碳损设备，承担了大部分负荷用能，GB 为最高㶲损和熵增设备，考虑到它也承担了较大一部分的负荷用能，可视其为有效能层面品质较差的能量转换设备；算例3 舍弃了电网提供的高品质电能，也未采用外部输入热能，因此该结构表现为三者中最高的能损、㶲损、熵增、碳损。

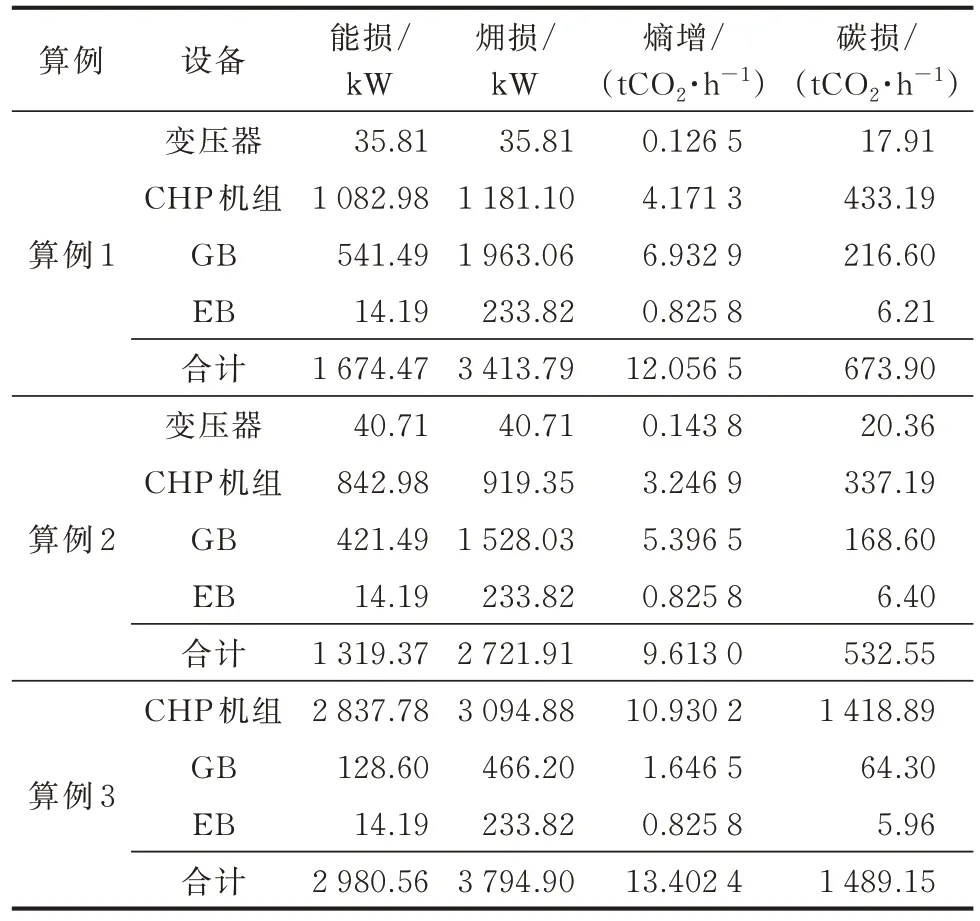
表9 合理化修正后设备的输出流计算结果Table 9 Calculation results of output flow of equipment after rationalization correction

若需要进一步探究如何精细化调整多能耦合环节的广义能量品质分布，可以选择任意具有比例系数的节点、广义源阻作为优化对象，视其系数为优化变量，采用输出流、输入流或内部多流损耗构建目标函数，进行管线规划、设备选型和运行优化。例如：本文算例中的CHP 机组可以视为运行可变热电比的工况，输入端对应的分配节点可以作为需求侧响应的动作元件，根据上述方法可以对二者的系数进行最优化求解。也可以针对内部管线拓扑进行优化，过程中可根据判定参数，判断可调节点、可控设备等约束条件是否存在不合理的配置情况。

本文限于篇幅，着重分析与介绍FH 与IES 广义能量品质，日后将开展针对IES 供能品质提升的规划与运行优化的研究。

4 结语

本文梳理了多能耦合环节的能量流、㶲流、熵增流、碳排放流多样性建模方法，分析各类方法的特点以及弊端，提出基于标准化矩阵架构的FH，以广义源阻元件以统一结构描述能量转化设备的多流转化特性，并总结了多能耦合环节约束条件合理性的判定与修正方法。该模型能够在一致的精细化和抽象化程度上，准确刻画多能耦合环节内部、输入、输出的广义能量品质情况，标准化求解多种流的分布。过程不涉及多次迭代，部分非变量在不同流的计算中是通用的，并且线性方程组等特征有利于模型的规模化应用。该模型可辅助IES 整体以及多能耦合环节的管线布局、选址定容、设备选型和运行优化等决策分析，以满足“双碳”背景下对高品质IES 的新发展要求。

本文限于篇幅，仅对某一时间断面的多能耦合环节稳态流分布建模和分析，后续将以IES 能量品质提升为目标，围绕流集线器多目标规划与多时间尺度运行优化开展研究。同时，本文假设能量转换设备具有线性多流转化与分配特性，后续将针对设备的动态响应特性和非线性参数，研究非线性广义源阻机理模型，以及相应流集线器模型的高效求解方法。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。