无相位量测的多环中压配电网线路参数辨识方法

2024-01-18李博通孙铭阳陈晓龙冀肖彤

电力系统自动化 2023年24期

李博通，孙铭阳，陈晓龙，李斌，冀肖彤，肖繁

（1.智能电网教育部重点实验室（天津大学），天津市 300072；2.国网湖北省电力有限公司，湖北省武汉市 430000；3.国网湖北省电力有限公司电力科学研究院，湖北省武汉市 430000）

0 引言

分布式电源和储能大规模接入配电网带来的随机性和波动性对配电网的运行和控制提出了新的挑战［1-3］。为在提升新能源发电消纳能力的同时保证高质量的安全可靠供电，需要对配电网开展更加精细化的监测、调控和保护。无论是调控精准度还是保护性能的提升，都需要以准确的线路参数为基础才能完成［4］。

线路参数可以由线路长度、电阻率及线路几何位置通过物理或经验公式求取［5］。但是，由于线路长期运行老化及环境（温度、湿度）等情况，线路实际参数与理论计算参数存在一定偏差［6］。为了获取更为准确的中压配电网线路参数，可以依靠现场量测装置获取的量测数据进行实时线路参数辨识。中压配电网的量测装置主要为数据采集与监控（supervisory control and data acquisition，SCADA）系统［7］和同步相量测量单元（phasor measurement unit，PMU）［8］两种。其中，SCADA 装置能采集到电气量的幅值，但无法获取电气量相位数据。目前，中压配电网中已广泛安装SCADA 装置。PMU 装置利用全球定位系统（global positioning system，GPS）同步技术可以实现电气量的全网同步相量采集，具有更高的量测精度。但是，由于PMU 装置价格远高于SCADA 装置，目前配电网还未大规模配置。因此，研究无相位电气量数据的中压配电线路参数辨识方法具有实际工程意义。

国内外学者对于无相位电气量数据下的配电网线路参数辨识的方法已经进行了一定的研究。文献［9-11］根据采集到的电压幅值和功率信息，从辐射状配电网末节点开始逐步推导上游节点的电压，再搭建优化模型进行求解。其中，文献［9］采用二次规划算法完成线路参数求解，该方法对小规模的电网结构有较高的精度；文献［10］采用遗传算法求解，该算法不需要将优化问题转化成特定形式即可求解；文献［11］采用差分进化算法求解，该算法通过较少的量测数据就能完成线路参数辨识。文献［12］首先利用线路阻抗初值，从负荷侧推导各线路的功率分布，从电源侧正推得到以电源电压为参考的各电气量，进而列写节点电压方程并用最小二乘法求解。再将求解结果作为初值重新计算，通过不断迭代来逼近阻抗实际值。文献［13］提出了一种改进的牛顿迭代法实现线路参数辨识，该方法改进了泰勒一阶展开，提高了算法收敛性。文献［14］提出了一种基于多创新最小二乘的线路参数辨识方法，该算法引入多个创新变量来处理非线性部分，进而可以使用线性化的方法求解。文献［9-14］均利用量测的冗余数据列写方程，采用最小二乘、差分进化或其他优化算法实现线路参数辨识。文献［15-16］提出基于拉格朗日乘子法的配电网不良线路参数辨识方法，利用正则化拉格朗日乘子判断线路中的可疑参数，进而对可疑参数进行修正。前者采用局部区域网络进行参数估计来提升算法的鲁棒性，后者采用变步长逐次修正的方案以提升算法效率。文献［9-16］针对辐射状配电网进行线路参数辨识，其中，文献［11-15］均实现了包含电纳在内的线路参数辨识，而其余3 篇文献没有考虑电纳。

随着现代社会对高可靠性电力需求的不断增加，环状配电网受到业内的广泛关注［17-18］。环状配电网具有高可靠性、高稳定性、节能环保等多种优点［19-20］。目前，已在雄安、北京等地建成了“双花瓣”配电网［21-22］；在天津、上海已经投运了蜂巢和钻石配电网［23］。相比于辐射状配电网，环状配电网功率流向更为复杂，尤其是多环结构下难以直接列写方程求解线路参数。这导致已有的辐射状网络的线路参数辨识方法无法应用，针对环状配电网的线路参数辨识方法研究尚未见文献涉及。

本文提出一种基于无相位电气量数据的多环中压配电网线路参数辨识方法。首先，将环状配电网从外围逐步解环，推导展开节点两侧线路的功率，进而逐步从外向内推导各节点电压；然后，利用推导所得电压与量测电压数据列写电压残差方程，使用遗传算法求解电压残差最小时对应的线路参数；最后，在MatPower 中搭建三环蜂巢状配电网，利用其生成的量测数据对本文提出的方法进行测试，证明该方法的准确性和鲁棒性。

1 单环中压配电网线路参数辨识方法

中压配电线路一般为10 kV 或35 kV，长度一般在20 km 以内，而且环状配电网多建设在城市，一般使用电缆输电。因此，线路参数中的电纳较大，故采用考虑电纳的集中参数的π 型等效模型如图1 所示。图中：Ui为节点i的电压幅值；Uj为节点j的电压幅值；Pi+jQi为由左侧流入节点i的功率；Pj+jQj为节点j流入右侧的功率；Rij为节点i与节点j之间的线路电阻；Xij为节点i与节点j之间的线路电抗；Bij为节点i与节点j之间的线路电纳。

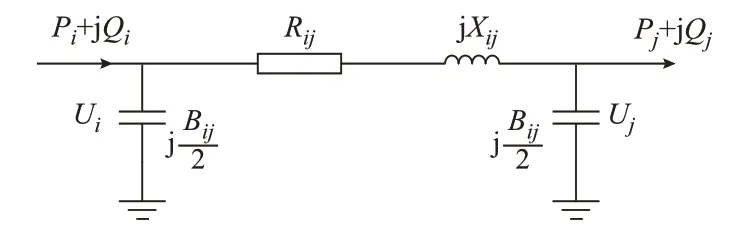
图1 π 型线路等效模型Fig.1 π-type line equivalent model

利用潮流计算的基本公式［24］，可以由图1 右侧节点电压和功率推导左侧节点电压和功率，有

式中：ΔUij为电压降落的纵分量；ΔU为电压降落的横分量。

ΔUij和ΔU'ij的表达式为：

将式（2）代入式（1），消去ΔUij和ΔU'ij，得到由右侧电压幅值Uj、功率Pj+jQj以及线路参数推导而来的左侧电压幅值Ui为：

左侧的功率为：

式（3）、式（4）表明可以利用图1 右侧节点电压幅值、功率和线路参数推导得到左侧的电压幅值和功率。

针对图2（a）中的单环配电网结构，可以通过解环操作展开成如图2（b）所示结构。图中：1 到m+n+1 均为节点编号。

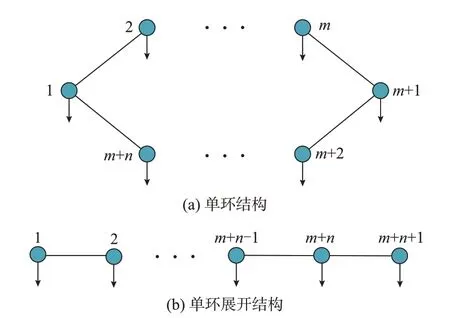
图2 m+n 节点单环结构及其展开结构Fig.2 m+n-node single-ring structure and its opening structure

将图2（a）中的单环状拓扑结构从节点1 处打开成图2（b）。图2（b）中，右侧的节点1 更名为节点m+n+1，节点1 的输出功率被分成两部分，有

式中：P1+jQ1为图2（a）中节点1 的输出功率；+jQ'1为图2（b）中节点1 的输出功率；Pm+n+1+jQm+n+1为图2（b）中节点m+n+1 的输出功率。

假设图2（a）所有负荷输出节点以及电源侧均装设SCADA 量测装置，利用量测得到的电压幅值和输出功率数值代入式（3），可以由图2（b）节点1 推导出节点2 的电压幅值U2为：

式中：R1，2为图2（b）中节点1 和节点2 之间的线路电阻；X1，2为图2（b）中节点1 和节点2 之间的线路电抗；B1，2为图2（b）中节点1 和节点2 之间的线路电纳。

同理，可以由右侧节点m+n+1 推导出节点m+n的电压幅值Um+n为：

式中：R1，m+n为图2（b）中节点m+n+1 和节点m+n之间的线路电阻；X1，m+n为图2（b）中节点m+n+1和节点m+n之间的线路电抗；B1，m+n为图2（b）中节点m+n+1 和节点m+n之间的线路电纳。

式（5）是复数方程，可以拆解为两个实数方程，故式（5）、式（6）和式（7）构成的方程组相当于4 个实数方程，理论上可以解出节点1 和节点m+n+1 输出功率P'1、Q'1、Pm+n+1、Qm+n+1与线路参数之间的关系。但是，包含式（6）和式（7）在内的方程组是复杂的非线性关系，求解困难。考虑一般情况下配电网相邻两节点电压相角差较小，忽略电压横分量，式（1）可以简化为：

利用式（8）求出式（6）、式（7）后，再联立方程式（5）、式（6）、式（7），此时方程组是关于输出功率的线性方程组，可以解得节点1 和节点m+n+1 输出功率与线路参数之间的关系（在式（6）和式（7）中，U2和Um+n代表已知的量测值。因此，在式（9）中未出现U2和Um+n）：

将式（9）代入式（6）可以消去P'1、Q'1，得到节点2的电压幅值为：

式（10）为节点2 的电压幅值与线路参数的关系。得到U2之后，可以利用每个节点的电压量测值和输出功率，通过式（3）和式（4）逐步从图2（b）单环展开结构的左侧节点1 推导至右侧节点m+n+1，得出每个节点的电压计算值（使用上一个节点的电压数据为量测电压，而非上一个节点推导出的电压，这有助于提升后续计算的精度），有

式中：Ui，cal为图2（b）中节点i的电压计算值；R∈Rm+n为图2（b）中m+n条线路的电阻组成的向量；X∈Rm+n为图2（b）中m+n条线路的电抗组成的向量；B∈Rm+n为图2（b）中m+n条线路的电纳组成的向量。

将所有的量测电压以及功率都代入式（11）后，有m+n个方程，但是由于未知数有3（m+n）个，因此，需要使用3 个及以上不同时刻下的量测数据才能完成线路参数辨识。考虑到有可能会出现某两个时刻下负荷情况几乎相同，列出的两个方程会近似线性相关，导致结果误差较大，应该使用更多时刻下的量测数据来进行综合求解。此外，采用更多时刻下的量测数据求解可以有效避免线性相关方程对结果的影响，而且可以有效降低量测误差对线路参数辨识的影响，提高算法的鲁棒性。

SCADA 装置采样间隔为2～10 s/次［25］，考虑在一个合理的时间T内，即能满足线路参数计算所需数据的最少采集时间。该时间越短，外界环境变化越小，计算出的线路参数更具实时性。式（11）对时间T内所有采集时刻进行推导。

式中：Ui，t，cal(i=2，3，…，m+n+1；t=1，2，…，T)为t时刻由节点i-1 推导出的节点i电压幅值；Ucal为电压计算值矩阵。

矩阵式（12）中所有的元素都是线路参数的函数。与式（12）相似，通过量测装置可以得到每个节点的电压量测值如下：

式中：Ui，t，mea(i=2，3，…，m+n+1；t=1，2，…，T)为t时刻节点i的电压量测值；Umea为由Ui，t，mea构成的电压量测值矩阵。

式中：J（R，X，B）为不同电路参数下的电压残差。

式（14）表示Ucal与Umea的欧氏距离，用2 范数来表示。当两矩阵之间的距离最近的时候，认为对应的线路参数即为待辨识的线路参数，即

2 多环中压配电网线路参数辨识方法

针对多环配电网结构，首先将最外围的环从连接两条干线的任意节点解环，利用上文方法求解节点两侧功率，从外围逐步向中间推导电压幅值以及功率；遇到环再次解环重复上述步骤；最后得到从外围逐步向内推导的电压幅值，列写类似式（14）的电压残差方程。

从原理上讲，只需要将环展开成辐射状就可以进行线路参数辨识。但是，针对大型复杂配电网，需要考虑计算效率以及计算精度。本文推导思路是从末节点逐条支路推导至中心节点，所经过的线路段数越多，优化方程越复杂，其辨识精度越低或计算时间越长（保证相同精度，需要增加迭代次数）。因此，为了使计算效率和辨识精度尽可能高，要求解环后最远的末节点距离中心节点之间的线路段数尽可能少。

基于拓扑学理论，可以使用深度优先搜索［26］或广度优先搜索［27］等遍历算法，以解环后距离中心节点最远的末节点与中心节点之间的线路段数最少为目标，寻找电网拓扑中的最优树。将该最优树作为解环后的主体结构，但由于树是拆分边得到的，不会增加节点数，而本文中需要拆分节点，每次拆分需要增加一个节点。因此，可以选择拆分距离根节点更远的末节点，以确保距离中心节点最远的末节点与中心节点之间的段数尽可能少。在这样解环后的拓扑中，根节点即为中心节点。

下面以三环状蜂巢配电网为例具体说明。

针对图3（a）所示的拓扑结构，分别从节点1、9、11 展开成图3（b）所示的开环状并增加新的节点14、15、16，此时所有末节点距离中心节点之间的线路段数是相等的，满足解环后最远的末节点距离中心节点之间的线路段数尽可能少，此时的计算效率和计算精度理论上是最高的。然而，实际中，图3（a）所示的节点较少的环状网路，因为该拓扑结构过于简单，在任意点解环构成辐射状，对于计算效率和计算精度基本无影响。

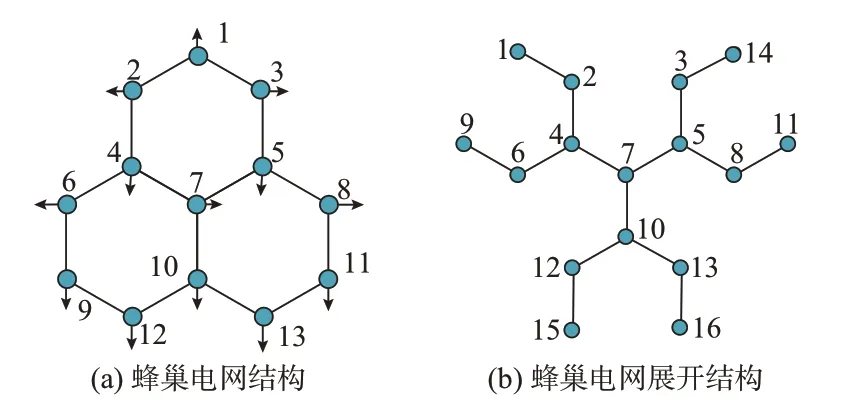
图3 三环状蜂巢配电网拓扑结构及其展开图Fig.3 Topology of three-ring honeycomb distribution network and its open-ring diagram

按照图3（b）的形式展开，从节点1、14 向节点2、3 推导电压，参考式（10）可以得出：

式中：U2、U3分别为图3（b）中节点2、节点3 的电压幅值；R1，2为图3（b）中节点1 和节点2 之间的电阻；X1，2为图3（b）中节点1 和节点2 之间的电抗；B1，2为图3（b）中节点1 和节点2 之间的电纳；R1，3为图3（b）中节点14 和节点3 之间的电阻；X1，3为图3（b）中节点14 和节点3 之间的电抗；B1，3为图3（b）中节点14和节点3 之间的电纳。

同理，可以推导出节点6、8、12、13 的电压。

再利用式（3）、式（4）进一步推导节点4、5、10、7的电压，其中由多节点推导出同一节点的电压幅值取均值即可，有

式中：Ni为可以直接推出节点i电压的节点数目（例如图3（b），有且仅有节点2 和节点6 都可以推导出节点4 的电压，即N4=2）；Ui，b为由不同节点b推出的节点i电压（例如图3（b），节点2 和节点6 都可以推导出节点4 的电压）。

由于从节点1、9、11、14、15、16 开始推导其节点电压，故认为这些节点的电压已知。为了方便编程计算，将这些节点的量测值直接代入电压计算值矩阵。同样，可以列写出类似式（12）的整个时间序列的电压计算值矩阵，即

电压量测值矩阵为：

利用式（15）可以计算得出待辨识线路参数。

3 参数辨识的最优化算法

本文的优化目标函数式（15）是非凸函数，有多个局部最优解。以图3 所示拓扑结构为例，目标函数将会有45 个未知数（15 条线路），就是45 维函数优化问题，该函数是高维函数。针对高维非凸函数优化问题，传统最小二乘法难以找到全局最优解，而遗传算法能够较好地处理高维非凸函数优化问题［28-29］，因为其不需要求解梯度，也不需要假设函数具有特定的形式［30］。因此，本文采用遗传算法进行线路参数辨识。

针对本问题，首先设定线路参数的变化范围以及种群大小M。然后，在规定的范围内随机产生由M组线路参数构成的种群{S1，S2，…，SM}，其中

式中：Sl为第l组线路参数解，也是种群中的一个个体，j=1，2，…，M；Rl为第l组线路电阻解；Xl为第l组线路电抗解；Bl为第l组线路电纳解。

针对种群中每一组线路参数，通过式（14）计算其电压残差，根据残差的大小评价种群中每组线路参数辨识结果的优劣程度。根据交叉概率，将式（20）中残差较低的线路参数矩阵中的部分对应元素进行互换，再根据变异概率将其部分元素在小范围内进行随机改变，产生新一代线路参数。将新一代线路参数加入原来种群中，并淘汰残差较高的线路参数，以保持种群大小M不变。得到新种群后重复之前的步骤，当迭代次数达到最大次数时，输出该种群中电压残差最小的线路参数，其流程图如图4所示。

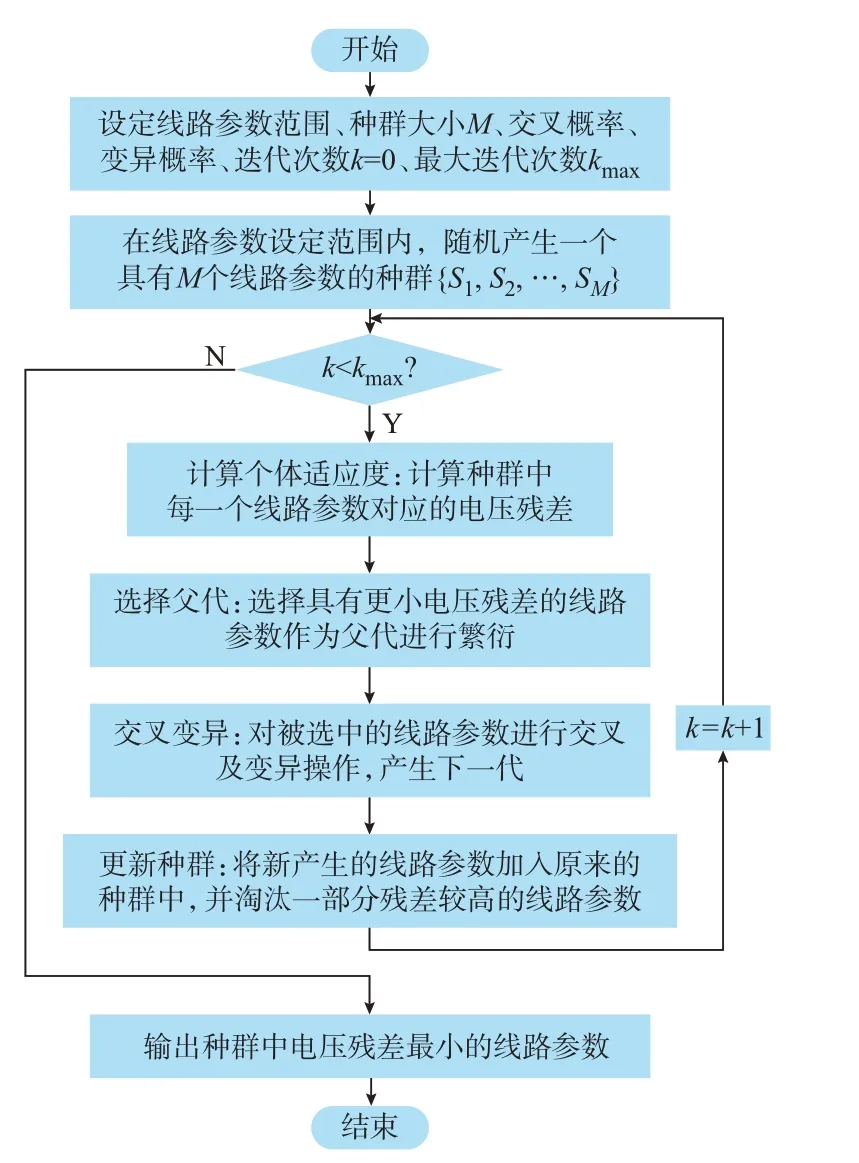
图4 实现线路参数辨识的遗传算法流程图Fig.4 Flow chart of genetic algorithm to realize line parameter identification

4 算例分析及对比

针对三环蜂巢配电网，在MATLAB 中使用本文提出的参数辨识方法进行仿真验证。利用MATLAB 中的MatPower 工具箱搭建如图3（a）所示的三环蜂巢配电网络结构。其中，节点1 接入系统，节点5、10、13 接入分布式电源，所有节点均接有负荷。设定所有负荷和分布式电源功率在额定功率的80%～120%随机波动，利用负荷和分布式电源的功率波动，重复100 次潮流计算来模拟实际电网运行状况。利用每个节点的电压幅值以及输出功率作为量测值来计算各线路参数。

本文参考遗传算法经验设定范围［31］：种群大小在20～200 之间，交叉概率在0.6～1.0 之间，变异概率在0.005～0.010 之间。本文以经验范围为起点，采用控制变量的方法寻找使遗传算法精度更高的参数。最终选定遗传算法的最大迭代次数为2 000，种群大小为100，交叉概率为0.5，变异概率为0.02。线路参数上下限设定为真实值的±20%，进行线路参数辨识。在i7-7700 CPU 和12 GB RAM 的台式计算机中整体辨识过程耗时46.21 s，辨识结果如表1所示。

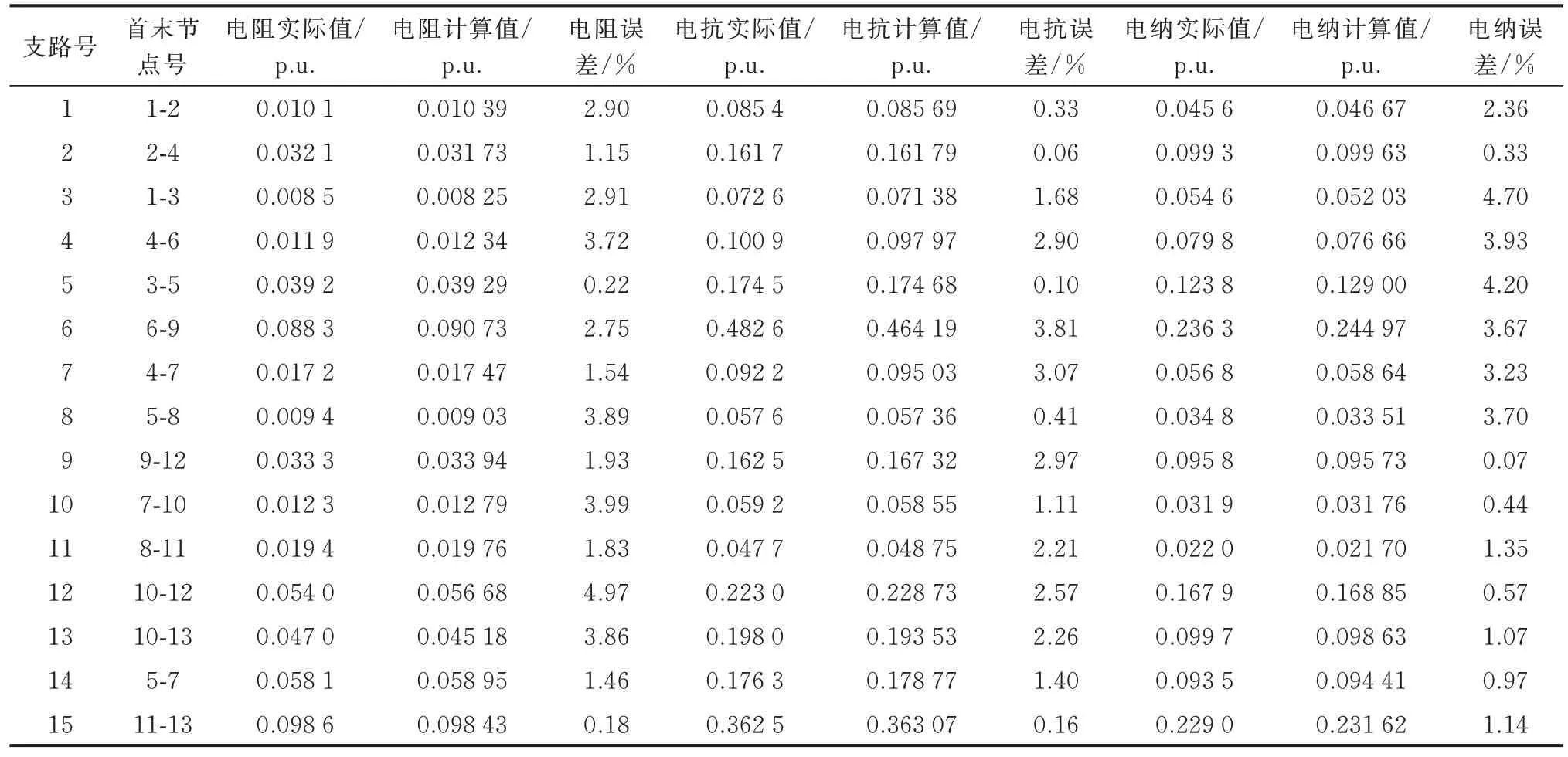
表1 量测数据准确时的线路参数辨识结果Table 1 Line parameter identification results when measuring data are accurate

根据表1 中结果可见，整体线路参数辨识结果具有较高精度，其中，电阻平均误差为2.49%，最大误差为4.97%；电抗平均误差为1.67%，最大误差为3.81%；电纳平均误差为2.12%，最大误差为4.70%。

电力系统正常运行时，节点电压波动较小，但节点的输出功率可能会短暂波动，从而导致功率量测误差的产生。为了模拟真实的量测误差，在原始量测功率基础上分别加入±0.2%、±0.4%、±0.6%、±0.8%、±1%的高斯白噪声。随后，使用遗传算法和最小二乘法重新计算线路参数，并绘制了平均误差和最大误差的折线图，如图5 所示。图5 展示了不同功率量测误差下的线路参数辨识结果（功率和电压均有量测误差时的线路参数辨识结果以及量测功率误差进一步增大时遗传算法的误差分别如附录A图A1、图A2 所示）。

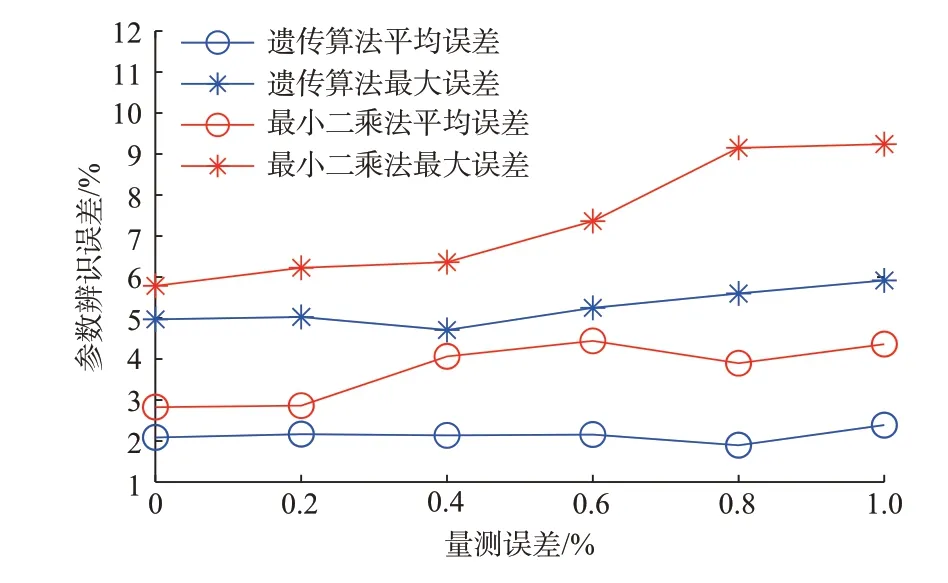
图5 功率量测有误差时的参数辨识误差Fig.5 Parameter identification error when there are errors in power measurement

由图5 可以看出，针对本文的优化模型，遗传算法在精度和鲁棒性方面都优于最小二乘法。这是因为遗传算法在处理高维非凸函数优化问题时具有全局搜索能力和适应复杂高维函数问题的优势［31］，能够更好地探索解空间并搜索到全局最优解。相比之下，最小二乘法可能受限于局部搜索和梯度求解的困难，难以搜索到全局最优解和满足高精度的要求。

图5 中，功率量测误差在1%时，使用遗传算法的平均误差为2.39%，最大误差为5.92%，这样的误差在配电网线路参数辨识中是可以接受的，原因如下：在配电网正常运行时，用户的阻抗远大于线路参数的阻抗，线路参数有一定的误差对电网调控影响不大；而在故障时，保护通常留有一定的裕度，所以线路参数有一定误差同样是可以接受的。

附录B 中展示了针对“双花瓣电网”［32］使用本文方法完成线路参数辨识的算例。

附录C 中使用了粒子群算法和模拟退火算法完成线路参数辨识，并与本文所使用的遗传算法进行了对比。可见，针对本文的优化函数，遗传算法相比于粒子群算法和模拟退火算法有更高的精度和鲁棒性。