电动汽车与直流配电网协同的分布式自适应滚动预测调度

2024-01-18邱馨洁王笑雪王守相

电力系统自动化 2023年24期

梁栋，邱馨洁，刘琪，王笑雪，王守相

（1.省部共建电工装备可靠性与智能化国家重点实验室（河北工业大学），天津市 300401；2.河北省电磁场与电器可靠性重点实验室（河北工业大学），天津市 300401；3.河北省智能配用电装备产业技术研究院（石家庄科林电气股份有限公司），河北省石家庄市 050222；4.山东科技大学电气与自动化工程学院，山东省青岛市 266590；5.智能电网教育部重点实验室（天津大学），天津市 300072）

0 引言

发展分布式电源（distributed generator，DG）及电动汽车（electric vehicle，EV）是推动落实中国“双碳”战略目标的重要手段。近年来，EV 充电桩和光伏等直流型源、荷在配电网中的比重不断升高，截至2022 年，全国新能源汽车保有量达1 310 万辆［1］，分布式光伏累计装机容量达157.62 GW［2］。

强随机性和波动性的直流型源、荷的大量、无序接入，威胁配电网的安全可靠运行。通过在台区低压侧的直流型源、荷聚集区组建直流配电网（direct current distribution network，DCDN），可省去大量交、直转换环节［3-5］，有效缓解源、荷波动带来的电压越限、变压器过载、新能源消纳困难等问题，提升台区运行灵活性。

高渗透率DG 接入下的配电网优化调度问题已受到业界广泛关注。其中，基于预测模型-滚动优化-反馈校正的模型预测控制（model predictive control，MPC）框架可在一定程度上削弱源、荷不确定性，在配电网日内调度中具有很强的适用性［6-7］。在调控手段方面，电压源型换流器（voltage source converter，VSC）具有快速调节潮流分布的能力，通过其优化调度提高新能源接纳能力已成为交直流配电网研究的重点［8-11］。上述研究主要通过系统侧优化调度提高配电网运行经济性和新能源接纳能力，未考虑负荷侧灵活性资源的调度潜力。

EV 是一种兼具源、荷双重属性的灵活性资源，现有EV 充电调度研究从时间尺度上可分为日前和实时两类。日前优化通过采集历史数据、统计用户出行规律或根据日前申报机制获得相关参数，计算出电网一天内各时段EV 充电需求，作为电网调度的依据［12-15］。由于EV 接入时刻状态及需求具有较大的不确定性，日前调度难以满足EV 的实时充电需求。实时优化通过采集当前时刻入网EV 的信息，对未来时段充放电功率进行优化［16-19］。文献［20］提出了基于虚拟电价和MPC 的动态EV 互动响应控制策略；文献［21-22］通过配电网全局优化获取充电站调度计划，进而控制充电站对各EV 进行功率分配；文献［23］提出了基于EV 参与调峰定价策略的区域电网两阶段优化调度方案。上述研究侧重将EV 充电站或EV 集群作为整体进行建模和调度，未在EV 实时随机接入场景下对单个EV 灵活性潜力进行充分挖掘，且集中在交流配电网领域。

本文提出了EV 与DCDN 协同的分布式自适应滚动预测调度方法。首先，建立了VSC、储能及直流潮流数学模型；然后，以网损和弃光最小为目标建立了DCDN 自适应滚动预测调度模型，通过实时EV 集群的最晚取车时间动态更新调度窗口，以满足每辆EV 的充电需求；最后，建立了DCDN 分布式滚动预测调度模型，并采用交替方向乘子法（alternating direction method of multipliers，ADMM）实现分布式求解。仿真结果表明，对VSC 与EV 的协同调度可显著降低电能损耗、提升DG 接纳能力。

1 协同调度框架与调度模型建立

1.1 协同调度框架

本文针对主从控制的DCDN 开展EV 与VSC、储能等灵活性资源的协同调度研究，主VSC 为Vdc-Q控制，以控制DCDN 电压Vdc稳定；从VSC 为有功功率-无功功率（P-Q）控制。如图1 所示，DCDN 分为多个区域，在每个调度周期起始时刻，采用分散式调度策略：各区域均配置本地控制器，根据本区域网络结构和参数，从上层云主站获取本区域源、荷超短期预测信息，收集本区域内实时入网EV 集群信息，通过本地优化计算和区域间信息交互，完成全网协同调度任务，计算完成之后仅对本地调度对象下发指令。分散式调度不依赖全局控制器集中通信，各区域控制器只需与本地调度对象进行本地通信并与相邻区域控制器之间进行点对点通信。

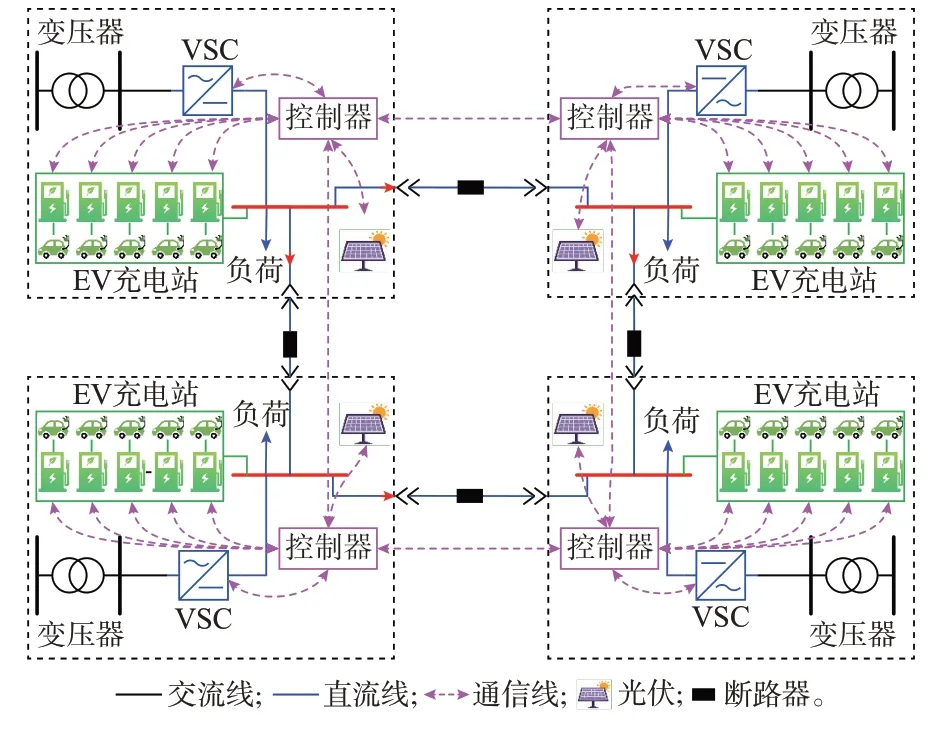
图1 整体调度结构Fig.1 Overall scheduling structure

1.2 VSC 稳态运行模型

假设VSC 功率注入DCDN 为正方向，VSC 在t时段需满足如下约束：

式中：Pi，t，VSC和Qi，t，VSC分别为t时段VSC 注入节点i的有功和无功功率；Plossi，t为t时段节点i处VSC 的有功传输损耗；Aloss为VSC 的损耗系数［24］；Pmin，VSC和Pmax，VSC分别为VSC 有功功率下限和上限；Qmin，VSC和Qmax，VSC分别为VSC 无功功率下限和上限；Si，max为接入节点i的VSC 允许通过的最大视在功率；i∈ΩVSC，其中，ΩVSC为所有VSC 节点集合。

VSC 容量约束式（1）中最后一式可松弛为二阶锥约束：

VSC 损耗也可采用其他VSC 损耗计算模型［9］。

1.3 储能稳态运行模型

储能在t时段需满足如下约束：

式中：P，ESS和P，ESS分别为t时段节点i处储能的充电功率和放电功率；P+i，max和Pax分别为节点i处储能的最大充电和放电功率；αi，t为0-1 变量，αi，t=1 表示储能充电，αi，t=0 表示储能放电；Ei，t为t时段节点i处储能存储的电量和分别为节点i处储能的充、放电效率；Ei，ESS为节点i处储能容量；Ei，max和Ei，min分别为节点i处储能的最大和最小荷电状态（state of charge，SOC）；Δt=15 min 为时间间隔；i∈ΩESS，其中，ΩESS为所有储能节点集合。

为避免引入表征储能充、放电状态的0-1 变量使调度模型变为求解较慢的混合整数规划问题，本文以变量Pi，t，ESS=P，ESS-P，ESS/表征充放电功率，式（3）变为：

式中：Pi，t，ESS为t时段节点i处储能的充放电功率，Pi，t，ESS＞0 表示储能充电，Pi，t，ESS＜0 表示储能放电；Pi，ESS，max为节点i处储能的最大充放电功率。

调度模型求解完毕后，根据PESS的正负及储能充放电效率即可由Pi，t，ESS=PESS-P，ESS/ηdi确定实际下发的储能充、放电指令。

1.4 直流配电网潮流模型

采用适用于辐射状和环状电网的支路潮流模型［25］，每个非平衡节点i在t时段需满足潮流约束：

式中：Pi，t为t时段节点i的注入有功功率；Pi，t，L和Pi，t，DG分别为t时段接入节点i的常规负荷有功功率和DG 注入有功功率；Pi，t，EVS为t时段接入节点i的EV 充电站负荷有功功率，Pi，t，EVS＞0 表示充电站从节点i抽取有功功率，Pi，t，EVS＜0 表示充电站向节点i注入有功功率；Pi，t，cut为t时段节点i舍弃的DG 注入有功功率；Pij，t和Iij，t分别为t时段支路ij的始端有功功率和电流幅值；rij为支路ij的电阻；Vi，t为t时段节点i的电压幅值；i∈Ωb，其中，Ωb为所有节点集合；ij∈Ωbr，其中，Ωbr为所有支路集合。

由于潮流方程非凸，可引入辅助变量ui，t、wij，t替换V、I，则式（5）变为：

1.5 EV 充电偏好模型

本节将EV 分为不可调度、只充电和可充放电3 类［17］。第1 类EV 不参与调度，接入后以额定功率充电直到SOC 达到期望值。接入节点i的第k∈ΩEV1(i)（ΩEV1（i）为节点i的充电站内第1 类EV 集合）辆第1 类EV 需满足：

式中：Pk，t，EV1为第k辆第1 类EV 在t时段的充电功率；Pc，k，rate为第k辆EV 的额定充电功率；Ek，t为第k辆EV 在t时段结束时刻的电池电量；Ek，cur-1为第k辆EV 在当前调度窗口时段集合ΩW初始时刻的电池电量；ηk为第k辆EV 的充电效率；Ek，ini为第k辆EV 入网时的初始电量；Ek，exp为第k辆EV 用户设置的期望电量；Ek，cap为第k辆EV 的额定电池容量；ΩQ为当前调度窗口时段初始时刻到t时段结束时刻之间的优化时段集合。

第2 类EV 在充电周期内充电功率可以灵活调节，但不允许进行放电。对接入节点i的第k∈ΩEV2(i)（ΩEV2（i）为节点i的充电站的第2 类EV 集合）辆第2 类EV 需满足：

式中：Pk，t，EV2为第k辆第2 类EV 在t时段的充电功率。

第3 类EV 在充电周期内可充电或放电。对接入节点i的第k∈ΩEV3(i)（ΩEV3（i）为节点i的充电站的第3 类EV 集合）辆第3 类EV 需满足：

式中：Pk，t，EV3为第k辆第3 类EV 在t时段的充放电功率；Pk，EV，rate为第k辆EV 的额定充放电功率；Emin，EV为EV 的最小SOC。

对第2、3 类EV，超出取车时间后设置充放电功率为0。在t时段，节点i接入的充电站总充电负荷Pi，t，EVS为上述3 类EV 充电负荷之和：

2 分布式自适应滚动预测调度策略

2.1 基于MPC 的滚动预测调度模型

日内滚动调度以15 min 为间隔，将一天划分为96 个时段。若将EV 充电站整体当作不可控的负荷，则控制变量包括储能充放电功率、VSC 传输功率。基于MPC 思想，令控制时域与预测时域相等，本文统称为调度窗口。在t时段初始时刻，基于当前调度窗口内各时段DG 和负荷的超短期预测值求解多时段优化问题；求解结束后，仅将t时段的储能充放电功率指令、VSC 传输功率指令下发；在t+1时段初始时刻，调度窗口向后推移，更新窗口内DG和负荷的预测信息，建立新的多时段优化模型并求解。MPC 调度窗口见附录A 图A1。

1）目标函数。考虑总有功损耗最小的目标函数f1和总弃光电量最小的目标函数f2，表示为：

2）约束条件，包括VSC 运行约束、储能运行约束、直流潮流约束及各节点电压、支路电流约束：

综合目标函数和约束条件，在每一时段的初始时刻，需求解的DCDN 滚动预测调度模型为：

式中：α和β分别为有功损耗与弃光电量权重系数。

模型经式（2）、式（6）转化后，已变为易于求解的二阶锥规划（second-order cone programming，SOCP）问题，可采用商业求解器高效求解。

2.2 基于自适应MPC 的滚动预测调度

模型式（13）将EV 充电站整体当作不可控的负荷，未考虑充电站内各EV 在充电时间选取上的灵活性。本节将第2、3 类EV 看作可调度的灵活性资源，将每辆EV 的数学模型集成到调度模型中，在EV 实时随机接入场景下对单个EV 灵活性潜力进行充分挖掘，实现对DCDN 的进一步优化，此时控制变量包括储能充放电功率、VSC 传输功率及所有第2、3 类EV 充放电功率指令。

在tcur时段的初始时刻，基于当前时刻所有充电站入网EV 集群的最晚取车时间确定调度窗口［16］，进而基于调度窗口内各时段DG 和负荷的超短期预测值求解多时段优化问题；求解结束后，仅将tcur时段的储能充放电功率指令、VSC 传输功率指令及所有第2、3 类EV 充放电功率指令下发；在tcur+1 时段的初始时刻，重新基于该时段所有充电站内入网EV 集群的最晚取车时间确定新的调度窗口，并更新窗口内DG 和负荷的预测信息，建立新的多时段优化模型并求解。与MPC 不同，自适应MPC 的调度窗口需自适应动态更新而不再是常数。自适应MPC 调度窗口见附录A 图A2。

可得当前时段tcur起始时刻的调度窗口为：

式中：tout，max为当前时段tcur起始时刻所有充电站接入EV 的最晚取车时间；NW为调度窗口长度。

综合目标函数和约束条件，在每一时段的初始时刻，需求解的自适应滚动预测调度模型为：

2.3 DCDN 分区解耦策略

当系统中EV 数量较多时，若对每一EV 进行集中式调度，则计算量大、通信负担重。因此，本文通过网络分区建立了DCDN 分布式滚动预测调度模型，并采用ADMM 实现分布式求解，以提高求解效率、降低通信负担。

以如图2（a）所示的四端环形DCDN 为例，4 个配电台区低压侧之间通过直流联络线实现柔性互联，各台区的直流型源、荷、储均接入其直流母线，形成低压DCDN。假定联络线功率正方向如图中红色箭头所示，据此可确定联络线的上、下游区域。例如，联络线1-3 的上游区域为不包括联络线1-3 的区域1，下游区域为包含联络线1-3 的区域3。

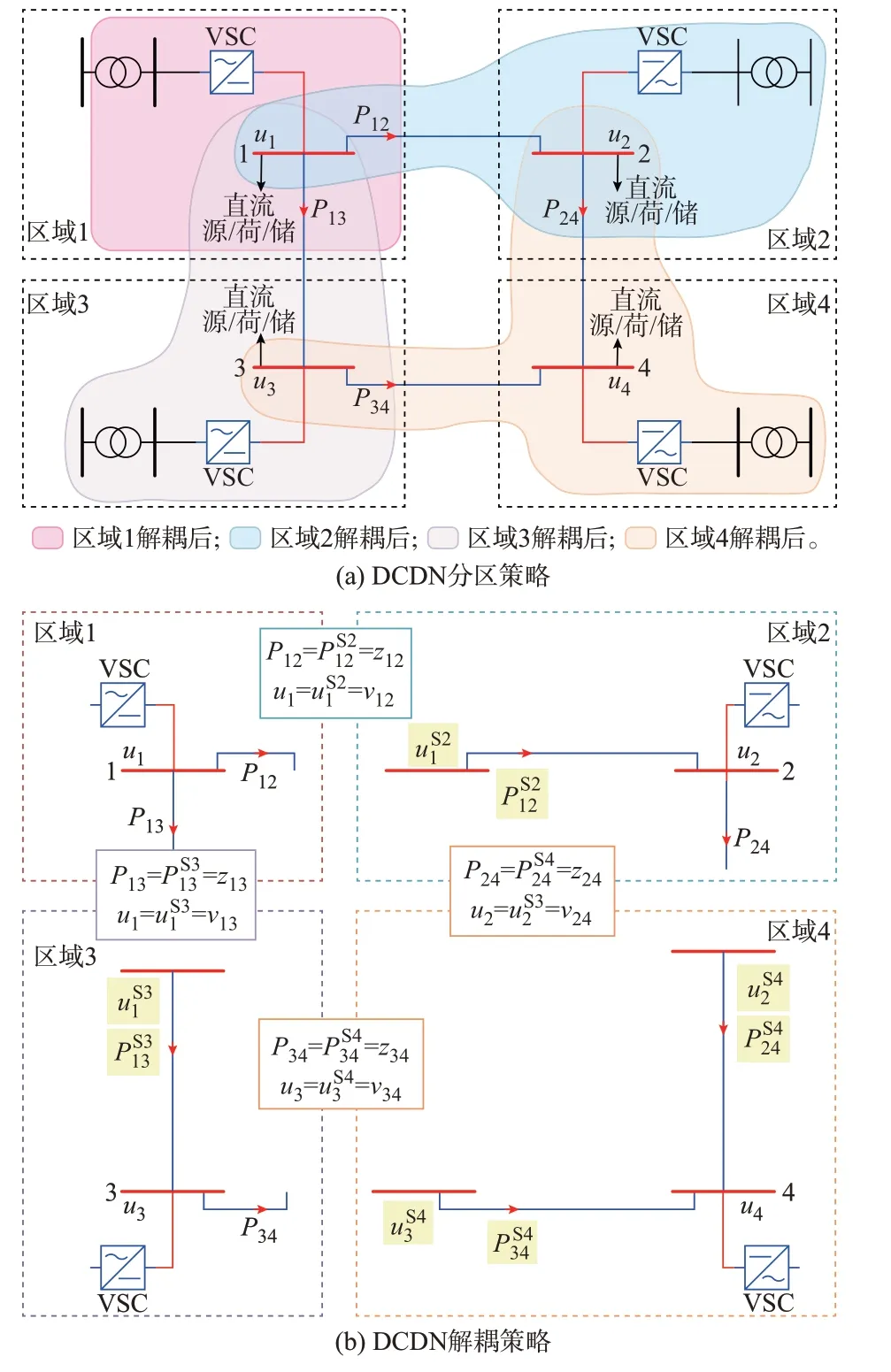
图2 DCDN 分区与解耦策略Fig.2 Partition and decoupling strategies of DCDN

分析DCDN 潮流模型可知，各区域之间仅通过线路始端有功功率和始端节点电压幅值平方相耦合。为实现模型分区解耦，将联络线上游区域的边界变量复制一份划入下游区域，如图2（a）所示。具体地，将联络线始端有功功率在下游区域复制一份，例如，联络线1-3 始端有功功率P13为区域1 的本地变量，引入复制变量P作为区域3 对P13的复制量，上标S3 表示该复制变量属于区域3，同时引入全局一致变量z13及约束P13=z13、z13=P，使P13和P二者保持一致；同样，将联络线1-3 上游区域的直流母线电压幅值平方在下游区域复制一份，这里的直流母线电压幅值平方用u1表示，复制变量为uS31，同时引入相应的全局一致变量v13及约束。P13、u1为上游区域分享给下游区域的变量，故称其为共享变量。分区解耦后的DCDN 如图2（b）所示。

2.4 分布式调度模型

将所有变量写作向量形式，t时段区域q与其上游区域的变量关系如下：

式中：K为所有区域集合；Nupq为区域q的上游区域集合；x[l]为t时段下游区域q对上游区域l的复制变量；x[q]为t时段上游区域l共享给下游区域q的共享变量；Pql，t为t时段联络线q-l的始端有功功率；P为区域q内Pql，t的复制变量；ul，t为t时段直流母线l的始端电压；u为区域q内ul，t的复制变量；xql，t为t时段区域q与区域l间复制变量和共享变量对应的全局一致变量；zql，t为Pql，t和P对应的全局一致变量；vql，t为ul，t和u对应的全局一致变量。

区域q与其下游区域的变量关系如下：

式中：N为区域q下游区域集合；x[l]为t时段上游区域q共享给下游区域l的共享变量；x[q]为t时段下游区域l对上游区域q的复制变量。

DCDN 分布式自适应滚动预测调度模型如下：

式中：f1，q和f2，q分别为区域q本地有功损耗和弃光电量；xq，t为t时段区域q所有本地变量组成的向量，包括对上游区域l的复制变量xupq，t[l]、分享给下游区域l的共享变量xdnq，t[l]及其他本地变量；λupql，t和λdnql，t为等式约束对应的拉格朗日乘子向量；Xq，t为t时段区域q所有本地变量组成的向量集合，如式（19）所示。

3 分布式协同调度模型求解

首先采用标准ADMM 进行求解，算法推导及算法流程见附录B。标准ADMM 需全局控制器进行协调，以计算全局一致变量。本章对此进行改进，得到不需全局控制器协调的分散式求解算法［26］。观察附录B 式（B5）可见，每个全局一致变量的值等于其所关联的上游本地变量、下游复制变量二者平均值。因此，每个全局一致变量的求解可分为2 步：

1）下游区域控制器将解得的复制变量值传给上游区域控制器；

2）上游区域控制器计算全局一致变量，并将其传给下游区域控制器。

通过上、下游区域控制器之间两两通信的方式，即可实现全局一致变量的分散式求解。由于上、下游区域之间仅通过两个变量相关联，通信量很少。针对分布式算法的收敛性问题，由于原始集中式模型为凸优化问题，而ADMM 求解凸优化问题的收敛性具有严格数学证明，可保证算法可靠收敛。

4 算例分析

4.1 仿真设置

采用附录A 图A3 所示DCDN 对所提方法进行测试。VSC1 为主VSC，其余VSC 为从VSC。负荷、光伏、储能、EV 充电站配置情况如图A3 所示。设置各节点允许的电压幅值范围为0.95～1.05 p.u.。采用AMPL 建模语言编程［27］，调用Cplex 12.7［28］进行求解。基于某地实际负荷及光伏、充电站数据构造的常规负荷、光伏和充电站的系数曲线见图A4，据此可得到超短期预测值曲线。每个EV 充电站设置30 个直流充电桩，最大充电功率为60 kW。通过随机抽样模拟产生各时段3 类EV 入网集群、EV 初始电量、取车时间，所有EV 期望SOC 均为90%，全天3 类EV 数量分别为138、136、58。

设置两种调度策略进行对比分析：

1）MPC 调度策略：将充电站整体看作直流负荷，调度窗口长度固定为16，窗口内各时段采用常规负荷、DG 和充电负荷的日内超短期预测值；

2）自适应MPC 调度策略：对每辆EV 进行调度，调度窗口根据当前时刻接入EV 的最晚取车时间确定，窗口内各时段采用常规负荷、光伏的日内超短期预测值。

当全天剩余时段长度小于调度窗口长度时，调度窗口变为全天所有剩余时段长度，直至全天滚动求解结束。两种调度策略的调度窗口对比见附录A图A5。

4.2 电能损耗和弃光电量分析

本节对两种调度策略下的DCDN 电能损耗与弃光电量进行对比，所有线路容量设置为1 MV·A。表1 为不同光伏装机容量下两种调度策略的日电能损耗（α=0.25）。由表1 可见，不同光伏装机容量下，自适应MPC 调度的日电能损耗均低于MPC 调度；全部EV 为第3 类时，自适应MPC 调度下的日电能损耗进一步降低，说明可控EV 越多，自适应MPC 调度在降低台区网损方面越有效。

表1 不同光伏装机容量的电能损耗Table 1 Energy losses with different photovoltaic installed capacities

表2 为不同光伏装机容量下两种调度策略的日弃光电量（α=0.25）。由表2 可见，MPC 调度与自适应MPC 调度的弃光电量相等，这是因为线路容量较小，受线路容量约束，即使增大弃光电量的惩罚系数β，也无法降低弃光电量。

表2 不同光伏装机容量的弃光电量Table 2 Photovoltaic curtailment with different photovoltaic installed capacities

图3 为不同光伏装机容量下的DCDN 各时段电能损耗对比。由图可见，自适应MPC 调度通过对EV 充电功率的实时调控，使其大部分时段网损低于MPC 调度；当全天332 辆EV 均为第3 类EV 时，各时段网损进一步降低。

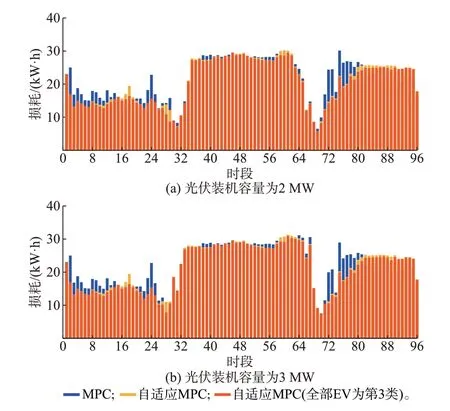
图3 不同光伏装机容量下的各时段电能损耗（β=1.00）Fig.3 Energy losses of each period with different photovoltaic installed capacities (β=1.00)

4.3 增加线路容量

本节将线路容量由1 MV·A 增加到2 MV·A。表3 为不同光伏装机容量下两种调度策略的日电能损耗。由表3 可见，不同光伏装机容量下自适应MPC 调度的日电能损耗均低于MPC 调度；全部EV为第3 类时，自适应MPC 调度策略下的日电能损耗进一步降低。

表3 不同光伏装机容量的电能损耗（线路容量为2 MV·A）Table 3 Energy losses with different PV installed capacities (line capacity is 2 MV·A)

表4 为不同光伏装机容量下两种调度策略的日弃光电量。由表4 可见，随着弃光权重系数β增大，日弃光电量均显著减小；当β增大到一定程度后，弃光电量达到定值，光伏消纳已饱和；此时MPC 调度与自适应MPC 调度的弃光电量相等，即使继续增大β，也无法降低弃光电量。当β=0.25 时，光伏消纳尚未达到饱和，自适应MPC 调度策略相比MPC 调度策略，通过EV 调度使得日弃光量更低；当全部EV 为第3 类时，自适应MPC 调度拥有更多的可调度EV，使日弃光电量再次降低。

表4 不同光伏装机容量的弃光电量（线路容量2 MV·A）Table 4 Photovoltaic curtailment with different photovoltaic installed capacities (line capacity is 2 MV·A)

此外，表1 和表2 对比可见，线路容量增大后，由于光伏消纳显著增加导致日弃光电量显著降低，同时由于线路潮流增大导致日电能损耗随之增大。

图4 和图5 为β=0.25 时不同光伏装机容量下两种调度策略的各时段电能损耗与弃光电量。由图可见，系统消纳光伏尚未达到饱和时，自适应MPC调度策略有一定调控空间，且可调度EV 越多，能够消纳的光伏越多，同时各时段网损越小。

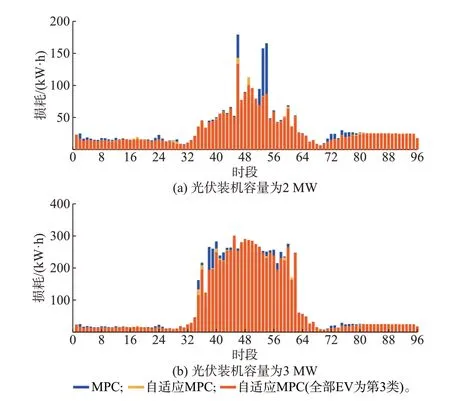
图4 不同光伏装机容量下的各时段电能损耗（β=0.25）Fig.4 Energy losses of each period with different photovoltaic installed capacities (β=0.25)

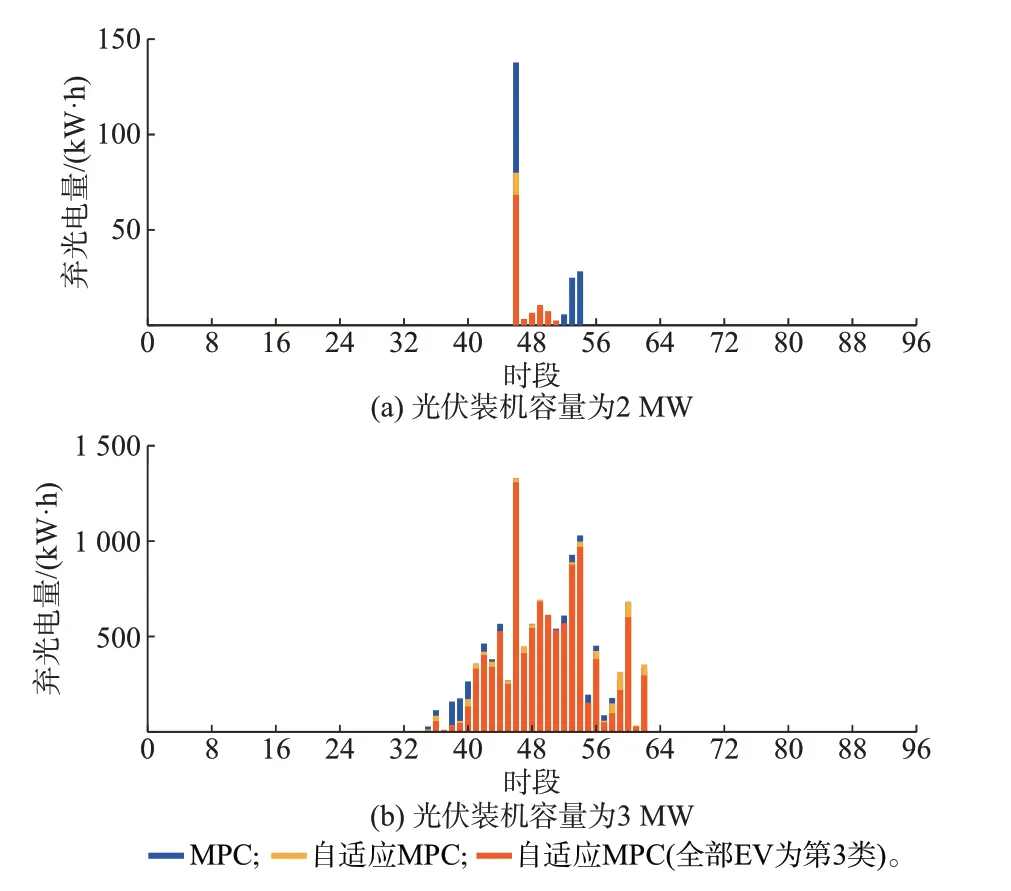
图5 不同光伏装机容量下的弃光电量（β=0.25）Fig.5 Photovoltaic curtailment with different photovoltaic installed capacities (β=0.25)

4.4 光伏接纳能力分析

由表1、表4 可见，在光伏达到可接纳容量上限时，继续增加分布式光伏容量，日电能损耗会增加。为解释该结果，分析如下两种场景：场景1，光伏装机容量为2 MW，β=0.25；场景2，光伏装机容量为3 MW，β=0.25。由表1 可见，场景2 下3 种策略的日电能损耗均高于场景1。以光伏支路1-4 为例，其在两种场景下的有功功率曲线如附录A 图A6 所示。图中支路有功功率为负，说明发生了功率倒送。由图A6（a）可见，受1 MV·A 线路容量限制，两种场景中光伏支路1-4 均会在中午的光伏出力高峰时段达到功率上限，区别在于：1）场景1 在时段35 才达到线路功率上限，而场景2 在时段33 即已达到线路功率上限，在时段24～35，场景2 中支路功率始终大于场景1，因此网损更大；2）场景1 在时段63 光伏功率即已小于线路功率上限，而场景2 在时段66 才小于线路功率上限，在时段63～80，场景2 中支路功率始终大于场景1，因此网损更大。

由此可知，虽然装机容量为2 MW 和3 MW 时，系统在中午光伏接纳能力均达到饱和，但装机容量大时饱和时间更长，非饱和时段的线路功率也更大，所以损耗更大。由附录A 图A6（b）可见，自适应MPC 调度策略下也可得到同样的分析结论。

将线路容量由1 MV·A 增加到2 MV·A，仍然分析上述两种场景。由表1 可见，场景2 网损高于场景1。两种场景下光伏支路1-4 的日有功功率曲线如附录A 图A7 所示，由图可得与线路容量为1 MV·A 时相同的结论。此外，对比图A7 中场景1、2 的3 条曲线可见，增加弃光惩罚系数β至5.00时，支路功率增大，说明线路容量增大后，可以通过增大弃光电量惩罚进一步消纳光伏发电、减少弃光电量。

4.5 EV 充电需求分析

附录A 图A8 为自适应MPC 调度策略下3 类EV 的电池电量曲线。由图可见，3 类EV 均能在离开之前电量达到其期望电量，区别在于第1 类EV 充电速度更快，第2 类EV 由于充电功率可调节，电量曲线较之第1 类EV 更为平缓，第3 类EV 能够响应指令进行放电，虽然电量会下降，但能在离开之前达到期望电量。这说明自适应MPC 调度策略能在降低系统日电能损耗和弃光电量的同时，满足各类EV 用户的不同充电需求。

4.6 分布式算法收敛性分析

附录A 图A9 为采用基于自适应MPC 调度策略的分布式协同调度时，算法原始残差与对偶残差的迭代收敛曲线。由图可见，将收敛精度设置为10-3时分布式算法仅需约50 次迭代即可收敛；若将收敛精度设置为更高精度如10-4时，计算结果与低收敛精度时的计算结果差别很小。因此，实际应用时无须设置很高的收敛精度，从而可减少迭代次数，进一步降低计算时间和通信量。

在求解时间方面，集中式调度单次求解用时约1.35 s，而分布式调度单次求解用时约12.32 s，这是由于算例规模相对较小，且模型中没有整数变量，导致集中式调度求解非常快，而分布式调度需要反复迭代，导致较为耗时。实际中分布式调度和集中式调度的有效性均会受到通信延迟的影响，由于分布式调度的通信对象更少、通信距离更短，其通信负担更轻、通信故障影响范围更小，且各区域可并行计算，在实际应用时总耗时与集中式调度的差距将缩小。若进一步增加EV 数量，则集中式调度模型变量和调度对象的数量均增加，求解用时和通信耗时也相应增加，尤其通信延迟问题将更加凸显，分布式调度的优势将更加明显。